2010年北京市崇文区高三数学一模试卷及答案
2010年高考北京市数学试卷-文科(含详细答案)

绝密 使用完毕前2010年普通高等学校招生全国统一考试数学(文)(北京)本试卷分第Ⅰ卷和第Ⅱ卷两部分。
第Ⅰ卷1至2页、第Ⅱ卷3至5页,共150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效,考试结束后,将本试卷和答题卡。
第Ⅰ卷(选择题 共140分)一、 本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
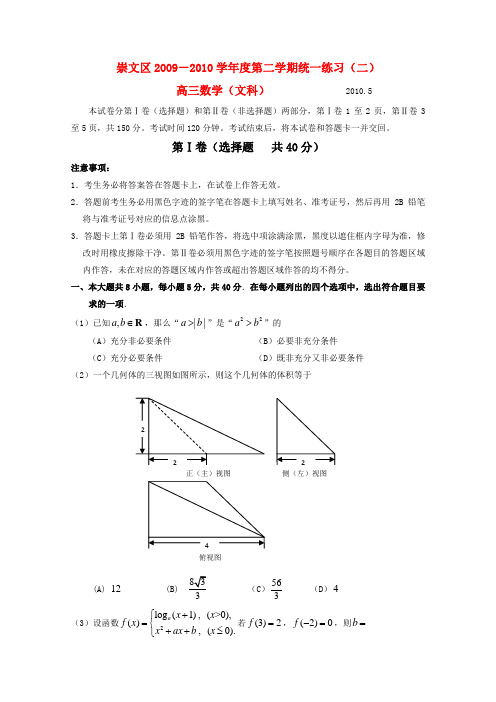
⑴ 集合2{03},{9}P x Z x M x Z x =∈≤<=∈≤,则P M I =(A) {1,2} (B) {0,1,2} (C){1,2,3} (D){0,1,2,3} ⑵在复平面内,复数6+5i, -2+3i 对应的点分别为A,B.若C 为线段AB 的中点,则点C 对应的复数是(A )4+8i (B)8+2i (C )2+4i (D)4+i⑶从{1,2,3,4,5}中随机选取一个数为a ,从{1,2,3}中随机选取一个数为b ,则b>a 的概率是 (A )45 (B)35 (C )25 (D)15⑷若a,b 是非零向量,且a b ⊥,a b ≠,则函数()()()f x xa b xb a =+⋅-是 (A )一次函数且是奇函数 (B )一次函数但不是奇函数(C )二次函数且是偶函数 (D )二次函数但不是偶函数(5)一个长方体去掉一个小长方体,所得几何体的 正视图与侧(左)视图分别如右图所示,则该集合体 的俯视图为:(6)给定函数①12y x =,②12log (1)y x =+,③|1|y x =-,④12x y +=,期中在区间(0,1)上单调递减的函数序号是(A )①② (B )②③ (C )③④ (D )①④ (7)某班设计了一个八边形的班徽(如图),它由腰长为1, 顶角为α的四个等腰三角形,及其底边构成的正方形所组成, 该八边形的面积为(A )2sin 2cos 2αα-+; (B )sin 3αα+(C )3sin 1αα+ (D )2sin cos 1αα-+ (8)如图,正方体1111ABCD-A B C D 的棱长为2, 动点E 、F 在棱11A B 上。
2010年北京崇文区高三数学理科一模试题含答案

崇文区2009-2010学年度第二学期统一练习(一)高三数学(理科) 2010.4 第Ⅰ卷(选择题 共40分)一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.(1)已知全集U =R ,集合{}|12A x x =->,{}2|680B x x x =-+<,则集合()UA B ⋂=ð(A ){}|14x x -≤≤ (B ){}|14x x -<< (C ){}|23x x ≤< (D ) {}|23x x <≤(2)一个单位共有职工200人,其中不超过45岁的有120人,超过45岁的有80人. 为了调查职工的健康状况,用分层抽样的方法从全体职工中抽出一个容量为25的样本,应抽取不超过45岁的职工人数为(A) 5 (B) 10 (C )15 (D )50 (3)已知PA 是O 的切线,切点为A ,2PA=,AC 是O的直径,PC 交O 于点B ,30PAB ∠=,则O 的半径为(A )1 (B )2(C(D )(4)已知等比数列{}n a 为递增数列,且373a a +=,282a a ⋅=,则117a a = (A )2 (B )43 (C ) 32(D )12(5)已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的为(A )若,,αγβγ⊥⊥则αβ (B )若,,m n αα⊥⊥则m n (C )若,m n αα,则m n (D )若,,m m αβ则αβ(6)设33,,2x yx y M N P ++===(其中0x y <<), 则,,M N P 大小关系为(A )M N P << (B )N P M << (C )P M N << (D )P N M << (7)2位男生和3位女生共5位同学站成一排.若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数为(A )36 (B )42 (C ) 48 (D ) 60(8)设定义在R 上的函数1,(1),1()1,(1)x x f x x ⎧≠⎪-=⎨⎪=⎩. 若关于x 的方程2()()0f x bf x c ++=有3个不同的实数解1x ,2x ,3x ,则123x x x ++等于(A ) 3 (B )2 (C )1b -- (D )c第Ⅱ卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分.(9)如果复数()()2i 1i m m ++(其中i 是虚数单位)是实数,则实数m =___________.(10)若12)a x的展开式中的常数项为220-,则实数a =___________. (11)将参数方程12cos ,2sin ,x y θθ=+⎧⎨=⎩(θ为参数)化成普通方程为 .(12)某程序框图如图所示,该程序运行后输出,M N 的值分别(131n nn S a S -⎧=⎨⎩若数列{}n b 的前n 项积为n T ,类比上述结果,则n b =_________;产品数量CA 此时,若2()n T n n *=∈N ,则n b =___________.(14)定义在R 上的函数满足1(0)0,()(1)1,()()52x f f x f x f f x =+-==, 且当1201x x ≤<≤时,12()()f x f x ≤,则1()2010f=_________________. 三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. (15)(本小题共12分)在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,满足sin 2A =,且A B C ∆的面积为2.(Ⅰ)求bc 的值;(Ⅱ)若6=+c b ,求a 的值.(16)(本小题共13分)为了调查某厂2000名工人生产某种产品的能力,随机抽查了m 位工人某天生产该产品的数量,产品数量的分组区间为[)10,15,[)15,20,[)20,25,[)25,30,[30,35],频率分布直方图如图所示.已知生产的产品数量在[)20,25之间的工人有6位. (Ⅰ)求m ;(Ⅱ)工厂规定从各组中任选1人进行再培训,则选取5人的概率是多少?(17)(本小题共14分)三棱柱111C B A A B C-中,侧棱与底面垂直,90=∠ABC ,12AB BC BB ===, ,M N 分别是AB ,1AC 的中点.(Ⅰ)求证:MN 平面11B BCC ; (Ⅱ)求证:⊥MN 平面C B A 11; (Ⅲ)求二面角11A C B M --的余弦值.(18)(本小题共14分)已知322()69f x x ax a x =-+(a ∈R ). (Ⅰ)求函数()f x 的单调递减区间;(Ⅱ)当0a >时,若对[]0,3x ∀∈有()4f x ≤恒成立,求实数a 的取值范围.(19)(本小题共14分)已知抛物线24y x =,点(1,0)M 关于y 轴的对称点为N ,直线l 过点M 交抛物线于,A B 两点.(Ⅰ)证明:直线,NA NB 的斜率互为相反数; (Ⅱ)求ANB ∆面积的最小值;(Ⅲ)当点M 的坐标为(,0)(0m m >,且1)m ≠.根据(Ⅰ)(Ⅱ)推测并回答下列问题(不必说明理由):① 直线,NA NB 的斜率是否互为相反数? ② ANB ∆面积的最小值是多少?(20)(本小题共13分)已知数列{}n a 中,11a =,21(0a a a =-≠且1)a ≠,其前n 项和为n S ,且当2n ≥时,1111n n n S a a +=-. (Ⅰ)求证:数列{}n S 是等比数列; (Ⅱ)求数列{}n a 的通项公式; (Ⅲ)若4a =,令19(3)(3)nn n n a b a a +=++,记数列{}n b 的前n 项和为n T .设λ是整数,问是否存在正整数n ,使等式13758n n T a λ++=成立?若存在,求出n 和相应的λ值;若不存在,请说明理由.崇文区2009-2010学年度第二学期统一练习(一)高三数学(理科)参考答案及评分标准 2010.4一、选择题(本大题共8小题,每小题5分,共40分)(9)1- (10)1- (11)()2214x y -+= (12)13,21(13)11(1)(2)n nn T n b T n T -=⎧⎪=⎨≥⎪⎩ ;()221(1)(2)1n n b n n n =⎧⎪=⎨≥⎪-⎩(14)132三、解答题(本大题共6小题,共80分) (15)(共12分) 解:(Ⅰ)∵,552sin=A π<<A 0 ∴cos25A =. ∴4sin 2sin cos 225A A A ==. ∵2sin 21==∆A bc S ABC , ∴5=bc . --------------------6分(Ⅱ)∵,552sin=A ∴532sin21cos 2=-=A A . ∵5=bc ,6=+c b ,∴A bc c b a cos 2222-+=)cos 1(2)(2A bc c b +-+=20=∴52=a . -----------12分(16)(共13分)解:(Ⅰ)根据直方图可知产品件数在[)20,25内的人数为50.066m ⨯⨯=,则20m =(位). ---------------- 6分(Ⅱ)根据直方图可知产品件数在[)10,15,[)15,20,[)20,25,[)25,30,[30,35],组内的人数分别为2,4,6, 5,3. 设选取这5人不在同组为B 事件,则5202465315()323P B C ⨯⨯⨯⨯==. 答:选取这5人不在同组的概率为15323. ---------------- 13分 (17)(共14分)(Ⅰ)证明: 连结1BC ,1AC . 在1ABC 中,,M N 是AB ,C A 1的中点, ∴||MN 1BC .又 MN ⊄平面11B BCC ,∴||MN 平面11B BCC . --------------------4分(Ⅱ)如图,以1B 为原点建立空间直角坐标系xyz B -1.则)0,0,0(1B ,(0,2,2)C ,1(2,0,0)A -,(1,0,2)M -,(1,1,1)N -∴1BC =(0,2,2),)0,0,2(11=B A ,(0,1,1)NM =-. 设平面C B A 11的法向量为(,,)x y z =n .111000B C x y z A B ⎧⋅==⎧⎪⇒⎨⎨=-⋅=⎩⎪⎩n n 令1=z ,则0,1x y ==-,∴(0,1,1)=-n .NM ∴n =.∴⊥MN 平面C B A 11. --------------9分(Ⅲ)设平面C MB 1的法向量为000(,,)x y z =m 1(1,0,2)B M =-. 001001200x z B C y z B M ⎧=⋅=⎧⎪⇒⎨⎨=-⋅=⎩⎪⎩m m令01z =,则002,1x y ==-∴(2,1,1)=-m .∴cos ,||||⋅<>===⋅n m n m n m . 所求二面角11A C B M --的余弦值为33. --------------------14分 (18)(共14分)解:(Ⅰ)22'()31293()(3)0f x x ax a x a x a =-+=--<(1)当3a a =,即0a =时,2'()30f x x =>,不成立.(2)当3a a >,即0a <时,单调减区间为(3,)a a .(3)当3a a <,即0a >时,单调减区间为(,3)a a .-------------------5分 (Ⅱ)22'()31293()(3)f x x ax a x a x a =-+=--,()f x 在(0,)a 上递增,在(,3)a a 上递减,在(3,)a +∞上递增.(1)当3a ≥时,函数()f x 在[0,3]上递增, 所以函数()f x 在[0,3]上的最大值是(3)f ,若对[]0,3x ∀∈有()4f x ≤恒成立,需要有(3)4,3,f a ≤⎧⎨≥⎩解得a ∈∅.(2)当13a ≤<时,有33a a <≤,此时函数()f x 在[0,]a 上递增,在[,3]a 上递减,所以函数()f x 在[0,3]上的最大值是()f a ,若对[]0,3x ∀∈有()4f x ≤恒成立,需要有()4,13,f a a ≤⎧⎨≤<⎩ 解得1a =.(3)当1a <时,有33a >,此时函数()f x 在[,3]a a 上递减,在[3,3]a 上递增, 所以函数()f x 在[0,3]上的最大值是()f a 或者是(3)f .由2()(3)(3)(43)f a f a a -=--, ①304a <≤时,()(3)f a f ≤, 若对[]0,3x ∀∈有()4f x ≤恒成立,需要有(3)4,30,4f a ≤⎧⎪⎨<≤⎪⎩解得3[1]4a ∈-.②314a <<时,()(3)f a f >, 若对[]0,3x ∀∈有()4f x ≤恒成立,需要有()4,31,4f a a ≤⎧⎪⎨<<⎪⎩ 解得3(,1)4a ∈.综上所述,[1a ∈. -------------14分 (19)(共14分)解:(Ⅰ)设直线l 的方程为()1(0)y k x k =-≠.由()21,4,y k x y x ⎧=-⎪⎨=⎪⎩ 可得 ()2222240k x k x k -++=.设()()1122,,,A x y B x y ,则21212224,1k x x x x k++==. 124y y ∴=-()1,0N -1212221212441144NA NB y y y yk k x x y y +=+=+++++ ()()()()()()2212212112222212124444(4444)04444y y y y y y y y y y y y ⎡⎤+++-+-+⎣⎦===++++. 又当l 垂直于x 轴时,点,A B 关于x 轴,显然0,NA NB NA NB k k k k +==-. 综上,0,NA NB NA NB k k k k +==-. ---------------- 5分 (Ⅱ)12NAB S y y ∆=-===4>. 当l 垂直于x 轴时,4NAB S ∆=.∴ANB ∆面积的最小值等于4. ----------------10分 (Ⅲ)推测:①NA NB k k =-;②ANB ∆面积的最小值为4 ---------------- 14分(20)(共13分)解:(Ⅰ)当2n ≥时,11+111111n n n n n n nS a a S S S S +-=-=---, 化简得211(2)n n n S S S n -+=≥,又由1210,0S S a =≠=≠,可推知对一切正整数n 均有0n S ≠, ∴数列{}n S 是等比数列. ---------------- 4分 (Ⅱ)由(Ⅰ)知等比数列{}n S 的首项为1,公比为a , ∴1n n S a -=.当2n ≥时,21(1)n n n n a S S a a --=-=-, 又111a S ==,∴21,(1),(1),(2).n n n a a a n -=⎧=⎨-≥⎩ ----------8分 (Ⅲ)当4,2a n =≥时,234n n a -=⨯,此时22119934(3)(3)(343)(343)n n n n n n n a b a a ---+⨯⨯==++⨯+⨯+ 221213411(41)(41)4141n n n n n -----⨯==-++++, 又111293(3)(3)8a b a a ==++,∴213,(1)811,(2)4141n n n n b n --⎧=⎪⎪=⎨⎪-≥⎪⎩++1138T b ==, 当2n ≥时,1222212131111()()841414141n n n n T b b b ----=+++=+-++-++++171841n -=-+. 若1n =,则等式13758n n T a λ++=为37858λ+=,52λ=不是整数,不符合题意.若2n ≥,则等式13758n n T a λ++=为11717841548n n λ---+=+⨯,15541n λ-=-+ λ是整数,∴141n -+是5的因数.∴当且仅当2n =时,1541n -+是整数, ∴4λ=综上所述,。
北京市崇文区2010年高三数学第二次高考模拟考试(文)新人教版
侧(左)视图正(主)视图俯视图崇文区2009-2010学年度第二学期统一练习(二)高三数学(文科) 2010.5本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至5页,共150分。
考试时间120分钟。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分)注意事项:1.考生务必将答案答在答题卡上,在试卷上作答无效。
2.答题前考生务必用黑色字迹的签字笔在答题卡上填写姓名、准考证号,然后再用2B 铅笔将与准考证号对应的信息点涂黑。
3.答题卡上第Ⅰ卷必须用2B 铅笔作答,将选中项涂满涂黑,黑度以遮住框内字母为准,修改时用橡皮擦除干净。
第Ⅱ卷必须用黑色字迹的签字笔按照题号顺序在各题目的答题区域内作答,未在对应的答题区域内作答或超出答题区域作答的均不得分。
一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.(1)已知,a b ∈R ,那么“||a b >”是“22a b >”的(A )充分非必要条件 (B )必要非充分条件 (C )充分必要条件 (D )既非充分又非必要条件 (2)一个几何体的三视图如图所示,则这个几何体的体积等于(A) 12 (B)3 (C )563(D )4 (3)设函数2log (1), (>0), (), (0).a x x f x x axb x +⎧=⎨++≤⎩若(3)2f =,(2)0f -=,则b =(A) 0 (B) 1- (C )1 (D )2 (4)把函数sin ()y x x =∈R 的图象上所有的点向左平移6π个单位长度,再把所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象所表示的函数为 (A )sin(23y x x π=-∈R (B )1sin(26y x x π=+∈R (C )sin(23y x x π=+∈R (D )1sin(),26y x x π=-∈R (5)已知椭圆2215x y m+=的离心率5e =,则m 的值为(A )3 (B)3(C(D )253或3 (6)将石子摆成如图的梯形形状.称数列5,9,14,20,为“梯形数”.根据图形的构成,数列的第10项10=a(A )90 (B )81 (C )77 (D )65 (7)已知命题p :对x ∀∈R0≥恒成立.命题q :x R ∃∈,使120x -≤成立.则下列命题中为真命题的是(A )()p q ⌝∧ (B )p q ∧ (C )()p q ∧⌝ (D )()()p q ⌝∧⌝(8)设O 为坐标原点,(1,1)A ,若点B 满足222210,12,12x y x y x y ⎧+--+≥⎪≤≤⎨⎪≤≤⎩,则OA OB ⋅的最小值为(A(B )2 (C )3 (D)2崇文区2009-2010学年度第二学期统一练习(二)高三数学(文科) 2010.5第Ⅱ卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分. (9)函数y =的定义域为 .(10)若复数(3i)(2i)m +-+(其中i 为虚数单位)在复平面内对应的点位于第四象限,则实数m 的取值范围为 .(11)甲、乙、丙三名射击运动员在某次测试中各射击20次,三人的测试成绩如下表123,,x x x 分别表示甲、乙、丙三名运动员的这次测试成绩的平均数,则123,,x x x 的大小关系是 ; 123,,s s s 分别表示甲、乙、丙三名运动员的这次测试成绩的标准差,则123,,s s s 的大小关系是 . (12)向量,a b满足||1,||2=-=a a b ,a 与b 的夹角为60,||=b . (13)若110a b<<,则下列不等式中, ①a b ab +< ②||||a b > ③a b < ④2b aa b+> 正确的不等式有 .(写出所有正确不等式的序号)(14)已知圆的方程2225x y +=,过(4,3)M -作直线,MA MB 与圆交于点,A B ,且,MA MB关于直线3y =对称,则直线AB 的斜率等于 .C 1D 1CA 1BA三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. (15)(本小题共12分)如图,在平面直角坐标系xOy 中,以x 轴为始边作两个锐角,αβ,它们的终边分别与单位圆交于,A B 两点.已知,A B (Ⅰ)求tan()αβ+的值; (Ⅱ)求2αβ+的值.(16)(本小题共14分)正方体1111D C B A ABCD -的棱长为2,O 是AC 与BD 的交点,E 为1BB 的中点. (Ⅰ)求证:直线1B D ∥平面AEC ; (Ⅱ)求证:⊥D B 1平面AC D 1; (Ⅲ)求三棱锥1D D OC -的体积.(17)(本小题共13分)在平面直角坐标系xOy 中,平面区域W 中的点的坐标(,)x y 满足225x y +≤,从区域W 中随机取点(,)M x y .(Ⅰ)若x ∈Z ,y ∈Z ,求点M 位于第四象限的概率;(Ⅱ)已知直线:(0)ly x b b =-+>与圆22:5O x y +=求y x b ≥-+的概率.(18)(本小题共14分)已知函数32()f x x ax bx c =+++在1x =-与2x =处都取得极值. (Ⅰ)求,a b 的值及函数()f x 的单调区间; (Ⅱ)若对[2,3]x ∈-,不等式23()2f x c c +<恒成立,求c 的取值范围.(19)(本小题共14分)已知椭圆的中心在原点,焦点在x 轴上,经过点P 且离心率e =.过定点)01(,-C 的直线与椭圆相交于A ,B 两点.(Ⅰ)求椭圆的方程;(Ⅱ)在x 轴上是否存在点M ,使MB MA ⋅为常数?若存在,求出点M 的坐标;若不存 在,请说明理由.(20)(本小题共13分)已知数列{}n a 的前n 项和为n S ,且满足*120(2,)n n n a S S n n -+⋅=≥∈N ,112a =. (Ⅰ)求证:{1nS }是等差数列; (Ⅱ)求数列{}n a 的通项公式;(Ⅲ)若*2(1)(2,)n n b n a n n =-≥∈N ,求证: 222231n b b b +++<.(考生务必将答案答在答题卡上,在试卷上作答无效)崇文区2009-2010学年度第二学期统一练习(二)高三数学(文科)参考答案及评分标准 2010.5一、选择题(本大题共8小题,每小题5分,共40分)(9)1(0,]4 (10)2(,1)3(11)123x x x ==;213s s s >> (12)12 (13)①,④ (14)43- 三、解答题(本大题共6小题,共80分) (15)(共12分)解:(Ⅰ)由已知得:cos 10αβ==. ∵,αβ为锐角 ∴sin αβ== ∴ 1tan 2,tan 7αβ==. ∴12tan tan 7tan()311tan tan 127αβαβαβ+++===-⋅-⨯.--------------------6分 (Ⅱ)∵22tan 44tan 21tan 143ααα===--- ∴41tan 2tan 37tan(2)1411tan 2tan 1()37αβαβαβ-+++===--⋅--⨯. ,αβ为锐角,∴3022παβ<+<, ∴324παβ+=. -----------12分 (16)(共14分)(Ⅰ)连接OE ,在1B BD ∆中,∵E 为1BB 的中点,O 为BD 的中点,∴OE ∥1B D 又∵1B D ⊄平面AEC∴直线1B D ∥平面AEC . --------------------4分 (Ⅱ)在正方体1111D C B A ABCD -中,1B B ⊥平面ABCD ,AC ⊂平面ABCD∴1B B AC ⊥.BD AC ⊥且1BB BD B ⋂= ∴1B D AC ⊥ ∴1AC B D ⊥ 同理可证11B D AD ⊥ ∵1AC AD A ⋂=∴⊥D B 1平面AC D 1. --------------------9分(Ⅲ)11111221333D D OC D DOC DOC V V DD S --∆==⋅⋅=⨯⨯=. -------------14分 (17)(共13分)解:(Ⅰ)若x ∈Z ,y ∈Z ,则点M 的个数共有21个,列举如下:(2,1),(2,0),(2,1)----;(1,2),(1,1),(1,0),(1,1),(1,2)-------; (0,2),(0,1),(0,0),(0,1),(0,2)--;(1,2),(1,1),(1,0),(1,1),(1,2)--; (2,1),(2,0),(2,1)- .当点M 的坐标为(1,1),(1,2),(2,1)---时,点M 位于第四象限. 故点M 位于第四象限的概率为17. ---------------- 6分 (Ⅱ)由已知可知区域W 的面积是5π.因为直线:l y x b =-+与圆22:5O x y +=如图,可求得扇形的圆心角为23π,所以扇形的面积为12555233S ππ=⨯=, 则满足y x b ≥-+的点M 构成的区域的面积为5122015355sin 32312S πππ-=-=, 所以y x b ≥-+的概率为20153433125πππ--=.---------------- 13分(18)(共14分)解:(Ⅰ)'2()32f x x ax b =++,由题意:''(1)0,(2)0,f f ⎧-=⎪⎨=⎪⎩ 即320,1240,a b a b -+=⎧⎨++=⎩ 解得326a b ⎧=-⎪⎨⎪=-⎩ ∴323()62f x x x x c =--+,'2()336f x x x =-- 令'()0f x <,解得12x -<<; 令'()0f x >,解得1x <-或2x >,∴()f x 的减区间为(1,2)-;增区间为(,1)-∞-,(2,)+∞.---------------5分 (Ⅱ)由(Ⅰ)知,()f x 在(,1)-∞-上单调递增;在(1,2)-上单调递减; 在(2,)+∞上单调递增.∴[2,3]x ∈-时,()f x 的最大值即为(1)f -与(3)f 中的较大者.7(1)2f c -=+; 9(3)2f c =-+ ∴当1x =-时,()f x 取得最大值. 要使23()2f x c c +<,只需23(1)2c f c >-+,即:2275c c >+解得:1c <-或72c >. ∴c 的取值范围为7(,1)(,)2-∞-⋃+∞. -------------14分 (19)(共14分)解:(Ⅰ)设椭圆方程为22221(0)x y a b a b+=>>O由已知可得22222211a b c c aa b ⎧=+⎪⎪⎪=⎨⎪⎪+=⎪⎩,解得 224,2a b ==.所求椭圆的方程为 22142x y +=. -------------5分 (Ⅱ)设1122(,),(,),(,0)A x y B x y M m当直线AB 与x 轴不垂直时,设直线AB 的方程为(1)y k x =+.222222(1)(12)4240240y k x k x k x k x y =+⎧⇒+++-=⎨+-=⎩ 2122412k x x k +=-+,21222412k x x k -=+,2221212121223(1)(1)(1)12k y y k x x k x x x x k=++=+++=-+ 21122121212(,)(,)()MA MB x m y x m y x x m x x m y y ⋅=--=-+++22222222443121212k mk k m k k k --=++++++ 2222(241)412m m k m k +-+-=+2222211(241)(21)(241)42212m m k m m m k +-+-+-+-=+227212(241)212m m m k +=+--+MA MB ⋅是与k 无关的常数,∴7202m += ∴74m =-,即7(,0)4M -. 此时,1516MA MB ⋅=-. 当直线AB 与x 轴垂直时,则直线AB 的方程为1x =-.此时点A B ,的坐标分别为(1,1,22--- 当74m =-时, 亦有1516MA MB ⋅=- 综上,在x 轴上存在定点7(,0)4M -,使MA MB ⋅为常数.------------ 14分(20)(共13分)解:(Ⅰ)由*120(2,)n n n a S S n n -+⋅=≥∈N ,得1120n n n n S S S S ---+⋅=,所以*1112(2,)n n n n S S --=≥∈N ,故{1nS }是等差数列.---------------- 4分 (Ⅱ) 由(Ⅰ)知,12n n S =,所以12n S n=. 111(2)22(1)n n n a S S n n n -=-=-≥- 所以1,(1),21,(2).2(1)n n a n n n ⎧=⎪⎪=⎨⎪-≥-⎪⎩---------------- 9分(Ⅲ)112(1)[](2)2(1)n b n n n n n=-⋅-=≥-所以221111(2)(1)1n b n n n n n n=<=-≥-- 2223b b ++...2n b +1111223<-+-+ (111)111n n n+-=-<-. ----------1 3分。
北京市崇文区2010年高三数学第二次高考模拟考试(理)新人教版

侧(左)视图正(主)视图俯视图崇文区2009-2010学年度第二学期统一练习(二) 高三数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至5页,共150分。
考试时间120分钟。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分)注意事项:1.考生务必将答案答在答题卡上,在试卷上作答无效。
2.答题前考生务必用黑色字迹的签字笔在答题卡上填写姓名、准考证号,然后再用2B 铅笔将与准考证号对应的信息点涂黑。
3.答题卡上第Ⅰ卷必须用2B 铅笔作答,将选中项涂满涂黑,黑度以遮住框内字母为准,修改时用橡皮擦除干净。
第Ⅱ卷必须用黑色字迹的签字笔按照题号顺序在各题目的答题区域内作答,未在对应的答题区域内作答或超出答题区域作答的均不得分。
一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.(1)“关于x 的不等式220x ax a -+>的解集为R ”是“01a ≤<” (A )充分非必要条件 (B )必要非充分条件 (C )充分必要条件 (D )既非充分又非必要条件 (2)一个几何体的三视图如图所示,则这个几何体的体积等于(A) 12(B) 4 (C )563(D (3)设函数2log (1), (>0), (), (0).a x x f x x axb x +⎧=⎨++≤⎩若(3)2f =,(2)0f -=,则a b +=(A) 1- (B) 0 (C )1 (D )2(4)把函数sin ()y x x =∈R 的图象上所有的点向左平移6π个单位长度,再把所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象所表示的函数为 (A )sin(2),3y x x π=-∈R (B )1sin(),26y x x π=+∈R (C )sin(2),3y x x π=+∈R (D )1sin(),26y x x π=-∈R (5)已知点P 是抛物线22y x =上的一个动点,则点P 到点(0,2)M 的距离与点P 到该抛物线准线的距离之和的最小值为(A )3 (B (C (D )92(6)若非零向量,a b 满足||||+=a b b ,则(A) |2||2|>+a a b (B) |2||2|<+a a b (C )|2||2|>+b a b (D )|2||2|<+b a b(7)用5,6,7,8,9组成没有重复数字的五位数,其中恰好有一个奇数夹在两个偶数之 间的五位数的个数为(A )120 (B )72 (C )48 (D )36(8)已知圆的方程2225x y +=,过(4,3)M -作直线,MA MB 与圆交于点,A B ,且,MA MB 关于直线3y =对称,则直线AB 的斜率等于 (A )43-(B )34- (C )54- (D )45-D崇文区2009-2010学年度第二学期统一练习(二)高三数学(理科) 2010.5 第Ⅱ卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分. (9)函数y =(10)如图,⊙O 中的弦AB 与直径点P ,M 为DC 延长线上一点,⊙O 的切线,N 为切点,若8AP =6PB =,4PD =,6MC =,则MN = .(11)甲、乙、丙三名射击运动员在某次测试中各射击20次,三人的测试成绩如下表123,,x x x 分别表示甲、乙、丙三名运动员这次测试成绩的平均数,则123,,x x x 的大小关系为 ;123,,s s s 分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则123,,ss s 的大小关系为 .(12)若直线l 的参数方程为31,545x t y t ⎧=-⎪⎪⎨⎪=⎪⎩(t 为参数),则直线l 的斜率为 ; 在极坐标系中,直线m 的方程为sin()42πρθ+=,则点7(2,)4A π到直线m 的距离为 ______.(13)给定下列四个命题: ①若110a b<<,则22b a >; ②已知直线l ,平面,αβ为不重合的两个平面.若l α⊥,且αβ⊥,则l ∥β; ③若1,,,,16a b c --成等比数列,则4b =-;④若55432543210(2)x a x a x a x a x a x a -=+++++,则123451a a a a a ++++=-.C 1D 1CA 1BA 其中为真命题的是 .(写出所有真命题的序号)(14)设不等式组*0,0,()4x y n y nx n >⎧⎪>∈⎨⎪≤-+⎩N ,所表示的平面区域n D 的整点个数为n a ,则 2420101()2010a a a +++= .三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. (15)(本小题共12分)如图,在平面直角坐标系xOy 中,以x 轴为始边作两个锐角,αβ,它们的终边分别与单位圆交于,A B 两点.已知,A B 的横坐标分别为510(Ⅰ)求tan()αβ+的值; (Ⅱ)求2αβ+的值.(16)(本小题共14分)正方体1111D C B A ABCD -的棱长为2,O 是AC 与BD 的交点,E 是1B B 上一点,且112B E =.(Ⅰ)求证:⊥D B 1平面AC D 1;(Ⅱ)求异面直线O D 1与D A 1所成角的余弦值; (Ⅲ)求直线1D O 与平面AEC 所成角的正弦值.(17)(本小题共13分)某学校高一年级开设了,,,,A B C D E 五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.(Ⅰ)求甲、乙、丙三名学生参加五门选修课的所有选法种数;(Ⅱ)求甲、乙、丙三名学生中至少有两名学生选修同一门课程的概率;(Ⅲ)设随机变量X 为甲、乙、丙这三名学生参加A 课程的人数,求X 的分布列与数学期望. (18)(本小题共14分)设函数1()(2)ln()2f x a x ax x=--++(a ∈R ). (Ⅰ)当0a =时,求()f x 的极值; (Ⅱ)当0a ≠时,求()f x 的单调区间.(19)(本小题共14分)已知椭圆()222210x y a b a b+=>>和圆O :222x y b +=,过椭圆上一点P 引圆O 的两条切线,切点分别为,A B .(Ⅰ)(ⅰ)若圆O 过椭圆的两个焦点,求椭圆的离心率e ;(ⅱ)若椭圆上存在点P ,使得90APB ∠=,求椭圆离心率e 的取值范围; (Ⅱ)设直线AB 与x 轴、y 轴分别交于点M ,N ,求证:2222a b ONOM+为定值.(20)(本小题共13分)设集合{}1,2,3,4,5,6M =,对于,i i a b M ∈,记ii ia eb =且i i a b <,由所有i e 组成的集合设为{}12,,,k A e e e =.(Ⅰ)求k 的值;(Ⅱ)设集合1'|',i i i i B e e e A e ⎧⎫==∈⎨⎬⎩⎭,对任意,'i j e A e B ∈∈,试求'i j i j e e ≠⋅∑; (Ⅲ)设,'i j e A e B ∈∈,试求'i j e e +∈Z 的概率.(考生务必将答案答在答题卡上,在试卷上作答无效)崇文区2009-2010学年度第二学期统一练习(二)高三数学(理科)参考答案及评分标准 2010.5一、选择题(本大题共8小题,每小题5分,共40分)(9)1(0,]4(10)(11)123x x x ==;213s s s >> (12)43-;2 (13)①,③ (14)3018三、解答题(本大题共6小题,共80分) (15)(共12分)解:(Ⅰ)由已知得:cos αβ==. ∵,αβ为锐角 ∴sin 510αβ==. ∴ 1tan 2,tan 7αβ==. ∴12tan tan 7tan()311tan tan 127αβαβαβ+++===-⋅-⨯.--------------------6分 (Ⅱ)∵22tan 44tan 21tan 143ααα===--- ∴41tan 2tan 37tan(2)1411tan 2tan 1()37αβαβαβ-+++===--⋅--⨯. ,αβ为锐角,∴3022παβ<+<, ∴324παβ+=. -----------12分 (16)(共14分)解:(Ⅰ)如图,以D为原点建立空间直角坐标系D xyz-.则(0,0,0)D,(0,2,0)C,(2,0,0)A,1(2,2,2)B,1(0,0,2)D∴1(2,0,2)AD=-,(2,2,0)AC=-,1(2,2,2)B D=---.114040AD B D⋅=+-=,14400AC B D⋅=-+=又AC与1AD交于A点11AD B D⊥,1AC B D⊥∴1B D⊥平面1D AC.------------4(Ⅱ)设DA1与OD1所成的角为θ.1(0,0,2)D ,(1,1,0)O,1(2,0,2)A.∴1(2,0,2)A D=--,1(1,1,2)DO=-.∴1111||cos6||||A D D OA D D Oθ⋅===⋅.所求异面直线DA1与OD1.---------------9分(Ⅲ)设平面AEC与直线OD1所成的角为φ.设平面AEC的法向量为(,,)x y z=n.3(2,2,2E,(0,2,0)C,(2,0,0)A,3(0,2,2AE=,3(2,0,2EC=--.30434x zAEEC y z⎧=-⎧⎪⋅=⎪⎪⇒⎨⎨⋅=⎪⎪⎩=-⎪⎩nn令1z=,则33,44x y=-=-∴33(,,1)44=--n.∴111|7sin|cos,|51||||D OD OD Oφ⋅=<>==⋅|nnn.所求平面AEC 与直线O D 1所成角的正弦值为51.--------------------14分 (17)(共13分)解:(Ⅰ)甲、乙、丙三名学生每人选择五门选修课的方法数是5种,故共有555125⨯⨯=(种).(Ⅱ)三名学生选择三门不同选修课程的概率为:35312525A =.∴三名学生中至少有两人选修同一门课程的概率为:121312525-=. (Ⅲ)由题意:0,1,2,3X =.33464(0)5125P X ===; 1233448(1)5125C P X ⋅===; 233412(2)5125C P X ⋅===; 3331(3)5125C P X ===.ξ的分布列为数学期望64481210123125125125125EX =⨯+⨯+⨯+⨯=35.---------------- 13分 (18)(共14分)解:(Ⅰ)依题意,知()f x 的定义域为(,0)-∞.当0a =时,1()2ln()f x x x =--+,'221()f x x x -=-2(21)x x-+=. 令'()0f x =,解得12x =-. 当x 变化时,'()f x 与()f x 的变化情况如下表:由上表知:当12x <-时,'()0f x >;当12x >-时,'()0f x <. 故当12x =-时, ()f x 取得极大值为2ln 22-.-------------------5分 (Ⅱ)'221()2a f x a x x -=-+22(2)12a x ax x --+=21(21)()a x x a x +-=若0a >,令'()0f x >,解得:12x <-;令'()0f x <,解得:102x -<<. 若0a <,①当20a -<<时,112a-> 令'()0f x >,解得:112x a <<-; 令'()0f x <,解得:1x a <或102x -<<. ②当2a =-时,112a-=,2'2(21)()0x f x x -+=≤ ③当2a <-时,112a-< 令'()0f x >,解得:112x a-<<; 令'()0f x <,解得:12x <-或10x a<<. 综上,当0a >时,()f x 的增区间为1(,)2-∞-,减区间为1(,0)2-;当20a -<<时,()f x 的增区间为11(,)2a -,减区间为1(,)a -∞,1(,0)2-; 当2a =-时,()f x 的减区间为(,0)-∞,无增区间;当2a <-时,()f x 的增区间为11(,)2a -,减区间为1(,)2-∞-,1(,0)a.-------------14分(19)(共14分)解:(Ⅰ)(ⅰ)∵ 圆O 过椭圆的焦点,圆O :222x y b +=,∴ b c =,∴ 2222b ac c =-=, ∴ 222a c =,∴2e =. (ⅱ)由90APB ∠=及圆的性质,可得OP =,∴2222,OP b a =≤ ∴222a c ≤ ∴212e ≥1e ≤<. ---------------- 6分 (Ⅱ)设()()()001122,,,,,P x y A x y B x y ,则011011y y x x x y -=--整理得220011x x y y x y +=+22211x y b +=∴PA 方程为:211x x y y b +=,PB 方程为:222x x y y b +=.∴11x x y y +=22x x y y +, ∴021210x y y x x y -=--,直线AB 方程为 ()0110x y y x x y -=--,即 200x x y y b +=. 令0x =,得20b ON y y ==,令0y =,得2b OM x x ==,∴2222222220022442a y b x a b a b a b b bONOM++===,∴2222a b ON OM +为定值,定值是22a b . ----------------14分 (20)(共13分)解:(Ⅰ)由题意知,,i i a b M ∈,i i a b <,首先考虑M 中的二元子集有 {}{}{}1,2,1,3,,,5,6,共15个,即2615C =个.又i i a b <,满足j i i ja ab b =的二元子集有: {}{}{}1,2,2,4,3,6,此时12i i a b =, {}{}1,3,2,6,此时13ii a b =, {}{}2,3,4,6,此时23ii ab =,共7个二元子集. 故集合A 中的元素个数157311k =-+=.---------------- 4分 (Ⅱ)列举11111223345{,,,,,,,,,,}23456354556A = 354556{2,3,4,5,6,,,,,,}223345B = 11111,11'''ij i j i j i j i j i j e e e e e e ≠====⋅=⋅-⋅∑∑∑ 111111115896039'111122040i j i j e e ===-=⋅-=∑∑.----------8分 (Ⅲ)由(Ⅱ)列举符合题意的有:13222+=,15322+=,15233+=,24233+=,35244+=,46255+=, 共6对. 所求概率为:6121p =. ----------13分。
2010年北京崇文数学一模答案

初三数学试題答樂第1页(共4页)数学试题参考答案及评分标准2010. S 崇文区2009-2010学年度第二学迎初三统一慈习(一)三■解答题(本18共30分.毎小卷5分)二.填空题(本題共16分■毎小题4分)】3.無= 3 *^"-2 x号-1 —5 ................................ .. ......................................... ………………,.… d 分=2矩・6. ........................................................................................................ .......... 5分14•解:去分酔■得3(3x・I)-2“3・ ........................................................... . ......................... .. 2分耕得工=2“ .............................................................................................................................. 4分经检验足原方程的解.•••原方廷的解足工=2 ......................................................................................................... 5分15. iE明匸ED1RD小乙0=90°□乙人•■•乙£+Z£CD=903. 又•••/1C丄CE”.乙ACB+ 乙ECD=90°・•••厶ACB 口」E・在LABC和ADCE中.厶ACB二乙E.BC^CE............................................................................................................................. 3分•••氐ABCMDCE.......................................................................................... ........................ 4分XAB^DC.............................................................................................................................. S分16.耶:由题意,可知点A的横坐标是2,白点A在正比^»y=2x的因象上.・••点4的燮标为(2.4). ..................................................................................................... 2£又•••点人左反比例函数尸迂1的田線上,・・・4 口罟.即肮=9. ......................................................................................................... 5;?初三数学过題答牢第2英(共4页)17・嵌4 ■亡HU1 T -2 1 (x-lX^+I )1 -X *1社 (*]), T %3 + x - 1 =O f .\ -x 2 =x-1・ ......................... .. ............ ........... .... ........... .. ........ . ...... 4 分 •••更式" ................................ . .... ...... ........... 5 分13.無:设火车从北京到式汉的平均时速为z 公里每小时,提連后丈汉到广州依平均时嚏为y公里每小时. ..................................... . ................. 1分 依題意•有y =2x + 50t!5x=Lr + (15-8-4)y- ............................................................................... 3 分解方程组,得严冋 .............. .... ................ly » 350.答:火车从北京到餒汉的平均时速为15€公里部小吋•提速后武汉到广州的平均吋遠为 350公里每小时.四、解答題(本麵共20分,第19越5分,篇20翹5分•第21貶6分■第22題4分)19. ......................................................................................... 烬:作朋丄DC 于E.DF 丄BC 于F ・....................................................... 1分A AEj^DF. v AD//BC. Z.A£F = 90°.・・・四边形AEFD 是矩形.A £F = .W=3r A£=DF. ......................................................... 2 分V BD = CD 、D"BC.:・DF 是4BDC 的BC 边上的中我.v 厶BDC DF 士BC “F =4・ ...................................... 3 分 A A£=4,BE = BF-£F»4 -3 -1. ............................................................................................. 4 分 在 R1A.4BE 中.AB 2 ^AE l+〃尸20. 解:(1)・4C 与OO 棉切.证罚如下:•••OC 丄 AD{ 話)............................................................................................................................ 3 分 •••^=74r +r 3分 4 o BA Z.4OC+Z.1 =90°. ..............................................又丁厶C = /BED =乙1.••• ZAOC+^C=90U. ...............................................AB LACIP4C与QO相切. .......................初三数学过題答牢第2英(共4页)初三数学试題答案第3页(共4页〉(2〉解:连接在 Rt bAOC 中■厶 CAO 二 90。
崇文高三一模及答案数学文.doc

北京市崇文区2009—2010学年度第二学期统一练习(一)数 学 试 题(文)2010.4本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。
考试时间120分钟。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分)答题区域内作答,未在对应的答题区域内作答或超出答题区域作答的均不得分。
一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.已知全集U =R ,集合{}|12A x x =->,{}2|680B x x x =-+<,则集合()UA B ⋂=ð( )A .{}|14x x -≤≤B .{}|23x x ≤<C . {}|23x x <≤D .{}|14x x -<<2.已知幂函数()y f x =的图象过(4,2)点,则1()2f =( )AB .12C .14D.23.有一个几何体的三视图及其尺寸如图(单位:cm ),该几何体的表面积和体积为 ( )A .2324πcm ,12πcm B .2315πcm ,12πcm C .2324πcm ,36πcm D .以上都不正确4.若直线y x b =+与圆222x y +=相切,则b 的值为( ) A .4±B .2±C.D.±5.将函数x y 2sin 2=的图象向右平移6π个单位后,其图象的一条对称轴方程为( ) A .3π=x B .6π=x B .125π=x D .127π=x6.已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的为( )A .若,,αγβγ⊥⊥则αβ B .若,,m m αβ则αβC .若,m n αα,则m nD .若,,m n αα⊥⊥则m n7.若01a <<,函数()log a f x x =,()11(),(),342m f n f p f ===,则( )A .m n p >>B .m p n >>C .n m p >>D .p m n >>8.如果对于任意实数x ,[]x 表示不超过x 的最大整数. 例如[]3.273=,[]0.60=. 那么“[][]x y =”是“1x y -<”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件第Ⅱ卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9.若),2(,53)2cos(ππααπ∈=-,则tan α= . 10.如果复数()()2i 1i m m ++(其中i 是虚数单位)是实数,则实数m =___________. 11.从52张扑克牌(没有大小王)中随机的抽一张牌,这张牌是J 或Q 或K 的概率为_______.12.某程序框图如图所示,该程序运行后输出,M N 的值分别为 .13.若数列{}n a 的前n 项和为n S ,则11,(1),,(2)n nn S n a S S n -=⎧=⎨-≥⎩.若数列{}n b 的前n 项积为n T ,类比上述结果,则n b =_________;此时,若2()n T n n *=∈N ,则n b =___________.14.关于平面向量有下列四个命题: ①若⋅=⋅a b a c ,则=b c ;②已知(,3),(2,6)k ==-a b .若a b ,则1k =-;③非零向量a 和b ,满足||=|a |=|b |a -b ,则a 与a +b 的夹角为30; ④()()0||||||||+⋅-=a b a b a b a b . 其中正确的命题为___________.(写出所有正确命题的序号)三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题共12分)在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,满足sin2A =,且ABC ∆的面积为2.(Ⅰ)求bc 的值;(Ⅱ)若6=+c b ,求a 的值. 16.(本小题共13分)为了调查某厂2000名工人生产某种产品的能力,随机抽查了m 位工人某天生产该产品的数量,产品数量的分组区间为[)10,15,[)15,20,[)20,25,[)25,30,[30,35],频率分布直方图如图所示.已知生产的产品数量在[)20,25之间的工人有6位. (Ⅰ)求m ;(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工人不在同一组的概率是多少?17.(本小题共14分)三棱柱111C B A ABC -中,侧棱与底面垂直, 90=∠ABC ,12AB BC BB ===, ,M N 分别是AB ,1A C 的中点.(Ⅰ)求证:||MN 平面11B BCC ;(Ⅱ)求证:⊥MN 平面C B A 11; (Ⅲ)求三棱锥-M C B A 11的体积. 18.(本小题共14分)已知函数322()69f x x ax a x =-+(a ∈R ). (Ⅰ)求函数()f x 的单调递减区间;(Ⅱ)当0a >时,若对[]0,3x ∀∈有()4f x ≤恒成立,求实数a 的取值范围. 19.(本小题共14分)已知椭圆()222210x y a b a b +=>>短轴的一个端点(D ,离心率12e =.过D作直线l 与椭圆交于另一点M ,与x 轴交于点A (不同于原点O ),点M 关于x 轴的对称点为N ,直线DN 交x 轴于点B . (Ⅰ)求椭圆的方程;(Ⅱ)求 OA OB ⋅的值.20.(本小题共13分)已知数列{}n a 的前n 项和为n S ,且211122n S n n =+. 数列{}n b 满足2120n n n b b b ++-+=(n *∈N ),且311b =,129153b b b +++=.(Ⅰ)求数列{}n a ,{}n b 的通项公式; (Ⅱ)设3(211)(21)n n n c a b =--,数列{}n c 的前n 项和为n T ,求使不等式57n kT >对一切n *∈N 都成立的最大正整数k 的值;(Ⅲ)设,(21,),(),(2,),n n a n l l f n b n l l **⎧=-∈⎪=⎨=∈⎪⎩N N 是否存在m *∈N ,使得(15)5()f m f m += 成立?若存在,求出m 的值;若不存在,请说明理由.参考答案一、选择题(本大题共8小题,每小题5分,共40分) 1—4 CDAB 5—8 CDBA二、填空题(本大题共6小题,每小题5分,共30分)9.34- 10.1-11.31312.13,2113.11(1)(2)n nn T n b T n T -=⎧⎪=⎨≥⎪⎩ ;()221(1)(2)1n n b n n n =⎧⎪=⎨≥⎪-⎩14.②③④三、解答题(本大题共6小题,共80分)15.(共12分)解:(Ⅰ)∵,552sin=A π<<A 0∴cos25A =. ∴4sin 2sin cos 225A A A ==. ∵2sin 21==∆A bc S ABC , ∴5=bc .--------------------6分(Ⅱ)∵,552sin=A ∴532sin21cos 2=-=A A . ∵5=bc ,6=+c b ,∴A bc c b a cos 2222-+=)cos 1(2)(2A bc c b +-+=20=.∴52=a . -----------12分 16.(共13分)解:(Ⅰ)根据直方图可知产品件数在[)20,25内的人数为 50.066m ⨯⨯=,则20m =(位). ---------------- 6分 (Ⅱ)根据直方图可知产品件数在 [)10,15,[)15,20,组内的人数分别为2,4.设这2位工人不在同一组为A 事件,则8()15P A =. 答:选取这2人不在同组的概率为815. ---------------- 13分 17.(共14分)(Ⅰ)证明: 连结1BC ,1AC ,,M N 是AB ,C A 1的中点∴||MN 1BC .又 MN ⊄平面11B BCC ,∴||MN 平面11B BCC . --------------------4分(Ⅱ) 三棱柱111C B A ABC -中,侧棱与底面垂直,∴四边形11B BCC 是正方形.11BC B C ∴⊥. 1MN B C ∴⊥.连结1,A M CM ,1AMA AMC ≅.1A M CM ∴=,又N 中1A C 的中点, 1MN AC ∴⊥. 1B C 与1A C 相交于点C ,∴⊥MN 平面C B A 11. --------------------9分(Ⅲ)由(Ⅱ)知MN 是三棱锥-M C B A 11的高.在直角MNC 中,1,MC AC ==MN ∴=又11A B CS=.11111433M A B C A B CV MN S-=⋅=. --------------------14分 18.(共14分)解:(Ⅰ)22'()31293()(3)0f x x ax a x a x a =-+=--< (1)当3a a =,即0a =时,2'()30f x x =>,不成立.(2)当3a a >,即0a <时,单调减区间为(3,)a a .(3)当3a a <,即0a >时,单调减区间为(,3)a a .--------------------5分 (Ⅱ)22'()31293()(3)f x x ax a x a x a =-+=--,()f x 在(0,)a 上递增,在(,3)a a 上递减,在(3,)a +∞上递增.(1)当3a ≥时,函数()f x 在[0,3]上递增, 所以函数()f x 在[0,3]上的最大值是(3)f ,若对[]0,3x ∀∈有()4f x ≤恒成立,需要有(3)4,3,f a ≤⎧⎨≥⎩解得a ∈∅.(2)当13a ≤<时,有33a a <≤,此时函数()f x 在[0,]a 上递增,在[,3]a 上递减,所以函数()f x 在[0,3]上的最大值是()f a , 若对[]0,3x ∀∈有()4f x ≤恒成立,需要有()4,13,f a a ≤⎧⎨≤<⎩ 解得1a =.(3)当1a <时,有33a >,此时函数()f x 在[,3]a a 上递减,在[3,3]a 上递增,所以函数()f x 在[0,3]上的最大值是()f a 或者是(3)f . 由2()(3)(3)(43)f a f a a -=--,①304a <≤时,()(3)f a f ≤, 若对[]0,3x ∀∈有()4f x ≤恒成立,需要有(3)4,30,4f a ≤⎧⎪⎨<≤⎪⎩解得3[1,]94a ∈-. ②314a <<时,()(3)f a f >, 若对[]0,3x ∀∈有()4f x ≤恒成立,需要有()4,31,4f a a ≤⎧⎪⎨<<⎪⎩ 解得3(,1)4a ∈.综上所述,[1a ∈. -------------14分 19.(共14分)解:(Ⅰ)由已知,2,a b ==.所以椭圆方程为 22143x y +=. -------------5分 (Ⅱ)设直线l方程为y kx =+0y =,得A k ⎛⎫-⎪ ⎪⎝⎭.由方程组223412y kx x y ⎧=+⎪⎨+=⎪⎩ 可得(223412x k x +=,即()22340k x++=.所以M x =, 所以222,3434M k k ⎛--+ ++⎝,222,3434N k k ⎛- ++⎝. 所以34DNk k ==.直线DN 的方程为34y x k= 令0y =,得,03B ⎛⎫-⎪ ⎪⎝⎭.所以 OA OB ⋅=4=. ---------------- 14分 20.(共13分)解:(Ⅰ)当1n =时, 116a S == 当2n ≥时, 221111111()[(1)(1)]52222n n n a S S n n n n n -=-=+--+-=+. 而当1n =时, 56n +=∴5n a n =+又2120n n n b b b ++-+=即211n n n n b b b b +++-=-,∴{}n b 是等差数列,又311b =,129153b b b +++=,解得15,3b d ==.∴32n b n =+. ---------------- 4分(Ⅱ)3(211)(21)n n n c a b =--1111()(21)(21)22121n n n n ==--+-+∴12n T c c =++…n c +1111[(1)()2335=-+-+…11()]2121n n +--+21n n =+ ∵11102321(23)(21)n n n nT T n n n n ++-=-=>++++∴n T 单调递增,故min 11()3n T T ==. 令1357k>,得19k <,所以max 18k =. ---------------- 9分 (Ⅲ),(21,),(),(2,),n n a n l l f n b n l l **⎧=-∈⎪=⎨=∈⎪⎩N N(1)当m 为奇数时,15m +为偶数,∴347525m m +=+,11m =.(2)当m 为偶数时,15m +为奇数,∴201510m m +=+,57m *=∉N (舍去).综上,存在唯一正整数11m =,使得(15)5()f m f m +=成立. ----------1 3分。
数学_2010年北京市某校高考数学模拟试卷(理科)(含答案)
2010年北京市某校高考数学模拟试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1. 已知i 是虚数单位,则−1+i 1+i=( )A −1B 1C −iD i2. 在△ABC 中,“sin2A =sin2B”是“A =B”的( )A 充分不必要条件B 必要不充分条件C 充分必要条件D 既不充分也不必要条件3.已知四棱锥P −ABCD 的三视图如图所示,则这个四棱锥的体积为( )A 13 B 1 C 23 D 434. 如果执行程序框图,那么输出的t =( )A 96B 120C 144D 3005. 某事件A 发生的概率为P(0<p <1),则事件A 在一次试验中发生的次数X 的方差的最大值为( )A 34 B 13 C 14 D 126. 已知实数x ,y 满足{x −y +1≥0x +y −3≥0x ≤2则yx 取值范围是( )A [12,2] B (−∞,12]∪[32,+∞) C [12,32] D (−∞,12]∪[2,+∞)7. 已知等差数列{a n }的前n 项和为S n ,若m >1且a m−1+a m+1−a m 2−1=0,S 2m−1=39,则m 等于( )A 10B 19C 20D 398. 设集合X 是实数集R 的子集,如果点x 0∈R 满足:对任意a >0,都存在x ∈X ,使得0<|x −x 0|<a ,称x 0为集合X 的聚点.用Z 表示整数集,则在下列集合中:①{n n+1|n ∈Z ,n ≥0}; ②{x|x ∈R, x ≠0};③{1n |n ∈Z ,n ≠0}; ④整数集Z 以0为聚点的集合有( )A ②③B ①④C ①③D ①②④二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上. 9. 在极坐标系中,曲线ρ=2sinθ所围成的平面图形的面积为________.10. 若(x +1x )n 展开式的二项式系数之和为64,则展开式的常数项的值为________.11. 已知PT 切⊙O 于点T ,PA 交⊙O 于A 、B 两点,AB =7,PT =12,如图所示.则PB =________. 12. 已知函数f(x)={(12)x ,(x ≤0)|log 2x|,(x >0)则函数F(x)=f(x)−1的零点的个数为________;使不等式F(x)≤1成立的x 的取值范围是________.13. 若椭圆和双曲线有相同焦点F 1,F 2,点P 是两条曲线的一个公共点,并且PF 1→⋅PF 2→=0,e 1,e 2分别为它们的离心率,则1e 12+1e 22的值是________.14. (1)对于数列{a n },若存在常数T ≥0,使得对于任意n ∈N ∗,均有|a n |≤T ,则称{a n }为有界数列.以下数列{a n }为有界数列的是________;(写出满足条件的所有序号) ①a n =n −2②a n =1n+2③a nan+1=2,a 1=1(2)数列{a n }为有界数列,且满足a n+1=−a n 2+2a n ,a 1=t(t >0),则实数t 的取值范围为________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15. 已知cosα=17,cosβ=1314且α,β∈(0,π2)(1)求tan2α的值; (2)求角α−β的大小.16. 某公司在“2010年上海世博会知识宣传”活动中进行抽奖游戏.抽奖规则是:在一个盒子中装有6张大小相同的精美卡片,其中3张印有“世博会会徽”图案,3张印有“世博会吉祥物海宝”图案.现每一次从盒子里无放回的随机抽取一张卡片,抽到印有海宝图案的卡片就中奖且游戏结束.(I)求最多抽取两次卡片游戏就结束的概率;(II)用X 表示游戏结束时所抽取卡片的次数,求X 的分布列和数学期望.17. 如图,在底面是菱形的四棱锥P −ABCD 中,∠ABC =60∘,PA =AC =2,PB =PD =2√2,点F 是PC 的中点. (1)求证:PC ⊥BD ;(2)求BF 与平面ABCD 所成角的大小;(3)若点E 在棱PD 上,当PEPD为多少时二面角E −AC −D 的大小为π6?18. 已知函数f(x)=ax −ln(2x +1),其中a ∈R .(1)当函数f(x)的图象在点(0, f(0))处的切线方程为y =2x 时,求a 值; (2)求函数f(x)的单调区间;(3)函数f(x)的图象总是在直线y =2ax +12a 的上方,求a 的取值范围.19. 已知圆C :x 2+(y −14)2=116,动圆M 与圆C 外切,圆心M 在x 轴上方且圆M 与x 轴相切. (1)求圆心轨迹M 的曲线方程;(2)若A(0, −2)为y 轴上一定点,Q(t, 0)为x 轴上一动点,过点Q 且与AQ 垂直的直线与轨迹M 交于D ,B 两点(D 在线段BQ 上),直线AB 与轨迹M 交于E 点,求AD →⋅AE →的最小值. 20. 现有一组互不相同且从小到大排列的数据:a 0,a 1,a 2,a 3,a 4,a 5,其中a 0=0,为提取反映数据间差异程度的某种指标,今对其进行如下加工:记T =a 0+a 1+...+a 5,x n =n5,y n =1T (a 0+a 1+...+a n ),作函数y =f(x),使其图象为逐点依次连接点P n (x n , y n )(n =0, 1, 2,…,5)的折线. (1)求f(0)和f(1)的值;(2)设P n−1P n 的斜率为k n (n =1, 2, 3, 4, 5),判断k 1,k 2,k 3,k 4,k 5的大小关系; (3)证明:当x ∈(0, 1)时,f(x)<x .2010年北京市某校高考数学模拟试卷(理科)答案1. D2. B3. C4. B5. C6. A7. C 8. A 9. π 10. 20 11. 912. 3,x ∈[−1, 0]∪[14, 4]13. 214. ②③;0<t ≤215. 解:(1)∵ cos2α=2cos 2α−1=−4749,且2α∈(0, π), ∴ sin2α=√1−cos 22α=8√349, 则tan2α=sin2αcos2α=−56√347;(2)∵ cosα=17,cosβ=1314且α,β∈(0,π2),∴ sinα=4√37,sinβ=3√314, 又∵ cosα<cosβ,∴ α>β,即π2>α−β>0, ∴ cos(α−β)=cosαcosβ+sinαsinβ=17×1314+4√37×3√314=12,则α−β=π3.16. 解:(1)由题意知最多摸两次中奖包括第一次模卡中奖和第二次摸卡中奖,这两种结果是互斥的,第一次摸卡中奖的概率为P 1=C 31C 61=12第二次摸卡中奖的概率为P 2=A 62˙=310则最多摸两次中奖的概率为P =P 1+P 2=45(2)由题意,摸卡次数X 的取值为:1,2,3,4 P(X =1)=P 1=12;P(X =2)=P 2=310P(X =3)=A 63˙=320 P(X =4)=A 33A 63=120∴ 则ξ的分布列为:∴ EX =1×12+2×310+3×320+4×120=7417. 解:令AC 与BD 的交点为O ,由于底面是菱形的四棱锥P −ABCD 中,∠ABC =60∘,PA =AC =2,可得AO =1,BO =√3又PB =PD =2√2,在等腰三角形PBD 中,由勾股定理可解得P0=√5故有PA 2+AO 2=5=PO 2,故有PO ⊥AC ,即有PO ,AC ,BD 三线两两垂直,由此,可以O 为坐标原点,,OB 方向为X 轴,OC 方向为Y 轴,OP 方向为Z 轴建立空间坐标系,故有A(0, −1, 0),B(√3, 0, 0),C(0, 1, 0),D(−√3, 0, 0),P(0, 0, √5)(I)PC →=(0, 1, −√5),BD →=(−2√3, 0, 0),因为PC →⋅BD →=0,故有PC ⊥BD ;(2)由前证易得P0⊥面ABCD ,故OP →即为平面ABCD 的法向量,其坐标为(0, 0, √5)又F 是PC 的中点,故其坐标为(0, 12, √52),所以BF→=(−√3, 12, √52)设线面角为θ,故有sinθ=||OP →||BF →|˙|=52√5×3√22=√106,故有θ=arcsin√106,即所求的线面角为arcsin√106(3)连接OE ,由于AC ⊥面PBD ,故可得∠EOD 即是二面角E −AC −D 的平面角, 设PEPD =t ,由PE =tPD ,可以得出,ED =(1−t)PD ,作EM 垂直OD 于M ,故点E 到底面的距离是EM =(1−t)√5,,OM =t √3又二面角E −AC −D 的大小为π6,可得tan π6=EMOM =√5t √3=√33,即有t =(1−t)√5,解得t =√51+√5=5−√5218. 解:(1)f′(x)=a −22x+1,∴ 函数f(x)的图象在点(0, f(0))处的切线方程为y =2x ,∴ f′(0)=a −2=2, ∴ a =4.(2)由已知得函数f(x)的定义域为(−12, +∞),且f′(x)=a −22x+1, ①当a ≤0时,f′(x)<0,函数f(x)在(−12, +∞)上单调递减, ②当a >0时,由f′(x)=0,解得x =2−a 2a>−12.f′(x)、f(x)随x 的变化情况如下表从上表可知 当x ∈(−12,2−a2a)时,f′(x)<0,函数f(x)在(−12,2−a 2a)上单调递减.当x ∈(2−a 2a ,+∞)时,f′(x)>0,函数f(x)在(2−a2a ,+∞)上单调递增. 综上所述:当a ≤0时,函数f(x)在(−12, +∞)上单调递减. 当a >0时,函数f(x)在(−12,2−a 2a )上单调递减,函数f(x)在(2−a 2a,+∞)上单调递增.(3)函数f(x)的图象总是在直线y =2ax +12a 的上方, 即ax −ln(2x +1)>2ax +12a 在(−12, +∞)上恒成立,即a <−2ln(2x+1)2x+1在(−12, +∞)上恒成立. 设G(x)=−2ln(2x+1)2x+1,则G′(x)=4ln(2x+1)−4(2x+1)2,令G′(x)>0得x >e−12,G′(x)<0得−12<x <e−12,G′(x)=0得x =e−12,∴ G(x)在x =e−12处取得最小值G(e−12)=−2e.∴ a <−2e .∴ a 的取值范围:a <−2e .19. 解:(1)设M(x, y),则MC =14+y ,即M 到C 的距离等于M 到直线y =−14的距离,从而圆心轨迹M 的曲线方程为x 2=y ;(2)由题意,不妨设t >0.设QB 方程为:y =−t2(x −t)与x 2=y 联立,求得D(t2,t 24),B(−t,t 2),从而AB 方程为y +2=t 2+2−tx ,与x 2=y 联立,求得E(−2t ,4t 2),∴ AD →⋅AE →=t 22+8t 2+4≥8,即AD →⋅AE →的最小值为8.20. 解:(1)解:f(0)=a 0a 0+a 1+a 2+a 3+a 4+a 5=0,f(1)=a 0+⋯+a5a 0+⋯+a 5=1.(2)解:k n =y n −y n−1x n−x n−1=5T na n ,n =1,2, (5)因为a1<a2<a3<a4<a5,所以k1<k2<k3<k4<k5.(3)证明:由于f(x)的图象是连接各点P n(x n, y n)(n=0, 1,…,5)的折线,要证明f(x)<x(0<x<1),只需证明f(x n)<x n(n=1, 2, 3, 4).事实上,当x∈(x n−1, x n)时,f(x)=f(x n)−f(x n−1)x n−x n−1(x−x n−1)+f(x n−1)=x n−xx n−x n−1f(x n−1)+x−x n−1x n−x n−1f(x n)<x n−xx n−x n−1x n−1+x−x n−1x n−x n−1x n=x.下面证明f(x n)<x n.对任何n(n=1, 2, 3, 4),5(a1+...+a n)=[n+(5−n)](a1+...+a n)=n(a1+...+a n)+(5−n)(a1+...+a n)≤n(a1+...+a n)+(5−n)na n=n[a1+...+a n+(5−n)a n] <n(a1+...+a n+a n+1+...+a5)=nT.所以f(x n)=a1+⋯+a nT <n5=x n.。
2010年北京西城区高考一模试题:数学(理科)
2010年北京崇文区高考一模试题:数学(理科)本试卷分第I 卷和第II 卷两部分,第I 卷1至2页,第II 卷3至5页,共150分。
考试时长120分钟。
考生务必将答案答在答题纸上,在试卷上作答无效。
考试结束后,将本试卷和答题纸一并交回。
第I 卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,选出符合题目要求的一项。
1.设集合{|1}P x x =>,2{|0}Q x x x =->,则下列结论正确的是 A .P Q = B .P Q R =C .P QÜD .Q PÜ2.函数sin cos y x x =+的最小值和最小正周期分别是A .2πB .2,2π-C .πD .2,π- 3.设等差数列{}n a 的前n 项和为nS ,246a a +=则5S 等于A .10B .12C .15D .304.甲乙两名运动员在某项测试中的8次成绩如茎叶图所示,1x ,2x 分别表示甲乙两名运动员这项测试成绩的平均数,1s ,2s 分别表示甲乙两名运动员这项测试成绩的标准差,则有A .1212,x x s s ><B .1212,x x s s =<C .1212,x x s s ==D .1212,x x s s <>5.阅读右面的程序框图,运行相应的程序,输出的结果为A .1321B .2113C .813D .1386.某会议室第一排共有8个座位,现有3人就座,若要求每人左右均有空位,那么不同的坐法种数为A .12B .16C .24D .327.已知平面区域1,||1,{(,)0,,{(,)0,1,y x y x x y y M x y y x ≤+⎧⎫≤-+⎧⎫⎪⎪Ω=≥=⎨⎬⎨⎬≥⎩⎭⎪⎪≤⎩⎭,向区域Ω内随机投一点P ,点P 落在区域M 内的概率为A .14B .13C .12D .238.如图,平面α⊥平面β,αβ =直线l ,A ,C 是α内不同的两点,B ,D 是β内不同的两点,且A ,B ,C ,D ∉直线l ,M ,N 分别是线段AB ,CD 的中点。
2010年北京市高考数学试卷(文科)答案与解析
2010年北京市高考数学试卷(文科)参考答案与试题解析一、选择题(共8小题,每小题5分,满分40分)1.(5分)(2010•北京)(北京卷理1)集合P={x∈Z|0≤x<3},M={x∈Z|x2<9},则P∩M=()A.{1,2}B.{0,1,2} C.{x|0≤x<3} D.{x|0≤x≤3}【考点】交集及其运算.【专题】集合.【分析】由题意集合P={x∈Z|0≤x<3},M={x∈Z|x2<9},分别解出集合P,M,从而求出P∩M.【解答】解:∵集合P={x∈Z|0≤x<3},∴P={0,1,2},∵M={x∈Z|x2<9},∴M={﹣2,﹣1,0,1,2},∴P∩M={0,1,2},故选B.【点评】此题考查简单的集合的运算,集合在高考的考查是以基础题为主,题目比较容易,复习中我们应从基础出发.2.(5分)(2010•北京)在复平面内,复数6+5i,﹣2+3i对应的点分别为A,B.若C为线段AB 的中点,则点C对应的复数是()A.4+8i B.8+2i C.2+4i D.4+i【考点】向量的线性运算性质及几何意义.【专题】平面向量及应用.【分析】根据两个复数对应的点的坐标分别为A(6,5),B(﹣2,3),确定中点坐标为C (2,4)得到答案.【解答】解:两个复数对应的点的坐标分别为A(6,5),B(﹣2,3),则其中点的坐标为C(2,4),故其对应的复数为2+4i.故选C.【点评】本题考查复平面的基本知识及中点坐标公式.求解此类问题要能够灵活准确的对复平面内的点的坐标与复数进行相互转化.3.(5分)(2010•北京)从{1,2,3,4,5}中随机选取一个数为a,从{1,2,3}中随机选取一个数为b,则b>a的概率是()A.B.C.D.【考点】等可能事件的概率.【专题】概率与统计.【分析】由题意知本题是一个古典概型,试验包含的所有事件根据分步计数原理知共有5×3种结果,而满足条件的事件是a=1,b=2;a=1,b=3;a=2,b=3共有3种结果.【解答】解:由题意知本题是一个古典概型,∵试验包含的所有事件根据分步计数原理知共有5×3种结果,而满足条件的事件是a=1,b=2;a=1,b=3;a=2,b=3共有3种结果,∴由古典概型公式得到P==,故选D.【点评】本题考查离散型随机变量的概率问题,先要判断该概率模型是不是古典概型,再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数.4.(5分)(2010•北京)若,是非零向量,且⊥,||≠||,则函数f(x)=(x+)(x﹣)是()A.一次函数且是奇函数B.一次函数但不是奇函数C.二次函数且是偶函数D.二次函数但不是偶函数【考点】平面向量数量积的运算.【专题】平面向量及应用.【分析】f(x)=x﹣x,因为||≠||,所以f(x)=()x,所以函数f(x)是一次函数且是奇函数.【解答】解:∵⊥,∴•=0∴f(x)=(x+)(xb﹣)=x﹣x,∵||≠||,∴所以f(x)=()x所以函数f(x)是一次函数且是奇函数故选A.【点评】本题主要考查平面向量的数量积运算和函数的奇偶性.求解中要明确两向量互相垂直等价于二者点乘等于0.5.(5分)(2010•北京)一个长方体去掉一个小长方体,所得几何体的正视图与侧(左)视图分别如图所,则该几何体的俯视图为()A. B.C. D.【考点】简单空间图形的三视图.【专题】立体几何.【分析】从正视图和侧视图上分析,去掉的长方体的位置应该在的方位,然后判断俯视图的正确图形.【解答】解:由正视图可知去掉的长方体在正视线的方向,从侧视图可以看出去掉的长方体在原长方体的左侧,由以上各视图的描述可知其俯视图符合C选项.故选:C.【点评】本题考查几何体的三视图之间的关系,要注意记忆和理解“长对正、高平齐、宽相等"的含义.6.(5分)(2010•北京)给定函数①,②,③y=|x﹣1|,④y=2x+1,其中在区间(0,1)上单调递减的函数序号是()A.①②B.②③C.③④D.①④【考点】函数单调性的判断与证明.【专题】函数的性质及应用.【分析】本题所给的四个函数分别是幂函数型,对数函数型,指数函数型,含绝对值函数型,在解答时需要熟悉这些函数类型的图象和性质;①为增函数,②为定义域上的减函数,③y=|x﹣1|有两个单调区间,一增区间一个减区间,④y=2x+1为增函数.【解答】解:①是幂函数,其在(0,+∞)上即第一象限内为增函数,故此项不符合要求;②中的函数是由函数向左平移1个单位长度得到的,因为原函数在(0,+∞)内为减函数,故此项符合要求;③中的函数图象是由函数y=x﹣1的图象保留x轴上方,下方图象翻折到x轴上方而得到的,故由其图象可知该项符合要求;④中的函数图象为指数函数,因其底数大于1,故其在R上单调递增,不合题意.故选B.【点评】本题考查了函数的单调性,要注意每类函数中决定单调性的元素所满足的条件.7.(5分)(2010•北京)某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成,该八边形的面积为()A.2sinα﹣2cosα+2 B.sinα﹣cosα+3C.3sinα﹣cosα+1 D.2sinα﹣cosα+1【考点】解三角形.【专题】解三角形.【分析】根据正弦定理可先求出4个三角形的面积,再由三角面积公式可求出正方形的边长进而得到面积,最后得到答案.【解答】解:由正弦定理可得4个等腰三角形的面积和为:4××1×1×sinα=2sinα由余弦定理可得正方形边长为:故正方形面积为:2﹣2cosα所以所求八边形的面积为:2sinα﹣2cosα+2故选A.【点评】本题考查了三角面积公式的应用和余弦定理的应用.正、余弦定理是考查解三角形的重点,是必考内容.8.(5分)(2010•北京)如图,正方体ABCD﹣A1B1C1D1的棱长为2,动点E、F在棱A1B1上.点Q是CD的中点,动点P在棱AD上,若EF=1,DP=x,A1E=y(x,y大于零),则三棱锥P﹣EFQ的体积()A.与x,y都有关B.与x,y都无关C.与x有关,与y无关D.与y有关,与x无关【考点】棱柱、棱锥、棱台的体积.【专题】立体几何.【分析】通过观察,发现点P到平面EFQ的距离是P到平面CDA1B1的距离,此距离只与x有关,面积EFQ为定值,推出结果.【解答】解:三棱锥P﹣EFQ的体积与点P到平面EFQ的距离和三角形EFQ的面积有关,由图形可知,平面EFQ与平面CDA1B1是同一平面,故点P到平面EFQ的距离是P到平面CDA1B1的距离,且该距离就是P到线段A1D的距离,此距离只与x有关,因为EF=1,点Q到EF 的距离为线段B1C的长度,为定值,综上可知所求三棱锥的体积只与x有关,与y无关.故选:C.【点评】本题考查空间几何体的结构特征和棱锥的体积问题,同时考查学生分析问题的能力以及空间想象能力.二、填空题(共6小题,每小题5分,满分30分)9.(5分)(2010•北京)已知函数y=,如图表示的是给定x的值,求其对应的函数值y的程序框图,①处应填写x<2;②处应填写y=log2x.【考点】设计程序框图解决实际问题.【专题】算法和程序框图.【分析】由题目可知:该程序的作用是计算分段函数y=的值,由于分段函数的分类标准是x是否大于2,而满足条件时执行的语句为y=2﹣x,易得条件语句中的条件①,及不满足条件时②中的语句.【解答】解:由题目可知:该程序的作用是计算分段函数y=的值,由于分段函数的分类标准是x是否大于2,而满足条件时执行的语句为y=2﹣x,易得条件语句中的条件为x<2不满足条件时②中的语句为y=log2x故答案为:x<2,y=log2x.【点评】要求条件结构对应的函数解析式,要分如下几个步骤:①分析流程图的结构,分析条件结构是如何嵌套的,以确定函数所分的段数;②根据判断框中的条件,设置分类标准;③根据判断框的“是”与“否”分支对应的操作,分析函数各段的解析式;④对前面的分类进行总结,写出分段函数的解析式.10.(5分)(2010•北京)在△ABC中,若b=1,c=,∠C=,则a=1.【考点】三角形中的几何计算.【专题】解三角形.【分析】先根据b,c,∠c,由正弦定理可得sinB,进而求得B,再根据正弦定理求得a.【解答】解:在△ABC中由正弦定理得,∴sinB=,∵b<c,故B=,则A=由正弦定理得∴a==1故答案为:1【点评】本题考查了应用正弦定理求解三角形问题.属基础题.11.(5分)(2010•北京)若点p(m,3)到直线4x﹣3y+1=0的距离为4,且点p在不等式2x+y<3表示的平面区域内,则m=﹣3.【考点】二元一次不等式(组)与平面区域.【专题】不等式的解法及应用.【分析】由点M到直线4x﹣3y+1=0的距离等于4求得m的值,代入不等式2x+y<3验证后得答案.【解答】解:∵点M(m,3)到直线4x﹣3y+1=0的距离为4,∴,解得:m=7或m=﹣3.当m=7时,2×7+3<3不成立;当m=﹣3时,2×(﹣3)+3<3成立.综上:m=﹣3.故答案为:﹣3.【点评】本题考查了点到直线的距离公式,考查了二元一次不等式表示的平面区域,是基础题.12.(5分)(2010•北京)从某小学随机抽取100名同学,将他们身高(单位:厘米)数据绘制成频率分布直方图(如图).由图中数据可知a=0.03.若要从身高在[120,130﹚,[130,140﹚,[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为3.【考点】频率分布直方图.【专题】概率与统计.【分析】欲求a,可根据直方图中各个矩形的面积之和为1,列得一元一次方程,解出a,欲求选取的人数,可先由直方图找出三个区域内的学生总数,及其中身高在[140,150]内的学生人数,再根据分层抽样的特点,代入其公式求解.【解答】解:∵直方图中各个矩形的面积之和为1,∴10×(0。
北京崇文区2010届高三统一练习数学文
崇文区2009 — 2010学年度第二学期统一练习(一)高三数学(文科)本试卷分第I 卷(选择题)和第n 卷(非选择题)两部分,第I 卷1至2页,第n 卷3至5页,共150分。
考试时间120分钟。
考试结束后,将本试卷和答题卡一并交回。
第I 卷(选择题 共40分)注意事项:1 •考生务必将答案答在答题卡上,在试卷上作答无效。
2.答题前考生务必用黑色字迹的签字笔在答题卡上填写姓名、准考证号,然后再用2B 铅笔将与准考证号对应的信息点涂黑。
3 •答题卡上第I 卷必须用 2B 铅笔作答,将选中项涂满涂黑,黑度以遮住框内字母为准,修改时用橡皮擦除干净。
第n 卷必须用黑色字迹的签字笔按照题号顺序在各题目的答题区 域内作答,未在对应的答题区域内作答或超出答题区域作答的均不得分。
一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.e u A B2010.4(1) 已知全集UR ,集合 A X | X 1X |X 2 6X8 0,则集合(2) (3) (A ) x| 1(C )X |2已知幕函数yf (X )的图象过(4, 2)有一个几何体的三视图及其尺寸如图(单位:cm ),该几何体的表面积和体积为 (A ) 24 n cm 2,12 n cm 3 (B ) (D )(B ) 15 n cm 2,12 n cm 3 (C ) 2324 n cm ,36 n cm (D ) 以上都不正确x|2 x| 1 f (1)正(主)视图侧(左)视图俯视图(4若直线y x b 与圆x 2 y 2相切,则b 的值为(A ) 4(B ) 2(C ) . 2(D ) 2:2(5)将函数y2sin2x 的图象向右平移 —个单位后,其图象的一条对称轴方程为6那么“ x y ”是“ x y 1”的 (A )充分而不必要条件 (D )既不充分也不必要条件(A )若,,则 P(B )若 m P , m P ,则 P(C )若 mP ,nP ,则 m Pn(D )若 m,n ,则 m Pn (7) 若0 a 1,函数f x log a X ,m1f ( ),n 41 f ( ), P 2f 3,则(A ) m n p (B ) m p n(C ) nm p(D ) p m n(8) 如果对于任意实数x , x 表示不超过x 的最大整数 .例如 3.27 3, 0.6 0(6)已知m,n 是两条不同直线,是三个不同平面,下列命题中正确的为(A) x 3(B)x(C)5 7x72 (D)5(B )必要而不充分条件(C )充分必要条件崇文区2009 — 2010学年度第二学期统一练习高三数学(文科) 2010.4第H 卷(共110分)(11 )从52张扑克牌(没有大小王)中随机的抽一张牌,这张牌是(12)某程序框图如图所示,该程序运行后输出M ,N 的值分别为 ___________________ .若数列{b n }的前n 项积为T n ,类比上述结果,贝U b n =________________________________________________ ;2此时,若 T n n (n N ),则 g = __________________ . (14) 关于平面向量有下列四个命题:①若 a b a c ,则 b c ;②已知 a (k,3),b(2,6).若 a Pb ,则 k 1 ;③非零向量a 和b ,满足|a|=|b| |a-b|,则a 与a+b 的夹角为30o;④(旦—)(——)0.|a| |b||a| |b|其中正确的命题为 ____________ .(写出所有正确命题的序号)、填空题:本大题共 6小题,每小题5分,共30 分. (9 )若 %)5,(-,),则 tan(10 )如果复数 m 2i 1 mi (其中i 是虚数单位)是实数,则实数(13)若数列{a n }的前n 项和为S n ,则a nS , (n 1),Si & 1, (n2)・J 或Q 或K 的概率为三、解答题:本大题共 6小题,共80分.解答应写出文字说明,演算步骤或证明过程 .(15) (本小题共12分)在 ABC 中,角A,B,C 所对的边分别为a,b,c ,满足si 丄5,且 ABC 的面2 5积为2 •(I)求bc 的值;(□)若b c 6,求a 的值.(16) (本小题共13分)为了调查某厂2000名工人生产某种产品的能力,随机抽查了 m 位工人某天生产该产品的数量,产品数量的分组区间为10,15 , 15,20 , 20,25 , 25,30 , [30,35],频率分布直方图如图所示•已知生产的产品数量在20,25之间的工人有6位.(I)求 m ;(n)工厂规定从生产低于 20件产品的工人中随机的选取 2位工人进行培训,则这 2位工人不在同一组的概率是多少?三棱柱ABC A ! B 1C 1中,侧棱与底面垂直,M,N 分别是AB , AC 的中点.(I)求证: MN ||平面 BCC 1B 1 ; (n)求证:MN 平面ABQ ;(川)求三棱锥 M A 1B 1C 的体积.(18)(本小题共14分)(17)(本小题共14分)ABC 90 , AB BC BB 1 2 ,人频率/组距BC(I)求数列 a n , b n 的通项公式;n N 都成立的最大正整数 k 的值;a n , (n 2l 1, l N ),是否存在 m N ,使得 f (m 15) 5 f (m)成b n , (n 2l ,l N ),立?若存在,求出 m 的值;若不存在,请说明理由.已知函数 f (x) x 3 6ax 2 9a 2x ( a R ).(I)求函数f(x)的单调递减区间; (n)当a 0时,若对 x 0,3有f(x)4恒成立,求实数 a 的取值范围.(19)(本小题共14分)已知椭圆b 2A1 a b 0短轴的一个端点D 0, , 3,离心率e -.过D2作直线I 与椭圆交于另一点 M ,与x 轴交于点 A (不同于原点 点为N ,直线DN 交x 轴于点B .(I)求椭圆的方程; (n)求(20)(本小题共13分)1 2 11已知数列a n 的前n 项和为S n ,且S n n n .2 2数列 b n 满足 b n 2 2b n 1 b n 0( nN ),且 b 3 11 , b 1 b 2 L b 9 153.(n)设c n3(2 a n 11)(2b n 1)数列C n 的前n 项和为T n ,求使不等式T n—对一切57(川)设f (n)的值.O ),点M 关于x 轴的对称(考生务必将答案答在答题卡上,在试卷上作答无效)崇文区2009 —2010学年度第二学期统一练习(一)高三数学(文科)参考答案及评分标准2010.4、选择题(本大题共8小题,每小题5分,共40分)题号(1) (2) (3) (4) (5) (6) (7) (8) 答案C D A B C D B A二、填空题(本大题共6小题,每小题5分,共30分)(9) 3(10) 1(11) 3(12) 13, 21 413T1(n1)1(n1)(13 ) b n T n;b n n2(14)②③④(n2)2(n2)Tn 1n 1三、解答题(本大题共6小题,共80分)(15)(共12 分)A 屈解:(I):sin , 0 A2 5A 2亦二cos2 5A A 4二si nA 2sin —cos—2 2 51T S ABC—bcsin A 2 ,2••• bc 5. --------------- 6 分A V5(n):sin ,2 52 A 3•- cosA 1 2sin2 5bc5, b c 6 ,a2b2 c22bc cos A2(b c) 2bc(1 cosA) 20.a 2.5.------ 12 分(16)(共13 分)解:(I)根据直方图可知产品件数在20,25内的人数为m 5 0.06 6,则m 20 (位). ---------- 6 分(n)根据直方图可知产品件数在设这2位工人不在同一组为A事件,则p(A)—.158答:选取这2人不在同组的概率为 --------- 13分15(17)(共14 分)(I)证明:连结BC1, AC1,M,N是AB , A1C的中点MN || BC1.又MN 平面BCC1B1,MN ||平面BCC1B1 . ----------------------------- 4 分(n)三棱柱ABC A1B1C1中,侧棱与底面垂直,四边形BCC1B1是正方形.BC1 RC .MN B1C .连结A,M ,CM , VAMA1 VAMC .A1M CM,又N中AC的中点,MN AC .Q B1C与AC相交于点C ,MN 平面A1B1C . -----------------9 分(川)由(n)知MN是三棱锥M A S B1C的高.在直角VMNC中,MC5,AC 2 3,MN . 2r.又S VA1B,C2-2 .VM A1B1C 1匚MN SVA1B1C343 .----------- 14分(18) (共14分)10,15 , 15,20,组内的人数分别为2, 4.解:(I) f'(x)3x2 12ax9a23(x a)(x3a) 0(1 )当a 3a,即a0时, f '(:x) 3x20 ,不成立.(2 )当a 3a,即a0时, 单调减咸区间为(3a, a).(3 )当a 3a,即a0时, 单调减咸区间为(a,3a). ------------- ---- 52 2(n) f'(x) 3x 2 12ax 9a 23(x a)(x 3a),f(x)在(0, a)上递增,在(a,3a)上递减,在(3a,)上递增.(1 )当a 3时,函数f (x)在[0,3]上递增, 所以函数f (x)在[0,3]上的最大值是f ⑶,f (3) 4,—若对x 0,3有f (x) 4恒成立,需要有解得a •a 3,(2)当1 a 3时,有a 3 3a ,此时函数f (x)在[0,a ]上递增,在[a,3]上递 减,所以函数f (x)在[0,3]上的最大值是f (a),(19)(共 14 分)2x所以椭圆方程为 一(n)设直线l 方程为y kx .3 . 令y0,得 A 一,0 .k若对 x 0,3有f (x) 4恒成立,需要有f(a) 4解得 a 1 . 1 a 3,(3)当 a1时,有3 3a ,此时函数f(x)在[a,3a ]上递减,在[3a,3]上递增,所以函数 f(x)在[0,3]上的最大值是 f (a)或者是f (3).由 f (a)2f (3) (a 3) (4 a 3), 3一时,f (a)4f(3),若对0,3 有 f(x)4恒成立,需要有解得a [1 孕,4]. 9 41 时,f (a)f(3),f(3)4,一J4若对 x0,3 有 f (x)4恒成立,需要有f (a)3 a 44,解得1,(弓,1).4综上所述,2罷a [1L ].14解:(1)由已知,a 2,b x3 .由方程组y kx .3 2 23x 4y2可得 3x 412kx . 3 2 12,即所以 X M所以所以3 4k 28.3k 3 4k 2 8.3k 3 4k 2,8 , '3k 8.3k 22,23 4k 3 4k8、、3k 34k4k 2直线DN 的方程为「3.令y 0,得B4,3k丁,° .4. 所以 14分(i)当n 1时, a 〔 S 1 6 当n 2 时,a n S n S n 1/1才而当n 1 时,n 56 …a nn 5又b n 2 2b n 1 b n 0即b n 2 b n 二 b n 是等差数列, 又b 3 11 ,•- b n 3n 2 .■)C n3(2a n 11)(2b n 1) (2n •- T n11 C 1 C2 … C n-[(1-(20)(共 13 分) 2 1 1解: bi 11n) Q(n 2 2 1)2珈1)] n5.b n 1b n, 153, 解得 b i5,d1)(2n 1) 2(2n 1 2n 1)1 )(3 1 5)1(2n 12n 12n 3 2n 1 (2n 3)(2 n 1)1二T n 单调递增,故(「)min h 3 •1 k令 ,得 k 19,所以 k max 18. ------------- 3 57 ••• 3m 47 5m 25, m 11. (2)当m 为偶数时, m 15为奇数,• m 20 15m 10, m N (舍去). 7 综上,存在唯一正整数 m 11,使得 f(m 15) 5f (m)成立. ----- 1 3 分a n , (n 2l 1, l N ),b n , (n 2l ,l N ),(出)f(n)(1)当m 为奇数时,m 15为偶数,。
