宿豫中学09届高三数学二轮复习天天练4
宿豫中学09届高三数学二轮复习天天练(2)

Read xIf x >0 Then1y x ←+Else1y x ←-End If Print y (第9题)09届高三数学天天练22一、填空题 1.设⎭⎬⎫⎩⎨⎧-∈3,21,1,1α,那么使函数αx y =的定义域为R 且为奇函数的所有α的值为. 2.空间直角坐标系中,点(4,3,7)P -关于平面xoy 的对称点的坐标为。
3.若复数()()2563i z m m m =-++-是纯虚数,那么实数m =. 4.已知集合{}22log (2)A y y x ==-,{}220B x x x =--≤,那么A B =.5.若)127cos(,31)12sin(παπα+=+则的值为. 6.椭圆221x my +=的焦点在y 轴上,长轴长是短轴长的两倍,那么m 的值为。
7.已知||1a =,||2b =,且()a a b ⊥-,那么向量a 与向量b 的夹角是。
8.在区间(0,1)中随机地取出两个数,那么两数之和小于65的概率是_________ 9.右边是根据所输入的x 值计算y 值的一个算法程序, 若x 依次取数列1100n ⎧⎫-⎨⎬⎩⎭()n N +∈中的前200项,那么所得y 值中的最小值为. 10.用一些棱长为1cm 的小正方体码放成一个几何体,图1为其俯视图,图2为其主视图,那么这个几何体的体积最大是cm 3.图1(俯视图) 图2(主视图)11.已知抛物线)0(22>=p px y 焦点F 恰好是双曲线22221x y a b-=的右焦点,且两条曲线交点的连线过点F ,那么该双曲线的离心率为。
12.若存在实数[]1,1p ∈-,使得不等式()2330px p x +-->成立,那么实数x 的取值范围为。
13.若()f n 表示2*1()n n N +∈的各位上的数字之和,如2141197,19717+=++=,所以(14)17f =,记*1211()(),()[()],,()[()],k k f n f n f n f f n f n f f n k N +===∈,那么2008(17)f =Q PFEC O B A14.下列说法:①当2ln 1ln 10≥+≠>xx x x 时,有且;②∆ABC 中,A B >是sin sin A B >成立的充要条件;③函数x y a =的图象可以由函数2x y a =(其中01a a >≠且)平移得到;④已知n S 是等差数列{}n a 的前n 项和,若75S S >,那么93S S >.;⑤函数(1)y f x =+与函数(1)y f x =-的图象关于直线1x =对称。
江苏省宿迁市高三数学模拟试卷(二)
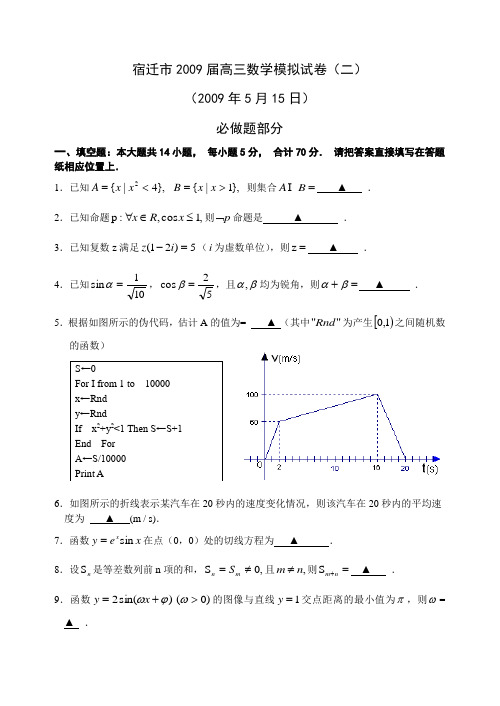
宿迁市2009届高三数学模拟试卷(二)(2009年5月15日)必做题部分一、填空题:本大题共14小题, 每小题5分, 合计70分. 请把答案直接填写在答题纸相应位置上.1.已知},4|{2<=x x A },1|{>=x x B 则集合=B A ▲ . 2.已知命题,1cos ,:p ≤∈∀x R x 则p ⌝命题是 ▲ . 3.已知复数z 满足5)21(=-i z (i 为虚数单位),则=z ▲ . 4.已知101sin =α,52cos =β,且βα,均为锐角,则=+βα ▲ .5.根据如图所示的伪代码,估计A 的值为= ▲ (其中""Rnd 为产生[)1,0之间随机数的函数)6.如图所示的折线表示某汽车在20秒内的速度变化情况,则该汽车在20秒内的平均速度为 ▲ (m / s). 7.函数x e y xsin =在点(0,0)处的切线方程为 ▲ .8.设n S 是等差数列前n 项的和,,0S ≠=m n S 且,n m ≠则=+n m S ▲ .9.函数)sin(2ϕω+=x y )0(>ω的图像与直线1=y 交点距离的最小值为π,则ω= ▲ .S ←0For I from 1 to 10000 x←Rnd y←RndIf x 2+y 2<1 Then S←S+1 End For A←S/10000 Print A10.抛物线x y 42=的焦点为F ,过点F 的直线交抛物线于A ,B 两点,且AF=2BF ,则A 点的坐标为 ▲ .11.若实数y ,x 满足,012222=+-++y x y x 则122--x y 的 最小值为 ▲ .12.设向量a ,b 满足|a |=|b |=1,|3a -2b |=3,则|3a +b |= ▲ . 13.棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,则图中三角形(正四面体的截面)的面积是 ▲ .14.一般地,在数列{n a }中,如果存在非零常数T ,使得m T m a a =+对任意正整数m 均成立,那么就称{n a }为周期数列,其中T 叫做数列{n a }的周期.已知数列{n x }满足11-+-=n n n x x x ),2(*N n n ∈≥,如果,11=x ,2a x =),0,1(≠≤a a 设2009S 为其前2009项的和,则当数列{n x }的周期为3时, 2009S = ▲ .二、解答题: 本大题共6小题, 15-17每题14分,18-20每题16分,共计90分. 请在答题纸指定的区域内作答, 解答时应写出文字说明, 证明过程或演算步骤.15.如图,圆O 为单位圆,(1,0),A 1),2B C 1(2D (0,1),E1(2F -为圆O 上的定点, 点M 为圆O 上的动点.M 第一次由点A 按逆时针方向运动到某定点,所形成的角为α;M 第二次由点A 按逆时针方向运动到某定点,所形成的角为β.(Ⅰ) 当点M 第一次由点A 按逆时针方向运动到定点C , 第二次由点A 按逆时针方向运动到定点D 时,求)(c βα-os 的值;(Ⅱ)在F E D C B A 、、、、、中是否存在两个点,能使角α,β同时满足,232πβα=+且323tan 2tan-=βα? 若不存在, 说明理由; 若存在, 找出定点并证明.16. 在直三棱柱111C B A ABC -中,3A 1===AA AC B ,2B =C ,D 是BC 的中点,F 是C C 1上一点,且CF=2,E 是1AA 上一点,且AE=2.(Ⅰ) 求证: ⊥F 1B 平面ADF ;(Ⅱ)求证: BE ∥平面ADF .17.某个体运输户购买某种汽车的第n 天,花费的维护保养费和油费为(n + 300)元人民币,若买车和办牌照的费用为60万元人民币,问买车后的第几天(从买车后的第二天算起)该个体运输户每天平均用车的总费用最低?每天平均用车的总费用最低为多少元?(参考数据,1.4142= 1.732=,结果精确到个位)18. 若椭圆1C :1x 2222=+by a )0(>>b a 过点)1,2(,离心率为22,21,F F 分别为其左、右焦点.(Ⅰ)若点P 与21,F F 的距离之比为31,求直线032=+-y x 被点P 所在的曲线2C 截得的弦长;(Ⅱ) 设21,A A 分别为椭圆1C 的左、右顶点,Q 为1C 上异于21,A A 的任意一点,直线Q 1A 交1C 的右准线于点M ,直线Q A 2交1C 的右准线于点N ,求证22NF MF ⊥.19.等差数列{n a }的首项和公差都是32,记{n a }前n 项和为n S .等比数列{nb }各项均为正数,公比为q ,记{n b }的前n 项和为n T . (Ⅰ) 写出i S (5,4,3,2,1=i )构成的集合A ;(Ⅱ) 若q 为正整数,问是否存在大于1的正整数k ,使得k T ,k T 2同时为集合A 中的元素?若存在,写出所有符合条件的{n b }的通项公式;若不存在,请说明理由; (Ⅲ) 若将n S 中的整数项按从小到大的顺序构成数列{n c },求{n c }的一个通项公式.20.已知函数),()(2R b bx x x f ∈+=),()(R a x ax x g ∈+=⎩⎨⎧<≥=).()()),((),()()),(()(x g x f x f g x g x f x g f x H(Ⅰ) 当1==b a 时,求);(x H(Ⅱ) 当1=a 时,在[2,)x ∈+∞上)),(()(x g f x H =求b 的取值范围;(Ⅲ) 当0>a 时,方程,0))((=+c x g f 在),0(∞+上有且只有一个实根,求证:c b 、中至少有一个负数.附加题部分21.[选做题] 在A ,B ,C ,D 四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明,证明过程或演算步骤. A .选修4—1:几何证明选讲 设PC 为⊙O 的切线,点C 为切点,割线PBA 经过圆心O ,CM ⊥PA ,且交PA 于M , 求证:APAM =.B .选修4—2:矩阵变换.已知圆C: 122=+y x 在矩阵A=⎥⎦⎤⎢⎣⎡b a 00)0,0(>>b a 对应的伸压变换下变为椭圆1422=+y x .试求b a ,的值.C .选修4-4:坐标系与参数方程.已知曲线C 的极坐标方程为θρ2cos =,M 是曲线C 上的动点.以极点为原点,极轴为x 轴的正半轴建立平面直角坐标系,直线l 的参数方程为⎩⎨⎧-=+-=.3,4t y t x (t 为参数),求点M 到直线l 距离的最小值.D .选修4-5:不等式选讲已知.131211)(n n f +⋅⋅⋅+++= )(*N n ∈求证: .2)()3(<-n f n f[必做题] 第22题, 第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时写出文字说明,证明过程或演算步骤.22. 如图,AB 是圆O 的直径且2=AB ,C 是圆O 上不同于B A ,的任一点,且60=∠BAC ,PC 垂直于圆O 所在的平面。
宿豫中学09届高三数学二轮复习天天练14

09届高三数学天天练14一、填空题1.已知全集U ={1,2,3,4,5,6,7},集合2{|650}M x x x =∈-+Z ≤,则集合UM = .2. 已知函数()32sin 2f x x x =+,则()f x 的最小正周期是 . 3. 经过点(-2,3),且与直线250x y +-=平行的直线方程为 . 4. 若复数z 满足3,iz i i++=则||z = . 5. 程序如下:t ←1 i ←2While i ≤4t ←t ×i i ←i +1End WhilePrint t 以上程序输出的结果是 .6. 若12320082009,,,,,x x x x x 的方差为3,则12200820093(2),3(2),,3(2),3(2)x x x x ----的方差为 . 7.正方体ABCD -A 1B 1C 1D 1的棱长为2311A B CD -的外接球的体积为 .8. 以椭圆22221(0)x y a b a b+=>>的左焦点(,0)F c -为圆心,c 为半径的圆与椭圆的左准线交于不同的两点,则该椭圆的离心率的取值范围是 . 9. 设a >0,集合A ={(x ,y )|3,40,20x x y x y a ⎧⎪+-⎨⎪-+⎩≤≤≥},B ={(x ,y )|222(1)(1)x y a -+-≤}.若点P (x ,y )x ∈A 是点P (x ,y )∈B 的必要不充分条件,则a 的取值范围是 . 10.在闭区间 [-1,1]上任取两个实数,则它们的和不大于1的概率是 . 11.数列{}n a 中,16a =,且111n n n a a a n n---=++(*n ∈N ,2n ≥),则这个数列的通项公式n a = . 12.在△ABC 中,π6A ∠=,D 是BC 边上任意一点(D 与B 、C 不重合),且22||||AB AD BD DC =+⋅,则B ∠等于 .13.设函数32()2ln f x x ex mx x =-+-,记()()f x g x x=,若函数()g x 至少存在一个零点,则实数m 的取值范围是 . 14.根据下面一组等式:1234561,235,45615,7891034,111213141565,161718192021111,s s s s s s ==+==++==+++==++++==+++++=…………可得13521n s s s s -+++⋅⋅⋅+= .二、解答题:(文科班只做15题,30分,理科班两题都做,每题15分)15.某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:日 期 12月1日12月2日 12月3日12月4日12月5日温差x (°C ) 10 11 13 12 8 发芽数y (颗)2325302616该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.(1)求选取的2组数据恰好是不相邻2天数据的概率;(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y 关于x 的线性回归方程y bx a =+;(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?16.将曲线1xy =绕坐标原点按逆时针方向旋转45°,求所得曲线的方程.09届高三数学天天练14答案一、填空题1.{6,7} 2.π 3.210x y ++= 417 5.24 6.27 7.36π 8.2( 9.0<a 2 10.78 11.(1)(2)n n ++ 12.5π12 13. 21(,]e e-∞+ 14.4n 15解:(1)设抽到不相邻两组数据为事件A ,因为从5组数据中选取2组数据共有10种情况,每种情况都是等可能出现的,其中抽到相邻两组数据的情况有4种, ……………2分所以 43()1105P A =-=.………………………………4分 答:略. …………………………………………………………………5分 (2)由数据,求得12,27x y ==.…………………………………………………7分由公式,求得52b =,3a y bx =-=-. …………………………………9分 所以y 关于x 的线性回归方程为5ˆ32yx =-. ……………………………10分 (3)当x =10时,5ˆ103222y =⨯-=,|22-23|<2;……………………………12分 同样,当x =8时,5ˆ83172y =⨯-=,|17-16|<2.…………………………14分 所以,该研究所得到的线性回归方程是可靠的. ……………………………………15分16.解:由题意,得旋转变换矩阵22cos 45sin 45[]sin 45cos 4522⎡⎢-⎢⎥==⎢⎥⎢⎥⎦M , ……3分 设1xy =上的任意点(,)P x y '''在变换矩阵M 作用下为(,)P x y ,2222x x y y ⎢⎢'⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥'⎢⎥⎣⎦⎣⎦⎢⎥⎦, ∴22,22.x y y y ⎧''=⎪⎪⎨⎪''=⎪⎩…………………………………………7分 得22122y x -=.将曲线1xy =绕坐标原点按逆时针方向旋转45°,所得曲线的方程为22122y x -=.……10分。
宿豫中学09届高三数学二轮复习天天练6

αβAC D P B 09届高三数学天天练6解答题:(文科班只做前四题,理科班全做,每题15分)1.设向量(cos ,sin )m θθ=,(22sin ,22cos )n θθ=+,),23(ππθ--∈,若1m n •=,求:(1))4sin(πθ+的值; (2))127cos(πθ+的值.2.某公司欲建连成片的网球场数座,用128万元购买土地10000平方米,该球场每座的建筑面积为1000平方米,球场的总建筑面积的每平方米的平均建筑费用与球场数有关,当该球场建n 个时,每平方米的平均建筑费用用f (n )表示,且f (n )=f (m )(1+20m n -)(其中n >m ,n ∈N),又知建五座球场时,每平方米的平均建筑费用为400元,为了使该球场每平方米的综合费用最省(综合费用是建筑费用与购地费用之和),公司应建几个球场?3. 如图已知平面,αβ,且,,AB PC αβα=⊥,,PD C D β⊥是垂足.(Ⅰ)求证:AB ⊥平面PCD ;(Ⅱ)若1,2PC PD CD ===,试判断平面α与平面β的位置关系,并证明你的结论.4.已知定义在R 上的函数)3()(2-=ax x x f ,其中a 为常数.(1)若x =1是函数)(x f 的一个极值点,求a 的值;(2)若函数)(x f 在区间(-1,0)上是增函数,求a 的取值范围;(3)若函数]2,0[),()()(∈'+=x x f x f x g ,在x =0处取得最大值,求正数..a 的取值范围.5.已知二阶矩阵M 有特征值8λ=及对应的一个特征向量111e ⎡⎤=⎢⎥⎣⎦,并且矩阵M 对应的变换将点(1,2)-变换成(2,4)-.(Ⅰ)求矩阵M ;(Ⅱ)求矩阵M 的另一个特征值,及对应的一个特征向量2e 的坐标之间的关系;(Ⅲ)求直线:10l x y -+=在矩阵M 的作用下的直线l '的方程.09届高三数学天天练6答案解答题:(文科班只做前四题,理科班全做,每题15分)1.解:(1)依题意,cos (22sin )sin 2cos )m n θθθθ•=+2(sin cos )θθ=+4sin()4πθ=+ 又1m n •=41)4sin(=+πθ (2)由于),23(ππθ--∈,则)43,45(4πππθ--∈+ 结合41)4sin(=+πθ,可得415)4cos(-=+πθ 则7cos()12θπ+ 11cos[()]43θππ=++15113(4242=-⨯-⨯3158=- 2.解:设建成x 个球场,则每平方米的购地费用为x 1000101284⨯=x1280 由题意知f (5)=400, f (x )=f (5)(1+205-x )=400(1+205-x ) 从而每平方米的综合费用为y =f (x )+x1280=20(x +x 64)+300≥64+300=620(元),当且仅当x =8时等号成立故当建成8座球场时,每平方米的综合费用最省.3、解:(Ⅰ)因为,PC AB αα⊥⊂,所以PC AB ⊥.同理PD AB ⊥.又PC PD P =,故AB ⊥平面PCD . 5分(Ⅱ)设AB 与平面PCD 的交点为H ,连结CH 、DH .因为AB ⊥平面PCD , 所以,AB CH AB DH ⊥⊥,所以CHD ∠是二面角C AB D --的平面角.又1,2PC PD CD ===,所以2222CD PC PD =+=,即90CPD ∠=︒. 在平面四边形PCHD 中,90PCH PDH CPD ∠=∠=∠=︒,所以90CHD ∠=︒.故平面α⊥平面β. 14分4. 解:(I )).2(363)(,3)(223-=-='-=ax x x ax x f x ax x f )(1x f x 是= 的一个极值点,2,0)1(=∴='∴a f ;(II )①当a =0时,23)(x x f -=在区间(-1,0)上是增函数,0=∴a 符合题意;②当ax x x f a x ax x f a 2,0:0)(),2(3)(,021==='-='≠得令时; 当a >0时,对任意0,0)(),0,1(>∴>'-∈a x f x 符合题意;当a <0时,当02,12,0)()0,2(<≤-∴-≤∴>'∈a ax f a x 时符合题意; 综上所述,.2-≥a(III )].2,0[,6)33()(,023∈--+=>x x x a ax x g a],2)1(2[36)33(23)(22--+=--+='x a ax x a ax x g令.044(*),02)1(2,0)(22>+=∆=--+='a x a ax x g 显然有即 设方程(*)的两个根为(*),,21由x x 式得0221<-=ax x ,不妨设210x x <<. 当202<<x 时,)(2x g 为极小值,所以)(x g 在[0,2]上的最大值只能为)0(g 或)2(g ; 当22≥x 时,由于)(x g 在[0,2]上是单调递减函数,所以最大值为)0(g ,所以在[0,2] 上的最大值只能为)0(g 或)2(g ,又已知)(x g 在x =0处取得最大值,所以),2()0(g g ≥即].56,0(,0,56,24200∈>≤-≥a a a a 所以又因为解得 5. (Ⅰ)设a b M c d ⎡⎤=⎢⎥⎣⎦,则1188118a b c d ⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦,故88a b c d +=⎧⎨+=⎩ 1224a b c d --⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,故2224a b c d -+=-⎧⎨-+=⎩ 联立以上方程组解得6,2,4,4a b c d ====,故6244M ⎡⎤=⎢⎥⎣⎦ (Ⅱ)由(Ⅰ)知,矩阵M 的特征多项式为2()(6)(4)81016f λ=λ-λ--=λ-λ+, 故其另一个特征值为2λ=.设矩阵M 的另一个特征向量是2x e y ⎡⎤=⎢⎥⎣⎦,则262244x y x M e x y y +⎡⎤⎡⎤==⎢⎥⎢⎥+⎣⎦⎣⎦,解得20x y +=. (Ⅲ)设点(,)x y 是直线l 上的任一点,其在矩阵M 的变换下对应的点的坐标为(,)x y '',则6444x x y y '⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦,即1113,4848x x y y x y ''''=-=-+,代入直线l 的方程后并化简得20x y ''-+=,即20x y -+=。
宿豫中学09届高三数学二轮复习天天练23
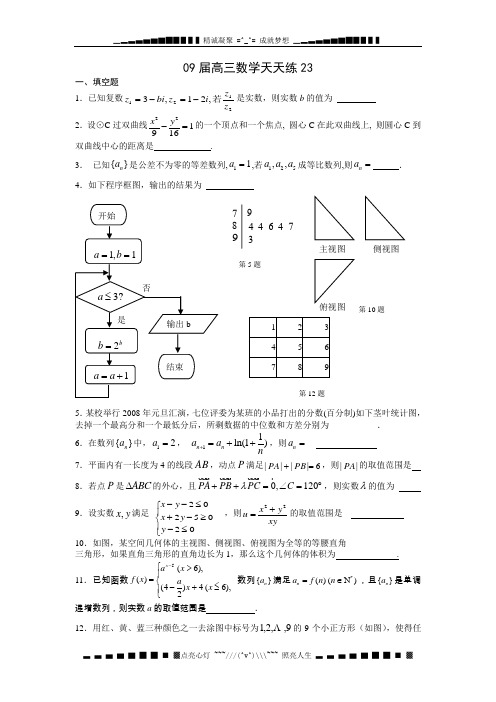
09届高三数学天天练23一、填空题1.已知复数2121,21,3z z i z bi z 若-=-=是实数,则实数b 的值为2.设⊙C 过双曲线221916x y -=的一个顶点和一个焦点, 圆心C 在此双曲线上, 则圆心C 到双曲线中心的距离是 . 3. 已知{}n a 是公差不为零的等差数列,11a =,若125,,a a a 成等比数列,则n a = . 4.如下程序框图,输出的结果为5.某校举行2008年元旦汇演,七位评委为某班的小品打出的分数(百分制)如下茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的中位数和方差分别为 __________. 6.在数列{}n a 中,12a =, 11ln(1)n n a a n+=++,则n a =7.平面内有一长度为4的线段AB ,动点P 满足6||||=+PB PA ,则||PA 的取值范围是 8.若点P 是ABC ∆的外心,且0,120PA PB PC C λ++=∠=︒,则实数λ的值为9.设实数,x y 满足 2025020x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩,则22x y u xy +=的取值范围是 10.如图,某空间几何体的主视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为 .11.已知函数5(6),()(4)4(6),2x a x f x ax x -⎧>⎪=⎨-+≤⎪⎩ 数列{}n a 满足*()(N )n a f n n =∈,且{}n a 是单调递增数列,则实数a 的取值范围是 .12.用红、黄、蓝三种颜色之一去涂图中标号为9,,2,1 的9个小正方形(如图),使得任7 8 994 4 6 4 7 3第12题意相邻(有公共边的)小正方形所涂颜色都不相同,且“3、5、7”号数字涂相同的颜色,则符合条件的所有涂法共有 ______ 种.13.如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横纵坐标分别对应数列{}*()n a n N ∈的前12项,如下表所示:按如此规律下去,则200920102011a a a ++= 14.某同学在研究函数()1xf x x=+ (x ∈R ) 时,分别给出下 面几个结论:①等()()0f x f x -+=在x R ∈时恒成立;②函数 f (x) 的值域为 (-1,1); ③若x 1≠x 2,则一定有f (x 1)≠f (x 2);④函数()()g x f x x =-在R 上有三个零点. 其中正确结论的序号有 . 二、解答题:(文科班只做15题,30分,理科班两题都做,每题15分)15. 2008年中国北京奥运会吉祥物由5个“中国福娃”组成,分别叫贝贝、晶晶、欢欢、迎迎、妮妮.现有8个相同的盒子,每个盒子中放一只福娃,每种福娃的数量如下表:从中随机地选取5只.(I )求选取的5只恰好组成完整“奥运吉祥物”的概率;(II )若完整地选取奥运会吉祥物记10分;若选出的5只中仅差一种记8分;差两种记6分;以此类推. 设ξ表示所得的分数,求ξ的分布列及数学期望.16.已知矩阵11A ⎡=⎢-⎣ 24⎤⎥⎦,向量74⎡⎤=⎢⎥⎣⎦α.(1)求矩阵A 的特征值1λ、2λ和特征向量1α、2α; (2)求5A α的值.09届高三数学天天练23答案第13题一、填空题:1. 6 2.1633.21n - 4.16 5.86,1.6 6.2ln n + 7.]5,1[ 8.1- 9.10[2,]310.16 11.(4,8)12.108 13.1005 14.①②③15.解:(Ⅰ)选取的5只恰好组成完整“奥运吉祥物”的概率.283566581312==⋅=C C C P ………………5分 (Ⅱ)10,8,6,4ξ的取值为…………………6分;2895618)()6(;5631)()()8(;283)10(5833233312232213582322332312132223581312==⋅+⋅+⋅===+⋅+⋅+⋅===⋅==C C C C C C C C P C C C C C C C C C P C C C P ξξξ .561)4(583322=⋅==C C C P ξ …………11分 ξ的分布列为:5.756285628=+++=ξE …………15分 16、解:(1)矩阵A 的特征多项式为1()1f λλ-= 24λ--256=-+λλ,令()0f =λ,得122,3λλ==,当12=λ时,得121⎡⎤=⎢⎥⎣⎦α,当23=λ时,得211⎡⎤=⎢⎥⎣⎦α. …………………7分(2)由12m n =+ααα得274m n m n +=⎧⎨+=⎩,得3,1m n ==.∴5A α5551212(3)3()A A A =+=+αααα55551122214353()32311339⎡⎤⎡⎤⎡⎤=+=⨯+=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦λαλα.……………………15分。
宿豫中学09届高三数学二轮复习天天练20
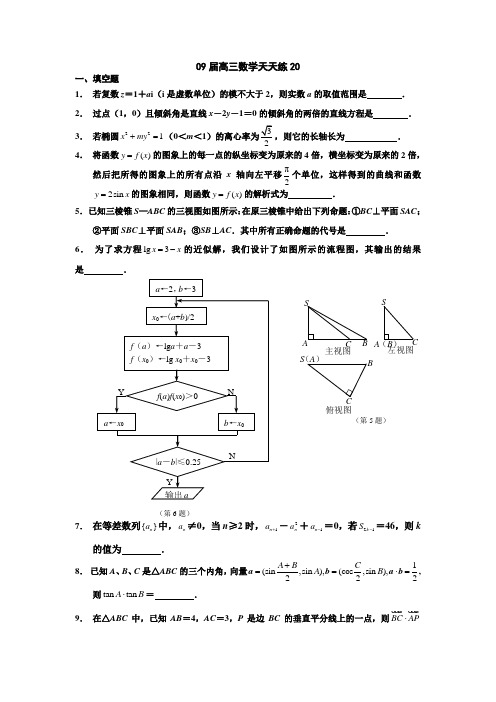
09届高三数学天天练20一、填空题1. 若复数z =1+a i (i 是虚数单位)的模不大于2,则实数a 的取值范围是 . 2. 过点(1,0)且倾斜角是直线x -2y -1=0的倾斜角的两倍的直线方程是 . 3. 若椭圆221x my +=(0<m <1,则它的长轴长为 . 4. 将函数()y f x =的图象上的每一点的纵坐标变为原来的4倍,横坐标变为原来的2倍,然后把所得的图象上的所有点沿x 轴向左平移π2个单位,这样得到的曲线和函数2sin y x =的图象相同,则函数()y f x =的解析式为 .5. 已知三棱锥S —ABC 的三视图如图所示:在原三棱锥中给出下列命题:①BC ⊥平面SAC ;②平面SBC ⊥平面SAB ;③SB ⊥AC .其中所有正确命题的代号是 . 6. 为了求方程lg 3x x =-的近似解,我们设计了如图所示的流程图,其输出的结果是 .7. 在等差数列{}n a 中,n a ≠0,当n ≥2时,1n a +-2n a +1n a -=0,若21k S -=46,则k的值为 .8. 已知A 、B 、C 是△ABC 的三个内角,向量1(sin,sin ),(cos ,sin ),222A B C A B +==⋅=a b a b ,则tan tan A B ⋅= .9. 在△ABC 中,已知AB =4,AC =3,P 是边BC 的垂直平分线上的一点,则BC AP⋅SSA (B ) CC S (A )B 主视图左视图 俯视图(第5题)(第6题)= .10.若圆锥的高是底面半径和母线的等比中项,则称此圆锥为“黄金圆锥”.已知某黄金圆锥的侧面积为S ,则这个圆锥的高为 .11.已知函数f (x )=cos ωx (ω>0)在区间π[0]4, 上是单调函数,且f (3π8)=0,则ω= .12.已知数列{} {}n n a b ,的前n 项和分别为n A ,n B ,且A 100=8,B 100=251.记n n n n n n n C a B b A a b =⋅+⋅-⋅ (n ∈N*),则数列{C n }的前100项的和为 .13.设()f x 是定义在R 上的奇函数,且当0x ≥时,2()f x x =,若对任意的[]2x t t ∈+,,不等式()2()f x t f x +≥恒成立,则实数t 的取值范围是 .14.已知集合A ={(x ,y )│| x |+| y |=4,x ,y ∈R}, B ={(x ,y )│x 2+y 2=r 2,x ,y∈R},若A ∩B 中的元素所对应的点恰好是一个正八边形的八个顶点,则正数r 的值为 .二、解答题:(文科班只做15题,30分,理科班两题都做,每题15分)15. 已知集合A ={ x | -1≤x ≤0},集合B ={210x x ax b +⋅-<,0≤a ≤2,1≤b ≤3}.(Ⅰ)若,a b ∈N ,求A B ≠∅的概率;(Ⅱ)若,a b ∈R ,求AB =∅的概率.16.设点P 在曲线sin 2ρθ=上,点Q 在曲线2cos ρθ=-上,求||PQ 的最小值.09届高三数学天天练20答案1.[2.4x -3y -4=0 3.4 4.1πsin 222y x =-()或1cos22y x =- 5.①6.2.5 7.128.139.-721011.43或4 12.2008 13.+∞)14. 8sin π8cos 815.解:(Ⅰ) 因为,a b ∈N ,(a ,b )可取(0,1),(0,2),(0,3),(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)共9组.………………………………2分令函数()21,[1,0]x f x ax b x =+⋅-∈-,则()ln22x f x a b '=+⋅.因为[0,2],[1,3],()0a b f x '∈∈>所以,即()f x 在[1,0]-上是单调增函数. ()f x 在[1,0]-上的最小值为12ba -+-.…………………………6分 要使AB ≠∅,只须102ba -+-<,即220a b -+>. 所以(a ,b )只能取(0,1),(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)7组.所以AB ≠∅的概率为79. ……………………………………9分 (Ⅱ)因为[0,2],[1,3]a b ∈∈,所以(a ,b )对应的区域边长为2的正方形(如图),面积为4.………………11分 由(Ⅰ)可知,要使AB =∅,只须min ()102202bf x a a b =-+-⇒-+≥≤, 所以满足AB =∅的(,)a b 对应的区域是如图阴影部分.所以S 阴影1111224=⨯⨯=.………………………………13分所以AB =∅的概率为114416P ==. …………………14分16.解:以极点为原点,极轴所在直线为x 轴建立直角坐标系.将曲线sin ρθ=2cos ρθ=-分别化为直角坐标方程,得 直线方程2y =,圆方程22(1)1x y ++=.………………6分所以圆心(-1,0)到直线距离为2,||PQ 的最小值为2-1=1.…………10分。
宿豫中学09届高三数学二轮复习天天练5
09届高三数学天天练5一、填空题 1.若数据123,,,,n x x x x 的平均数x =5,方差22σ=,则数据12331,31,31,,31n x x x x ++++的平均数为 ,方差为 。
2.函数xxx f +-=11)(的定义域是 . 3.用数学归纳法证明等式:aa a a a n n --=++++++111212(1≠a ,*N n ∈),验证1=n时,等式左边= .4.从4名男生和3名女生中选出4人参加迎新座谈会,若这4人中必须既有男生又有女生,不同的选法共有5.等差数列}{n a 中,公差1=d ,143=+a a ,则2042a a a +++ = . 6.函数())(cos 22sin 32R x x x x f ∈-=的最小正周期为 . 7.在二项式10)1(+x 的展开式中任取一项,则该项的系数为奇数的概率是 . 8.“41=a ”是“对任意的正数,x 均有1≥+x ax ”的 条件9.如图,ABC ∆中, 90=∠C ,30=∠A ,1=BC 。
在三角形内挖去半圆(圆心O 在边AC 上,半圆与BC 、AB 相切于点C 、M ,与AC 交于N ),则图 中阴影部分绕直线AC 旋转一周所得旋转体的体积为 . 10.函数624301+-=+x x y , ]1,0[∈x 的值域是 .11.对于函数|1|)(+-=x mx x f (),2[+∞-∈x ),若存在闭区间],[b a ),2[+∞-)(b a <, 使得对任意],[b a x ∈,恒有)(x f =c (c 为实常数),则实数m = .12.研究问题:“已知关于x 的不等式02>+-c bx ax 的解集为)2,1(,解关于x 的不等式 02>+-a bx cx ”,有如下解决方案:解:由02>+-c bx ax ⇒0)1()1(2>+-xc x b a ,令xy 1=,则)1,21(∈y ,所以不等式02>+-a bx cx 的解集为)1,21(.参考上述解法,已知关于x 的不等式0<++++cx bx a x k 的解集为)3,2()1,2( --, 则关于x 的不等式0111<++++cx bx ax kx 的解集为 . ≠⊂13.已知函数)(x f 满足,002)2()(≥<⎩⎨⎧+=x x x f x f x,则)5.7(-f = . 14.以下有四种说法:(1)若q p ∨为真,q p ∧为假,则p 与q 必为一真一假; (2)若数列}{n a 的前n 项和为*2,1N n n n S n ∈++= ,则*,2N n n a n ∈=; (3)若0)(0'=x f ,则)(x f 在0x x =处取得极值;(4)由变量x 和y 的数据得到其回归直线方程:l y bx a =+,则l 一定经过点(,)P x y .以上四种说法,其中正确说法的序号为 .二、解答题:(文科班只做15题,30分,理科班两题都做,每题15分)15.ABC ∆中,三个内角A 、B 、C 所对的边分别为a 、b 、c ,若60=B , c a )13(-=. (1)求角A 的大小;(2)已知当]2,6[ππ∈x 时,函数x a x x f sin 2cos )(+=的最大值为3,求ABC ∆的面积.16. 求曲线x x x y 223++-=与x 轴所围成的图形的面积.09届高三数学天天练5答案一、填空题1. 16,18 2.]1,1(- 3.21a a ++ 4.34种 5.80 6.π 7.114 8.充分非必要条件 9.π2735 10.]6,5[ 11.1± 12.)21,31()21,1( -- 13.2 14.(1)(4) 二、解答题:(文科班只做15题,30分,理科班两题都做,每题15分)15.[解](1)因为60=B ,所以120=+C A , A C -=120 ………………1分 因为c a )13(-=,由正弦定理可得:C A sin )13(sin -= ………………3分)s i n 32c o s c o s 32)(s i n 13()32s i n ()13(s i nA A A A πππ--=--= )sin 21cos 23)(13(A A +-=,整理可得:1tan =A ………………5分 所以,45=A (或4π) ………………6分(2)x a x x f sin sin 21)(2+-=,令x t sin =,因为]2,6[ππ∈x ,所以]1,21[∈t 7分18)4(212)()(222++--=++-==a a t at t t g x f ,]1,21[∈t ………………9分若214<a ,即2<a ,2121)21(max +==a g f ,32121=+a ,则5=a (舍去)…… 10分 若2114≤≤a ,即42≤≤a ,18)4(2max +==a a g f ,3182=+a ,得4=a …… 11分 若14>a,即4>a , a g f +-==21)1(max 1-=a ,31=-a ,得4=a (舍去)12分 故4=a ,326+=∆ABC S ………………14分 16.解 函数x x x y 223++-=的零点:11-=x ,02=x ,23=x .…………………4分 又易判断出在)0 , 1(-内,图形在x 轴下方,在)2 , 0(内,图形在x 轴上方,所以所求面积为dx x x x A ⎰-++--=0 1 23)2(dx x x x ⎰++-+2 0 23)2(1237=………10分。
宿豫中学届高三数学二轮复习天天练
关于 x 的方程 f ( x) kx k 1 ( k R 且 k 1 )有 4 个不同的根,则 k 的取值范围是
9.在某项测量中, 测量结果
服从正态分布
N (1,
2
)(
0) .若 在 (0,1) 内取值的概率
为 0.4,则 在 (0,2) 内取值的概率为
.
10.将 5 本不同的书全发给 4 名同学,每名同学至少有一本书的分配方案有
设 CP CC1, P( x, y, z)
则 (x, y 1, z) (0,1, 3)
得 P(0,1 , 3 ) BP ( 3,1 , 3 ) ……………………9 分
4
设 n3 平面 DA1C1
n3
则
n3
A1C1 设 n3
DA1
( x3 , y3, z3 )
2 y3 0
得到
3x 3 3z3
不妨取 n3 0
“平行线面组 ”,在一个
长方体中,由两个顶点确定的直线与含有四个顶点的平面构成的
“平行 线面组 ”的个数
是
14.给出下列四个命题:①命题 “ x R, x2 0 ”的否定是 “ x R, x2 0 ”;②线性相关
系数 r 的绝对值越接近于 1,表明两个随机变量线性相关性越强;③若 a,b [ 0,1] ,则
x 1 t cos
3 x1 t
16.( 1)直线的参数方程为
6 ,即
2.
5′
y 1 t sin
y 1 1t
6
2
x 1 3t
( 2)把直线
2 代入 x 2 y 2 4 ,
1
y1 t
2
得 (1 3 t)2 (1 1 t)2 4, t 2 ( 3 1)t 2 0 , t1t2
宿豫中学09届高三数学二轮温习天天练7
ICME -7 图甲 O A 1A 2A 3A 4A 5A 6A 7A 8 图09届高三数学天天练7一、填空题1. 设集合102M x x ⎧⎫=-<⎨⎬⎩⎭,{}210N x x =+>,则N M ⋂= .2. 已知复数z 知足z 2+1=0,则(z 6+i )(z 6-i )= .3. 在整体中抽取了一个样本,为了便于统计,将样本中的每一个数据乘以100后进行分析,得出新样本平均数为3,则估量整体的平均数为 .4. 幂函数()y f x =的图象通过点1(2,)8--,则知足()f x =27的x 的值是 .5. 下列四个命题:①2n n n ∀∈R ,≥;②2n n n ∀∈<R ,;③2n m m n ∀∈∃∈<R R ,,;④n m m n m ∃∈∀∈⋅=R R ,,.其中真命题的序号是 .6. 如图甲是第七届国际数学教育大会(简称ICME -7)的会徽图案,会徽的主体图案是由如图乙的连续串直角三角形演化而成的,其中11223781OA A A A A A A =====,若是把图乙中的直角三角形继续作下去,记12,,,,n OA OA OA 的长度组成数列{}n a ,则此数列的通项公式为n a= .7. 以下伪代码: Read xIf x ≤ 0 Then ()f x ← 4xElse ()f x ←2x End If Print ()f x依照以上算法,可求得(3)(2)f f -+的值为 .8. 在半径为1的圆周上按顺序均匀散布着A 1,A 2,A 3,A 4,A 5,A 6六个点.则122323343445455656616112A A A A A A A A A A A A A A A A A A A A A A A A ⋅+⋅+⋅+⋅+⋅+⋅= .9. 若()sin() 1 (0,||<π)f x A x ωϕωϕ=++>对任意实数t ,都有()()ππ33f t f t +=-+.记()cos()1g x A x ωϕ=+-,则π()3g = .10.已知函数f (x )=log a | x |在(0,+∞)上单调递增,则f (-2) f (a +1).(填写“<”,“=”,“>”之一) 11.过抛物线22(0)y px p =>的核心F 的直线l 交抛物线于A 、B 两点,交准线于点C .若2CB BF =,则直线AB 的斜率为 .12.有一根长为6cm ,底面半径为0.5cm 的圆柱型铁管,用一段铁丝在铁管上缠绕4圈,并使铁丝的两个端点落在圆柱的同一母线的两头,则铁丝的长度最少为 cm . 13.若不等式组0,22,0,x y x y y x y a-⎧⎪+⎪⎨⎪⎪+⎩≥≤≥≤ 表示的平面区域是一个三角形及其内部,则a 的取值范围是 .14.已知△ABC 三边a ,b ,c 的长都是整数,且a b c ≤≤,若是b =m (m ∈N*),则如此的三角形共有 个(用m 表示). 二、解答题:(文科班只做15题,30分,理科班两题都做,每题15分)15.已知椭圆2221(01)y x b b+=<<的左核心为F ,左、右极点别离为A 、C ,上极点为B .过F 、B 、C 作⊙P ,其中圆心P 的坐标为(m ,n ).(Ⅰ)当m +n >0时,求椭圆离心率的范围; (Ⅱ)直线AB 与⊙P 可否相切?证明你的结论.1六、过点P (-3,0)且倾斜角为30°的直线和曲线1,()1x t tt y t t ⎧=+⎪⎪⎨⎪=-⎪⎩为参数相交于A 、B 两点.求线段AB 的长.09届高三数学天天练7答案一、填空题:1.{}1122x x -<< 2.2 3. 4.13 5.④ 67.-8 8.3 9.-1 10.< 11.1213.4(0,1][,)3+∞ 14.(1)2m m + 1五、解:(Ⅰ)设F 、B 、C 的坐标别离为(-c ,0),(0,b ),(1,0),则FC 、BC 的中垂线别离为12cx -=,11()22b y x b -=-.联立方程组,解出21,2.2c x b c y b -⎧=⎪⎪⎨-⎪=⎪⎩21022c b cm n b--+=+>,即20b bc b c -+->,即(1+b )(b -c )>0, ∴ b >c .从而22b c >即有222a c >,∴212e <.又0e >,∴0e <<.(Ⅱ)直线AB 与⊙P 不能相切.由AB k b =,22102PBb cb b kc --=--=2(1)b c b c +-.若是直线AB 与⊙P 相切,则b ·2(1)b c b c +-=-1. 解出c =0或2,与0<c <1矛盾,因此直线AB 与⊙P 不能相切.评讲建议:此题要紧考查直线与直线、直线与圆和椭圆的相关知识,要求学生明白得三角形外接圆圆心是三边中垂线的交点,从而斗胆求出交点坐标,构造关于椭圆中a ,b ,c 的齐次等式得离心率的范围.第二小题亦能够用平几的知识:圆的切割线定理,假设直线AB 与⊙P 相切,则有AB 2=AF ×AC ,易由椭圆中a ,b ,c 的关系推出矛盾.16解:直线的参数方程为3,()12x s y s ⎧=-+⎪⎪⎨⎪=⎪⎩为参数,………………………………3分 曲线1,()1x t tt y t t ⎧=+⎪⎪⎨⎪=-⎪⎩为参数能够化为224x y -=.………………………5分将直线的参数方程代入上式,得2100s -+=.设A 、B 对应的参数别离为12s s ,,∴121210s s s s +==.…………………………8分AB 12s s =-==.………………………………………10分 说明:把握直线,圆,圆锥曲线的参数方程及简单的应用.。
江苏省宿迁市宿豫中学届高考数学(二轮复习)专题检测:再谈“三个二次”的转化策略.docx
4 再谈“三个二次”的转化策略1.若A ={x |x 2+(p +2)x +1=0,x ∈R },B ={x |x >0},且A ∩B =∅,则实数p 的取值范围是________.答案 (-4,+∞)解析 当A =∅时,Δ=(p +2)2-4<0,∴-4<p <0.当A ≠∅时,方程x 2+(p +2)x +1=0有一个或两个非正根,∴⎩⎪⎨⎪⎧Δ≥0,x 1+x 2=-(p +2)≤0,∴p ≥0. 综上所述,p >-4.2.已知函数f (x )=x 2-2x +3在闭区间[0,m ]上的最大值为3,最小值为2,则m 的取值范围为________.答案 [1,2]解析 ∵f (x )=(x -1)2+2,其对称轴为x =1,当x =1时,f (x )min =2,故m ≥1,又∵f (0)=3,f (2)=3,∴m ≤2.综上可知1≤m ≤2.3.方程x 2-32x -m =0在x ∈[-1,1]上有实根,则m 的取值范围是________. 答案 [-916,52] 解析 m =x 2-32x =⎝ ⎛⎭⎪⎫x -342-916,x ∈[-1,1].当x =-1时,m 取最大值为52, 当x =34时,m 取最小值为-916,∴-916≤m ≤52. 4.已知函数f (x )=⎩⎪⎨⎪⎧ x +1,x ≤0,x 2-2x +1,x >0,若关于x 的方程f 2(x )-af (x )=0恰有5个不同的实数解,则a 的取值范围是________.答案 (0,1)解析设t =f (x ),则方程为t 2-at =0,解得t =0或t =a ,即f (x )=0或f (x )=a .如图,作出函数f (x )的图象,由函数图象,可知f (x )=0的解有两个,故要使方程f 2(x )-af (x )=0恰有5个不同的解,则方程f (x )=a 的解必有三个,此时0<a <1.所以a 的取值范围是(0,1).5.(2013·重庆改编)若a <b <c ,则函数f (x )=(x -a )(x -b )+(x -b )(x -c )+(x -c )(x -a )的两个零点分别位于下列哪个区间________.(填序号)①(a ,b )和(b ,c )内②(-∞,a )和(a ,b )内③(b ,c )和(c ,+∞)内④(-∞,a )和(c ,+∞)内答案 ①解析 由于a <b <c ,所以f (a )=0+(a -b )(a -c )+0>0,f (b )=(b -c )(b -a )<0,f (c )=(c -a )(c -b )>0.因此有f (a )·f (b )<0,f (b )·f (c )<0,又因f (x )是关于x 的二次函数,函数的图象是连续不断的曲线,因此函数f (x )的两零点分别位于区间(a ,b )和(b ,c )内.6.已知函数f (x )=x 3+ax 2+bx +c 有两个极值点x 1,x 2.若f (x 1)=x 1<x 2,则关于x 的方程3(f (x ))2+2af (x )+b =0的不同实根的个数为________.答案 3解析 因为函数f (x )=x 3+ax 2+bx +c 有两个极值点x 1,x 2,可知关于导函数的方程f ′(x )=3x 2+2ax +b =0有两个不等的实根x 1,x 2.则方程3(f (x ))2+2af (x )+b =0的根的个数就是方程f (x )=x 1和f (x )=x 2的不等实根的个数之和,再结合图象可看出函数y =f (x )的图象与直线y =x 1和直线y =x 2共有3个不同的交点,故所求方程有3个不同的实根.7.若关于x 的不等式(2x -1)2<ax 2的解集中整数恰好有3个,则实数a 的取值范围是__________.答案 ⎝ ⎛⎦⎥⎤259,4916 解析 因为不等式等价于(-a +4)x 2-4x +1<0,其中(-a +4)x 2-4x +1=0中的Δ=4a >0,且有4-a >0,故0<a <4,不等式的解集为12+a <x <12-a ,14<12+a <12,则一定有{1,2,3}为所求的整数解集.所以3<12-a≤4,解得a 的范围为⎝ ⎛⎦⎥⎤259,4916. 8.已知函数f (x )=x 2-2ax +2,当x ∈[-1,+∞)时,f (x )≥a 恒成立,则a 的取值范围________.答案 [-3,1]解析 因为f (x )=(x -a )2+2-a 2,所以此二次函数图象的对称轴为x =a .①当a ∈(-∞,-1)时,f (x )在[-1,+∞)上单调递增,所以f (x )min =f (-1)=2a +3.要使f (x )≥a 恒成立,只需f (x )min ≥a ,即2a +3≥a ,解得a ≥-3,即-3≤a <-1.②当a ∈[-1,+∞)时,f (x )min =f (a )=2-a 2.要使f (x )≥a 恒成立,只需f (x )min ≥a ,即2-a 2≥a ,解得-2≤a ≤1,即-1≤a ≤1.综上,实数a 的取值范围为[-3,1].9.已知函数f (x )=2ax 2+2x -3.如果函数y =f (x )在区间[-1,1]上有零点,则实数a 的取值范围为______________.答案 ⎣⎢⎡⎭⎪⎫12,+∞ 解析 若a =0,则f (x )=2x -3,f (x )=0⇒x =32∉[-1,1],不合题意,故a ≠0. 下面就a ≠0分两种情况讨论:①当f (-1)·f (1)≤0时,f (x )在[-1,1]上有一个零点,即(2a -5)(2a -1)≤0,解得12≤a ≤52. ②当f (-1)·f (1)>0时,f (x )在[-1,1]上有零点的条件是⎩⎪⎨⎪⎧ f ⎝ ⎛⎭⎪⎫-12a f (1)≤0,-1<-12a <1,f (-1)·f (1)>0,解得a >52. 综上,实数a 的取值范围为⎣⎢⎡⎭⎪⎫12,+∞. 10.已知定义在R 上的单调递增奇函数f (x ),若当0≤θ≤π2时,f (cos 2θ+2m sin θ)+f (-2m -2)<0恒成立,则实数m 的取值范围是________.答案 (-12,+∞) 解析 方法一 f (cos 2θ+2m sin θ)+f (-2m -2)<0⇒f (cos 2θ+2m sin θ)<f (2m +2)⇒cos 2θ+2m sin θ<2m +2⇒2m (1-sin θ)>-1-sin 2θ.当θ=π2时,2m ·0>-2,此时m ∈R ; 当0≤θ<π2时,m >-1+sin 2θ2(1-sin θ),令t =1-sin θ, 则t ∈(0,1],此时m >-12×1+(1-t )2t =-12(t +2t-2). 设φ(t )=-12(t +2t-2), 而φ(t )在t ∈(0,1]上的值域是(-∞,-12], 故m >-12. 方法二 同方法一,求得2m (1-sin θ)>-1-sin 2θ,设sin θ=t ,则t 2-2mt +2m +1>0对于t ∈[0,1]恒成立.设g (t )=t 2-2mt +2m +1,其图象的对称轴方程为t =m .①当m <0时,g (t )在[0,1]上单调递增,从而g (0)=2m +1>0,即m >-12, 又m <0,所以-12<m <0. ②当0≤m ≤1时,g (t )在[0,m ]上单调递减,在[m,1]上单调递增,从而g (m )=m 2-2m 2+2m +1>0,即m 2-2m -1<0,所以1-2<m <1+ 2.又m ∈[0,1],所以0≤m ≤1.③当m >1时,g (t )在[0,1]上单调递减,从而g (1)=1-2m +2m +1=2>0恒成立,所以m >1.综合①②③,可知m >-12. 11.已知函数f (x )=2a sin 2x -2 3a sin x cos x +a +b (a ≠0)的定义域是⎣⎢⎡⎦⎥⎤0,π2,值域是[-5,1],求常数a ,b 的值.解 f (x )=2a ·12(1-cos 2x )- 3a sin 2x +a +b =-2a ⎝ ⎛⎭⎪⎫12cos 2x +32sin 2x +2a +b =-2a sin ⎝⎛⎭⎪⎫2x +π6+2a +b , 又∵0≤x ≤π2,∴π6≤2x +π6≤76π, ∴-12≤sin ⎝⎛⎭⎪⎫2x +π6≤1. 因此,由f (x )的值域为[-5,1]可得⎩⎪⎨⎪⎧ a >0,-2a ×(-12)+2a +b =1,-2a ×1+2a +b =-5, 或⎩⎪⎨⎪⎧ a <0,-2a ×1+2a +b =1,-2a ×(-12)+2a +b =-5, 解得⎩⎪⎨⎪⎧ a =2,b =-5或⎩⎪⎨⎪⎧ a =-2,b =1. 12.已知函数f (x )=ax 2+ax 和g (x )=x -a ,其中a ∈R ,且a ≠0.若函数f (x )与g (x )的图象相交于不同的两点A 、B ,O 为坐标原点,试求△OAB 的面积S 的最大值.解 依题意,f (x )=g (x ),即ax 2+ax =x -a ,整理得ax 2+(a -1)x +a =0,①∵a ≠0,函数f (x )与g (x )的图象相交于不同的两点A 、B , ∴Δ>0,即Δ=(a -1)2-4a 2=-3a 2-2a +1 =(3a -1)(-a -1)>0,∴-1<a <13且a ≠0.设A (x 1,y 1),B (x 2,y 2),且x 1<x 2,由①得x 1x 2=1>0,x 1+x 2=-a -1a .设点O 到直线g (x )=x -a 的距离为d ,则d =|-a |2,∴S =121+12|x 1-x 2|·|-a |2=12-3a 2-2a +1=12 -3⎝ ⎛⎭⎪⎫a +132+43. ∵-1<a <13且a ≠0,∴当a =-13时,S 取得最大值33.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
09届高三数学天天练4
一、填空题:
1、已知向量))(sin 2,cos 2(),1,1(),1,1(R ∈=-==ααα,实数,m n 满足
,m a n b c +=则22(3)m n -+的最大值为 .
2、对于滿足40≤≤a 的实数a ,使342
-+>+a x ax x 恒成立的x 取值范围_ . 3、扇形OAB 半径为2,圆心角∠AOB =60°,点D 是弧AB 的中点,点C 在线段OA 上,且3=OC .则⋅的值为 4、已知函数x x f 2sin )(=,)62cos()(π
+
=x x g ,直线x =t (t ∈⎥⎦
⎤
⎢⎣⎡2,0π)与函数f (x )、g (x )的图像分别交于M 、N 两点,则|MN |的最大值是 .
5、对于任意实数x ,符号[x ]表示x 的整数部分,即“[x ]是不超过x 的最大整数” .在实数轴R (箭头向右)上[x ]是在点x 左侧的第一个整数点,当x 是整数时[x ]就是x .这个函数[x ]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用.那么
]1024[log ]4[log ]3[log ]2[log ]1[log 22222+++++ =__________ .
6. 已知抛物线的顶点在原点,焦点在x 轴的正半轴上,F 为焦点,,,A B C 为抛物线上的三点,且满足0FA FB FC ++=,FA +FB +6FC =,则抛物线的方程为 7、方程θθ
cos 2
sin =在[)π2,0上的根的个数
8、|x log |y 2=的定义域为]b ,a [ , 值域为]2,0[ 则区间]b ,a [ 的长度a b -的最小值为
9、若数列{}
n a 的通项公式为)(5245251
2
2+--∈⎪
⎭
⎫ ⎝⎛⨯-⎪
⎭
⎫ ⎝⎛⨯=N n a n n n ,{}
n a 的最大值为第x 项,最小
项为第y 项,则x+y 等于
10、若定义在R 上的减函数()y f x =,对于任意的,x y
R ∈,不等式22(2)(2)f x x f y y -≤--成立.且函数(1)y f x =-的图象关于点(1,0)
对称,则当 14x ≤≤时,
y
x
的取值范围 . 11、已知函数()f x 满足()12f =,()()
()
111f x f x f x ++=-,
则()()()()1232007f f f f ⋅⋅⋅
⋅的值为 .
12、已知函数()2sin f x x ω=在区间[,]34
ππ
-
上的最小值为2-,则ω的取值范围是 .
13、与圆x 2 + y 2-4x=0外切,又与Y 轴相切的圆的圆心轨迹方程是 14、设集合{}1,2,3,
,n S n =,若n X S ⊆,把X 的所有元素的乘积称为X 的容量(若X
中只有一个元素,则该元素的数值即为它的容量,规定空集的容量为0)。
若X 的容量为奇(偶)数,则称X 为n S 的奇(偶)子集。
若4n =,则n S 的所有奇子集的容量之和为____ .
二、解答题:(文科班只做15题,30分,理科班两题都做,每题15分)
15、在直三棱柱111ABC A B C -中,13AB AC AA a ===,
2BC a =,D 是BC 的中点,F 是1C C 上一点,且2CF a =.
(1)求证:1B F ⊥ 平面ADF ; (2)求三棱锥1D AB F -的体积;
(3)试在1AA 上找一点E ,使得//BE 平面ADF .
16、已知直线l 的参数方程:12x t y t
=⎧
⎨
=+⎩(t 为参数)和圆C 的极坐标方程:
)4
sin(22π
θρ+=.(1)将直线l 的参数方程化为普通方程,圆C 的极坐标方程化为直
角坐标方程;(2)判断直线l 和圆C 的位置关系.
A
B
C
D
1A
1B
1C
F
09届高三数学天天练4答案
1、 16
2、),3()1,(+∞⋃--∞
3、3
4、3
5、8204
6、x y 42=
7、 2 8、43 9、3 10、1[,1]2- 11、3 12、3
(,2][,)2
-∞-+∞
13、y 2=8x(x>0)或y=0 (x<0) 14、7
15、(1)证明:,AB AC D =为BC 中点
AD BC ∴⊥,又直三棱柱中:1BB ⊥底面
,ABC AD ⊂底面ABC ,1AD BB ∴⊥,AD ∴⊥平面11BCC B ,1B F ⊂平面11BCC B
1AD B F ∴⊥.在 矩形11BCC B 中:1C F CD a ==,
112CF C B a == 11Rt DCF Rt FC B ∴∆≅∆,11CFD C B F ∴∠=∠ 190B FD ∴∠=,即 1B F FD ⊥,
AD
FD D =,1B F ∴⊥平面AFD ; -----------5分
(2)解:
AD ⊥平面11BCC B 1111
3
D A B F
A B D F B D
F V V S A D -
-∴==⋅⋅
=11132B F FD AD ⨯⋅⨯= -------10分
(3)当2AE a =时,//BE 平面ADF .
证明:连,EF EC ,设EC AF M =,连DM ,2AE CF a == AEFC ∴为矩形,M ∴为EC 中点,D 为BC 中点,//MD BE ∴,M D ⊂平面ADF ,BE ⊄平面ADF //BE ∴平面ADF . -------15分
16、解:(1)消去参数t ,得直线l 的普通方程为12+=x y ;
)4
(sin 22π
θρ+=即)cos (sin 2θθρ+=,
两边同乘以ρ得)cos sin (22θρθρρ+=, 消去参数θ,得⊙C 的直角坐标方程为:
2)1()1(22=-+-x x
(2)圆心C 到直线l 的距离25
5
212|112|2
2<=
++-=
d , 所以直线l 和⊙C 相交.。
