lagrange插值作业

合集下载

实验四 Lagrange插值法画函数图像

实验四 : Lagrange 插值法画函数图像学号: 姓名:指导老师：马季骕班级:计算机科学与技术（非师范）1、算法说明：先研究线形插值和二次插值，在线性插值中，若逼近函数用两点式表示出来，则有F （x ）=y0*((x-x1)/(x0-x1))+y1*((x-x0)/(x1-x0))过三个点的二次插值可以确定一条抛物线，经过化简之后，被逼近函数可以表示称F(x)=y0*((x-x1)*(x-x2)/(x0-x1)/(x0-x2))+y1*((x-x0)*(x-x2)/(x1-x0)/(x1-x2))+y2*((x-x0)*(x-x1)/(x2-x0)/(x2-x1));经过分析对比可以总结出：对于具有n+1个节点的函数，都可以表示成该节点的函数值与其对应基函数的乘积的线形组合。

其中要求逼近函数是n 次多项式，并且逼近函数过所有的型值点。

（1）原函数图像的绘制：对于给定函数11-,2511)(2≤≤+=x xx f 。

在区间[]11-，上画出f (x )的函数图像。

（2）Lagrange 插值函数图像的绘制：根据题目要求取11个等距插值节点)(10210,1,...10i i x i =+-=，求出每一个结点处的基函数)(x l j （j=0,1,…n ），然后根据Lagrange 插值多项式的一般形式把ϕ(x )写成与节点相对应的函数值)(i x f （i=0,1,2…n ）与其插值基函数)(x l j （j=0,1,…n ）的线形组合的形式。

即)()()(x l x f x jn0j i ∑==ϕ 2、源代码：// 数值分析Dlg.cpp : implementation file//#include "stdafx.h"#include "数值分析.h"#inc-lude "数值分析Dlg.h"#ifdef _DEBUG#define new DEBUG_NEW#undef THIS_FILEstatic char THIS_FILE[] = __FILE__;#endif/////////////////////////////////////////////////////////////////////////////// CAboutDlg dialog used for App Aboutclass CAboutDlg : public CDialog{public:CAboutDlg();// Dialog Data//{{AFX_DATA(CAboutDlg)enum { IDD = IDD_ABOUTBOX };//}}AFX_DATA// ClassWizard generated virtual function overrides//{{AFX_VIRTUAL(CAboutDlg)protected:virtual void DoDataExchange(CDataExchange* pDX); // DDX/DDV support //}}AFX_VIRTUAL// Implementationprotected://{{AFX_MSG(CAboutDlg)//}}AFX_MSGDECLARE_MESSAGE_MAP()};CAboutDlg::CAboutDlg() : CDialog(CAboutDlg::IDD){//{{AFX_DATA_INIT(CAboutDlg)//}}AFX_DATA_INIT}void CAboutDlg::DoDataExchange(CDataExchange* pDX){CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(CAboutDlg)//}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(CAboutDlg, CDialog)//{{AFX_MSG_MAP(CAboutDlg)// No message handlers//}}AFX_MSG_MAPEND_MESSAGE_MAP()/////////////////////////////////////////////////////////////////////////////// CMyDlg dialogCMyDlg::CMyDlg(CWnd* pParent /*=NULL*/): CDialog(CMyDlg::IDD, pParent){//{{AFX_DATA_INIT(CMyDlg)// NOTE: the ClassWizard will add member initialization here //}}AFX_DATA_INIT// Note that LoadIcon does not require a subsequent DestroyIcon in Win32 m_hIcon = AfxGetApp()->LoadIcon(IDR_MAINFRAME);}void CMyDlg::DoDataExchange(CDataExchange* pDX){CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(CMyDlg)// NOTE: the ClassWizard will add DDX and DDV calls here //}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(CMyDlg, CDialog)//{{AFX_MSG_MAP(CMyDlg)ON_WM_SYSCOMMAND()ON_WM_PAINT()ON_WM_QUERYDRAGICON()ON_BN_CLICKED(IDC_NEW, OnNew)ON_BN_CLICKED(IDC_LAG, OnLag)ON_BN_CLICKED(IDC_LINE, OnLine)ON_BN_CLICKED(IDC_HER, OnHer)//}}AFX_MSG_MAPEND_MESSAGE_MAP()/////////////////////////////////////////////////////////////////////////////// CMyDlg message handlersBOOL CMyDlg::OnInitDialog(){CDialog::OnInitDialog();// Add "About..." menu item to system menu.// IDM_ABOUTBOX must be in the system command range.ASSERT((IDM_ABOUTBOX & 0xFFF0) == IDM_ABOUTBOX);ASSERT(IDM_ABOUTBOX < 0xF000);CMenu* pSysMenu = GetSystemMenu(FALSE);if (pSysMenu != NULL){CString strAboutMenu;strAboutMenu.LoadString(IDS_ABOUTBOX);if (!strAboutMenu.IsEmpty()){pSysMenu->AppendMenu(MF_SEPARATOR);pSysMenu->AppendMenu(MF_STRING, IDM_ABOUTBOX, strAboutMenu);}}// Set the icon for this dialog. The framework does this automatically// when the application's main window is not a dialogSetIcon(m_hIcon, TRUE); // Set big iconSetIcon(m_hIcon, FALSE); // Set small icon// TODO: Add extra initialization herereturn TRUE; // return TRUE unless you set the focus to a control}void CMyDlg::OnSysCommand(UINT nID, LPARAM lParam){if ((nID & 0xFFF0) == IDM_ABOUTBOX){CAboutDlg dlgAbout;dlgAbout.DoModal();}else{CDialog::OnSysCommand(nID, lParam);}}// If you add a minimize button to your dialog, you will need the code below// to draw the icon. For MFC applications using the document/view model,// this is automatically done for you by the framework.void CMyDlg::OnPaint(){if (IsIconic()){CPaintDC dc(this); // device context for paintingSendMessage(WM_ICONERASEBKGND, (WPARAM) dc.GetSafeHdc(), 0);// Center icon in client rectangleint cxIcon = GetSystemMetrics(SM_CXICON);int cyIcon = GetSystemMetrics(SM_CYICON);CRect rect;GetClientRect(&rect);int x = (rect.Width() - cxIcon + 1) / 2;int y = (rect.Height() - cyIcon + 1) / 2;// Draw the icondc.DrawIcon(x, y, m_hIcon);}else{CDialog::OnPaint();}}// The system calls this to obtain the cursor to display while the user drags// the minimized window.HCURSOR CMyDlg::OnQueryDragIcon(){return (HCURSOR) m_hIcon;}void CMyDlg::OnNew(){// TODO: Add your control notification handler code hereint i;int j;int x00=331;int y00=225;double x;CDC *pDC=GetDC();pDC->SetMapMode(MM_LOMETRIC);pDC->SetViewportOrg(x00,y00);for(i=-750; i<=750; i++){pDC->SetPixel(i,0,RGB(0,0,0));pDC->SetPixel(0,i,RGB(0,0,0));}for(x=-1; x<=1; x+=0.001){double j=400.0/(1+25*x*x);pDC->SetPixel(x*500,j,RGB(0,0,0));}}void CMyDlg::OnLag(){// TODO: Add your control notification handler code here int i;int j;int x00=331;int y00=225;double x;CDC *pDC=GetDC();pDC->SetMapMode(MM_LOMETRIC);pDC->SetViewportOrg(x00,y00);for(i=-750; i<=750; i++){pDC->SetPixel(i,0,RGB(0,0,0));pDC->SetPixel(0,i,RGB(0,0,0));}double yx[]={-1,-0.8,-0.6,-0.4,-0.2,0,0.2,0.4,0.6,0.8,1};double yy[12],lx[12],ly[12];double l_fenzi[12],l_fenmu[12];double l_x,l_y;for(i=0; i<=10; i++){yy[i]=1.0/(1+25*yx[i]*yx[i]);}for(i=0; i<=10; i++){l_fenmu[i]=1.0;for(j=0; j<=10; j++){if(i!=j)l_fenmu[i]=l_fenmu[i]*(yx[i]-yx[j]);}}double qq,pp;for(qq=-1; qq<=1; qq+=0.0003){for(i=0; i<=10; i++){l_fenzi[i]=1.0;for(j=0; j<=10; j++){if(i!=j)l_fenzi[i]=l_fenzi[i]*(qq-yx[j]);}}pp=0;for(i=0; i<=11; i++){pp=pp+1.0/(1+25*yx[i]*yx[i])*l_fenzi[i]/l_fenmu[i];}pDC->SetPixel(qq*500,pp*390+5,RGB(50,12,225));}}void CMyDlg::OnLine()// TODO: Add your control notification handler code here int i;int j;int x00=331;int y00=225;double x;CDC *pDC=GetDC();pDC->SetMapMode(MM_LOMETRIC);pDC->SetViewportOrg(x00,y00);for(i=-750; i<=750; i++){pDC->SetPixel(i,0,RGB(0,0,0));pDC->SetPixel(0,i,RGB(0,0,0));}double yx[]={-1,-0.8,-0.6,-0.4,-0.2,0,0.2,0.4,0.6,0.8,1};double yy[14];for(i=0; i<=10; i++){yy[i]=1.0/(1+25*yx[i]*yx[i]);}CPen pen;CPen*oldpen;pen.CreatePen(PS_SOLID,5,RGB(127,255,212));oldpen=pDC->SelectObject(&pen);for(i=0; i<10; i++){pDC->MoveTo(yx[i]*480,yy[i]*400);pDC->LineTo(yx[i+1]*480,yy[i+1]*400);}}void CMyDlg::OnHer()// TODO: Add your control notification handler code hereint x00=331,y00=225,i,j;double x;CDC *pDC=GetDC();pDC->SetMapMode(MM_LOMETRIC);pDC->SetViewportOrg(x00,y00);for(i=-750; i<=750; i++){pDC->SetPixel(i,0,RGB(0,0,0));pDC->SetPixel(0,i,RGB(0,0,0));}double yx[]={-1,-0.8,-0.6,-0.4,-0.2,0,0.2,0.4,0.6,0.8,1};double yy[12];for(i=0; i<=10; i++){yy[i]=1.0/(1+25*yx[i]*yx[i]);}double x0,x1,yd1,yd0,y1,y0;for(i=0; i<10; i++){x0=yx[i],x1=yx[i+1];y0=1.0/(1+25*x0*x0);y1=1.0/(1+25*x1*x1);yd0=-(50*x0)*1.0/((1+25*x0*x0)*(1+25*x0*x0));yd1=-(50*x1)*1.0/((1+25*x1*x1)*(1+25*x1*x1));for(double qq=x0; qq<x1; qq+=0.005){double pp= y0*(1+2*(qq-x0)/(x1-x0)) * (qq-x1)/(x0-x1) * (qq-x1)/(x0-x1)+y1*(1+2*(qq-x1)/(x0-x1)) * (qq-x0)/(x1-x0) * (qq-x0)/(x1-x0)+yd0*(qq-x0) * (qq-x1)/(x0-x1) * (qq-x1)/(x0-x1)+yd1*(qq-x1) * (qq-x0)/(x1-x0) * (qq-x0)/(x1-x0);pDC->SetPixel(qq*500,pp*400,RGB(255,215,0));}}}2、实验结果：4、结果分析：本次实验，对用Lagrange插值法求f(x)的逼近函数 (x)有了更深刻的理解，学会了用程序来求解Lagrange插值基函数（j=0,1,…n），求出逼近函数 (x)并绘制出其图像，当插值函数次数很高时出现了Runge现象，可以通过函数图像很直观地看到Lagrange插值法的这个缺点。

数值计算方法Lagrange插值算法实验

Lagrange插值【实验目的】１、掌握Matlab基本语句,学会编写.M文件２、编写Lagrange算法【实验内容】1.编写Lagrange的Matlab程序lagrange.m，调用该程序，求解例2中的近似值。

补：例2已知：利用此三值的二次插值多项式求lg12的近似值。

【算法】//xi为插值自变量，yi为与xi对应的插值//x为插值自变量数组，y为插值数组float lagrange(x,y,xi){Float p=1.0;s=0.0;yi=0.0;for (k=1;k++;k<=n){for(j=1;j++;j<=n){If(k!=j){p*=(xi-x[j])/(x[k]-x[j]);}}s+=p*y[k];p=1.0;}yi=s;return yi;}【实验要求】本次实验要求写实现代码。

实验报告请写明【实验目的】、【实验内容】、【源代码及注释】和【实验心得】function [ yi ] = lagrange( x,y,xi )% Lagrange插值% x,y分别为已知节点及其函数值向量% xi为插值点，yi为插值n=length(x);m=length(y);if(n~=m)error('The length of x must be equal the length of y!'); ends=0;z=xi;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x(j))/(x(k)-x(j));endends=p*y(k)+s;end yi=s; end。

Lagrange 插值

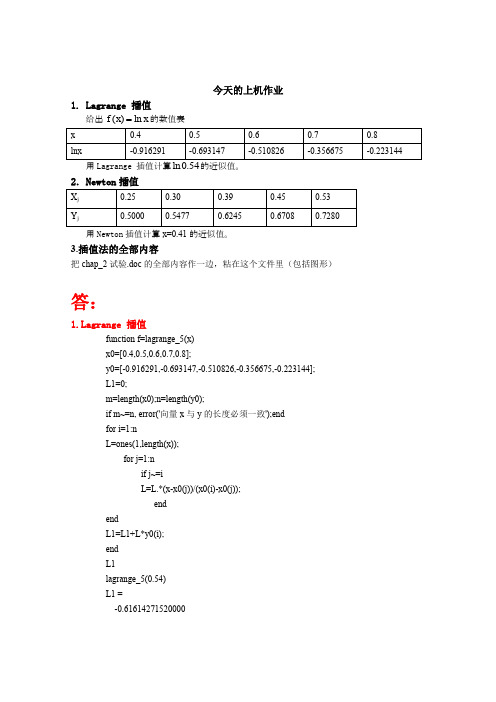
今天的上机作业1. Lagrange 插值给出()ln f x x 的数值表用Lagrange 插值计算ln 0.54的近似值。

2．Newton 插值用Newton 插值计算x=0.41的近似值。

3.插值法的全部内容把chap_2试验.doc 的全部内容作一边，粘在这个文件里（包括图形）答：grange 插值function f=lagrange_5(x) x0=[0.4,0.5,0.6,0.7,0.8];y0=[-0.916291,-0.693147,-0.510826,-0.356675,-0.223144]; L1=0;m=length(x0);n=length(y0);if m~=n, error('向量x 与y 的长度必须一致');end for i=1:nL=ones(1,length(x)); for j=1:n if j~=iL=L.*(x-x0(j))/(x0(i)-x0(j)); end endL1=L1+L*y0(i); end L1lagrange_5(0.54) L1 =-0.616142715200002．Newton插值function f=newton_li5(x) %x0为入的节点值，y0相应节点的函数值x0=[0.25 0.30 0.39 0.45 0.53];y0=[0.5000 0.5477 0.6245 0.6708 0.7280];n=length(x0)%syms xfor i=1:nf(i,1)=y0(i);endhx=f(1,1);xx=(1.0);for k=2:nfor i=k:nf(i,k)=(f(i,k-1)-f(i-1,k-1))/(x0(i)-x0(i-k+1)); %构造差商表endxx=xx*(x-x0(k-1));hx=hx+f(k,k)*xx; %计算函数的近似值end%f=expand(hx)Hxnewton(0.41)n =5hx =0.64030542443064ans =0.50000000000000 0 0 0 00.54770000000000 0.95400000000000 0 0 00.62450000000000 0.85333333333333 -0.71904761904761 0 00.67080000000000 0.77166666666666 -0.54444444444446 0.87301587301575 00.72800000000000 0.71500000000000 -0.40476190476189 0.60731538992422 -0.948930296755483.插值法的全部内容把chap_2试验.doc的全部内容作一边，粘在这个文件里（包括图形）P28 例22点插值function f=lagrange_2(x)x0=[0.32,0.34];y0=[0.314567,0.333487];L1=0;m=length(x0);n=length(y0);if m~=n, error('向量x与y的长度必须一致');endfor i=1:nL=ones(1,length(x));for j=1:nif j~=iL=L.*(x-x0(j))/(x0(i)-x0(j));endendL1=L1+L*y0(i);endL1lagrange_2(0.3367)L1 =0.330365200000003点插值function f=lagrange_3(x)x0=[0.32,0.34,0.36];y0=[0.314567,0.333487,0.352274];L1=0;m=length(x0);n=length(y0);if m~=n, error('向量x与y的长度必须一致');endfor i=1:nL=ones(1,length(x));for j=1:nif j~=iL=L.*(x-x0(j))/(x0(i)-x0(j));endendL1=L1+L*y0(i);endL1lagrange_3(0.3367)L1 =0.33037436203750Lagrange插值法%eg1_lagr.mclear;clf;xx=linspace(-5,5,50); y=sin(xx); %作被插函数的图象disp('n x=4.5处的插值绝对误差的绝对值')x1=linspace(-5,5,3); y1=sin(x1); yy1=lagr1(x1,y1,xx); %2次插值chazhi_y45_2=lagr1(x1,y1,4.5);gd_wucha_limit_y45_2=abs(chazhi_y45_2-sin(4.5));disp(sprintf('%d %15.4f %15.4f',2,chazhi_y45_2,gd_wucha_limit_y45_2))x2=linspace(-5,5,5); y2=sin(x2); yy2=lagr1(x2,y2,xx); %4次插值chazhi_y45_4=lagr1(x2,y2,4.5);gd_wucha_limit_y45_4=abs(chazhi_y45_4-sin(4.5));disp(sprintf('%d %15.4f %15.4f',4,chazhi_y45_4,gd_wucha_limit_y45_4))x3=linspace(-5,5,9); y3=sin(x3); yy3=lagr1(x3,y3,xx); %8次插值chazhi_y45_8=lagr1(x3,y3,4.5);gd_wucha_limit_y45_8=abs(chazhi_y45_8-sin(4.5));disp(sprintf('%d %15.4f %15.4f',8,chazhi_y45_8,gd_wucha_limit_y45_8))plot(xx,y,'m-');hold on,pause,plot(x1,y1,'rs',xx,yy1,'r-'); hold on,pause,plot(x2,y2,'b*',xx,yy2,'b-'); hold on,pause,plot(x3,y3,'ko',xx,yy3,'k-'); hold on计算函数值function f=newton_li4(x) %x0为入的节点值，y0相应节点的函数值x0=[0.40,0.55,0.65,0.80,0.90,1.05];y0=[0.41075,0.57815,0.69675,0.88811,1.02652,1.25382];n=length(x0)%syms xfor i=1:nf(i,1)=y0(i);endhx=f(1,1);xx=(1.0);for k=2:nfor i=k:nf(i,k)=(f(i,k-1)-f(i-1,k-1))/(x0(i)-x0(i-k+1)); %构造差商表endxx=xx*(x-x0(k-1));hx=hx+f(k,k)*xx; %计算函数的近似值end%f=expand(hx)hxnewton(0.596)n =5hx =0.77193768707246ans =0.50000000000000 0 0 0 00.54770000000000 0.95400000000000 0 0 00.62450000000000 0.85333333333333 -0.71904761904761 0 00.67080000000000 0.77166666666666 -0.54444444444446 0.87301587301575 00.72800000000000 0.71500000000000 -0.40476190476189 0.60731538992422 -0.94893029675548Newton插值法%eg1_newton.mclear;clf;xx=linspace(-5,5,50); y=sin(xx); %作被插函数的图象disp('n x=4.5处的插值绝对误差的绝对值')x1=linspace(-5,5,3); y1=sin(x1); yy1=newton1(x1,y1,xx,2); %2次插值chazhi_y45_2=newton1(x1,y1,4.5,2);gd_wucha_limit_y45_2=abs(chazhi_y45_2-sin(4.5));disp(sprintf('%d %15.4f %15.4f',2,chazhi_y45_2,gd_wucha_limit_y45_2))x2=linspace(-5,5,5); y2=sin(x2); yy2=newton1(x2,y2,xx,4); %4次插值chazhi_y45_4=newton1(x2,y2,4.5,4);gd_wucha_limit_y45_4=abs(chazhi_y45_4-sin(4.5));disp(sprintf('%d %15.4f %15.4f',4,chazhi_y45_4,gd_wucha_limit_y45_4))x3=linspace(-5,5,9); y3=sin(x3); yy3=newton1(x3,y3,xx,8); %8次插值chazhi_y45_8=newton1(x3,y3,4.5,8);gd_wucha_limit_y45_8=abs(chazhi_y45_8-sin(4.5));disp(sprintf('%d %15.4f %15.4f',8,chazhi_y45_8,gd_wucha_limit_y45_8))plot(xx,y,'m-');hold on,pause,plot(x1,y1,'rs',xx,yy1,'r-'); hold on,pause,plot(x2,y2,'b*',xx,yy2,'b-'); hold on,pause,plot(x3,y3,'ko',xx,yy3,'k-'); hold on。

数值分析Lagrange插值多项式

其余的将M值及f2[x_]修改即可，得到插值函数修改分f3[x_]即可。
1 n+1 !
f
n+1
(εx )
n i=0(x
− xi )
其中 εx 为区间内一点
但 Lagrange 插值法没有承接性，可以进行改良。
【Lagrange 插值算法描述】 1. 对给定函数选取其区间上的一系列节点并计算其函数值，得到点列（x0 ， y0 ）,…,( xn , yn )； 2. 通过上述点列构造 Lagrange 基函数li x = 出 Lagrange 插值函数Ln x =
【实验】通过 Mathematica 编写程序得到如下结果： N=5： 1. 取xi = 5 −
10 N
i ， i = 0,1， … ，N 得到：
（1）插值点为：
（2）由上述插值点构造出 Lagrange 插值函数：
（3）由题目所给出的条件计算误差得到：
插值函数与原函数的图像为：
其中蓝色为原函数图像，红色为插值函数图像，可以看出在 0 点误差最大，与我们的计算结果相吻合。
n k=0 yk lk (x)； n x −x i j=0 x −x i j j ≠i
,并由该基函数构造
3. 由多项式插值误差定理来估计其误差： f x −p x =
1 n+1 !
f
n+1
(εx )
n i=0(x
− xi )
其中 εx 为区间内一点
但此题有自己的估计误差的要求，则我们依照题意估计误差。
n x −x i j=0 x −x i j j ≠i
,
li x = δij
n k=0 yk lk (x)
来构造 Lagrange 插值多项式： Ln x =

拉格朗日(Lagrange)插值

p2(7) =
(1–4)(1–9)
*1 + (4–1)(4–9)
*2
(7–1)(7–4)
+ (9–1)(9–4) * 3
= 2.7
例5.4 已知函数y=f(x)在节点上满足
x x0 x1 x2
y y0 y1 y2
求二次多项式 p(x) = a0 + a1x + a2x2
使之满足 p(xi) = yi
li (x的) 插值
lk (x0 ) 0,,lk (xk1) 0,lk (xk ) 1,lk (xk1 ) 0,,lk (xn ) 0
即
lk
(xi )
ki
1 0
(i k) (i k)
由条件 lk (xi ) 0 ( i k)知, x0 , x1,, xk1, xk1,, xn
都是n次 lk (x) 的零点,故可设
l0 (x)
再由另一条件 l0 (x0
c(x
) 1
x1 )( x x2
确定系数
)
c
(x0
1 x1)( x0
x2
)
从而导出
l0 (x)
(x (x0
x1)( x x2 ) x1 )( x0 x2 )
类似地可以构造出满足条件： l1(x1) 1, l1(x0 ) 0,
的插值多项式
l1 ( x)
lk (x)
j0 jk
n
x xj
n
(xk x j )
j0 xk x j
jk
j0 jk
称 lk (x) 为关于基点 xi 的n次插值基函数(i=0,1,…,n)
以n+1个n次基本插值多项式 lk (x)(k 0,1,, n) 为基础,就能直接写出满足插值条件

多项式插值,Lagrange插值,Lagrange反插值,牛顿插值

数学软件实验任务书实验一多项式插值1实验原理()y f x =在区间[,]a b 上的1n +个互异点01n a x x x b =<<= 出得值为012,,,,n y y y y ，存在次数不超过n 的多项式：2012()n n n P x a a x a x a x =++++使得满足条件：()()n i i p x f x =2 数据来源X=[1 1.4 1.8 2.0]Y=[-2 -0.8 0.4 1.2]3 实验程序clcclear allX=[1 1.4 1.8 2.0];Y=[-2 -0.8 0.4 1.2]';n=length(X);A=zeros(n,n);for i=1:nfor j=1:n-1A(i,j+1)=X(i)^j;endendB=zeros(n,1);for i=1:nB(i,1)=1;endA(:,1)=B;A1=A;%%%%%%%%范德蒙行列式a=inv(A1)*Ysyms x;f=a(1)+a(2)*x+a(3)*x^2+a(4)*x^3%%%%%检验subs(f,1)4 实验结果%%%%%%%%%%多项式系数a =-9.200012.5333-7.00001.666723()0.9212.537 1.67f x x x x =-+-+%%%%%%%%%%%%%%%代入1x =检验subs(f,1)ans =-2.000000003实验二 Lagrange 插值1 实验原理通过平面上不同两点可以确定一条直线经过这两点，这就是拉格朗日线性插值问题，对于不在同一条直线的三个点得到的插值多项式为抛物线。

这里给出一般的插值公式，拉格朗日插值的基多项式为：10(),0,1,2,,n i j i jj i x x l x i n x x =≠-==-∏ 有了基函数以后就可以直接构造插值多项式，插值多项式为：0()()nn i i i p f x l x ==∑2 数据来源X=[0 1 2 4]Y=[1 9 23 3]3 实验程序function laglange(X,Y,x0)syms xn=length(X);w=1;for i=1:nw=w*(x-X(i));enda=diff(w,x);f=0;for i=1:nb=w/(x-X(i));l=b/(subs(a,x,X(i)));f=f+l*Y(i);endf=expand(f)%subs(f,x,x0)sprintf('f(%f)=%f',x0,subs(f,x,x0))end4 实验结果运行程序在Matlab 窗口显示f =3 2- 11/4 x + 45/4 x - 1/2 x + 1 即：3211451()1442f x x x x =-+-+ 实验三牛顿插值1 实验原理函数()f x 的差商定义为：[]()k k f x f x =111[][][,]k k k k k kf x f x f x x x x ----=-111[,,][,,][,,,]k j k k j k k k j k k k j f x x f x x f x x x x x -+------=-下面给出牛顿插值多项式为：001001011()[][,]()[,,,]()()()n n n N x f x f x x x x f x x x x x x x x x -=+-++---如果记：011()()(),1,2,,k k w x x x x x x k n -=---=则牛顿插值可以表达为： 001101()[][,][,,,]n n n N x f x f x x w f x x x w =+++2 数据来源X=[1.0 1.3 1.6 1.9 2.2]Y=[0.7651977 0.6200860 0.4554022 0.2818186 0.1103623] 3 实验程序1 计算差商表程序clcclearX=[1.0 1.3 1.6 1.9 2.2];Y=[0.7651977 0.6200860 0.4554022 0.2818186 0.1103623]; f0=Y;n=length(X);f=zeros(n);f(1,:)=Y;for i=1:n-1f(2,i)=(f0(i+1)-f0(i))/(X(i+1)-X(i))endfor k=2:n-1for i=1:n-kf(k+1,i)=(f(k,i+1)-f(k,i))/(X(k+i)-X(i)) endend2 牛顿差值程序function s=niudun(x,y,t)syms p;s=y(1);xishu=0;dxs=1;n=length(x);%%构造牛顿插值方法for(i=1:n-1)for(j=i+1:n)xishu(j) = (y(j)-y(i))/(x(j)-x(i));endtemp1(i)=xishu(i+1);dxs=dxs*(p-x(i));s=s+temp1(i)*dxs;y=xishu;endsimplify(s)end4 实验结果差商表：f =0.7652 0.6201 0.4554 0.2818 0.1104-0.4837 -0.5489 -0.5786 -0.5715 0-0.1087 -0.0494 0.0118 0 00.0659 0.0681 0 0 00.0018 0 0 0 0在命令窗口输入x=[1.0 1.3 1.6 1.9 2.2];y=[0.7651977 0.6200860 0.4554022 0.2818186 0.1103623]; yt=niudun(x,y,1.5)得到结果yt =[0.5118199945]。

三次lagrange插值多项式例题

三次lagrange插值多项式例题
Lagrange插值多项式是一种用于数据拟合的方法，它可以根据给定的数据点，构造一个多项式函数，从而在数据点之间进行插值。

以下是一个三次Lagrange插值多项式的例题：
假设有如下数据点：（1，3），（2，5），（4，1），（5，7）
构造三次Lagrange插值多项式，求当x=3时，函数的取值。

首先，我们需要根据给定的数据点，构造出Lagrange插值多项式的基函数。

对于三次Lagrange插值多项式，其基函数可以表示为：
L0(x) = (x-2)(x-4)(x-5)/(-12)
L1(x) = (x-1)(x-4)(x-5)/6
L2(x) = (x-1)(x-2)(x-5)/(-4)
L3(x) = (x-1)(x-2)(x-4)/6
其中，Li(x)表示第i个基函数，其分母为所有数据点的x坐标之差的乘积，分子为除去第i个数据点的x坐标之差的乘积。

接下来，我们可以将基函数和对应的y坐标代入插值多项式的公式中，得到：
P(x) = 3L0(x) + 5L1(x) + L2(x) - 7L3(x)
当x=3时，P(x)的取值为：
P(3) = 3L0(3) + 5L1(3) + L2(3) - 7L3(3)
= 3(-2*1*2/12) + 5((3-1)*(3-4)*(3-5)/6) + (-2*1*2/4) -
7((3-1)*(3-2)*(3-4)/6)
= -2.33
因此，当x=3时，函数的取值为-2.33。

以上就是三次Lagrange插值多项式的例题。

通过构造基函数和代入公式，可以轻松求解出插值多项式在任意点的取值。

数值分析Lagrange插值法计算实验

数值分析实验报告（01）一、实验目的通过实验锻炼和掌握的能力掌握Lagrange 插值方法并学会利用计算机编程计算函数值。

二、实验内容给出()ln f x x =的数值表 x0.4 0.5 0.6 0．7 0.8 ln x-0.916291 -0.693147 -0.510826 -0.356675 -0.223144用线性插值和二次插值计算的近似值。

计算ln(0.54)。

三、编程思路0.5图1 程序框图四、Matlab 程序代码function y0=lagrange(x,y,x0)nx=length(x);ny=length(y);if nx~=nyreturn;endn=nx;y0=0;for k=1:np=1;for j=1;nif j~=kp=p.*(x0-x(j))./(x(k)-x(j));endendy0=y0+p*y(k);end% x=[0.5 0.6];% y=[-0.693147 -0.510826];x0=0.54;y0=lagrange(x,y,x0);y0% x=[0.4 0.5 0.6];% y=[-0.916296 -0.693147 -0.510826];x0=0.54;y0=lagrange(x,y,x0);y0五、数值结果及分析（数值运行结果及对结果的分析）y0 =-0.6202y0 =-0.6202六、实验体会（计算中出现的问题，解决方法，实验体会）输入程序时括号含义不明，或者输入括号减少，导致结果错误。

仔细检查，寻找错误，一定要仔细认真。

拉格朗日（Lagrange）插值算法

拉格朗⽇（Lagrange）插值算法拉格朗⽇插值（Lagrange interpolation）是⼀种多项式插值⽅法，指插值条件中不出现被插函数导数值，过n+1个样点，满⾜如下图的插值条件的多项式。

也叫做拉格朗⽇公式。

这⾥以拉格朗⽇3次插值为例，利⽤C++进⾏实现：1//利⽤lagrange插值公式2 #include<iostream>3using namespace std;45double Lx(int i,double x,double* Arr)6 {7double fenzi=1,fenmu=1;8for (int k=0;k<4;k++)9 {10if (k==i)11continue;12 fenzi*=x-Arr[k];13 fenmu*=Arr[i]-Arr[k];14 }15return fenzi/fenmu;16 }1718int main()19 {20double xArr[4]={};21double yArr[4]={};22//输⼊4个节点坐标23 cout<<"请依次输⼊4个节点的坐标:"<<endl;24for (int i=0;i<4;i++)25 cin>>xArr[i]>>yArr[i];2627//输⼊要求解的节点的横坐标28 cout<<"请输⼊要求解的节点的横坐标:";29double x;30 cin>>x;31double y=0;32for (int i=0;i<4;i++)33 y+=Lx(i,x,xArr)*yArr[i];34 printf("x=%lf时，y=%lf\n",x,y);3536//分界，下⾯为已知y求x37 cout<<"请输⼊要求解的节点的纵坐标:";38 cin>>y;39 x=0;40for (int i=0;i<4;i++)41 x+=Lx(i,y,yArr)*xArr[i];42 printf("y=%lf时，x=%lf\n",y,x);4344 system("pause");45return0;46 }作者：耑新新，发布于转载请注明出处，欢迎邮件交流：zhuanxinxin@。

Lagrange 插值多项式与Newton插值

专业序号姓名日期实验1Lagrange 插值多项式【实验目的】1．掌握用MATLAB计算拉格朗日插值方法，改变节点的数目，对插值结果进行初步分析；2．掌握用MATLAB的插值方法并通过实例学习用插值解决实际问题。

3. 观察Runge现象的演示。

【实验内容】Lagrange 插值多项式按照 P74 图4-4 的方法编 Lagrange 插值多项式function y = mylagpoly(X,Y,x)X,Y 采样点x 自变量(向量)y 多项式的函数值要特别注意大小写,x,y 和 t 都是向量【程序如下】:% exp4_2.m --- Runge现象的演示(内含 L 和 N 插值多项式)function try_Runge% 见 P84f = inline('1./(1+25*x.^2)'); % 定义函数n = 11;X = linspace(-1,1,n); % n 等分( n+1 个点),插值点横坐标Y = f(X); % 插值点纵坐标x = -1 : 0.01 : 1; % 加细 xy = mylagpoly(X,Y,x)plot(x,f(x),'r',X,Y,'o',x,y,'b')title('Runge现象') % 加标题legend('y=1/(1+25*x^2)','插值点 ','等分的10次插值多项式',0) % 加标签function y = mylagpoly(X,Y,x)n = length(X);y = zeros(size(x));for i = 1:nt=1;for j = 1:nif j ~= it = t.*((x-X(j))/(X(i)-X(j))); % 注意这里是点乘,字母与书上不同,此时t变成向量了endendy=y+ t.*Y(i);end【运行结果如下】：【结果分析】：拉格朗日插值实验通过离散的点来构造一个函数来逼近原来的函数，理论上应该是点越多，构造函数应该会越来越逼近原函数，但是却发生了Range现象，所以在利用拉格朗日插值法来构造函数来逼近原函数时，应该选择适当的点来逼近原函数，但即使如此，依然不能有效的避免Range现象。

数值计算方法实验之Lagrange多项式插值（Python代码）

数值计算⽅法实验之Lagrange多项式插值（Python代码）⼀、实验⽬的在已知f(x),x∈[a,b]的表达式，但函数值不便计算,或不知f(x),x∈[a,b]⽽⼜需要给出其在[a,b]上的值时，按插值原则f(x i)= y i(i= 0,1…….,n)求出简单函数P(x)(常是多项式),使其在插值基点x i,处成⽴P(x i)=y i(i=0,1,……,n),⽽在[a,b]上的其它点处成⽴f(x)≈P(x).⼆、实验原理三、实验内容求之f(x)=x4在[0,2]上按5个等距节点确定的Lagrange插值多项式.四、实验程序1import matplotlib.pyplot as plt2from pylab import mpl34#计算插值多项式的系数。

5 x = [0, 0.5, 1, 1.5, 2]6 y = [0, 0.0625, 1, 5.0625, 16]78def ParametersOfLagrangeInterpolation(data_x,data_y,size):9 parameters=[]1011 i=0;#i⽤来控制参数的个数12while i < size:13 j = 0;#j⽤来控制循环的变量做累乘14 temp = 1;15while j < size:16if(i != j):17 temp*=data_x[i]-data_x[j]18 j+=1;19 parameters.append(data_y[i]/temp)20 i += 1;21return parameters2223#计算拉格朗⽇插值公式的值。

2425def CalculateTheValueOfLarangeInterpolation(data_x,parameters,x):26 returnValue=027 i = 0;28while i < len(parameters):29 temp = 130 j = 0;31while j< len(parameters):32if(i!=j):33 temp *=x-data_x[j]34 j+=135 returnValue += temp * parameters[i]36 i += 137return returnValue3839#将函数绘制成图像40def Draw(data_x,data_y,new_data_x,new_data_y):41 plt.plot(new_data_x, new_data_y, label="拟合曲线", color="red")42 plt.scatter(data_x,data_y, label="离散数据",color="yellow")43 plt.scatter(1.75, 9.37890625, label="真实数据", color="orange")44 plt.scatter(1.25, 2.44140625, color="green")45 mpl.rcParams['font.sans-serif'] = ['SimHei']46 mpl.rcParams['axes.unicode_minus'] = False47 plt.title("Lagrange插值拟合数据")48 plt.legend(loc="upper left")49 plt.show()5051 parameters=ParametersOfLagrangeInterpolation(x,y,5)52 datax=[0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2]53 datay=[]54for temp in datax:55 datay.append(CalculateTheValueOfLarangeInterpolation(x,parameters,temp))56 x.append(1.75)57 y.append(CalculateTheValueOfLarangeInterpolation(x,parameters,1.75))58 Draw(x,y,datax,datay)59print("得到的四次Lagrange插值多项式为：L(x) = %f(x-0)(x-1)(x-1.5)(x-2) + %f(x-0)(x-0.5)(x-1.5)(x-2) + %f(x-0)(x-0.5)(x-1)(x-2) + %f(x-0)(x-0.5)(x-1)(x-1.5)"%(parameters[1],parameters[2],parameters[3],parameters[4]))五、运算结果(1)图像得到的四次Lagrange插值多项式为：L(x) = -0.166667(x-0)(x-1)(x-1.5)(x-2) + 4.000000(x-0)(x-0.5)(x-1.5)(x-2) + -13.500000(x-0)(x-0.5)(x-1)(x-2) + 10.666667(x-0)(x-0.5)(x-1)(x-1.5)。

数值分析报告Lagrange差值和牛顿插值

、实验名称Lagra nge 插值多项式和牛顿插值多项式、实验目的与要求：实验目的：掌握Lagrange 插值多项式和牛顿插值多项式的算法。

实验要求：1.给出Lagrange 插值和牛顿插值算法思路，2. 用C 语言实现算法，运行环境为Microsoft VisualC++，3. 计算误差（这里只要求给出（-5,5 ）内101个点的误差）。

三、实验内容：1. 对Lagrange 插值多项式算法作编程练习和上机运算，2. 对牛顿插值多项式算法作编程练习和上机运算，3. 比较两种方法。

算法思路：1. Lagrange 算法是把多项式p 写成如下形式:x x j j o x X j 称为Lagrange 基函数。

j i计算Lagrange 基函数的方法:fx=0.0;for(i=0;i< 二n ;i++){实验P(x) y °l °(x) y 」1(x)+y 」n (x)，其中 l i (x)tmp=1.0;for(j=0;j<i;j++)tmp二tmp*(x-x[j])/(x[i]-x[j]);for(j=i+1;j <n ;j++)tmp=tmp*(x-x[j])/(x[i]-x[j]);fx=fx+tmp*y[i];}return(fx);2.牛顿算法是把多项式p写成如下形式：p(x) C o q(x X o)…+Cm(x x o)(x N)…(x x^) 其中x0, x l, , xn是插值点，C0,C l,, C i 1是待定系数。

可以通过插值点X o, X i，…,X n和插值点处的函数值y o, y i,…，y n算出待定系数C0,C1,…,Cn 1，方法如下：(1)P k(xQ C q(X k x0)…+C k1(X k x°)…区X k-J⑵ P k1(X k) C0 q(X k X0)…+C k2(X k X。

)…(X k X k-2) 将(1)-⑵并利用y k P k(xQ，得- F k(X<) F k 1(人)（人X））（兀N）••化人1）y k鮎(人)(X k X))(人X i)-<X k X ki)算法：c[0]=y1[0];for( k=1; k <= N; k++){ d=x1[k]-x1[k -1];u=c[k-1];for( i =k-2 ; i >= 0 ; i --){ u=u*(x1[k 卜x1[i])+c[i];d=d*(x1[k] -x1[i]);}c[k]=(y1[k]-u)/d;}3.这里，我们先编写两个函数px1和px2，分别用来计算插值10. 2i 1节点取X 5 二~1 和Chebyshev point K 5cos( )，N J2N 2i=0,1,…，N时的Lagrange多项式函数或牛顿多项式函数，然后在main 函数中，主要目的是计算误差|f(x) - p(x)|在(-5,5)内101个点处的最大值，其中当然要引用前面编写的两个函数px1和px2，最后将N=5,10,20,40时两种情况下的最大误差输出，并分析结果。

数值分析实验四(Lagrange插值)

《数值分析》实验报告实验编号：实验四课题名称：Lagrange插值一、算法介绍对Lagrange型的n次插值多项式，先构造n+1个插值节点x[0],x[1],…,x[n]上的n次插值基函数对任一点xi所对应的插值基函数l[i](x)=[(x-x[0])…(x-x[i-1])(x-x[i+1])…(x-x[n])]/[(x[i]-x[0])…(x[i]-x[i-1])(x[i]-x[i+1 ])…(x[i]-x[n])]，其中i=0,1,2,…,n。

有了这n+1个n次插值基函数，n次Lagrange 型插值多项式就容易写出来了，表达式为：f(x)=y[1]*l[1](x)+y[2]*l[2](x)+…+y[n]*l[n](x)。

此程序中n=10。

二、程序代码// testView.cpp : implementation of the CTestView class//#include "stdafx.h"#include "test.h"#include "testDoc.h"#include "testView.h"#ifdef _DEBUG#define new DEBUG_NEW#undef THIS_FILEstatic char THIS_FILE[] = __FILE__;#endif/////////////////////////////////////////////////////////////////////////////// CTestViewIMPLEMENT_DYNCREATE(CTestView, CView)BEGIN_MESSAGE_MAP(CTestView, CView)//{{AFX_MSG_MAP(CTestView)// NOTE - the ClassWizard will add and remove mapping macros here.// DO NOT EDIT what you see in these blocks of generated code!//}}AFX_MSG_MAP// Standard printing commandsON_COMMAND(ID_FILE_PRINT, CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_DIRECT, CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_PREVIEW, CView::OnFilePrintPreview)END_MESSAGE_MAP()/////////////////////////////////////////////////////////////////////////////// CTestView construction/destructionCTestView::CTestView(){// TODO: add construction code here}CTestView::~CTestView(){}BOOL CTestView::PreCreateWindow(CREATESTRUCT& cs){// TODO: Modify the Window class or styles here by modifying // the CREATESTRUCT csreturn CView::PreCreateWindow(cs);}/////////////////////////////////////////////////////////////////////////////// CTestView drawingvoid CTestView::OnDraw(CDC* pDC){CTestDoc* pDoc = GetDocument();ASSERT_V ALID(pDoc);// TODO: add draw code for native data hereint i,j,k;double x,y,p_x,p_y,l,xx[100],f[100],F[100],sum,p_sum;CPen MyPen,*OldPen;pDC->SetViewportOrg(400,400); //定义坐标原点for(i=-500;i<500;i++){pDC->SetPixel(0,i,RGB(0,0,0));pDC->SetPixel(i,0,RGB(0,0,0)); //画出坐标}pDC->TextOut(-210,5,"-1");pDC->TextOut(196,5,"1");//原函数MyPen.CreatePen(PS_SOLID,1,RGB(255,0,0));//定义画笔颜色OldPen=pDC->SelectObject(&MyPen);x=-1.0,y=1/(1+25*x*x);p_x=x*200;p_y=-y*200;pDC->MoveTo(p_x,p_y);for (x=-1.0;x<=1.0;x+=0.0001){y=1/(1+25*x*x);p_x=x*200;p_y=-y*200;pDC->LineTo(p_x,p_y);}pDC->SelectObject(OldPen);MyPen.DeleteObject();//Lagrange插值x=-1.0;MyPen.CreatePen(PS_SOLID,1,RGB(0,255,0));OldPen=pDC->SelectObject(&MyPen);for(i=0;i<=10;i++){f[i]=1/(1+25*x*x);xx[i]=x;x+=0.2;}x=-1.0;y=1/(1+25*x*x);p_x=x*200,p_y=-y*200; //将x和y坐标各放大200倍pDC->MoveTo(p_x,p_y);for(k=0;k<=1000;k++){sum=0;for(i=0;i<=10;i++){l=1;for(j=0;j<=10;j++){if(i!=j)l=l*(x-xx[j])/(xx[i]-xx[j]);}sum+=f[i]*l;}p_x=x*200;p_y=-sum*200;pDC->LineTo(p_x,p_y);x+=0.002;}pDC->SelectObject(OldPen);MyPen.DeleteObject();}/////////////////////////////////////////////////////////////////////////////// CTestView printingBOOL CTestView::OnPreparePrinting(CPrintInfo* pInfo){// default preparationreturn DoPreparePrinting(pInfo);}void CTestView::OnBeginPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/){// TODO: add extra initialization before printing}void CTestView::OnEndPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/){// TODO: add cleanup after printing}/////////////////////////////////////////////////////////////////////////////// CTestView diagnostics#ifdef _DEBUGvoid CTestView::AssertValid() const{CView::AssertValid();}void CTestView::Dump(CDumpContext& dc) const{CView::Dump(dc);}CTestDoc* CTestView::GetDocument() // non-debug version is inline{ASSERT(m_pDocument->IsKindOf(RUNTIME_CLASS(CTestDoc)));return (CTestDoc*)m_pDocument;}#endif //_DEBUG/////////////////////////////////////////////////////////////////////////////// CTestView message handlers三、运算结果截屏红色的曲线为原函数图像，绿色曲线为Lagerange插值多项式函数对应的图像四、算法分析上述图像中绿色的曲线为Lagrange插值多项式所对应的图像，通过观察可见函数图像在靠近区间端点的地方出现了Runge现象。

Lagrange插值法和Newton插值法

插值法函数逼近一、实验目的：通过上机操作掌握插值法函数逼近的算法实现，掌握Lagrange 插值法和Newton 插值法的思想和区别。

二、实验内容：Lagrange 插值法和Newton 插值法的算法实现。

三、理论基础：（一）、Lagrange 插值法：n 次Lagrange 插值基函数：ni x x x x x l j i j ij j i ...,1,0,)()()(n0=--∏=≠= ，l i ，i=0,1,…,n 是n 次多项式并满足 l i (x j )=⎩⎨⎧≠=.,0,j 1i j i ，n 次Lagrange 插值多项式： ,)()()(0n ∑==ni i i x l x f x L显然，L ,n n P ∈并满足插值条件 L )()(n j j x f x =，j=0,1,…,n. （二）、Newton 插值法均差: f[x k ]=f(x k ), f[x k ,x k+1]=(f[x k+1]-f[x k ])/(x k+1-x k ) f[x k ,x k+1]=(f[x k+1]-f[x k ])/(x k+1-x k )为f 在x k 上的零阶均差，在x 1,+k k x 上的一阶均差和在21,,++k k k x x x 上的二阶均差. n 次Newton 插值多项式：f(x)=f(x 0)+f[x 0,x 1](x-x 0)+f[x 0,x 1,x 2](x-x 0)(x-x 1)+…+f[x 0,x 1,…x n ](x-x 0)(x-x 1)…(x-x n )Lagrange 插值法：代码：function yh= lagrange( x,y,xh ) n=length(x); m=length(xh); x=x(:); y=y(:); xh=xh(:);yh=zeros(m,1);c1 = ones(1,n-1);c2 = ones(m,1);for i=1:n,xp = x([1:i-1 i+1:n]);yh = yh + y(i) * prod((xh*c1-c2*xp')./(c2*(x(i)*c1-xp')),2); end运行结果：x(1)=0.4;x(2)=0.50;x(3)=0.70;x(4)=0.80;y(1)=-0.916281;y(2)=-0.693147;y(3)=-0.356675;y(4)=-0.223144;xh=0.6;lagrange(x,y,xh)ans =-0.5100Newton 插值法：代码：function newtoncz(a,b,n,f)ln=length(n);for k=1:lnm=n(k)-1;y=zeros(1,m+1);A=zeros(m+1);w=zeros(1,m+1);h=(b-a)/m;for i=1:m+1x(i)=a+(i-1)*h;y(i)=subs(f,findsym(f),x(i));endA(:,1)=y';for i=2:m+1for j=i:m+1A(j,i)=(A(j,i-1)-A(j-1,i-1))/(x(j)-x(j-i+1));endendp=A(1,1);w=vpa(w,4);syms X;w(1)=X-x(1);for i=2:m+1w(i)=w(i-1)*(X-x(i));p=A(i,i)*w(i-1)+p;p=simplify(p);endp=vpa(p,4);fprintf('n=%d的newton插值多项式为：',n(k));disp(p);运行结果：>> a=-1;>> b=1;>> n=[5,7,13];>> syms X;>> f=1/(1+25*X.^2);>> newtoncz(a,b,n,f)n=5的newton插值多项式为：3.316*X^4-4.277*X^2+1.n=7的newton插值多项式为：-13.13*X^6+20.96*X^4+.3475e-14*X^3-8.784*X^2-.2420e-15*X+1.n=13的newton插值多项式为：909.9*X^12-.3411e-12*X^11-2336.*X^10+.6632e-12*X^9+2202.*X^8-.1573 e-12*X^7-955.4*X^6+.2341e-12*X^5+198.7*X^4-.3535e-13*X^3-19.58*X^2 +.7881e-15*X+1.000四、比较分析：Lagrange插值多项式结构简单紧凑，在理论分析中甚为方便，在数值分析中经常使用，但在使用过程中也存在不便之处，当插值节点增加（相应的插值多项式的次数增加）、减少（相应的插值多项式的次数减少）时，构造差值多项式的基函数均需重新构造。

实验四 Lagrange函数插值方法(新)

实验四 Lagrange函数插值方法一、问题提出对于给定的一元函数的n+1个节点值。

试用Lagrange公式求其插值多项式或分段二次Lagrange插值多项式。

数据如下：试构造Lagrange多项式L，计算和的值。

二、要求1、利用Lagrange插值公式编写出插值多项式程序；2、给出插值多项式或分段三次插值多项式的表达式；3、根据节点选取原则，对问题（2）用三点插值或二点插值，其结果如何；4、对此插值问题用Newton插值多项式其结果如何。

三、目的和意义1、学会常用的插值方法，求函数的近似表达式，以解决其它实际问题；2、明确插值多项式和分段插值多项式各自的优缺点；3、熟悉插值方法的程序编制；4、如果绘出插值函数的曲线，观察其光滑性。

四、实验源代码#include<stdio.h>#define N 7float x[] = {1,2,3,4,5,6,7};float y[] = {0.368,0.135,0.050,0.018,0.007,0.002,0.001};float p(float xx){int i,k;_______________for( i=0; i<N; i++ ){m1 = 1; m2 = 1;_______________if( k != i ) {________________ ________________________________ }return pp;}main(){printf( "f(1.8)=%lf\n", p(1.8) ); ____________________}五、实验结果六、实验心得与体会。

实验一lagrange插值

实验一：拉格朗日插值算法的实现实验目的：1.验证拉格朗日插值算法对于不同函数的插值效果；2.验证随着插值结点的增多插值曲线的变化情况。

实验内容:根据课本P18的一般情形的过程编写拉格朗日插值方法的程序，实现拉格朗日插值。

源程序如下：#include<iostream>using namespace std;int main(){double x_[10],y_[10],t,y=0,x;int i,n,j,k;cout<<"多少个插值点？"<<endl;cin>>n;for(i=0;i<n;i++) //输入已知条件，即已知点{cout<<"输入插值节点x和y--(x,y):";cin>>x_[i]>>y_[i];}cout<<"输入x:"<<endl; //确定插值的位置cin>>x;for(k=0;k<n;k++) //实现插值的关键程序{t=1;for(j=0;j<n;j++){if(j!=k)t=((x-x_[j])/(x_[k]-x_[j]))*t; //插值基函数的计算}y=y+t*y_[k]; //求插值的结果}cout<<"近似的y值是: "<<y<<endl; //输出插值结果return 0;}实验结果：1）对y=x进行插值，已知（1,1）（2,2,）（3,3,），求当x=5时的插值结果2）对y=x^2进行插值3）（验证随着插值结点的增多插值曲线的变化情况）对y等于根号x插值用计算器计算根号8的值：可以知道：随着插值点的增多，插值结果越精确。

实验10 lagrange插值

《数值分析》实验10一．实验名称：Lagrange 插值二、实验目的：（1）学会Lagrange 插值。

三、实验要求（1）按照题目要求完成实验内容（2）写出相应的实验原理与程序代码（3）给出实验结果(有相应的图像，对比真实函数与插值函数)（4）写出相应的实验报告。

四、实验题目1、用六点Lagrange 插值计算sin(1)的近似值.2、考虑函数2()1f x x=+,[5,5]x ∈-, 在[-5,5]上取1n +个等距节点5k k x n =-+ (n k ,,2,1,0 =)作为插值节点构造n 次Lagrange 插值多项式。

(1) 做5次Lagrange 插值，计算()k f xi 的近似值（其中，105k k xi m =-+，0,1,2,,,20k m m ==）。

(2) 做10次Lagrange 插值，计算()k f xi 的近似值，并将结果与其真实值相比较。

1.程序：#include<math.h>#include<stdio.h>int main(){int n = 6,m=20, start_n=0,end_n=n+start_n,i,kk, k; //n:对应插值选用的节点double x[]={0.7,0.9,1.1,1.3,1.5,1.7} ,y[]={0.6442,0.7833,0.8912,0.9636,0.9975,0.9917} ;double xx=1;double sum=0;for(k=start_n;k<end_n;k++){double p=y[k];for(i=start_n;i<end_n;i++)if(i!=k)p*=(xx-x[i])/(x[k]-x[i]);sum+=p;}printf("sin(%.0f)=%.4f,\n",xx,sum);}结果：sin(1)=0.8414,2.（1）程序：#include<math.h>#include<stdio.h>int main(){int n=5,m=20,start=0,end=n+start+1,i,k1,k;//n:对应n次插值double x[n+1],y[n+1],z;for(k=0;k<=n;k++){x[k]=-5+10*k/n;y[k]=1/(1+pow(x[k],2));}printf("%d次插值,\n");for(k1=0;k1<=m;k1++){z=double(-5+0.5*k1);printf("f(%0.1f)=",z);double sum=0;for(k=start;k<end;k++){double p=y[k];for(i=start;i<end;i++)if(i!=k)p*=(z-x[i])/(x[k]-x[i]);sum+=p;}printf("%f,\n",sum);}}结果：5次插值,f(-5.0)=0.038462,f(-4.5)=-0.046034,f(-4.0)=-0.048077,f(-3.5)=0.007813,f(-3.0)=0.100000,f(-2.5)= 0.209736,f(-2.0)=0.321154,f(-1.5)=0.421274,f(-1.0)=0.500000,f(-0.5)=0.550120,f(0.0)=0.567308, f(0.5)=0.550120,f(1.0)=0.500000,f(1.5)=0.421274,f(2.0)=0.321154,f(2.5)=0.209736,f(3.0)=0.100 000,f(3.5)=0.007813,f(4.0)=-0.048077,f(4.5)=-0.046034,f(5.0)=0.038462,（2）程序：#include<math.h>#include<stdio.h>int main(){int n=10,m=20,start=0,end=n+start+1,i,k1,k;//n:对应n次插值double x[n+1],y[n+1],z;for(k=0;k<=n;k++){x[k]=-5+10*k/n;y[k]=1/(1+pow(x[k],2));}printf("%d次插值,\n",n);for(k1=0;k1<=m;k1++){z=double(-5+0.5*k1);double y_x=1/(1+pow(z,2));printf("f(%0.1f)=",z);double sum=0;for(k=start;k<end;k++){double p=y[k];for(i=start;i<end;i++)if(i!=k)p*=(z-x[i])/(x[k]-x[i]);sum+=p;}printf("%f,f(%.1f)-f*(%.1f)=%f\n",sum,z,z,sum-y_x);}}结果：10次插值,f(-5.0)=0.038462,f(-5.0)-f*(-5.0)=0.000000，f(-4.5)=1.578721,f(-4.5)-f*(-4.5)=1.531662 f(-4.0)=0.058824,f(-4.0)-f*(-4.0)=0.000000，f(-3.5)=-0.226196,f(-3.5)-f*(-3.5)=-0.301668 f(-3.0)=0.100000,f(-3.0)-f*(-3.0)=0.000000，f(-2.5)=0.253755,f(-2.5)-f*(-2.5)=0.115824 f(-2.0)=0.200000,f(-2.0)-f*(-2.0)=0.000000，f(-1.5)=0.235347,f(-1.5)-f*(-1.5)=-0.072346 f(-1.0)=0.500000,f(-1.0)-f*(-1.0)=0.000000，f(-0.5)=0.843407,f(-0.5)-f*(-0.5)=0.043407 f(0.0)=1.000000,f(0.0)-f*(0.0)=0.000000，f(0.5)=0.843407,f(0.5)-f*(0.5)=0.043407f(1.0)=0.500000,f(1.0)-f*(1.0)=0.000000，f(1.5)=0.235347,f(1.5)-f*(1.5)=-0.072346f(2.0)=0.200000,f(2.0)-f*(2.0)=0.000000，f(2.5)=0.253755,f(2.5)-f*(2.5)=0.115824f(3.0)=0.100000,f(3.0)-f*(3.0)=0.000000，f(3.5)=-0.226196,f(3.5)-f*(3.5)=-0.301668f(4.0)=0.058824,f(4.0)-f*(4.0)=0.000000，f(4.5)=1.578721,f(4.5)-f*(4.5)=1.531662f(5.0)=0.038462,f(5.0)-f*(5.0)=0.000000。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

给定函数211)(x x f +=
，现考察在区间【-5，5】上)(x f 上的等距插值问题。

1. 利用matlab 可以得到211)(x x f +=的图形如下图所示： x=-5:0.1:5;
y=1./(1+x.^2);
plot(x,y)
2. 作)(x f 的20个节点的分段线性插值)(20x lin ，其实现代码及图形如下：
x=-5:0.1:5;
y=1./(1+x.^2);
x1=linspace(-5,5,20)；
y1=interp1(x,y,x1,'linear')；
plot(x,y,’r ’,x1,y1,’b ’)
所得图形如下：
其中兰线我分段线性插值函数)(20x lin 的曲线
此处需说明由于此处利用的PLOT 函数其绘制曲线的原理既是描点，连线，其所得图形是折线。

所以通过plot 函数绘制)(x f 函数时，如果取点不够多，且恰好去20个等距节点时，其所得的图形和通过分段线性插值所得的)(20x lin 图形是一样，即若运行下列代码会得到下面图形：
x=linspace(-5,5,20)；
y=1./(1+x.^2)；
plot(x,y)
即其和通过分段线性插值所得的函数)(20x lin 的曲线是重合的。

3. 作)(x f 的21个等距节点的20次lagrange 插值函数)(20x l 。

此处由于matlab 中没有固定的lagrange 插值函数，所以定义lagrange 函数如下，并将其放入matlab 可搜索到的工作目录中:\\....\matlab7.0\work 中。

所定义的lagrange 函数如下：
（此处参考：Numerical Computing with MATLAB 【M 】 Cleve Moler, 并下载其附带的lagrange 函数）
% textbook page 35
function yh = lagrange(x,y,xh)
n = length(x);
m = length(xh);
x = reshape(x,n,1); % x = x(:);
y = reshape(y,n,1); % y = y(:);
xh = reshape(xh,m,1); % xh = xh(:);
yh = zeros(m,1);
c1 = ones(1,n-1);
c2 = ones(m,1);
for i=1:n,
xp = x([1:i-1,i+1:n]);
yh = yh + y(i) * prod((xh*c1-c2*xp')./(c2*(x(i)*c1-xp')),2);
end
然后运行下列代码：
x=linspace(-5,5,21)
y=1./(1+x.^2)
x1=linspace(-5,5,23)
y1=lagrange(x,y,x1)
plot(x,y,'r',x1,y1,'b')
可得到如下图形；
这里需说明用plot 函数所得的被插值函数)(x f 与20次lagrange 插值函数的曲线都不是其精确值，由于在绘制)(x f 曲线时，只取了【-5，5】上的21个点，而绘制)(20x l 函数时只取了【-5，5】上的23个点。

以下分别做出10次lagrange 插值函数)(10x l 与16次lagrange 插值函数)(16x l 以作比较。

如：)(x f 在【-5，5】上取11个点，再作10次lagrange 插值函数)(10x l ，然后运行下列代码：
x=linspace(-5,5,11)
y=1./(1+x.^2)
x2=linspace(-5,5,23)
y2=lagrange(x,y,x2)
plot(x,y,'r',x2,y2,'b')
即得如下图形
如：)(x f 在【-5，5】上取17个点，再作16次lagrange 插值函数)(16x l ，然后运行下列代码：
x=linspace(-5,5,17)
y=1./(1+x.^2)
x3=linspace(-5,5,23)
y3=lagrange(x,y,x3)
plot(x,y,'r',x3,y3,'b')
即得如下图形：
若将其绘制在一起则可得下面图形：plot(x1,y1,'r',x2,y2,'b',x3,y3,'g')。