收益法主要公式
评估 收益法公式

评估收益法公式收益法公式是一种在金融领域常用的评估方法,用于估计资产或投资的价值。
它主要基于预期未来的现金流,以及投资的风险和回报。
在这篇文章中,我们将介绍收益法公式的基本原理和应用。
收益法公式的基本原理是基于现金流的贴现。
它假设资产或投资的价值取决于预期未来的现金流的大小和时间。
根据这一原理,我们可以使用下面的公式来计算资产或投资的价值:V = (CF1 / (1+r)1) + (CF2 / (1+r)2) + ... + (CFn / (1+r)n)其中,V表示资产或投资的价值,CF代表未来每期的现金流量,r是折现率,n是现金流的期数。
这个公式的基本思想是通过将未来现金流的价值折现到现在,来计算资产或投资的现值。
在应用收益法公式时,我们需要确定以下几个关键要素:1. 未来现金流量:我们需要预测资产或投资未来每期的现金流量。
这包括预计的收入和支出,以及可能的资本回收。
2. 折现率:折现率反映了投资的风险和回报。
通常,较高的风险会导致较高的折现率。
折现率可以根据市场情况、行业标准或个体评估来确定。
3. 现金流的期数:我们需要确定现金流的期数,即预计现金流的持续时间。
这取决于资产或投资的特性和预测的可靠性。
使用收益法公式进行评估时,我们需要收集和分析相关数据,进行现金流的预测,并确定适当的折现率和现金流的期数。
然后,将这些数据代入收益法公式,计算资产或投资的价值。
需要注意的是,收益法公式作为一种估值方法,它的准确性受到许多因素的影响,包括数据质量、预测的可靠性、折现率的选择等。
因此,在使用收益法公式进行评估时,需要谨慎分析和判断,并结合其他评估方法和信息来综合判断资产或投资的价值。
综上所述,收益法公式是一种常用的评估方法,基于未来现金流的贴现来估计资产或投资的价值。
它的应用需要对未来现金流、折现率和现金流的期数进行合理的预测和选择。
然而,评估的准确性受到多个因素的影响,因此在使用时需要谨慎分析和判断。
收益法公式

收益法公式This model paper was revised by the Standardization Office on December 10, 2020收益法中的主要技术方法收益法实际上是在预期收益还原思路下若干具体方法的集合。
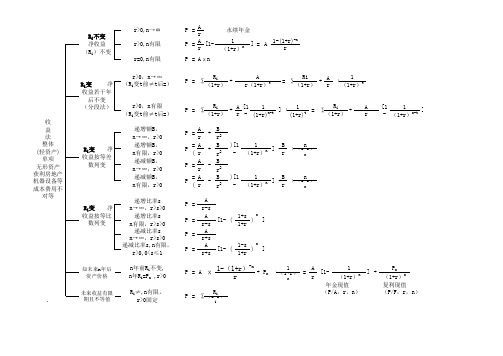
收益法中的具体方法可以分为若干类:(1)针对评估对象未来预期收益有无限期的情况划分,可分为有限期和无限期的评估方法;(2)针对评估对象预期收益额的情况划分,又可分为等额收益评估方法、非等额收益评估方法等。
为了便于学习收益法中的具体方法,先对这些具体方法中所用的字符含义做统一的定义:P——评估值;i——年序号;P n——未来第n年的预计变现值;R i——未来第i年的预期收益;r——折现率或资本化率;n——收益年期;t——收益年期;A——年金。
(一)纯收益不变1.在收益永续,各因素不变的条件下,有以下计算公式:P=A/r其成立条件是:(1)纯收益每年不变;(2)资本化率固定且大于零;(3)收益年期无限。
2.在收益年期有限,资本化率大于零的条件下,有以下计算公式:P=Ar[1−1(1+r)n]这是一个在估价实务中经常运用的计算公式,其成立条件是:(1)纯收益每年不变;(2)资本化率固定且大于零;(3)收益年期有限为n。
3.在收益年期有限,资本化率等于零的条件下,有以下计算公式:P=A×n其成立条件是:(1)纯收益每年不变;(2)收益年期有限为n;(3)资本化率为零。
(二)纯收益在若干年后保持不变1.无限年期收益。
其基本公式为:P=∑R i(1+r)i+Ar(1+r)nni=1其成立条件是:(1)纯收益在n年(含第n年)以前有变化;(2)纯收益在n年(不含第n年)以后保持不变;(3)收益年期无限;(4)r 大于零。
2.有限年期收益。
其计算公式为:P=∑R i()+Ar(1+r)[1−1()]t i=1其成立条件是:(1)纯收益在t 年(含第t 年)以前有变化;(2)纯收益在t 年(不含第t 年)以后保持不变;(3)收益年期有限为n ;(4)r 大于零。
资产评估市场法、收益法、成本法及年金现值终值主要公式
Ri变 净 收益按等差
数列变
递增额B, n→∞,r>0
递增额B, n有限,r>0
递减额B, n→∞,r>0
递减额B, n有限,r>0
Ri变 净 收益按等比
数列变
递增比率s n→∞,r>s>0
递增比率s n有限,r>s>0
递减比率s n→∞,r>s>0 递减比率s,n有限, r>0,0<s≤1
A r
[1 -
1 (1+r)n-t
]
P
=
A r
P
= (
A r
P
=
A r
P
= (
A r
+Leabharlann B r2+
B r2
-
B r2
-
B r2
)[1 -
1 (1+r)n
] -Br
ⅹ(1+nr)
n
)[1 -
1 (1+r)n
] +Br
ⅹ(1+nr)
n
P=
A r-s
P=
A r-s
[1- (
1+s 1+r
n
)]
P=
A r+s
收 益 法 整体 (轻资产) 单项 无形资产 获利房地产 机器设备等 成本费用不 对等
.
Ri不变 净收益 (Ri)不变
r>0,n→∞ r>0,n有限 r=0,n有限
P
=
A r
P
=
A r
[1-
P = Aⅹn
永续年金
收益法全部公式

一、收益法中的必须死记的两个公式:1、F=P×(1+i)n2、P=A/i×[1-1/(1+i)n] (年金现值公式)二、需要巧记的公式等比现值公式P=A/i-s×[1-(1+s/1+i)n] [当i≠s时]P=nA/(1+i) [当I=s时]三、需理解记忆的公式1、《理论与方法》P163中涉及土地使用权在不同年限,收益率等的换算,给出了好几个公式,让人一时无法记住。
如:V∞=VN×1/KNVn=VN×YN/Yn×(1+YN)N/(1+Yn)n×[(1+Yn)n-1]/[(1+YN)N-1]实际这些公式都无需死记,因为这里都隐含了一个前提,土地的年收益都是相同的,只是在不同年限,不同报酬率下折现值不同而已。
如果理解了这个道理,那例题中的解法都会变成以下的解题思路了。
解题思路:设土地年收益=a,30年土地价格=X则2500=a/10%×[1-1/(1+10%)40]X=a/10%×[1-1/(1+10%)30]2500/X= a/10%×[1-1/(1+10%)40]/ a/10%×[1-1/(1+10%)30]50年的土地价格。
解题思路:设土地年收益=a,50年土地价格=X3000=a/8%×[1-1/(1+8%)30]X=a/10%×[1-1/(1+10%)50]3000/X= a/8%×[1-1/(1+8%)30]/ a/10%×[1-1/(1+10%)50]X=2642元/平方米2、《理论与方法》P198,抵押贷款常数公式这个公式也不好记,不过仔细观察以下,就会发现,它不过是年金现值公式的变形,且是以年抵押贷款常数表示的,那样就好理解了。
P=A/I×[1-1/(1+i)n]记住按年金现值公式计算出的抵押贷款常数往往要换算成年抵押贷款常数。
收益法

0.87 5.00% 365 81.17 15.00%
3673
20814 6.00% 5.00% 35 58.77 7239.7
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
请输入评估价值
换算出评估对象建筑面积
收益法公式(净收益按一定比例递增): V=[A/(R-g)]×[1-(1+g) /(1+R) ] V:房地产价格 A:年纯收益 g:年均增长率 R:还原利率 n:未来可取得收益的年限 序号 项 目 数 基准 值 实际 求出值 (元) 24487
n n
一、 有效毛收入 1 日租金 2 空租及收租损失 3 计算周期(年) 4 建筑面积 运营费用 二、 1 房产税 2 维修费 3 管理费、保险费等 4 营业税、教育附加、维护建设 5 其他 三、 净收益 四、 还原利率 五、 年增长率 六、 可收益年限(年) 七、 委估房屋收益价值(万元) 八、 委估房屋收益单价(元/平方米)
143.00
100.84
特殊情况
非阁楼建筑面积 阁楼建筑面积 评估非阁楼单价 评估阁楼单价
(除地下室)非阁楼房屋价值(万元) (除地下室)阁楼房屋价值(万元)
100.84 0.00 14181 9927 143.00 0.00 46 0.00 #DIV/0! 0.00 0.00 #DIV/0! 0.00
401.27 70.81 472.09
请输入剩余年限 请输入地下室面积 地下室单价 地下室价值(万元) 请输入车库面积 请输入车库单价 车库价值(万元)
计算出年净收益值 计算出年运营费用 计算出年有效毛收入
收益法公式

收益法中得主要技术方法收益法实际上就是在预期收益还原思路下若干具体方法得集合。
收益法中得具体方法可以分为若干类:(1)针对评估对象未来预期收益有无限期得情况划分,可分为有限期与无限期得评估方法;(2)针对评估对象预期收益额得情况划分,又可分为等额收益评估方法、非等额收益评估方法等。
为了便于学习收益法中得具体方法,先对这些具体方法中所用得字符含义做统一得定义:P—-评估值;i-—年序号;Pn——未来第n年得预计变现值;R i——未来第i年得预期收益;r——折现率或资本化率;n——收益年期;t——收益年期;A——年金。
(一)纯收益不变1.在收益永续,各因素不变得条件下,有以下计算公式:P=A/r其成立条件就是:(1)纯收益每年不变;(2)资本化率固定且大于零;(3)收益年期无限、2。
在收益年期有限,资本化率大于零得条件下,有以下计算公式:这就是一个在估价实务中经常运用得计算公式,其成立条件就是:(1)纯收益每年不变;(2)资本化率固定且大于零;(3)收益年期有限为n。
3、在收益年期有限,资本化率等于零得条件下,有以下计算公式:P=A×n其成立条件就是:(1)纯收益每年不变;(2)收益年期有限为n;(3)资本化率为零。
(二)纯收益在若干年后保持不变1.无限年期收益、其基本公式为:其成立条件就是:(1)纯收益在n年(含第n年)以前有变化;(2)纯收益在n年(不含第n年)以后保持不变;(3)收益年期无限;(4)r大于零。
2.有限年期收益、其计算公式为:其成立条件就是:(1)纯收益在t年(含第t年)以前有变化;(2)纯收益在t年(不含第t年)以后保持不变;(3)收益年期有限为n;(4)r大于零。
这里要注意得就是,纯收益A得收益年期就是(n—t)而不就是n。
(三)纯收益按等差级数变化1。
在纯收益按等差级数递增,收益年期无限得条件下,有以下计算公式:其成立条件就是:(1)纯收益按等差级数递增;(2)纯收益逐年递增额为B;(3)收益年期无限;(4)r大于零。
收益法的公式

对于土地与建筑物合一的估价对象,当建筑物耐用年限短于土地使用权年限时,可采用下列方式之一处理:
1 先根据建筑物耐用年限确定未来可获收益的年限,选用对应的有限年的收益法计算公式,净收益中不应扣除建筑物折旧和土地取得费用的摊销;然后再加上土地使用权年限超出建筑物耐用年限的土地剩余使用年限价值的折现值。
2 将未来可获收益的年限设想为无限年,选用无限年的收益法计算公式,净收益中应扣除建筑物折旧和土地取得费用的摊销。
收益法的基本公式如下:
n Ai
V =∑ --------------
i=1 (1+R)i
式中V ─ 收益价格(元,元/m2);
Ai ─ 未来第i年的净收益(元,元/m2);
R ─ 资本化率(%);
n ─ 未来可获收益的年限(年)。
当利用土地与地上建筑物共同产生的收益单独求取土地价值时,在净收益每年不变、可获收益无限期的情况下,应采用下式:
AO-VB·RB
VL =------------------- ………………(5.3.9-1)
RL
当利用土地与地上建筑物共同产生的收益单独求取建筑物价值时,在净收益每年不变、可获收益无限期的情况下,应采用下式:
AO-VL·RL
VB =------------------- ………………(5.3.9-2)
RB
式中AO ─ 土地与地上建筑物共同产生的净收益(元,元/m2);
VL ─ 土地价值(元,元/m2);
VB ─ 建筑物价值(元,元/m2)。
收益法计算估值公式

收益法计算估值公式收益法是一种在资产评估和企业价值评估中常用的方法,通过预测未来的收益,并将其折算为现值来确定资产或企业的价值。
收益法计算估值的公式看起来可能有点复杂,但只要咱们一步步来,其实也没那么难理解。
先来说说收益法的基本原理哈。
想象一下,你有一家水果店,每年都能稳定地赚到一定的利润。
如果有人想买下你的水果店,他出的价格应该和这个店未来能给他带来的收益有关系,对吧?收益法就是基于这样的想法,认为资产的价值取决于它未来能产生的经济利益的现值。
那收益法的计算公式是啥呢?一般来说,常见的公式是这样的:V = ∑[Rt / (1 + i)^t]这里的 V 就是资产的评估价值,Rt 是第 t 年的预期收益,i 是折现率,t 是收益期限。
举个例子吧,比如说有一家小型制造企业,预计未来 5 年每年的净利润分别是 10 万元、12 万元、15 万元、18 万元和 20 万元。
咱们假设折现率是 10%。
第一年的现值= 10 / (1 + 10%)^1 ≈ 9.09 万元第二年的现值= 12 / (1 + 10%)^2 ≈ 9.92 万元第三年的现值= 15 / (1 + 10%)^3 ≈ 11.27 万元第四年的现值= 18 / (1 + 10%)^4 ≈ 12.42 万元第五年的现值= 20 / (1 + 10%)^5 ≈ 12.42 万元把这五年的现值加起来,9.09 + 9.92 + 11.27 + 12.42 + 12.42 ≈ 55.12 万元,这大概就是这家企业的评估价值啦。
在实际应用中,确定预期收益、折现率和收益期限可不容易。
就拿预期收益来说,得对市场趋势、行业竞争、企业自身的经营状况等好多因素进行深入分析。
我之前接触过一个案例,是一家传统的服装加工厂。
他们想评估一下企业的价值,以便考虑引入新的投资者。
我们在预测预期收益的时候,可费了不少功夫。
先是详细研究了他们过去几年的销售数据,发现他们的主打产品在市场上的份额逐渐被一些新兴品牌挤占。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
收益法主要公式第二节报酬资本化法的公式-2五、净收益按一定比率递增的公式(掌握)净收益按一定比率递增的公式根据收益期限,分为有限年和无限年两种。
(一)收益期限为有限年的公式收益期限为有限年的公式如下:【例7-10】某宗房地产的受益期限为48年;未来第一年的净收益为16万元,此后每年的净收益在上一年的基础上增长2%;该类房地产的报酬率为9%。
请计算该房地产的收益价值。
【解】该房地产的收益价值计算如下:(二)收益期限为无限年的公式收益期限为无限年的公式为:公式原型为:此公式的假设前提是:?净收益未来第1年为此后按比率g逐年递增:?报酬率为,且g,;?收益期限为无限年。
此时要求g,的原因是,从数学上看,如果g?,就会无穷大。
但这种情况在现实中不可能出现,原因之一是任何房地产的净收益都不可能以极快的速度无限递增下去,原因之二是较快的递增速度意味着较大的风险,从而要求提高报酬率。
【例7-11】预测某宗房地产未来第一年的净收益为16万元,此后每年的净收益在上一年的基础上增长2%,收益期限可视为无限年,该类房地产的报酬率为9%。
请计算该房地产的收益价值。
【解】该房地产的收益价值计算如下:六、净收益按一定比率递减的公式(了解)净收益按一定比率递减的公式根据收益期限,分为有限年和无限年两种。
(一)收益期限为有限年的公式式中:g——净收益逐年递减的比率,其中,净收益未来第一年为,未来第二年为 (1-g),2n-1未来第三年为 (1-g),以此类推,未来第n年为 (1-g)。
公式原型为:此公式的假设前提是:?净收益未来第1年为,此后按比率g逐年递减:?报酬率为y,y?0;?收益期限为有限年。
(二)收益期限为无限年的公式公式原型为:此公式的假设前提是:?净收益未来第1年为a,此后按比率g逐年递减:?报酬率为y,y大于零;?收益期限为无限年。
净收益等于有效毛收入减去运营费用。
如果有效毛收入与运营费用逐年递增或递减的比率不等,也可以利用净收益按一定比率递增或递减的公式计算估价对象的收益价格。
例如,假设有效毛收入逐年递增的比率为g,运营费用逐年递增的比率为g,收益期限为有限ie年,则计算公式为:式中 i—有效毛收入;—运营费用;gi—i逐年递增的比率;ge—e逐年递增的比率。
公式原型为:此公式的假设前提是:?有效毛收入i按比率g逐年递增,运营费用e按比率g 逐年ie递增;?g或g不等于报酬率y;?收益期限为有限年n,并且满足 ie同理,如果有效毛收入与运营费用逐年递减的比率不等,或者一个逐年递增另一个逐年递减,其计算公式都能较容易地推导出。
其中,在有效毛收入始终大于运营费用的前提下,收益期限为无限年的计算公式为:在上述公式中,有效毛收入逐年递增时,g前取“一”,逐年递减时,g前取“,”;ii前取“,”。
运营费用逐年递增时,g前取“一”,逐年递减时,gee【例7-12】预测某宗房地产未来第一年的有效毛收入为20万元,运营费用为12万元,此后每年的有效毛收入会在上一年的基础上增长5%,运营费用增长3%,收益期限可视为无限年,该类房地产的报酬率为8%。
请计算该宗房地产的收益价值。
【解】该宗房地产的收益价格计算如下:【例7-13】预测某宗房地产未来每年的有效毛收入不变,为16万元,运营费用第一年为8万元,此后每年会在上一年的基础上增长2%,该类房地产的报酬率为10%。
请计算该宗房地产的收益价值。
【解】由于一定期限之后,该宗房地产的运营费用会超过有效毛收入,所以在计算其收益价格之前,先计算其合理经营期限n:七、净收益在前后两段变化规律不同的公式(熟悉)净收益在前后两段变化规律不同的公式,根据前段净收益的变化,有无规律变化、每年不变、按一定数额递增、按一定数额递减、按一定比率递增、按一定比率递减等情形;后段净收益的变化,在实际估价中主要是假定每年不变,也可根据具体情况设定为按一定数额递增、按一定数额递减、按一定比率递增、按一定比率递减等情形;根据收益期限,又分为有限年和无限年两种。
下面以后段净收益每年不变的情形来说明。
(,)收益期限为有限年的公式收益期限为有限年的公式为:式中t——净收益有变化的期限。
公式原型为:此公式的假设前提是:?净收益在未来t年(含第t年)有变化,分别为a,a,…,12a,在第t年以后无变化为a,?报酬率为y,且y不等于零;?收益期限为有限年n。
t(二)收益期限为无限年的公式收益期限为无限年的公式为:公式原型为:此公式的假设前提是:?净收益在未来t年(含第t年)有变化,分别为a1,a2…,;?报酬率为y,且y大于零;?收益期限为无限年。
at,在第t年以后无变化为a净收益在前后两段变化规律不同的公式有重要的实用价值。
因为在现实中每年的净收益是不同的。
但如果如果采用净收益一直每年不变或者有规律变化的公式,如公式: 或者来估价,有时未免太片面;而如果根据净收益每年都有变化的实际情况来估价,又不大可能(除非收益期限较短)。
为了解决这个矛盾,一般是根据估价对象的经营状况和市场环境,预测其未来5年~10年的净收益,并假设此后的净收益每年不变或者按一定规律变动,然后对这两段净收益进行折现处理,计算出房地产的价值。
特别是像商店、旅馆、餐饮、娱乐之类的房地产,在建成后的前几年由于试营业等原因收益可能不稳定,更适用这种公式来估价。
【例7-14】某宗房地产的收益期限为38年,预测其来来5年的净收益分别为20万元、22万元、25万元、28万元、30万元,从未来第6年到第38年每年的净收益将稳定在35万元左右,该类房地产的报酬率为10%。
请计算该房地产的收益价值。
【解】该宗房地产的收益价格计算如下:【例7-15】预测某宗房地产未来5年的净收益分别为20万元、22万元、25万元、28万元、30万元,从未来第6年到无穷远每年的净收益将稳定在35万元左右,该类房地产的报酬率为10%。
请计算该宗房地产的收益价值。
【解】该宗房地户的收益价格计算如下:,310(20(万元)与例7- 14的38年收益期限的房地产价格300(86万元相比,例7-15收益期限为无限年的房地产价格要高9(34万元(310(20,300(86,9(34)。
八、预知未来若干年后价格的公式(掌握)预测房地产未来t年期间的净收益分别为a,a,…,a,第t年末的价格为v,则其12tt现在的价格为:式中 v——房地产现在的价格。
t——预测净收益的期限。
如果购买房地产的目的是为了持有一段时间后转售,则t为持有房地产的期限,简称持有期。
a——房地产未来t年期间的净收益,简称期间收益。
iv——房地产在未来第t年末的价格(为第t年末的市场价值或残值。
如果购买房地t产的目的是持有一段时间后转售,则为预测的第t年末转售时的价格减去销售税费后的净值,称为净转售价值或期末转售收益,是在持有期末转售房地产时可以获得的净收益)。
公式原型为:此公式的假设前提是:?已知房地产未来t年期间的净收益为a,a,…a;?房地产12t在第t年末的价格为v;?期间报酬率和期末报酬率相同,为y。
t上述公式根据期间收益的变化,可具体化为下列公式:(1)期间收益每年不变的公式上述公式中如果期间收益每年不变为a,则公式为:(2)期间收益按一定数额递增的公式上述公式中如果期间收益按数额b逐年递增,则公式为:(3)期间收益按一定数额递减的公式上述公式中如果期间收益按数额b逐年递减,则公式为:(4)期间收益按一定比率递增的公式上述公式中如果期间收益按比率g逐年递增,则公式为:(5)期间收益按一定比率递减的公式上述公式中如果期间收益按比率g逐年递减,则公式为:上述公式中如果难以预测未来的价格,而能预测未来价格相对于当前价格的变化率(即相对价值变动),例如增值率为?,即v,v(1,?),以期间收益每年不变的情形为例, t则公式为:对此公式进行整理,可得到下列公式:t如果预测的是未来价格每年的上涨率为g,即v=v(1+g),则公式为: t对此公式进行整理,可得到下列公式:预知未来若干年后的价格的公式,一是适用于房地产目前的价格难以知道,但根据发展前景比较容易预测其未来的价格或未来价格相对于当前价格的变化率时,特别是在某地区将会出现较大改观或者房地产市场行情预期有较大变化的情况下。
二是对于收益期限较长的房地产,有时不是按照其收益期限来估价,而是先确定一个合理的持有期,然后预测持有期间的净收益和持有期末的价值,再将它们折算为现值。
实际上,收益性房地产是一种投资品,作为投资品的典型收益包括两部分:一是在持有房地产期间每单位时间(如每月、每年)所获得的租赁收益或经营收益;二是在持有期末转售房地产时所获得的增值收益。
因此,预知未来若干年后的价格的公式成了评估收益性房地产价值的最常用公式。
下面举几个例子予以具体说明。
【例7-16】某宗房地产现行的价格为2000元/?,年净收益为200元/?,报酬率为10%。
现获知该地区将兴建一座大型的现代化火车站,该火车站将在6年后建成投入使用,到那时该地区将达到该城市现有火车站地区的繁华程度。
在该城市现有火车站地区,同类房地产的价格为5000元/?。
据此预计新火车站建成投入使用后,新火车站地区该类房地产的价格将达到5000元/?。
请计算获知兴建火车站后该宗房地产的价格。
【解】获知兴建火车站后该宗房地产的价格计算如下:可见,该宗房地产在获知兴建火车站之后,价格由2000元/?上涨到3693元/?。
【例7-17】某写字楼过去的市场价格为12000元/?,目前房地产市场不景气,其市场租金为每天3元/?。
该类写字楼的净收益为市场租金的70%。
预测房地产市场3年后会回升,那时该写字楼的市场价格将达12500元/?,转让该写字楼的税费为市场价格的6%。
如果投资者要求该类投资的报酬率为10%,请求取该写字楼目前的价值。
【解】该写字楼目前的价值求取如下:【例7-18】某出租的旧办公楼的租约尚有2年到期,在此最后2年的租期中,每年可收取净租金80万元(没有费用支出),到期后要拆除作为商业用地。
预计作为商业用地的价值为1100万元,拆除费用为50万元,该类房地产的报酬率为10%。
请求取该旧办公楼的价值。
【解】该旧办公楼的价值求取如下:,1006(61(万元)【例7-19】预测某宗房地产未来两年的净收益分别为55万元和60万元,两年后的价格比现在的价格上涨5%。
该类房地产的报酬率为10%。
请计算该宗房地产现在的价格。
【解】该宗房地产现在的价格求取如下:【例7-20】预测其未来第一年的净收益为24000元,未来5年的净收益每年增加1000元,价格每年上涨3%,报酬率为9(5%。
请求取该宗房地产当前的价格。
【解】选用下列公式求取该宗房地产当前的价格:根据题意已知:将上述数据代入公式后计算如下:对上述等式进行合并同类项并计算后得到:v,376096(65(元)下面是赠送的几篇网络励志文章需要的便宜可以好好阅读下,不需要的朋友可以下载后编辑删除~~谢谢~~出路出路,走出去才有路“出路出路,走出去才有路。
