控制系统的极坐标图
控制工程 第5章 系统的频率特性
频响函数 幅频特性 相频特性
1 G ( j ) 1 j 0.005 1 | G ( j ) | 1 (0.005 )2 0 0.005 ( ) arctan arctan 1 1 arctan(0.005 )
可见:输入信号频率越高,稳态输出幅值衰减越大,相移越大(这正是惯性环节 的频响特性)。
18:10:18
5-1 频率特性
本例题也可以采用第 4 章介绍的求时间响应的方法获 得稳态响应,即利用传递函数求出零状态响应,然后分 解出其中的稳态响应。 而利用频响函数可直接求出稳态 响应。
21
y( t ) L [Y ( s )] 0.555e 200 t
m k f (t)/x (t) f(t)—力
A
f(t) = Asin(ωt)
A B
x(t)—位移 B
0 -A
ωt
υ
单自由度有阻尼振动 x(t) = Bsin(ωt+υ)+瞬态响应 系统力学模型 教材101页图5-2中的标注“υ”不对,应改成“υ/ω”,
18:10:18
或将横坐标标尺改成“ωt”。
5-1 频率特性
相频特性 = 正弦信号稳态响应相角 - 正弦输入信号相角
幅频特性和相频特性合起来描述了系统的频响特 性或频率特性。
18:10:18
13
5-1 频率特性
系统频率特性的获得 解析法 令输入x(t)=x0sin(t),求解微分方程的特解(稳 态解)。可以利用拉氏变换求解;
利用频率响应函数;
实验法
输入正弦信号,测量稳态输出。
18:10:18
5-1 频率特性
利用频率响应函数求频率特性 频率响应函数的定义:对连续线性定常系统,输出 的付立叶变换 C(j) 与输入的付立叶变换 R(j) 之比 ,叫频率响应函数,简称频响函数,也称为正弦传 递函数,记作G(j) 。即
自动控制原理课后习题答案,第5章(西南科技大学)

j
1(
j
5
1)
由频率特性可得:
解:
20
lg
0.4
1
L()
20 20
lg lg
0.41 5
20
lg
20
3
5
1 0.4 1
L() 3 2 10 4 3 20 5
可见:c 0.4
()
arctan
90
arctan 5
2
arc
tan 10
2
将 代c 入 ()
)( 1
1
s
1)
其中 1 10n 1
因 20lg K 20得K 10
因 20lg Mr 40 20
由Mr 2
1
12
得 0.05
10s2
G(s) (s2 0.1s 1)(0.1s 1)
5-8 已知单位反馈系统开环传递函数
G(s)H
(s)
s(s2
20(s 1) 2s 10)(s
1
2 10 时,直线斜率由
0dB/dec 变 为 -40dB/dec 、
10 5
40 60
当3 5 时,直线斜率由-
40dB/dec变为-20dB/dec 。
相频特性曲线由各环节的相频特性相加获得,计算几个点的 值绘出大致曲线。
num=[20 20]; den=[1 7 20 50 0]; bode(num,den) grid
20 lg K
由
lg1 lg10
得K= 100
40
G(s)
100(0.316s 1) s2 (0.00316s 1)
解(c) :系统最左端直线的斜率为40dB/dec,得 v = -2,系统有两 个纯微分环节。1 和n 分别是振荡和惯性环节的转折频 率,则系统开环传递函数为:
自动控制原理习题
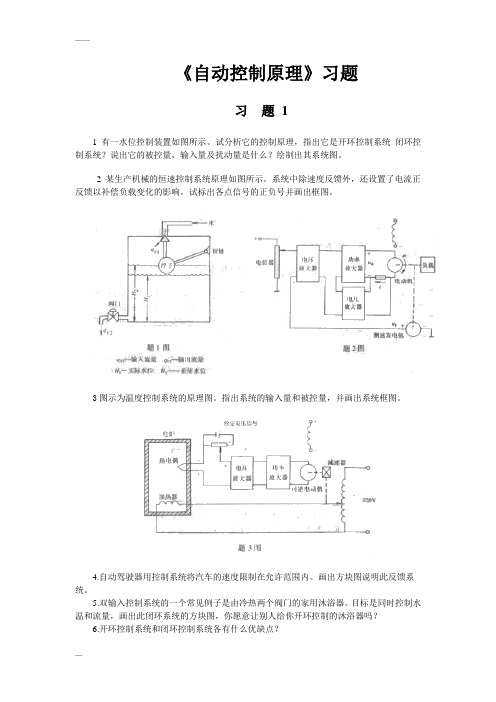
《自动控制原理》习题习题11有一水位控制装置如图所示。
试分析它的控制原理,指出它是开环控制系统闭环控制系统?说出它的被控量,输入量及扰动量是什么?绘制出其系统图。
2 某生产机械的恒速控制系统原理如图所示。
系统中除速度反馈外,还设置了电流正反馈以补偿负载变化的影响。
试标出各点信号的正负号并画出框图。
3图示为温度控制系统的原理图。
指出系统的输入量和被控量,并画出系统框图。
4.自动驾驶器用控制系统将汽车的速度限制在允许范围内。
画出方块图说明此反馈系统。
5.双输入控制系统的一个常见例子是由冷热两个阀门的家用沐浴器。
目标是同时控制水温和流量,画出此闭环系统的方块图,你愿意让别人给你开环控制的沐浴器吗?6.开环控制系统和闭环控制系统各有什么优缺点?7.反馈控制系统的动态特性有哪几种类型?生产过程希望的动态过程特性是什么?习题21 试分别写出图示各无源网络的传递函数。
习题1图2 求图示各机械运动系统的传递函数。
(1)求图a的=?(2)求图b的=?(3) 求图c的=?习题2图3 试分别写出图中各有源网络的传递函数U2(s)/ U1(s)。
习题3图4交流伺服电动机的原理线路和转矩-转速特性曲线如图所示。
图中,u为控制电压.T 为电动机的输出转矩。
N为电动机的转矩。
由图可T与n、u呈非线性。
设在某平衡状态附近用增量化表示的转矩与转速、控制电压关系方程为k n、k c为与平衡状态有关的值,可由转矩-转速特性曲线求得。
设折合到电动机的总转动惯量为J,粘滞摩擦系数为f,略去其他负载力矩,试写出交流伺服电动机的方程式并求输入为u c,输出为转角θ和转速为n时交流伺服电动机的传递函数。
习题4图5图示一个转速控制系统,输入量是电压V,输出量是负载的转速 ,画出系统的结构图,并写出其输入输出间的数学表达式。
习题5图6 已知一系统由如下方程组组成,试绘制系统框图,求出闭环传递函数。
7 系统的微分方程组如下:其中K0,K1,K2,T均为正常数。
控制工程基础第四章频域响应法

幅频特性A(): 稳态输出信号的幅值与输入信号的幅值之比: A() Ac G( j) A
相频特性(): 稳态输出信号的相角与输入信号相角之差:
() G( j)
幅相频率特性G(j) : G(j) 的幅值和相位均随输入正弦信
号角频率的变化而变化。 G( j ) A(w)e j ()
在系统闭环传递函数G(s)中,令s= j,即可得到系统的频率 特性。
控制工程基础第四章频 域响应法
2021/7/13
频率响应法是二十世纪三十年代发展起来的一种经典工 程实用方法,是一种利用频率特性进行控制系统分析的图解方 法,可方便地用于控制工程中的系统分析与设计。频率法用于 分析和设计系统有如下优点:
(1)不必求解系统的特征根,采用较为简单的图解方法 就可研究系统的稳定性。由于频率响应法主要通过开环频率特 性的图形对系统进行分析,因而具有形象直观和计算量少的特 点。
对相角进行线性分度;横轴:对频率取以10为底的对数后进行分度)
,合称为伯德图(Bode图)。
对数幅频特性记为
单位为分贝(dB)
对数相频特性记为
单位为弧度(rad)
L(w) (dB) ... 40 20
0
0.01
-20
-4...0
(w)
... 90o
45o
0o 0.01
-45o -9...0o
0. 1
(3)具有相同幅值的两个系统, 由0时, 最小相位系统的相角迟后最小, 而非最小相位系统的相角迟后则较大。
1 : 0 90o Ts 1
1 : 180o 90o Ts 1
Ts 1: 0 90o Ts 1: 180o 270o
(4)非最小相位一般由两种情况产生: 系统内包含有非最小相位元件(如 延迟因子); 内环不稳定。
自动控制理论_哈尔滨工业大学中国大学mooc课后章节答案期末考试题库2023年

自动控制理论_哈尔滨工业大学中国大学mooc课后章节答案期末考试题库2023年1.对于惯性环节【图片】,下列说法错误的是()。
参考答案:其微分方程为。
2.负反馈系统的开环极点为-1、-4(两重极点),开环零点为-2;若该系统具有一对实部为-3.75的共轭复极点,那么该系统的另外一个极点为()。
参考答案:-1.53.某单位负反馈控制系统的开环传递函数为【图片】,若使该系统在单位斜坡信号作用下的稳态误差小于0.2 ,那么K的范围应为()。
参考答案:44.传递函数为【图片】,在阶跃输入下,输出响应的形式为()。
参考答案:单调上升5.系统的开环传递函数是指()。
参考答案:所指定的闭环回路主反馈点断开后,反馈信号和偏差信号之比6.设单位反馈系统的开环传递函数为【图片】,当K由0增大时,闭环系统()。
参考答案:由不稳定到稳定7.控制系统的稳态响应是指【图片】时()。
参考答案:系统对某一输入信号的固定响应8.系统的开环传递函数为【图片】,当增大K时,闭环系统阶跃响应的超调量(),调整时间()。
(调整时间近似取【图片】)参考答案:增加;不变9.已知单位反馈系统的开环传递函数为【图片】,其闭环系统稳定的条件是()。
参考答案:K>1510.控制系统如图所示,若使系统在斜坡输入下的稳态误差为零,【图片】应取为()。
(定义误差e(t)=r(t)-c(t))【图片】参考答案:1/K11.已知单位反馈系统的开环传递函数为【图片】,当输入信号为【图片】时,闭环系统输出的稳态误差为()。
参考答案:0.212.求取控制系统的时域响应的方法有()。
参考答案:求取系统的输出,并求其拉氏反变换_求得其微分方程的通解和特解之和_求得暂态分量和稳态分量之和_求得零输入响应和零状态响应之和13.减小或消除系统稳态误差的方法主要有()。
参考答案:增大系统的开环增益_引入适当的前馈环节_在前向通道中串联积分环节14.如果一个线性系统是稳定,那么()。
孙炳达版 《自动控制原理》第5章 控制系统的频率特性分析法-3

比例环节可以完全、真实地复现任何频率的输入 信号,幅值上有放大或衰减作用;υ (ω)=0º ,表示输 出与输入同相位,既不超前也不滞后。
5.3 典型环节的频率特性
二、积分环节 1.代数表达式 传递函数
G (s) 1 s 1
频率特性 相频特性
幅频特性
A( )
1 1 1 j 90 G( j ) j e j () 90
对数频率特性曲线是一条斜线, 斜率为-20dB/dec, 称为高频渐 近线,与低频渐近线的交点为ωn=1/T,ωn称为交接频率或转 折频率,是绘制惯性环节的对数频率特性时的一个重要参数。
5.3 典型环节的频率特性
3.伯德图 对数幅频图
L( ) 20lg A( ) 20lg 1 1 2T 2 20lg 1 2T 2
G ( j ) 1 j 2 2 2 (1 2 2 ) j 2 (1 2 2 ) 2 (2 ) 2 e
2 T j arctan 1 2 2
5.3 典型环节的频率特性
2.极坐标图 理想微分环节的极坐标图在0 <<的范围内,与正虚轴重合。 可见,理想微分环节是高通滤 波器,输入频率越高,对信号的 放大作用越强;并且有相位超前 作用,输出超前输入的相位恒为 90º ,说明输出对输入有提前性、 预见性作用。 (纯微分)
在控制工程中,采用分段直线表示对数幅频特征 曲线,作法为: a.当Tω<<1(ω<<1/T)时,系统处于低频段 L( ) 20lg1 0 b.当Tω>>1(ω>>1/T)时,系统处于高频段
L( ) 20lg T
此直线方程过(1/T,0)点, 且斜率为-20dB/dec。
实验5 控制系统的极坐标图,

实验5 控制系统的极坐标图一.实验目的1.利用计算机作出开环系统的极坐标图;2.极坐标图系统分析二.实验步骤1.在Windows界面上用鼠标双击matlab图标,即可打开MATLAB 命令平台。
2.练习相关M函数极坐标绘图函数:(nyquist图)nyquist(sys)nyquist(sys,w)[re,im,w]=nyquist(sys)函数功能:奈奎斯特轨线作图命令,即极坐标图。
格式1:给定开环系统的模型对象sys,作极坐标。
频率w的范围自动给定。
格式2:给定开环系统的模型对象sys,作极坐标。
频率w的范围人工给定。
格式3:返回极坐标图参数向量,不作图。
re为复变函数的实部向量,real[G(jωre=。
)G(jω)]im为复变函数的虚部向量,imagim=。
G(jω)][G(jω)w为频率向量,单位为[弧度]/秒。
例如,系统开环传递函数为10s 2s 10)s (G 2o ++= 作图程序为num =[0 0 10]; %作多项式模型图奈奎斯特图 den=[1 2 10]; sys =tf(num,den); %系统对象nyquist(sys); %绘制极坐标图如果作图趋势不明显,可以采用下述方法改进:(1)使用命令axis()改变坐标显示范围axis([-1,1.5,-2,2]) %改变坐标显示范围(2)给定角频率变量w =0:0.1:100;nyquist(sys,w);绘制的极坐标图如图14所示。
三.实验内容1.)1Ts (s 1)s (G += 要求:作极坐标图。
如展示不清,可改变坐标范围或者设定角频率变量(w=w1:Δw:w2)。
2.212121T T or T T ,)1s T (s )1s T (K )s (G <>++=要求:(1)作极坐标图。
可改变坐标范围或者设定角频率变量w ; (2)比较时与21T T >21T T <时两图的区别与特点。
3.2121221T T or T T ,)1s T (s )1s T (K )s (G >>++=要求:(1)作极坐标图。
自控原理复习练习题

⾃控原理复习练习题电科10《⾃动控制原理》复习参考练习题⼀、单项选择题:1.控制系统的上升时间t r,调节时间t s等反映出系统的()A.相对稳定性 B.绝对稳定性 C.快速性 D.平稳性2.根据给定值信号的特征分类,控制系统可分为()A.恒值控制系统、随动控制系统和程序控制系统B.反馈控制系统、前馈控制系统、反馈复合控制系统C.最优控制系统和模糊控制系统D.连续控制系统和离散控制系统3.系统的传递函数()A.与输⼊信号有关B.与输出信号有关C.完全由系统的结构和参数决定D.既由系统的结构和参数决定,也与输⼊信号有关4.⼀阶系统的阶跃响应()A.当时间常数T较⼤时有超调 B.当时间常数T较⼩时有超调C.有超调 D.⽆超调5.随动系统中最常⽤的典型输⼊信号是抛物线函数和()A.脉冲函数 B.阶跃函数 C.斜坡函数 D.正弦函数6.确定系统闭环根轨迹的充要条件是()A.根轨迹的模⽅程 B.根轨迹的相⽅程C.根轨迹增益 D.根轨迹⽅程的阶次7.正弦信号作⽤于线性系统所产⽣的频率响应是()A.输出响应的稳态分量 B.输出响应的暂态分量C.输出响应的零输⼊分量 D.输出响应的零状态分量8.Ⅱ型系统对数幅频特性的低频段渐近线斜率为()A.-60(dB/dec) B.-40(dB/dec)C.-20(dB/dec) D.0(dB/dec)9.设开环系统频率特性G (j ω)=3)1(10ωj +,则其频率特性相位移?(ω)=-180 时,对应频率ω为() A . 10(rad/s ) B .3(rad/s ) C .3(rad/s ) D . 1(rad/s )10. 进⾏串联滞后校正后,校正前的截⽌频率ωc 与校正后的截⽌频率ωc ′的关系,通常是()A .ωc = ωc ′B .ωc > ωc ′C .ωc < ωc ′D .ωc 与ωc ′⽆关11. 常⽤的⽐例、积分与微分控制规律的另⼀种表⽰⽅法是()A . PIB . PDC .ID D . PID12. 伯德图中的⾼频段反映了系统的()A .稳态性能B .动态性能C .抗⼲扰能⼒D .以上都不是13.结构类似的最⼩相位系统和⾮最⼩相位系统相⽐,最⼩相位系统⼀定满⾜()A .两者幅频特性不同,相频特性也不同B 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
控制系统的极坐标图
电气三班 李向辉 201230050615
一.实验目的
1. 利用计算机作出开环系统的极坐标图(Nyquist 图);
2. 利用极坐标图进行系统分析。
w 的范围自动设定。
函数格式2:角频率向量w 的范围可以由人工给定(例如,w =1:0.1:100)。
函数格式3:返回变量格式。
计算所得的实部Re 、虚部Im 及角频率w 返回至MATLAB 命令窗口,不作图。
三.实验内容
1.)
1(1)(+=Ts s s G ,要求作极坐标图(如展示不清,可改变坐标范围或者设定角频率变量(2::1w w w w ∆=)),令T =1。
num=1;
den=[1 1 0];
nyquist(num,den);
2.2121,)
1()1()(T T s T s s T k s G >++= or 21T T < 要求:(a )作极坐标图(可改变坐标范围或者设定角频率变量w ); 令2=k ,1,221==T T or 2,121==T T
num=[4 2];
den=[1 1 0];
nyquist(num,den);
hold on
num=[2 2];
den=[2 1 0];
nyquist(num,den);
hold on
曲线关于虚轴对称。
3.21221,)
1()1()(T T s T s s T k s G >++= or 21T T < 要求:(a )作极坐标图(可改变坐标范围或者设定角频率变量w ); 令2=k ,1,221==T T or 2,121==T T
num=[4 2];
den=[1 1 0 0];
nyquist(num,den);
hold on num=[2 2];
den=[2 1 0 0];
nyquist(num,den);
hold on
曲线轨迹相同,方向相反。
四.实验报告要求
完成上述各题给定要求并做好实验记录。
