3-3物理抽气 打气问题
选修3-3中打气和抽气问题

分析:对打了40次的总的空气运用波意耳定律列式求解即可. 解答:每打一次把一个大气压强的空气打进去125ml,打了40次,总体积 V1=0.125×40=5L,气压为P1=1atm; 压入胎内后,体积减小为V2=2L, 根据玻意耳定律得: P1V1=P2V2 解得:P2=2.5atm 答:打了40次后胎内空气压强为2.5atm
解析:设打入的空气体积为V1,到湖底后,这部分空气的体积为V2. 湖底的压强P2=P0+p水=p0+ρ水gh=2 atm T2 = 280K 铁箱充气后所受浮力为F浮=ρ水gV2 上浮的条件是ρ水gV2-mg≥0 有V2≥ρ水(m)=103(560) m3=0.56 m3 由题意可知:P1=1 atm T1 = 300K 由理想气体状态方程有: P0V1/T1=P2V2/T2 得V1=P2V2T1/T2·P0≤280(2×0.56)×1(300) m3=1.2 m3 故至少需要打入1.2 m3的1 atm、27 °C的空气.
3、用打气筒给自行车内胎打气,一次可打入温度为27℃、压强为105Pa 的空气400cm3.如果车胎与地面接触时自行车内胎的容积为1600cm3,接 触面积为20cm2,要使它在370C时能负重820N,应打气几下?(没打气前 车胎内少量的气体可忽略) 设要打n次气达到要求. 据题,打n次气后胎内气体的压强应达到: P2=F/S=820/20×10-4=4.1×105Pa; 每打一次可压入压强为105Pa的空气400×10-6m3, 则打了n次,总体积为:V1=n×400×10-6m3,气压为:P1=105Pa,温度 为:T1=300K; 压入胎内后,体积减小为:V2=1.6×10-3m3,气压为:P2=4.1×105Pa, 温度为T2=310K; 根据理想气体状态方程得:P1V1/T1=P2V2/T2, 代入数据有:105×n×400×10-6/300 = 4.1×105×1.6×10-3/310 解得:n=16次
高中物理

【高中物理】难点突破:
选修3-3:打气问题
【例题】:如图a所示是常见的饮水机压水器,可以简化为如图模型,上面气囊的体积V1=0.5L,挤压时可以把里面气体全部压入下方水桶中,它桶的横截面积是S=0.05m²,假设温度不变,细管的体积可以忽略。
大气压为P0=10Pa,水的密度为ρ=10kg/m³,开始时,桶内气体体积为
V2=12.5L,挤压一次后,水恰好上升到管口处,求桶中液面离出水口多高?
【解析】:变质量问题的破解方法:
方法一:利用理想气体状态方程
设液面离出水口高度为h,则:
P0(V1+V2)=PV2,注意求压强易错,
P=P0+ρgh,代入数据计算可以得出:h=?
方法二:利用克拉波龙方程
PV=nRT,n是物质的量,n摩尔,因为两部分气体总的物质的量总和不变。
所以可用
P1V1/T1+P2V2/T2=P3V3/T3
对于本题,P0V1/T+P0V2/T=PV2/T
代入数据可以求出结果。
2018届高考物理选修3-3大题气体计算专题
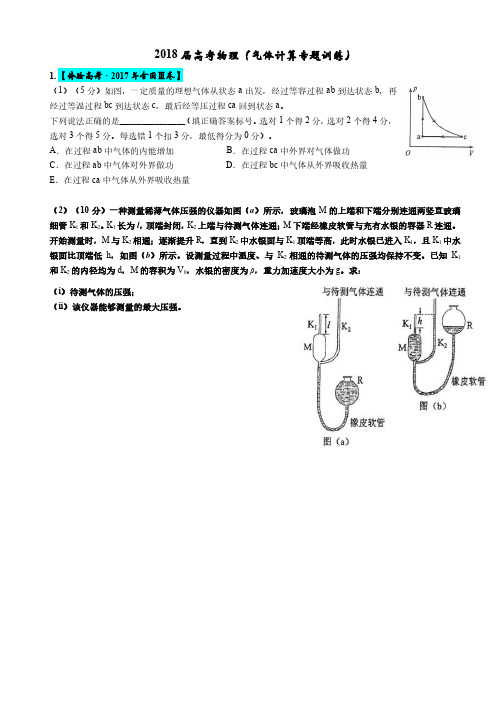
(ⅱ)气球内热空气所受的重力 G (Ta )Vg ⑦
⑤
⑥
联立④⑦解得
G
Vg 0
T0 Ta
⑧
(ⅲ)设该气球还能托起的最大质量为 m ,由力的平衡条件可知: mg f G m0g
⑨
Hale Waihona Puke 联立⑥⑧⑨可得: m
0VT0 Tb
0VT0 Ta
m0
【全国Ⅰ卷】
【解析】(i)设打开 K2 后,稳定时活塞上方气体的压强为 p1 ,体积为V1 。依题意,被活塞分开的两部分气体都
1.小方同学在做托里拆利实验时,由于操作不慎,玻璃管漏进了一些空气。当大气压强为 76 cmHg 时,管内外 水银面高度差为 60 cm,管内被封闭的空气柱长度是 30 cm,如图所示.问:
①此时管内空气的压强是多少 cmHg; ②现保持下端水银槽不动,将玻璃管向下插入 10 cm,则此时的空气柱长度是多少.(设此时玻璃管还未触 到水银槽底,不考虑水银槽液面的变化,且整个过程温度不变)
①求放出部分水银后 A 侧空气柱的长度 ②此后再向 B 侧注入水银,使 A、B 两侧的水银达到同一高度,求注入水银在管内的长度
10.某氧气瓶的容积V 30 L ,在使用过程中,氧气瓶中的压强由 P1 100 atm 下降到 P2 50 atm ,且温度始终 保持 0℃。已知在标准状况1 mol 气体的体积 22.4 L 。求:使用掉的氧气分子数为多少? (阿伏加德罗常数为 NA 6.0 1023 mol-1 ,结果保留两位有效数字)
0VT0 Ta
m0
【解析】(i)设
1
个大气压下质量为
m
的空气在温度
T0 时的体积为
物理抽气 打气问题

抽气和打气抽气和打气的问题是属于气体变质量问题的常见题型.若抽气和打气过程中的温度不变,则一般用玻意耳定律求解.[例一] 用最大容积为ΔV的活塞打气机向容积为V的容器中打气.设容器中原来空气压强与外界大气压强PO相等,打气过程中,设气体的温度保持不变.求:连续打n次后,容器中气体的压强为多大[解答]如图所示是活塞充气机示意图.由于每打一次气,总是把ΔV体积,相等质量(设Δm)压强为PO 的空气压到容积为V的容器中,所以打n次后,共打入压强为P的气体的总体积为nΔV,因为打入的nΔV体积的气体与原先容器里空气的状态相同,故以这两部分气体的整体为研究对象.取打气前为初状态:压强为PO、体积为V+nΔV;打气后容器中气体的状态为末状态:压强为Pn、体积为V.由于整个过程中气体质量不变、温度不变,由玻意耳定律得:P O (V+nΔV)=PnV∴Pn = PO(V+nΔV)/ V[例二]用容积为ΔV的活塞式抽气机对容积为VO的容器中的气体抽气、设容器中原来气体压强为P,抽气过程中气体温度不变.求抽气机的活塞抽动n次后,容器中剩余气体的压强Pn为多大[解答]如图是活塞抽气机示意图,当活塞上提抽第一次气,容器中气体压强为P1,根据玻意耳定律得:P1(V+nΔV)=PVP1=PV/(V+nΔV)当活塞下压,阀门a关闭,b打开,抽气机气缸中ΔV体积的气体排出.活塞第二次上提(即抽第二次气),容器中气体压强降为P2.根据玻意耳定律得:P 2(V+nΔV)=P1VP 2=P1V/(V+nΔV)= P[V/(V+nΔV)]2抽第n次气后,容器中气体压强降为:P n =P[V/(V+nΔV)]n打气和抽气不是互为逆过程,气体的分装与打气有时可视为互为逆过程.气体的分装有两种情况,一种是将大容器中的高压气体同时分装到各个小容器中,分装后各个小容器内气体的状态完全相同,这种情况实质上是打气的逆过程,每个小容器内的气体相当于打气筒内每次打进的气体,大容器中剩下的气体相当于打气前容器中的原有气体.另一种是逐个分装,每个小容器中所装气体的压强依次减小,事实上,逐个分装的方法与从大容器中抽气的过程很相似,其解答过程可参照抽气的原理.[例三]钢筒容积20升,贮有10个大气压的氧气,今用5升真空小瓶取用,直到钢筒中氧气压强降为2个大气压为止,设取用过程中温度不变,小瓶可耐10个大气压.(l )若用多个5升真空小瓶同时分装,可装多少瓶(2)若用5升真空小瓶依次取用,可装多少瓶[解答](l )用多个5升真空小瓶同时分装,相当于打气的逆过程,则由玻意耳定律可解为:P 1V 1=P 2(V 1+nΔV)代入数据,得n=16(瓶)即用5升真空小瓶同时分装可装16瓶。
物理抽气打气问题

抽气和打气抽气和打气的问题是属于气体变质量问题的常见题型.若抽气和打气过程中的温度不变,则一般用玻意耳定律求解.用最大容积为ΔV的活塞打气机向容积为V的容器中打气.设容器中原来空气压强与外界大气压强PO相等,打气过程中,设气体的温度保持不变.求:连续打n次后,容器中气体的压强为多大如图所示是活塞充气机示意图.由于每打一次气,总是把ΔV体积,相等质量(设Δm)压强为PO 的空气压到容积为V的容器中,所以打n次后,共打入压强为P的气体的总体积为nΔV,因为打入的nΔV体积的气体与原先容器里空气的状态相同,故以这两部分气体的整体为研究对象.取打气前为初状态:压强为PO、体积为V+nΔV;打气后容器中气体的状态为末状态:压强为Pn、体积为V.由于整个过程中气体质量不变、温度不变,由玻意耳定律得:P O (V+nΔV)=PnV∴Pn = PO(V+nΔV)/ V用容积为ΔV的活塞式抽气机对容积为VO的容器中的气体抽气、设容器中原来气体压强为P,抽气过程中气体温度不变.求抽气机的活塞抽动n次后,容器中剩余气体的压强Pn为多大如图是活塞抽气机示意图,当活塞上提抽第一次气,容器中气体压强为P1,根据玻意耳定律得:P1(V+nΔV)=PVP1=PV/(V+nΔV)当活塞下压,阀门a关闭,b打开,抽气机气缸中ΔV体积的气体排出.活塞第二次上提(即抽第二次气),容器中气体压强降为P2.根据玻意耳定律得:P 2(V+nΔV)=P1VP 2=P1V/(V+nΔV)= P[V/(V+nΔV)]2抽第n次气后,容器中气体压强降为:P n =P[V/(V+nΔV)]n打气和抽气不是互为逆过程,气体的分装与打气有时可视为互为逆过程.气体的分装有两种情况,一种是将大容器中的高压气体同时分装到各个小容器中,分装后各个小容器内气体的状态完全相同,这种情况实质上是打气的逆过程,每个小容器内的气体相当于打气筒内每次打进的气体,大容器中剩下的气体相当于打气前容器中的原有气体.另一种是逐个分装,每个小容器中所装气体的压强依次减小,事实上,逐个分装的方法与从大容器中抽气的过程很相似,其解答过程可参照抽气的原理.钢筒容积20升,贮有10个大气压的氧气,今用5升真空小瓶取用,直到钢筒中氧气压强降为2个大气压为止,设取用过程中温度不变,小瓶可耐10个大气压.(l)若用多个5升真空小瓶同时分装,可装多少瓶(2)若用5升真空小瓶依次取用,可装多少瓶(l)用多个5升真空小瓶同时分装,相当于打气的逆过程,则由玻意耳定律可解为:P1V1=P2(V1+nΔV)代入数据,得n=16(瓶)即用5升真空小瓶同时分装可装16瓶。
高中物理选修3-3气体压强专项练习题(附答案)

高中物理选修3-3气体压强专项练习题(附答案)选修3-3 气体压强计算专项练1.一定质量的理想气体从状态A变化到状态B再变化到状态C,其状态变化过程的p-V图象如图所示。
已知该气体在状态A时的温度为27℃。
求:①该气体在状态B和C时的温度分别为多少℃?②该气体从状态A经B再到C的全过程中是吸热还是放热?传递的热量是多少?2.一定质量理想气体经历如图所示的A→B、B→C、C→A三个变化过程,TA=300K,气体从C→A的过程中做功为100J,同时吸热250J,已知气体的内能与温度成正比。
求:i)气体处于C状态时的温度TC;ii)气体处于C状态时内能UC。
3.如图所示,一个内壁光滑的导热气缸竖直放置,内部封闭一定质量的理想气体,环境温度为27℃。
现将一个质量为m=2kg的活塞缓慢放置在气缸口,活塞与气缸紧密接触且不漏气。
已知活塞的横截面积为S=4.0×10^-4m^2,大气压强为P=1.0×10^5Pa,重力加速度g取10m/s,气缸高为h=0.3m,忽略活塞及气缸壁的厚度。
i)求活塞静止时气缸内封闭气体的体积。
ii)现在活塞上放置一个2kg的砝码,再让周围环境温度缓慢升高,要使活塞再次回到气缸顶端,则环境温度应升高到多少摄氏度?4.如图所示,一汽缸固定在水平地面上,通过活塞封闭有一定质量的理想气体,活塞与缸壁的摩擦可忽略不计,活塞的截面积S=100cm^2.活塞与水平平台上的物块A用水平轻杆连接,在平台上有另一物块B,A、B的质量均为m=62.5kg,物块与平台间的动摩擦因数μ=0.8.两物块间距为d=10cm。
开始时活塞距缸底L1=10cm,缸内气体压强p1等于外界大气压强p=1×10^5Pa,温度t1=27℃。
现对汽缸内的气体缓慢加热,g=10m/s。
求:①物块A开始移动时,汽缸内的温度;②物块B开始移动时,汽缸内的温度。
5.如图所示,一导热性能良好、内壁光滑的气缸水平放置,横截面积为S=2×10^-3m^2,质量为m=4kg厚度不计的活塞与气缸底部之间封闭了一部分气体,此时活塞与气缸底部之间的距离为24cm,在活塞的右侧12cm处有一对与气缸固定连接的卡环,气体的温度为300K,大气压强P=1.0×10^5Pa。
物理抽气-打气问题

抽气和打气抽气和打气的问题是属于气体变质量问题的常见题型.若抽气和打气过程中的温度不变,则一般用玻意耳定律求解.用最大容积为ΔV的活塞打气机向容积为V的容器中打气.设容器中原来空气压强与外界大气压强PO相等,打气过程中,设气体的温度保持不变.求:连续打n次后,容器中气体的压强为多大?如图所示是活塞充气机示意图.由于每打一次气,总是把ΔV体积,相等质量(设Δm)压强为PO 的空气压到容积为V的容器中,所以打n次后,共打入压强为P的气体的总体积为nΔV,因为打入的nΔV体积的气体与原先容器里空气的状态相同,故以这两部分气体的整体为研究对象.取打气前为初状态:压强为PO、体积为V0+nΔV;打气后容器中气体的状态为末状态:压强为Pn、体积为V.由于整个过程中气体质量不变、温度不变,由玻意耳定律得:PO(V+nΔV)=PnV∴P n= P O(V0+nΔV)/ V0用容积为ΔV的活塞式抽气机对容积为VO的容器中的气体抽气、设容器中原来气体压强为P,抽气过程中气体温度不变.求抽气机的活塞抽动n次后,容器中剩余气体的压强Pn为多大?如图是活塞抽气机示意图,当活塞上提抽第一次气,容器中气体压强为P1,根据玻意耳定律得:P 1(V+nΔV)=PVP 1=PV/(V+nΔV)当活塞下压,阀门a关闭,b打开,抽气机气缸中ΔV体积的气体排出.活塞第二次上提(即抽第二次气),容器中气体压强降为P2.根据玻意耳定律得:P 2(V+nΔV)=P1VP 2=P1V/(V+nΔV)= P[V/(V+nΔV)]2抽第n次气后,容器中气体压强降为:P n=P0[V0/(V0+nΔV)]n打气和抽气不是互为逆过程,气体的分装与打气有时可视为互为逆过程.气体的分装有两种情况,一种是将大容器中的高压气体同时分装到各个小容器中,分装后各个小容器内气体的状态完全相同,这种情况实质上是打气的逆过程,每个小容器内的气体相当于打气筒内每次打进的气体,大容器中剩下的气体相当于打气前容器中的原有气体.另一种是逐个分装,每个小容器中所装气体的压强依次减小,事实上,逐个分装的方法与从大容器中抽气的过程很相似,其解答过程可参照抽气的原理.钢筒容积20升,贮有10个大气压的氧气,今用5升真空小瓶取用,直到钢筒中氧气压强降为2个大气压为止,设取用过程中温度不变,小瓶可耐10个大气压.(l)若用多个5升真空小瓶同时分装,可装多少瓶?(2)若用5升真空小瓶依次取用,可装多少瓶?(l)用多个5升真空小瓶同时分装,相当于打气的逆过程,则由玻意耳定律可解为:P1V1=P2(V1+nΔV)代入数据,得n=16(瓶)即用5升真空小瓶同时分装可装16瓶。
3-3物理抽气-打气问题(1)
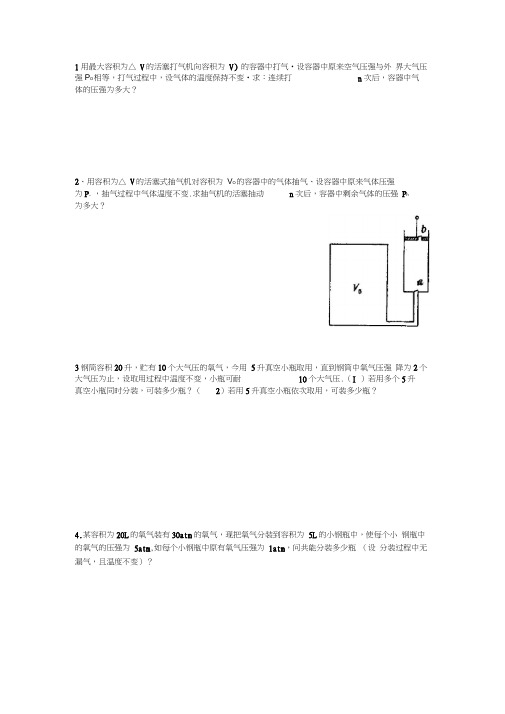
1用最大容积为△ V的活塞打气机向容积为V)的容器中打气•设容器中原来空气压强与外界大气压强P O相等,打气过程中,设气体的温度保持不变•求:连续打n次后,容器中气体的压强为多大?
2、用容积为△ V的活塞式抽气机对容积为V O的容器中的气体抽气、设容器中原来气体压强
为P。
,抽气过程中气体温度不变.求抽气机的活塞抽动n次后,容器中剩余气体的压强P n
为多大?
3钢筒容积20升,贮有10个大气压的氧气,今用5升真空小瓶取用,直到钢筒中氧气压强降为2个大气压为止,设取用过程中温度不变,小瓶可耐10个大气压.(I )若用多个5升
真空小瓶同时分装,可装多少瓶?(2)若用5升真空小瓶依次取用,可装多少瓶?
4.某容积为20L的氧气装有30atm的氧气,现把氧气分装到容积为5L的小钢瓶中,使每个小钢瓶中的氧气的压强为5atm,如每个小钢瓶中原有氧气压强为1atm,问共能分装多少瓶(设分装过程中无漏气,且温度不变)?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
抽气和打气的问题是属于气体变质量问题的常见题型.若抽气和打气过程中的温度不变,则一般用玻意耳定律求解.
[例一]
用最大容积为ΔV的活塞打气机向容积为V0的容器中打气.设容器中原来空气压强与外界大气压强P O相等,打气过程中,设气体的温度保持不变.求:连续打n次后,容器中气体的压强为多大?
[解答]
如图所示是活塞充气机示意图.由于每打一次气,总是把ΔV体积,相等质量(设Δm)压强为P O的空气压到容积为V0的容器中,所以打n次后,共打入压强为P0的气体的总体积为nΔV,因为打入的nΔV体积的气体与原先容器里空气的
状态相同,故以这两部分气体的整体为研究对象.取打
气前为初状态:压强为P O、体积为V0+nΔV;打气后容
器中气体的状态为末状态:压强为P n、体积为V0.由于
整个过程中气体质量不变、温度不变,由玻意耳定律得:
P O(V0+nΔV)=P n V0
∴P n= P O(V0+nΔV)/ V0
[例二]
用容积为ΔV的活塞式抽气机对容积为V O的容器中的气体抽气、设容器中原来气体压强为P0,抽气过程中气体温度不变.求抽气机的活塞抽动n次后,容器中剩余气体的压强P n为多大?
[解答]
如图是活塞抽气机示意图,当活塞上提抽第一次气,容
器中气体压强为P1,根据玻意耳定律得:
P1(V0+ΔV)=P0V0
P1=P0V0/(V0+ΔV)
当活塞下压,阀门a关闭,b打开,抽气机气缸中ΔV
体积的气体排出.活塞第二次上提(即抽第二次气),容器
中气体压强降为P2.根据玻意耳定律得:
P2(V0+ΔV)=P1V0
P2=P1V0/(V0+ΔV)= P0[V0/(V0+ΔV)]2
抽第n次气后,容器中气体压强降为:
P n=P0[V0/(V0+ΔV)]n
打气和抽气不是互为逆过程,气体的分装与打气有时可视为互为逆过程.气体的分装有两种情况,一种是将大容器中的高压气体同时分装到各个小容器中,分装后各个小容器内气体的状态完全相同,这种情况实质上是打气的逆过程,每个小容器内的气体相当于打气筒内每次打进的气体,大容器中剩下的气体相当于打气前容器中的原有气体.另一种是逐个分装,每个小容器中所装气体的压强依次减小,事实上,逐个分装的方法与从大容器中抽气的过程很相似,其解答过程可参照抽气的原理.
[例]
钢筒容积20升,贮有10个大气压的氧气,今用5升真空小瓶取用,直到钢筒中氧气压强降为2个大气压为止,设取用过程中温度不变,小瓶可耐10个大气压.(l)若用多个5升真空小瓶同时分装,可装多少瓶?(2)若用5升真空小瓶依次取用,可装多少瓶?[解答]
(l)用多个5升真空小瓶同时分装,相当于打气的逆过程,则由玻意耳定律可解为:P1V1=P2(V1+nΔV)
代入数据,得n=16(瓶)
即用5升真空小瓶同时分装可装16瓶。
(2)用5升真空小瓶依次取用;相当于抽气过程,则由
P n=P0[V1/(V1+ΔV)]n
代人数据得:n=7(瓶)
只两用的活塞打气筒,其筒体积为V0,现在它与另一只容积为V的容器连接,V容器内空气的压强为po,打气时,活塞工作n次后,容器内气体压强为多少?若是抽气,n次后压强又为多少?
打气时比较简单,每次增大的压强是一定的。
活塞工作n次后,容器内气体压强为p。
+np。
v。
/v
抽气时比较麻烦,每次抽气是将体积v增大到v+v。
;压强减为原来的v/(v+v。
);n次后压
强为p。
[v/(v+v。
)]^n。
