2011-2012(1)《信号与系统》A试卷答案
《信号与系统》试卷
2012–2013学年第一学期期终考试试卷（A 卷）开课学院： 物理与电子信息学院 课程名称： 信号与系统 （评分标准及参考答案） 考试形式：闭卷，所需时间120分钟2、学生答题前将密封线外的内容填写清楚，答题不得超出密封线；3、答题请用蓝、黑钢笔或圆珠笔。
一、选择题（共20分，每题2分）1. 系统r (t )=e (t )u (t )的性质是（ C ）。
A 线性、时不变B 非线性、时不变C 线性、时变D 非线性、时变2. 若y (n)=x 1(n )*x 2(n )，其中x 1(n )=u (n +2)-u (n -2)，x 2(n )=n [u (n -2)-u (n -5)]，则y (1)=（ D ）。
A 0B 1C 3D 53. 已知某LTI 系统的单位冲激响应h (t )如图1所示，若输入信号为u (t )，则y(3/2)=( C )。
A 0B 1C 11/4D 2 4. 理想不失真传输系统的传输函数H(jω)是（ B ）。
A 0j t Ke ω-B 0t j Ke ω-C 00j t Keω-D []0()()j t c c Keu u ωωωωω-+--（其中00,,,c t k ωω为常数）5. 如图2所示周期信号的傅里叶级数的特点是（ A ）。
A 只有奇次谐波的正弦分量 B 只有偶次谐波的正弦分量 C 只有奇次谐波的余弦分量 D 只有偶次谐波的余弦分量6. 系统的幅频特性和相频特性如图3所示,当激励为e (t )=2sin6πt +sin8πt 时,系统响应r (t )的失真情况为（ A ）。
A 无失真B 仅有幅度失真C 仅有相位失真D 幅度和相位均有失真 7. 某LTI 系统H(s)具有三个极点(p 1=-2, p 2=-1, p 3=1)和一个零点(z 1=2)，则该系统可能的收敛域数量为（ D ）。
A 1B 2C 3D 4 8. 信号()()tf t h t d λλλ=-⎰的拉氏变换为（ C ）。
信号与系统a答案
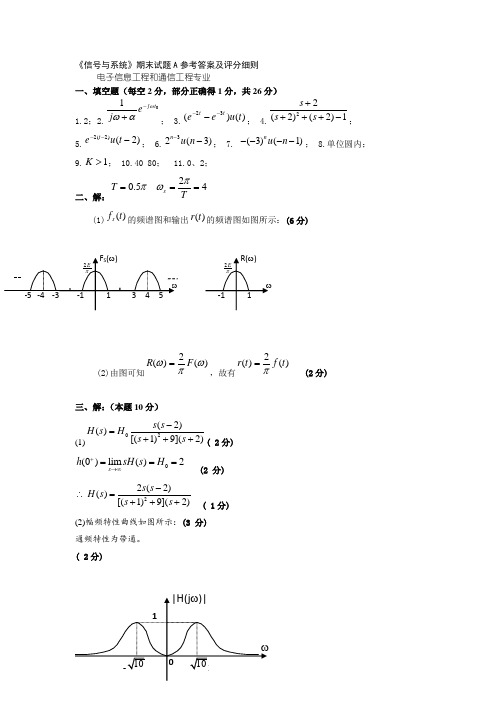
《信号与系统》期末试题A 参考答案及评分细则电子信息工程和通信工程专业 一、填空题（每空2分，部分正确得1分，共26分）1.2；2.01t j ej ωαω-+； 3.)()(32t u eett---； 4.22(2)(2)1s s s ++++-；5.)2()2(2---t u et ； 6.32(3)n u n --； 7. (3)(1)n u n ----； 8.单位圆内；9.1K >； 10.40 80； 11.0、2；二、解：425.0===TT s πωπ(1))(t f s 的频谱图和输出)(t r 的频谱图如图所示：(6分)(2)由图可知)(2)(ωπωF R =，故有)(2)(t f t r π=(2分)三、解：（本题10分）(1)2(2)()[(1)9](2)s s H s H s s -=+++( 2分)0(0)lim ()2s h sH s H +→∞=== (2 分)22(2)()[(1)9](2)s s H s s s -∴=+++ ( 1分)(2)幅频特性曲线如图所示：(3 分) 通频特性为带通。
( 2分)四、解：3212()()(2)zH z z z -=-- (1)收敛域的三种情况：2z >12z <122z << (2分)(2) 12()2z zH z z z =--- (2分)2z >时 12()[()2]()nnh n u n =- 系统因果不稳定 (2分) 12z <时 12()[()2](1)nn h n u n =-+-- 系统非因果不稳定 (2分)122z <<时12()()()2(1)nnh n u n u n =+-- 系统非因果稳定 (2分)五、求解各题1.(1)电路的S 域模型为：525)(2++=s s s H (3分)极、零点图如图所示： (2分)极点位于左半平面系统是稳定系统。
(完整word版)信号与系统考试试题及答案,推荐文档
长沙理工大学拟题纸课程编号 1拟题教研室（或老师）签名 教研室主任签名 符号说明：)sgn(t 为符号函数，)(t δ为单位冲击信号，)(k δ为单位脉冲序列，)(t ε为单位阶跃信号，)(k ε为单位阶跃序列。
一、填空（共30分，每小题3分）1. 已知)()4()(2t t t f ε+=，求_______)("=t f 。
)('4)(2)("t t t f δε+2. 已知}4,2,4,3{)(},1,2,2,1{)(=-=k h k f ，求______)()(=*k h k f 。
}4,6,8,3,4,10,3{)()(-=*k h k f3. 信号通过系统不失真的条件为系统函数_______)(=ωj H 。
0)(t j Kej H ωω-=4. 若)(t f 最高角频率为m ω，则对)4(t f 取样的最大间隔是______。
m T ωπωπ4max max ==5. 信号t t t f ππ30cos 220cos 4)(+=的平均功率为______。
101122222=+++==∑∞-∞=n n F P6. 已知一系统的输入输出关系为)3()(t f t y =，试判断该系统是否为线性时不变系统______。
故系统为线性时变系统。
7. 已知信号的拉式变换为)1)(1(1)(2-+=s s s F ，求该信号的傅立叶变换)(ωj F =______。
故傅立叶变换)(ωj F 不存在。
8. 已知一离散时间系统的系统函数2121)(---+=z z z H ，判断该系统是否稳定______。
故系统不稳定。
9. =+-+⎰∞∞-dt t t t )1()2(2δ______。
310. 已知一信号频谱可写为)(,)()(3ωωωωA e A j F j -=是一实偶函数，试问)(t f 有何种对称性______。
关于t=3的偶对称的实信号。
二、计算题（共50分，每小题10分）1. 已知连续时间系统的单位冲激响应)(t h 与激励信号)(t f 的波形如图A-1所示，试由时域求解该系 统的零状态响应)(t y ，画出)(t y 的波形。
《信号与系统》2011—2012学年1期末考试卷(陈红娟)
成都理工大学2011—2012学年第一学期《信号与系统》考试试卷（闭卷)一、单项选择题（依题意,选择唯一正确的答案，填入横线内,每小题3分，共30分）1．在某些离散的时刻才有确定函数值，而在其他时刻无定义的信号，称之为 B .A 。
连续信号B 。
离散信号C 。
随机信号D 。
非周期信号2。
利用冲激函数的抽样性质,求得()()dt t t t f δ⎰∞∞--0的函数值为 B .A.()0t f B 。
()0t f - C 。
0t D. 0t -3．下列四个等式中，不成立的是 D .A 。
()()()t f t t f =δ* B.()()()00*t t f t tt f -=-δC ．()()()n yn x n Rxy-=*D 。
()()ττ--=xx xx R R4. 单位阶跃函数()t u的拉氏变换结果为 C .得 分A 。
sB 。
2sC. s1D. 21s5。
设()n x 为离散序列，则()n x 的双边边Z 变换定义为 C 。
A 。
()()nn zn x z X -∞=∑=B 。
()()nn zn x z X ∑∞==C. ()()nn zn x z X -∞-∞=∑=D 。
()()nn z n x z X ∑∞-∞==6。
整个系统的完全响应是由自身特性决定的_____A______和与外加激励信号e （t)有关的_______________两部分组成。
A 。
自由响应,强迫响应B. 稳态响应,瞬态响应 C 。
零输入响应，零状态响应D.自由响应,稳态响应7. 已知系统为()()()()t x t r dtt dr dt t r d 422=++,其中x(t ）为激励信号,r （t)为系统响应，试判断该系统的类别___A_______A 。
线性非时变系统B. 非线性时变系统 C 。
非线性非时变系统D. 线性时变系统8。
函数()()t u e t f t 2-=的收敛域为 B 。
(最新整理)-(1)《信号与系统》期末考试试卷A答案
2014-2015(1)《信号与系统》期末考试试卷 A 答案
3．若
p(t)
(t
n
)
，画出
ys
(t)
的频谱 Ys
(
j)
，并写出 Ys (
j)
的表示式。
n
40
答案:
1．Y ( j) E[u( 5) u( 5)]
2．
Ys
(
j
)
1 2
Y[
j(
1000)]
Y
[
j(
1000)]
3）
Ys
(
j
)
40
[u
1
密封
2014-2015(1)《信号与系统》期末考试试卷 A 答案
西南交通大学 2014－2015 学年第(1）学期考试试卷
课程代码 3122400 课程名称 信号与系统 A 考试时间 120 分钟
题
总成
一二三四五六七八九十
号
绩
得
分
姓名
密封装订线
学号
阅卷教师签字：
一、选择题：（20 分）
本题共 10 个小题，每题回答正确得 2 分,否则得零分。每小题所给答案中只有一
1
1 0.5 z 1
，收敛域
z
0.5
，求逆变换得
x（n）为（
A
)
A． 0.5n u(n)
B. 0.5n u(n 1) C。 0.5n u(n)
D。 0.5n u(n 1)
二、（14 分)画图题 1.已知 f (1 2t) 波形如图所示，画出 f (t) 的波形。
解： f (1 2t) tt f (2t 1) tt12 f (2t) t12t f (t)
2022年《信号与系统》试卷
《信号与系统》卷子〔A 卷〕一、填空题〔每空1分，共18分〕1．假设)()(s F t f ↔，则↔)3(t F 。
2．ℒ()n t t ε⎡⎤=⎣⎦，其收敛域为 。
3．()(21)f t t ε=-的拉氏变换)(s F = ，其收敛域为 。
4．利用拉氏变换的初、终值定理，可以不经反变换计算，直接由)(s F 决定出()+o f 及)(∞f 来。
今已知)3)(2(3)(+++=s s s s s F ，[]Re 0s > 则)0(+f ，)(∞f = 。
5．已知ℒ[]022()(1)f t s ωω=++，Re[]1s >-，则()F j ω=ℱ[()]f t = 。
6．已知ℒ0220[()](1)f t s ωω=-+，Re[]1s >，则()F j ω=ℱ[()]f t = 。
7．已知()[3(1)](1)t f t e Sin t t ε-=--，试写出其拉氏变换()F s 的解析式。
即()F s = 。
8．对连续时间信号进行均匀冲激取样后，就得到 时间信号。
9．在LTI 离散系统分析中， 变换的作用类似于连续系统分析中的拉普拉斯变换。
10．Z 变换能把描述离散系统的 方程变换为代数方程。
11．ℒ 0(3)k t k δ∞=⎡⎤-=⎢⎥⎣⎦∑ 。
12．已知()()f t F s ↔，Re[]s α>，则↔--)1()1(t t f e t ε ，其收敛域为 。
13．已知22()(1)sse F s s ω-=++，Re[]1s >-，则=)(t f 。
14．单位样值函数)(k δ的z 变换是 。
二、单项选择题〔在每题的备选答案中，选出一个正确答案，并将正确答案的序号填在括号内。
每题1分，共8分〕 1．转移函数为327()56sH s s s s=++的系统，有〔 〕极点。
A ．0个 B ．1个 C ．2个 D ．3个 2．假设11)(1+↔s t f ，Re[]1s >-；)2)(1(1)(2++↔s s t f ，Re[]1s >-，则[]12()()()y t f t f t =-的拉氏变换()Y s 的收敛区是〔 〕。
(完整版)《信号与系统》期末试卷与答案
《信号与系统》期末试卷A 卷班级： 学号：__________ 姓名：________ _ 成绩：_____________一． 选择题（共10题，20分） 1、n j n j een x )34()32(][ππ+=，该序列是 D 。
A.非周期序列B.周期3=NC.周期8/3=ND. 周期24=N2、一连续时间系统y(t)= x(sint)，该系统是 C 。
A.因果时不变B.因果时变C.非因果时不变D. 非因果时变3、一连续时间LTI 系统的单位冲激响应)2()(4-=-t u et h t，该系统是 A 。
A.因果稳定B.因果不稳定C.非因果稳定D. 非因果不稳定4、若周期信号x[n]是实信号和奇信号，则其傅立叶级数系数a k 是 D 。
A.实且偶B.实且为奇C.纯虚且偶D. 纯虚且奇5、一信号x(t)的傅立叶变换⎩⎨⎧><=2||02||1)(ωωω，，j X ，则x(t)为 B 。
A.tt22sin B.t t π2sin C. t t 44sin D. ttπ4sin 6、一周期信号∑∞-∞=-=n n t t x )5()(δ，其傅立叶变换)(ωj X 为 A 。
A.∑∞-∞=-k k )52(52πωδπB. ∑∞-∞=-k k)52(25πωδπ C. ∑∞-∞=-k k )10(10πωδπD.∑∞-∞=-k k)10(101πωδπ7、一实信号x[n]的傅立叶变换为)(ωj e X ，则x[n]奇部的傅立叶变换为C 。
A. )}(Re{ωj eX j B. )}(Re{ωj e X C. )}(Im{ωj e X j D. )}(Im{ωj e X8、一信号x(t)的最高频率为500Hz ，则利用冲激串采样得到的采样信号x(nT)能唯一表示出原信号的最大采样周期为 D 。
A. 500 B. 1000 C. 0.05D. 0.0019、一信号x(t)的有理拉普拉斯共有两个极点s=－3和s=－5，若)()(4t x e t g t=，其傅立叶变换)(ωj G 收敛，则x(t)是 C 。
2011年重庆理工大学信号与系统A试卷答案
课程测试、考核评分标准科目： 信号分析与处理（A 卷）班级： 109070301 109070302 测试、考核时间： 2011年05月25日试卷评分标准及答案一、填空题（每题2分，共20分）1．[][][]n n f n f δ*= （1分）、[][][]1--=n n n εεδ 或者[][][]∑∑-∞=∞=δ=-δ=εnk k k k n n 0 （1分）2．幅值频谱（1分）、相位频谱（1分）3．()0t t K -δ 4．()()()t f dt t dy dtt y d =+22 5． a α> 6．()()n n nεδ⎪⎭⎫⎝⎛-+-21327． 所有的极点均位于单位圆之内或者[]∞<∑∞-∞=n n h8．ω∆3；3ω∆ 9．abj e a F a ωω⎪⎭⎫ ⎝⎛-1 10．t e 33--二、单项选择题（每小题2分，共20分）（1）B （2）A （3）A （4）C （5）C （6）C （7）D （8）D （9）C （10）A三、简单分析题（每小题5分，共30分）1．答：周期矩形脉冲信号的频谱与周期T 和脉冲持续时间τ的关系是：当保持周期T 不变，而脉冲宽τ减小，则频谱的幅度随之减小，相邻谱线的间隔不变，频谱包络线过零点的频率增高，频率分量增多，频谱幅度的收敛速度相应变慢。
当脉冲宽度τ不变时，而周期T 变化时，频谱包络线有过零点的位置不变，周期T 增大，频谱幅度随着减小，相邻谱线的间隔变小，频谱变密。
如果周期无限增长，此时，相邻谱线的间隔将趋近于零，周期信号的离散频谱就过流到非周期信号的连续频谱。
2．解：因()22sinωτωτττ↔t G ,取πωωτ=2，故得πτ2=， （1分） 则 ()πωπωππsin 22↔t G故 ()πωπωππsin 212↔t G （1分） 故根据傅立叶变换的对称性，有()()ωωππππππ22212sin G G t t =⨯↔ 故()()()ωπωππj e G t t -↔--211sin （1分） 由此可得幅值谱图如下图所示： （2分）3． 解：()()()()()()()12112+-→+-→+→-→-→t t t t t f t f t f δδδδ（2分）（各图0.5分）4．解：设零输入响应为()t y zi ，零状态响应为()t y zs ，则由题意知()()()()te t y t y t e t y t y tzi zs t zi zs 2cos 222cos 2+=++=+-- （2分）由此可得：()()()()()t e t y t t t et y t zi tzs εεε--=+-=32cos （2分）则当激励为()t f 4时，系统的全响应为：()()()()()t et t y t y t y tzi zs ε--=+=2cos 44 （1分）5．解：设()()()()n n y n y n y zs zi ε=+=111 （1） （1分）()()()()n n y n y n y n zs zi ε⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛=+=1312222（2） （1分）考虑()()()()n y n y n y n y zs zs zi zi 1221-==代入式（2）得 （1分）()()()()n n y n n y n zs nzi εε⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛=3113111 （1分）应用零输入响应、零状态齐次性可得()()()()n n y n y n y n zs zi ε⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=+⨯=31332113 （2分）6．解： ()()()224j F G e ωπωπδωω-=+ （1分）因有： ()2G t Sa τωττ⎛⎫⇔⎪⎝⎭取2τπ=，有()()()()()()222222G t Sa G Sa t G Sa t πππππωπωππωπ⇔⇔⇔ （2分） 故： ()()()222j G e Sa t ωπωπ-⇔- （1分） 又有： ()()4222πδωπδω=⨯⇔所以原函数为： ()()()22f t Sa t π=+- （1分）四、综合计算题（每小题10分，共30分）1．解：当开关闭合后，电路的S 域等效模型如图所示，列出系统的S 域方程，有 （3分）()()()()()()()⎪⎪⎩⎪⎪⎨⎧+-=⎪⎭⎫ ⎝⎛+-++=+-+⋅2112212121232121s s s I s s I s s s I s s I （4分）计算得()()()()()()235221115423212121231221212--++++-=+⎪⎭⎫⎝⎛++++-+⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛+=s s s s s s s s s s s s I （1分）即可得输出电压为 ()()235421215822--++++-==s s s s I s V o （1分） 进行拉普拉斯反变换得 ()0;542582321≥-+-=--t e e e t v t t t o （1分）2．解：（1）设 ()()()()131-++=z z z z A z H （2分）由终值定理()()()()()()()213111lim lim 11=-++-=-=∞→→z z z z Az z H z h z z （2分） 由此可得， 4=A （1分）即得该系统函函数为： ()()()()1314-++=z z z z z H （1分） 这样系统的单位脉冲响应为： ()()[]()n n h n ε132+-= （2分） 故得描述该系统的差分方程为：()()()()()124312141-+=---+n f n f n y n y n y （2分）3．解：（1）、())(82)(4)(4)(2ωωωωωωωωF F j Y Y j Y j +=++ （1分）4482)()()(2+++==ωωωωωωj j j F Y H （1分） ()()2224224482)(22212+++=+++=+++=ωωωωωωωωj j j K j K j j j H （2）分[])(22)(22t e te t h t t ε--+= （1分）（2）11)()()(+==-ωωεj F t e t f t （1分） ()()2626162211)2(82)()()(232212+-++-++=+++++=+++==ωωωωωωωωωωωωj j j j K j K j K j j j F H Y （3分）())(666)(22t e te e t y t t t ε-----= （1分）。
西农大 2011—2012学年第1学期《信号与系统》课程 A 卷答案
第 1 页 共 5 页西北农林科技大学本科课程《信号与系统》考试试卷A 卷参考答案一、单项选择题（每小题3分，共30分）1. C ；2. A ；3. A ；4. D ；5. A ；6. C ；7. D ；8. B ；9. B ；10. B二、填空题（每空2分，共10分） 1. 11；2. 2sin t ；3. 0；4. 1，50三、证明题（10分） 证明：以下5行推导，每行2分。
2**22|[]|[][] 1[]()21()[]21()()21|()|2n n j j n n j j n n j j j x n x n x n x n X e e d X e x n e d X e X e d X e d πππππππππππ∞∞*=-∞=-∞*∞ΩΩ-=-∞∞ΩΩ-=-∞ΩΩ-Ω=⎡⎤=Ω⎢⎥⎣⎦=Ω=Ω=Ω∑∑∑⎰∑⎰⎰⎰四、简答题（每小题3分，共15分）1. 答：当采用连续时间傅里叶级数有限项部分和近似连续信号时，（1分） 在信号的不连续点处附近，部分和会偏离原信号，（1分）其峰值与部分和的项数几乎无关，过冲是不连续点处高度的9%。
（1分）2. 答：时域卷积定理：时域卷积对应频域相乘或x(t)*y(t) ⇔ X(w)Y(w)。
（2分） 频域卷积定理：频域卷积对应时域相乘或X(w)*Y(w) ⇔ 2πx(t)y(t)。
（1分）第 2 页 共 5 页3．答：零输入时系统的响应称为零输入响应；（2分）零初始状态时系统的响应称为零状态响应。
（1分）4．答：DFT ：离散傅立叶变换。
（2分）1(2/)0[][],0,1,2,1N j k N n n X k x n e k N π--===-∑ （1分）5. 答：时域连续，则频域非周期；时域离散，则频域周期。
（2分） 时域周期，则频域离散；时域非周期，则频域连续。
（1分）五、计算题（共35分）1. 解：（1）以下3行每行给1分11223314[]2cos(), 8;42818[]sin(), 16;821612[]2cos(), 4;2624x n n N x n n N x n n N ππππππππππ==⇒===⇒==-+=⇒= （2）因为123,,N N N 皆为有理数，故该函数为周期函数。
《信号与系统》A试卷答案
西南交通大学2011－2012学年第(1)学期考试试卷课程代码 3122400 课程名称 信号与系统A 考试时间 120分钟阅卷教师签字： 一、选择题：（20分）本题共10个小题，每题回答正确得2分，否则得零分。
每小题所给答案中只有一个是正确的。
1. 已知f (t )的傅里叶变换为)(ωj F ，则f (1-t )的傅里叶变换为（ C ） （A ）ωωj e j F )(-- （B ）ωωj ej F -)(（C ）ωωj e j F --)(（D ）ωωj ej F )(-2．连续周期信号的频谱具有( D )（A ）连续性、周期性 （B ）连续性、非周期性 （C ）离散性、周期性 （D ）离散性、非周期性3．某系统的系统函数为H （s ），若同时存在频响函数H （j ω），则该系统必须满足条件（C ） （A ）时不变系统 （B ）因果系统 （C ）稳定系统 （D ）线性系统4. 已知)(1n f 是1N 点的时限序列，)(2n f 是2N 点的时限序列，且12N N >，则)()()(21n f n f n y *= 是（ A ）点时限序列。
（A ）121-+N N （B ）2N （C ）1N （D ）21N N +5. 若对f （t ）进行理想取样，其奈奎斯特取样频率为f s ，则对)231(-t f 进行取样，其奈奎斯特取样频率为（ B ）。
（A ）3f s （B ）s f 31 （C ）3（f s -2） （D ）)2(31-s f 班 级 学 号 姓 名密封装订线 密封装订线 密封装订线6. 周期信号f(t)如题图所示，其直流分量等于（ B ）（A ）0 （B ）4 （C ）2（D ）67. 理想不失真传输系统的传输函数H （jω）是 （ B ）。
（A ）0j tKe ω- （B ）0t j Ke ω-（C ）0t j Ke ω-[]()()c c u u ωωωω+--（D ）00j t Keω- （00,,,c t k ωω为常数）8．已知)()(ωj F t f ↔,则信号)5()()(-=t t f t y δ的频谱函数 )(ωj Y 为（ A ）。
信号与系统( A卷答案 )
淮南师范学院201 -201学年第 学期《信号与系统》A 卷参考答案及评分标准一、填空题（每题2分，共10分）1．离散信号2．()f t3．冲激信号或()t δ4．可加性5．()t δ二、选择题（每题2分，共10分）1. (B)2. (C)3. (C)4. (A)5. (C)三、判断题（每题2分，共10分）1. ×2. √3. √4. √5. √四、简答题（每题5分，共10分）1. 简述根据数学模型的不同，列出系统常用的几种分类。
（本题5分）答：根据数学模型的不同,系统可分为4种类型. -----------------------(1分)(1) 即时系统与动态系统 -----------------------(1分)(2) 连续系统与离散系统 -----------------------(1分)(3) 线性系统与非线性系统 -----------------------(1分)(4) 时变系统与时不变系统 -----------------------(1分)2. 简述稳定系统的概念及连续时间系统时域稳定的充分必要条件。
（本题5分）答：（1）一个系统（连续的或离散的）如果对任意的有界输入，其零状态响应也是有界的则称该系统是有界输入有界输出稳定系统。
-----------------------(2分)（2）连续时间系统时域稳定的充分必要条件是()h t dt M ∞-∞≤⎰-----------------------(3分)五、计算题（每题10分，共60分）1、如有两个序列试求卷积和12()()()f k f k f k =*（本题10分）解： 1 1 1⨯ 1 2 3--------------------------3 3 32 2 21 1 1---------------------------------1 3 6 5 3 -----------------------(5分){}12()()()0,1,3,6,5,3,00f k f k f k k =*=↑= -----------------------(5分)2、求象函数2()(2)(4)s F s s s =++的拉普拉斯逆变换()f t （本题10分） 解：12()24k k F S s s =+++2424s s =-+++ -----------------------(5分) 24()(24)()t t f t e e t ε--∴=-+ -----------------------(5分)3. 已知某LTI 离散系统的差分方程为()(1)2(2)2()y k y k y k f k +---=, 求单位序列响应()h k （本题10分）解：12()()2()2()Y Z Z Y Z Z Y Z F Z --+-= -----------------------(2分) ()()()Y Z H Z F Z =12212z Z --=+-2222Z Z Z =+- -----------------------(2分) ()2(2)(1)H Z Z Z Z Z =+-21413132Z Z =⋅+⋅-+ -----------------------(2分) 24()3132Z Z H Z Z Z =⋅+⋅-+ -----------------------(2分) 24()[(2)]()33k h k k ε=+⋅- -----------------------(2分) 4. 已知002,()0,F jw ωωωω⎧<⎪=⎨>⎪⎩ ，求()F jw 的傅里叶逆变换（本题10分）解：1()()2j t f t F j e d ωωωπ+∞=-∞⎰ 0011j t e d ωωωωπ=⋅-⎰ -----------------------(5分)0011j t e jtωωωπ=⋅⋅- 02sin()t t ωπ= -----------------------(5分) 5. 已知某系统框图其中()()f t t ε=(1) 求该系统的冲激响应()h t(2) 求该系统的零状态响应()zs y t（本题10分）解：''()3'()2()4'()()y t y t y t f t f t ++=+2(32)()(41)()S S Y S S F S ++=+ -----------------------(2分) 2()(41)()()(32)Y S S H S F S S S +==++ 113712S S =-⋅+⋅++ -----------------------(2分) (1) 冲激响应 2()[(3)7]()t t h t ee t ε--=-⋅+ -----------------------(2分) (2) 41()()()(1)(2)zs S Y S H S F S S S S +=⋅=++ -----------------------(1分)1117132122S S S =⋅+⋅-⋅++ -----------------------(1分) 零状态响应217()(3)()22t t zs y t e e t ε--=+- -----------------------(2分) 6. 如图所示的电路，写出以)(t u s 为输入，以)(t u c 为响应的微分方程。
电子科大信号与系统期中考试试卷及答案11-12学年
………密………封………线………以………内………答………题………无………效……电子科技大学二零 一 一 至二零 一 二 学年第 一 学期期 中 考试SIGNALS AND SYSTEMS 课程考试题 卷 （ 120 分钟） 考试形式： 闭卷 考试日期 20 11 年 月 日课程成绩构成：平时 10 分， 期中 20 分， 实验 10 分， 期末 60 分1(56points).Each of the following questions may have one or two right answers, justify your answers and write it in the blank. (1)()cos 221πδ+∞-∞-=⎰t t dt ( d ).(a) 1 (b) -1 (c) 0.5 (d) -0.5(2) The fundamental period of the signal []23cos sin 32ππ⎡⎤⎡⎤=-⎢⎥⎢⎥⎣⎦⎣⎦x n n n is ( a ). (a) 12N = (b) 6N = (c) 8N = (d) 24N = (3) Let ()1tx t e -= and ()()()14k x t x t t k δ+∞=-∞=*-∑. The Fourier series coefficients of ()x t may be ( a ).(a) {} and Im 0-==k k k a a a (b) {} and Im 0-=-=k k k a a a (c) {} and Re 0-==k k k a a a (d) {} and Re 0k k k a a a -=-=(4) Consider an LTI system with unit impulse response ()h t illustrated in Figure 1， if the input is ()()d t x t dtδ=, the output () 0.5t y t =- is( b ).(a) -1 (b) 1 (c) -0.5 (d) 0.5(5) The convolution integral ()222t te e u t -*=( c ).(a) 2 (b)214te (c)212te (d)()212te u t(6) Which of the following systems is an linear system ( a ). In each example, []y n denotes the system output and []x n is the systeminput.(a) [][][]cos y n n x n = (b) [][]{}cos 3y n x n = (c) [][]()ln y n x n = (d) [][]2y n x n =(7) Which of the following systems are causal and stable system ( ad ). In each example, ()h t denotes the impulse response of thefollowing systems.(a) ()()()13h t t t δδ=-+- (b) ()()()0.5cos 2t h t t e u t =- (c) ()()()13h t t t δδ=+++ (d) ()()()cos 2t h t t e u t -=-(8) Determine the following signals which have finite total energy ( bc ). (a) []()[]1x n n u n =+ (b) ()()23tx t eu t -=+(c) []()[]1cos /32nx n n u n π⎛⎫= ⎪⎝⎭(d) () , tx t e t =-∞<<+∞tFigure 1………密………封………线………以………内………答………题………无………效……(9) Consider a continuous-time LTI system whose frequency response is ()()sin /2Hj ωωω=. If we know the output ()y t to some periodicinput signals are ()0y t =. The fundamental period of the input signal may be ( ac ). (a) 1T = (b) 2T = (c) 0.5T = (d) 3T =2(12points). A continuous-time signal ()32-+x t is illustrated in Figure 2.(a) Determine the signal ()x t . (b) Sketch and label carefully ()x t .3(10 points).Consider an LTI system whose response to the signal ()t x 1 in Figure 3 is the signal ()t y 1 illustrated in Figure 4. Determine the response of the system to the input ()t x 2 depicted in Figure 5 .4(12 points). Consider a continuous-time LTI system whose frequency response ()H j ω is illustrated in Figure 6. If the input signal()1cos 3sin 6ππ=++x t t t , determine the output of the system.12Figure 3ωFigure 6tFigure 2………密………封………线………以………内………答………题………无………效……14(10points). Consider an LTI system whose input []x n and unit impulse response []h n are given by []{}1,0,1,1,0,1x n n =-=-，[]{}2,1,3,2,2,3,4,5h n n ==. Determine the output [][][]n h n x n y *= of this system.《信号与系统》半期考试评分标准说明1.填空题（56分）⑴. (d) ⑵ (a) ⑶ (a) ⑷ (b) ⑸ (c) ⑹ (a) ⑺ (ad) ⑻ (bc) ⑼ (ac) ⑽ (ab) 本部分评分规则：1) 选择题共14个正确答案，1-6题为单选，7-10题为双选； 2) 若只填写了1个答案，正确得4分，错误得0分；3) 若填写了2个答案，2个正确得8分，1个正确、1个错误得4分，2个错误得0分；4) 若填写了3个答案，2个正确、1个错误得4分，1个正确、2个错误得2分，3个错误得0分； 5) 若填写了4个答案，得0分。
信号与系统试卷及参考答案
试卷及答案信号与系统试卷（1）（满分：100分，所有答案一律写在答题纸上）考试班级学号姓名成绩考试日期：年月日，阅卷教师：考试时间 120分钟，试卷题共2页一一线性非时变离散系统，具有一初始状态x(0)，当激励为时f(k)，响应为y(k)=((1/2)k+1)u(k)；若初始状态不变，当激励为-f(k)时，响应y(k)=((-1/2)k-1)u(k)为；试求当初始状态2x(0)为，激励为4f(k)时，系统的响应？（10分）二绘出下列函数的图形（1）.已知一连续时间信号x(t)如图所示，试概略画出信号y(t)=x(2-t/3)的波形图。
（8分）(2). 试概略画出信号y(t)=u(t 2-4) 的波形图。
（8分）三 计算下列函数(1). y(t)=⎰-44(t 2+3t+2)(δ(t)+2δ(t-2))dt （4分） (2). f(t)=e -2t u(t), h(t)= e -2t u(t), y(t)=f(t)*h(t) （8分） (3).f(k)=1,k=0,1,2,3,h(k)=1,k=0,1,2,3,y(k)=f(k)*h(k) （8分）（4） 已知f(t)=e -2t u(t), 求y(t)=[t f(2t)] 的富立叶变换 （8分）（5）y ’(t)+2y(t)=δ(t)+u(t), y(0)=0, 试求y(t)=? （8分） （6）. y(k)-y(k-1)-2y(k-2)=u(k)+2u(k-2), y(-1)= 2,y(-2)= -1/2,试求零输入响应y x (k)=? 零状态响应y f (k)=? （8分）四 一线性非时变因果系统，当激励为u(t)时，响应为)]2()([cos )(cos )(ππ---+=-t u t u t t tu e t g t ，求当激励f(t)=δ(t)时的响应)(t h 。
（10分）五 某一子系统，当输入f(t)=e -t u(t)时，零状态响应y f (t) = (1/2 e -t - e -2t +1/2e -3t )u(t), 试求将两个这样的子系统串联时，总系统的冲激响应。
安徽大学信号(A)及答案
安徽大学2011—2012学年第 2 学期《信号与系统 》考试试卷（A 卷）（闭卷 时间120分钟）考场登记表序号一、选择题（每小题2分，共10分） 1．已知()f t ，为求(25)f t -应按照下列哪种运算求得正确结果（ D ） A ．(5)f t -左移2 B.(5)f t 右移2 C.(5)f t 左移25 D.(5)f t -右移252．已知系统的激励e (t )与响应r (t )的关系为：()()de t r t dt=，则该系统为（ A ） A 、线性时不变系统 B 、线性时变系统 C 、非线性时不变系统 D 、非线性时变系统 3．若信号f(t)的最高频率是4kHz ，则2tf()的乃奎斯特抽样频率为（ B ） A ．4kHz B. 2kHz C. 8kHz D.3kHz4. 因果序列的Z 变换1121 1.50.5z X(z)z z---=-+，则该因果序列的终值()x ∞为（ A ） A ． 0 B. 1 C. 2 D. 3 5．若系统函数23()32s H s s s +=-+，则该系统(A ) A ．不稳定 B. 稳定 C. 临界稳定 D. 以上均不对院/系 年级 专业 姓名 学号答 题 勿 超 装 订 线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------二、填空题（每小题2分，共10分）1．求()()f t u t *= 。
2．某连续时间系统由两个冲击响应分别为1h (t)和2h (t)子系统串联构成，则该系 统的冲击响应为 。
3．对连续时间最小相移系统，其在S 平面的________平面无零点。
4．若信号的113s F(s)=(s+)(s+)-，求该信号的=)j (F ω 。
信号与系统2011-2012参考答案
(1 分)
c1
6s 18 2 ( s 4)( s 16) s 3 25 6s 3 2 ( s 3)( s 16) s 4 4
6s (0.015 0.105 j ) ( s 3)( s 4)( s 4 j ) s 4 j 6s (0.015 0.105 j ) ( s 3)( s 4)( s 4 j ) s 4 j
10 10 1 ； H (50) 0 j 10 j 50 10
y (t ) 2 0.3922 cos(50t 1.974)
5. Determine whether the following linear time-invariant systems are
stable, marginally stable or unstable. (a) H ( z ) Answer: Unstable (b) H ( s ) Answer: Stable (3 分)
x[0] x[1] x[2] x[3] 1 2 4 8 v[0] v[2] v[3] 2 0 6 2 3 0 6 4 6 0 12 8 0 24 16 0 48 v[1] 3 12 24
（1 分）
（1 分）
y[0]=2, y[6]=48
y[1]=14]= -12, (3 分)
y (t ) 2 3e t e2t cos 2t , t 0 . Determine the transfer function for the
system. Answer:
X ( s) Y (s) 1 s 1 2 3 s2 s s 1 ( s 2) 2 4 Y ( s ) s 2 2 s 16 H ( s ) s 3 4 s 2 8s
《信号与系统》试题及答案
信号与系统》试题及答案2012 年度教学质量综合评估测验卷《信号与系统》试题 题组：：1、开课学院：信息工程学院学院 题组2、：题纸上。
电子3、类适专用业班级：信息工程学院通信工程专业及 电子4、类在专答业写所要求填 卷面题型及分值：)题 答 不 内 线 封 密名姓研12组0 分钟，所有答案均写在答 发两张答题纸上认真填 。
总总分二 三 四 五 六 七 八 九 十100 20 20 60一、选择题(每小题 2 分，共 10小题。
每一小题仅有一个选项是正确的。
共计 20 分)列说法不正确的是( 一般周期信号为功率信号。
时限信号 (仅在有限时间区间不为零的非周期信号 )为能量信号。
ε(t)是功率信号； 1、 A 、 B 、 C 、)。
D 、 e t 为能量信号 列关于冲激函数性质的表达式不正确的是( 2、 A 、 C 、 3、 A 、 4、 f (t) (t) f (0) (t)H(s)B、(at))d (t)D 、 1ta(-t)(t)(s2s 1()s (s 2)2)，属于其极点的是(B 、2C 、 )。
1 If f1(t) ←→ F1(j ω)， f2(t) ←→ F2(j ω) A 、[a f1(t) + b f2(t) ] ←→ [a F1(j ω) *b F2(j ω) ] B 、[a f1(t) + b f2(t) ] ←→ [aF1(j ω) - b F2(j ω) ] C 、[a f1(t) + b f2(t) ] ←→ [a F1(j ω) + b F2(j ω) ] D 、[a f1(t) + b f2(t) ] ←→ [a F1(j ω) /b F2(j ω) ] 5、下列说法不正确的是( )。
A 、H(z)在单位圆内的极点所对应的响应序列为衰减的。
即当趋于 0。
Then[ D 、-2k →∞时，响应均B 、H(z)在单位圆上的一阶极点所对应的响应函数为稳态响应。
C 、H(z) 在单位圆上的高阶极点或单位圆外的极点， 其所对应的响应序列都是递 增的。
2011年12月考试信号与系统第一次作业
2011年12月考试信号与系统第一次作业题号 一 二 三 四 五 六 七 合计 已做/题量 9 / 9 1 / 1 5 / 5 2 / 2 10 / 10 5 / 5 10 / 1042 / 42 得分/分值18 / 184 / 410 / 108 / 89 / 1010 / 1040 / 4099 / 100一、单项选择题 （共9题、总分18分、得分18分） 1.连续信号f(t) 与 δ(t −t0)的乘积，即 f(t)*δ(t −t0)=( ) (本题分数：2 分，本题得分：2 分。
)A 、B 、C 、D 、题目信息 难度： 2 正确答案： B 解题方案：2. 已知f(t)，为求f(t 0−at) 应按下列哪种运算求得正确结果？（式中t 0,a 都为正值） (本题分数：2 分，本题得分：A 、f(-at)左移t 0B 、f(-at) 右移t 0C 、f(at) 左移t0/aD 、f(at)右移t0/a题目信息 难度： 2 正确答案： D 解题方案：3. 已知 f(t)，为求f(t 0-at) 应按下列哪种运算求得正确结果？（式中t 0,a 都为正值） (本题分数：2 分，本题得分A 、B 、f(at) 右移t0 C 、f(at) 左移t 0/a D 、f(-at) 右移t 0/a题目信息 难度： 3 正确答案： D 解题方案：4. 下列论断正确的为（ ）。
(本题分数：2 分，本题得分：2 分。
)A 、两个周期信号之和必为周期信号；B 、非周期信号一定是能量信号；C 、能量信号一定是非周期信号；D 、两题目信息 难度： 3 正确答案： C 解题方案：5. 信号f1(t),f2(t)波形如图所示，设f(t)=f1(t)*f2(t)，则f(0)为（ ）(本题分数：2 分，本题得分：2 分。
)A 、1B 、2C 、3D 、4题目信息 难度： 4 正确答案： B解题方案：卷积的图解法计算。
如直接用卷积定义式更加简单。
信号与系统答案
赣 南 师 范 学 院2011—2012学年度第1学期期末考试试卷（C 卷）开课学院：物电 课程名称：信号与系统 考试形式：闭卷 所需时间：120分注意事项：1、教师出题时请勿超出边界虚线；2、学生答题前将密封线外的内容填写清楚，答题不得超出密封线；．3、答题请用蓝、黑钢笔或圆珠笔。
一．填空题：(每题2分,共20分)1．[()(2)](22)u t u t t δ---等于 1()(1)2t δ-2．计算下列卷积32()3()t te u t e u t --*等于33()()tte e u t ---3．若()f t 的傅里叶变换为()F w ，求20()cos f t w t 的傅里叶变换2000001()cos [()*()()*()]4f t w t F w w F w w F w w F w w π↔+++-- 4．()dt t e t 12-⎰+∞∞--δ= e -2 。
5．计算下列信号的傅里叶变换[]sin()cos()2x n n n π=+，则()jw X e =()[()()]22[(1)(1)],jw X e w w j w w w πππδδπδδππ=--++--+-≤≤6. 下列是各离散时间信号的傅里叶变换2113()11148jwjw jw j w e X e e e ----=--，求相应于每一变换的信号[]x n =2171[][][]9294n nx n u n u n ⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭7. 线性时不变离散系统，若该系统的单位阶跃响应为1()[]4n u n ，则该系统的单位脉冲响应为 111[]()[]()[1]44n n h n u n u n -=--8. 有一个因果LTI 滤波器，其频率响应()H jw 如图所示，给定的输入1()()(6)X jw jw jw =+，求经过滤波后的输出()y t = 6()2()t y t e u t -=-9. 已知10(2)(5)()(1)(3)s s F s s s s ++=++，{}0Re s >，求逆变换()f t =310010()20e e ()33t t f t u t --⎛⎫=-- ⎪⎝⎭10.已知象函数2()(1)(2)z F z z z =+-,其收敛域分别为1<⎪z ⎪<2,求逆z 变换()f n =12()(1)()(2)(1)33n n f n u n u n =----二．判断题：(每题2分,共10分，填入“√”或“×”)1. 若t<0时，有f(t)=0 , t ≥0时，有f(t) ≠0 ,则f(t)称为因果信号。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
西南交通大学2011－2012学年第(1)学期考试试卷课程代码 3122400 课程名称 信号与系统A 考试时间 120分钟阅卷教师签字： 一、选择题：（20分）本题共10个小题，每题回答正确得2分，否则得零分。
每小题所给答案中只有一个是正确的。
1. 已知f (t )的傅里叶变换为)(ωj F ，则f (1-t )的傅里叶变换为（ C ） （A ）ωωj e j F )(-- （B ）ωωj ej F -)(（C ）ωωj e j F --)(（D ）ωωj ej F )(-2．连续周期信号的频谱具有( D )（A ）连续性、周期性 （B ）连续性、非周期性 （C ）离散性、周期性 （D ）离散性、非周期性3．某系统的系统函数为H （s ），若同时存在频响函数H （j ω），则该系统必须满足条件（C ） （A ）时不变系统 （B ）因果系统 （C ）稳定系统 （D ）线性系统4. 已知)(1n f 是1N 点的时限序列，)(2n f 是2N 点的时限序列，且12N N >，则)()()(21n f n f n y *= 是（ A ）点时限序列。
（A ）121-+N N （B ）2N （C ）1N （D ）21N N +5. 若对f （t ）进行理想取样，其奈奎斯特取样频率为f s ，则对)231(-t f 进行取样，其奈奎斯特取样频率为（ B ）。
（A ）3f s （B ）s f 31 （C ）3（f s -2） （D ）)2(31-s f 班 级 学 号 姓 名密封装订线 密封装订线 密封装订线6. 周期信号f(t)如题图所示，其直流分量等于（ B ）（A ）0 （B ）4 （C ）2（D ）67. 理想不失真传输系统的传输函数H （jω）是 （ B ）。
（A ）0j tKe ω- （B ）0t j Ke ω-（C ）0t j Ke ω-[]()()c c u u ωωωω+--（D ）00j t Keω- （00,,,c t k ωω为常数）8．已知)()(ωj F t f ↔,则信号)5()()(-=t t f t y δ的频谱函数 )(ωj Y 为（ A ）。
(A) ω5)5(j e f -(B) ωω5)(j e j F -(C) )5(f (D) )(ωj F9．以下表达式能正确反映)(n δ与)(n u 的是（ A ）。
(A)∑∞=-=0)()(k k n n u δ (B) ∑∞=-=1)()(k k n n u δ(C) )1()()(+--=n u n u n δ (D) ∑∞==0)()(k k n u δ10. 若系统函数有两个极点在虚轴上，当激励为单位冲激函数时，响应中含有（ B ） （A ）衰减的正弦振荡分量 （B ）等幅的正弦振荡分量 （C ）阶跃函数分量 （D ）衰减的指数分量二、（10分）试求下图所描述离散线性时不变系统的单位取样响应()h n 。
(x其中线性时不变子系统的单位取样响应分别为：()()14()(1)(2)(3)h n R n n n n n δδδδ==+-+-+-，()()()()2212h n n n n δδδ=+---，()()()()33212h n n n n δδδ=+-+-。
解：()[]123()()()h n h n h n h n =+*()()()()()()()()645114193142101113-+-+-+-+-+-+=n n n n n n n n h δδδδδδδ三、（20分）画图题1.（5分）已知信号)25(t f -波形如图所示，试给出)(t f 的波形。
解：)25(t f - t t →- (52)f t + 12t t → (5)f t + 5t t →- ()f t1.反褶2.展缩3.平移2.（5分）某线性时不变系统在零状态条件下的输入e （t ）与输出r （t ）的波形如题图所示，当输入波形为x （t ）时，试画出输出波形y （t ）。
t t解：t3.（10分）已知=)(ωj F F ⎥⎦⎤⎢⎣⎡22sin t t ,画出频率)(ωj F ～ω图形解：设sin ()()tx t Sa t t==，则[]()(1)(1)X j u u ωπωω=+--因为()()()f t x t x t =⋅，所以1()()()2F j X j X j ωωωπ=*四、（20分）某因果系统的微分方程为22()()3()()d y t dy t ay t x t dt dt++=，已知该系统的一个极点为-1。
（1）求参数a 的值；（2）求系统所有的零、极点，并画出零极点分布图； （3）判断系统的稳定性；（4）求该系统的单位冲激响应()h t 。
解：（1）根据微分方程，两边取拉氏变换，可得系统函数为：21()3H s s s a=++ 因为系统的一个极点为-1，故当s=-1时，系统函数的分母为0，即2(1)3(1)0a -+⨯-+=，得2a =（2）所以系统函数为：21()32H s s s =++1(1)(2)s s =++极点为121,2s s =-=-，无零点。
（3）由于系统是因果的，且所有极点都在s 平面的左半开平面，所以收敛域包含虚轴，系统是稳定的。
（4）2111()3212H s s s s s ==-++++ 且系统因果，所以2()()t th t e e u t --⎡⎤=-⎣⎦五、（10分） 已知信号f （t ）=Sa （2πt ），用单位冲激序列∑∞-∞=-=n sT nT t t )()(δδ对其进行取样，取样周期T s =0.25秒，1．画出f （t ）及)()()(t t f t f T s δ=的波形；2．求取样后信号f s （t ）的频谱函数F s （j ω），并画出频谱图F s （j ω）； 3．从该取样信号f s （t ）能否恢复原信号f （t ）？说明理由。
答案：1）2）1()[(2)(2)]2F j u u ωωπωπ=+--∞3）从该取样信号能恢复f （t ），因为原信号是带限信号，而且取样频率大于原信号最高频率的两倍，满足取样定理，只需将取样信号f s （t ）通过一个截止频率为26c πωπ<<的低通滤波器，即可恢复f （t ）。
六、（10分）设系统由下面的差分方程描述：3[][1][2][]2y n y n y n x n +---= （1）求系统的系统函数()H z ，并画出极零点分布图；（2）限定系统是因果的，写出()H z 的收敛域，并求出其单位脉冲响应[]h n ； （3）限定系统是稳定的，写出()H z 的收敛域，并求出其单位脉冲响应[]h n解：（1）对差分方程两端进行Z 变换：123()()()()2Y z z Y z z Y z X z --+-=，12()1()3()12Y z H z X z z z --==+-2(0.5)(2)z z z =-+ 0.20.8()0.52z zH z z z =+-+ （2）若系统因果，收敛域为2z >， 此时[]0.2(0.5)[]0.8(2)[]n n h n u n u n =+- （3）若系统稳定，收敛域为0.52z << 此时[]0.2(0.5)[]0.8(2)[1]n n h n u n u n =----七、（10分）图（a ）所示系统中sin 2000()te t tππ=，1()sin(2000),s t t π=2()cos(2000),s t t t π=-∞<<∞。
理想低通滤波器的传输函数如图（b ）所示。
（1） 画出A 、B 、C 处的频谱图。
（2） 求输出信号)(t r 。
解：（1）根据抽样信号的傅里叶变换[]()()()Sa Tt u T u T Tπωω↔+--sin 2000sin 2000()20002000(2000)2000t te t Sa t t tπππππ===，则其傅里叶变换为()(2000)(2000)E j u u ωωπωπ=+--1()sin(2000),s t t π=其频谱为[]1()(2000)(2000)S j j ωπδωπδωπ=+--所以，A 点的频谱()A j ω为：11()()()2A j E j S j ωωωπ=*[]1()(2000)(2000)2E j j ωπδωπδωππ=*+-- [][]{}(2000(20002jE j E j ωπωπ=+--ω图 （b ）1图（a ）2ω2()cos(2000)s t t π=其频谱[]2()(2000)(2000)S j ωπδωπδωπ=++-所以B 点的频谱()B j ω为：21()()()2B j A j S j ωωωπ=*[]1()(2000)(2000)2A j ωπδωπδωππ=*++- [][]{}1(2000(20002A j A j ωπωπ=++-所以C 点的频谱()C j ω为()()()0C j B j H j ωωω==（2）输出信号()0r t =。