六年级数学竞赛上册奥数高思第1讲:计算综合二(20200403194556)
六年级奥数培训教材

六年级拔尖数学目录第1讲定义新运算第2讲简单的二元一次不定方程第3讲分数乘除法计算第4讲分数四那么混合运算第5讲估算第6讲分数乘除法的计算技巧第7讲简单的分数应用题〔1〕第8讲较复杂的分数应用题〔2〕第9讲阶段复习与测试〔略〕第10讲简单的工程问题第11讲圆和扇形第12讲简单的百分数应用题第13讲分数应用题复习第14讲综合复习〔略〕第15讲测试〔略〕第16讲复杂的利润问题〔2〕第一讲 定义新运算在加.减.乘.除四那么运算之外,还有其它许多种法那么的运算。
在这一讲里,我们学习的新运算就是用“ #〞“*〞“Δ〞等多种符号按照一定的关系“临时〞规定的一种运算法那么进展的运算。
例1:如果A*B=3A+2B ,那么7*5的值是多少?例2:如果A#B 表示3B A + 照这样的规定,6#〔8#5〕的结果是多少?例3:规定YX XY Y X +=∆ 求2Δ10Δ10的值。
例4:设M*N 表示M 的3倍减去N 的2倍,即M*N=3M-2N(1) 计算〔14 *10〕*6(2) 计算 〔58*43〕 *〔1 *21〕例5:如果任何数A 和B 有A ¤B=A ×B-〔A+B 〕求〔1〕10¤7〔2〕〔5¤3〕¤4〔3〕假设2¤X=1求X例6:设P ∞Q=5P+4Q ,当X ∞9=91时,1/5∞〔X ∞ 1/4〕的值是多少?例7:规定X*Y=XY Y AX +,且5*6=6*5那么〔3*2〕*〔1*10〕的值是多少?例8:▽表示一种运算符号,它的意义是))((A Y A X XY Y X +++=∇11 3211212112=+++=∇))((A 那么20218▽2021=?稳固练习1、2▽3=2+22+222=246; 3▽4=3+33+333+3333=3702;按此规那么类推(1) 3▽2 〔2〕5▽3〔3〕1▽X=123,求X 的值2、1△4=1×2×3×4;5△3=5×6×7计算〔1〕〔4△2〕+〔5△3〕 〔2〕〔3△5〕÷〔4△4〕3、如果A*B=3A+2B,那么〔1〕7*5的值是多少?〔2〕〔4*5〕*6 〔3〕〔1*5〕*〔2*4〕4、如果A>B,那么{A,B}=A;如果A<B,那么{A,B}=B;试求〔1〕{8,0.8}〔2〕{{1.9,1.901}1.19}5、N为自然数,规定F〔N〕=3N-2 例如F〔4〕=3×4-2=10试求:F〔1〕+F〔2〕+F〔3〕+F〔4〕+F〔5〕+……+F〔100〕的值6、如果1=1!1×2=2!1×2×3=3!……1×2×3×4×……×100=100!那么1!+2!+3!+……+100!的个位数字是几?〔第四届小学生“迎春杯〞数学决赛试题〕7、假设“+、-、×、÷、=、〔〕〞的意义是通常情况,而式子中的“5”却相当于“4”。
高思教育数学课本第1讲加减法巧算讲义

在进行加减法计算时,“先计算括号中的部分,再从左往右依次计算”是基本的运算法则.但除此之外,还有许多运算技巧,熟练掌握各种运算技巧可以使你算得更快更准.“凑整法”是最常用的巧算方法,就是在计算时优先计算可以得到整十、整百、整千的部分,从而达到巧算的目的.要想凑出整十,两个数的末位相加应该得0,这样的情况除了00+,55+,46+.同学们在做题时要注意观察各+,28+,37+外,还有19加数的个位,看能不能找到合适的凑法.除了加法可以凑整以外,减法同样可以凑整,个位相同的两个数相减后便能得到整十的数.在进行加减法混合运算时,经常会遇到能够巧算的数不在一起的情况,这时候就需要通过调整运算顺序,把能巧算的放在一起先算.但需要注意的是,在调整的过程中,每个数都必须带着自己左边的符号一起移动,这种调整可以形象地称作“带符号搬家”.如果搬家的是算式中的第一个数,前面没有符号,在这个数之前添上一个加号即可.分析 (1)通过个位凑十来配对,但其中以1和9结尾的都分别有2个,应该如何配对呢?(2)加法配对看末位,减法应该如何配对?练习1.(1)计算:36973264168103+++++;(2)计算:24681925323922241234−++−+.除了“带符号搬家”可以调整运算次序外,“脱括号”与“添括号”也是改变运算顺序的常用手段.加减法算式中“脱括号”要遵循下面的规则:括号前面是加号,脱去括号不变号;括号前面是减号,脱去括号变符号.分析 去掉括号会变成什么样?练习2.(1)计算:()()12323454567−−−−;(2)(2(2)计算:()()437200836353−−+−. 小笑话从前,山东省有个大军阀,他横行霸道,却不学无术,经常闹笑话.一次会议开始时,他想点点名,了解一下哪些人来了,哪些人没来.可是,他一看到会的人数比较多,点名很费事.于是这个不学无术的军阀就想了一个“办法”.他认为没有来的人总是少数,只要知道哪些人没来,来的人不用一一点名,也会清楚了.于是他便大声地叫道:“没有来的人举手!”他这么喊过之后,到会的人面面相觑,都感到莫名其妙.上面只是一个小笑话,但是其实这个军阀运用了数学中“补数”的思想,只要知道了没到的人数,再用总人数减去没到的人数就可以了,只是他脱离了实际,结果闹了笑话.其实补数是速算和心算时一个重要的概念.比如,在计算45798−时,可以把98看成1002−来计算,()4579845710024571002359−=−−=−+=.在运用补数进行巧算的时候要注意补数前的符号到底是加还是减.分析 把题目中接近整百整十的数都变成补数的形式,应该怎么变?练习3.(1)计算:999999999++;(2)计算:23452993981198−−−.前面学习了“脱括号”的巧算方法,其实“添括号”也是一个重要的技巧,“添括号”与“脱括号”类似,同样要注意:括号前面是加号,添上括号不变号;(2)当然,这里所说的“括号前面”是指要添上的括号之前,而要改变的符号是新括号里的那些符号.分析 题(1)中全都是减号,在什么位置添上括号可以简化计算?题(2)中有加有减,有哪些数之间是可以凑整的?练习4.(1)计算:379131588742−−−−;(2)计算:9811451813235577+−−+−.最后我们来看两个与数字特点有关的计算:分析 仔细观察每一问里的数字都有什么特点?试着利用这些特点进行巧算.练习5. 计算:(1)714147471555++−;(2)1827364554637281+−+−+−+.(2(2)例题5本讲知识点汇总一、通过末位找到凑整的关系:加法末位和为10,减法末位相同.二、脱括号、添括号的原则:括号前面是加号,脱去/添上括号不变号;括号前面是减号,脱去/添上括号变符号.三、巧用补数:对于靠近整十整百整千的数,可以先用那些整的进行计算,再计算它们的补数.四、把每个数位分开计算.作业1. 计算:2589127175373289−++++.2. 计算:()()62235778600457−−−−.−−−.3.计算:100197396298−−−+.4.计算:3579862138734234++−.5.计算:334343433111。
小学数学奥数基础教程(六年级)目30讲全

小学奥数基础教程(六年级)第1讲比较分数的大小第2讲巧求分数第3讲分数运算的技巧第4讲循环小数与分数第5讲工程问题(一)第6讲工程问题(二)第7讲巧用单位“1”第8讲比和比例第9讲百分数第10讲商业中的数学第11讲圆与扇形第12讲圆柱与圆锥第13讲立体图形(一)第14讲立体图形(二)第15讲棋盘的覆盖第16讲找规律第17讲操作问题第18讲取整计算第19讲近似值与估算第20讲数值代入法第21讲枚举法第22讲列表法第23讲图解法第24讲时钟问题第25讲时间问题第26讲牛吃草问题第27讲运筹学初步(一)第28讲运筹学初步(二)第29讲运筹学初步(三)第30讲趣题巧解第一讲比较分数的大小同学们从一开始接触数学,就有比较数的大小问题。
比较整数、小数的大小的方法比较简单,而比较分数的大小就不那么简单了,因此也就产生了多种多样的方法。
对于两个不同的分数,有分母相同,分子相同以及分子、分母都不相同三种情况,其中前两种情况判别大小的方法是:分母相同的两个分数,分子大的那个分数比较大;分子相同的两个分数,分母大的那个分数比较小。
第三种情况,即分子、分母都不同的两个分数,通常是采用通分的方法,使它们的分母相同,化为第一种情况,再比较大小。
由于要比较的分数千差万别,所以通分的方法不一定是最简捷的。
下面我们介绍另外几种方法。
1.“通分子”。
当两个已知分数的分母的最小公倍数比较大,而分子的最小公倍数比较小时,可以把它们化成同分子的分数,再比较大小,这种方法比通分的方法简便。
如果我们把课本里的通分称为“通分母”,那么这里讲的方法可以称为“通分子”。
2.化为小数。
这种方法对任意的分数都适用,因此也叫万能方法。
但在比较大小时是否简便,就要看具体情况了。
3.先约分,后比较。
有时已知分数不是最简分数,可以先约分。
4.根据倒数比较大小。
5.若两个真分数的分母与分子的差相等、则分母(子)大的分数较大;若两个假分数的分子与分母的差相等,则分母(子)小的分数较大。
小学奥数之第2讲-计算综合(二)

第2讲计算综合(二)本讲主要是补充[计算综合(I)]未涉及和涉及不深的问题,但不包括多位数的运算. 1.n×(n+1)=[n×(n+1)×(n+2)-(n-1)×n×(n+1)]÷3;2.从1开始连续n个自然数的平方和的计算公a式:()()222211231216n n n n++++=⨯⨯+⨯+3.平方差公式:a2-b2=(a+b)(a-b).1.已知a=11,,112211331119999100b=+++++++试比较a、b的大小.【分析与解】11,,1122113311119898a bA B==++++++++其中A=99,B=99+1.100因为A<B,所以98+1A>98+1B,11119797,9696,111198989797119898A BA B+<++>+++++++1122,1133114411119898A B+>+++++++++所以有a<b.2.试求11112111311143114120052005++++++++++的和?【分析与解】记1,131412005x=+++则题目所要求的等式可写为:11,1211xx++++而11111.122211xx x xx++=+=+++++所以原式的和为1.评注:上面补充的两例中体现了递推和整体思想.2.试求1+2+3+4+…4+100的值?【分析与解】方法一:利用等差数列求和公式,(首项+末项)×项数÷2=(1+100)×100÷2=5050.方法二:倒序相加,1+ 2+ 3+ 4+ 5+… 97+ 98+ 99+ 100100+ 99+ 98+ 97+ 96+…4+ 3+ 2+ 1,上下两个数相加都是101,并且有100组,所以两倍原式的和为101×100,那么原式的和为10l×100 ÷2=5050.方法三:整数裂项(重点),原式=(1×2+2×2+3×2+4×2+…+100×2)÷2=[]122(31)3(42)4(53)100(10199)2⨯+⨯-+⨯-+⨯-++⨯-÷=(12⨯23+⨯12-⨯34+⨯23-⨯45+⨯34-⨯10010199100++⨯-⨯)2÷=1001012⨯÷=5050.3.试求l×2+2×3+3×4+4×5+5×6+…+99×100.【分析与解】方法一:整数裂项原式=(1×2×3+2×3×3+3×4×3+4×5×3+5×6×3+…+99×100×3)÷3=[1×2×3+2×3×(4-1)+3×4×(5-2)+4×5×(6-3)+5×6×(7-4)+…+99×100×(101-98)]÷3(123⨯⨯234+⨯⨯123-⨯⨯345+⨯⨯234-⨯⨯456+⨯⨯345-⨯⨯567+⨯⨯456-⨯⨯99100101 9899100++⨯⨯-⨯⨯)3991001013331011003333100333300.÷=⨯⨯÷=⨯⨯=⨯=方程二:利用平方差公式12+22+32+42+…+n2=2(1)(21).6n n nn⨯+⨯+=原式:12+l+22+2+32+3+42+4+52+5+…+992+99=12+22+32+42+52+…+992+1+2+3+4+5+…+99=991001999910062⨯⨯⨯+=328350+4950=333300.5.计算下列式子的值:0.1×0.3+0.2⨯0.4+0.3×0.5+0.4×0.6+…+9.7×9.9+9.8⨯10.0【分析与解】这个题看上去是一个关于小数的问题,实际上我们可以先把它们变成整数,然后再进行计算.即先计算1×3+2⨯4+3×5+4⨯6+…+97⨯99+98×100。
小学六年级学而思奥数讲解

某科室有 12 人,其中 6 人会英语, 5 人会俄语, 5 人会日语, 3 人既会英语又会俄语, 2 人 既会俄语又会日语, 2 人既会英语又会日语, 1 人三种语言全会。只会 1 种外语的人比 1 种 外语也不会的人多 ______个。
2006 盏亮着的电灯,各有一个拉线开关控制,按顺序编号为
1、 2、, 2006。将编号为 2 的
第 2008 次截去剩余长度的 米?
1 20092 ,此时该铁丝还剩
2010 厘米,那么该铁丝原长为
______厘
【附加练习】
1 1
13
1 1
24
1 1
35
1 1
2007 2009
4
已知
1 A=
3
5
24 6
97 99
246
, B=
98 100
357
试求 A、B、 C 三者大小关系。
96 98
1
, C= 。
97 99
10
【开裆裤的课堂笔记总结】 1.整体约分:
被除数、除数中的分母对应相等: 要么带化假、 要么假化带, 考虑提取公因数后整体约分; 2.连锁约分:
多分数连乘,将分子、分母都化成乘积形式,伺机约分。
测试题
例 1 测: 计算: 3 2 2 1 35
2 2 13 35
11 A.1
8
11 B.
8
1 C. 1
11
【举一反三】 还是用数字 0、1、2、3、4、5 六个数字可组成 _____个没有重复数字且能被 5 整除的四位数?
(2010 年北大附中小升初试题 ) 一个三位数,若它的中间数字恰好为首尾数字的平均值,则称它为“好数” 共有 ______个。
6华数奥赛教材六年级

《华数奥赛教材(6年级)》目录
上册
第一讲速算与巧算(一)
第二讲速算与巧算(二)
第三讲估算
第四讲计数问题(一)
第五讲计数问题(二)
第六讲分数与百分数(一)
第七讲分数与百分数(二)
第八讲圆的面积
第九讲圆的面积及综合问题
第十讲工程问题(一)
第十一讲工程问题(二)
第十二讲整除问题
第十三讲余数问题
《华数奥赛教材(6年级)》目录
下册
第一讲比和比例(一)
第二讲比和比例(二)
第三讲立体图形的计算(一)
第四讲立体图形的计算(二)
第五讲列方程解应用题(一)
第六讲列方程解应用题(二)
第七讲不定方程
第八讲逻辑推理问题
第九讲行程问题
第十讲时钟问题
第十一讲观察与归纳
第十二讲周期性问题
综合练习(一)综合练习(二)综合练习(三)综合练习(四)综合练习(五)综合练习(六)综合练习(七)综合练习(八)。
高思奥数导引小学六年级含详解答案第01讲 分数数列计算
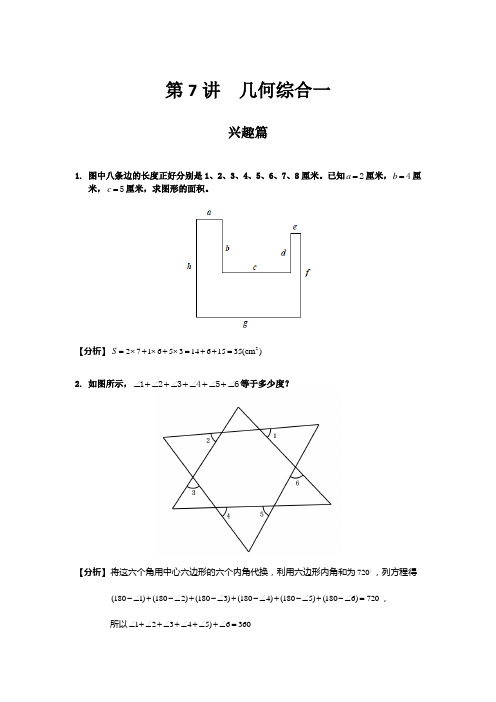
第7讲几何综合一兴趣篇1. 图中八条边的长度正好分别是1、2、3、4、5、6、7、8厘米。
已知a=2厘米,b=4厘米,c=5厘米,求图形的面积。
【分析】2S=⨯+⨯+⨯=++=2716531461535(cm)2. 如图所示,∠+∠+∠+∠+∠+∠123456等于多少度?【分析】将这六个角用中心六边形的六个内角代换,利用六边形内角和为720,列方程得(1801)(1802)(1803)(1804)(1805)(1806)720-∠+-∠+-∠+-∠+-∠+-∠=,所以12345)6360∠+∠+∠+∠+∠+∠=3. 如图,平行四边形ABCD 的周长为75厘米。
以BC 为底时高是14厘米,以CD 为底时高是16厘米。
求平行四边形ABCD 的面积。
【分析】 75237.5BC CD +=÷=,根据面积相等,底的比与高的比成反比例,所以:16:148:7BC CD ==,因此37.5(87)820BC =÷+⨯=,平行四边形ABCD 的面积是2014280⨯=平方厘米4. 如图所示,一个边长为1米的正方形被分成4个小长方形,它们的面积分别是310平方米、25平方米、15平方米和110平方米。
已知图中的阴影部分是正方形,那么它的面积是多少平方米?【分析】 1251110CH HD ==,因此23CH =,13HD =,3310245AE EB ==,所以37AE =,47EB =,因此2353721FG =-=,那么它的面积是252521441⎛⎫= ⎪⎝⎭平方米5. 如图,红、黄、绿三块大小一样的正方形纸片,放在一个正方体盒内,它们之间相互重叠。
已知露在外面的部分中,红色的面积是20,黄色的面积是14,绿色的面积是10。
那么,正方体盒子的底面积是多少?绿黄红【分析】 将黄色纸片推到左边,则每块纸片露出的形状如右上图.黄、绿两色的面积之和保持14+10=24不变,则在右图中这两块面积相等,均为24212÷=.根据公式可知,空白处面积=黄⨯绿÷红=1212207.2⨯÷=,则正方形盒底面积是7.212122051.2+++=.6. 如图,在三角形ABC 中,IF 和BC 平行,GD 和AB 平行,HE 和AC 平行。
高斯竞赛数学六年级

第1讲 分数数列计算内容概述建立抵消的思想,特别是灵话运用裂项的方法求解一些分数数列的计算问题.典型问题兴趣篇1.计算:⋅⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯1091981871761651541431321211 2.计算:⋅⨯++⨯+⨯+⨯99972752532312 3.计算:⋅⨯++⨯+⨯+⨯100981861641421 4.计算:.90172156142130120112161+++++++ 5.计算:⋅+++++97001130170128141 6.计算:⋅⨯++⨯+-⨯++⨯+-⨯+1091099898878776766565 7.计算:⋅+-+-+-+-901972175615421330112091276523 8.计算:⋅⨯⨯++⨯⨯+⨯⨯+⨯⨯10099982543243223212 9.计算:⋅++++++240239210209201912116521 10.计算:⋅+⨯-⨯⨯+⨯-⨯+⨯-)911()911()311()311()211()211(拓展篇1.计算:⋅⨯++⨯+⨯+⨯+⨯+⨯200820071651541431321211 2.计算:⋅⨯++⨯+⨯+⨯+⨯101983141131183853523 3.计算:⋅⨯-⨯+⨯-⨯+⨯-⨯1311241192097167512538314 4.计算:;90117721155611342111301920171215613211)1(++++++++ ⋅⨯-⨯-⨯+⨯++⨯+⨯-⨯-⨯+⨯+⨯-⨯-⨯+⨯42408241398040387839377611920108189716861475126410538426314)2( 5.计算:)10921()921(10)4321()321(4)321()21(3)21(121++++⨯++++++++⨯+++++⨯+++⨯+ 6.计算:⋅++++++83975939231137.计算:⋅⨯⨯++⋅⨯⨯+⨯⨯+⨯⨯10097999810798746541328.计算:⋅+++++++++++++++206421864216421421219.计算:⋅⨯⨯++⨯⨯+⨯⨯+⨯⨯504948154314321321110.计算:⋅⨯⨯++⨯⨯+⨯⨯+⨯⨯109811543643253214 11.计算:⋅-⨯⨯⋅-⨯-)9911()311()211(222 12.计算:⋅⨯+⨯⨯⨯+⨯⨯+⨯⨯+)2009200711()5311()4211()3111(超越篇1.计算:⋅⨯++⨯+++⨯++⨯+201920191918191832322121222222222.计算:.1201201181181414121222222222⋅-++-+++-++-+3.已知算式)19189()17168()542()321(+⨯+⨯⨯+⨯+ 的结果是一个整数,那么它的末两位数字是多少?4.计算:⋅⨯⨯++⨯⨯+⨯⨯+⨯⨯201918375437432532135.计算:!10099!43!32!21++++ (最后结果可以用阶乘表示)6.已知22226411019181,81++++==B A ,请比较A 和B 的大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
1+ 21 1
8 =
. 11
+ 1
4 x+
分析 第( 1 )题就是一个简单连分数的计算, 从下往上一层层算即可.但第( 2 )
题则是一个连分数方程,而且未
数在最底层,不可能把左侧的分数先算出来.
此时,为了将分数线减少,我
以采取方程左右两侧同时取倒数的想法,这
样一来,就容易求解了.
练习
5.( 1 )计算:
12 4. ( 1)计算:
;
7
9
+
3 84
+
5 1+
4
(2)已知
a ?b = a - b + 1 ,求:
5. 规定运算
a ×b
1
66 ,求 x .
=
1
1
1 107
+
+
6
1
1
1
1
+
+
5
2
1
1
+ x+
4
3
(1) (2 ?1)?(4 ?3) ;
(2) (99?97 ) + (97 ?95 ) (95 ?93 ) + + (3 ?1) ;
b
++
531 579 753 579 753 135 357 975
531
357 975
++
-
+++
753 135 531 579 753 135 579
357 975 531
135 357 975
a
+
3
身体健康
六年级
上册第 1 讲
我们不妨把这两块重叠部分,一个设为 b 的式子把原式表示出来吗?
已知 “*”表示一种运算符号,它的含义是:
m
a ?b =
+ a ×b ,并且 2 ?3 = 7 .
a ×b
( 1 )请问: m 等于多少?
(2 )计算: (1 ?2 )+ (2 ?3 ) + (3 ? 4 ) + + (19 ?20 ).
分析( 1)由 “*”的定义,以及 2 ?3 = 7 ,不难求出 m ; ( 2)对于 “*”,我们不清楚它有什么运算性质,但可以按照它的定义,
(2 ) (1 ?4 ) + (1 ?9 ) + (1 ?16 ) + + (1 ?100 ).
思考题
算式 1
1+1+1+1+1+1+1+1+ 1 + 1 + 1 + ×
2004 的计算结果,
2 3 4 5 6 7 8 9 10 11 12
13 小数点后第 2004 位数字是几?
本讲知 识点 汇总
一、提公因数法. 二、复杂的繁分数计算. 三、连分数的计算. 四、换元法及整体思想. 五、与整数裂项、分数裂项关联的自定义运算问题.
" " 和用来表示增加的 “+ ”.1489 年,德国数学家魏德迈( Widman , 1460 — ?)在
他的著作中首先使用 “+ ”、“ ”这两个符号表示剩余和不足. 1514 年荷兰数学家赫克
(Hoecke )把它们用作代数运算符号.后来又经过法国数学家韦达(
Vieta , 1540 — 1603 )
a ,另一个设为 b .你能用带有 a 和
练习
4. 计算: ++++
11 1 1 1
++ + + 11111 1
- +++++
+++
1 11 1 1 11 1 1
. 2345
23456
2 34 5 6 23 4 5
例 4 中用到了换元的运算技巧.换元,指的是用字母来代表一块算式,把算式当成 一个整体进行计算的方法,是一种很实用的计算技巧.换元的目的是让我们省去很多不
计算综合二
1
计算综合二
课本
到了六年级,我们对四则运算提出了新的要求,出现的都是比较复杂的混合四则运
算的题目,因而要求有较
的计算基本功.注意在计算的同时,综合运用以前学过的各
种巧算技巧,往往能使题目的计算过程变得简洁.但是现在的巧算技巧不再像以前那么
直接,而是蕴藏在计算的细节之中.
例题 1
÷5 + × 4
1+ 1+1
1+ 2
2
1+
+
55
1
4
身体健康
计算综合二
课本
连分数计算最重要的就是把分数线减少.仔细观察一下上述过程,大家不难发现,连分 数的计算顺序是由短分数线开始算,每次算完,分数线就变少,分数形式变得越来越简单.
例题 5
(1)将下面这个连分数化简为最简真分数:
1 ;
1
5+ 1
4+ 1
3+ 2
( 2)若等式成立, x 等于多少?
13 ;
8 +1
5
+3 3
1+
( 2 )计算: 1+ 1+ 1+
1 +1 ;
1 +1
1 +1
1
2
1+ +1
1
( 3 )已知
1
10 , 求 x .
=
3
1 17
+
5
12
+
7 12
+
12
x+
2
5
身体健康
六年级
上册第 1 讲
连分数的灯与塔
很多连分数具有很漂亮且有趣的形式,它们具有与花灯和宝塔相似的形状.请看下
?1 + 1 ?1 + 1 ?1 + + 1 ? 1
(3) 1
2
23
34
. 99 100
8
身体健康
.
×+
4
7
18 2 6 2
÷ 计算:
1 35 8
13 - 3 ÷
3 4 16
分析 题目看上去很繁琐,似乎需要大量的计算.对于这种含有带分数的运算, 我们一般先把带分数化成假分数,这样便于在乘除法中进行约分.
练习
91 7 3
.
×+ ×
92 3
6
35 3 24 11 2
2. 计算:
31 1
×
1
17
6 -3 4
把 “*”运算换成四则运算,如
1 ? 2 可以替换成
m + × , 2 ?3 可以替换成 12
1 ×2
6
身体健康
m + × , …… 23
2 ×3
计算综合二
课本
练习
a ?b = 1 ,求:
6. 定义新运算:
b- a
1 ?1 + 1 ?1 + 1 ?1 + + 1 ?
(1)
1;
98 87 7 6
2
的宣传和提倡,才开始普及,直到 1630 年,才得到大家的公认.
乘号曾经出现过十几种,现在通用两种.一个是 “×,”最早是由英国数学家奥屈特
1631 年提出的;一个是 “·”,最早是由英国数学家赫锐奥特首创的.德国数学家莱布尼 茨认为 “×号”像拉丁字母 “X”,加以反对,而赞成用 “·”号.他自己还提出用 “п”
必要的计算,这样能够大大简化计算过程.有时候,不一定要用换元才能够省去计算,
只要带着这个想法考虑问题就行了.
下面我们学习连分数.什么是连分数呢,举几个简单的例子:
1+ 1 1+ 2 1 1+ +3 1
1
2+
3+ 1
1
4
1+
1
1
像上面这样包含若干层分数线的复杂分数就是连分数.连分数本质上讲应该是一个 算式,而不仅仅只是一个数,所以我们通常需要将这样的连分数化简成最简分数的形式. 那究竟如何化简呢?
表示相乘.到了 18 世纪,美国数学家欧德莱确定把 “×作”为乘号.他认为 “,×是”“+”
斜起来写,是另一种表示增加的符号
除号 “÷”,最初这个符号是作
号在欧洲大陆流行,奥屈特用 “: ”表示除或比.
也有人用分数线表示比,后来有人把二者结合起来就变成了
“÷”.瑞士数学家拉哈的著
作中正式把 “÷”作为除号.
接下来我们学习一种特殊的计算技巧:换元法.请同学们先看例题
4.
例题 4
计算:
++ 531 579 753
++ 579 753 135
-
+++
+
531 579 753 135 579 753
. 135 357 975
357 975 531
135 357 975 531
357 975
分析 算式中的四个括号其实有很大一部分是重叠的,如下所示:
作业
×7 +
÷6
.
5
1. 计算:
51
34.5
12
7
14
7
身体健康
六年级
上册第 1 讲
2. 计算:
15
;
1 ×10 + 4.5 ÷
21 (1) 3 7
8 - 0.5 ×1.5 + × ÷+ .
