192特殊的平行四边形分课时练
2020-2021学年人教版数学 八年级下册 课时训练 18.2 特殊的平行四边形(含答案)
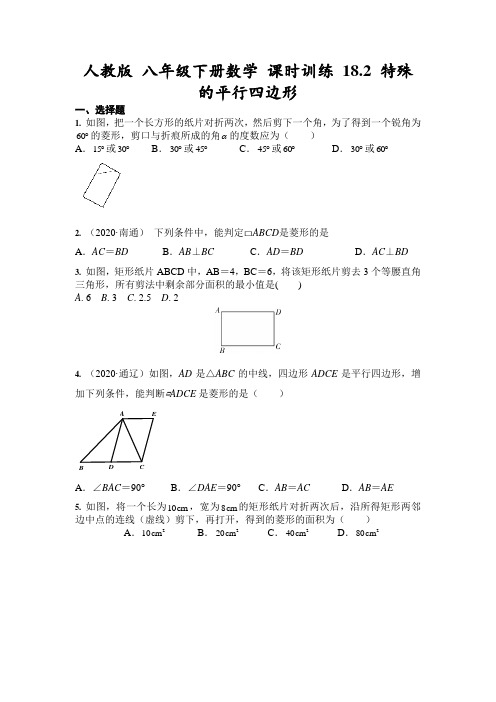
人教版 八年级下册数学 课时训练 18.2 特殊的平行四边形一、选择题1. 如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个锐角为60︒的菱形,剪口与折痕所成的角α的度数应为( )A .15︒或30︒B .30︒或45︒C .45︒或60︒D .30︒或60︒2. (2020·南通)下列条件中,能判定□ABCD 是菱形的是 A .AC =BDB .AB ⊥BCC .AD =BDD .AC ⊥BD3. 如图,矩形纸片ABCD 中,AB =4,BC =6,将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是( ) A . 6 B . 3 C . 2.5 D. 24. (2020·通辽)如图,AD是△ABC 的中线,四边形ADCE 是平行四边形,增加下列条件,能判断▱ADCE 是菱形的是( )EAA .∠BAC =90°B .∠DAE =90°C .AB =ACD .AB =AE5. 如图,将一个长为10cm ,宽为8cm 的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )A .210cmB .220cmC .240cmD .280cm6. (2020·滨州)下列命题是假命题的是()A .对角线互相垂直且相等的平行四边形是正方形B .对角线互相垂直的矩形是正方形C .对角线相等的菱形是正方形D .对角线互相垂直且平分的四边形是正方形7. (2020·黑龙江龙东)如图,菱形ABCD 的对角线AC 、BD 相交于点O ,过点D 作DH ⊥AB 于点H ,连接OH ,若OA =6,OH =4,则菱形ABCD 的面积为( )A .72B .24C .48D .96 8. (2020·泰安)如图,矩形ABCD 中,AC ,BD 相交于点O ,过点B 作BF ⊥AC 交CD 于点F ,交AC 于点M ,过点D 作DE ∥BF 交AB 于点E ,交AC 于点N ,连接FN ,EM .则下列结论:① DN ﹦BM ;②EM ∥FN ;③AE ﹦FC ;④当AO ﹦AD 时,四边形DEBF 是菱形.其中,正确结论的个数是( ) A .1个 B .2个 C . 3个 D .4个AB CDEFOMN 二、填空题9. 菱形ABCD 中,E 、F 分别是BC 、CD 的中点,且AE BC ⊥,AF CD ⊥,那么EAF ∠等于 .10. 已知正方形BDEF 的边长是正方形ABCD 的对角线,则:BDEF ABCD S S =正方形正方形11. 如图,已知P 是正方形ABCD 内的一点,且ABP ∆为等边三角形,那么DCP ∠=PDCBA12.如图,在矩形ABCD 中,点E F ,分别在边AB CD ,上,BF DE ∥,若12cm 7cm AD AB ==,,且:5:2AE EB =,则阴影部分EBPD 的面积为FE A BC D13. 如图,在菱形ABCD 中,E 、F 分别是AD 、BD 的中点,若EF =2,则菱形ABCD 的周长为________.14. 如图,在矩形ABCD 中,点E 是BC 上一点,AE AD =,DF AE ⊥,垂足为F.线段DF 与图中的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明。
18_2_1特殊的平行四边形(第二课时)练习

18.2.1 特殊的平行四边形(第二课时)练习练习1 现在你能帮小明解决问题了吗?小明判定相框为矩形的以下方法中哪些准确?为什么?(1)有一个角是直角的四边形是矩形;( )(2)四个角都相等的四边形是矩形;( )(3)对角线相等的四边形是矩形;( )(4)对角线互相平分且相等的四边形是矩形;( )(5)两组对边分别平行,且对角线相等的四边形是矩形.( )设计意图:考查学生对判定定理1,2,3的理解。
练习2 在“?”号处填上恰当的条件:设计意图:通过练习2的辨别,更进一步帮学生理清矩形判定定理思路随堂检测1.(选择)以下说法准确的是( ).(A )有一组对角是直角的四边形一定是矩形(B )有一组邻角是直角的四边形一定是矩形(C )对角线互相平分的四边形是矩形 (D )对角互补的平行四边形是矩形 设计意图:考查学生对判定定理的理解。
2.工人师傅做铝合金窗框分下面三个步骤实行:⑴ 先截出两对符合规格的铝合金窗料(如图①),使AB =CD ,EF =GH ;⑵ 摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是: ; ⑶ 将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,根据的数学道理是: ;设计意图:考查学生平行四边形的性质判定和在实际生活中的应用。
3.如图四边形ABCD 的对角线AC 、BD 相交于点O 已知O 是AC 的中点AE=CF,DF ∥BE(1)求证:△BOE ≌△DO F ,(2)若OD=21AC,则四边形ABCD 是什么特殊四边形?请证明你的结论。
设计意图:考查综合应用平行四边形的性质,矩形的性质与判定知识实行推理论证的水平。
九年级上特殊平行四边形课时练习题及答案

九(上)第一章特殊平行四边形重点题目菱形的性质1、菱形具有而一般平行四边形不具有的性质是()A. 对角相等B. 对边相等C. 对角线互相垂直D. 对角线相等2、菱形的周长为100cm;一条对角线长为14cm;它的面积是()A. 168cm2B. 336cm2C. 672cm2D. 84cm23、下列语句中;错误的是()A. 菱形是轴对称图形;它有两条对称轴B. 菱形的两组对边可以通过平移而相互得到C. 菱形的两组对边可以通过旋转而相互得到D. 菱形的相邻两边可以通过旋转而相互得到4、菱形的两条对角线分别是6 cm;8 cm;则菱形的边长为_____;面积为______.5、四边形ABCD是菱形;点O是两条对角线的交点;已知AB=5;AO=4;求对角线BD和菱形ABCD的面积.6、如图;在菱形ABCD中;∠ADC=120°;则BD:AC等于().(A)3:2 (B)3:3(C)1:2 (D)3:17、菱形ABCD的周长为20cm;两条对角线的比为3∶4;求菱形的面积。
8、如左下图;菱形ABCD的对角线AC、BD交于点O;且AC=16cm;BD=12cm;求菱形ABCD的高DH。
9、如右上图;在菱形ABCD中;∠BAD=80°;AB的垂直平分线交对角线AC于点F;E为垂足;连接DF;则∠CDF的度数为.10、在菱形ABCD中;∠A与∠B的度数比为1:2;周长是48cm.求:(1)两条对角线的长度;(2)菱形的面积.11、如图所示;在平面直角坐标系中;菱形MNPO的顶点P的坐标是(3;4);则顶点M、N的坐标分别是()A.M(5;0);N(8;4)B.M(4;0);N(8;4)C.M(5;0);N(7;4)D.M(4;0);N(7;4)12、(2010•襄阳)菱形的周长为8cm;高为1cm;则该菱形两邻角度数比为()A.3:1 B.4:1 C.5:1 D.6:113、如左下图;菱形ABCD的对角线AC、BD相交于点O;且AC=8;BD=6;过点O作OH丄AB;垂足为H;则点0到边AB的距离OH=_________.EOB第7题CF DA 15、【提高题】 如图;在菱形ABCD 中;顶点A 到边BC 、CD 的距离AE 、AF 都为5; EF =6;那么;菱形ABCD 的边长是_____菱形的判定1、能够判别一个四边形是菱形的条件是( )A. 对角线相等且互相平分B. 对角线互相垂直且相等C. 对角线互相平分D. 一组对角相等且一条对角线平分这组对角2、平行四边形ABCD 的两条对角线AC 、BD 相交于点O ; AB=5; AO=2; OB=1. 四边形ABCD 是菱形吗?为什么?3、 如左下图;AD 是△ABC 的角平分线。
八年级数学下册18.2特殊的平行四边形同步练习(二)(含解析)(新版)新人教版

18.2 特别的平行四边形同步练习( 二)一、单项选择题(本大题共有15 小题,每题 3 分,共 45 分)1、矩形拥有而菱形不拥有的性质是()A.两组对角分别相等B.对角线相互均分C.两组对边分别平行D.对角线相等2、以下说法中错误的选项是().A.对角线垂直的矩形是正方形B.对角线相等的菱形是正方形C.四条边相等的四边形是正方形D.四个角相等的四边形是矩形3、如图,在中,,,,为边上一动点,于,于,为的中点,则的最小值为()A.B.C.D.4、在中,,是边上一点,交于点,交于点,若要使四边形是菱形,只要增添条件().A.B.C.D.5、正方形四边中点的连线围成的四边形(最正确的说法)必定是()A.平行四边形B.正方形C.菱形D.矩形6、如图,正方形的边长为,在各边上按序截取,则四边形的面积是()A.B.C.D.7、如图,已知是正方形对角线上一点,且,则度数是()A.B.C.D.8、过矩形的四个极点作对角线、的平行线分別交于、、、四点,则四边形是().A. 正方形B. 菱形C. 矩形D. 平行四边形9、如图,四边形为平行四边形,延伸到,使,连结,,,增添一个条件,不可以使四边形成为矩形的是()A.B.C.D.10、如图,在锐角中,点是边上的一个动点,过作直线,设交的均分线于点,交的外角均分线于点,以下结论中正确的选项是()①;②;③若,,则的长为;④当时,四边形是矩形.A.①②B.①④C.①③④D.②③④11、以下命题中,真命题是()A.两条对角线相等的四边形是矩形B.两条对角线相互垂直的四边形是菱形C.两条对角线相互垂直且相等的四边形是正方形D.两条对角线相互均分的四边形是平行四边形12、如图,在四边形中,、、、分别是、、、的中点,要使四边形是菱形,则四边形只要要知足一个条件,是()A. 四边形是梯形B. 四边形是菱形C. 对角线D.13、如图,在菱形中,,分别在,上,且,与交于点,连结.若,则的度数为()A.B.C.D.14、在中,,、分别是、的中点,在延伸线上,,,,则四边形的周长为()A.B.C.D.15、以下图,设表示平行四边形,表示矩形,表示菱形,表示正方形,则以下四个图形中,能表示它们之间关系的是()A.B.C.D.二、填空题(本大题共有 5 小题,每题 5 分,共 25 分)16、如图,在菱形中,对角线、交于点,为边的中点,若菱形的周长为,则的长为.17、如图,已知矩形的对角线长为,、、、分别是、、、的中点,则四边形的周长等于.18、如图,在矩形中,,点和点分别从点和点出发,按逆时针方向沿矩形的边运动,点和点的速度分别为和,则最快后,四边形成为矩形.19、图,在中,点是的中点,点,分别在线段及其延伸线上,且.给出以下条件:①;②;③;从中选择一个条件使四边形是菱形,你以为这个条件是________(只填写序号).20、如图,在中,,点,分别是边,的中点,延伸到点,使.若,则的长是.三、解答题(本大题共有 3 小题,每题10 分,共 30 分)21、如图已知正方形的边长为,点分别为各边的中点,求图中阴影部分的面积.22、如图,平面直角坐标系中,的三个极点坐标分别为,,.(1)请画出对于直线作轴对称变换获得的,求点的坐标(2)将四边形向左平移个单位得四边形.则四边形与四边形重叠部分图形的形状什么?它的面积是多少?23、已知垂直均分,,,(1)证明四边形是平行四边形.(2)若,,求的长.18.2 特别的平行四边形同步练习( 二 )答案部分一、单项选择题(本大题共有15 小题,每题 3 分,共 45 分)1、矩形拥有而菱形不拥有的性质是()A.两组对角分别相等B.对角线相互均分C.两组对边分别平行D.对角线相等【答案】 D【分析】解:矩形拥有的性质是:对角线相等且相互均分,两组对边分别平行,两组对角分别相等;菱形拥有的性质是:两组对边分别平行,对角线相互均分,两组对角分别相等;矩形拥有而菱形不拥有的性质是:对角线相等.2、以下说法中错误的选项是().A.对角线垂直的矩形是正方形B.对角线相等的菱形是正方形C.四条边相等的四边形是正方形D.四个角相等的四边形是矩形【答案】 C【分析】解:四个角相等的四边形则每个角为90°,所以是矩形,该说法正确,不切合题意;四条边相等的四边形是菱形,不必定是正方形,该说法错误,切合题意;对角线相等的菱形是正方形,该说法正确,不切合题意;对角线垂直的矩形是正方形,该说法正确,不切合题意.故正确答案选:四条边相等的四边形是正方形.3、如图,在中,,,,为边上一动点,于,于,为的中点,则的最小值为()A.B.C.D.【答案】 D【分析】解:连结,以下图:,,,,,,四边形是矩形,.是的中点,,依据直线外一点到直线上任一点的距离,垂线段最短,即时,最短,相同也最短,当时,,最短时,,当最短时,.4、在中,,是边上一点,交于点,交于点,若要使四边形是菱形,只要增添条件().A.B.C.D.【答案】 C【分析】解:只要增添,四边形是平行四边形四边形是菱形故正确答案是:5、正方形四边中点的连线围成的四边形(最正确的说法)必定是()A.平行四边形B.正方形C.菱形D.矩形【答案】 B【分析】解:连结、,交于,正方形,,,是的中点,是的中点,是的中点,是的中点,,,,,,,,四边形是平行四边形,平行四边形是正方形.6、如图,正方形的边长为,在各边上按序截取,则四边形的面积是()A.B.C.D.【答案】 B【分析】解:四边形是正方形,,,,.在、、和中,,(),,,四边形是菱形,,,,四边形是正方形,,,,四边形的面积是:,7、如图,已知是正方形对角线上一点,且,则度数是()A.B.C.D.【答案】 B【分析】解:是正方形,,,,.8、过矩形的四个极点作对角线、的平行线分別交于、、、四点,则四边形是().A.正方形B.菱形C.矩形D.平行四边形【答案】 B【分析】解:由题意知,,,四边形是平行四边形,.四边形为矩形,矩形的对角线相等,,,平行四边形是菱形 .故答案为:菱形.9、如图,四边形为平行四边形,延伸到,使,连结,,,增添一个条件,不可以使四边形成为矩形的是()A.B.C.D.【答案】 B【分析】解:四边形为平行四边形,,且,又,,且,四边形为平行四边形,,,,平行四边形为矩形;,,四边形不可以为矩形;,,平行四边形为矩形;,,平行四边形为矩形.10、如图,在锐角中,点是边上的一个动点,过作直线,设交的均分线于点,交的外角均分线于点,以下结论中正确的选项是()①;②;③若,,则的长为;④当时,四边形是矩形.A.①②B.①④C.①③④D.②③④【答案】 B【分析】解①交的均分线于点,交的外角均分线于点,,,,,,,,,,;①正确;②当时,;故②错误;③,,,,,,;故③错误;④当点在边上运动到中点时,四边形是矩形.证明:当为的中点时,,,四边形是平行四边形,,平行四边形是矩形.故④正确;11、以下命题中,真命题是()A.两条对角线相等的四边形是矩形B.两条对角线相互垂直的四边形是菱形C.两条对角线相互垂直且相等的四边形是正方形D.两条对角线相互均分的四边形是平行四边形【答案】 D【分析】解:两条对角线相等且相互均分的四边形才是矩形,该选项命题错误;两条对角线相互垂直且均分的四边形才是菱形,该选项命题错误;两条对角线相互垂直且相等且相互均分的四边形是才正方形,该选项命题错误;两条对角线相互均分的四边形是平行四边形,该命题正确.故答案为:两条对角线相互均分的四边形是平行四边形.12、如图,在四边形中,、、、分别是、、、的中点,要使四边形是菱形,则四边形只要要知足一个条件,是()A.四边形是梯形B.四边形是菱形C. 对角线D.【答案】 D【分析】解:在四边形中,、、、别是、、、的中点,,,;同理,,四边形是平行四边形;若四边形是梯形时,,则,这与平行四边形的对边相矛盾;若四边形是菱形时,点四点共线;若对角线时,四边形可能是等腰梯形;当时,;所以平行四边形是菱形;13、如图,在菱形中,,分别在,上,且,与交于点,连结.若,则的度数为()A.B.C.D.【答案】 C【分析】解:四边形为菱形,,,,,在和中,,(),,,,,,,.14、在中,,、分别是、的中点,在延伸线上,,,,则四边形的周长为()A.B.C.D.【答案】 A【分析】解:在中,,,,是的中点,,,,,,、分别是、的中点,,,四边形是平行四边形,四边形的周长.15、以下图,设表示平行四边形,表示矩形,表示菱形,表示正方形,则以下四个图形中,能表示它们之间关系的是()A.B.C.D.【答案】 D【分析】解:四个边都相等的矩形是正方形,有一个角是直角的菱形是正方形,正方形应是N 的一部分,也是的一部分,矩形形、正方形、菱形都属于平行四边形,它们之间的关系是:.二、填空题(本大题共有 5 小题,每题 5 分,共 25 分)16、如图,在菱形中,对角线、交于点,为边的中点,若菱形的周长为,则的长为.【答案】 4【分析】解:四边形是菱形,,,,又,,在中,是斜边上的中线,,故答案为:.17、如图,已知矩形的对角线长为,、、、分别是、、、的中点,则四边形的周长等于.【答案】 16【分析】解:如图,连结、,、、、分别是、、、的中点,,,则四边形的周长等于.故正确答案是.18、如图,在矩形中,,点和点分别从点和点出发,按逆时针方向沿矩形的边运动,点和点的速度分别为和,则最快后,四边形成为矩形.【答案】 4【分析】解:设最快秒,是矩形,,要使是矩形,则,得.解得.19、图,在中,点是的中点,点,分别在线段及其延伸线上,且.给出以下条件:①;②;③;从中选择一个条件使四边形是菱形,你以为这个条件是________(只填写序号).【答案】③【分析】解:由题意得:,,四边形是平行四边形,①,依据这个条件只好得出四边形是矩形,②,依据是平行四边形已能够得出,所以不可以依据此条件得出菱形,③,,,,(),,四边形是菱形.20、如图,在中,,点,分别是边,的中点,延伸到点,使.若,则的长是.【答案】 7【分析】解:如图,连结.是的中位线,,,,,,是平行四边形,.是斜边上的中线,,.三、解答题(本大题共有 3 小题,每题10 分,共 30 分)21、如图已知正方形的边长为,点分别为各边的中点,求图中阴影部分的面积.【分析】解:连结、,∵ 、分别为边、的中点,∴,,同理,,,,,∵四边形是正方形,∴,,∴四边形是正方形,∴暗影部分的面积.22、如图,平面直角坐标系中,的三个极点坐标分别为,,.(1) 请画出对于直线作轴对称变换获得的,求点的坐标.【分析】解:(1)所作图形以下:点的坐标为.(2)将四边形向左平移个单位得四边形.则四边形与四边形重叠部分图形的形状什么?它的面积是多少?【分析】解:重叠图形为四边形,则四边形与四边形重叠部分图形的形状为菱形,它的面积为.23、已知垂直均分,,,(1)证明四边形是平行四边形.【分析】证明:垂直均分,,,在与中,,(),,,,,,,四边形是平行四边形.(2)若,,求的长.【分析】解:四边形 ABDF是平行四边形,,平行四边形是菱形,,,设,则,,即解得:,,.。
特殊的平行四边形练习题

特殊的平行四边形练习题一、选择题1.下列命题中,真命题是( )A .两条对角线垂直的四边形是菱形B .对角线垂直且相等的四边形是正方形C .两条对角线相等的四边形是矩形D .两条对角线相等的平行四边形是矩形 2.下列命题中正确的是( )A .两条对角线互相平分的四边形是平行四边形B .两条对角线相等的四边形是矩形C .两条对角线互相垂直的四边形是菱形D .两条对角线互相垂直且平分的四边形是正方形 3.下列命题不正确的是( )A .对角线相等且互相平分的四边形是矩形B .邻边相等的矩形是正方形C .对角线互相垂直的四边形是菱形D .对角线相等的菱形是正方形 4.菱形具有而平行四边形不具有的性质是( )A.两组对边分别平行B.两组对角分别相等 C .对角线互相平分 D .对角线互相垂直 5.菱形的两条对角线的长分别是6和8 ,则这个菱形的周长和面积分别为( )A .24 ,48B .20 ,24C . 10 ,24D . 5 ,48 6.在平面直角坐标系中,已知点A (0,2),B (,0),C (0,),D (,0),则以这四个点为顶点的四边形是( ) A .矩形 B .菱形 C .正方形 D .梯形 7.如图1,菱形ABCD 中,∠B =60°,AB =2,E 、F 分别是BC 、CD 的中点,连接AE 、EF 、AF ,则△AEF 的周长为( )A .B .C .D .图2 图3 图48.如图2,在平行四边形ABCD 中,对角线和相交于点,则下面条件能判定平行四边形ABCD 是矩形的是( )A .B .C .且D . 9.如图3,平行四边形ABCD 中,AC ,BD 是两条对角线,如果添加一个条件,即可推出平行四边形ABCD 是菱形,那么这个条件是( ) A . AB =CD B .AC =BD C . AC ⊥BD D .AB ⊥BD 10.如图4,菱形中,对角线AC 、BD 交于点O ,E 为AD 边中点,菱形ABCD 的周长为28,则OE 的长等于( )A .3.5B .4C .7D .14 11.下列命题中错误..的是( ) A.平行四边形的对边相等 B.两组对边分别相等的四边形是平行四边形 C.矩形的对角线相等 D.对角线相等的四边形是矩形 12.下列命题中错误..的是( ) A.平行四边形的对角线互相平分 B.对角线互相垂直平分且相等的四边形是正方形 C.矩形的对角线互相垂直平分 D.四边相等的四边形是菱形32-2-32ABCD 3233343AC BD O AC BD =AC BD ⊥AC BD =AC BD ⊥AB AD =图1 FAD E B CA CB D13.如图5,菱形ABCD 中,AB=4,∠BAD=120°,AE ⊥BC ,AF ⊥CD ,垂足分别为E ,F ,连接EF ,则的△AEF 的面积是( ) A .4 B .3 C .2 D .图5 图6 图7 图814.如图6,把矩形ABCD 沿EF 翻折,点B 恰好落在AD 边的B ′处,若AE =2,DE =6,∠EFB =60°,则矩形ABCD 的面积是( )A .12 B. 24 C. 12 3 D. 16 315.如图7,在菱形ABCD 中,AC 与BD 相交于点O ,AC=8,BD=6,则菱形的边长AB 等于( )A .10B .C .6D .5 16.如图8,下列条件之一能使平行四边形ABCD 是矩形的为( ) ① ② ③ ④ A .①③ B .②③ C .②④ D .③④二、填空题1. 如图9,菱形中,,对角线,则菱形的周长等于 .图9 图10 图11 图122.如图10,矩形ABCD 中,AB =2,BC =3,对角线AC 的垂直平分线分别交AD ,BC 于点E 、F ,连接CE ,则CE 的长________.3.如图11,在四边形中,,,若再添加一个条件,就能推出四边形是矩形,你所添加的条件是 .(写出一种情况即可)4.如图12,菱形的边长为2,,则点的坐标为 . 5.如图13,在矩形ABCD 中,对角线AC ,BD 相交于点O ,若∠AOD =120°,AB =4cm ,则AC 的长为________cm .图13图14图15 6.如图14,已知P 是正方形ABCD 对角线BD 上一点,且BP = BC ,则∠ACP 度数是 °. 7.如图15, 正方形ABCD 的边长为4,点P 在DC 边上,且DP =1,点Q 是 AC 上一动点,则DQ +PQ 的最小值为____________.AC BD ⊥90BAD ∠=AB BC =AC BD =ABCD 60A ∠=8BD =ABCD ABCD AD BC ∥90D ∠=ABCD ABCD 45ABC ∠=D A B CD A B D F A D OE B C B C D A PF D OB E A 三、解答题1.如图,矩形ABCD 中,O 是AC 与BD 的交点,过O 点的直线EF 与AB CD ,的延长线分别交于E F ,.(1)求证:BOE DOF △≌△; (2)当EF 与AC 满足什么关系时,以A E C F ,,,为顶点的四边形是菱形?证明你的结论.2.如图,在Rt △ABC 中,∠BAC=90°,D 是BC 的中点,E 是AD 的中点,过点A 作AF ∥BC 交BE 的延长线于点F .(1)求证:△AEF ≌△DEB ; (2)证明四边形ADCF 是菱形;(3)若AC=4,AB=5,求菱形ADCF 的面积.3.如图,在△ABC 中,D 、E 分别是AB 、AC 的中点,过点E 作EF ∥AB ,交BC 于点F . (1)求证:四边形DBFE 是平行四边形;(2)当△ABC 满足什么条件时,四边形DBFE 是菱形?为什么?4.已知:如图,在▱ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC 于E,F两点,连结BE,DF.(1)求证:△DOE≌△BOF;(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.5.如图,在△ABC中,点D是BC的中点,点E,F分别在线AD及其延长线上,且DE=DF.给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是(只填写序号).请说明理由.6.已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.(1)求证:△ABM≌△DCM;(2)判断四边形MENF是什么特殊四边形,并证明你的结论;(3)当AD∶AB=__________时,四边形MENF是正方形(只写结论,不需证明).1.如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是,并证明.(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.2.如图,在△ABC中,AB=AC,点D(不与点B重合)在BC上,点E是AB的中点,过点A作AF∥BC交DE延长线于点F,连接AD,BF.(1)求证:△AEF≌△BED.(2)若BD=CD,求证:四边形AFBD是矩形.3.如图,将平行四边形ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC 于点O.(1)求证:△ABD≌△BEC;(2)连接BD,若∠BOD=2∠A,求证:四边形BECD是矩形.4.如图,在△ABC中,AB=BC,BD平分∠ABC.四边形ABED是平行四边形,DE交BC 于点F,连接CE.求证:四边形BECD是矩形.A B P D E5.已知:如图,点E 是正方形ABCD 的边AB 上任意一点,过点D 作DF DE ⊥交BC 的延长线于点F .求证:DE DF =.6.已知:如图,在正方形ABCD 中,点E 、F 分别在BC 和CD 上,AE = AF . (1)求证:BE = DF ;(2)连接AC 交EF 于点O ,延长OC 至点M , 使OM = OA ,连接EM 、FM .判断四边形AEMF 是什么特殊四边形?并证明你的结论.7.如图,P 是边长为1的正方形ABCD 对角线AC 上一动点(P 与A 、C 不重合),点E 在射线BC 上,且PE=PB . (1)求证:PE=PD ;(2)PE ⊥PD ; 8.如图12,B 、C 、E 是同一直线上的三个点,四边形ABCD 与四边形CEFG 是都是正方形.连接BG 、DE.(1)观察猜想BG 与DE 之间的关系,并证明你的结论.(2)在图中是否存在通过旋转能够互相重合的两个三角形?若存在,请指出,并说出旋转过程;若不存在,请说明理由.图12G FEDC BAA EBCFD 12330.(2015•简阳市模拟)已知:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证:(1)AE=AB;(2)如果BM平分∠ABC,求证:BM⊥CE.3.(2014•江苏盐城,第25题10分)菱形ABCD中,对角线AC、BD相交于点O,过点O作一条直线分别交DA、BC的延长线于点E、F,连接BE、DF.(1)求证:四边形BFDE是平行四边形;(2)若EF⊥AB,垂足为M,tan∠MBO=,求EM:MF的值.4、(2008泰州市)在矩形ABCD中,AB=2,AD=3.(1)在边CD上找.一点E,使EB平分∠AEC,并加以说明;(3分)(2)若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.①求证:点B平分线段AF;(3分)②△PAE能否由△PFB绕P点按顺时针方向旋转而得到,若能,加以证明,并求出旋转度数;若不能,请说明理由.(4分)5.(2014•山东临沂,第25题11分)【问题情境】如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.【探究展示】(1)证明:AM=AD+MC;(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.【拓展延伸】(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.14.(2013年内蒙古赤峰)如图4-3-47,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t s(0 < t≤ 15).过点D作DF⊥BC于点F,连接DE,EF.(1)求证:AE=DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;(3)当t为何值时,△DEF为直角三角形?请说明理由.新课标第一网图4-3-4713、(2008年江苏省苏州市)如图,在等腰梯形ABCD 中,AD BC ∥,5AB DC ==,6AD =,12BC =.动点P 从D 点出发沿DC 以每秒1个单位的速度向终点C 运动,动点Q 从C 点出发沿CB 以每秒2个单位的速度向B 点运动.两点同时出发,当P 点到达C 点时,Q 点随之停止运动.(1)梯形ABCD 的面积等于 ;(2)当PQ AB ∥时,P 点离开D 点的时间等于 秒;(3)当P Q C ,,三点构成直角三角形时,P 点离开D 点多少时间?26、(2008上海市)如图,已知平行四边形ABCD 中,对角线AC BD ,交于点O ,E 是BD 延长线上的点,且ACE △是等边三角形. (1)求证:四边形ABCD 是菱形;(2)若2AED EAD ∠=∠,求证:四边形ABCD 是正方形.38、(2008鸡西)已知:正方形ABCD 中,45MAN ∠=,MAN ∠绕点A 顺时针旋转,它的两边分别交CB DC ,(或它们的延长线)于点M N ,.EB ACB当MAN ∠绕点A 旋转到BM DN =时(如图1),易证BM DN MN +=. (1)当M A N ∠绕点A 旋转到BM DN ≠时(如图2),线段BM DN ,和MN 之间有怎样的数量关系?写出猜想,并加以证明.40.(2010福建南平)如图1,在△ABC 中,AB=BC ,P 为AB 边上一点,连接CP ,以PA 、PC 为邻边作□APCD ,AC 与PD 相交于点E ,已知∠ABC=∠AEP=α(0°<α<90°).(1)求证:∠EAP=∠EPA;(2)□APCD 是否为矩形?请说明理由;(3)如图2,F 为BC 中点,连接FP ,将∠AEP 绕点E 顺时针旋转适当的角度,得到∠MEN(点M 、N 分别是∠MEN 的两边与BA 、FP 延长线的交点).猜想线段EM 与EN 之间的数量关系,并证明你的结论.43.(2010 山东莱芜)在平行四边形ABCD 中,AC 、BD 交于点O ,过点O 作直线EF 、GH ,分别交平行四边形的四条边于E 、G 、F 、H 四点,连结EG 、GF 、FH 、HE . (1)如图①,试判断四边形EGFH 的形状,并说明理由;图1BBBMBCNCNM CNM 图1图2图3AAADDD(2)如图②,当EF ⊥GH 时,四边形EGFH 的形状是 ;(3)如图③,在(2)的条件下,若AC =BD ,四边形EGFH 的形状是 ;(4)如图④,在(3)的条件下,若AC ⊥BD ,试判断四边形EGFH 的形状,并说明理由.46.(2010福建宁德)如图,四边形ABCD 是正方形,△ABE 是等边三角形,M 为对角线BD (不含B 点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM.⑴ 求证:△AMB≌△ENB;⑵ ①当M 点在何处时,AM +CM 的值最小;②当M 点在何处时,AM +BM +CM 的值最小,并说明理由;⑶ 当AM +BM +CM 的最小值为时,求正方形的边长.13B C H G F EO D C B A 图① H G F E OD C B A 图② A B C DOE F G H 图③ A B C D OEF GH图④。
北师九上3.2特殊的平行四边形同步练习

3。
2特殊平行四边形(时间100分钟满分:100分)教材跟踪训练(一)填空题(共16分)1。
(2分)矩形除了具备平行四边形的性质外,还有一些特殊性质:四个角 ,对角线。
2.(1分)在矩形ABCD中,对角线AC、BD交于点O,若100∠=,AOB 则OAB∠=。
3.(1分)已知菱形一个内角为120,且平分这个内角的一条对角线长为8cm,则这个菱形的周长为 .4.(3分)矩形的两条对角线把这个矩形分成了四个三角形.菱形的两条对角线把这个菱形分成了四个三角形。
正方形的两条对角线把这个正方形分成了四个三角形。
5.(2分)如图,把两个大小完全相同的矩形拼成“L”型图案,则∠=。
∠= ,FCAFAC6.(2分)正方形的边长为a,则它的对角线长,若正方形的对角线长为b,它的边长为。
7.(1分)边长为a的正方形,在一个角剪掉一个边长为的b正方形,则所剩余图形的周长为。
8.(4分)顺次连接四边形各边中点,所得的图形是。
顺次连接对角线的四边形的各边中点所得的图形是矩形。
顺次连接对角线的四边形的各边中点所得的四边形是菱形.顺次连接对角线的四边形的各边中点所得的四边形是正方形。
(二)选择题(每小题2分,共14分)1。
正方形具备而菱形不具备的性质是()A.对角线互相平分B.对角线互相垂直 C。
对角线相等 D。
每条对角线平分一组对角2。
下列命题是真命题的是()A.有一个角是直角的四边形是矩形 B。
有一组邻边相等的四边形是菱形C. 有三个角是直角的四边形是矩形D. 有三条边相等的四边形是菱形3.从菱形的钝角顶点,向对角的两边条垂线,垂足恰好在该边的中点,则菱形的内角中钝角的度数是()A.150B. 135C. 120 D 。
1004.顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形满足条件的是()①平行四边形 ②菱形 ③等腰梯形 ④对角线互相垂直的四边形A.①③ B 。
②③ C 。
③④ D.②④5.在平行四边形、菱形、矩形、正方形中,能够找到一个点,使该点到各顶点距离相等的图形是()A 。
特殊的平行四边形(第2课时)-2020-2021学年八年级数学下册课时同步练(人教版)(解析版)
第十八章平行四边形专题18.2 特殊第平行四边形(第2课时)基础巩固一、单选题(共10小题)1.正方形具有而矩形不一定有的性质是()A.对角线互相垂直B.对角线相等C.对角互补D.四个角相等【答案】A【分析】根据正方形的性质,余角和补角,矩形的性质逐一进行判断即可.【解答】解:A.因为对角线互相垂直,正方形具有而矩形不具有,所以A选项符合题意;B.因为对角线相等,正方形具有而矩形也具有,所以B选项不符合题意;C.因为对角互补,正方形具有而矩形也具有,所以C选项不符合题意;D.因为四个角相等,正方形具有而矩形也具有,所以D选项不符合题意.故选:A.【知识点】正方形的性质、余角和补角、矩形的性质2.如图,在菱形ABCD中,对角线AC=6,∠BAD=120°,则菱形ABCD的周长为()A.24B.30C.36D.18【答案】A【分析】根据菱形的邻角互补求出∠B=60°,再根据菱形的四条边都相等可得AB=BC,然后求出△ABC 是等边三角形,根据等边三角形的三条边都相等可得AB,然后利用菱形的周长公式计算即可得解.【解答】解:在菱形ABCD中,∠BAD=120°,∴∠B=180°﹣120°=60°,又∵AB=BC,∴△ABC是等边三角形,∴AB=AC=6,∴菱形ABCD的周长=6×4=24.故选:A.【知识点】菱形的性质、等边三角形的判定与性质3.若菱形的周长为16,高为2,则菱形两邻角的度数之比为()A.4:1B.5:1C.6:1D.7:1【答案】B【分析】如图,AH为菱形ABCD的高,AH=2,利用菱形的性质得到AB=4,利用正弦的定义得到∠B=30°,则∠C=150°,从而得到∠C:∠B的比值.【解答】解:如图,AH为菱形ABCD的高,AH=2,∵菱形的周长为16,∴AB=4,在Rt△ABH中,sin B===,∴∠B=30°,∵AB∥CD,∴∠C=150°,∴∠C:∠B=5:1.故选:B.【知识点】菱形的性质4.如图,在菱形ABCD中,对角线AC、BD相交于点O,H为BC中点,AC=6,BD=8.则线段OH的长为()A.B.C.3D.5【答案】B【分析】先根据菱形的性质得到AC⊥BD,OB=OD=BD=4,OC=OA=AC=3,再利用勾股定理计算出BC,然后根据直角三角形斜边上的中线性质得到OH的长.【解答】解:∵四边形ABCD为菱形,∴AC⊥BD,OB=OD=BD=4,OC=OA=AC=3,在Rt△BOC中,BC===5,∵H为BC中点,∴OH=BC=.故选:B.【知识点】直角三角形斜边上的中线、菱形的性质、三角形中位线定理5.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6cm,BC=8cm.则EF的长是()A.2.2cm B.2.3cm C.2.4cm D.2.5cm【答案】D【分析】根据矩形性质得出∠ABC=90°,BD=AC,BO=OD,根据勾股定理求出AC,进而求出BD、OD,最后根据三角形中位线求出EF的长即可.【解答】解:∵四边形ABCD是矩形,∴∠ABC=90°,BD=AC,BO=OD,∵AB=6cm,BC=8cm,∴由勾股定理得:AC===10(cm),∴BD=10cm,DO=5cm,∵点E、F分别是AO、AD的中点,∴EF是△AOD的中位线,∴EF=OD=2.5cm,故选:D.【知识点】勾股定理、三角形中位线定理、矩形的性质6.如图,在Rt△ABC中,∠ACB=90°,点H、E、F分别是边AB、BC、CA的中点,若EF+CH=8,则CH的值为()A.3B.4C.5D.6【答案】B【分析】根据三角形的中位线定理和直角三角形斜边上的中线等于斜边的一半求得即可.【解答】解:∵在Rt△ABC中,∠ACB=90°,点H,E,F分别是边AB,BC,CA的中点,∴EF=AB,CH=AB,∴EF=CH,∵EF+CH=8,∴CH=EF=8=4,故选:B.【知识点】三角形中位线定理、直角三角形斜边上的中线7.如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有()A.2条B.4条C.6条D.8条【答案】B【分析】根据轴对称的性质即可画出对称轴进而可得此图形的对称轴的条数.【解答】解:如图,因为以正方形的边长为直径,在正方形内画半圆得到的图形,所以此图形的对称轴有4条.故选:B.【知识点】轴对称图形、轴对称的性质、正方形的性质8.如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为()A.4B.2C.D.2【答案】C【分析】根据正方形的对角线互相垂直可得OA⊥OD,对角线平分一组对角可得∠OAD=45°,然后求出四边形OEPF为矩形,△AEP是等腰直角三角形,再根据矩形的对边相等可得PF=OE,根据等腰直角三角形的性质可得PE=OE,从而得到PE+PF=OA,然后根据正方形的性质解答即可.【解答】解:在正方形ABCD中,OA⊥OB,∠OAD=45°,∵PE⊥AC,PF⊥BD,∴四边形OEPF为矩形,△AEP是等腰直角三角形,∴PF=OE,PE=AE,∴PE+PF=AE+OE=OA,∵正方形ABCD的边长为2,∴OA=AC==.故选:C.【知识点】正方形的性质9.如图,矩形ABCD的边AD沿折痕AE折叠,使点D落在BC边上的点F处,已知AB=3,BF=4,则CE的长等于()A.B.C.D.【答案】A【分析】由勾股定理可求AF的长,由折叠的性质可得AD=AF=5,DE=EF,由勾股定理可求EC的长.【解答】解:∵AB=3,BF=4,∴AF===5,∵矩形ABCD的边AD沿折痕AE折叠,∴AD=AF=5,DE=EF,∴BC=AD=5,∴CF=BC﹣BF=1,∵EF2=EC2+CF2,∴(3﹣CE)2=EC2+1,∴CE=,故选:A.【知识点】矩形的性质、翻折变换(折叠问题)10.如图,在平行四边形ABCD中,AD=2AB,作CE⊥AB于点E,点F是AD的中点,连接CF,EF.关于下列四个结论:①∠BCF=∠DCF;②∠FEC=∠FCE;③∠AEF=∠CFD;④S△CEF=S△BCE,则所有正确结论的序号是()A.①②③④B.①②③C.②③④D.③④【答案】B【分析】由平行四边形的性质结合等腰三角形的判定与性质可得∠DFC=∠BCF,DFC=∠DCF,可证明①;取EC的中点G,连接FG,则FG为梯形AECD的中位线,再证明FG⊥CE,可证明②;根据平行线的性质可得∠AEC=∠DCE=90°,进而可证明③;而无法证明④.【解答】解:∵四边形ABCD为平行四边形,∴AB∥CD,AD∥BC,AB=CD,∴∠DFC=∠BCF,∵点F是AD的中点,∴AD=2DF,∵AD=2AB,∴AD=2CD,∴DF=CD,∴∠DFC=∠DCF,∴∠BCF=∠DCF,故①正确;取EC的中点G,连接FG,则FG为梯形AECD的中位线,∴FG∥AB,∵CE⊥AB,∴FG⊥CE,∴EF=CF,∴∠FEC=∠FCE,故②正确;∵CE⊥AB,AB∥CD,∴CE⊥CD,∴∠AEC=∠DCE=90°,即∠AEF+∠FEC=∠DCF+∠FCE=90°,∴∠AEF=∠DCF,∵∠DCF=∠CFD,∴∠AEF=∠CFD,故③正确;根据现有条件无法证明S△CEF=S△BCE,故错误④.故选:B.【知识点】全等三角形的判定与性质、直角三角形斜边上的中线、平行四边形的性质二、填空题(共6小题)11.已知四边形ABCD是矩形,点E是矩形ABCD的边上的点,且EA=EC.若AB=6,AC=2,则DE的长是.【分析】由勾股定理可求BC=2,分点E在CD上或在AB上两种情况讨论,由勾股定理可求解.【解答】解:如图,∵四边形ABCD是矩形,∴CD=AB=6,AD=BC,∠ABC=∠ADC=90°,∴BC===2,∴AD=2,当点E在CD上时,∵AE2=DE2+AD2=EC2,∴(6﹣DE)2=DE2+4,∴DE=;当点E'在AB上时,∵CE'2=BE'2+BC2=E'A2,∴AE'2=(6﹣AE')2+4,∴AE'=,∴DE'===,综上所述:DE=或,故答案为:或.【知识点】矩形的性质、勾股定理12.如图,在菱形ABCD中,对角线AC,BD交于点O,其中OA=1,OB=2,则菱形ABCD的面积为.【答案】4【分析】根据菱形的面积等于对角线之积的一半可得答案.【解答】解:∵OA=1,OB=2,∴AC=2,BD=4,∴菱形ABCD的面积为×2×4=4.故答案为:4.【知识点】菱形的性质13.如图,在Rt△ABC中,∠ABC=90°,D、E、F分别为AB、BC、CA的中点,若BF=5,则DE=.【答案】5【分析】首先由直角三角形的性质求得AC=2BF,然后根据三角形中位线定理得到DE=AC,此题得解.【解答】解:如图,∵在Rt△ABC中,∠ABC=90°,F为CA的中点,BF=5,∴AC=2BF=10.又∵D、E分别为AB、BC的中点,∴DE是Rt△ABC的中位线,∴DE=AC=5.故答案是:5.【知识点】三角形中位线定理、直角三角形斜边上的中线14.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.【答案】135【分析】由正方形的性质可得∠ACB=∠BAC=45°,可得∠2+∠BCP=45°=∠1+∠BCP,由三角形内角和定理可求解.【解答】解:∵四边形ABCD是正方形,∴∠ACB=∠BAC=45°,∴∠2+∠BCP=45°,∵∠1=∠2,∴∠1+∠BCP=45°,∵∠BPC=180°﹣∠1﹣∠BCP,∴∠BPC=135°,故答案为:135.【知识点】正方形的性质15.如图,点E是正方形ABCD的边DC上一点,点F是CB延长线上一点,且△ADE≌△ABF,四边形AECF的面积为8,DE=1,则AE的长为.【答案】3【分析】由:△ADE≌△ABF,可得正方形ABCD的面积等于四边形AECF的面积,从而可得AD2=8,在Rt△ADE中,由勾股定理可求得答案.【解答】解:∵△ADE≌△ABF,∴正方形ABCD的面积等于四边形AECF的面积,∵四边形AECF的面积为8,∴正方形ABCD的面积为8.∴AD2=8,在Rt△ADE中,AE===3,故答案为:3.【知识点】全等三角形的性质、正方形的性质、勾股定理16.如图,在菱形ABCD中,对角线AC、BD相交于点O,点E在线段BO上,连接AE,若CD=2BE,∠DAE=∠DEA,EO=1,则线段AE的长为.【分析】设BE=x,则CD=2x,根据菱形的性质得AB=AD=CD=2x,OB=OD,AC⊥BD,再证明DE =DA=2x,所以1+x=x,解得x=2,然后利用勾股定理计算OA,再计算AE的长.【解答】解:设BE=x,则CD=2x,∵四边形ABCD为菱形,∴AB=AD=CD=2x,OB=OD,AC⊥BD,∵∠DAE=∠DEA,∴DE=DA=2x,∴BD=3x,∴OB=OD=x,∵OE+BE=BO,∴1+x=x,解得x=2,即AB=4,OB=3,在Rt△AOB中,OA===,在Rt△AOE中,AE===2.故答案为2.【知识点】菱形的性质拓展提升三、解答题(共6小题)17.如图,四边形AFDC是正方形,∠CEA和∠ABF都是直角,且点E,A,B三点共线,CE=5,求AB的长.【分析】由正方形的性质可得CA=AF,∠CAF=90°,由“AAS”可证△CEA≌△ABF,可得AB=CE =5.【解答】解:∵四边形AFDC是正方形,∴CA=AF,∠CAF=90°,∵点E,A,B三点共线,∴∠EAC+∠BAF=180°﹣∠CAF=90°,又∵∠CEA=∠ABF=90°,∴∠EAC+∠ECA=90°,∴∠ECA=∠BAF,∴△CEA≌△ABF(AAS),∴AB=CE=5.【知识点】全等三角形的判定与性质、正方形的性质18.如图,点E是正方形ABCD的CD边上一点,连接AE,将△ADE顺时针旋转,使AD与AB重合,点E落在CB的延长线上的F处.(1)旋转中心是,旋转角为度;(2)若CE=3cm,BF=2cm,求四边形AFCE的面积.【答案】【第1空】点A【第2空】90【分析】(1)由旋转的性质可求解;(2)由旋转的性质可得△ADE≌△ABF,进而可得DE=BF=2cm,S△ADE=S△ABF,即可求解.【解答】解:(1)∵将△ADE顺时针旋转,使AD与AB重合,∴旋转中心是点A,旋转角为∠DAB=90°,故答案为点A,90;(2)∵将△ADE顺时针旋转,使AD与AB重合,∴△ADE≌△ABF,∴DE=BF=2(cm),S△ADE=S△ABF,∴CD=CE+DE=5(cm),∴四边形AFCE的面积=S正方形的面积=25(cm2).【知识点】三角形的面积、正方形的性质、旋转的性质19.如图,在正方形ABCD的外侧,作等边三角形DCE,连接BE,求∠DEB的度数.【分析】由正方形的性质可得BC=CD,∠BCD=90°,由等边三角形的性质可得BC=CE,∠DCE=∠DEC=60°,由等腰三角形的性质可求∠BEC=15°,即可求解.【解答】解:∵四边形ABCD是正方形,∴BC=CD,∠BCD=90°,∵△DCE是等边三角形,∴BC=CE,∠DCE=∠DEC=60°,∴BC=CE,∠BCE=150°,∴∠BEC=∠EBC=(180°﹣∠BCE)=15°,∴∠DEB=∠DEC﹣∠BEC=60°﹣15°=45°.【知识点】正方形的性质、等边三角形的性质20.如图,四边形ABCD是正方形,G是BC上任意一点,DE⊥AG于点E,BF∥DE,且交AG于点F.(1)求证:△ADE≌△BAF;(2)求证:DE﹣BF=EF;(3)若AB=2,BG=1,求线段EF的长.【分析】(1)由“AAS”可证△DAE≌△ABF;(2)由全等三角形的判定和性质可得AE=BF,DE=AF,即可得结论;(3)由勾股定理可求AG的长,由面积法可求BF的长,由勾股定理可求AF的长,即可求解.【解答】证明:(1)∵四边形ABCD是正方形,∴AB=AD,∠ABC=∠BAD=90°,∵DE⊥AG,∴∠AED=∠DEF=90°,∵BF∥DE,∴∠AFB=∠DEF=∠DEA=90°,∴∠BAF+∠DAE=∠ADE+∠DAE=90°,∴∠BAF=∠ADE,在△ABF和△DAE中,,∴△DAE≌△ABF(AAS);(2)∵△DAE≌△ABF,∴AE=BF,DE=AF,∵AF﹣AE=EF,∴DE﹣BF=EF;(3)∵∠ABC=90°,∴AG2=AB2+BG2=12+22=5,∴AG=,∵S△ABG=AG•BF,∴BF=,在Rt△ABF中,AF2=AB2﹣BF2=22﹣=,∴DE=AF=,∴EF=DE﹣BF=.【知识点】全等三角形的判定与性质、正方形的性质21.如图,E是正方形ABCD对角线BD上一点,连接AE,CE,并延长CE交AD于点F.(1)求证:△ABE≌△CBE;(2)若∠AEC=140°,求∠DFE的度数.【分析】(1)由“SAS”可证△ABE≌△CBE;(2)由全等三角形的性质可求∠CEB=70°,由三角形的外角的性质可求解.【解答】(1)证明:∵四边形ABCD是正方形,∴AB=CB,∠ABC=∠ADC=90°,,在△ABE和△CBE中,,∴△ABE≌△CBE(SAS);(2)∵△ABE≌△CBE,∴∠AEB=∠CEB,又∵∠AEC=140°,∴∠CEB=70°,∵∠DEC+∠CEB=180°,∴∠DEC=180°﹣∠CEB=110°,∵∠DFE+∠ADB=∠DEC,∴∠DFE=∠DEC﹣∠ADB=110°﹣45°=65°.【知识点】正方形的性质、全等三角形的判定与性质22.如图,矩形ABCD的对角线相交于点O,分别过点C、D作CE∥BD、DE∥AC,CE、DE交于点E.(1)求证:四边形OCED是菱形.(2)将矩形ABCD改为菱形ABCD,其余条件不变,连结OE.若AC=10,BD=24,则OE的长为.【答案】13【分析】(1)根据矩形性质和已知条件即可判断四边形OCED是菱形;(2)根据菱形的性质和勾股定理可得CD=13,再根据矩形的判定和性质即可得OE的长.【解答】(1)证明:∵DE∥AC、CE∥BD,∴四边形OCED是平行四边形.∵四边形ABCD是矩形,∴AC=BD,,.∴OC=OD.∴四边形OCED是菱形;(2)解:∵四边形ABCD是菱形,∴AC⊥BD,=5,=12.∴CD==13,∵DE∥AC、CE∥BD,∴四边形OCED是平行四边形.∵AC⊥BD,∴四边形OCED是矩形,∴OE=CD=13.故答案为:13.【知识点】菱形的判定与性质、矩形的性质。
人教版数学八年级下册第19章19.2 特殊的平行四边形 课时同步训练-2.doc
第十九章 四边形 19.2 特殊的平行四边形19.2.2菱形 第1课时(共2课时)课前预习篇1.菱形的定义:有一组 邻边 相等的平行四边形叫菱形.2.菱形的性质:菱形具有平行四边形一切性质,此外,它还具有如下特殊性质: (1)边: 菱形的对边平行且四边相等 . (2)角: 菱形的对角相等邻角互补 .(3)对角线: 菱形的两条对角线互相垂直,且每一条对角线平分一组对角 . (4)对称性:.菱形是轴对称图形也是中心对称图形,两条对角线所在的直线是它的两条对称轴.3.菱形的面积公式:(1) S 菱形=对角线乘积的一半 ;(2) S 菱形=底×高 .典例剖析篇【例1】已知:如图,菱形ABCD 的周长为8 cm ,∠ADC=120°,对角线AC ,BD 相交于点O ,求这个菱形的对角线长和面积.【解析】此题考查了菱形的性质:四边相等,对角线互相垂直平分,且每一条对角线平分一组对角.根据已知可确定存在30°角的直角三角形,所以再结合菱形的性质,问题可解. 解:因为四边形ABCD 是菱形, 所以AD=AB=BC=CD ,AC ⊥BD ,∠ADB=12∠ADC . 因为菱形ABCD 的周长为8 cm ,∠ADC=120°, 所以AD=AB=2 cm ,∠AOD=90°,∠ADB=60°. 所以在Rt △AOD 中,∠DAO=30°. 所以DO=12AD=1 cm ,==因为DO=12BD ,AO=12AC ,所以BD=2 cm ,AC=cm .所以S 菱形=12A C ·BD=12×2×cm .基础夯实篇1.菱形具有而一般平行四边形不具有的特征是( D ) A .对角相等 B .对边平行且相等 C .对角线互相平分 D .对角线互相垂直 2.菱形具有而矩形不一定具有的特征是( B )A .对角相等且互补B .对角线互相垂直平分C .四个内角都相等D .一组对边平行,另一组对边相等 3.依次连接菱形四条边的中点所构成的四边形是( B ) A .菱形 B .矩形 C .一般平行四边形 D .一般四边形4.(2010北京)若菱形两条对角线的长分别为6和8,则这个菱形的周长为(A ) A .20 B .16 C . 12 D .105..(2010南通) 如图,菱形ABCD 中,AB = 5,∠BCD = 120°,则对角线AC 的长是( D )A .20B .15C .10D .56.如图,在菱形ABCD 中,E ,F 分别是AB ,AC 的中点,如果EF=2,那么菱形ABCD 的周长是( D ) A .4 B .8C .12D .16 7.(2010珠海)如图,P 是菱形ABCD 对角线BD 上一点,PE ⊥AB 于点E ,PE =4cm ,则点P 到BC 的距离是___ 4__cm . 8.(2010嘉兴)如图,已知菱形ABCD 的一个内角∠BAD =80º,对角线AC 、BD 相交于点O ,点E 在AB 上且BE =BO ,则∠EOA =__25 º _____. 9.(2010陕西)若一个菱形的边长为2,则这个菱形两条对角线的平方和为 ( A ) A 16 B 8 C 4 D 1BACD11.(2010烟台)如图,在平面直角坐标系中,点O 为原点,菱形OABC 的对角线OB 在x 轴上,顶点A 在反比例函数2y x=的图像上,则菱形的面积为______4______.决胜中考篇12.(2009安顺)如图所示,两个全等菱形的边长为1 m ,一个微型机器人由A 点开始按ABCDEFCGA 的顺序沿菱形的边循环运动,行走2009 m 停下,则这个微型机器人停在___B ___点.13.(2010益阳)如图7,在菱形ABCD 中,∠A =60°,AB =4,O 为对角线BD 的中点,过O 点作OE ⊥AB ,垂足为E . (1) 求∠ABD (2)求线段BE 的长.解:⑴ 在菱形ABCD 中,AB=AD ,∠A =60°,所以ABD ∆为等边三角形 所以∠ABD=60°⑵由(1)可知BD=AB=4,又因为O 为BD 的中点所以OB=2。
特殊的平行四边形专项练习(含答案)
特殊的平行四边形(含答案)一、选择题(本大题共49小题,共147.0分)1.一个菱形的周长是20cm,两条对角线长的比是4︰3,则这个菱形的面积是()A. 12cm2B. 96cm2C. 48cm2D. 24cm22.若菱形的周长为8,高为1,则菱形两邻角的度数之比是()A. 3:1B. 4:1C. 5:1D. 6:13.如图,在矩形ABCD中,O为AC中点,EF过O点,且EF⊥AC分别交DC于F,交AB于E,点G是AE中点,且∠AOG=30°.①DC=3OG;②OG=12BC;③△OGE是等边三角形;④S△AOE=16S矩形ABCD.则结论正确的个数为()A. 4B. 3C. 2D. 14.如图,ABCD是一张平行四边形纸片,要求利用所学知识作出一个菱形,甲、乙两位同学的作法如下:则关于甲、乙两人的作法,下列判断正确的为()A. 仅甲正确B. 仅乙正确C. 甲、乙均正确D. 甲、乙均错误5.如图,在菱形ABCD中,∠A=130°,连接BD,∠DBC等于()A. 25°B. 35°C. 50°D. 65°6.如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为()A. 5cmB. 4.8cmC. 4.6cmD. 4cm7.如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为()A. 36°B. 27°C. 18°D. 9°8.如图,四边形ABCD是菱形,AC=12,BD=16,AH⊥BC于H,则AH等于()A. 4B. 5C. 245D. 4859.菱形具有而一般平行四边形不具有的性质是()A. 两组对边分别相等B. 两条对角线相等C. 四个内角都是直角D. 每一条对角线平分一组对角10.如图,在菱形ABCD中,∠BAD=100°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF等于()A. 60°B. 50°C. 30°D. 20°11.如图,在矩形ABCD中,F是BC中点,E是AD上一点,且∠ECD=30°,∠BEC=90°,EF=4cm,则矩形的面积为().A. 16cm2B. 8√3cm2C. 16√3cm2D. 32cm212.如图,正方形ABCD中,BE=FC,CF=2FD,AE,BF交于点G,连接AF,给出下列结论:①AE⊥BF;②AE=BF;③BG=43GE;④S四边形CEGF=S▵ABG.其中正确的个数为()A. 1个B. 2个C. 3个D. 4个13.在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE//AC,DF//AB,分别交AB,AC于E、F两点,下列说法错误的是()A. 四边形AEDF是平行四边形B. 若AB⊥AC,则四边形AEDF是矩形C. 若BD=CD,则四边形AEDF是正方形D. 若AD平分∠BAC,则四边形AEDF是菱形14.如图,在矩形ABCD中,AB>BC,点E,F,G,H分别是边DA,AB,BC,CD的中点,连接EG,HF,则图中的矩形共有()A. 5个B. 8个C. 9个D. 11个15.如图,将长方形纸片折叠,使A点落BC上的F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是()A. 邻边相等的矩形是正方形B. 对角线相等的菱形是正方形C. 两个全等的直角三角形构成正方形D. 轴对称图形是正方形16.平行四边形、矩形、菱形、正方形都具有的性质是()A. 对角线互相平分B. 对角线互相垂直C. 对角线相等D. 对角线互相垂直平分且相等17.如图,在菱形ABCD中,E,F,G,H分别是菱形四条边的中点,连结EG与FH,交点为O,则图中的菱形共有()A. 4个B. 5个C. 6个D. 7个18.如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60∘,则花坛对角线AC的长等于()A. 6√3米B. 6米C. 3√3米D. 3米19.如图,在平行四边形ABCD中,AD=2AB,CE⊥AB于点E,点F、G分别是AD、BC的中点,连接CF、EF、FG,下列结论:①CE⊥FG;②四边形ABGF是菱形;③EF=CF;④∠EFC=2∠CFD.其中正确的个数是()A. 1个B. 2个C. 3个D. 4个20.如图①,正方形A的一个顶点与正方形B的对称中心重合,重叠部分面积是正方形A面积的12,如图②,移动正方形A的位置,使正方形B的一个顶点与正方形A 的对称中心重合,则重叠部分面积是正方形B面积的()A. 12B. 14C. 16D. 1821.如图①、图②,在给定的一张矩形纸片上作一个正方形,甲、乙两人的作法如下:甲:以点A为圆心,AD长为半径画弧,交AB于点E,以点D为圆心,AD长为半径画弧,交CD于点F,连接EF,则四边形AEFD即为所求;乙:作∠DAB的平分线,交CD于点M,同理作∠ADC的平分线,交AB于点N,连接MN,则四边形ADMN即为所求.对于以上两种作法,可以做出的判定是()A. 甲正确,乙错误B. 甲、乙均正确C. 乙正确,甲错误D. 甲、乙均错误22.如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点,当AB︰AD的比为()时,四边形MENF是正方形.A. 1︰1B. 1︰2C. 2︰3D. 1︰423.如图,在菱形ABCD中,∠ADC=72∘,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB的度数是()A. 108∘B. 72∘C. 90∘D. 100∘24.在一次数学课上,张老师出示了一个题目:“如图,▱ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,BE.请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:小青:OE=OF;小何:四边形DFBE是正方形;小夏:S四边形AFED=S四边形FBCE;小雨:∠ACE=∠CAF.这四位同学写出的结论中不正确的是()A. 小青B. 小何C. 小夏D. 小雨25.如图,将边长为2cm的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为()A. (√3,−1)B. (2,−1)C. (1,−√3)D. (−1,√3)26.七巧板是我国祖先的一项卓越创造,流行于世界各地.由边长为2的正方形可以制作一副中国七巧板或一副日本七巧板,如图1所示.分别用这两副七巧板试拼如图2中的平行四边形或矩形,则这两个图形中,中国七巧板和日本七巧板能拼成的个数分别是()A. 1和1B. 1和2C. 2和1D. 2和227.四边形ABCD的对角线AC,BD,下面给出的三个条件中,选取两个,能使四边形ABCD是矩形,①AC,BD互相平分;②AC⊥BD;③AC=BD,则正确的选法是()A. ①②B. ①③C. ②③D. 以上都可以28.如图,菱形ABCD周长为20,对角线AC、BD相交于点O,E是CD的中点,则OE的长是()A. 2.5B. 3C. 4D. 529.如图,在正方形ABCD中,E是BC边上的一点,BE=2,EC=4,将正方形边AB沿AE折叠到AF,延长EF交DC于G,连接AG.现在有如下四个结论:①∠EAG=45°;②FG=FC;③FC//AG;④S△GFC=3.6.其中结论正确的个数是()A. 1B. 2C. 3D. 430.在菱形ABCD中,AC、BD为对角线,若AC=4,BD=8,则菱形ABCD的面积是()A. 12B. 16C. 24D. 3231.四边形具有不稳定性,对于四条边长确定的四边形.当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′.若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是()A. 1B. 12C. √22D. √3232.一个菱形的边长为6,面积为28,则该菱形的两条对角线的长度之和为()A. 8B. 12C. 16D. 3233.矩形OABC在平面直角坐标系中的位置如图所示,已知B(2√3,2),点A在x轴上,点C在y轴上,P是对角线OB上一动点(不与原点重合),连接PC,过点P作PD⊥PC,交x轴于点D.下列结论:①OA=BC=2√3;②当点D运动到OA的中点处时,PC2+PD2=7;③在运动过程中,∠CDP是一个定值;④当△ODP为等腰三角形时,点D的坐标为(2√33,0).其中正确结论的个数是()A. 1个B. 2个C. 3个D. 4个34.如图,矩形ABCD中,点E在BC边上,DF⊥AE于F,若EF=CE=1,AB=3,则线段AF的长为()A. 2√5B. 4C. √10D. 3√235.如图,在矩形ABCD中,BC=8,CD=6,E为AD上一点,将△ABE沿BE折叠,点A恰好落在对角线BD上的点F处,则折线BE的长为()A. 2√5B. 3√3C. 3√5D. 6√336.如图,菱形ABCD的边长为13,对角线AC=24,点E、F分别是边CD、BC的中点,连接EF并延长与AB的延长线相交于点G,则EG=()A. 13B. 10C. 12D. 537.下列说法正确的是()A. 一组对边平行另一组对边相等的四边形是平行四边形B. 对角线互相垂直平分的四边形是菱形C. 对角线相等的四边形是矩形D. 对角线互相垂直且相等的四边形是正方形38.如图,在菱形ABCD中,∠BCD=60°,BC的垂直平分线交对角线AC于点F,垂足为E,连接BF、DF,则∠DFC的度数是()A. 130°B. 120°C. 110°D. 100°39.若菱形的周长为16,高为2,则菱形两邻角的度数之比为()A. 4:1B. 5:1C. 6:1D. 7:140.已知四边形ABCD是平行四边形,AC,BD相交于点O,下列结论错误的是()A. OA=OC,OB=ODB. 当AB=CD时,四边形ABCD是菱形C. 当∠ABC=90°时,四边形ABCD是矩形D. 当AC=BD且AC⊥BD时,四边形ABCD是正方形41.下列是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是()A. 由②推出③,由③推出①B. 由①推出②,由②推出③C. 由③推出①,由①推出②D. 由①推出③,由③推出②42.菱形不具备的性质是()A. 是轴对称图形B. 是中心对称图形C. 对角线互相垂直D. 对角线一定相等43.如图,矩形ABCD的对角线AC,BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为()A. 485B. 325C. 245D. 12544.下列说法正确的有几个()①对角线互相平分的四边形是平行四边形;②对角线互相垂直的四边形是菱形;③对角线互相垂直且相等的平行四边形是正方形;④对角线相等的平行四边形是矩形.A. 1个B. 2个C. 3个D. 4个45.在矩形ABCD中,AC、BD相交于点O,若△AOB的面积为2,则矩形ABCD的面积为()A. 4B. 6C. 8D. 1046.如图,已知正方形ABCD边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE长为()A. 2√2−2B. √3−1C. 2−√2D. √2−147.如图,在菱形ABCD中,对角线AC、BD相交于点O,H为BC中点,AC=6,BD=8.则线段OH的长为()A. 125B. 52C. 3D. 548.如图所示,点O是矩形ABCD对角线AC的中点,OE//AB交AD于点E.若OE=3,BC=8,则OB的长为()A. 4B. 5C. √342D. √3449.菱形的对角线不一定具有的性质是()A. 互相平分B. 互相垂直C. 每一条对角线平分一组对角D. 相等二、填空题(本大题共21小题,共63.0分)50.如图,将两条宽度都为6的纸片重叠在一起,使∠ABC=60°,则四边形ABCD的面积为________.51.如图,在菱形ABCD中,对角线AC、BD相交于点O,H为边AD的中点,菱形ABCD的周长为28,则OH的长等于________.52.已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是______.53.在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,下面四个结论中,①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.所有正确结论的序号是______.54.菱形的面积是24,一条对角线长是6,则菱形的边长是______.55.如图,四边形ABCD为菱形,四边形AOBE为矩形,O,C,D三点的坐标为(0,0),(2,0),(0,1),则点E的坐标为______.56.如图,在菱形ABCD中,AB=18cm,∠A=60°,点E以2cm/s的速度沿AB边由A向B匀速运动,同时点F以4cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为______.57.如图1,已知四边形ABCD是正方形,将△DAE,△DCF分别沿DE,DF向内折叠得到图2,此时DA与DC重合(A、C都落在G点),若GF=4,EG=6,则DG的长为______.58.已知矩形ABCD,对角线AC、BD相交于点O,点E为BD上一点,OE=1,连接AE,∠AOB=60°,AB=2,则AE的长为______.59.菱形ABCD中,∠A=60°,AB=9,点P是菱形ABCD内一点,PB=PD=3√3,则AP的长为______.60.如图,在平面直角坐标系中,菱形OABC的一个顶点在原点O处,且∠AOC=60°,A点的坐标是(0,4),则直线AC的表达式是______.61.如图,将菱形ABCD折叠,使点B落在AD边的点F处,折痕为CE.若∠D=70°,则∠AEF=______.62.如图,已知点P(2,0),Q(8,0),A是x轴正半轴上一动点,以OA为一边在第一象限内作正方形OABC,当PB+BQ取最小值时,点B的坐标是______.63.已知正方形ABCD,以∠BAE为顶角,边AB为腰作等腰△ABE,连接DE,则∠DEB=______.64.一个菱形的周长为52cm,一条对角线长为10cm,则其面积为______ cm2.65.菱形有一个内角为60°,较短的对角线长为6,则它的面积为______.66.如图,在菱形ABCD中,对角线AC、BD相交于点O,点E在线段BO上,连接AE,若CD=2BE,∠DAE=∠DEA,EO=1,则线段AE的长为______.67.如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2019次,点B的落点依次为B1,B2,B3,…,则B2019的坐标为______.68.如图,在Rt△ABC中,∠A=90°,AB=6,BC=10,P是BC边上的一点,作PE垂直AB,PF垂直AC,垂足分别为E、F,求EF的最小值是______.69.如图1,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为3的正方形中(纸片在结合部分不重叠无缝隙),则图2中阴影部分面积为______.70.若顺次连接四边形ABCD四边中点形成的四边形为矩形,则四边形ABCD满足的条件为______.三、解答题(本大题共19小题,共152.0分)71.如图,在▵ABCD中,E,F分别为边AB,CD的中点,BD是对角线.(1)求证:△ADE≌△CBF;(2)若∠ADB是直角,请证明四边形BEDF是菱形.72.如图,在△ABC中,D,E分别是AB,AC的中点,连接DE并延长DE至点F,使EF=DE,连接CF.(1)求证:四边形DBCF是平行四边形;(2)探究:当△ABC满足什么条件时,四边形ADCF是矩形,并说明理由.73.如图1,直角梯形ABCD中,AD//BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.(1)AM=______,AP=______.(用含t的代数式表示)(2)当四边形ANCP为平行四边形时,求t的值;(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由②使四边形AQMK为正方形,则AC=______.74.如图,在长方形纸片ABCD中,AD//BC,将长方形纸片折叠,使点D与点B重合,点C落在点C′处,折痕为EF.(1)求证:BE=BF.(2)若∠ABE=18°,求∠BFE的度数.(3)若AB=4,AD=8,求AE的长.75.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于点D,交AB于点E,点F在DE的延长线上,且AF=CE.(1)四边形ACEF是平行四边形吗?说明理由.(2)当∠B的大小满足什么条件时,四边形ACEF为菱形?请说明你的结论.(3)四边形ACEF有可能是正方形吗?为什么?76.如图,P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足,若CF=3,CE=4,求AP的长.77.如图,长方形纸片ABCD中,AB=8cm,把长方形纸片沿直线AC折叠,点B落在点E处,AE交cm,求AD.DC于点F,AF=25478.如图,在▱ABCD中,AE⊥BC,AF⊥CD,垂足分别为点E、F,且BE=DF.求证:▱ABCD是菱形.CE.79.如图,AE=AC,点B是CE的中点,且AD//CE,AD=12(1)若AE=25,CE=14,求△ACE的面积;(2)求证:四边形ABCD是矩形.80.如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.(1)求证:四边形AMDN是平行四边形;(2)在点M移动过程中:①当四边形AMDN成矩形时,求此时AM的长;②当四边形AMDN成菱形时,求此时AM的长.81.如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时旋转90°,得到线段CQ,连接BP,DQ.(1)如图1,求证:△BCP≌△DCQ;(2)如图,延长BP交直线DQ于点E.①如图2,求证:BE⊥DQ;②如图3,若△BCP为等边三角形,判断△DEP的形状,并说明理由.82.如图,在四边形ABCD中,BC=CD,∠C=2∠BAD.O是四边形ABCD内一点,且OA=OB=OD.求证:(1)∠BOD=∠C;(2)四边形OBCD是菱形.83.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.(1)求证:四边形AEFD是矩形;(2)连接OE,若AD=10,EC=4,求OE的长度.84.如图,在▱ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.(1)求证:△ADE≌△CBF;(2)连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.85.如图,以矩形OABC的顶点O为坐标原点,OA所在直线为x轴,OC所在直线为y轴建立平面直角坐标系.已知,OA=2,OC=4,点D为x轴上一动点,以BD为一边在BD右侧作正方形BDEF.(1)若点D与点A重合,请直接写出点E的坐标;(2)若点D在OA的延长线上,且EA=EB,求点E的坐标;(3)若OE=2√17,求点E的坐标.86.如图,BD是△ABC的角平分线,过点D作DE//BC交AB于点E,DF//AB交BC于点F.(1)求证:四边形BEDF为菱形;(2)如果∠A=90°,∠C=30°,BD=6,求菱形BEDF的面积.87.已知抛物线y=ax2+bx+c(a≠0)过点A(1,0),B(3,0)两点,与y轴交于点C,OC=3.(1)求抛物线的解析式及顶点D的坐标;(2)过点A作AM⊥BC,垂足为M,求证:四边形ADBM为正方形;(3)点P为抛物线在直线BC下方图形上的一动点,当△PBC面积最大时,求点P的坐标;QC是否存在最小值?若存在,求岀(4)若点Q为线段OC上的一动点,问:AQ+12这个最小值;若不存在,请说明理由.88.如图所示,顺次延长正方形ABCD的各边AB,BC,CD,DA至E,F,G,H,且使BE=CF=DG=AH.求证:四边形EFGH是正方形.89.已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE//AC,AE//BD.(1)求证:四边形AODE是矩形;(2)若AB=2,DE=1,求四边形AODE的面积.答案和解析1.【答案】D【解析】【分析】此题主要考查菱形的性质,根据菱形的对角线互相垂直平分,利用勾股定理求解.【解答】解:设菱形的对角线长分别为8x cm和6x cm,已知菱形的周长为20cm,故菱形的边长为5cm,根据菱形的性质可知,菱形的对角线互相垂直平分,即可知(4x)2+(3x)2=25,解得x=1,故菱形的对角线长分别为8cm和6cm,×8×6=24(cm2).所以菱形的面积为122.【答案】C【解析】【分析】本题考查了菱形的性质、含30°角的直角三角形的判定;熟练掌握菱形的性质和含30°角的直角三角形的判定是解决问题的关键.先根据菱形的性质求出边长AB=2,再根据直角三角形的性质求出∠B=30°,得出∠DAB=150°,即可得出结论.【解答】解:如图所示:∵四边形ABCD是菱形,菱形的周长为8,∴AB=BC=CD=DA=2,∠DAB+∠B=180°,∵AE=1,AE⊥BC,∴AE=1AB,2∴∠B=30°,∴∠DAB=150°,∴∠DAB:∠B=5:1;故选C.3.【答案】B【解析】【分析】本题考查了矩形的性质,直角三角形斜边上的中线等于斜边的一半的性质,等边三角形的判定与性质,等腰三角形的判定与性质,三角形的面积,设出AE、OG,然后用a表示出相关的边更容易理解,根据直角三角形斜边上的中线等于斜边的一半可得OG= AG=GE=12AE,再根据等边对等角可得∠OAG=30°,根据直角三角形两锐角互余求出∠GOE=60°,从而判断出△OGE是等边三角形,判断出③正确;设AE=2a,根据等边三角形的性质表示出OE,利用勾股定理列式求出AO,从而得到AC,再求出BC,然后利用勾股定理列式求出AB=3a,从而判断出①正确,②错误;再根据三角形的面积和矩形的面积列式求出判断出④正确.【解答】解:∵EF⊥AC,点G是AE中点,∴OG=AG=GE=12AE,∵∠AOG=30°,∴∠OAG=∠AOG=30°,∠GOE=90°−∠AOG=90°−30°=60°,∴△OGE是等边三角形,故③正确;设AE=2a,则OE=OG=a,由勾股定理得,AO=√AE2−OE2=√(2a)2−a2=√3a,∵O为AC中点,∴AC=2AO=2√3a,∴BC=12AC=12×2√3a=√3a,在Rt△ABC中,由勾股定理得,AB=√(2√3a)2−(√3a)2=3a,∵四边形ABCD是矩形,∴CD=AB=3a,∴DC=3OG,故①正确;∵OG=a,12BC=√32a,∴OG≠12BC,故②错误;∵S△AOE=12a⋅√3a=√32a2,S ABCD=3a⋅√3a=3√3a2,∴S△AOE=16S ABCD,故④正确;综上所述,结论正确是①③④共3个.故选B.4.【答案】C【解析】【分析】此题主要考查了菱形的判定,关键是掌握菱形的判定方法:①菱形定义:一组邻边相等的平行四边形是菱形(平行四边形+一组邻边相等=菱形);②四条边都相等的四边形是菱形.③对角线互相垂直的平行四边形是菱形(或“对角线互相垂直平分的四边形是菱形”).【解答】解:甲的作法正确;∵四边形ABCD是平行四边形,∴AD//BC,∴∠DAC=∠ACB,∵EF是AC的垂直平分线,∴AO=CO,在△AOE和△COF中,{∠EAO =∠FCO AO =CO ∠AOE =∠COF, ∴△AOE≌△COF(ASA),∴AE =CF ,又∵AE//CF ,∴四边形AECF 是平行四边形,∵EF ⊥AC ,∴四边形AECF 是菱形;乙的作法正确;∵AD//BC ,∴∠1=∠2,∠6=∠7,∵BF 平分∠ABC ,AE 平分∠BAD ,∴∠2=∠3,∠5=∠6,∴∠1=∠3,∠5=∠7,∴AB =AF ,AB =BE ,∴AF =BE∵AF//BE ,且AF =BE ,∴四边形ABEF 是平行四边形,∵AB =AF ,∴平行四边形ABEF 是菱形;故选C .5.【答案】A【解析】【试题解析】【分析】此题主要考查了菱形的性质,正确应用菱形的性质是解题关键.直接利用菱形的性质得出∠ABC 的度数,进而得出∠DBC 的度数.【解答】解:∵在菱形ABCD中,∠A=130°,∴∠ABC=180°−130°=50°,∴∠DBC=12∠ABC=25°.故选:A.6.【答案】A【解析】【分析】本题主要考查菱形的判定和性质,证得四边形ABCD是菱形是解题的关键.作AR⊥BC于R,AS⊥CD于S,根据题意先证出四边形ABCD是平行四边形,再由AR= AS得平行四边形ABCD是菱形,再根据根据勾股定理求出AB即可.【解答】解:如图,作AR⊥BC于R,AS⊥CD于S,连接AC,BD交于点O,由题意知,AD//BC,AB//CD,∴四边形ABCD是平行四边形.∵两张纸条等宽,∴AR=AS.∵AR⋅BC=AS⋅CD,∴BC=CD,∴平行四边形ABCD是菱形,∴AC⊥BD.在Rt△AOB中,OA=12AC=3cm,OB=12BD=4cm,∴AB=√OA2+OB2=√32+42=5cm.故选A.7.【答案】C【解析】【分析】本题考查了矩形的性质、等腰三角形的判定与性质、角的互余关系,熟练掌握矩形的性质,并能进行推理计算是解决问题的关键,解答此题由矩形的性质得出OC=OD,得出∠ODC=∠OCD,求出∠EDC=36°,再由角的互余关系求出∠ODC,即可得出∠BDE的度数.【解答】解:∵四边形ABCD是矩形,∴∠ADC=90°,OC=12AC,OD=12BD,AC=BD,∴OC=OD,∴∠ODC=∠OCD,∵∠ADE:∠EDC=3:2,∴∠EDC=25×90°=36°,∵DE⊥AC,∴∠DEC=90°,∴∠ODC=∠OCD=90°−36°=54°,∴∠BDE=∠ODC−∠EDC=54°−36°=18°.故选C.8.【答案】D【解析】【分析】本题考查了菱形的性质,也涉及了勾股定理,要求我们掌握菱形的面积的两种表示方法,及菱形的对角线互相垂直且平分.根据菱形的性质得出BO、CO的长,在Rt△BOC中求出BC,利用菱形面积等于对角线乘积的一半,也等于BC×AH,即可得出AH的长度.【解答】解:∵四边形ABCD是菱形,AC=12,BD=16,∴CO=12AC=6,BO=12BD=8,CO⊥BO,∴BC=√BO2+CO2=√62+82=10,∴S菱形ABCD =12AC⋅BD=12×16×12=96,∵S菱形ABCD=BC×AH,∴BC×AH=96,∴AH=9610=485.故选D.9.【答案】D【解析】【分析】此题主要考查了菱形的性质和平行四边形的性质,关键是根据菱形对角线垂直及平行四边形对角线平分的性质的理解.根据菱形的特殊性质可知对角线互相垂直.【解答】解:A.两组对角分别相等,两者均有此性质,故此选项不正确;B.两条对角线相等,两者均没有此性质,故此选项不正确;C.四个内角都是直角,两者均不具有此性质,故此选项不正确;D.每一条对角线平分一组对角,菱形具有而一般平行四边形不具有此性质,故此选项正确.故选D.10.【答案】C【解析】【分析】本题考查了三角形外角的性质,全等三角形性质和判定,线段垂直平分线性质,菱形的性质的应用,注意:菱形的四条边相等,菱形的对角线互相平分、垂直,且每一条对角线平分一组对角.连接BF,根据菱形性质得出AD=AB,∠DCB=100°,∠DCA= 50°,∠DAC=∠BAC=50°,根据线段垂直平分线得出AF=BF,求出∠FAB=∠FBA= 50°,求出∠AFB=80°,证△DAF≌△BAF,求出∠DFA=∠BFA=80°,根据三角形外角性质求出即可.【解答】解:如图,连接BF.∵在菱形ABCD中,∠BAD=100°,∴∠DAC=∠BAC=50°,∠ADC=∠ABC=180°−100°=80°.∵EF是线段AB的垂直平分线,∴AF=BF.∴∠ABF=∠CAB=50°.在△ADF与△ABF中,∵{AD=AB,∠DAF=∠BAF, AF=AF,∴△ADF≌△ABF(SAS),∴∠ADF=∠ABF=50°,∴∠CDF=∠ADC−∠ADF=80°−50°=30°.11.【答案】C【解析】【分析】本题考查了矩形的性质,直角三角形斜边上的中线等于斜边的一半的性质,等边三角形的判定及性质,求出矩形的宽是解题的关键.根据直角三角形斜边上的中线等于斜边的一半求出BC,然后判断出△CEF是等边三角形,过点E作EG⊥CF于G,根据等边三角形的性质及勾股定理求出EG,然后根据矩形的面积公式列式进行计算即可得解.【解答】解:作EG⊥BC于G.∵F是BC中点,∠BEC=90°,∴EF=BF=FC,BC=2EF=2×4=8(cm),∵∠ECD=30°,∴∠BCE=60°,∴△CEF是等边三角形,∴CE=EF=4cm,∠CEG=30°,∴CG=12CE=2cm,则EG=√CE2−CG2=2√3(cm),∴矩形的面积=8×2√3=16√3(cm2).故选C.12.【答案】C【解析】【分析】此题考查三角形全等的判定和性质、正方形的性质和勾股定理。
人教版八年级下册19.1平行四边形课时练
数学:19.1平行四边形课时练(人教新课标八年级下)课时一平行四边形的性质(一) 一、选择题1.平行四边形的两邻角的角平分线相交所成的角为( ) A.锐角 B.直角 C.钝角 D.不能确定2.平行四边形的周长为24cm ,相邻两边的差为2cm ,则平行四边形的各边长为( ) A.4cm ,4cm ,8cm ,8cm B.5cm ,5cm ,7cm ,7cm C.5.5cm ,5.5cm ,6.5cm ,6.5cm D.3cm ,3cm ,9cm ,9cm3. 如图所示,四边形ABCD 是平行四边形,∠D =120°,∠CAD =32° .则∠ABC 、∠CAB 的度数分别为( )A.28°,120°B.120°,28°C.32°,120°D.120°,32° 4. 在□ABCD 中,∠A ∶∠B ∶∠C ∶∠D 的值可以是( )DA.1∶2∶3∶4B.1∶2∶2∶1C.1∶1∶2∶2D.2∶1∶2∶1 5下面的性质中,平行四边形不一定具有的是( )A.对角互补B.邻角互补C.对角相等D.对边相等.6.在□ABCD 中,∠A 的平分线交DC 于E ,若∠DEA=30°,则∠B =( ) A100° B.120° C.135° D.150° 二、填空题7. .如图所示,A ′B ′∥AB ,B ′C ′∥BC ,C ′A ′∥CA ,图中有 个平行四边形8. 已知:平行四边形一边AB =12 cm,它的长是周长的61,则BC =______ cm,CD =______ cm. 9.平行四边形的一组对角度数之和为200°,则平行四边形中较大的角为 . 10.. ABCD 中,若∠A ∶∠B =1∶3,那么∠A =________,∠B =________, ∠C =________,∠D =________.11. 如图所示,,在ABCD 中,对角线AC 、BD 相交于点O ,图中全等三角形共有________对12.如图所示,在ABCD 中,∠B =110°,延长AD 至F ,CD 至E ,连结EF ,则∠E+∠F= 三、解答题13. 在四边形ABCD 中,AB ∥CD ,∠A =∠C ,求证:四边形ABCD 是平行四边形. 14. 在□ABCD 中, ∠A+∠C=160°, , 求∠A,∠C,∠B,∠D 的度数第3题图 第7题图 第11题图 第12题图第14题图15. .如图所示,四边形ABCD 是平行四边形,BD ⊥AD ,求BC ,CD 及OB 的长.16. 如图,在□ABCD 中,E 、F 分别是BC 、AD 上的点,且AE ∥CF ,AE 与CF 相等吗?说明理由.课时一答案:一、1.B ,提示:平行四边形的两邻角的和为180°,所以它们的角平分线的夹角为90°;2.B ,提示:设相邻两边为,,ycm xcm 根据题意得⎩⎨⎧=-=+212y x y x ,解得⎩⎨⎧==57y x ;3. B ,提示:根据平行四边形的性质对角相等得∠D =∠ABC=120°,邻角互补得∠CAB +∠CAD+∠D =180°,则∠CAB =180°-32°-120°=28°;4. D ,提示:根据平行四边形的对角相等,得对角的比值相等故选D ;5.A ;6.B ,由题意得∠A =60°,根据平行四边形的邻角互补,得∠B =180°-60°=120°; 二、7.3个即四边形ABCB ′,C ′BCA ,ABA ′C 都是平行四边形;8.24 ,CD =12;9.100°,提示:先求出对角为100°,另一组对角为80°,所以较大的为100°;10.45°,135°,45°,135°11.4;15.70°,提示:根据平行四边形的对角互补得∠B=∠ADC=110°,则∠FDC=70°,再根据三角形的外角等于其不相邻的两个角的和,故为∠E+∠F=70°;三、13. 证明:∵AB ∥CD ,∴∠A+∠D=180°,又∵∠A =∠C,∴∠C+∠D=180°, ∴AD ∥CB, ∴四边形ABCD 是平行四边形.. 14.解:在□ABCD 中, ∠A =∠C,又∵∠A+∠C=160°∴∠A =∠C=80°∵在□ABCD 中AD ∥CB,∴∠A+∠B=180°, ∴∠B =∠D=180°-∠A=180°-80°=100° 15. 解:∵ABCD ,∴BC =AD =12,CD =AB =13,OB=21BD ∵BD ⊥AD ,∴BD =22AD AB -=221213-=5∴OB =25 16. AE =CF ;证明∵四边形ABCD 为平行四边形,∴AF ∥CE ,又∵AE ∥CF ∴四边形AECF 为平行四边形,AE=CF ;第15题图 第16题图课时二:平行四边形的性质(二)1. 如图所示,如果该平行四边形的一条边长是8,一条对角线长为6,那么它的另一条对角线长x 的取值范围是________.2.如图,□ABCD 中,EF 过对角线的交点O ,AB =4,AD =3,OF =1.3,则四边形BCEF 的周长为( )A.8.3B.9.6C.12.6D.13.63. 如图,在□ABCD 中,对角线AC ,BD 相交于点O ,MN 是过O 点的直线,交BC 于M ,交AD 于N ,BM =2,AN =2.8,求BC 和AD 的长.4.平行四边形的周长为25cm ,对边的距离分别为2cm 、3cm为( )A.15cm 2B.25cm 2C.30cm 2D.50cm 25. 如图所示,已知ABCD 的对角线交于O ,过O 作直线交AB 、CD 的反向延长线于E 、F ,求证:OE =OF .6. 如图所示,在□ABCD 中,O 是对角线AC 、BD 的交点,BE ⊥AC ,DF ⊥AC ,垂足分别为E 、F .那么OE 与OF 是否相等?为什么?7.已知O 为平行四边形ABCD 对角线的交点,△AOB 的面积为1,则平行四边形的面积为( )第1题图第2题图 第3题图 第5题图 第6题图A.1B.2C.3D.48.平行四边形的对角线分别为y x ,,一边长为12,则y x ,的值可能是下列各组数中的( ) A.8与14 B.10与14 C.18与20 D.10与28 9. □ABCD 中,若,6,10,30cm AB cm BC B ===∠ο则□ABCD 的面积是 .10. 如图,在平行四边形ABCD 中,AE ⊥BC 于E ,AF ⊥CD 于F ,∠EAF =45°,且AE+AF =22,则平行四边形ABCD 的周长是 .11.如图所示,已知D 是等腰三角形ABC 底边BC 上的一点,点E ,F 分别在AC,AB 上,且DE ∥AB ,DF ∥AC 求证:DE+DF=AB12. 如图,□ABCD O 为D 的对角线AC 的中点,过点O 作一条直线分别与AB 、CD 交于点M 、N ,•点E 、F 在直线MN 上,且OE=OF .(1)图中共有几对全等三角形,请把它们都写出来; (2)求证:∠MAE=∠NCF .课时二答案:1. 10<x <22,提示:根据三角形的三边关系得11215<<x ,解得2210<<x ;2. B ;3. BC =AD =4.8;4.A ;提示:根据面积法求出邻边的比为3∶2,则邻边为7.5,5,则面积为7.5×2=15cm 2;5. 证明:∵ABCD ,∴OA =OC ,DF ∥EB ∴∠E =∠F ,又∵∠EOA =∠FOC ∴△OAE ≌△OCF ,∴OE =OF ;6. OE =OF , 在□ABCD 中,OB=OD ,∵BE ⊥AC ,DF ⊥AC ∴∠BEO =∠DFO ,又∠BOE =∠DOF ,∴△BOE ≌△DOF ,∴OE =OF .7.D ,提示:因为平行四边形的对角线把平行四边形分成面积相等的4个小三角形,所以平行四边形的面积为4;8.C ,提示:根据三角形的两边之和大于第三边,两边之差小于第三第10题图 第11题图边,若y x >,则⎪⎪⎩⎪⎪⎨⎧<->+12221222yx yx ,所以符合条件的y x ,可能是18与20;9.302cm ;10.8;11.证明:∵DE ∥AB ,DF ∥AC∴四边形AEDF 是平行四边形,∴DF=AE ,又∵DE ∥AB ,∴∠B=∠EDC ,又∵AB=AC,∴∠B=∠C ,∴∠C=∠EDC ,∴DE=CE ,∴DF+DE=AE+CE=AC=AB. 12. 解:(1)有4对全等三角形.分别为△AMO ≌△CNO ,△OCF ≌△OAE ,△AME ≌△CNF ,△ABC ≌△CDA . (2)证明:∵OA=OC ,∠1=∠2,OE=OF , ∴△OAE ≌△OCF ,∴∠EAO=∠FCO . 在YABCD 中,AB ∥CD ,∴∠BAO=∠DCO ,∴∠EAM=∠NCF . 课时三平行四边形的判定(一) 一、选择题1.下列条件中不能判定四边形ABCD 为平行四边形的是( ) A.AB=CD,AD=BC B.AB ∥CD ,AB=CD C.AB=CD ,AD ∥BC D. AB ∥CD ,AD ∥BC2.已知:四边形ABCD 中,AD ∥BC ,分别添加下列条件之一:①AB ∥CD ;② AB=CD, ③AD=BC ,④∠A=∠C ,⑤∠B=∠D ,能使四边形ABCD 成为平行四边形的条件的个数是( ) A.4 B.3 C.2 D.13.把两个全等的非等腰三角形拼成平行四边形,可拼成的不同平行四边形的个数为( ) A.1 B.2 C.3 D.44. 在四边形ABCD 中,AC 与BD 相交于点O ,如果只给出条件“AB ∥CD ”,那么还不能判定四边形ABCD 为平行四边形,给出以下六个说法中,正确的说法有( )(1)如果再加上条件“AD ∥BC ”,那么四边形ABCD 一定是平行四边形; (2)如果再加上条件“AB =CD ”,那么四边形ABCD 一定是平行四边形;(3)如果再加上条件“∠DAB =∠DCB ”那么四边形ABCD 一定是平行四边形; (4)如果再加上“BC =AD ”,那么四边形ABCD 一定是平行四边形; (5)如果再加上条件“AO =CO ”,那么四边形ABCD 一定是平行四边形; (6)如果再加上条件“∠DBA =∠CAB ”,那么四边形ABCD 一定是平行四边形. A.3个 B.4个 C.5个 D.6个 二、填空题5.已知:四边形ABCD 中,AD ∥BC ,要使四边形ABCD 为平行四边形, 需要增加条件 .(只需填上一个你认为正确的即可).6.如图所示,ABCD 中,BE ⊥CD,BF ⊥AD,垂足分别为E 、F ,∠EBF=60°AF=3cm ,CE=4.5cm ,则∠C= ,AB= cm ,BC= cm .7.如图所示,在ABCD 中,E,F 分别是对角线BD 上的两点, 且BE=DF ,要证明四边形AECF 是平行四边形,最简单的方法 是根据 来证明.第6题图8. 将两个全等的不等边三角形拼成平行四边形,可拼成的不同的平行四边形的个数为______. 三、解答题9.已知:如图所示,在ABCD 中,E 、F 分别为AB 、CD 的中点,求证四边形AECF 是平行四边形.10. 如图所示,BD 是ABCD 的对角线,AE ⊥BD 于E ,CF ⊥BD 于F ,求证:四边形AECF 为平行四边形.11. 如图所示,平行四边形ABCD 的对角线A C 、BD 相交于点O,E 、F 是直线AC 上的两点,并且AE=CF,求证:四边形BFDE 是平行四边形.12. 如图,E F ,是平行四边形ABCD 的对角线AC 上的点,CE AF .请你猜想:BE 与DF 有怎样的位置..关系和数量..关系? 并对你的猜想加以证明:课时三答案:一、1.C ;2.B ,提示:AD ∥BC ,添加条件①③④能使四边形ABCD 成为平行四边形;3.C ;4.B ;二、5. AD =BC (或AB ∥CD 或∠A=∠C 或∠B=∠D );6.30°,6,9;7.对角线互相平分;8. 3; 三、9.在ABCD 中,AD=CB,AB=CD,∠D =∠B ,∵E 、F 分别为AB 、CD 的中点,∴DF=BE , 又∵AB ∥CD ,AB=CD ,∴AE=CF ,∴四边形AECF 是平行四边形. 10. 证明:∵ABCD∴AB =CD ,AB ∥CD ∴∠1=∠2AE ⊥BD ,CF ⊥BD第9题图 第10题图 第11题图ABC DE F第12题图∴∠AEB =∠CFD =90°,AE ∥CF ∴△AEB ≌△CFD ,∴AE =CF ∴AECF 为平行四边形11. 证明:∵四边形ABCD 是平行四边形,∴OA=OC,OB=OD又∵AE=CF ,∴OE=OF ∴四边形BFDE 是平行四边形. 12. 猜想:BE DF ∥,BE DF = 证明:证法一:如图第12-1.Q 四边形ABCD 是平行四边形. BC AD ∴= 12∠=∠ 又CE AF =Q BCE DAF ∴△≌△ BE DF ∴= 34∠=∠BE DF ∴∥证法二:如图第12-2.连结BD ,交AC 于点O ,连结DE ,BF . Q 四边形ABCD 是平行四边形 BO OD ∴=,AO CO = 又AF CE =Q AE CF ∴= EO FO ∴=∴四边形BEDF 是平行四边形BE DF ∴∥ 课时四平行四边形的判定(二)1.如图所示,D 、E 、F 为△ABC 的三边中点, 则图中平行四边形有( ) A.1个 B2个 C 3个 D.4个2. D 、E 、F 为△ABC 的三边中点,L 、M 、N 分别是△DEF 三边的中点,若△ABC 的周长为20cm ,则△LMN 的周长是( ) A.15cm B.12cm C.10cm D.5cm3.已知等腰三角形的两条中位线长分别为3和5, 则此等腰三角形的周长为 .4.□ABCD 中,对角线AC 、BD 相交于点O ,E 、F 分别是OB 、OD 的中点,四边形AECF 是_______.5. 如图,DE ∥BC ,AE =EC ,延长DE 到F ,使EF =DE , 连结AF 、FC 、CD ,则图中四边形ADCF 是______.ABCDEF第12-2OAB CDE F 第12-1 2 3 4 1第1题图第5题图6. 如图,在□ABCD 中,点E 是AD 的中点,BE 的延长线与CD 的延长线相交于点F (1)求证:△ABE ≌△DFE ;(2)试连结BD 、AF ,判断四边形ABDF 的形状,并证明你的结论.7. 如图所示,某城市部分街道示意图,AF ∥BC ,EC ⊥BC ,BA ∥DE ,BD ∥AE ,EF=FC ,甲、乙两人同时从B 站乘车到F 站,甲乘1路车,路线是B →A →E →F ,乙乘2路,路线是B →D →C →F ,假设两车速度相同,途中耽误时间相同,那么谁先到达F 站,请说明理由.8. 如图所示,已知AD 与BC 相交于E ,∠1=∠2=∠3,BD=CD ,∠ADB=90°,CH ⊥AB 于H ,CH 交AD 于F . (1)求证:CD ∥AB ; (2)求证:△BDE ≌△ACE ; (3)若O 为AB 中点,求证:OF=12BE .9.. 已知如图:在ABCD 中,延长AB 到E ,延长CD 到F ,使BE =DF ,则线段AC 与EF 是否互相平分?说明理由.第6题图 第7题图 第8题图 第9题图10. 如图所示,□ABCD 的对角线AC 、BD 交于O ,EF 过点O 交AD 于E ,交BC 于F ,G 是OA 的中点,H 是OC 的中点,四边形EGFH 是平行四边形,说明理由.11.如图所示,平行四边形ABCD 中,M 、N 分别为AD 、BC 的中点,连结AN 、DN 、BM 、CM ,且AN 、BM 交于点P ,CM 、DN 交于点Q .四边形MGNP 是平行四边形吗?为什么?课时四答案:1.C;2.D ,提示:根据三角形中位线的性质定理:;21,21DEF LMN ABC DEF L L L L ∆∆∆∆==3.26或22,提示:当两腰上的中位线长为3时,则底边长为6,腰长为10,三角形的周长为26,当两腰上的中位线长为5时,则底边长为10,腰长为6,三角形的周长为22;4.平行四边形 ;5.平行四边形;6.证明:(1)∵ 四边形ABCD 是平行四边形,∴AB ∥CF . ∴∠1=∠2,∠3=∠4 ∵E 是AD 的中点,∴ AE=DE . ∴△ABE ≌△DFE .(2)四边形ABDF 是平行四边形.∵△ABE ≌△DFE ∴AB=DF 又AB ∥CF .∴四边形ABDF 是平行四边形. 7.解:∵BA ∥DE ,BD ∥AE ,∴四边形ABDE 是平行四边形 ∴AB=DE ,BD=AE ,又EF=FC 且AF ∥BC ,EC ⊥BC ,∴DE=DC , ∴EA+AE+EF=BD+DC+CF ,∴二人同时到达F 站.8.证明:(1)∵BD=CD ,∴∠BCD=∠1.∵ ∠l=∠2,∠BCD=∠2.∴CD ∥AB . (2) ∵ CD ∥AB ∴∠CDA=∠3.第10题图第10题图 第11题图∠BCD=∠2=∠3.且BE=AE.且∠CDA=∠BCD.∴DE=CE.在△BDE和△ACE中,DE=CE,∠DEB=∠CEA,BE=AE.∴△BDE≌△ACE (3) ∵△BDE≌△ACE∠4=∠1,∠ACE=∠BDE=90°.∴∠ACH=90°一∠BCH又CH⊥AB,.∴∠2=90°一∠BCH∴∠ACH=∠2=∠1=∠4.AF=CF∵∠AEC=90°一∠4,∠ECF=90°一∠ACH∠ACH=∠4 ∠AEC=∠ECF.CF=EF.∴EF=AFO为AB中点,OF为△ABE的中位线∴OF=12BE9.线段AC与EF互相平分.理由是:∵四边形ABCD是平行四边形.∴AB∥CD,即AE∥CF,AB=CD,∵BE=DF,∴AE=CF∴四边形AECF是平行四边形,∴AC与EF互相平分.10.是平行四边形,△AOE≌△COF.11是平行四边形,四边形AMCN、BMDN是平行四边形.。
