时间序列实验报告2
应用统计实验 实验二 时间序列分析与预测

实验报告实验名称:时间序列分析与预测分组组长:组员及分工:专业班级:姓名:学号:实验日期:一、实验目的能熟练运用Excel数据分析工具进行长期趋势的预测,掌握平均发展水平和平均发展速度的计算方法,了解季节变动的分析方法二、实验内容(1)时间序列水平分析指标(2)速度分析指标(3)长期趋势的测定与预测(4)季节变动的测定与预测三、实验过程和结果实验(1)打开数据表,找到作业1,(1)在单元格A3、A4、A5、A6中分别输入“逐期增长量”、“累计增长量”、“平均增长量=”和“平均增长量=”。
(2)在单元格C3中输入“=C2-B2”,回车得1996年的逐期增长量(3)依次在单元格D3至G3中重复步骤(2),或把光标移至C3单元格右下角,当光标变为黑十字星时,按住鼠标右键并拖到G3区域松开,得2001~2005各年的逐期增长量(4)选择单元格C4,输入“=C2-$B$2”,回车得1996年的累计增长量(5)依次在单元格D4~G4中重复步骤(4),得到2001年~2005各年的累计增长量(6)选择单元格G5,在其中输入“=L4/10”,得到2001~2005年期间的平均增长量(7)或在单元格G6中输入“=(C3+D3+E3+F3+G3)/(6-1)”,按回车得2001~2005年期间的平均增长量(1)在单元格A7、A8、A9、A10、A11、A12、A13、A14中分别输入“环比发展速度”、“定基发展速度”、“环比增长速度”、“定基增长速度”、“平均发展速度”、“平均发展速度”、“平均发展速度”、“平均增长速度”。
(2)在单元格C7中输入“=C2/B2*100”,按回车得2001年的环比发展速度(3)依次在单元格D7至G7中重复步骤(2),或把光标移至C7单元格右下角,当光标变为黑十字星时,按住鼠标右键并拖到G7区域松开,得2002~2005各年的环比发展速度(4)在单元格C8中输入“=C2/$B$2*100”,回车后得到2001年的定基发展速度(5)把光标移至D8单元格右下角,当光标变为黑十字星时,按住鼠标右键并拖到G8区域松开,得到2002~2005各年的定基发展速度(6)在单元格C9中输入“C7-100”,回车后得到2001年的环比增长速度(7)把光标移至C9单元格右下角,当光标变为黑十字星时,按住鼠标右键并拖到G9区域松开,得2002~2005各年的环比增长速度(8)在单元格C10中输入“C8-100”,回车后得到2001年的定基增长速度(9)依次在单元格D10至G10中重复步骤(4),或者把光标移至C10单元格右下角,当光标变为黑十字星时,按住鼠标右键并拖到G10区域松开,得到2002~2005各年的定基增长速度(10)在单元格G11中输入“=(G2/B2)^(1/5)”,回车后得到2000~2005年期间的平均发展水平速度(11)在单元格G12中输入“=(C7/100*D7/100*E7/100*F7/100*G7/100)^(1/5)”,回车后得到2000~2005年期间的平均发展速度(12)在单元格G13中输入“=(G8/100)^(1/5)”,回车后得到2000~2005年期间的平均发展速度(13)在单元格G14中输入“=G11-1”或“G12-1”,回车得到2000~2005年期间的平均增长速度。
时间序列分析试验报告

时间序列分析试验报告
一、试验简介
本次试验旨在探索时间序列分析,以分析日期变化的影响与规律。
时
间序列分析是数据分析的一种,目的是预测未来正确的趋势,并且分析既
有趋势的影响及其变化。
二、试验材料
本次试验使用的资料为最近12个月(即2024年1月到2024年12月)的电子商务网站销售数据。
该电子商务网站以每月总销售量、每月总销售
额及每月交易次数三个变量作为试验数据。
三、试验方法
1.首先,收集2024年1月到2024年12月的电子商务销售数据,记
录每月总销售量、总销售额及交易次数。
2.然后,编制时间序列分析图表,反映每月总销售量、总销售额及
交易次数的变化情况。
3.最后,分析每月的变化趋势,比较每月的销售数据,并进行相关
分析推断。
四、实验结果
1.通过时间序列分析图表可以看出,每月总销售量、总销售额及交
易次数均呈现出稳定上升趋势。
2.从图表中可以推断,在2024年底到2024年底,当月的总销售量、总销售额及交易次数均较上月有所增加。
3.从表中可以推断,每月的总销售量、总销售额及交易次数都在逐渐增加,最终在2024年末达到高峰。
五、结论
通过本次实验可以得出结论。
实验报告-时间序列

实验报告----平稳时间序列模型的建立08经济统计I60814030王思瑶一.实验目的从观察到的化工生产过程产量的70个数据样本出发,通过对模型的识别、模型的定价、模型的参数估计等步骤建立起适合序列的模型。
以下是化工生产过程的产量数据:obs BF obs BF1 47 36582 64 37453 23 38544 71 39365 38 40546 64 41487 55 42558 41 43459 59 445710 48 455011 71 466212 35 474413 57 486414 40 494315 58 505216 44 513817 80 525918 55 535519 37 544120 74 555321 51 564922 57 573423 50 583524 60 595425 45 604526 57 616827 50 623828 45 635029 25 646030 59 653931 50 665932 71 674033 56 685734 74 695435 50 7023可以明显看出序列均值显著非零,所以用样本均值作为其估计对序列进行零均值化。
obs BF 零均值化后的数据Y obs BF零均值化后的数据Y1 47 -4.12857 3658 6.871432 64 12.87143 3745-6.128573 23 -28.12857 3854 2.871434 71 19.87143 3936-15.128575 38 -13.12857 4054 2.871436 64 12.87143 4148-3.128577 55 3.87143 4255 3.871438 41 -10.12857 4345-6.128579 59 7.87143 4457 5.8714310 48 -3.12857 4550-1.1285711 71 19.87143 466210.8714312 35 -16.12857 4744-7.1285713 57 5.87143 486412.8714314 40 -11.12857 4943-8.1285715 58 6.87143 50520.8714316 44 -7.12857 5138-13.1285717 80 28.87143 52597.8714318 55 3.87143 5355 3.8714319 37 -14.12857 5441-10.1285720 74 22.87143 5553 1.8714321 51 -0.12857 5649-2.1285722 57 5.87143 5734-17.1285723 50 -1.12857 5835-16.1285724 60 8.87143 5954 2.8714325 45 -6.12857 6045-6.1285726 57 5.87143 616816.8714327 50 -1.12857 6238-13.1285728 45 -6.12857 6350-1.1285729 25 -26.12857 64608.8714330 59 7.87143 6539-12.1285731 50 -1.12857 66597.8714332 71 19.87143 6740-11.1285733 56 4.87143 6857 5.8714334 74 22.87143 6954 2.8714335 50 -1.12857 7023-28.12857二.实验步骤1.模型识别零均值平稳序列的自相关函数与偏相关函数的统计特性如下:模型 AR(n) MA(m) ARMA(n,m)自相关函数拖尾截尾拖尾偏自相关函数截尾拖尾拖尾所以,作零均值化后数据的自相关函数与偏自相关函数图Date: 04/25/11 Time: 22:35Sample: 2001 2070Included observations: 70Autocorrelation Partial Correlation AC PAC Q-Stat Prob***| . | ***| . | 1 -0.382 -0.382 10.638 0.001. |** | . |** | 2 0.325 0.209 18.444 0.000**| . | . | . | 3 -0.193 -0.018 21.234 0.000. |*. | . | . | 4 0.090 -0.049 21.857 0.000.*| . | .*| . | 5 -0.162 -0.126 23.900 0.000. | . | .*| . | 6 0.014 -0.094 23.916 0.001. | . | . | . | 7 0.012 0.065 23.928 0.001.*| . | .*| . | 8 -0.085 -0.079 24.519 0.002. | . | . | . | 9 0.039 -0.051 24.644 0.003. | . | . |*. | 10 0.033 0.080 24.736 0.006. |*. | . |*. | 11 0.090 0.125 25.426 0.008.*| . | . | . | 12 -0.077 -0.054 25.942 0.011. | . | . | . | 13 0.063 -0.045 26.291 0.016. | . | . |*. | 14 0.051 0.134 26.524 0.022. | . | . |*. | 15 -0.006 0.079 26.528 0.033. |*. | . |*. | 16 0.126 0.145 28.016 0.031.*| . | . | . | 17 -0.090 -0.040 28.792 0.036. | . | .*| . | 18 0.017 -0.084 28.820 0.051.*| . | . | . | 19 -0.099 -0.017 29.795 0.054. | . | . | . | 20 0.006 -0.036 29.798 0.073. | . | . | . | 21 0.015 0.055 29.820 0.096. | . | . | . | 22 -0.037 -0.015 29.968 0.119. | . | . | . | 23 0.013 -0.051 29.985 0.150. | . | . | . | 24 0.010 0.010 29.997 0.185. | . | . | . | 25 0.015 -0.016 30.023 0.223. | . | . | . | 26 0.036 0.023 30.172 0.261. | . | . | . | 27 -0.016 -0.036 30.202 0.305. | . | . | . | 28 0.033 0.030 30.335 0.347. | . | . | . | 29 -0.057 -0.015 30.735 0.378. | . | . | . | 30 0.051 -0.003 31.064 0.412.*| . | . | . | 31 -0.070 -0.053 31.706 0.431. | . | . | . | 32 0.057 -0.003 32.141 0.460由上图可知Autocorrelation与Partial Correlation序列均有收敛到零的趋势,可以认为Y的自相关函数与偏自相关函数均是拖尾的,所以初步判断该序列适合ARMA模型。
时间序列实验报告

重庆交通大学学生实验报告实验课程名称时间序列分析开课实验中心数统学院实验教学中心开课学院数学与统计学院专业年级应用统计学2015级1班姓名XXXX学号6315XXXXXXXX任课老师XXXXX开课时间2017—2018学年第1学期此页空页!实验一R语言简介: 基本操作一实验目的1、了解软件R:安装、启动、退出、帮助等。
2、熟悉R的操作界面。
二、实验内容及要求:1、实验内容:(1)R的安装;(2)启动与退出;(3)包的安装及R的更新;(4)帮助及移除多个对象等;(5)常见命令2、实验要求:(1)熟悉R的操作环境;(2)熟悉包的安装与帮助;(3)学习常见命令,熟悉 R 的操作界面。
三、实验过程及结果1、(1)R的安装(2)启动与退出;(3)包的安装及R的更新;A、包的安装> chooseCRANmirror()> install.packages()B、R的更新> install.packages("installr") > library(installr)> updateR()(4)帮助及移除多个对象等;> ?关键字> ??关键字> help.start()#帮助> rm()> rm(list=ls())#移除多个对象(5)常见命令四、实验心得了解了R的一些基本使用及其常见的命令,为自己深入学习r的使用打下了基础。
实验二R语言简介: 数据集创建与处理一实验目的1、掌握R数据集的不同创建形式。
2、熟悉并掌握利用R对时间序列数据集进行变换与处理。
二、实验内容及要求1、实验内容:(1)利用data.frame函数创建数据集;(2)读取 d.txt 型数据框;(3)读取 excel 数据及对某变量数据进行某些处理(4)导出 R 中数据集(5)时间序列数据输入(6)对已有数据集中数据的处理2、实验要求:熟悉R数据集的不同创建方法,掌握利用R对时序数据集进行变换与处理三、实验过程及结果1、实验内容:(1)利用data.frame函数创建数据集;(2)读取 d.txt 型数据框;m(3)读取 excel 数据及对某变量数据进行某些处理(4)导出 R 中数据集(5)时间序列数据输入(6)对已有数据集中数据的处理(5)(6)合> library(readxl)> X2_7<- read_excel("C:/Users/Administrator/Desktop/2.7.x lsx")> summary(X2_7)330.45 330.97 331.64 332.87 333.61Min. :331.6 Min. :330.1 Min. :328.6 Min. :328.3 Min. :329.41st Qu.:332.9 1st Qu.:332.4 1st Qu.:331.9 1st Qu.:33 1.5 1st Qu.:332.8Median :334.7 Median :334.4 Median :333.7 Median :33 4.4 Median :335.1Mean :335.0 Mean :334.2 Mean :333.9 Mean :334.3 Mean :335.23rd Qu.:336.8 3rd Qu.:336.1 3rd Qu.:335.9 3rd Qu.:33 7.0 3rd Qu.:337.7Max. :339.2 Max. :338.2 Max. :339.9 Max. :340.6 Max. :341.2333.55Min. :330.61st Qu.:333.9Median :336.0Mean :335.73rd Qu.:338.0Max. :340.9四、实验心得通过本次实验,首先,我知道了文件其他格式的文件如何导入R,知晓乐数据集的创建,使用及一些简单的处理。
统计学实验报告--时间序列分析
实验目的:
1.综合运用统计学时间序列相关知识,并结合经济学等方面的知识进
行回归分析,预测2012年社会投资额。
2.根据时间序列预测结果,建立回归方程,预测该地2012年GDP。
实验步骤:
1.对所搜集的数据资料进行分类整理。
2.绘制表格及频数分布直方图。
3.运用时间数列,进行回归分析,预测2012年社会投资额。
4.运用时间数列预测结果,建立回归方程,预测2012年GDP。
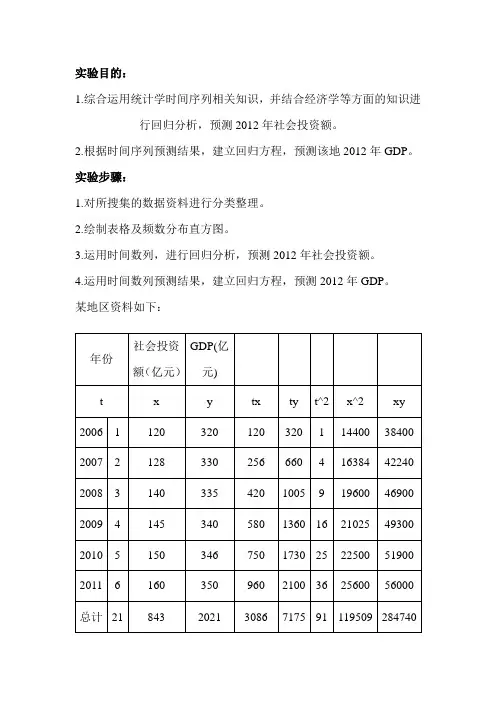
某地区资料如下:
分析: (1)设X=a+bt b=(∑xt -n
/1∑∑t x )/[∑2^t -2)^(/1∑t n ]
=(3086-1/6*384*21)/(91-1/6*21^2) =7.7429 x =140.5 t =3.5 a=x -b t
=140.5-7.7429*3.5 =113.3999+7.7429t
故,2012年,即t=7时,社会投资额为167.6002亿元。
(2)设ŷ=c+dx
d=(∑xy-1/n∑∑y
/1
n
x]
2^x
x)/[∑∑
-2
)^
(
=(284740-1/6*2021*843)/(179509-1/6*843^2)
=0.74
c=y-d x=232.86
故,2012年该地GDP为356.88亿元。
实验结论:运用时间序列进行回归分析,可以根据以往的经济数据进行预测分析,提高经济活动的目的性与计划性。
应用时间序列分析实训报告

《应用时间序列分析》实训报告实训项目名称非平稳时间序列模型的建立实训时间 2013年12月16日实训地点实验楼308班级计科1001班学号姓名《应用时间序列分析》实训(实践) 报告实训名称平稳时间序列模型的建立一、实训目的本次实验是一个综合试验,通过自己选定问题,收集数据,确定研究方法,建立合适模型,解决实际问题,增强学生动手能力,提高学生综合分析的能力。
二、实训内容学生根据自己喜好,选定一个实际问题,确定指标,收集相关数据,利用所学时间序列分析方法队进行研究,建立时间序列模型,揭示其研究对象内部的规律,并对未来进行预测。
并写出分析报告。
具体实验内容如下:1 确定研究问题2 收集数据3 建立合适模型1.ARIMA模型建模前的准备:判断序列是否平稳.①通过序列自相关图、趋势图等进行判断②若序列不平稳:均值非平稳序列通过差分变换转换为平稳方差非平稳序列通过对数变换等转化为平稳序列③模型平稳化以后,将序列零均值化2.模型识别主要通过序列的自相关函数、偏自相关函数表现的特征,进行初步的模型识别3.模型参数估计①在Eviews中估计ARMA模型的方法②估计模型以后要能写出模型的形式(差分方程形式和用B算子表示的形式)4.模型的诊断检验①根据模型残差是不是白噪声来判断模型是否为适应性模型②能根据输出结果判断模型是否平稳,是否可逆③若有多个序列是模型的适应性模型,会用合适的方法从这些模型中进行选择,如比较模型的残差方差,AIC,SC等。
5.模型应用①掌握追溯预测的操作方法②外推预测的操作方法四、实训分析与总结1)输入数据2)生成时序图观测序列时序图,可知序列具有线性长期趋势,需要进行一阶差分观测差分时序图看出并无明显的趋势性或者循环性,得出一阶差分平稳。
由图知,序列一阶自相关显著,序列平稳;Q 统计量P 值小于0.05,非白噪声;同时偏自相关拖尾、自相关一步截尾,可建立ARIMA (0,1,1)模型。
3)模型参数估计ARMA 模型估计方程:t )708169.01(015566.5εB x t ++=∇SBC 值为7.013764由图知偏自相关,C 的值大于0.05,则去掉C,继续建立模型:ARIMA 模型估计方程:t 652119.011εBx t -=∇SBC 值为7.055671比较两个模型的SBC 值,建立ARMA 模型最优。
应用时间序列实验报告
工程学院课程设计《时间序列分析课程设计》学生学号:学院:理学院专业班级:专业课程:时间序列分析课程设计指导教师:2017年 6 月 2 日目录1. 实验一澳大利亚常住人口变动分析 (1)1.1 实验目的 (2)1.2 实验原理 (2)1.3 实验容 (2)1.4 实验过程 (4)2. 实验二我国铁路货运量分析 (9)2.1 实验目的 (10)2.2 实验原理 (10)2.3 实验容 (11)2.4 实验过程 (12)3. 实验三美国月度事故死亡数据分析 (15)3.1 实验目的 (17)3.2 实验原理 (17)3.3 实验容 (18)3.4 实验过程 (18)课程设计体会 (22)1.实验一澳大利亚常住人口变动分析1971年9月—1993年6月澳大利亚常住人口变动(单位:千人)情况如表1-1所示(行数据)。
表1-1(1)判断该序列的平稳性与纯随机性。
(2)选择适当模型拟合该序列的发展。
(3)绘制该序列拟合及未来5年预测序列图。
1.1 实验目的掌握用SAS软件对数据进行相关性分析,判断序列的平稳性与纯随机性,选择模型拟合序列发展。
1.2 实验原理(1)平稳性检验与纯随机性检验对序列的平稳性检验有两种方法,一种是根据时序图和自相关图显示的特征做出判断的图检验法;另一种是单位根检验法。
(2)模型识别先对模型进行定阶,选出相对最优的模型,下一步就是要估计模型中未知参数的值,以确定模型的口径,并对拟合好的模型进行显著性诊断。
(3)模型预测模型拟合好之后,利用该模型对序列进行短期预测。
1.3 实验容(1)判断该序列的平稳性与纯随机性时序图检验,根据平稳时间序列均值、方差为常数的性质,平稳序列的时序图应该显示出该序列始终在一个常识值附近波动,而且波动的围有界。
如果序列的时序图显示该序列有明显的趋势性或周期性,那么它通常不是平稳序列。
对自相关图进行检验时,可以用SAS系统ARIMA过程中的IDENTIFY语句来做自相关图。
计量经济学实验报告(实验项目:时间序列计量经济学模型) (2)
实验项目:时间序列计量经济学模型一实验目的通过上机实验掌握计量经济学软件EViews,运用EViews软件进行时间序列计量经济学模型的分析,掌握时间序列计量经济学模型,包括建立模型,了解其单整性、平稳性。
二预备知识单位根检验、单整性检验、ADF检验、最小二乘估计原理。
三实验内容下表给出了1978—2006年中国居民消费价格指数CPI.(1990年=100)(1)做出时间序列CPI的样本相关图,并通过图形判断该序列时间序列的平稳性。
(2)对CPI序列进行单位根检验,以进一步明确它们的平稳性。
(3)检验CPI的单整性。
四实验步骤(一)启动软件包Eviews 的启动步骤:双击E views 快捷方式,进入E Views 窗口;或点击开始 /程序/ Eviews 6,进入E Views 窗口。
(二)创建工作文件。
1 建立工作文件并录入数据,如图1所示。
图 12 平稳性检验2.1 平稳性的图示判断给出一个随机时间序列,首先可以通过该序列的事件路径图来粗略地判断它是否是平稳的。
使用语句T=@TREND+1978产生时间点的序列T,画出CPI跟时间T的关系图,即时序图,如图2所示。
图 2由图2,我们可以直观地看到CPI关于时间T有明显递增的趋势,不同时间段的均值不同,有持续上升,即CPI序列不平稳。
当然,这种直观的图示也常长生误导,因此需要进行进一步的判断。
2.2 样本自相关图判断点击主界面Quick\Series Statistics\Correlogram...,在弹出的对话框中输入CPI,点击OK就会弹出Correlogram Specification对话框,选择Level,并输入要输出的阶数(一般为12),点击OK,即可得到CPI的样本相关函数图,如图3所示。
图 3一个时间序列的样本自相关函数定义为:121()(),1,2,3,...()n kt t k t k ntt XX X X r k XX -+==--==-∑∑易知,随着k 的增加,样本自相关函数下降且趋于零。
时间序列法实验报告
一、实验目的1. 了解时间序列分析方法的基本原理和应用。
2. 学习如何使用时间序列分析方法对实际数据进行预测和分析。
3. 通过实验,提高对时间序列数据处理的实际操作能力。
二、实验内容本次实验选取了一组某城市过去三年的月均降雨量数据,旨在通过时间序列分析方法预测未来一个月的降雨量。
三、实验步骤1. 数据预处理- 读取实验数据,确保数据格式正确。
- 检查数据是否存在缺失值,如有,进行插补处理。
- 对数据进行初步的描述性统计分析,了解数据的分布情况。
2. 时间序列平稳性检验- 对原始数据进行ADF(Augmented Dickey-Fuller)检验,判断时间序列是否平稳。
- 若不平稳,进行差分处理,直至序列平稳。
3. 时间序列建模- 根据平稳时间序列的特点,选择合适的模型进行拟合。
- 本实验选取ARIMA模型进行拟合,其中AR项数为1,MA项数为1,差分次数为1。
4. 模型参数估计- 使用最小二乘法对模型参数进行估计。
5. 模型检验- 对拟合后的模型进行残差分析,检查是否存在自相关或异方差。
- 若存在自相关或异方差,对模型进行修正。
6. 预测- 使用拟合后的模型对未来一个月的降雨量进行预测。
四、实验结果与分析1. 数据预处理- 实验数据共有36个观测值,无缺失值。
- 描述性统计分析结果显示,降雨量数据呈正态分布。
2. 时间序列平稳性检验- 对原始数据进行ADF检验,结果显示P值小于0.05,拒绝原假设,说明原始数据不平稳。
- 对数据进行一阶差分后,再次进行ADF检验,结果显示P值小于0.05,接受原假设,说明一阶差分后的数据平稳。
3. 时间序列建模- 根据平稳时间序列的特点,选择ARIMA(1,1,1)模型进行拟合。
4. 模型参数估计- 使用最小二乘法对模型参数进行估计,得到AR系数为0.8,MA系数为-0.9。
5. 模型检验- 对拟合后的模型进行残差分析,发现残差序列存在自相关,但不存在异方差。
- 对模型进行修正,加入自回归项,得到修正后的ARIMA(1,1,1,1)模型。
时间序列报告精选
时间序列报告精选2020-11-17时间序列报告精选篇一:时间序列报告ARIMA在客货运输量预测的应用摘要:本次实验利用时间序列中ARIMA模型,建立了客货运输总量预测模型,模型确定为ARIMA(1,1,1)12和ARIMA(12,1,12)12,并对数据进行预测,通过AIC准则和SBC准则确定ARIMA(12,1,12)12为相对最优模型。
关键词:时间序列,ARIMA,AIC准则,SBC准则AbstractThe experiment applied the ARIMA model of the time series to formulate the prediction model of passenger and freight transport. With two deterministic models including ARIMA(1,1,1)12andARIMA(12,1,12)12 and data prediction, the experiment determined ARIMA(12,1,12)12as a relative optimization model by means of AIC criterion and SBC criterion.Keyword:time series, ARIMA,AIC,SBC1. 引言随着经济的高速发展,我国客货运总量数据也在逐年增高,对客货运总量数据的预测有利于制定未来运输的发展战略,合理利用资源,合理调度,使得流通更快捷便利。
2. 模型简介ARIMA模型定义ARIMA 模型(Autoregressive Integrated Moving Average model)是研究时间序列的重要方法,由自回归模型(简称AR模型)、滑动平均模型(简称MA模型)和使之成为平稳序列所做的差分次数(阶数)为基础“混合”构成。
ARIMA模型表示为:(1iL)(1L)Xt(1iLi)t idi1i1pqp0,p0E(t)0,Var(t)2,E(ts)0,stExst0,st其中L是滞后算子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
姓名 时间序列分析实验报告(二)
学号
Problem 1: Establish an AR(2) model for data “ ar2.xls” and answer the following questions. 1. Create a new integer-data workfile named ar2 and import the data series named x; 2. Check whether series x is stationary by liner graph; 3. Display the autocorrelation and partial autocorrelation functions by correlogram, and store the frozen graph object named xg; 4. Establish an AR(2) model for series x and save the estimation output as ar2; 注意 1:为什么该数据用 AR(2)过程建模呢?Give you reasons of the choice of p briefly. It follows from the correlogram of series x that the partially autocorrelation function breaks off after 2 . This argues for an AR(2) process, i.e., p=2. 注意 2: 要求大家以后在 Eviews 采用 AR 的输入形式。 即在方程估计的对话框中输入 “x c ar(1) ar(2)” 估计 AR(2)。此时对应形式 xt 1 ( xt 1 ) 2 ( xt 2 ) ut ,其中 为该序列的均值。输出 的回归方程中各数据对应方程中的参数如下:
ARMA(2,1):
ARMA(2,2):
3
班级
姓名
学号
ARMA(1,2):
6. Write out the preferred estimated equation by lag operator; 5 分 Answers: yt 0.516 yt 1 0.360ut 1 ut (1 0.516L) yt (1 0.360L)ut
1
班级
姓名
学号
存在问题: (1)残差非连续相关是什么概念? (2)只给出 Q 值,怎么得到的结论没有给出说明。还需要说明是通过 p 值和显著性对比得到的结 论。 (3)LBQ 检验统计量括号中的数字是所服从卡方分布的自由度,而不是相关系数的个数。自由度 为相关系数的个数 m 减去回归方程中自变量的个数。 (4)部分同学只是指出要拒绝原假设,结论太含糊。结论要明确,落脚在序列是否自相关上。 (5)有同学是根据临界值和检验统计量的观测值对比得到 LM 检验的结论。最为简单的方法是根 据 p 值和显著性水平对比得到结论,因为 LM 检验结果输出中给出了 p 值,而没有给出临界值。 (6)考试时不需要写 Eviews 操作过程,原因要用英语陈述清楚,结果要明确。 6. Write the estimated equation in the form of lag operator; 5 分 Answers: (1 0.454L 0.394 L )( xt 3.293) ut
2
存在问题: (1)忘记残差项 ut 或者 xt 。 (2)符号写错,写成了 (1 0.454 L 0.394 L ) xt 0.501 ut 。
2
(3)方程书写不规范,写成 (1 0.454* L 0.394* L ^ 2) xt 0.501 Ut (4)AR(2)过程的估计和 LM 检验混淆。LM 检验是通过建立自回归方程对残差的自相关性检验。 (5)估计方程时样本会自动调整,不需要调整为 1-298. (6)考试要求保留三位小数。 7. Compute the 299th value and 300th value by dynamic forecast. 5 分 Answers: x299 2.913 , x300 3.007 . 注意:预测期为“299 300” ,而不是“1 300” 。即在“Forecast”对话框中,将“Forecast sample” 选项调整为“299 300” ,默认是全部样本。即根据 1 到 298 个数据进行一步预测得到第 299 个数据 的预测值,进行二步预测得到第 300 个数据的预测值。 如果预测期写成“1 300” 。那么,Eviews 会将第一个数据和第二个数据当作真实数据。而从第 三个数据到第 300 个数据全部是基于第一个数据和第二个数据预测得到的。大家会发现,从第 123 个数据开始到第 300 个数据全部相等。这是因为,随着预测期 的增加,预测值会收敛到该序列的 均值。后面的这些相等的预测数据实际上是该序列的均值。 也就是说,真实数据越多,预测期越短,所掌握的信息越多,预测的结果越准确。 存在问题: (1)没有用 Eviews 计算,而是根据公式推导的。
2
班级
(2)预测期写成“1 300”或者“298 300” 。
姓名
学号
ቤተ መጻሕፍቲ ባይዱ
Problem2: Estimate ARMA models by Box-Jenkins method for data in“arma2.xls”. Ask: 1. Create a new integer-data workfile named arma2 and import the data series named y; 2. Check whether series y is stationary by liner graph; 3. In order to estimate an ARMA model for new series y, identify the possible highest order by correlogram: pmax=?, qmax=? Answers: It follows from the correlogram of series y that the partially autocorrelation function breaks off after 2 and that the autocorrelation function breaks off after 3 . Thus, pmax=2 and qmax==3. 4. Establish ARMA models from low order to high: AR(1), MA(1), ARMA(1,1), ARMA(2,1), ARMA(2,2), ARMA(1,2). Name the estimation outputs as eq01, eq02, eq03, eq04, eq06, eq06 respectively; 5. Select the preferred model by Q-statistic, LM-test and information criterions and compute the 2-step forecast of y by dynamic method; 注意:AR(1),MA(1):残差存在自相关性,不合适。 ARMA(1,1),ARMA(2,1),ARMA(2,2),ARMA(1,2):残差不存在自相关性。 赤池信息准则: ARMA(1,2)=3.414466>ARMA(2,1)=3.408219>ARMA(1,1)=3.407955>ARMA(2,2)=3.399235。 2 步预测误差(RMSE): ARMA(1,1)=1.828790 <ARMA(1,2)=1.834662<ARMA(2,1)=1.881183<ARMA(2,2)=1.889910。 ARMA(2,1)和 ARMA(2,2)的预测误差较 ARMA(1,1)和 ARMA(1,2)有些高,而所有模型的信息 准则相差不大。综合来看,选择较简单的 ARMA(1,1)。 ARMA(1,1):
yt 0126 0.505 yt 1 0.365ut 1 ut (1 0.505L) yt 0126 (1 0.365L)ut
4
班级
姓名
学号
回归方程输出结果中 MA(q)对应的值就是自变量 ut q 的系数,不需要加负号。 (3) 将 AR 项和 MA 项混淆,写成了
截图结果如下:
存在问题: (1)不明白 AR(2)模型的一般形式是什么,经常不出现 AR(1)部分。 (2)对 x 差分得到序列 y,对序列 y 估计的 AR 方程。用 ADF 检验下,序列 x 是平稳的,无需消 除趋势。 5. Test whether there is serial correlation for the residuals by Q-statistics and LM-test ( 0.05 ). Give your reason briefly; Answers: According to the correlogram of residuals, the Ljung-Box Q statistic which is calculated with 12 correlation coefficients is Q(10)=11.383. Its corresponding p value is 0.328, which is larger than 0.05. This implies that the residuals are not autocorrelated ( 0.05 ). Since LM(12)=11.767 and the corresponding p value is 0.465, the residuals are not autocorrelated ( 0.05 ). 注意:当在 Eviews 中采用 ar 输入时,P 值已经进行了修正。自相关输出结果中有说明, “Q-statistic probabilities adjusted for 2 ARMA term(s)” 。
