多元函数全微分
《高等数学B》第八章 多元函数微分学 第三节 全微分及其应用
∆ z = A∆ x + B∆ y + o( ρ ) 总成立 ,
上式仍成立, 当 ∆ y = 0 时,上式仍成立,此时 ρ = | ∆ x | ,
f ( x + ∆ x , y ) − f ( x , y ) = A ⋅ ∆ x + o(| ∆ x |) ,
所求全微分 dz = e 2dx + 2e 2dy .
y yz 例2 计算函数 u = x + sin + e 的全微分 . 2
y ∂u 1 ∂u ∂u yz yz 解 = ye , =1, = cos + ze , ∂y 2 2 ∂z ∂x
所求全微分
1 y yz yz du = dx + ( cos + ze )dy + ye dz . 2 2
例4 试证函数
1 , ( x , y ) ≠ ( 0 , 0) , xy sin 2 2 x +y f ( x , y) = 0, ( x , y ) = ( 0 , 0) .
在点 (0 , 0) 连续且偏导数存在,但偏导数在点 (0 , 0) , 0) 可微 . 不连续, (证明略) 证明略)
∂u ∂u ∂u du = dx + dy + dz . ∂x ∂y ∂z
例1 计算函数 z = e x y在点 ( 2 , 1) 处的全微分 . 解
∂z = ye xy , ∂x
∂z = e2 , ∂x ( 2 , 1 )
∂z = xe xy , ∂y
∂z = 2e 2 , ∂y ( 2 , 1 )
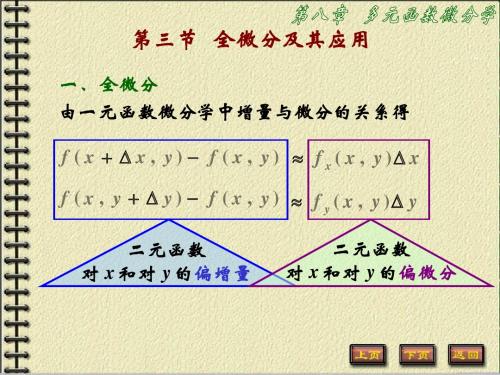
∆ z ≈ dz = f x ( x , y )∆ x + f y ( x , y )∆ y .
多元函数的全微分与偏导数

多元函数的全微分与偏导数多元函数是数学分析中非常重要的一个概念,它描述了多个自变量对应的函数值的变化规律。
全微分和偏导数则是研究多元函数性质的重要工具。
在本文中,我们将探讨多元函数的全微分与偏导数的定义、性质和应用。
一、全微分的概念与性质1.1 全微分的定义设函数 $f(x_1,x_2,\cdots,x_n)$ 在点$(x_{1_0},x_{2_0},\cdots,x_{n_0})$ 具有一阶连续偏导数,则在该点的全微分为:$$\mathrm{d} f=f_{x_1}\mathrm{d} x_1+f_{x_2}\mathrm{d}x_2+\cdots+f_{x_n}\mathrm{d} x_n$$其中 $f_{x_i}$ 表示 $f$ 对 $x_i$ 的偏导数,$\mathrm{d}x_i$ 表示 $x_i$ 的微小增量。
1.2 全微分的性质全微分具有以下性质:(1)全微分的值与路径无关。
即,从点 $A$ 到点 $B$ 的全微分值相等。
(2)全微分对各变量的求导顺序不影响结果。
(3)全微分的二阶导数与求导顺序无关。
二、偏导数的定义与求解方法2.1 偏导数的定义函数 $f(x_1,x_2,\cdots,x_n)$ 对自变量 $x_i$ 的偏导数定义为:$$\frac{\partial f}{\partial x_i}=\lim_{\Delta x_i\rightarrow0}\frac{f(x_1,x_2,\cdots,x_{i-1},x_i+\Delta x_i,x_{i+1},\cdots,x_n)-f(x_1,x_2,\cdots,x_n)}{\Delta x_i}$$偏导数表示 $f$ 在某一自变量上的变化率。
2.2 偏导数的求解方法对于多元函数 $f(x_1,x_2,\cdots,x_n)$,求偏导数的方法如下:(1)保持其他自变量不变,对于某个自变量求导数。
(2)对于每个自变量都求一遍偏导数。
全微分的计算公式

全微分的计算公式全微分是微积分中一个重要的概念,它用于描述函数变量之间的微小变化关系。
全微分的计算可以使用泰勒展开、导数定义和偏导数等方法。
本文将介绍全微分的计算公式和应用。
一、一元函数的全微分设函数y = f(x)在点(x0, y0)处可微分。
此时,函数f(x)在x0附近可以用其局部线性近似代替。
根据导数的定义,可得到函数f(x)在点x0处的导数f'(x0)。
函数f(x0)的全微分df表示函数f(x)在x0附近的微小变化量,可以通过以下公式计算:df = f'(x0)dx其中,f'(x0)表示函数f(x)在x0处的导数,dx表示自变量x的微小变化量。
二、二元函数的全微分对于二元函数z = f(x, y),如果在点(x0, y0)处可微分,那么z在(x0, y0)处的全微分dz可以表示为:dz = ∂f/∂x*dx + ∂f/∂y*dy其中,∂f/∂x表示函数f(x, y)对x的偏导数,∂f/∂y表示函数f(x, y)对y的偏导数,dx表示自变量x的微小变化量,dy表示自变量y的微小变化量。
需要注意的是,在计算二元函数的全微分时,要先对函数进行偏导数运算,然后与自变量的微小变化量相乘,再将结果相加。
三、多元函数的全微分对于多元函数z = f(x1, x2, ..., xn),如果在点(x1^0,x2^0, ..., xn^0)处可微分,那么z在(x1^0, x2^0, ..., xn^0)处的全微分dz可以表示为:dz = ∂f/∂x1*dx1 + ∂f/∂x2*dx2 + ... + ∂f/∂xn*dxn其中,∂f/∂x1表示函数对变量x1的偏导数,∂f/∂x2表示函数对变量x2的偏导数,dx1表示自变量x1的微小变化量,dx2表示自变量x2的微小变化量,以此类推。
四、全微分的应用例如,在概率论与统计学中,我们常常需要计算函数的期望和方差。
对于连续型随机变量,若已知其概率密度函数f(x)和函数g(x),可以通过全微分的公式计算函数g(x)的期望和方差。
多元函数的全微分和偏导数.

注 (1) z f ( x, y) 在点( x0 , y0 )可微反映的是函数在点
( x0 , y0 ) 具有这样的性质:
“在点( x0 , y0 ) 全增量可以用自变量增量的线性函数近似” (2) z f ( x, y)在点( x0 , y0 )微分dz是 z f ( x, y)在点
[1 x 6 1 x 4] 11 x 8x 8 lim lim x 0 x 0 x x
2 2
1 3(2 y) 2 y 2 11 z lim 7 y (1, 2) x0 y
1 y 2
lim 又 y 0 sin
不存在, 故
不存在 注 分段函数求偏导数时,要分在分段点和非分段点考虑,
分段点通常采用定义去求.
机动
目录
上页
下页
返回
结束
(三)可导与连续 函数在某点各偏导数都存在,但在该点不一定连续. xy , x2 y2 0 2 显然 z f ( x, y ) x y 2 例 0 , x2 y2 0
为函数 z f ( x, y )在 ( x0 , y0 ) 处对 y 的偏增量。
机动 目录 上页 下页 返回 结束
定义 8.3.2 设函数 z f ( x, y ) 在点( x0 , y0 )的某邻域内极限
存在, 则称此极限为函数 z f ( x, y ) 在 ( x0 , y0 )对 x 的偏导数, 记为 同样可定义对 y 的偏导数:
的二阶偏导数 .按求导顺序不同, 有下列四个二阶偏导数:
z ( z ) f ( x, y ); xx x x 2 x
2
2 z z ( ) f x y ( x, y ) x y y x
多元函数的全微分公式

多元函数的全微分公式
微分
多元函数的全微分公式
一、定义
全微分是对多元函数的求导,并且把多元函数的求导公式写成一个全微分的公式形式。
二、公式
多元函数的全微分为:
dF=Fx1dx1+Fx2dx2+…+Fxndxn
其中,F为多元函数,x1,x2,…,xn为多元函数的变量,
Fx1,Fx2,…,Fxn为多元函数求导的部分,dx1,dx2,…,dxn是多元函数变量的微小变化量。
三、应用
多元函数的全微分公式可以用来计算某些复杂的多元函数的求
导结果,简化多元函数的求导过程,和解决关于多元函数的求导问题。
它还可以用来帮助计算函数的极值问题。
- 1 -。
多元函数的微分知识点介绍 整理人王浩

多元函数的微分知识点介绍整理人王浩多元函数的微分是求解多元函数的局部变化率的方法。
在微分学中,多元函数的微分包括偏导数和全微分两个概念。
偏导数是指某一变量在其他变量不变的情况下所产生的变化率,而全微分则是指所有变量同时改变时函数值的变化率。
1. 偏导数偏导数是导数概念在多元函数中的应用。
对于一个多元函数f(x,y),它的偏导数df/dx和df/dy表示当变量x或y分别增加一个微小的量时,函数f的局部变化率。
它们的定义如下:df/dx = lim(f(x+Δx,y)-f(x,y))/Δx (当Δy=0时)其中,Δx和Δy分别表示x和y的增量。
需要注意的是,偏导数只对某一变量求导,其他变量视作常数,可以将其视为单变量函数的导数。
2. 全微分全微分是将多元函数视为一个整体来求解其局部变化率的方法。
如果函数f(x,y)在某一点(x0,y0)处可微分,那么它的全微分df可以表示为:df = ∂f/∂x * dx + ∂f/∂y * dy其中,dx和dy分别表示x和y的增量,∂f/∂x和∂f/∂y分别表示函数f在(x0,y0)处的偏导数。
需要注意的是,全微分只适用于可微分的函数。
如果函数在某些点处不可微分,那么全微分也不存在。
3. 链式法则在多元函数求导中,链式法则是一种常用的方法。
它用于求解由多个函数复合而成的函数的导数。
如果h(x)是一个由f(u)和g(v)复合而成的函数,且u=u(x)和v=v(x)是关于x的函数,那么h(x)在x处的导数可以表示为:4. 梯度梯度是多元函数中的一种重要概念,它表示函数在某一点的最大变化方向。
对于一个多元函数f(x,y),它在某一点(x0,y0)的梯度grad(f)(x0,y0)可以表示为:可以看出,梯度是一个向量,它的方向是函数在某一点的最大变化方向,大小则表示变化率的大小。
总之,多元函数的微分是一个重要的数学工具,它可以帮助我们研究各种复杂的自然现象和社会现象,如气象学、地质学、金融学等。
多元函数微积分学 6.3偏导数与全微分
=1+ 2×0.04 + 0×0.02 =1.08.
24
2. 全微分的运算公式 设二元函数 u(x,y) , v(x,y) 均可微 , 则 ((v(x,y) ≠0)), 也可微 且 也可微,
d( ku)
(k为常数 为常数), 为常数
(k为常数), (k为常数), 为常数
= du ± dv, = vdu + udv,
26
f (x, y),
处连续. 即 z = f (x, y) 在点 (x, y) 处连续
17
定理4 (充分条件) 若函数
∂z ∂z 的偏导数 , ∂x ∂y 在 (x, y) 连 , 则函数在该点可微分 点 续 则函数在该点可微分. 证 ∆z = f (x + ∆x, y + ∆y) − f (x, y)
∂u =− sin( x2 − y2 − ez ) ⋅ (−2 y) = 2 y sin( x2 − y2 − ez ) ∂y
∂z 2 2 z z z 2 2 z u = −sin( x − y − e ) ⋅ (−e ) = e sin( x − y − e ) ∂z
10
2. 二元函数偏导数的几何意义
∂f ; z′ x ∂ x (x0 , y0 )
( x0 , y0 )
;
f1′(x0, y0 ) .
2
同样可定义对 y 的偏导数
f (x0, y0 + ∆y ) − f (x0, y0 ) f y′(x0, y0 ) = lim ∆ y→0 ∆y
若函数 z = f ( x , y ) 在域 D 内每一点 ( x , y ) 处对 x 或 y 偏导数存在 , 则该偏导数称为偏导函数 也简称为 则该偏导数称为偏导函数 偏导函数, 偏导数 , 记为
多元函数的偏导数与全微分
上相等。
如果函数z f ( x, y)在点( x, y)的某邻域内 有定义,并设 P( x x, y y)为这邻域内的
任意一点,则称这两点的函数值之差
f ( x x, y y) f ( x, y) 为函数在点 P 对应于自变量增量x, y的全增 量,记为z, 即 z= f ( x x, y y) f ( x, y)
同理, f (0,0) 0. y
可以证明,对本例中的函数f (x,y),
lim f(x,y)
(x,y)(0,0)
不存在,因此它在原点不连续,但在原点的两个偏函数
都存在,这一点和一元函数是不同的.在一元函数中,
高阶偏导 数
xxzx2z2fxx(x,y), xyzy2zxfyx(x,y) yxzx2zyfxy(x,y), yyzy2z2fyy(x,y)
偏导数的几何意义
例1
求 z = x 2 + 3 xy + y2在点 (1,2)处的偏导数.
解
z x
2x3y;
z y
3x2y.
z x
x 1 y2
2 1 3 2 8 ,
z y
x1 y2
3 1 2 2 7 .
例2
设 z = arcsin
x
¶z ¶z
,求 ,
x2 + y2
¶x ¶y
y0
y
记为 z y
, f x x0 y
,zy
x x0
或 x x0
y y0
f y ( x0 ,
y0 ).
y y0
y y0
xzxx0,fxxx0,zxxyxy00或fx(x0,y0). yy0 yy0
如果函数z f ( x, y)在区域 D内任一点
高等数学第六章多元函数微分法及应用第三节 全微分
dz f x (1,2)dx f y (1,2)dy 2 0.04 0 0.02 0.08
(1.04)2.02 1.08
V 2rhr r 2h
其余部分是 (r)2 (h)2的高阶无穷小,所以
V 2rhr r 2h o( (r)2 (h)2 )
2020/2/13
线性主部
无穷小量
3
二 全微分的定义
(Definition of total differential)
全微分存在.
xy
例如,
f
(
x,
y)
x2 y2
0
x2 y2 0 .
x2 y2 0
在 点 (0 ,0 )处 f x (0 ,0 ) f y (0 ,0 ) 0
z [ f x (0,0) x f y (0,0) y]
x y , (x)2 (y)2
2020/2/13
14
记全微分为 dz z dx z dy. x y
通常我们把二元函数的全微分等于它的两个 偏微分之和这件事称为二元函数的微分符合叠加 原理.
叠加原理也适用于二元以上函数的情况. 全微分的定义可推广到三元及三元以上函数
du u dx u dy u dz. x y z
2020/2/13
20
证 令 x cos , y sin ,
则 lim xy sin 1
( x , y )(0,0)
x2 y2
lim 2 sin cos sin 1
多元函数微分学—全微分及其运用(高等数学课件)
典 型 例 题 讲 解
例2 求函数 z ( x y )e xy 在点(1,2)处的全微分.
z
解: e xy y ( x y )e xy (1 xy y 2 )e xy,
x
z
例2
e xy 求函数计算函数,在点(1,2)处的全微分。
x( x y )e xy (1 xy x 2 )e xy,
用公式(1):
z dz f x( x0 , y0 )x f y ( x0 , y0 )y
二、典型例题讲解
例1 有一金属制成的圆柱体,受热后发生形变,它的半径由20 cm 增大到
20.05 cm ,高由50 cm 增加到50.09cm,求此圆柱体体积变化的近似值.
解: 设圆柱体的半径、高和体积分别为 、ℎ 和, 它们的增量分别记为
多元函数的微分学
多元函数的全微分
知识点讲解
1.全微分的定义
2.可微、连续、可偏导之间的关系
3.全微分的求法
全微分的定义
1.全改变量
设函数 z f ( x, y ) 在点 P0 ( x0 , y0 ) 的某个邻域内有定义,自变量、在0 、0
的改变量分别为 x, y ,全增量:
z f ( x0 x, y0 y ) f ( x0 , y0 )
x
y
z
由公式知:求全微分的步骤如下:
1.求偏导数;
2.套公式得全微分.
f ( x, y )
典 型 例 题 讲 解
例1 求函数 z x 2 y xy 2 的全微分.
解:
z
z
2 xy y 2 , x 2 2 xy
x
y
dz (2 xy y 2 )dx ( x 2 2 xy)dy.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∆z = f ( x0 + ∆x , y0 + ∆y ) − f ( x 0 , y0 )
(∆x ) + (∆y ) 上式仍成立, 当∆y = 0时,上式仍成立, 此时 ρ =| ∆x |, f ( x0 + ∆x , y0 ) − f ( x0 , y0 ) = A⋅ ∆x + o(| ∆x |),
4 例 试 函 证 数
1 , ( x, y) ≠ (0,0) xy sin 2 2 x +y f ( x, y) = 0, ( x, y) = (0,0)
在 (0,0)(1)连 ; (2)偏 数 在 (3)偏 数 点 连 续 偏 导 存 ; 偏 导 在 点(0,0)不 续 连 ; (4)f 在 (0,0)可 . 点 微
∂z = xe xy , ∂y
∂z ∂z 2 2 =e , = 2e , ∂x ( 2 , 1 ) ∂y ( 2 , 1 )
所求全微分 dz = e 2dx + 2e 2dy .
π 例 2 求 数z = y cos( x − 2 y), x = ,y = π, 函 当 4
dx = ,dy = π时的 微分. 全 4
∆x → 0 ∆y → 0
∴ f x′ ( x0 + θ 1 ∆x , y0 + ∆y ) = f x′ ( x0 , y0 ) + ε 1
(无穷小) 且当 ∆x → 0, ∆ y → 0 时,ε 1 → 0 . 无穷小) 同理 f ( x 0 , y 0 + ∆ y ) − f ( x 0 , y 0 ) = f y′ ( x 0 , y 0 )∆ y + ε 2 ∆ y ,
且当 ∆x → 0, ∆y → 0 时, ε 2
→ 0.
∆ z = f x ( x 0 , y 0 )∆ x + ε 1 ∆ x + f y ( x 0 , y 0 ) ∆ y + ε 2 ∆ y ′ ′
ε1∆x + ε2∆y ∆x ∆y ρ→0 → Q ≤ ε1 + ε2 ≤ ε1 + ε2 0, ρ ρ ρ
则
∆x ⋅ ∆y 2 2 (∆x) + (∆y )
ρ
∆x ⋅ ∆y = 2 2 (∆x) + (∆y )
当 ρ → 0时,上式极限不存在,说明它 上式极限不存在, 不能随着 ρ → 0而趋于0,0) ⋅ ∆x + f y (0,0) ⋅ ∆y ] ≠ o( ρ ),
ρ →0
∆x → 0 ∆y → 0
lim f ( x0 + ∆x , y0 + ∆y ) = f ( x0 , y0 )
∆x → 0 ∆y → 0
故函数 z = f ( x , y ) 在点 ( x0 , y0 ) 处连续.
可微分, 在点( 定理 2:如果函数 z = f ( x , y )在点( x 0 , y0)可微分, 则函数 z = f ( x , y )的两个偏导数 f x′ ( x 0 , y0 ), f y′ ( x 0 , y 0 )存在,且 存在, dz ( x
函 在 故 数 点(0,0)连 , 续
(
)
f ( ∆x ,0) − f (0,0) 0−0 ′ f x (0,0) = lim = lim = 0, (2) ∆x → 0 ∆x → 0 ∆ x ∆x
同理
可导 可偏导
可微 可微分
xy x2 y2 例如, 例如, + f ( x, y) = 0
x2 + y2 ≠ 0 x2 + y2 = 0
.
在点(0,0) 处有
′ ′ f x (0,0) = f y (0,0) = 0
∆x ⋅ ∆ y ′ ′ , ∆z − [ f x (0,0) ⋅ ∆x + f y (0,0) ⋅ ∆y ] = 2 2 ( ∆ x ) + ( ∆y )
思路:按有关定义讨论; 思路:按有关定义讨论;对于偏导数需分
( x , y ) ≠ (0,0) ,( x , y ) = (0,0) 讨论 讨论.
证 (1) xy sin
1 x2 + y2
≤ xy
1 2 ( x , y )→ (0 , 0 ) 2 ≤ x + y → 0 2 1 则 lim xy sin 2 2 = 0 = f ( 0,0 ), ( x , y )→ ( 0 , 0 ) x +y
y=f(x)在某点处: 可导 在某点处: 在某点处 z=f(x,y)在某点处:可偏导 在某点处: 在某点处 可微 连续 可微分 连续
连续
8.3.2 全微分存在的必要条件和充分条件
可微分, 1 定理 如果函数 z = f ( x , y ) 在点 ( x0 , y0 ) 可微分 则 函数在该点连续. 函数在该点连续
通常我们把二元函数的全微分等于它的两个偏 微分之和这件事称为二元函数的微分符合叠加原 微分之和这件事称为二元函数的微分符合叠加原 理. 全微分的定义可推广到三元函数: 全微分的定义可推广到三元函数
∂u ∂u ∂u u = f ( x , y , z ), du = dx + dy + dz . ∂x ∂y ∂z
0 , y0 )
= f x′ ( x 0 , y0 )∆x + f y′ ( x 0 , y0 )∆y
即可微分定义中 ∆z = A∆x + B∆y + o( ρ) A = f x′ ( x0 , y0 ),B = f y′ ( x0 , y0 )
证: 如果函数 z = f ( x , y ) 在点 P ( x0 , y0 ) 可微分 可微分,
= A∆x + B∆y + o( ρ ), ρ =
2 2
f ( x0 + ∆x, y0 ) − f ( x0 , y0 ) lim =A ∆x →0 ∆x
′ A = f x ( x0 , y0 ), 同理可得 B = f y ( x0 , y0 ). ′
y=f(x)在某点处: 在某点处: 在某点处 z=f(x,y)在某点处: 在某点处: 在某点处
= [ f ( x0 + ∆x, y0 + ∆y) − f ( x0 , y0 + ∆y)]
+ [ f (x0 , y0 + ∆y) − f (x0 , y0 )]
两个方括号内, 在 两个方括号内,应用拉格朗日中值定理
f ( x 0 + ∆x , y0 + ∆y ) − f ( x 0 , y 0 + ∆y )
ρ=
(∆x ) + (∆y ) ρ → 0, ∆x → 0, ∆y → 0.
2 2
故函数 z = f ( x , y )在点 ( x 0 , y0 ) 处可微
注:习惯上记 ∆x = dx , ∆y = dy , 全微分记为 ′ ′ dz ( x , y ) = f x ( x0 , y0 )dx + f y ( x0 , y0 )dy
解
π
∂z = − y sin( x − 2 y ), ∂x ∂z = cos( x − 2 y ) + 2 y sin( x − 2 y ), ∂y dz ( π , π )
4
∂z ∂z dx + dy = 2 π (4 + 7π ). = ∂y ( π , π ) ∂x ( π , π ) 8 4
0 0
上每一点( 都可微, 如果函数 z = f ( x , y )在定义域D上每一点( x , y)都可微, 上可微, 则称函数 f在区域D上可微,函数 f在区域D上的全微分记为
∂z ∂z dz = fx′(x, y)∆x + f y′(x, y)∆y 或 dz = dx + dy. ∂x ∂y
∂z ∂z dz = dx + dy. ∂x ∂y
叠加原理也适用于n元函数的情况 叠加原理也适用于 元函数的情况: 元函数的情况
′ ′ ′ u = f ( x1, x2 ,Lxn ),du= f x1dx1 + f x2dx2 +L+ f xndxn
例1 计 函 z = e 在 (2,1) 处 全 分 算 数 点 的 微 .
xy
解
∂z xy = ye , ∂x
8.3.1 全微分的定义
如果函数 z = f ( x , y )在点( x0 , y0 )的全改变量 ∆z = f ( x0 + ∆x , y0 + ∆y ) − f ( x0 , y0 )可表示为
∆z = A∆x + B∆y + o(ρ)
y
其中A, B不依赖于 ∆x , ∆y 而仅与 x , y有关,
∆y
∆x∆y
∆z = f ( x 0 + ∆ x , y 0 + ∆ y ) − f ( x 0 , y 0 ) = ( x0 + ∆x )( y0 + ∆y ) − x0 y0 = y0 ∆x + x0 ∆y + ∆x∆y
线性主要部分
o( (∆x)2 + (∆y)2 )
y0
x0
∆x
′ ′ f x ( x0 , y0 ) = y0 , f y ( x0 , y0 ) = x0
f ( x + ∆x , y + ∆y ) − f ( x , y ) 为函数在点 P 对应于自变量改变量∆x , ∆y 的全 改变量(全增量) 改变量(全增量),记为∆z
即 ∆z= f ( x + ∆x, y + ∆y) − f ( x, y)
例如: 例如:设矩形边长 x , y , 则面积为 z = f ( x , y ) = xy . 矩形面积在点( x0 , y0 )的改变量为
