六年级组合图形周长计算
小学六年级【小升初】数学《平面图形的测量专题课程》含答案
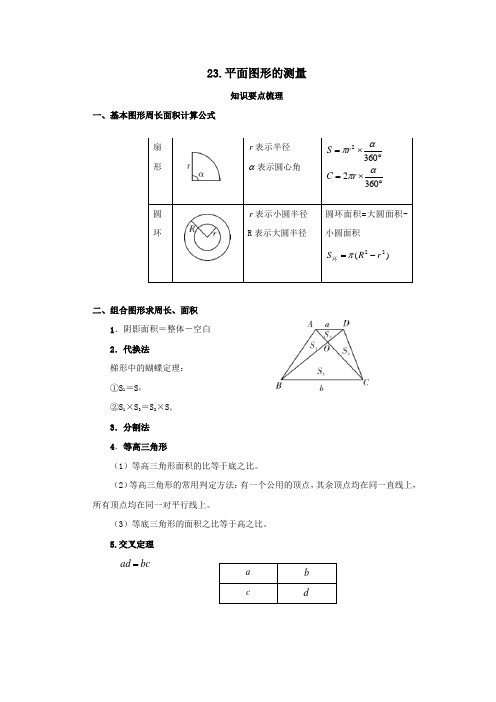
23.平面图形的测量知识要点梳理一、基本图形周长面积计算公式二、组合图形求周长、面积 1．阴影面积＝整体－空白 2．代换法梯形中的蝴蝶定理： ①S 1＝S 4 ②S 1×S 3＝S 2×S 4 3．分割法 4．等高三角形（1）等高三角形面积的比等于底之比。
（2）等高三角形的常用判定方法：有一个公用的顶点，其余顶点均在同一直线上，所有顶点均在同一对平行线上。
（3）等底三角形的面积之比等于高之比。
5.交叉定理 bc ad =扇形r 表示半径α表示圆心角︒⨯=3602απr S ︒⨯=3602απr C圆环 r 表示小圆半径R 表示大圆半径圆环面积=大圆面积-小圆面积)(22r R S -=π环a bcd考点精讲分析典例精讲考点1组合图形的周长和面积【例1】 求下面图形的周长和面积。
（单位：米） 【精析】 要求它的周长，可用长方形的2个长＋1个宽＋圆的周长的一半；要求它的面积，可用图中长方形的面积加上半圆的面积即可。
【答案】 周长：2.5×2＋2＋3.14×2÷2 ＝5＋2＋3.14 ＝10.14（米）面积：2.5×2＋3.14×2)22(÷2 ＝5＋3.14×1÷2 ＝5＋1.57 ＝6.57（平方米）答：这个图形的周长是10.14米，面积是6.57平方米【归纳总结】 组合图形的计算，一般都要把它分割成规则图形再进行计算。
考点2 等积变换法求面积【例2】 如图，ABCD 是直角梯形，AB ＝3厘米，AD ＝4厘米，BC ＝6厘米，求阴影部分的面积。
【精析】 阴影部分的面积为三角形ABE 和三角形DEC 的面积之和，利用△ABE 和△DEC 是等高三角形则阴影部分的面积可以变换为BC 边的长乘以高，再除以2。
【答案】 6×3÷2＝9（平方厘米）【归纳总结】 高一定，阴影部分面积＝底之和×高÷2。
六年级数学上册组合图形的周长和面积讲解
六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。
(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解：最基本的方法之一。
用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。
例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。
(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。
(完整版)六年级数学上册组合图形的周长和面积
六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。
(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解：最基本的方法之一。
用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。
例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。
(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。
数学(小升初) 组合图形周长、面积的计算
第2讲组合图形面积的计算一、计算公式例1、如图，正方形ABCD的边长为6厘米，△ABE、△ADF与四边形AECF的面积彼此相等，求三角形AEF的面积.例2、下图，求阴影部分的面积。
其他常用的基本方法有：一、相加法这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积。
例如：求下图整个图形的面积二、相减法这方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。
例如：下图，求阴影部分的面积。
一句话：正方形面积减去圆的面积即可。
三、直接求法这种方法是根据已知条件，从整体出发直接求出不规则图形面积。
例如：下图，求阴影部分的面积。
一句话：通过分析发现阴影部分就是一个底是2、高是4的三角形。
四、重新组合法这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可。
例如：下图，求阴影部分的面积。
一句话：拆开图形，使阴影部分分布在正方形的4个角处，如下图。
五、辅助线法这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可例如：下图，若求阴影部分的面积。
六、割补法法这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形，从而使问题得到解决。
例如：求阴影部分的面积．七、平移法这种方法是将图形中某一部分切割下来平行移动到一恰当位置，使之组合成一个新的基本规则图形，便于求出面积。
例如：下图，求阴影部分的面积。
一句话：可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内，这样整个阴影部分恰是一个正方形。
八、旋转法这种方法是将图形中某一部分切割下来之后，使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧，从而组合成一个新的基本规则的图形，便于求出面积。
例如图（1），求阴影部分的面积。
一句话：左半图形绕B点逆时针方向旋转180°，使A与C重合，从而构成右图（2）的样子，此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法这种方法是作出原图形的对称图形，从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半。
六年级5.4组合图形的周长与面积练习题
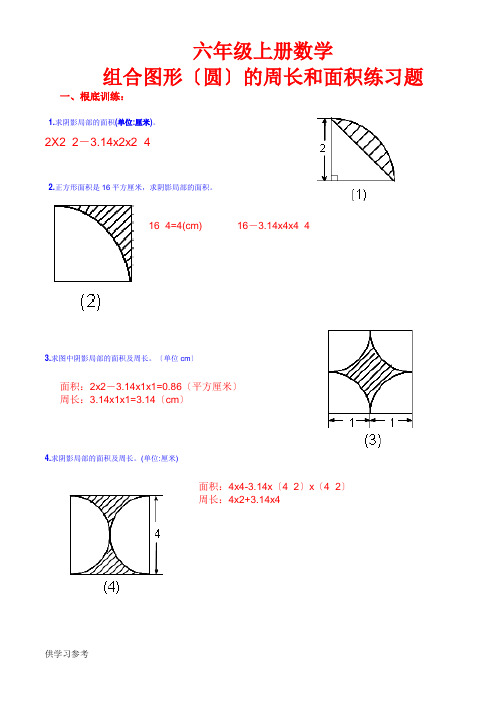
六年级上册数学组合图形〔圆〕的周长和面积练习题一、根底训练：1.求阴影局部的面积(单位:厘米)。
2X2÷2－3.14x2x2÷42.正方形面积是16平方厘米，求阴影局部的面积。
16÷4=4(cm) 16－3.14x4x4÷43.求图中阴影局部的面积及周长。
〔单位cm〕面积：2x2－3.14x1x1=0.86〔平方厘米〕周长：3.14x1x1=3.14〔cm〕4.求阴影局部的面积及周长。
(单位:厘米)面积：4x4-3.14x〔4÷2〕x〔4÷2〕周长：4x2+3.14x45.求阴影局部的面积。
7.如图〔8〕，求阴影局部的面积。
(单位:厘米)8.如图〔9〕求阴影局部的面积。
(单位:厘米)S=〔2+1〕X2=6〔平方厘米〕9. 如图〔11〕求阴影局部的面积。
(单位:厘米)〖3.14x4x4-3.14x3x3〗÷610.在如图〔12〕是正三角形中求阴影局部的面积及周长。
(单位:厘米) 面积：3.14x3x3÷2 周长：3.14x3+3x612. 如图〔13〕求阴影局部的面积。
(单位:厘米)13.如图〔14〕求阴影局部的面积。
(单位:厘米)16.如右图〔33〕，求阴影局部的面积及周长。
(单位:厘米)二、能力提升：17.如右图〔19〕正方形边长为4厘米，求阴影局部的面积及周长。
18.如图〔20〕，正方形ABCD的面积是36平方厘米，求阴影局部的面积。
19.如图〔22〕，正方形边长为8厘米，求阴影局部的面积。
20.如图〔28〕求阴影局部的面积。
(单位:厘米)21.如图〔33〕求阴影局部的面积。
六年级圆的周长奥数题
六年级圆的周长奥数题一、基础题型1. 一个圆的半径是3厘米，它的周长是多少厘米？- 解析：根据圆的周长公式C = 2π r（其中C表示周长，π通常取3.14，r为半径）。
当r = 3厘米时，C=2×3.14×3 = 18.84厘米。
2. 已知圆的直径是8分米，求这个圆的周长。
- 解析：因为圆的周长C=π d（d是直径），当d = 8分米时，C = 3.14×8=25.12分米。
3. 一个圆的半径扩大到原来的2倍，它的周长扩大到原来的几倍？- 解析：设原来圆的半径为r，则原来的周长C_1 = 2π r。
半径扩大2倍后变为2r，此时周长C_2=2π×(2r) = 4π r。
C_2div C_1=(4π r)div(2π r)=2，所以它的周长扩大到原来的2倍。
4. 有一个圆形花坛，半径是5米，在它的周围铺一条宽1米的小路，求小路的外沿周长是多少米？- 解析：小路的外沿半径为5 + 1=6米。
根据圆的周长公式C = 2π r，当r = 6米时，C=2×3.14×6 = 37.68米。
5. 一个半圆的直径是10厘米，求这个半圆的弧长（周长的一半）。
- 解析：圆的周长C=π d，半圆的弧长为(1)/(2)π d。
当d = 10厘米时，弧长=(1)/(2)×3.14×10 = 15.7厘米。
二、组合图形中的圆周长问题6. 正方形的边长为10厘米，在正方形内画一个最大的圆，求这个圆的周长。
- 解析：正方形内最大的圆的直径等于正方形的边长，即d = 10厘米。
根据圆的周长公式C=π d，C = 3.14×10 = 30.4厘米。
7. 长方形的长是12厘米，宽是8厘米，在长方形内画一个最大的半圆，求这个半圆的弧长。
- 解析：因为长方形的长是12厘米，宽是8厘米，所以这个半圆的直径最大为12厘米。
半圆的弧长=(1)/(2)π d=(1)/(2)×3.14×12 = 18.84厘米。
北师大版六年级上册数学圆的周长和面积组合图形计算
专题01 圆的周长和面积（组合图形）注意事项：1．答题前，填写好自己的姓名、班级、考号等信息，请写在答题卡规定的位置上。
2．所有题目必须在答题卡上作答，在试卷上作答无效。
3．考试结束后将试卷和答题卡一并交回。
一．计算题（共20小题）1．计算下面图形阴影部分的周长和面积。
（单位：厘米）2．如图中，大圆的半径等于小圆的直径。
请计算阴影部分的周长。
3．计算下面图形的周长与面积。
4．计算下边图形的周长和面积。
5．计算如图形阴影部分的周长和面积。
（单位：dm）6．求下面各图中阴影部分的周长和面积。
（1）（2）7．求阴影部分的周长。
（单位：)cm8．计算图中阴影部分的面积。
（单位：)cm9．求阴影部分的周长。
10．求如图阴影部分的周长（单位：厘米）．11．求阴影部分的周长。
（大圆 4.5R =，小圆2r =，单位：)cm12．求图中形阴影部分的面积．（可以直接用π表示，也可以π取3.14)13．如图，求阴影部分的周长。
(π取3.14)14．计算右图的面积（单位：)dm 。
15．已知三角形的面积是29m，求圆的面积。
16．按要求计算下列各题。
（1）求图中图形的周长。
（2）求图中阴影部分的面积。
17．求阴影部分的面积：（单位：)cm18．求阴影部分的周长。
（单位：)cm19．求下列阴影部分的面积．20．求如图阴影部分面积。
（单位：厘米）专题01 圆的周长和面积（组合图形）答案解析一．计算题（共20小题）1．计算下面图形阴影部分的周长和面积。
（单位：厘米）【分析】根据题意，圆的直径为（4×3）厘米，阴影部分的周长等于圆的周长的一半加上5条4厘米长的线段之和，利用圆的周长公式：C＝πd，代入数据即可求出阴影部分的周长；阴影部分的面积等于圆的面积的一半减去边长为4厘米的正方形面积，分别利用圆的面积和正方形的面积公式求出这两个图形的面积，再相减即可得解。
××÷+×【解答】3.14(43)245×÷+＝3.1412220+＝18.8420＝38.84（厘米）2××÷÷−×3.14(432)244＝2×÷−3.146216×÷−＝3.1436216−＝56.5216＝40.52（平方厘米）即阴影部分的周长是38.84厘米，面积是40.52平方厘米。
第五单元不规则或组合图形的周长“拓展型”专项练习(解析版)人教版
2023-2024学年六年级数学上册典型例题系列第五单元：不规则或组合图形的周长“拓展型”专项练习一、图形计算。
【分析】1(1) (2)（1）（2）二、解答题。
10．如图，是篮球场的一部分。
篮球场上的3分线是由两条平行线和一个半圆组成的。
请你根据图中的数据计算出3分线的长度（图中粗线为3分线）。
（得数保留一位小数）【答案】24.3米【分析】观察图形可知，3分线的长度＝圆周长的一半＋2条平行线的长度；根据圆的周长公式C＝πd，代入数据计算即可。
【详解】3.14 6.7522 1.5752⨯⨯÷+⨯圈（接头不计）。
至少需要铁丝多少厘米？【答案】142.8厘米【分析】由图可知铁丝紧紧地捆绑一圈，最左边和最右边各一个半圆，上面的铁丝是2个直径，下面的铁丝是2个直径，所以总的长度实际上是由一个圆的周长加上4个直径的长度【详解】3.14×20＝62.8（厘米）4×20＝80（厘米）80＋62.8＝142.8（厘米）答：至少需要铁丝142.8厘米【点睛】此题考查了学生的观察能力以及求圆的周长的方法，熟练掌握圆周长的公式，并灵活掌握。
13．请用直尺和圆规画一个如图一模一样的图形（保留作图痕迹，不用涂色），并计算这个图形的周长。
【答案】见详解；12.56厘米【分析】根据题意，先确定大半圆圆心的位置，以2厘米为半径画一个大半圆，再把这个大半圆的直径平均分成4份，分别以左起第一份、第三份的末尾为圆心，以1厘米为半径画两个小半圆，一个在左上，一个在右下，据此画出与原图一样的图形。
观察图形可知，两个小半圆可以组成一个圆，这个图形的周长＝半径为2厘米的大半圆周长的一半＋半径为1厘米的圆的周长；根据圆的周长公式C＝2πr ＝πd，代入数据计算即可。
【答案】42.98厘米【分析】绳子的总长度由两部分组成，曲线部分绳子的长度刚好等于直径为7厘米圆的周长，直线部分绳子的长度是直径的3倍，需要绳子的长度＝圆的周长＋直径×3，据此解答。
六年级上册数学教案-第九讲组合图形的周长与面积人教版
六年级上册数学教案第九讲组合图形的周长与面积人教版教学内容本讲主要介绍组合图形的周长与面积的计算方法。
学生需要掌握组合图形的构成，理解组合图形可以分解为简单的几何图形，如三角形、矩形、圆形等。
学生需要学习如何计算组合图形的周长和面积，包括分解图形、计算各部分周长和面积、求和等步骤。
本讲还将介绍一些常见的组合图形的周长与面积的求解技巧和注意事项。
教学目标1. 理解组合图形的构成，能够将组合图形分解为简单的几何图形。
2. 学会计算组合图形的周长和面积，能够熟练运用相关公式和定理。
3. 掌握一些常见的组合图形的周长与面积的求解技巧和注意事项。
4. 培养学生的观察能力、分析能力和解决问题的能力。
教学难点1. 如何正确地将组合图形分解为简单的几何图形。
2. 如何准确地计算组合图形的周长和面积，特别是涉及到多个几何图形的情况。
3. 如何灵活运用求解技巧和注意事项，解决实际问题。
教具学具准备1. 教师准备：组合图形的模型或图片，用于讲解和演示。
2. 学生准备：直尺、圆规、计算器等学习工具。
教学过程1. 导入：通过展示一些组合图形的图片或模型，引起学生的兴趣和好奇心，激发他们的学习欲望。
2. 讲解：讲解组合图形的构成，如何分解为简单的几何图形，以及如何计算组合图形的周长和面积。
通过示例和练习，让学生理解和掌握相关的概念和计算方法。
3. 练习：让学生进行一些练习题，巩固所学知识，提高计算能力。
同时，教师可以给予指导和解答，帮助学生解决遇到的问题。
4. 应用：通过解决实际问题，让学生将所学知识应用到实际中，提高解决问题的能力。
同时，教师可以给予指导和评价，帮助学生提高解题能力。
板书设计1. 组合图形的周长与面积2. 内容：包括组合图形的构成、分解方法、周长和面积的计算公式、示例和练习题等。
作业设计1. 基础题：计算给定组合图形的周长和面积。
2. 提高题：解决实际问题，应用所学知识。
3. 挑战题：探索一些特殊的组合图形的周长和面积的计算方法。
六年级圆的组合图形阴影面积与周长计算
例1.求阴影部分的面积。
(单位:厘米)例2.正方形面积是7平方厘米，求阴影部分的面积。
(单位:厘米)例 3.求图中阴影部分的面积。
(单位:厘米)例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米)例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？例7.求阴影部分的面积。
(单位:厘米)例8.求阴影部分的面积。
(单位:厘米) 例9.求阴影部分的面积。
(单位:厘米) 例10.求阴影部分的面积。
(单位:厘米) 例11.求阴影部分的面积。
(单位:厘米) 例12.求阴影部分的面积。
(单位:厘米)例13.求阴影部分的面积。
(单位:厘米)例14.求阴影部分的面积。
(单位:厘米)例15.已知直角三角形面积是12平方厘米，求阴影部分的面积。
例16.求阴影部分的面积。
(单位:厘米)例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)例18.求阴影部分的面积。
(单位:厘米)例19.正方形边长为2厘米，求阴影部分的面积。
例20.如图，正方形ABCD的面积是36平方厘米，求阴影部分的面积。
例21.如图，正方形边长为8厘米，求阴影部分的面积。
例21.如图，三角形ABC是直角三角形，阴影部分甲比阴影部分乙面积大28平方厘米，AB=40厘米。
求BC的长度。
.例22求阴影部分的面积例23求阴影部分的周长与面积例24求阴影部分的周长与面积例25求阴影部分的周长与面积例26求阴影部分的周长与面积例27求阴影部分的周长与面积例28求阴影部分的周长与面积例29求阴影部分的面积例30求阴影部分的面积例31正方形面积是7平方厘米，求阴影部分的面积和周长。
(单位:厘米)例32求图中阴影部分的面积和周长。
(单位:厘米)例33求图中阴影部分的面积和周长。
(单位:厘米)例34求图中阴影部分的面积和周长。
(单位:厘米)例35求图中阴影部分的面积和周长。
(单位:厘米)例36求图中阴影部分的面积和周长。
六年级数学 分数应用题及组合图形的周长与面积的计算
六年级数学上册校本教材（B ）班级： 姓名：训练内容：分数应用题及组合图形的周长与面积的计算。
知识要点：1、灵活掌握分数与比的应用题的解题技巧；2、巧解组合图形部分的周长及面积；典型例题：有两根蜡烛，一根长8cm ，另一根长6cm ，把两根都燃烧掉同样长的一部分后，短的一根剩下的长度是长的一根剩下的35 。
每段燃掉多少厘米?解题思路：这两根蜡烛的差没有变。
两根都燃掉同样长的一部分，两根燃烧后的长度都相差8-6=2（厘米），2厘米相当于长的一段所剩的1-35 =25 ，（8-6）÷（1-35 ）=5（厘米）8-5=3（厘米） 答：每段燃掉3厘米。
巩固练习1、上层书架上有40本书，下层书架上有30本书。
从两层书架上取同样本数的书以后，下层书架上剩下的书是上层书架上所剩书的本数的35 。
每层书架上各取走多少本书？2、上下两层书架放书本数之比为4：3。
如果从上层取出80本放到下层，则本数之比为4：5。
那么上、下两层书架现在分别放有图书多少本？3、甲乙两车分别从A 、B 两地同时相对而行，甲车每小时行40千米，乙车每小时行45千米，当甲行了全程的25 时，乙车离中点还有8千米，A 、B 两地相距多少千米？（提示：当行驶时间相同时，两车行驶的路程比等于它们的速度比）4、甲、乙两根绳子共长22米，甲绳截去15后，乙绳和甲绳的长度比是3:2，甲、乙两根绳原来各长多少米？（2011年升中试题）5、6、求阴影部分的周长和面积。
7、把一个圆平均分成若干等份后，能拼成一个周长为20.7分米的长方形，这个圆的面积是多少？8、一种压路机的前轮直径是2.5米，前轮每分钟转5周，它每分钟前进多少米？如果压路机车轮的宽度是2.2米，则10分钟压路机压过的路面时多少平方米？9、一块长方形铁片，长50厘米，宽40厘米，剪下最大直径的圆盘后，还剩下多少平方厘米？剩下的铁片还能剪出几个直径是10厘米的圆盘？8163。
组合图形的面积周长计算
组合图形的面积周长计算
组合图形
1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
（单位：厘米）②圆的
周长是18.84cm，求阴影部分面积。
③长方形的面积和圆的面积相等，已知圆④求直角
三角形中阴影部分的面积。
的半径是3cm，求阴影部分的周长和面积。
（单位：分米）
⑤下图中长方形长6cm，宽4cm，已知阴影⑥图中阴
影①比阴影②面积小48平方厘米，
①比阴影②面积少3cm2，求EC的长。
AB=40cm，求BC的长。
⑦平行四边形的面积是30cm2，⑧一个圆的半
径是4cm，求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm，AD=12cm，三角形ABE和三角形ADF的面积，
各占长方形ABCD的1/3，求三角形AEF的面积。
⑩梯形上底8cm，下底16cm，阴影⑾求阴
影部分面积。
（单位：cm）
部分面积64cm2，求梯形面积。
⑿梯形面积是48平方厘米，阴影部分比空白⒀阴影部分比空白部分大6cm2，求S阴。
部分12平方厘米，求阴影部分面积。
3、求下列图形的体积。
（单位：厘米）。
6年级上册数学圆形组合图形周长和面积计算图形汇总
6-组合图形周长长方形周长=
正方形周长=
圆的周长=
【方法】1、数边2、爱拼才会赢 3.加法
【隐藏完整圆】求阴影部分周长
单位：dm单位：m
单位：dm
单位：m
单位：m
2、求下图的周长（单位：米）
【二分之一圆
】求阴影部分周长
←6dm
6dm
2cm
单位：m
单位：cm
单位：cm 单位：cm
单位：cm
【四分之一圆
】求阴影部分周长
cm
单位：cm
单位：cm
单位：cm
6-4组合图形面积
【基础准备】1、图形面积公式2、求不完整面积的方法
【拼凑变完整】求阴影部分面积。
2cm
单位：cm
【陈年旧事】
计算下面图形面积。
单位：cm
单位：m
【挖空图：大减小】求阴影部分的面积。
单位：m
单位：cm
【叶子形：对半分】求阴影部分面积（单位：厘米）。
cm。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 1 2 3.14 3 ＋2 3.14 （2＋3） ＋2＋2 4 4 4.71 ＋7.85 ＋4 16.56
2. 半径为5的圆周长的四分之一
1 2 3.14 (2＋3) 4
将半径分别为3厘米和2厘米的两个计算
一个运动场，它的两头是 半圆形，中间是长方形，小 明沿着这个运动场跑2周。 请你算一算跑了多少米？
阴影部分周长包括哪几个部分？
3.14×15÷2＋3.14×10÷2＋3.14×5÷2 =23.55＋15.7＋7.85 =47.1
计算下面阴影部分的周长 2. 直径为10的圆周长的一半 3.14×10÷2
1. 直径为15的圆周长的一半
3. 直径为5的圆周长的一半 3.14×5÷2
3.14×15÷2
从图中你能发现这个图形有什么特点？
组成阴影部分的四条曲线合起来是一个直 径为8的圆的周长 3.14×8=25.12
阴影部分周长包括哪几个部分？
1. 半径为3的圆周长的四分之一
1 2 3.14 3 4