5.3 非平衡载流子的扩散运动与爱因斯坦关系
载流子的迁移率、扩散系数和Einstein关系

载流子的迁移率、扩散系数和Einstein关系2009-11-02 20:25:18| 分类:微电子物理| 标签:|字号大中小订阅作者:Xie M. X. (UESTC,成都市)* 载流子的迁移率μ是表征载流子在电场作用下加速运动快慢的一个物理量,等于单位电场作用下的漂移速度:μ=vd/E [cm2/V-s],E为电场[V/cm],vd为平均漂移速度[cm/s]。
载流子迁移率的大小决定于在运动过程中遭受散射的情况:μ=qt/m*,t是散射时间(等于散射几率的倒数,在简单情况下就是平均自由时间),m*是有效质量,q为电子电荷。
注意:由于载流子的平均漂移速度是定向运动,是一它总是小于混乱的热运动速度(室温下载流子的热运动速度大约为107cm/s)。
浓度为n、迁移率为μ的电子,在电场E作用下,所产生的漂移电流密度为:j=nqμE,即漂移电流密度与载流子浓度成正比。
因此,多数载流子对漂移电流的贡献是主要的。
* 载流子的扩散系数D是表征载流子在浓度梯度驱动下、从高浓度处往低浓度处扩散运动快慢的一个物理量,等于单位浓度梯度作用下的粒子流密度,单位为[cm2/s]。
扩散系数为D的电子,在浓度梯度为dn/dx的驱动下,所产生的扩散电流密度为:j=qD(dn/dx),即扩散电流密度与载流子浓度梯度成正比,而与载流子浓度本身的大小无关。
因此,即使是少数载流子,只要它具有较大的浓度梯度,则也可以尝试较大的电流。
* Einstein关系:因为载流子的迁移率和扩散系数都是表征载流子运动快慢的物理量,所以迁移率和扩散系数之间存在有正比的关系——Einstein关系。
载流子按能量分布的规律不同,则将得到不同的Einstein关系。
对于非简并半导体,载流子遵从Boltzmann分布,即可得到简单的Einstein 关系:D=(kT/q)μ;但是对于简并半导体,载流子遵从Fermi-Dirac分布,则将得到比较复杂的Einstein关系。
半导体物理第五章教材

➢ 光照停止时,半导体中仍然存在非平衡载流子。由于电子 和空穴的数目比热平衡时的增多了,它们在热运动中相遇 而复合的机会也将增大。这时复合超过了产生而导致一定 的净复合,非平衡载流子逐渐消失,最后恢复到平衡值, 半导体又回到了热平衡状态。
13
思考题
1. 掺杂、改变温度和光照激发都可以改变半导体的 电导率,试从三者的物理过程说明其区别。
nt0 Nt f(Et)1expNEttk0TEF 45
用半导体的光磁电效应的原理,该方法适合于测量短的寿 命,在砷化镓等Ⅲ-Ⅴ族化合物半导体中用得最多; ✓还有扩散长度法、双脉冲法及漂移法等。
不同的材料寿命很不相同。纯度和完整性特别好硅、锗 材料,寿命分别可达103μs、104μs;砷化镓的寿命极短,约为 10-5~10-6μs,或更低。即使是同种材料,在不同的条件 下,寿命也可在—个很大的范围内变化。
电子在导带和价 带之间的直接跃 迁,引起电子和 空穴的直接复合
电子和空穴通过 禁带的能级(复合 中心)进行复合
27
28
二、非子复合时释放能量的方式
非平衡载流子复合时释放能量的方式有三种: ➢ 发射光子:伴随着复合,将有发光现象,常称为发光复合
或辐射复合; ➢ 发射声子:载流子将多余的能量传给晶格,加强晶格的振
nt0 Nt f(Et)1expNEttk0TEF
41
n1 Nc expEtk0TEc
费米能级EF与复合中 心能级Et重合时导带
的平衡电子浓度
srnNcexpEtk 0TEcrnn1 Gn snt
内在 联系
Gn rnn1nt
42
(二) 空穴俘获与发射
1.俘获空穴 电子由复合中心能级Et落入价带与空穴复合,或者说复合
半导体物理课件 (6)非平衡载流子

p
0
p(x) Ae1x Be2x
L2p2 Lp ( ) 1 0
Lp ( )
L2p ( ) 4L2p
2L2p
1 Lp ( )
L2p ( ) 4L2p
2L2p
0
2
Lp ( )
L2p ( ) 4L2p
2L2p
0
对很厚的样品: p() 0
x ,
0 Ae1 Be2
A=0, p(x) Be2x
(1) 表面粗糙度 (2) 表面积与总体积的比例 (3) 与表面的清洁度、化学气氛有关 在考虑表面复合后,总的复合几率为:
1 1 1
v s
§5.4 陷阱效应
一、陷阱效应的类型
● 对于 rn rp 的杂质,
电子的俘获能力远大于俘获空穴的能力, 称为电子陷阱。
● 对于 rp rn 的杂质,
俘获空穴的能力远大于俘获电子的能力,
当复合达到稳态时
ui rn (Nt nt )n rnn1nt
其中:nt为复合中心的电子浓度
nt
N t (rn n rp p1 ) rn (n n1 ) rp ( p
p1 )
ui
rn (n
rn rp N t n1 ) rp ( p
p1 )
(np
n1 p1 )
其中:
Ec Et
n1 Nce KT
Et Ev
p1 N v e KT
ui
rn (n
N t rn rp n1 ) rp ( p
p1 )
(np
ni2 )
热平衡时
n p n0 p0 ni2
ui 0
非平衡态时
n n0 n
p p0 p
p n nt
载流子的漂移扩散爱因斯坦关系式

公式推导
当v增大到一定值时,a=0,此时载流子做匀速运动,速度不再增大。
根据以上推导,得到爱因斯坦关系式:v=u√(2kT/m),其中v为载流子速度,u为电 场迁移率,T为温度。
公式含义
爱因斯坦关系式表明了载流子 在电场中的运动速度与温度和
迁移率的关系。
当温度升高时,载流子速度 增大;当迁移率增大时,载
流子速度也增大。
该公式是半导体物理中的基本 公式之一,对于研究半导体器 件的性能和应用具有重要意义。
公式应用
1
爱因斯坦关系式可以用于计算半导体器件中的电 流和电压关系。
2
通过测量不同温度下的电流和电压数据,可以计 算出迁移率和温度系数等重要参数。
浓度
载流子浓度对漂移扩散的影响主要体现在费米能级和能级填 充上。在低浓度时,费米能级附近的能级较少,载流子容易 达到较高的漂移速度。
随着浓度的增加,费米能级附近的能级增多,载流子的平均 自由程减小,漂移速度降低。同时,浓度还影响扩散系数的 大小,浓度越高,扩散系数越大。
电场
电场对载流子漂移扩散的影响主要体现在电场对载流子的加速作用上。在电场的作用下,载流子获得加速度,导致其漂移速 度增加。
新理论的发展
要点一
量子力学与半经典理论的结合
在研究具有复杂能带结构的材料时,将量子力学与半经典 理论相结合,可以更准确地描述载流子的行为,为载流子 漂移扩散的研究提供更可靠的理论基础。
要点二
多尺度模拟方法
随着计算机技术的发展,多尺度模拟方法逐渐成为研究复 杂电子器件的有力工具,通过模拟不同尺度下的载流子行 为,可以更全面地理解载流子的漂移扩散过程。
半导体物理-第五章非平衡载流子

注入:通过外场产生过剩
载流子
np>ni2
抽取:通过外加电压使得
载流子浓度减小 UESTC Nuo Liu
np<ni2
当非平
衡载流子的
浓度△n和
△p《平衡多
子浓度时,
这就是小注 入条件。
p0 p n n0 (n型半导体) n0 p n p0 ( p型半导体)
EFn EF
和 e k0T
EFp Ev
p Nve k0T
p0
EF Ev
Nve k0T
EF EFp
e k0T
而 n n0 n n0 1
EFn EF
n0
n0
n0
EFp
p p0 p p 1
p0
p0
p0
所以 n p
n0 p0
即
E
n F
EF
EF EFp
e k0T e k0T
即
E
Up
非平衡空穴的复合率
1
n
n
Un
非平衡电子的复合率
则在单位时间内非平衡载流子的减少数 dpt
dt
而在单位时间内复合的非平衡载流子数 p
p
UESTC Nuo Liu
如果在t 0时刻撤除光照,小注入下的复 合过程是一个驰豫过程,此复合过程满足
为常数
dpt p 1
dt
p
解方程1得到
同理也有 UESTC Nuo Liu
n F
-
EF
EF
E
p F
UESTC Nuo Liu
对P型半导体,在小注入下,有
Ec
EFn - EF EF EFp
半导体物理基础4
5.5 非平衡载流子的扩散(Diffusion)运动
(1)扩散运动与扩散电流(diffusion current)
考察p型半导体的非少子扩散运动
沿x方向的浓度梯度 dn dx
电子的扩散流密度
(单位时间通过单位 截面积的空穴数)
Sn x
dn dx
Sn x dnx
dx
Sn x
Dn
dn dx
扩散定律
价带空穴增加,意味 着EF更靠近EV。
引入准费米能级:
EC EFn
n NCe k0T
EFp EV
p NV e k0T
EFn EFP
np n0 p0e k0T
EFn
E
P F
ni2e k0T
非平衡态时,
np ni2
5.3. 非平衡载流子的衰减 寿命
若外界条件撤除(如光照停止),经过一段时间后, 系统才会恢复到原来的热平衡状态。有的非子生存时间长、 有的短。非子的平均生存时间称为非子的寿命τ。
n(
x)
(n)(0 1
x W
)
相应的 Sn=常数
❖ 扩散电流密度
电子的扩散电流密度
J n扩
qSn x
qDn
dnx
dx
空穴的扩散电流密度
J
p扩
qSp x
qDp
dpx
dx
J n扩
qSn x qDn
dnx q
dx
Dn Ln
x
n0 e Ln
q
Dn Ln
nx
J p扩
qSp x qDp
dpx q Dp
n, p noneguilibrium carriers
excess carries (过剩载流子)
半导体物理与器件 第五章非平衡载流子解读
D p
d 2p dx 2
p
Dn
d 2n dx 2
n
但p( x)、n( x)仍是空间x的函数
上述两个方程的解:
p(x) Aexp( x ) B exp( x )
Lp
Lp
n(x) C exp( x ) B exp( x )
Ln
Ln
Lp Dp p 空穴扩散长度 Ln Dn n 电子扩散长度
第五章非平衡载流子
5.1非平衡载流子的注入与复合 5.2 非平衡载流子的寿命 5.3准费米能级 *5.4复合理论 *5.5 陷阱效应 5.6 载流子的扩散方程 5.7 载流子的漂移运动,爱因斯坦关系式 5.8 连续性方程
5.1非平衡载流子的注入与复合
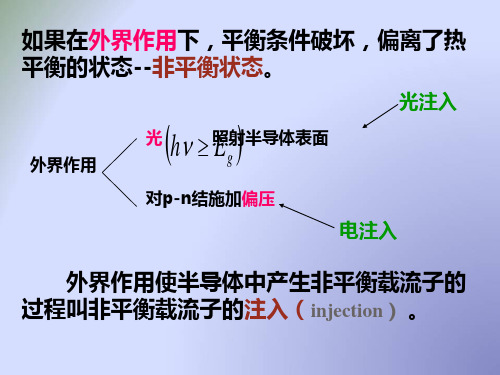
过剩载流子的产生: ①光注入
光照使半导体产生非平衡载流子
光照
1
1
0
2 0
R
L S
l
s
2 0
V IR p
半导体R1
V R2>>R1
5.1非平衡载流子的注入与复合
②电注入:
二极管加正向电场,n区的 电子扩散到p区,p区的空穴 扩散到n区
p
n
P区
p n
p0 n0
p n
n区
p n
p0 p n0 n
加反向电场,少子抽取,n区空穴飘移到p区,p 区的电子飘移到n区
5.1非平衡载流子的注入与复合
光生过剩电子和过剩空穴的浓度 非平衡载流子通常指非平衡少数载流子
5.1非平衡载流子的注入与复合
非简并半导体,处于热平衡时,电子浓度n0,空穴
浓度P0
Eg
n0 p0 ni2 Nc Nve k0T
如果对半导体施加外界作用,半导体处于非平衡状
半导体物理基础(5)扩散运动
在光照和外场同时存在的情况下:
J总 J n J p
(3) Einstein Relationship(爱因斯坦关系)
D
k 0T q
平衡条件下:
J p漂 J p扩 0
当W<<Ln时,
x n( x) (n)( ) 0 1 W
相应的 Sn=常数
扩散电流密度
电子的扩散电流密度
dnx J n 扩 qS n x qDn dx
空穴的扩散电流密度
dp x J p 扩 qS p x qD p dx
Dn dnx n0 e J n 扩 qSn x qDn q dx Ln
5.5 非平衡载流子的扩散(Diffusion)运动
(1)扩散运动与扩散电流(diffusion current)
考察p型半导体的非少子扩散运动 沿x方向的浓度梯度
电子的扩散流密度
dn dx
S n x
(单位时间通过单位 截面积的电子数)
dn S n x dx
dn x dx
x Ln
Dn q nx Ln
Dp dpx p 0 e J p 扩 qS p x qDp q dx Lp
x Lp
q
Dp Lp
px
(2)总电流密度
dnx J n J n漂 J n扩 qn n qDn dx
J p漂 qp ( 0 x) p
dp0 x J p 扩 qS p x qD p dx
qp ( 0 x) p
半导体物理第5章非平衡载流子
热平衡态: 产生率等于复合率,△n =0; 外界作用: 非平衡态,产生率大于复合率,△n 增大; 稳定后: 稳定的非平衡态,产生率等于复合率,△n 不变; 撤销外界作用: 非平衡态,复合率大于产生率,△n 减小; 稳定后 : 初始的热平衡态(△n =0)。
2. 非平衡载流子的检验
费米能级相同的原因:
半导体处于热平衡状态,即从价带激发 到导带的电子数等于从导带跃迁回价带的电子 数,使得导带中的电子的费米能级和和价带中 空穴的费米能级产生关联,即相等。
从而使得电子和空穴的浓度满足:
np
NC
NV
exp-
Eg K0T
=n
2 i
当半导体处于非平衡态时,有附加的载流 子产生。此时电子和空穴间的激发和复合的 平衡关系被破坏,导带中的电子分布和价带 中的空穴分布不再有关联,也谈不上它们有 相同的费米能级。
可见,EF和n E的Fp 偏离的大小直接反映出 (n或p )
与 相n0差p0的程度n,i2 即反映出半导体偏离热平衡
态的程度。
若两者靠得越近,则说明非平衡态越 接近平衡态。
对于n型半导体,准费米能级偏离平衡费米能级 示意图如下图所示:
EC
EF
EFn
EFp
特点:
EV
E
n F
- EF
EF
EFp
课堂练习5 证明对于n型半导体,准费米能级偏离平衡费米能级满足
恢复平衡态 产生率=复合率
n0、p
不变
0
非平衡载流子复合过程的两种基本形式:
直接复合: 电子在导带和价带之间直接跃迁而产生复合
间接复合:
Ec
电子和空穴通过禁带的能级进行复
5.6 载流子的扩散运动(雨课堂课件)
The end
拉普拉斯方程在球坐标系中的表达式
1 r2
r 2 r
u r
1
r 2 sin
s in
u
r
2
1 sin
2
2u
2
0...9.1.1
z
r
y
x
二阶常系数齐次线性微分方程的解
y py qy 0
特征方程r 2 pr q 0的两根r1 , r2 微分方程的解
两个不相等的实根r1, r2
因此,单位时间单位体积内由于扩散积累的空穴数为
dSp x
dx
又因为
dp x
S p Dp dx
所以,单位时间单位体积内由于扩散积累的空穴数为
dSp
dx
x
Dp
d
2p
dx2
x
(5-80)
一、非平衡载流子的扩散运动、扩散电流—浓度梯度
➢ 单位时间单位体积内由于复合而消失的空穴数: p x
其中 是非平衡载流子平均寿命。
研究对象:均匀掺杂的n型半导体中的非平衡少子Δp
扩散运动:表面光照,表面处
产生非平衡载流子(Δn, Δp),浓度
不均匀,引起扩散。一维
目标:非平衡载流子的变化规 律;扩散运动产生的电流
一维
图5-13 非平衡载流子的扩散
一、非平衡载流子的扩散运动、扩散电流—浓度梯度
(1) 非平衡少数载流子-空穴的扩散运动
两个不相等的实根r1, r2
y c1er1x c2er2x
两个相等的实根r1 r2
y c1 c2 x er1x
一对共轭复根r1,2 i
y ex c1 cos c2 sin
一、非平衡载流子的扩散运动、扩散电流—浓度梯度
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.3 载流子的扩散运动与爱因斯
坦关系式
n 适当波长的光照射样品的一侧,引起非平衡载流子由表面向内部扩散。
n 扩散运动是非平衡载流子的主要运动形式之一。
均匀掺杂的半导体,处于热平衡状态时,不产生扩散运动。
1. 一维平面扩散
空穴扩散系数,表示在单位浓度梯度下,单位时间内通过
单位面积的空穴数目;
反映了非平衡少子扩散能力的强弱; 负号表示扩散由高浓度向低浓度方向进行。
()()p p
d p x S x D dx
∆=-扩散流密度空穴扩散流密度:
扩散定律
——单位时间由于扩散通过垂
直于x 轴单位面积的载流子数。
(1)稳态扩散方程
()()p
p τx Δp dx x Δp d D =2
2
空穴的积累率等于复合率:
积累率复合率
稳态扩散方程
在恒定光照下,非平衡载流子的分布不随时间变化,形成稳定分布,这种情况称为稳定扩散。
()()
()()
2
p p p p
2
Δx S x S x Δx dS x d Δp x lim
D Δx
dx
dx
→-+=-
=空穴的积累率为:
p p p τD L =(2)稳态扩散方程的解
,系数A 和B 要根据边界条件确定。
()p
p
L x L x Be
Ae
x Δp +=-①样品足够厚
Δp (∞)→0
Δp (0)=(Δp )0边界条件:
解出:
A=(Δp )0B =0
()()p
L x e
Δp x Δp -=0空穴扩散长度
非平衡载流子浓度浓度由降低到所经过的距离。
()0p ∆()e
p 0
∆反映了非平衡载流子因扩散而深入样品的平均距离。
空穴的扩散流密度:
()()()
p
p p
p
D d p x S x D p x dx
L ∆∆=-=具有速度的量纲
称为空穴的扩散速度
()e
p 0
∆p
L
可得到:
②样品厚度为W ,且在另一端全部抽出
若
p W L <<()()01x Δp x p W ∆⎛
⎫≈- ⎪⎝
⎭
()()()0
00
p p p W ∆=∆⎧⎪⎨
∆=⎪⎩边界条件:当样品厚度很薄时,非平衡载流子在样品内呈线性分布。
则:()()⎪⎪⎭
⎫ ⎝⎛⎪
⎪⎭⎫
⎝⎛-∆=∆p p L W L x W p x p sh sh 0
扩散流密度:
()()()
p p p p
D d p x S x D p S dx
W
∆∆=-==在晶体管结构中,基区宽度比扩散长度小得多,从发射区注入基区的非平衡载流子在基区的分布近似符合上述结果。
是常数,说明非平衡载流子来不及复合就扩
散到了样品的另一端。
若
p W L <<()()0x Δp x p 1W ∆⎛
⎫≈- ⎪
⎝⎭
电子和空穴的扩散电流密度:
()()n n d n x S x D dx
∆=-()
()2
n
2
n
d n x n x D dx
τ∆∆=
对p 型半导体中的非平衡电子可做同样的讨论:电子的扩散流密度: 稳态扩散方程:
电子扩散系数
()
()dx
x p d qD qS J p
p Dif
p ∆-==()()dx
x n d qD qS J n
n Dif
n ∆=-=
2.
球形(径向)扩散运动
22
p p
D d d p p
r r dr dr ∆∆τ⎛⎫= ⎪⎝⎭三维探针注入:探针尖陷入半导体表面形成半径为r 0半球面用球坐标表示扩散方程:
可解得:
()()⎪⎪⎭⎫ ⎝
⎛--
∆==∆p L r r r r p r r f p 000exp
在注入面处,沿径向的扩散流密度:
()0000p p pr p r r p D D d p S D p dr r L ∆∆=⎛⎫⎛⎫=-=+ ⎪ ⎪ ⎪⎝⎭⎝⎭径向运动引起的扩散()()0
0p p p D S p L ∆=
一维平面扩散,注入面的扩散流密度:
复合引起的扩散
径向扩散的效率比平面注入时的高,因为除
了复合引起的扩散(D p /L p )外,还存在由径
向运动引起的扩散(D p /r 0)。
3.爱因斯坦关系式
爱因斯坦关系:
反映了非简并情况下,载流子迁移率和扩散系数之间的关系。
反映了漂移运动和扩散运动之间的内在联系。
0n n D k T q μ=对于电子:
对于空穴:q T k D p p 0=μ爱因斯坦关系仅适用于非简并半导体。
Ø依据爱因斯坦关系,可以对电流密度表达式进行化简(1)均匀半导体
n型半导体加以均匀电场;
表面处光注入非平衡载流子
半导体内的总电流密度为:
n p J J J =+电子的总电流密度为:空穴的总电流密度为:()()0()n n n n n drf dif d n J J J n n q E qD dx μ∆=+=+∆+()()0()p p p p p drf dif d p J J J p p q E qD dx
μ∆=+=+∆-平衡电子和非平衡电子平衡空穴和非平衡空穴
⎪⎪⎭⎫ ⎝
⎛∆-+⎪⎪⎭⎫ ⎝⎛∆+=+=dx p d q T k pE q dx n d q T k nE q J J J p n p n 00μμ非平衡电子非平衡空穴
(2)非均匀半导体 总的电流密度为:
⎪⎪⎭
⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛+=+=dx dp q T k pE q dx dn q T k nE q J J J p n p n 00μμ式中:()()()()x p x p p x n x n n ∆+=∆+=00,n 型的非均匀半导体,平衡载流子浓度沿x 方向存在浓度差;沿x 方向对其施加均匀电场;表面处光注入非平衡载流子。
