人教版初一数学相反数1
人教版初一数学知识点总结
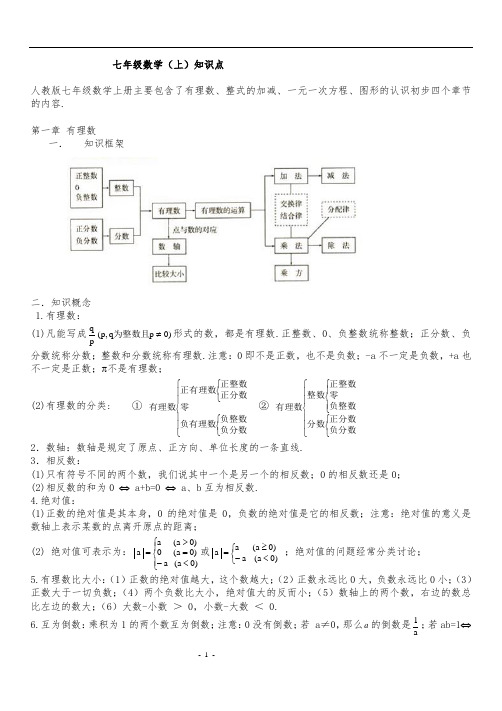
七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一. 知识框架二.知识概念 1.有理数: (1)凡能写成)0p q ,p (pq≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数 2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0; (2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数. 4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (aa ;绝对值的问题经常分类讨论;5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0. 6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a1;若ab=1⇔a 、b 互为倒数;若ab=-1 a 、b 互为负倒数. 7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值; (3)一个数与0相加,仍得这个数. 8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ). 10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘; (2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定. 11 有理数乘法的运算律: (1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc ); (3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a.13.有理数乘方的法则:(1)正数的任何次幂都是正数; (2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n ,当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n. 14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
人教版初一数学知识点总结

人教版初一数学知识点总结人教版七年级数学上册主要包含有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容。
其中第一章是有理数。
1.有理数有理数是指能够写成 p/q(p、q 为整数且p ≠ 0)形式的数,包括正整数、负整数、正分数、负分数以及零。
注意,π 不是有理数。
有理数可以分为零、正有理数、负有理数、正整数、负整数、正分数和负分数。
2.数轴数轴是一条带有原点、正方向和单位长度的直线。
3.相反数只有符号不同的两个数互为相反数,它们的和为零。
4.绝对值正数的绝对值是其本身,负数的绝对值是它的相反数。
绝对值的意义是数轴上表示某数的点离开原点的距离。
5.有理数比大小正数的绝对值越大,这个数越大。
正数永远比负数大,两个负数比大小,绝对值大的反而小。
在数轴上,右边的数总比左边的数大。
大数减去小数大于零,小数减去大数小于零。
6.互为倒数乘积为 1 的两个数互为倒数,如果a ≠ 0,则 a 的倒数是1/a。
7.有理数加法法则同号两数相加,取相同的符号,并把绝对值相加;异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;一个数与零相加,仍得这个数。
8.有理数加法的运算律加法的交换律:a+b=b+a;加法的结合律:(a+b)+c=a+(b+c)。
9.有理数减法法则减去一个数,等于加上这个数的相反数;即 a-b=a+(-b)。
10.有理数乘法法则两数相乘,同号为正,异号为负,并把绝对值相乘;任何数同零相乘都得零。
11.当几个数相乘时,如果有一个因式为零,那么积就为零;如果所有因式都不为零,那么积的符号由负因式的个数决定。
12.有理数除法的法则是,除以一个数等于乘以这个数的倒数。
但需要注意的是,零不能做除数,因为这是无意义的。
13.有理数乘方的法则包括以下两点:正数的任何次幂都是正数;负数的奇次幂是负数,偶次幂是正数。
此外,当n为正奇数时,(-a)n=-an或(a-b)n=-(b-a)n;当n为正偶数时,(-a)n=an或(a-b)n=(b-a)n。
2019学年新初一数学上(人教版)第一章《有理数》1.2.3 相反数(素材)

1.2.3相反数情景导入置疑导入归纳导入复习导入类比导入悬念激趣图1-2-21情景导入活动内容:(多媒体出示“南辕北辙”的图片)成语故事《南辕北辙》讲了一个人从魏国要到楚国去,楚国在南边,他硬要往北边走.他的马越好,赶车的本领越大,盘缠带得越多,走得越远,就越到不了楚国.1.如果点O表示魏国的位置,点A表示楚国的位置,我们假设楚国与魏国的距离为30 km,以魏国为原点,我们规定向南为正方向,而此人从魏国出发向北到了点B也走了30 km,请同学们把这3个点在数轴上表示出来.图1-2-222.你还能在数轴上表示出类似于A,B这样的点吗?[说明与建议] 说明:利用学生感兴趣的成语故事《南辕北辙》,培养学生的学习兴趣,激发求知欲,同时也让学生进一步加深对数轴的理解,表示30,-30的点与原点的距离相等,但方向相反,引出了相反数,为新课的导入做好铺垫.建议:首先用简短的成语故事《南辕北辙》激发学生的兴趣,然后让一名学生在黑板上画出数轴,将30,0,-30这3个数用数轴上的点表示出来,其余学生在练习本上完成.完成后教师引导学生复习数轴的三要素,加深学生对数轴的理解,体会用数轴上的点表示一个给定的有理数的方法.问题2由学生口答完成,让学生体会解决问题所用的数形结合的方法,从而引出新课.复习导入回答下列问题:问题1:如果支出50元记作-50元,那么收入50元记作什么?问题2:如果河道中的水位比正常水位高3厘米记作+3厘米,那么比正常水位低3厘米记作什么?比较上述问题中的两组数据,除了发现它们表示具有相反意义的量之外,你还有什么发现吗?[说明与建议] 说明:用正负数表示具有相反意义的量,并发现特殊的一对数,从而为本节课的学习做好铺垫.建议:引导学生通过类比的方法,完成上述两个问题的解答.然后教师总结这些问题的共性,即实际生活中存在着许多具有相反意义的量,因此产生了正数与负数,并且像+3与-3这样的一对数较为特殊,比较后发现两数只有符号不同,从而引出新课.悬念激趣一天,有理数王国的公民+1不小心掉进了一个魔瓶里.谁知出来后竟变成胖乎乎的0,你说怪不怪?冷眼旁观的2说:“谁叫这瓶里睡着他的相反数兄弟呢?幸好我没掉进去!”同学们,你想知道+1的相反数兄弟是谁吗?为什么他俩见面后就变成了0呢?就让我们一起走进神奇的相反数的世界吧![说明与建议] 说明:七年级的学生还是很可爱,很喜欢听故事的.所以这里通过小故事,激发同学们的兴趣,引入我们今天的学习内容——相反数.建议:先留给学生自主思考的时间,然后教师要引导学生进行分析,为进一步学习积累数学活动经验.教材母题——教材第10页练习第2题写出下列各数的相反数:6,-8,-3.9,,-,100,0.【模型建立】求一个数的相反数,可以在这个数的前面添一个“-”号.如-5的相反数可表示为-(-5),我们知道-5的相反数是5,所以-(-5)=5.【变式变形】1.-1的相反数是1;-2是2的相反数;-与互为相反数.2.-(-2)的相反数是-2.3.若-x=10,则x的相反数在原点的右侧;若x的相反数是-3,则x=3;若-x的相反数是-5.7,则x=-5.7.4.写出下列各数的相反数,并在数轴上把这些相反数表示出来:+2,-3,0,-(-1),-3,-(+2).[答案:-2,+3,0,-1,+3,+2在数轴上表示略]5.化简下列各数:(1)-(-100);(2)--5;(3)++;(4)+(-2.8);(5)-(-7);(6)-(+12).[答案:(1)100(2)5(3)(4)-2.8(5)7(6)-12][命题角度1] 求一个数的相反数在任意一个数的前面添上“-”号,就可以得到该数的相反数.其中0比较特殊,其相反数等于它本身.例如果a与-2互为相反数,那么a等于(B)A.-2B.2C.-D.[命题角度2] 相反数的数学意义相反数是成对出现的,且互为相反数的两个数的和为0.例已知x+y=0,则x与y(B)A.互为倒数B.互为相反数C.都为0D.以上均不正确[命题角度3] 多重符号的化简在一个数的前面添上“-”号,表示这个数的相反数;在一个数的前面添上“+”号,仍表示这个数本身.当a前面有偶数个“-”号时,结果为a;当a前面有奇数个“-”号时,结果为-a.例-(-2)等于 (B)A.-2B.2C.D.±2[命题角度4] 已知数轴上的点判断互为相反数的点给出数轴上的一些点,从中找出互为相反数的点,一般可以直接从各个点所代表的有理数判断,或从是否在原点的两侧并且到原点的距离相等进行判断.例如图1-2-23,数轴上的单位长度为1,有三个点A,B,C,若点A,B表示的数互为相反数,则图中点C表示的数是(C)图1-2-23A .-2B .0C .1D .4P10练习1.判断下列说法是否正确:(1)-3是相反数; (2)+3是相反数; (3)3是-3的相反数; (4)-3与+3互为相反数.[答案] (1)错误,相反数是成对出现的,单独的一个数不是相反数; (2)错误;(3)正确;(4)正确. 2.写出下列各数的相反数: 6,-8,-3.9,52,-211,100,0.[答案] -6,8,3.9,-52,211,-100,0.3.如果a =-a ,那么表示a 的点在数轴上的什么位置? [答案] 在数轴上的原点处. 4.化简下列各数:-(-68),-(+0.75),-⎝⎛⎭⎫-35,-(+3.8). [答案] 68,-0.75,35,-3.8.[当堂检测]1.-9的相反数是( )A .-91B .91C .-9D .92. 如果a 的相反数是2,那么a 等于( )A .-2B .2C .21D .- 213.下列说法:(1)-a是相反数,(2)a的相反数一定是负数, (3)a与-a互为相反数,(4)互为相反数的两个数符号一定相反, (5)互为相反数的两个数到原点的距离相等. 其中正确的有( ) A .一个B. 二个C. 三个D. 四个4.化简下列各数(1)-(- 4)=____,(2) – (+32)=____ ,(3) – [- (-5)]=______ .5. 已知数轴上点A 和点B 分别表示互为相反数的两个数a 、b (a <b ),并且A 、B 两点间的距离是10,求a ,b 两数。
相反数的表示

歸納: 數1-數2= 數1+ 數2的相反數
a - b = a + (-b)
將有理數的減法 變成加法去運算
結論: 有理數減法法則: 數1-數2=數1+數2的相反數 (文字表述)___________________________
a - b = a + ( -b ) (公式表述)___________________________
複習: 相反數
數
5 0 -8
相反數的表示
-(+5) 0 -(-8)
相反數
-5 0 8
b
-b
-b
有理數減法
設計一: 計算下列各式 3 5-2=ˍˍˍ 4 5-1=ˍˍˍ 5 5-0=ˍˍˍ 6 5-(-1)=ˍˍˍ 7 5-(-2)=ˍˍˍ 3 5+(-2)=ˍˍˍ 4 5+(-1)=ˍˍˍ 5 5+0=ˍˍˍ 6 5+(+1)=ˍˍˍ 7 5+(+2)=ˍˍˍ
(2) 2 Box -(-3 Box )=ˍˍˍˍˍˍˍˍ a+b -3 c + 2 a+b c (3) -3 a+b -(-2 a+b )=ˍˍˍˍ___ c c = - (3-2) a+b 〔提示:把 a+b 看成x〕 c c = - a+b c
預習: 計算27-18+(-7)-32的值 Q1) 以上算式中包含有有理數的甚麼運算? Q2) 我們可以怎樣計算出它的值? (即我們可以運用甚麼方法去求出它的值?) Q3) 以上算式的值應為多少呢?
觀察並發現: 5-2 5-1 5-0 = ______ 5+(-2) = ______ 5+(-1) = ______ 5+0
= 5-(-1) ______ 5+(+1) = 5-(-2) ______ 5+(+2)
初一数学绝对值与相反数课件

具备什么样特点的两个数才互为相反数呢?(小组讨论) 具备什么样特点的两个数才互为相反数呢?(小组讨论)
像+2与-2,+5与-5这样只有符号不同两个数叫做互为相反数
0的相反数是??
???
0的相反数是0。
2.分别说出9,-7,0,-0.2的相反数. 3.指出(--29.4,,7,,-01.,7,01.2各)是什么数的相反数? 4. a 的相反数是什么?
我怎么就变胖 了呢?
哈哈!我还 是我!
请两位同学背靠背,一人向前走5步,一人向后走5步。 如果向前为正,向前走5步,向后走5步,分别记作什么?
向前5步记作+5,向后5步记作-5。 +5与-5就叫做互为相反数。
你能在数轴上找两个点,使它们所代表的数互为相反数吗?
哈哈! 我来了。
我的相反数在 哪?
请同学们把自己最喜欢的数写给同桌,由他(她)写出这个数的绝对值。
小窍门:在写一个数的绝对值时,首先判断这个数是正数,负数,还是零,然后再选择相应法 则。
做一做
( 1 )在数轴上表示下列各数,并比较它们的大小: - 1.5 , - 3 , - 1 , - 5
( 2 ) 求出(1)中各数的绝对值,并比较它们的大小 ( 3 )你发现了什么?
在一个数前面加上“+”仍表示这个数,“+”号可省略.
想一想 数轴上表示相反数的两个点和原点有什么关系?
在数轴上表示相反数(0除外)的两个点位于原点的
,且与原点的距离 . 两侧
相等
课堂练习
1.-1.6是____的相反数,___的相反数是0.3.
2.下列几对数中互为相反数的一对为( ).
A. 和
B. 与
建立数学模型 规定
人教版初一上册数学知识点总结整理

这篇⼈教版初⼀上册数学知识点总结整理的⽂章,是特地为⼤家整理的,希望对⼤家有所帮助!1.有理数:(1)凡能写成形式的数,都是有理数,整数和分数统称有理数.注意:0即不是正数,也不是负数;-a不⼀定是负数,+a也不⼀定是正数; 不是有理数;(2)有理数的分类: ①②(3)注意:有理数中,1、0、-1是三个特殊的数,它们有⾃⼰的特性;这三个数把数轴上的数分成四个区域,这四个区域的数也有⾃⼰的特性;(4)⾃然数 0和正整数; a>0 a是正数; a<0 a是负数;a≥0 a是正数或0 a是⾮负数; a≤ 0 a是负数或0 a是⾮正数.2.数轴:数轴是规定了原点、正⽅向、单位长度的⼀条直线.3.相反数:(1)只有符号不同的两个数,我们说其中⼀个是另⼀个的相反数;0的相反数还是0; (2)注意: a-b+c的相反数是-a+b-c;a-b的相反数是b-a;a+b的相反数是-a-b;(3)相反数的和为0 a+b=0 a、b互为相反数.(4)相反数的商为-1.(5)相反数的绝对值相等4.绝对值:(1)正数的绝对值等于它本⾝,0的绝对值是0,负数的绝对值等于它的相反数;注意:绝对值的意义是数轴上表⽰某数的点离开原点的距离;(2) 绝对值可表⽰为:或;(3) ;;(4) |a|是重要的⾮负数,即|a|≥0;5.有理数⽐⼤⼩:(1)正数永远⽐0⼤,负数永远⽐0⼩;(2)正数⼤于⼀切负数;(3)两个负数⽐较,绝对值⼤的反⽽⼩;(4)数轴上的两个数,右边的数总⽐左边的数⼤;(5)-1,-2,+1,+4,-0.5,以上数据表⽰与标准质量的差,绝对值越⼩,越接近标准。
6.倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若ab=1 a、b互为倒数;若ab=-1 a、b互为负倒数.等于本⾝的数汇总:相反数等于本⾝的数:0倒数等于本⾝的数:1,-1绝对值等于本⾝的数:正数和0平⽅等于本⾝的数:0,1⽴⽅等于本⾝的数:0,1,-1.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较⼤加数的符号,并⽤较⼤的绝对值减去较⼩的绝对值;(3)⼀个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b)+c=a+(b+c).9.有理数减法法则:减去⼀个数,等于加上这个数的相反数;即a-b=a+(-b).10 有理数乘法法则:(1)两数相乘,同号得正,异号得负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)⼏个因式都不为零,积的符号由负因式的个数决定.奇数个负数为负,偶数个负数为正。
初一数学学科课程资源库相反数
相反数
翻转独学探究单
学习要求:1. 理解相反数的概念。
2. 会求一个数的相反数。
3. 会在数轴上表示两个相反数。
1.-9的相反数是()
2.写出互为相反数的一组数()
3.如果一个数的相反数是35,那么这个数是。
4.已知数轴上A、B表示的数互为相反数,并且两点间的
距离是6,点A在点B的左边,则点A、B表示的数分别是。
练一练:在纸上画出数轴,并用数轴上的点表示下列各数的其相反数
翻转课堂探究单
活动一:复习引入
引例:填空(请用正负数表示)
1.如果规定向东走为正,那么向东走5米表示为_____米;向西走5米应表示为___米。
2.若规定收入为正,那么收入10万元应表示为____万元;支出10元应表示为____万元。
3.某校初二男生测试引体向上,如果以5次为标准,超过标准的个数记为正数,不足标准个数记为负数,那么甲同学做7个应记录____个;乙同学做3个应记录____个。
活动二:总结归纳
+5和-5;+10和-10;+2和-2。
思考:观察以上三个问题中所填入的三对数,有什么共同特点?
总结:每对数都只有符号不同的数。
初一上数学课件(华东师大)-《相反数》
课堂小结 1.相反数的概念及表示方法. 2.相反数的代数意义和几何意义. 3.符号的化简.
-5
-2
+2
+5
- 5 -4 -3 -2 -1 0 1 2 3 4 5
三、新知探究 探究一:相反数 问题1:体验对称的图形的特点,为描述相反数在数轴上的特征作准备. 深化相反数的概念;“零的相反数是零”是相反数定义的一部分.强化互 为相反的数在数轴上表示的点的几何意义. 给出相反数的定义.
有两位同学背靠背,一人向前走5步,一人向 后走5步。
探究二:多重符号的化简 问题3:-(+5)和-(-5)分别表示什么意思?你能化简它们吗?
四、点点对接 例1:填空. (1)-5的相反数为________; (2)2m是________的相反数. 解析:(1)-5中去掉负号即可得其相反数; (2)在2m的前面加上负号即可得其相反数. 解:(1)5;(2)-2m.
例2 化简下列各数:
(1) -(+3);
(2) -(-2);
(3) -[-(-5)]; (4) -[-(+5)];
(5) -(-m);
(6) +(-a);
(7) -(a-b); (8) -(a+b).
分析 在一个数前面加上“+”号,所得数还是
原来的数;在一个数前ห้องสมุดไป่ตู้加上“-”号,表示求这
个数的相反数.如:(1)题表示求+3的相反数;
的相反数.
一般地,数a的相反数是-a,a可以是正数、 负数或0。
求一个数的相反数即在这个数的前面加上“—”号 。
规定:0的相反数是0, 即-0=0.
说明:(1)相反数是相对而言的,即6是-6的相反数,-6也是6的相反数.所 以说相反数是成对出现的.
初一数学上册教案1.2 相反数与绝对值(教师版)
个性化教学辅导教案——进门测评分_____1.★★(2015秋•龙岩校级月考)已知下列各数:﹣8、2.89、0、、﹣0.25、、.其中非负数有()A.1个B.2个C.3个D.4个【考点】12:有理数.【分析】有理数包括整数和分数,整数包括正整数、0、负整数,分数包括正分数和负分数,根据以上内容判断即可.【解答】解:非负数有2.89,0,,1,共4个.故选D.【点评】本题考查了有理数的定义的应用,能理解有理数的定义是解此题的关键,注意:有理数包括整数和分数,整数包括正整数、0、负整数,分数包括正分数和负分数.2.★★(2015秋•衡阳校级期中)下列说法正确的是()A.带有“+”号的数是正数B.带有“﹣”号的数是负数C.数轴上的两个点可以表示同一个有理数D.有理数分为自然数、负整数、分数【考点】12:有理数.【分析】根据有理数的分类,正数和负数的定义,有理数与数轴的关系,可得答案.【解答】解:A、大于零的数是正数,故A错误;B、小于零的数是负数,故B错误;C、数轴上每一个点表示一个有理数,故C错误;D、有理数分为自然数、负整数、分数,故D正确.故选:D.【点评】本题考查了有理数,利用了有理数的分类,注意数轴上的点与实数一一对应.3.★★(2017•邢台县模拟)如图,数轴上有A,B,C,D四个点,其中到原点距离相等的两个点是()A.点B与点D B.点A与点C C.点A与点D D.点B与点C【考点】数轴.【分析】根据数轴上表示数a的点与表示数﹣a的点到原点的距离相等,即可解答.【解答】解:由数轴可得:点A表示的数为﹣2,点D表示的数为2,根据数轴上表示数a的点与表示数﹣a的点到原点的距离相等,∴点A与点D到原点的距离相等,故选:C.【点评】此题主要考查了数轴,关键是掌握互为相反数的两个数,它们分别在原点两旁且到原点距离相等.4.★★★(2015秋•秀英区校级期中)数轴上的点A、B、C、D、O分别表示、﹣5、2、、0.(1)在如图所示的数轴上画出点A、B、C、D、O;(2)比较这五点所表示的数的大小,用“<”号连接起来;(3)有同学说:“B、D两点间的距离恰好是A、C两点间的距离的3倍”,你觉得这位同学的说法正确吗?请你作出判断,并说明理由.【考点】数轴;有理数大小比较.【分析】(1)把各点在数轴上表示出来即可;(2)从左到右用“<”把各数连接起来即可;(3)根据数轴上两点间距离的定义即可得出结论.【解答】解:(1)如图所示:;(2)由图可知,﹣5<﹣1<0<2<4;(3)错误.∵B、D两点间的距离是9,AC两点间的距离是3,∴BD≠3AC.【点评】本题考查的是数轴,熟知数轴上右边的数总比左边的数大的特点是解答此题的关键.1.★★(2017•新野县一模)﹣的相反数是()A.4B.﹣C.D.﹣4【考点】相反数.【分析】根据一个数的相反数就是在这个数前面添上“﹣”号,求解即可.【解答】解:﹣的相反数是,故选:C.【点评】本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号:一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.不要把相反数的意义与倒数的意义混淆.2.★★(2017•宁波模拟)﹣2的绝对值是()A.﹣2B.2C.D.﹣【考点】绝对值.【分析】根据绝对值的定义,可直接得出﹣2的绝对值.【解答】解:|﹣2|=2,故选:B.【点评】本题考查了绝对值的定义,是中考的常见题型,比较简单,熟记绝对值的定义是本题的关键.3.★★★若﹣x=﹣[﹣(﹣2)],求x的相反数.【考点】14:相反数.【分析】先根据多重符号的化简方法得出﹣[﹣(﹣2)]=﹣2,即﹣x=﹣2,即可求解.【解答】解:∵﹣x=﹣[﹣(﹣2)],∴﹣x=﹣2,即x的相反数为﹣2.【点评】本题考查了相反数的概念,多重符号的化简规律.用到的知识点:只有符号不同的两个数叫做互为相反数.求一个数的相反数的方法就是在这个数的前边添加“﹣”,a的相反数是﹣a.多重符号的化简:与“+”个数无关,有奇数个“﹣”号结果为负,有偶数个“﹣”号,结果为正.4.★★★已知|a﹣1|=﹣(a﹣1),求a的范围.【考点】绝对值.【分析】根据负数的绝对值等于它的相反数,零的绝对值是零得:a﹣1≤0,解出即可.【解答】解:因为|a﹣1|=﹣(a﹣1),所以a﹣1≤0,a≤1.【点评】本题考查了绝对值的意义,明确①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数﹣a;③当a是零时,a的绝对值是零.知识点一:相反数(1)相反数的概念:只有符号不同的两个数叫做互为相反数.(2)相反数的意义:掌握相反数是成对出现的,不能单独存在,从数轴上看,除0外,互为相反数的两个数,它们分别在原点两旁且到原点距离相等.例题:1.★★(2017•钦州一模)﹣5的相反数是()A.5B.﹣5C.D.【考点】相反数.【分析】根据只有符号不同的两个数互为相反数,可得一个数的相反数.【解答】解:﹣5的相反数是5,故选:A.【点评】本题考查了相反数,在一个数的前面加上负号就是这个数的相反数.2.★★★(2017•临沂模拟)若x=﹣7,则﹣x的相反数是()A.+7B.﹣7C.±7D.【考点】相反数.【分析】先根据x=﹣7求得﹣x=7,然后再来求7的相反数即可.【解答】解:﹣x的相反数是:﹣(﹣x)=x=﹣7.故选:B.【点评】本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号;一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.3.★★(2014秋•东西湖区校级月考)化简:(1)+(﹣0.5)(2)﹣(+10.1)(3)+(+7)(4)﹣(﹣20)(5)+[﹣(﹣10)](6)﹣[﹣(﹣)].【考点】相反数.【分析】(1)直接去括号化简求出即可;(2)直接去括号化简求出即可;(3)直接去括号化简求出即可;(4)直接去括号化简求出即可;(5)直接去括号化简求出即可.【解答】解:(1)+(﹣0.5)=﹣0.5;(2)﹣(+10.1)=﹣10.1;(3)+(+7)=7;(4)﹣(﹣20)=20;(5)+[﹣(﹣10)]=10;(6)﹣[﹣(﹣)]=﹣.【点评】此题主要考查了相反数的定义以及去括号法则,正确化简各数是解题关键.4.★★★若x+1是﹣9的相反数,求x的值.【考点】14:相反数.【分析】根据互为相反数的两个数的和等于0列出方程求解即可.【解答】解:∵x+1与﹣9互为相反数,∴x+1=9,解得x=8.【点评】本题考查了相反数的定义,熟记概念并列出方程是解题的关键.知识点二:绝对值(1)概念:数轴上某个数与原点的距离叫做这个数的绝对值.①互为相反数的两个数绝对值相等;②绝对值等于一个正数的数有两个,绝对值等于0的数有一个,没有绝对值等于负数的数.③有理数的绝对值都是非负数.(2)如果用字母a表示有理数,则数a 绝对值要由字母a本身的取值来确定:①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数﹣a;③当a是零时,a的绝对值是零.例题:1.★★(2016•泉州)﹣3的绝对值是()A.3B.﹣3C.﹣D.【考点】绝对值.【分析】计算绝对值要根据绝对值的定义求解.第一步列出绝对值的表达式;第二步根据绝对值定义去掉这个绝对值的符号.【解答】解:﹣3的绝对值是3.故选:A.【点评】此题主要考查了绝对值的定义,规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.2.★★(2017•临沂模拟)绝对值等于9的数是()A.9B.﹣9C.9或﹣9D.【考点】绝对值.【专题】计算题.【分析】根据绝对值的意义得|9|=9,|﹣9|=9.【解答】解:∵|9|=9,|﹣9|=9,∴绝对值等于9的数是9或﹣9.故选C.【点评】本题考查了绝对值:若a>0,则|a|=a;若a=0,则|a|=0;若a<0,则|a|=﹣a.【解答】解:∵|a|=5,|b|=4,∴a=±5,b=±4,∵a>b,∴a=5,b=4 或a=5,b=﹣4.【点评】本题考查了绝对值:当a>0,|a|=a;当a=0,|a|=0;当a<0,|a|=﹣a.1.★★(2017•天桥区一模)﹣的相反数是()A.B.C.D.【考点】相反数.【分析】根据只有符号不同的两个数互为相反数,可得一个数的相反数.【解答】解:的相反数是,故选:D.【点评】本题考查了相反数,在一个数的前面加上负号就是这个数的相反数.2.★★★(2017•长安区一模)比2的相反数小的是()A.5B.﹣3C.0D.﹣1【考点】相反数.【分析】根据一个数的相反数就是在这个数前面添上“﹣”号,求解即可.【解答】解:2的相反数是﹣2,比﹣2小的数是﹣3,故选:B.【点评】此题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号:一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.不要把相反数的意义与倒数的意义混淆.3.★★★(2017•金乡县一模)a(a≠0)的相反数是()A.﹣a B.a C.|a|D.【考点】相反数.【分析】依据相反数的定义解答即可.【解答】解:a(a≠0)的相反数是﹣a.故选:A.【点评】本题考查了相反数的定义,掌握相反数的定义是解题的关键.4.★★(2017•长春一模)﹣5的绝对值是()A.﹣B.5C.﹣5D.±5【考点】绝对值.【分析】绝对值的性质:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.【解答】解:根据负数的绝对值是它的相反数,得|﹣5|=5.故选B.【点评】此题考查了绝对值的知识,解题的关键是掌握绝对值的性质.5.★★(2014秋•本溪校级月考)化简:(1)﹣{+[﹣(+3)]};(2)﹣{﹣[﹣(﹣|﹣3|)}.【考点】相反数.【分析】根据只有符号不同的两个数互为相反数,可得一个数的相反数.【解答】解:(1)原式=﹣{+[﹣3]}=﹣{﹣3}=3;(2)原式=﹣{﹣[﹣(﹣3)]}=﹣{﹣[+3]}=﹣{﹣3}=3.【点评】本题考查了相反数,去小括号、中括号、大括号的顺序,得出答案.6.★★★化简下列各数:(1)﹣(﹣5)(2)﹣(+7)(3)﹣[﹣(+)](4)﹣[﹣(﹣a)](5)|﹣(+7)|(6)﹣|﹣8|(7)|﹣|+||(8)﹣|﹣a|(a<0)【考点】15:绝对值;14:相反数.【分析】(1)根据相反数定义求出即可;(2)根据相反数定义求出即可;(3)根据相反数定义求出即可;(4)根据相反数定义求出即可;(5)根据绝对值定义求出即可;(6)根据绝对值定义求出即可;(7)根据绝对值定义求出即可;(8)根据绝对值定义求出即可.【解答】解:(1)﹣(﹣5)=5;(2)﹣(+7)=﹣7;(3)﹣[﹣(+)]=;(4)﹣[﹣(﹣a)]=﹣a;(5)|﹣(+7)|=7;(6)﹣|﹣8|=﹣8;(7)|﹣|+||=;(8)﹣|﹣a|(a<0)=﹣(﹣a)=a.【点评】本题考查了绝对值,相反数的应用,注意:一个负数的绝对值等于它的相反数,一个正数的绝对值等于它本身,0的绝对值是0.7.★★★已知|3﹣2a|=5,求a的值.【考点】15:绝对值.【分析】根据绝对值的化简法则,化简求解.【解答】解:由题意得,3﹣2a=±5,解得:a=4或a=﹣1.【点评】本题考查了绝对值的知识,掌握绝对值的概念是解答本题的关键.8.★★★(2013秋•黔江区月考)已知4a﹣6与﹣6互为相反数,求a的值.【考点】14:相反数.【分析】根据互为相反数的两个数的和为0,可得一元一次方程,根据解一元一次方程,可得答案.【解答】解:4a﹣6与﹣6互为相反数,4a﹣6+(﹣6)=04a=12 a=3. 【点评】本题考查了相反数,互为相反数的两个数的和为0是解题关键.9.★★★如果|a |=1,|b |=5,且a >b ,求a ,b 的值.【考点】15:绝对值.【分析】先根据绝对值的性质分别解出a ,b ,然后根据a >b ,解出a ,b 的值.【解答】解:∵|a |=1,|b |=5,∴a=1或a=﹣1,b=5或b=﹣5.又∵a >b ,∴a=1或a=﹣1,b=﹣5.【点评】本题主要考查绝对值的意义,能够由绝对值的值求出这个数,并正确进行讨论.【规律方法】1. 多重符号的化简:与“+”个数无关,有奇数个“﹣”号结果为负,有偶数个“﹣”号,结果为正.2. 求相反数:求一个数的相反数的方法就是在这个数的前边添加“﹣”,如a 的相反数是﹣a ,m +n 的相反数是﹣(m +n ),这时m +n 是一个整体,在整体前面添负号时,要用小括号.3. 去掉绝对值:⎪⎩⎪⎨⎧<-=>=)0(,)0(,0)0(,a a a a a a——出门测 评分_____1.★★(2017•枝江市模拟)﹣的相反数是( )A .﹣3B .C .3D .﹣【考点】相反数.【分析】根据相反数的定义直接得出答案.【解答】解:﹣的相反数是.故选:B.【点评】本题考查了相反数的定义,掌握相反数的定义是解题的关键.2.★★(2017•宝丰县一模)计算:﹣(﹣1)=()A.1B.﹣1C.﹣2D.±1【考点】相反数.【分析】根据相反数的意义,可得答案.【解答】解:﹣(﹣1)=1,故选:A.【点评】本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号:一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.不要把相反数的意义与倒数的意义混淆.3.★★(2016•宿迁)﹣2的绝对值是()A.﹣2B.﹣C.D.2【考点】绝对值.【分析】计算绝对值要根据绝对值的定义求解.第一步列出绝对值的表达式;第二步根据绝对值定义去掉这个绝对值的符号.【解答】解:∵﹣2<0,∴|﹣2|=﹣(﹣2)=2.故选D.【点评】本题考查了绝对值的意义,任何一个数的绝对值一定是非负数,所以﹣2的绝对值是2.部分学生易混淆相反数、绝对值、倒数的意义,而错误的认为﹣2的绝对值是,而选择B.4.★★★(2016•顺义区二模)如图,数轴上有A,B,C,D四个点,其中表示互为相反数的点是()【分析】根据相反数的定义得到3x﹣3+(﹣15)=0,然后解一次方程即可.【解答】解:根据题意得3x﹣3+(﹣15)=0,解得x=6.【点评】本题考查了相反数:只有符号不同的两个数叫做互为相反数.8.★★★已知|x|=3,|y|=2,且x>y,求x和y的值.【考点】15:绝对值.【分析】利用绝对值得性质得出x,y的值,进而得出答案.【解答】解:∵|x|=3,|y|=2,∴x=±3,y=±2,∵x>y,∴当x=3,则y=2或﹣2.【点评】此题主要考查了绝对值,熟练应用绝对值的性质是解题关键.——课后作业1.★★(2017春•鄂州期中)|﹣8|的相反数是()A.﹣8B.8C.D.﹣【考点】绝对值;相反数.【分析】先根据绝对值的意义得到|﹣8|=8,然后根据相反数的意义求解.【解答】解:∵|﹣8|=8,而8的相反数为﹣8,∴|﹣8|的相反数为﹣8.故选:A.【点评】本题考查了绝对值:若a>0,则|a|=a;若a=0,则|a|=0;若a<0,则|a|=﹣a.也考查了相反数.2.★★(2017•合肥模拟)|﹣6|=()A.B.6C.﹣6D.±6【考点】绝对值.【分析】原式利用绝对值的代数意义计算即可得到结果.【解答】解:原式=6,故选B【点评】此题考查了绝对值,熟练掌握绝对值的代数意义是解本题的关键.3.★★(2016秋•太原期中)若|a|=6,则a的值等于±6.【考点】绝对值.【分析】直接利用绝对值的性质得出a的值,进而得出答案.【解答】解:∵|a|=6,∴a=±6.故答案为:±6.【点评】此题主要考查了绝对值的性质,正确利用绝对值的性质得出a的值是解题关键.4.★★填表.原数﹣5﹣39.2047相反数53﹣9.20﹣4﹣7【考点】14:相反数.【分析】根据相反数的定义,a的相反数是﹣a,分别得出即可.【解答】解:填表如下:原数﹣5﹣39.2047相反数53﹣9.20﹣4﹣7【点评】此题主要考查了相反数的定义,熟练掌握相关定义是解题关键.5.★★化简下列各数:(1)﹣(﹣100);(2)﹣(﹣5);(3)+(+);(4)+(﹣2.8);(5)﹣(﹣7);(6)﹣(+12).【考点】相反数.【专题】计算题.【分析】根据互为相反数的两数之和为0可求出各数的相反数.【解答】解:(1)100;(2)5;(3);(4)﹣2.8;(5)7;(6)﹣12.【点评】本题考查了相反数的知识,属于基础题,掌握互为相反数的两数之和为0.6.★★(2014秋•阳谷县校级月考)化简:(1)﹣|+2.5|;(2)﹣(﹣3.4)(3)|+5|(4)|﹣(﹣3)|(5)+(﹣4)(6)﹣[﹣(+5)].【考点】15:绝对值;14:相反数.【专题】1 :常规题型.【分析】根据绝对值和相反数的意义求解.【解答】解:(1)﹣|+2.5|=﹣2.5;(2)﹣(﹣3.4)=3.4;(3)|+5|=5;(4)|﹣(﹣3)|=3;(5)+(﹣4)=﹣4;(6)﹣[﹣(+5)]=5.【点评】本题考查了绝对值:若a>0,则|a|=a;若a=0,则|a|=0;若a<0,则|a|=﹣a.以及相反数的意义.∵x<0,∴x=﹣5.【点评】本题考查了绝对值的性质,一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.【思考】10.★★★已知A为数轴上的一点,将A先向右移动7个单位,再向左移动4个单位,得到点B,若A、B两点对应的数恰好互为相反数,求A点对应的数.【考点】14:相反数;13:数轴.【分析】设A表示的数是a,根据题意得出方程a+7﹣4=﹣a,求出即可.【解答】解:设A表示的数是a,则根据题意得:a+7﹣4=﹣a,a=﹣1.5,即a点对应的数是﹣1.5.【点评】本题考查了相反数的应用,注意:a的相反数是﹣a.11.★★★★(2012秋•南溪县校级月考)化简下列各式的符号,并回答问题:(1)﹣(﹣2);(2)+(﹣);(3)﹣[﹣(﹣4)](4)﹣[﹣(+3.5)];(5)(﹣{﹣[﹣(﹣5)]})(6)﹣{﹣[﹣(+5)]}问:①当+5前面有2012个负号,化简后结果是多少?②当﹣5前面有2013个负号,化简后结果是多少?你能总结出什么规律?【考点】相反数.【专题】规律型.【分析】根据相反数的定义分别进行化简即可;根据化简的结果回答问题即可.【解答】解:(1)﹣(﹣2)=2;(2)+(﹣)=﹣;(3)﹣[﹣(﹣4)]=﹣4;。
人教版初一数学知识点总结
七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章有理数一.知识框架二.知识概念1.有理数:(1)凡能写成)0pq,p(pq≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a不一定是负数,+a也不一定是正数;π不是有理数;(2)有理数的分类: ①⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数②⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a、b互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a(a)0a()0a(aa或⎩⎨⎧<-≥=)0a(a)0a(aa;绝对值的问题经常分类讨论;5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a 1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ). 10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a . 13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(二) 概念的理解 例1. 判断:(1)-5是5的相反数( );
(2)5是-5的相反数( );
(3)2 1
2
与
1 互为相反数(
2
);
(4)-5是相反数( ).
例2 判断: (1)-2是-(-2)的相反数 (2)-3和+3都是相反数 (3)-3是3的相反数 (4)-3与+3互为相反数 (5)+3是-3的相反数 (6)一个数的相反数不可能是它本身
注意:到原点的距离相等。
观察这两个数,有什么相同和不同?
符号不同
2.5 2.5
数字相同
像-2和2,3和-3,-2.5和2.5这样, 只有符号不同的两个数叫做互为
相反数。
例如:8的相反数是-8,7的相反数是-7。
5的相反数是
.
由此可知,求一个数的相反数就是在这个数的
前面添上“-”号。
• 一般地,a的相反数是 -a
请说出下列各式表示的含义: -(+1.1)表示什么呢? -(-7)表示什么呢?, -(-9.8)表示什么呢? 它们的结果应是多少?
典型例题
例题1 (1) 4 是____的相反数,4_____.____
(2)
1 5
是 ____的相反数,
. 1 __________ 5
(3)7.1是_____的相反数, 7.1____.______
(4) 100是_____的相反数, 100_____ .___
例3 化简下列各数中的符号: (1) (2 1 )
3 (2)-(+5)
(3)(7)
(4)(3)
今日作业
课堂练习
1.-1.6是____的相反数,___的相反数是0.3. 2.下列几对数中互为相反数的一对为( ). A.(8)和 (8)B.(8)与 (8) C. (8)与 (8)
3.5的相反数是____;a 的相反数是___;ab的相
反数是____. 4.若 a13,则 a______;___ 若 a6,则 a_______.__
5.若 a是负数,则 a是___数;若a是负数,则 a
是______数.
2x 3
例4 填空: (1)a-4的相反数是 相反数是 。
,3-x的
(2)2 x 是 的相反数
2、观察所画的及数轴及表示的点回答下列问 题:
(1)3与-3分别在原点的 和 。它们
到原点的距离为:
。
(2)数轴上与原点距离是2 的点有
这些点表示的数是
。
个,
(3)数轴上与原点距离是5 的点有
这些点表示的数是
。
个,
一般地,设a是一个正数,数轴上与原点的 距离是a 的点有 两 个,它们分别在原点 的左侧和右侧 ,表示 -a和a ,我们说 这两点关于 原点对称。
.
-a的相反数是 a
.
a和-a互为相反数.如:
???
0的相反数是??(从数轴上考虑) 0的相反数是0。 一个正数的相反数是一个 负数 。 一个负数的相反数是一个 正数 。 一个数的相反数是它本身的数是:0.
想一想
数轴上表示相反数的两个点和原点 有什么关系?
在数轴上表示互为相反数的两个数的 点,分别位于原点的两旁,且与原点的 距离相等。
• 例3 求下列各数的相反数:
(1)-5
(2) 1 (3)0
2
(4)a 3
(5)-2b
(6) a-b
பைடு நூலகம்
(7) a+2
2.在数轴上任意标出4个数,并标出它们的相反 数.
3.分别说出9,-7,0,-0.2的相反数.
3
4.指出-2.4,5 ,-1.7,1各是什么数的相反数?
5.a 的相反数是什么?
a 的相反数是-a , 求任意一个 数的相反数就可以在这个数前加一 个“-”号.
3
(3)如果-a=-9,那么-a的相反数
是
。
课堂小结
本节课学习了以下内容: 1.相反数的概念:只有符号不同的两个数,我们说 其中一个是另一个的相反数.
2.a表示求 a的相反数.
(xy)
例5 填空: (1)若-(a-5)是负数,则a-5 0.
(2)(xy)若是负数,则x+y 0.
今日作业
例6 已知a、b在数轴上的位置如 图所示。 在数轴上作出它们的相反数; 用“<”按从小到大的顺序将这 四个数连接起来。
今日作业
九州娱乐网 www.jiuzhouyule.me 九州娱乐网 uyd31vau
说:“是这样的,树和庄禾一样,长得过密了就会合挤着往上窜!”耿直不解,瞪着俩眼儿问爹爹:“那又是为什么呢?”耿 老爹怜爱地看着小儿子骨碌碌转动黑眼珠,伸手摸摸他的脑袋意味深长地说:“它们得晒太阳啊!晒不着太阳,它们就长不结 实哩!”“唔,我明白了。这树和庄禾晒太阳,敢情就好像我们人吃饭一样啊!”耿直的话把大家都给逗乐了。小青拍着手说: “我终于知道了,为什么你们三个吃饭都那么香呢,原来是争着晒太阳啊!”耿英追上去要打小青,嘴里直嚷着:“好你这张 利嘴,看我怎么收拾你!”小青咯咯地笑着拐个弯儿突然不见了。大家快步追上去也都来了一个90度的急转弯,这才发现,眼 前已经是齐刷刷的一排淋灰池子了。小青调皮地说:“怎么样,我就说藏着的嘛!”耿正说:“真还别说,要不是到了跟前, 谁会想到就在这里了呢!”小青用手指着十几步之外的几间平房说:“耿伯伯,卖石灰膏的人就住在那里!”于是,大家一起 向那几间平房走去。还没有走出几步,一只硕大的黑狗突然窜了出来,冲着众人“汪汪汪”直叫,凶巴巴的大有随时就要冲上 来的样子。耿正赶快就手捡起一根木棍拿在手里,挺身挡在大家的面前。耿直也随手拾起一块儿石头做出要扔出去的姿势。大 黑狗不敢往前冲了,但仍然还站在原地狂吠不止。耿老爹说:“你们不要打它!它一叫,卖石灰膏的人就会出来了。”果然, 耿老爹话音未落,就见一个略显肥胖的中年男人走了出来。他上下打量着对面的五个人,突然认出小青来了,大声说:“哦, 这不是小青姑娘吗?这几个人是”小青接过他的话音说:“来买你们的石灰膏!”中年男人笑了,说:“好一个嘎巴萝卜脆! 来买我们的石灰膏,好啊,快请屋里坐!”说着,轻轻踢一脚那只大黑狗:“去,一边去!”大黑狗乖乖地溜达到一边卧着去 了。耿老爹说:“这位兄弟啊,不用进屋啦,我们就在这里说话吧。喏,我先看看你们的货。可以吗?”中年男人说:“当然 可以了。靠西边这五个池子里的石灰膏都已经熟透了,你随便看啊。”说着,弯下腰挨着个儿掀起覆盖在池子上面的油布,请 大家逐个查看池子里的石灰膏。耿老爹看到每一个池子里的石灰膏都非常干净细腻,实在无可挑剔,就说:“行,我要买五间 新屋亮家所需要的石灰膏,价格就按照你们的销售价吧。我不砍你们的价,但你们一定得给我把料装足了!”中年男人说: “大哥你办事痛快,我自然也要够意思了!”他说完这话,随即大声地冲屋子里喊:“大伢子,肥子,你们快出来,装石灰膏 送货去啊!你们推两挂车过来,再带上八只最大号的桶!”只见一个大个子的年轻后生和另一个胖墩墩的大男娃儿应声而出。 俩人从旁边的一间房子里推出来两挂大块头的平车
第一章 有理数
1.2.3 相 反 数
保康县实验中学七年级备课组
1、画数轴,在数轴上表示出以下各点: 2,-3,2.5,-2.5,-2,3
2、观察所画的及数轴及表示的点回答下列问 题:
(1)3与-3分别在原点的 和
原点的距离为:
。
。它们到
(2)数轴上与原点距离是2 的点有
这些点表示的数是
。
个,
1、画数轴,在数轴上表示出以下各点: 2,-3,2.5,-2.5,-2,3
