第四章热力学第一定律
合集下载
第四章 热力学第一定律 4
1 V4 T1 T2 V1
Q2 Q1
V3 V2
V2 V1 V2 V1
V4 V1
V3 V4
V2 V1
Q 2 R T 2 ln
V2 V1
R T 2 ln
T2 T1
R T1 ln
Q2 Q1
V R T 2 ln 2 V1
Q 2 Q1 j
j1
n
§4.6.2 卡诺热机
为了对热机的最大可能效率进行理论研究，1824年法国工 程师卡诺设想了一种理想的热机，称为卡诺热机；这种热机的 循环过程称为卡诺循环。 卡诺循环在温度为T1、T2的两个热源间工作，由两个等温 过程和两个绝热过程构成。一般所说的卡诺循环是准静态的， 且无摩擦等耗散现象。 P 当工质是气体时，卡诺循 环可以用P-V图表示。 可见：在卡诺循环中，工质从T1 热源吸热Q1，向T2热源放热 Q 2 ， 向外输出功W′ 。
T
⑵ 转换点、转换曲线：
同一工质在不同的温度段对应的焦汤系 数的趋势是可以不同的。 从T-P 图上看，这种现象是由等焓线的斜率决定的。
P
⑵ 转换点、转换曲线： 同一工质在不同的温度段对应的焦汤系数的趋势是可以不同的。 从T-P 图上看，这种现象是由等焓线的斜率
T P H
则有：
W' Q1
Q1 Q2 Q1 1 Q2 Q1
——热机效率
说明
若循环存在m个高温热源，n个低温热源，热机的吸放热为：
Q 1 i ( i 1, 2 , m ) 及 Q 2 j ( j 1, 2 , n )
则热机效率公式中的吸放热为：
第4章热力学基本定律
（1）系统内发生的所有变化都必须可逆
（2）系统与环境之间的相互作用也是可逆进行；
• （1）封闭体系
Wid U p0 V T0 S
• （2）稳流系统
体积功
1 2 Wid H u gZ T0 S 2
Wid H T0 S
动能和势能忽略
理想功
• 理想功实际上是一个理论上的极限值，在 与实际过程一样的始终态下，通常作为评 价实际过程能量利用率的标准；
（1）设备内各点的状态不随时间变化 （2）垂直于流向的各个截面处的质量流率相等。
1 1 m1 m2 Q Ws d mE H u 2 gZ H u 2 gZ 2 2 dt dt dt 1 dt 2 dt
4.2 热力学第二定律的各种文字表述
克劳修斯说法：热不可能自动从低温物体传给高 温物体
开尔文说法：不可能从单一热源吸热使之完全变
为有用的功而不引起其他变化
自发的过程是不可逆的
热机的热效率
高温热源 T1
W Q1 Q2 Q1 Q1
火力发电厂的热效率大约为35% 卡诺热机的效率
Q1 Q2 T1 T2 Q1 Q2 W Q1 Q1 T1 Q1
低温热源 T2
W 1 Q1
热与功不等价
熵的概念
T1 T2 Q1 Q2 T1 Q1
Q1 Q2 0 T1 T2
无限小的可逆的卡诺热机有：
Q1
T1
Q2
T2
0
任意的可逆循环
Qrev
T
0
熵是状态函数
dS
Qrev
T
化工热力学第四章热力学第一定律及其应用课件
400
2.0
23.80J mol 1K 1
化工热力学 第四章 热力学第一定律及其应用
熵变为正值。对于绝热过程，环境没有熵变，因而孤立体系 熵变也为正值，这表明节流过程是不可逆的。此例说明，第三章 的普遍化关联法也可以应用于节流过程的计算。
化工热力学 第四章 热力学第一定律及其应用
例 4—3 300℃、4.5 MPa乙烯气流在透平机中绝热膨胀到 0.2MPa。试求绝热、可逆膨胀（即等熵膨胀）过程产出的轴功。 （a）用理想气体方程；（b）用普遍化关联法，计算乙烯的热
即：
能入 能出 能存
封闭体系非流动过程的热力学第一定律：
U Q W
化工热力学 第四章 热力学第一定律及其应用 第一节
§4-2 开系流动过程的能量平衡
开系的特点： ① 体系与环境有物质的交换。 ② 除有热功交换外，还包括物流输入和 输出携带能量。
开系的划分： ➢ 可以是化工生产中的一台或几台设备。 ➢ 可以是一个过程或几个过程。 ➢ 可以是一个化工厂。
化工热力学 第四章 热力学第一定律及其应用
例 4—2 丙烷气体在2MPa、400K时稳流经过某节流装置后 减压至0.1MPa。试求丙烷节流后的温度与节流过程的熵变。
[解] 对于等焓过程，式（3—48）可写成
H
CP T2 T1
H
R 2
H1R
0
化工热力学 第四章 热力学第一定律及其应用
已知终压为0.1MPa，假定此状态下丙烷为理想气体，
S
C* pms
ln T2 T1
R ln
P2 P1
S1R
因为温度变化很小 ，可以用
C* pms
C* pmh
92.734J
mol 1
第4章热力学第一定律及其应用
2)求状态2的 U 2 和 Q ： 2)求状态 求状态2 Q 忽略液体的体积： v2sv = 1V1 = 11000 = 254.8cm3 ⋅ g −1 = 2v1sv 忽略液体的体积：
2
m
z
2
×7.85
查表：（近似值） 查表：（近似值）P2 = 7.917×105 Pa ：（近似值
2 2
sv ∴U 2 = 2576.5J ⋅ g −1
sl sv sl U 2 = 718.33J ⋅ g −1 ∴U 2 = 1 (U 2 + U 2 ) = 1 ( 2576.5+ 718.33) = 1647.4 J ⋅ g −1
∴Q = 7.85 × (1647.4− 2595.3) = −7441J = −7.44KJ
“-”表示需从体系移出热量
4.1闭系非流动过程的能量平衡 4.1闭系非流动过程的能量平衡
热力学第一定律表达式为： 热力学第一定律表达式为： 式中： 式中： —物质内能的变化 —动能的变化， 动能的变化，
—位能的变化
∆u 2 g ∆Z ∆U + + = Q −W 2 gC gC
式中: 式中:
—由于系统与环境之间存在的温差而导致的 能量传递。 能量传递。 —由于系统的边界运动而导致的系统与环境 之间的能量传递。 之间的能量传递。 范围：适用于任何物质的可逆与不可逆过程。 范围：适用于任何物质的可逆与不可逆过程。
状态1 状态1： P1=15.54×105Pa 1 L =15.54× 饱和水蒸汽 mz 1)容器内蒸汽的质量 mz 和 U1 ： 1)容器内蒸汽的质量
状态2 状态2： 1 L
1 m汽 = m液 = mz 2
查水蒸汽表压力表（陈新志） 查水蒸汽表压力表（陈新志）P250： P1=15.54×105Pa 干饱和蒸汽 t1=20℃ =15.54× =20℃
4-3热力学第一定律
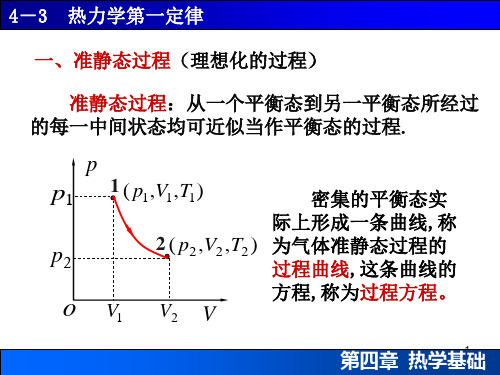
方程,称为过程方程。
第四章 热学基1础
4－3 热力学第一定律 二、内能
气体的内能就是气体内大量分子热运动的能 量与分子之间相互作用的势能的总和.
理想气体内能:表征系统状态的单值函数,理 想气体的内能仅是温度的函数 .
E E(T )
当系统状态变化时，系统 内能的增量只与系统起始和 终了状态有关，与系统所经 历的过程无关 .
系统放热 内能减少 外界对系统做功
物理意义
Q E A
1）能量转换和守恒定律 . 第一类永动机是不 可能制成的 .
2）实验经验总结，自然界的普遍规律 .
第四章 热学基5础
4－3 热力学第一定律
四、气体做功的公式
p
Ⅰ*
*Ⅱ
S
o V1 V V dV V2 V
F pS
S
dx
准静态过程功的计算
三、热力学第一定律
p
Ⅰ*
Q E A
*Ⅱ
o V1
V2 V
热力学第一定律：在系统变化的过程中,系统所 吸收的热量,等于系统内能的增量与系统对外界作功 的和.
微小过程 dQ dE dA
第四章 热学基4础
4－3 热力学第一定律
第一定律的符号规定
Q
E2 E1
A
+ 系统吸热 内能增加 系统对外界做功
4－3 热力学第一定律
一、准静态过程（理想化的过程）
准静态过程：从一个平衡态到另一平衡态所经过 的每一中间状态均可近似当作平衡态的过程.
p
p1 1 ( p1,V1,T1)
密集的平衡态实
际上形成一条曲线,称
p2
2 ( p2 ,V2 ,T2 ) 为气体准静态过程的 过程曲线,这条曲线的
热学第二版-秦允豪-第四章答案
第四章热力学第一定律(题号有所不同)5－1.0.020Kg的氦气温度由升为，若在升温过程中：（1）体积保持不变；（2）压强保持不变；（3）不与外界交换热量，试分别求出气体内能的改变，吸收的热量，外界对气体所作的功，设氦气可看作理想气体，且，解：理想气体内能是温度的单值函数，一过程中气体温度的改变相同，所以内能的改变也相同，为：热量和功因过程而异，分别求之如下：（1）等容过程：V=常量A＝0由热力学第一定律，（2）等压过程：由热力学第一定律，负号表示气体对外作功，（3）绝热过程Q＝0由热力学第一定律5－2.分别通过下列过程把标准状态下的0.014Kg氮气压缩为原体积的一半；（1）等温过程；（2）绝热过程；（3）等压过程，试分别求出在这些过程中气体内能的改变，传递的热量和外界对气体所作的功，设氮气可看作理想气体，且，解：把上述三过程分别表示在P-V图上，（1）等温过程理想气体内能是温度的单值函数，过程中温度不变，故由热一、负号表示系统向外界放热（2）绝热过程由或得由热力学第一定律另外，也可以由及先求得A（3）等压过程，有或而所以＝＝＝由热力学第一定律，也可以由求之另外，由计算结果可见，等压压缩过程，外界作功，系统放热，内能减少，数量关系为，系统放的热等于其内能的减少和外界作的功。
5－3 在标准状态下的0.016Kg的氧气，分别经过下列过程从外界吸收了80cal的热量。
（1）若为等温过程，求终态体积。
（2）若为等容过程，求终态压强。
（3）若为等压过程，求气体内能的变化。
设氧气可看作理想气体，且解：（1）等温过程则故（2）等容过程（3）等压过程5－4 为确定多方过程方程中的指数n，通常取为纵坐标，为横坐标作图。
试讨论在这种图中多方过程曲线的形状，并说明如何确定n。
解：将两边取对数或比较知在本题图中多方过程曲线的形状为一直线，如图所示。
直线的斜率为可由直线的斜率求n。
或即n可由两截距之比求出。
5－5 室温下一定量理想气体氧的体积为，压强为。
新版热学(秦允豪编)习题解答第四章热力学第一定律-新版.pdf
CV T0 2
CV （
R 2R
1
1
27 3 2
T2 T0
T0
（2）由（ 1）式：
8
3
1.5 ）
（3）左侧初态亦为 P0 T 0 V 0 ，终态为 P1V1T1
27
P1 P2
P0
∵ 活塞可移动，
8 ，由 PV
RT
RT 2
P0 V 0 T 2
V2
P2
T0
P2
14
V 1 2V 0 V 2
V0
9
P0V 0
3 T0
19
23
q 2 1 .60 10
6 .02 10 C
（ q 2N Ae ）
两极间电压为 ， A q
19
A 1 .229 2 1 .60 10
6 .02
Q'
5
2. 858 10
23
10
82 . 84 %
4.4.7 设 1mol 固 体状 态 方程 为： v v 0 aT bP ， 内 能 表示 为： u CT
Py L y S
P0 LS
其中 P0
gh 0
Py P0 可改写为
L Ly
1 P0
对微小振动 y L
Py P0
y 1
L
y
1 P0
1
1 P0
L
y P0
L
h0 gy
L
由功能关系：
m gy
1 mv 2 2
m max gy max
AP
式中 A P 是由于右端空气压强 P y 与左端空气压强 P0 对水银柱作功之和，且
2
T0
27 P0
8
热学学 第四章 热力学第一定律.
《论有机体的运动与物质代谢关系》1845 植物吸收了太阳能，把它转化为化学能。动物摄取
植物，通过氧化把化学能转化为热和机械能。
16
亥姆霍兹 德国 物理学家（1821～1894） 《力之守恒》 化学、力学、电磁学、热学
17
• 2 内能
内能：在热学参考系下，所有分子的无规则运动的能量之和。
热学参考系：使系统宏观静止的参考系
用的能量，在过程中保持为常数，因此可以省略。
• 内能具体包含哪些能量---普遍
分子的动能(包括平动、转动、振动)
+分子内部的振动势能
+分子间的势能
18
---原子核内的能量，不能被运用，省略。 ---系统整体运动的能量，不是内能，排除。 (系统的整体平动、转动的动能) ---对于理想气体，分子间势能在任何过程中始终保持为常数， 可以省略。 • 例子：单原子分子理想气体的内能。 每个分子的动能之和。---热学坐标系。 • 例子：刚性双(多)原子分子理想气体的内能。 每个分子的平动动能之和，每个分子的转动动能之和。 • 例子：非刚性双(多)原子分子理想气体的内能。 每个分子的平动动能之和，每个分子的转动动能之和。每个分 子的振动动能之和，每个分子的振动势能之和。 • 例子：前面的例子都为非理想气体时。 都要包含分子间的势能之和。
系统和外界在非功过程交换的能量，称为热量
注意：1）热量过程量。
2）系统和外界必须有温度差，才能交换热量。
3）系统和外界交换能量的方式只有两种：功，热量。
§4.3 热力学第一定律
本质：能量转化和守恒定律在热学系统的表现。
1 历史
14
焦耳(1818-1889),英国。 热功当量
w电＝I 2Rt＝JQ w重力＝JQ Q cmT
植物，通过氧化把化学能转化为热和机械能。
16
亥姆霍兹 德国 物理学家（1821～1894） 《力之守恒》 化学、力学、电磁学、热学
17
• 2 内能
内能：在热学参考系下，所有分子的无规则运动的能量之和。
热学参考系：使系统宏观静止的参考系
用的能量，在过程中保持为常数，因此可以省略。
• 内能具体包含哪些能量---普遍
分子的动能(包括平动、转动、振动)
+分子内部的振动势能
+分子间的势能
18
---原子核内的能量，不能被运用，省略。 ---系统整体运动的能量，不是内能，排除。 (系统的整体平动、转动的动能) ---对于理想气体，分子间势能在任何过程中始终保持为常数， 可以省略。 • 例子：单原子分子理想气体的内能。 每个分子的动能之和。---热学坐标系。 • 例子：刚性双(多)原子分子理想气体的内能。 每个分子的平动动能之和，每个分子的转动动能之和。 • 例子：非刚性双(多)原子分子理想气体的内能。 每个分子的平动动能之和，每个分子的转动动能之和。每个分 子的振动动能之和，每个分子的振动势能之和。 • 例子：前面的例子都为非理想气体时。 都要包含分子间的势能之和。
系统和外界在非功过程交换的能量，称为热量
注意：1）热量过程量。
2）系统和外界必须有温度差，才能交换热量。
3）系统和外界交换能量的方式只有两种：功，热量。
§4.3 热力学第一定律
本质：能量转化和守恒定律在热学系统的表现。
1 历史
14
焦耳(1818-1889),英国。 热功当量
w电＝I 2Rt＝JQ w重力＝JQ Q cmT
《热学》第四章和第五章复习
第四章 热力学第一定律 基本要求一、 可逆和不可逆过程 （1）准静态过程（2）理解什么是可逆过程，什么是不可逆过程.知道只有无耗散的准静态过程才是可逆过程。
二、 功和热量 （1）明确功是在力学相互作用过程中能量转移，热量是在热学相互作用过程中的能量的转移，它们都是过程量，它们都是过程量。
知道“作功”是通过物体宏观位移来完成；而“热传递”是通过分子之间的相互作用来完成。
（2）知道功有正负，熟练掌握从体积膨胀功微分表达式pdV W d -=出发计算体积膨胀功。
从几何上理解功的大小等于p-V 图上热力学过程曲线下面的面积。
三、热力学第一定律（1）知道能量守恒与转化定律应用到热学中就是热力学第一定律。
明确热力学第一定律是把内能、功和热量这三个具有能量量纲的物理量结合在一个方程中：即 W Q U +=∆； （2）一微小过程中热力学第一定律表示为：W d Q d dU +=；对于准静态过程热力学第一定律表示为：pdV Q d dU -=（3）内能是态函数，内能一般应是温度和体积的函数。
内能应当包含分子的热运动动能和分子之间的相互作用势能，也应包括分子内部的能量；在热学中的内能一般不包括系统做整体运动的机械能。
四、热容和焓（1）知道热容的定义、热容是过程量、热容与物体的量有关。
（2）知道焓的定义pV U H +=;知道焓的物理意义。
五、热力学第一定律对理想气体的应用（1）知道焦耳定律；即理想气体的内能仅是温度的函数；知道理想气体的焓也只是温度的函数。
内能和焓的微分可分别表示为：dT C dU m V ,ν=；dT C dH m p ,ν=；这两个公式适用于理想气体任何过程。
（2）理想气体的准静态过程的热力学第一定律可表示为pdV dT C dQ m V +=,ν；利用上式可得迈耶公式：R C C m V m p =-,,ν；（3）会熟练利用热力学第一定律处理一些常见热力学过程。
（4）会推导准静态绝热过程方程，熟记并会熟练利用绝热过程方程，同时应知道绝热过程方程的适用条件。
大学物理第4章-热力学第一定律
mol 理想气体的内能：
i E νRT 2
理想气体的内能是温度 T 的单值函数
i ΔE νR ΔT 2
QUIZ Jack’s death due to the loss of a) love b) temperature c) heat d) internal energy
热量是过程量，内能是状态量。
二、热 量
dQ 0 表示系统从外界吸热； dQ 0 表示系统向外界放热。
在SI制中：焦耳(J)
准静态过程中传递的热量是过程量。
三、热量的单位
结 论：
热量和功是系统状态变化中伴随发生的两种 不同的能量传递形式。它们的物理本质不同 宏观运动 分子热运动 功 热量 分子热运动 分子热运动
作功和传热的大小不但与系统的初、末态有关， 而且与过程有关，它们都是过程量，不是状态量， 因而微量功和微量传热分别写成 dA和dQ,它们不是全 微分。
dQ Cp ( )p dT
摩尔定压热容 Cp,m
i i Q E A RT RT 1 RT 2 2
Cp，m 1 dQ i 1 R dT p 2
：摩尔数
i：自由度数
三、迈耶公式及比热容比 摩尔定体热容 CV,m 摩尔定压热容 Cp,m 迈耶公式 比热容比
CV,m 3 R 2
5 R 2
Cp,m 5 R 2 7 R 2
1.67 1.40
刚性多原子分子
3R
4R
1.33
思考：为什么理想气体任意两状态间内能的变 化可表示成摩尔定体热容 CV,m 与温度变化乘积 的关系，而不是摩尔定压热容 Cp,m 与温度变化 乘积的关系？
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
w = pdv - dl - dA +…...
简单可压缩系统
w =pdv
可逆过程
q = Tds
w = pdv
适用于任何工质 、可逆过程 的热一律表达式
q = du + pdv
q = u + pdv Tds = du + pdv
单位工质
Tds = u + pdv
（2）在2B1过程中
Q2B1 (U1 U2 ) W2B1 10 5 15(kJ)
由于工质沿1A2B1回到初态系统经历了一个循 环，内能变化量为
U U1 U1 0 工质沿1A2B1回到初态时的净功为
W Q U Q 35 kJ
工质沿1A2B1回到初态时的净吸热量为：
适用条件： 1）任何工质 2) 任何过程
• 系统吸热：Q＞0； 系统放热： Q ＜0。
• 系统对外做功：W ＞0； 外界对系统做功： W＜0
• 系统内能增加： △U ＞0； 系统内能减少： △U ＜0
功 （ w） 是广义功
闭口系与外界交换的功量
容积功 拉伸功 表面张力功
pdv
w拉伸= - dl w表面张力= - dA
适用于理想气体 、任意过程的热一律表达式
q = cvdT + w q = cvT+ w
单位工质
适用于理想气体 、可逆过程的热一律表达式
q = cvdT+ pdv q = cvT+ pdv
Tds = cvdT + pdv Tds = cv T + pdv
单位工质
例1 ： 有一定质量的工质从状态1沿1A2到达 终态2，又沿2B1回到初态1，并且
定义：
在温差作用下,系统与外界通过界面传递的能量。
规定: 系统吸热热量为正，系统放热热量为负
单位： kJ 或 kcal 且l kcal=4.1868kJ 特点:
是传递过程中能量的一种形式，与热力过程有关
可逆过程： q Tds q Tds
功
定义: 种类:
除温差以外的其它不平衡势差所引起 的系统与外界传递的能量.
变化 3、w推＝pv与所处状态有关，是状态量 4、并非工质本身的能量（动能、位能）变化
引起，由外界做出，流动工质所携带的能量
第二节 闭口系统热一律表达式
Energy balance for closed system
•一般式 Q = dU + W Q = U + W
Q
W
q = du + w 单位工质 q = u + w
任何工质、可逆过程
•理想气体内能变化计算
定容过程: w 0 q = u + w 用定值比热计算: u cvT
u qv
用平均比热计算: u cvmT
t2
t2
t1
u
cvdt
cvdt
cvdt
cvm
t2 0
t2
cvm
t1 0
t1
t1
0
0
适用于理想气体一切过程或者实际气体定容过程
分子位能（相互作用） (v)
binding forces
说明：
内能是状态量
理想气体u=f(T) 实际气体u=f(T,v)
U : 广延参数 [ kJ ] u : 比参数 [kJ/kg]
内能总以变化量出现，内能零点人为定
2.外部储存能
macroscopic forms of energy
重力位能 系统工质与重力场的相互作用 potential 所具有的能量
三、热力学第一定律的一般表达式
输入系统的 能量
系统输出 的能量
系统中储存能量 的变化量
能量
系统储存的能量 传递中的能量
（一）系统的储存能
系统储 存的能
量
内部
储存能
热力学 能
状 态
参
外部
数
储存能
机械能
1.内部储存能
•
热 力 学 能
（ 内 能 ）
分子动能（移动、转动、振动） (T)
translation rotation vibration
第一节 热力学第一定律
一、实质：
能量转换及守恒定律在热力过程中的应用
二、热力学第一定律的表述：
•热能可以从一个物体传递给另一个物体，也可 以与机械能或其他能量相互转换，在传递和转换 过程中，能量的总值不变。
•“第一类永动机(Perpetual –motion machine of the first kind)是不可能制成的”
Ep mgz
宏观动能 以外界为参考坐标的系统宏观
kinetic 运动所具有的能量
Ek
1 2
mwg
2
系统总储存能 total energy
E = U + Ek + Ep e = u + ek + ep
（二）系统与外界传递的能量
热量
热源
过 程
系
功
参
功源 数
统
随物质传递的能量 质源
状 态 参
数
热量
第四章 热力学第一定律
The First Law of Thermodynamics
学习目标：
•深刻理解热力学第一定律的实质 •深刻理解能量、储存能、热力学能的概念，及 热力学能、焓的物理意义;掌握理想气体热力学 能及焓的变化量的计算；理解容积功、轴功、 技术功、流动功等概念
•熟练应用热力学第一定律解决具体问题
Q1A2 50 kJ
U2 U1 10 kJ W2B1 5 kJ
试判断沿过程1A2工质是膨胀还是压缩，并 且求工质沿1A2B1回到初态时的净吸热量和 对外作的净功。
解：（1）在1A2过程中
W1A2 Q1A2 (U2 U1) 50 10 40(kJ)
因为 W1A2 0 所以系统对外界做功，工质膨胀。
随物质传递的能量
流动工质本身 具有的能量
E
U
1 2
mwg 2
mgz
流动功(或推动功)
为推动流体通过控制体界 面而传递的机械功.
推进功（流动功、推动功）
A
W推 = p A dl = pV w推= pv
面工质的热力状态
流动功与其它功区别
对推进功的说明
1、与宏观流动有关，流动停止，推进功不存在 2、作用过程中，工质仅发生位置变化，无状态
•容积功W： 在力差作用下，通过系统容积变化与外界传递的能量。
规定: 系统对外作功为正，外界对系统作功为负。
膨胀功是热变功的源泉
可逆过程： w pdv w pdv
•轴功Ws: Shaft work 通过轴系统与外界传递的机械功
单位：l J=l Nm •其他准静态功：拉伸功，表面张力功，电功等