电路基础理论中关于网孔数目的计算方法
电路分析基础 4网孔法
5
4
6
• 独立KVL回路选择： • 方法1. 每选一个回路，让该回路包含新的支路，
选满b-n+1个为止。（如上例中1、3、7回路。） • 方法2. 对平面电路， b-n+1个网孔是一组独立
回路。（如上例中1、2、4回路。）
一、电路分析方法
1、 2b法: （2b个联立方程）
例9 求图示电路的输入电阻（不含受控源）
Ri
Ri 1
例10 求图示单口网络的输入电阻 R。i
i A+
u
RL
B-
解： i u 2i
RL
i u
2i
RL
Ri
u i
RL
结论：对于不含独立源但含有受控源的单口网络可 以等效为一个电阻，而且等效电阻还可能为负值。
X
第二章 电阻电路的基本分析法
本章重点： 1、了解支路分析法 2、熟练掌握网孔分析法 3、熟练掌握节点分析法 4、掌握含运放电路的分析
KCL方程的独立性
对于节点1、 2、 3、 4可列出KCL方程(电流流出
节点取“+”号， 流入取“-”号)为
2
（1） i1 i4 i6 0
1
2
（2） i1 i2 i3 0
1
3
3
（3） i2 i5 i6 0
（4） i3 i4 i5 0
4
5
4
6
有线性代数知识：上述4个方程线性不独立，其 中任意3个方程可组成独立方程组。独立的KCL方程 数为n-1个。
§2. 1 支路分析法
问题：已知b条支路，n个节点的电路 如何求解？有无规范化的方法?
待求变量：b个支路电压、 b个支路电流
2b变量需2b个方程
03-2网孔电流法
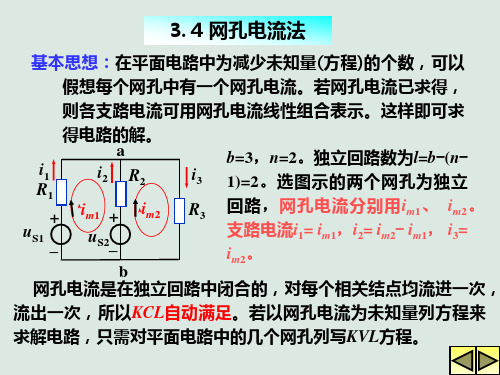
基本思想：在平面电路中为减少未知量(方程)的个数，可 以假想每个网孔中有一个网孔电流。若网孔电流已求得， 则各支路电流可用网孔电流线性组合表示。这样即可求 得电路的解。 a b=3 ， n=2 。 独 立 回 路 数 为 l=bi1 i2 R2 i3 (n-1)=2。选图示的两个网孔为独 R1 R3 立 回 路 ， 网 孔 电 流 分 别 用 im1 、 im1 + im2 + im2。支路电流i1= im1，i2= im2- im1， uS1 uS2 – – i3= im2。 b 网孔电流是在独立回路中闭合的，对每个相关结点均流进一 次，流出一次，所以KCL自动满足。若以网孔电流为未知量列方 程来求解电路，只需对平面电路中的几个网孔列写KVL方程。
压源的电势升。
例：给定直流电路如图（a）所示，其中R1＝R2＝R3＝1，
R4＝R5＝R6＝2，uS1＝4V，uS2＝2V。试选择一组独立回 路，并列出回路电流方程。 us1 +
Il1
R1
R2
解：电路的图如图（b）所示，
R6
选择支路4、5、6为树，3个独 立回路（基本回路）绘于图中。
Il1
R5
R4
3. 5 回路电流法
网孔电流法仅适用于平面电路，回路电流法则无
此限制，它适用于平面或非平面电路。因此回路电流
法是一种适用性较强并获得广泛应用的分析方法。
如同网孔电流是在网孔中连续流动的假想电流，
回路电流是在一个回路中连续流动的假想电流。
回路电流法是以一组独立回路电流为电路变量的
求解方程。
通常选择基本回路（单连支回路）作为独立回路，
R12= R21=－R2 —网孔1、网孔2之间的互电阻。 互电阻Rjk－当两个网孔电流流过相关支路方向相同时，互 电阻前取正号；否则取负号 (平面电路中，各个网孔的绕 行方向都取为相同的方向时，互电阻Rjk均为负值) 。
第3章网孔分析法和节点分析法
5 13 1 2 1 2
i1 i3 2ia
补充方程
5i1 10 4i3 4 5i2 8 4ib
18 i1 8
1 i2
0
0 i3 0
练习
10Ω
_ 4ib +
+ 2ia _
ib
+
+
4Ω
8V
_
u_a 5Ω
0.2ua
ia
作业
+ 4ix _ 4Ω
ix
2Ω
2Ω
2Ω
1A
3.2 节点（结点）电压法 (node voltage method)
4Ω
网孔1和网孔2看
i
+ 4V _
3
成一个网孔，即 超级网孔
2Ω 2Ω
4Ω
2Ω
+ 12V_
i
i
2A
1
2
+ 6_V
超级网孔 方程
超级网孔 自电阻
4i1 6i2 6i3 12 6 4
i1 i2 2 补充方程 2i1 4i2 10i3 4
超级网孔 与网孔3的
互电阻
作业1
列写网孔方程，并求出u0 4Ω
3Ω
i
+
4Ω
3
6Ω
8V
_
i
2Ω i
1
2 2A
网孔电流等于支路电 流等于电流源电流
i2 2A
6i1 2i2 4i3 8 i2 2A 4i1 6i2 13i3 0
6i1 4i3 12 4i1 13i3 12
6 4
4
13
i1 i2
12 12
2、等效变换
5Ω + 6V _
电路3.4网孔电流法
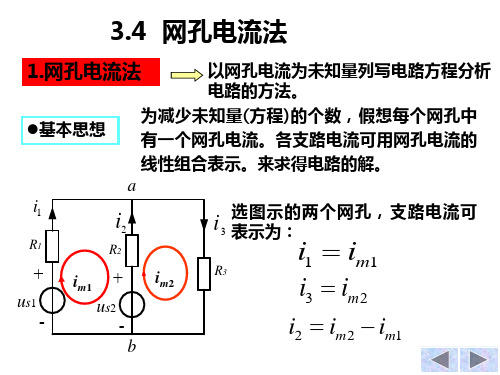
别用有关结点电压表示：
i1
u1 R1
is1
un1 R1
is1
①
i3
R3
i2
u2 R2
un2 R2
+
us3
i3
u3
us3 R3
un3 us3 R3
-
i4
u4 R4
un1 un2 R4
i5
u5 R5
un2 un3 R5
i6
u6 R6
is6
un1 un3 R6
is6
把支路电流用结点电压表示：
网孔电流法
网孔方程的一般形式(全部顺时)
R I11 m1 R I12 m2 R1m I mm U s11
RI 21 m1
RI 22 m2
RI 2m mm
U s 22
Rm1I m1 R I m2 m2 R I mm mm U smm
其中
Rjj为网孔j的自电阻(取正) Rij为网孔i,j的互电阻(取负)
例 列出图示电路的网孔分析法方程
1Ω
+ 1V -
Im1
0.1Ω 0.5Ω +
3A
1Ω
2V
Im2
Im3
-
(a)网孔2包括一个电流源，且等于网孔电流Im2， 相当于Im2已知，可不列该网孔的KVL方程。 如非要列，必须注意如何在该网孔方程中 考虑该电流源上的电压。
(b)应尽可能使电流源为网孔电流。
例 要点：独立源的处理
-G4Un2+(G4+G5)Un3 =－I
G5
看 成 电
①
增补方程Un1-Un3 = US ①
流 源
（2） 选择合适的参考点
《电路基础》第7讲 回路法、网孔法、节点法
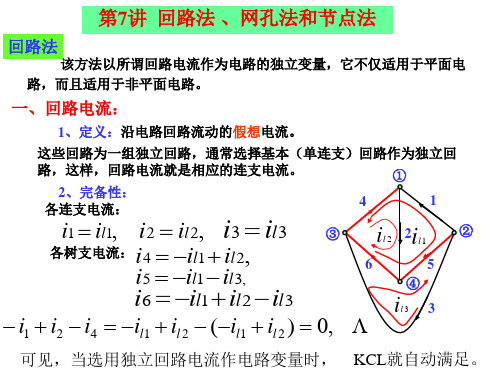
网孔法：回路法应用于平面电路时，选网孔电流作电路变 量，此时称网孔法。
结点电压法
结点电压法：以结点电压为未知变量列写电路方程分析电路的方法。
iS6
R6
①i6 iS1 i1 i4
R1
R4 ② R5
③
i2 R2 i5 i3 R3
+
一、结点电压：
o
-- uS3
1、定义：设定某一个结点为参考结点后，其它结点与参考结点之间的电压称 之结点电压。
代入KVL方程并整理得：
I4 R4 + _ US4
I1 R1
+ US1_
I2 R2
Ia + US2_
I3
Ib
R3 Ic
(R1+R2)Ia -R2Ib
= US1- US2
-R2Ia + (R2+R3)Ib - R3Ic
= US2
-R3Ib + (R3+R4)Ic = -US4
经观察，可找出以下规律：
1、自电阻Rkk： 恒取正号；回路k中所有电阻之和。 2、互电阻Rkj （kj）： 绕向一致取正号； 3、电压源项： 与绕向不一致的取正号；
I4 R4 + _ US4
小结：回路电流方程一般形式：
因为回路电流自动满足KCL，故只需列出 b-(n-1) 个 KVL方程，其一般形式为：
i i i u R R R 11 l1
网孔法：
i1
①
i3
R1
i2 R3
+ us1_
im1 R2
+
im2
+ _ us3
us2_
①
1
im1
2 im2
网孔电流法
R i1 + R i2 +... + R im = uS11 11 12 1m R21i1 + R22i2 +... + R2mim = uS22 ........................ Rm1i1 + Rm2i2 +... + Rm im = uSmm m
三、网孔电流法的应用
网孔分析法的计算步骤如下： 网孔分析法的计算步骤如下： 1．在电路图上标明网孔电流及其参考方向。规定各回路 ．在电路图上标明网孔电流及其参考方向。 绕行方向均与对应的网孔电流方向一致. 绕行方向均与对应的网孔电流方向一致 2．用观察法列出全部网孔电流方程,注意自电阻均为正值 ．用观察法列出全部网孔电流方程 注意自电阻均为正值 注意自电阻均为正值, 可为负值. 互电阻 可为负值 3．解联立方程组，求出各网孔电流。 ．解联立方程组，求出各网孔电流。 4．选定支路电流及参考方向。将支路电流用网孔电流表 ．选定支路电流及参考方向。 求得各支路电流。 示，求得各支路电流。 5．根据题目要求 计算支路电压和功率等 ．根据题目要求,计算支路电压和功率等 计算支路电压和功率等.
用网孔电流法求图示电路的支路电流。 例3 用网孔电流法求图示电路的支路电流。
解：设电流源电压为 ，考虑了电压 的网孔方程为： 设电流源电压为u，考虑了电压u的网孔方程为 的网孔方程为：
(1)i1 + u = 5V (2)i2 u = 10V
补充方程: 补充方程:
i1 i2 = 7A
i1 = 3A i2 = 4A u = 2V
i1
R1
② i5
R2
i2
i1 + i3 i4 = 0
us2
us1
电路分析网孔分析法和节点分析
电路分析网孔分析法和节点分析电路分析是电路理论和实际电路设计中的重要部分。
在电路分析中，有两种主要的方法，即网孔分析法和节点分析法。
本文将详细介绍这两种方法，并从理论和实践两个层面对这两种方法进行比较和对比。
首先，我们来看网孔分析法。
网孔分析法是通过将电路划分为若干个网孔来进行分析的方法。
网孔是由电路元件组成的闭合路径。
在网孔分析法中，我们可以根据基尔霍夫定律和欧姆定律，得到各个网孔中的电流和电压之间的关系。
通过解这些方程，我们可以得到电路中各个元件的电流和电压。
相对而言，网孔分析法适用于复杂的电路，因为通过合理划分网孔，可以降低计算复杂度。
其次，我们来看节点分析法。
节点分析法是通过将电路划分为若干个节点来进行分析的方法。
节点是电路中的交叉点或连接点。
在节点分析法中，我们可以根据基尔霍夫定律和欧姆定律，得到各个节点的电流和电压之间的关系。
通过解这些方程，我们可以得到电路中各个元件的电流和电压。
相对而言，节点分析法适用于简单的电路，因为节点分析法只需要解线性方程组，计算较为简单。
接下来，我们比较和对比这两种分析方法。
首先，网孔分析法和节点分析法都是基于基尔霍夫定律和欧姆定律进行分析的。
这两个定律是电路分析的基础，无论是网孔分析法还是节点分析法，都离不开这两个定律。
其次，网孔分析法和节点分析法在计算复杂度上有所不同。
网孔分析法需要对每个网孔进行分析和计算，所以在实际应用中可能需要解较多的方程，计算复杂度较高。
而节点分析法只需要解线性方程组，所以计算复杂度相对较低。
因此，网孔分析法适用于复杂的电路，而节点分析法适用于简单的电路。
最后，网孔分析法和节点分析法在电路分析结果的表示上有所不同。
在网孔分析法中，我们通常会得到各个网孔中的电流值，而在节点分析法中，我们通常会得到各个节点的电压值。
所以，在实际应用中，我们可以根据需要选择不同的方法，以得到更加直观和实用的分析结果。
综上所述，网孔分析法和节点分析法都是重要的电路分析方法，在不同的场景下，可以选择不同的方法进行电路分析。
[电路分析]网孔电流法
![[电路分析]网孔电流法](https://img.taocdn.com/s3/m/578688a2cc7931b764ce15b7.png)
网孔电流法一、网孔电流方程出发点进一步减少方程数，用未知的网孔电流代替未知的支路电流来建立方程。
图3.3-1所示电路，共有n=4个节点，b=6条支路（把电压源和电阻串联的电路看成一条支路）。
显然，独立的网孔数为b－n＋1=3个。
1、网孔电流设想每个网孔中有一个假想的电流沿着构成该网孔的各条支路循环流动，把这一假想的电流称为网孔电流（mesh current），如图3.3-1中的分别表示网孔a、b、c的网孔电流。
电路中各支路电流就可以用网孔电流表示结论：用3个网孔电流表示了6个支路电流。
进一步减少了方程数。
2、网孔电流方程根据KVL，可得图3.3-1电路的网孔电流方程网孔电流方程的一般形式自电阻×本网孔电流±Σ（互电阻×相邻网孔电流）= 本网孔中沿网孔电流方向的所有电压源的电位升之和自电阻（self resistance）是各网孔中所有支路电阻之和，互电阻（mutual resistance）是两个相邻网孔之间的共有电阻。
第二项前的正负号由相邻网孔电流与本网孔电流在互电阻上流过的方向是否一致来决定，若一致取正号；反之取负号。
网孔电流法分析电路的一般步骤确定电路中的网孔数，并设定各网孔电流的符号及方向。
按常规，网孔电流都取顺时针或逆时针方向。
列写网孔电流方程，并求解方程，求得各网孔电流。
由求得的网孔电流，再求其他的电路变量，如支路电流、电压等。
例3.3-1 图3.3-1所示电路中，已知us1=21V，us2=14V，us3=6V，us4=us5=2V，R1=3Ω，R2=2Ω，R3=3Ω，R4=1Ω，R5=6Ω，R6 =2Ω，求各支路电流。
解：1. 电路的网孔为3个。
设定3个网孔电流的符号及方向如图3.3-1所示。
2．列写网孔方程网孔a：网孔b：网孔c：代入参数，并整理，得解得网孔电流为：3．由网孔电流求各支路电流2、全欧姆定律只有一个网孔的电路，称为单回路电路（single loop circuit）。
电工基础——网孔电流法
电工基础——网孔电流法
网孔电流法（Mesh-Current Method）是一种分析任意拓扑复杂电路的分析方法，可以用来计算各个支路上的电压、电流和功率。
此方法以每个网格线段作为未知量，即电流在每个网格线段上的流动方向及大小为不确定因素，通过列方程的形式来求出网格线段上电流的值，最后求出相应的电压和电流，从而实现电路分析。
网孔电流法常用于处理复杂拓扑，即电路中有大量的支路，而这些电子元件之间又有多条连接线夹杂其中，可以使得这些电子元件形成连接在一起的电路结构。
在网孔电流法中，所有的支路用一个网格图表示，在网格上布放一个网格，每个支路由一条网格线段表示，电子元件的位置由网格线段的连接处表示，这种表示就叫做网格法。
首先，将电路中的所有主要构成元件都用一条网格线段表示，再将网格线段的交点（即支路交叉处）作为节点（node），将其他支路连接处（即没有交汇点）作为终端（terminal），全部构成一个网格结构。
其次，给出原始的方程组，其中以网格线段上的电流数值为未知量，每一条网格线段上的电流的大小都是未知的，然后利用电路的构成规律或理论推导来建立关于未知量的方程组，如Kirchhoff 电流定律（KCL）、Kirchhoff 电压定律（KVL）等，把这些方程组求解出相应的未知量，最后可以得到整个电路中所有未知量的值。
由于网格法是以网格线段为基础，因此可以灵活地处理电路中的支路，可以节省大量的计算量，因此，网孔电流法已经成为解决复杂电路问题的重要方法。
电工基础4.2 网孔电流法
I3=Im2、I4=Im3、
I5=Im1-Im3、I6=Im3-Im3
电第路三基章本电分路析分析的网络方程法
第五节 网孔分析法
对Im1、Im2、Im3、网孔列KVL方程有：
R1Im1+R5(Im1-Im3)+R2(Im1-Im2) =Us1-Us2
R2(-Im1+Im2)+R6(Im2-Im3)+R3Im3 =Us2
整理为： 5Im1-2Im2-Im3=6 -2Im1+11Im2-6Im3=3 -Im1-6Im2+10Im3=9.5 (第四步)解联立方程得： Im1=-0.5A Im2=1A Im3=1.5A
电第路三基章本电分路析分析的网络方程法
第五节 网孔分析法
（第五步）求解原题未知量：
I1=Im1=-0.5A I2=Im2=1A I3= Im3=1.5A I4=- Im1 + Im3 = 2A I5 = Im1 - Im2 =-1.5A I6= - Im2 + Im3 =0.5A
下面通过几个具体实例应用来介绍网孔 法的解题步骤 举例说明
例3-6 对图3-14所示电路，试用网孔法求 各支路电流。
电第路三基章本电分路析分析的网络方程法
第五节 网孔分析法
电第路三基章本电分路析分析的网络方程法
第五节 网孔分析法
解：（第一步）设网孔电流如图示
电第路三基章本电分路析分析的网络方程法
未知量，列写根据KVL、KCL及VCR 整理出的方程，求解未知量的方法。 以图3-13所示电路来说明网孔法的方 程。
电第路三基章本电分路析分析的网络方程法
第五节 网孔分析法
电路基础节点网孔法
运用节点法和网孔法进行电路分析众所周知，运用基尔霍夫定律和欧姆定律，我们可以对任何一个电路进行分析，以确定其运行条件（电流和电压值）。
一般电路分析的难点在于用最少的联立方程描述电路的运行特性。
在这一讲里，我们将介绍两种非常有效的可用于对任意电路进行分析的方法：节点法和网孔法。
这些方法是建立在对基尔霍夫定律的系统应用基础上的，我们将通过图1的例子电路来说明求解的步骤。
图1 一个典型的电阻电路节点法电压被定义为两点之间的电势差。
当我们讨论一个电路中某个确定节点的电压时，这就意味着我们已经设定了一个参考点。
通常这个参考点被定义为地。
节点法或节点电压法，是一种建立在KCL、KVL和欧姆定律基础之上的一种非常有效的电路分析法。
运用节点电压法分析一个电路的步骤如下：1.清楚地标注所有电路参数，并确定未知参数和已知参数。
2.确定电路中的所有节点。
3.选择一个节点作为参考节点，也可以叫做地，并把这个点的电势赋值为0。
电路中其他所有节点的电压都以参考节点作为参考。
4.标出其他所有节点的电压值。
5.赋值并标出极性。
6.在每个节点运用KCL定律，并用节点电压表示支路电流。
7.列出节点电压方程，并算出结果。
8. 得到各节点电压值后，可由欧姆定律确定各支路电流值。
我们利用图1的电路来示范节点法的求解过程。
图2 所显示的是第一步和第二步的执行。
图中已经标注了电路中的所有的元件并确定了电路中所有的相关节点。
图二 标记了节点的电路第三步要在这些确定了的节点当中选择一个作为参考节点。
我们可以有四种不同选择。
原则上，这些节点中的任意一个都可以被选为参考节点。
然而，有些节点比其他一些节点更有用。
所谓有用的节点就是那些能够使问题更容易地被理解和解决的节点。
我们需要记住一些通用的指导方针，以用于参考节点的选择。
1. 一个有用的参考节点应与最多数量的元件相连。
2. 一个有用的参考节点应与最多数量的电压源相连。
如我们的电路中，以节点作为参考节点的选择是最佳选择。
网孔分析法简单步骤及简单例题
网孔电流法的特点：仅适用于平面电路。 网孔分析法简单例题 1、网孔分析法求解电流 I 2、网孔分析法求解各支路电流
网孔分析法简单步骤及简单例题
什幺是网孔分析法 网孔分析法是电路基本分析方法的一种，以网孔电流为待求变量，按 KVL 建立方程求解电路的方法。 根据基尔霍夫定律：可以提供独立的 KVL 方程的回路数为 b-n+1 个， 网孔只是其中的一组。 网孔电流：沿每个网孔边界自行流动的闭合的假想电流。 一般对于 M 个网孔，自电阻×本网孔电流 + ∑（±）互电阻×相邻。 网孔电流 + ∑本网孔中电压升。 网孔分方向（常设为顺时针方向） 2、按照规律，采用观察法分析网孔 a、网孔中电流源视为开路，电压源视为短路。 b、以 KVL 为基础，列出网孔内的自导与互导的电压方程 3、解网孔电流 4、由网孔电流计算其它待求量 注意：电流源及受控源的处理 网孔分析法的一般步骤：
的方法称为网孔分析法。其网孔电流方程也称为网孔方程。 【例 3-2-1】图 3-2-1 所示电路列写网孔方程。 解：假定网孔电流分别在网孔 1、2、3 中流动，网孔电流的参考方向 如图 3-2-1 所示。 以支路电流为变量，列写各网孔的 KVL 方程为 为得到以网孔电流为未知变量的电路方程，用网孔电流表示各支路电 流，即有
（1）选定一组网孔，标明网孔电流及其参考方向; （2）以网孔电流的方向为网孔的巡行方向，列写各网孔 KVL 方程; （3）求解上述方程，得各网孔电流; （4）原电路韭公共支路的电流就等于网孔电流。 原电路公共支路的电流等于网孔电流的代数和。 网孔分析方程 【网孔电流】根据电流的连续性，可以假定一个电流在指定的网孔中 流动，这种电流称为网孔电流，对于电路中每一个结点，网孔电流流入一次 又流出一次，所以当以网孔电流作为电路待求变量时，电路的 KCL 方程自动 满足，只需列写 b-n+1 个网孔的 KVL 方程。 【网孔分析法】以网孔电流为待求变量，按 KVL 建立方程求解电路
电工基础——网孔电流法
例3 用网孔电流法求图示电路的支路电流。
解：设电流源电压为u，考虑了电压u的网孔方程为：
(1)i1 + u = 5V (2)i2 - u = -10V 补充方程: i1 - i2 = 7A
联立求解以上方程得到：
i1 = 3A i2 = -4A u = 2V 13
例4 用网孔电流法求解图示电路的网孔电流。
来表示。
2
i1 R1 ② R2 i2
us1 ① i4 R4
i5
R5 ④ R6 i6
us2
③
i3 R3 us3
i1 + i3 - i4 = 0 - i1 - i2 + i5 = 0 i2 - i3 - i6 = 0
i4 = i1 + i3 i5 = i1 + i2 i6 = i2 - i3
电流i4、i5和i6是非独立电流，它们由独立电流i1、i2和i3的线性 组合确定。这种线性组合的关系，可以设想为电流i1、i2和i3沿每个 网孔边界闭合流动而形成，如图中箭头所示。这种在网孔内闭合流
11
当电路中含有无伴电流源支路或含有受控源时的 处理方法:
1.无伴电流源在电路的边界支路上,设网孔电流就等于电流源 的电流,不再列写该回路的网孔电流方程。 2。无伴电流源在两个网孔的公共支路上，可以将电流源的端 电压u设为未知量，将其视为电压源的电压，列写网孔电流方 程。因增加了未知量，故必须补充一个方程。 3.如果电路中含有受控源,将其视为独立电源,列写网孔电流方 程,并将受控源的控制量用网孔电流表示,代入网孔电流方程中, 使方程中只含有网孔电流.
8
例1 用网孔电流法求图示电路各支路电流。
图2-22
解：①选定两个网孔电流i1和i2的参考方向，如图所示。 ②用观察电路的方法直接列出网孔方程：
电路分析基础网孔分析法
R21im1
R22im2
R1nimn us11 R2nimn us22
Rn1im1 Rn2im2 Gnnimn usnn
X
2.网孔分析法
R ii :网孔i的自电阻(self resistance)，等于网孔i内的所有电阻之和。
自电阻恒为正。
R ij :网孔i与网孔j之间的互电阻(mutual resistance)，等于i、j两网
的、具有特定功能的集成电路。
Offset null 1
Inverting input 2
NC
8
7 V
6 Output
+
Offset null 1 Inverting input 2 Noninverting input 3
8 NC
7 V
6 Output
Noninverting input 3
5 Offset null
4
V¯
金属外壳封装
V¯ 4
5 Offset null
DIP封装
1.运算放大器及其外部特性
7
39kΩ
4.5kΩ
3
2
30pF 7.5kΩ
25kΩ 6
50kΩ
1 1kΩ 50kΩ
5 1kΩ 5kΩ
50kΩ 50kΩ 4
LM741的电路原理图
1.运算放大器及其外部特性
a
符号 u - -
A
ud
+
b
o uo
电路分析基础网孔分析法
内容提要
定义 网孔分析法 几种特殊情况
X
1.定义
网孔分析法是以网孔电流作为电路变量列写方程求 解的一种方法。 网孔电流是一种假想的沿着网孔边界流动的电流。 基本思路：首先指定网孔电流方向；然后对各网孔列 写KVL方程，并根据各支路的VCR，将支路电压用网 孔电流表示；最后将用网孔电流表示的各支路的VCR 代入KVL方程，整理即得所求的网孔电流方程。 网孔分析法的实质：网孔的KVL方程。
网孔分析法PPT课件
i2 R2
us1 us4
i5
R5 us2
R4 i4 R6 i6
i3
R3
us3
15
2
4
6
3
说明：1）网孔分析法是回路分析法的特例
2）一个图G可以有很多种树，因此回路法 在变 量的选择上较网孔法更灵活。
例2：用回路分析法求 i 。
6
4A 2
i
3 2A
3V
4
2
1
3 6 5
说明：用回路法时尽可把电流源支路选为连支， 使之未知独立变量数减少。
2）一个图G可以有很多种树，因此割集法在 独立变量的选择上比节点法更灵活。
例1：用割集法求 i1
① 6V
5i2
2A ② 12V ③
i2
i1 ①
20 8 C1
④
1
4② 6
2
④
C2
5③
3
C3
说明：用割集法时尽可把电压源支路选为树支， 使之未知的独立变量减少。
§3-7 回路分析法
以连支电流作为求解量,对每一基本回 路列写支路电压以连支电流和电阻表示的 KVL方程求解电路的方法。
§3-4 网孔分析法
以网孔电流作为求解量,将网孔的KVL方程与支路 VAR相结合列写方程求解电路的方法。
说明：网孔法只适用于平面网络
网孔电流是独立的完备的电路变量
非平面网络
一）网孔电流方程式的建立过程
第一步：设网孔电流及其参考方向
第二步：对每一网孔列写 KVL方程(A）
第三步：各支路电流用网孔
i2
a)含受控电流源时
①
例4：列出图示电路的
节点方程 。
2A
2S
网孔与节点法
u6
-
-C +
u5=C u6=B - C
u4 -
独立性：节点电压彼此独立，不能互求。
u5
- -
对回路1: - u1 + u2 + u4=0
用节点电压表示: - A+（A - B）+B=0
《电路分析基础》
第3章网孔与节点分析方法
二、节点电压法：
依据：(1) KCL 步骤： (2) 支路VCR
基本步骤： 1）先将受控源暂当独立电源列方程；
2） 将控制量用网孔电流表示；
3）整理、化简方程，并求解。
举例1：求图示电路网孔电流。
6Ia - Ib-3Ic=0 -Ia+4 Ib-3Ic=-6 -3Ia -3 Ib+8 Ic=12-2U
Ib - Ia = U
Ia =1.29A
Ib=0.61A
Ic=2.38A
10 4 2
2
则：
1.6 70 2
43.06V
( 1 11) 10 4 2
若电路只一个独立节点，其节点方程为：
求得：
I1 = -4.306A
I2 = 10.765A
I3 = -13.471A
I sk Gk
( 弥尔曼定理)
《电路分析基础》
三、无阻电压源的处理
方法1： 选合适的参考节点使无阻电 压源成为一个已知节点电位，列 写其余节点电位方程。
U= -0.68V
Ia
Ib
Ic
《电路分析基础》
举例2：求图示电路网孔电流。
第3章网孔与节点分析方法
解：设受控电流源端电压为u，则：
3Ia - Ib-2Ic=10-u
电路基础-§2-3网孔电流法
第二章电阻电路§2-3 网孔电流法本章前面几节是利用等效变换,将电路简化成单回路电路,然后求出未知的电压和电流。
这些方法对简单电路很适合，但对于复杂电路，则用到下面两节要介绍的线性电路的一般分析方法。
主要讲述网孔电流法以及节点电压法，在讲述这两种方法之前，先了解网络分析法的概念。
一、网络分析法的概念网络分析法就是采用直接列写电路方程来分析线性电路的方法。
所以应用网络分析法首先必须选定电路的待求量（变量），这些变量可以是支路电流、支路电压、网孔电流、节点电压等。
然后根据KCL、KVL以及各元件的伏安特性建立网络方程，方程数应与变量数相同。
最后求解联立方程组，从而得出所求变量的值。
列写网络方程最基本的方法是支路电流法，这种方法就是以支路电流为变量来列写方程，电路中有b条支路，就设b 个支路电流变量，同时列写b个独立方程，求解该方程组，得到b个支路电流值。
以下例来简单说明支路法的特点。
【例2-10】用支路法分析图2-23电路的支路电流I 1、I 2、I 3。
⎪⎩⎪⎨⎧=+=-+-=-+3213231082040882I I I I I I I 解A I 781-=A I 7172=A I 793=二、网孔电流法（一）网孔电流的概念⎪⎭⎪⎬⎫+=+++---=-+++--=--++43364326142362652154134251451)()()(s s m m m s m m m s s m m m u u i R R R i R i R u i R i R R R i R u u i R i R i R R R ⎪⎭⎪⎬⎫=++=++=++333332321312232322212111313212111s m m m s m m m s m m m u i R i R i R u i R i R i R u i R i R i R ⎪⎪⎭⎪⎪⎬⎫=+++=+++=+++snn mn nn m n m n s mn n m m s mn n m m u i R i R i R u i R i R i R u i R i R i R 2211222222121111212111（二）网孔电流方程（三）网孔电流法的解题步骤（1）选定各网孔电流的参考方向，同时它们也是列KVL方程的绕行方向。
L10-1 网孔电流法
网孔电流法（一）
网孔电流法的一般步骤：
（1）选定l=b-n+1个网孔， 标明各网孔电流及方向。 （2）对l个网孔，以 网孔电流为未知量，列写KVL
方程； （3）求解KVL方程，得各网孔电流，进一步求得
各支路电压、电流。
I5
Im—3
网孔3 R31Im1 +R32Im2 +R33Im3 ＝ US
网孔电流法（一）
例1 桥式电路中， US=12 V，R1=R2=R4=5Ω， R3=10Ω， 中间支路是一检 流计，其电阻RG=10Ω。求检流计中电流。
R11＝R1+RG+ R3 =5+10+10=25Ω
Im1
Im2
IG
R22 ＝RG+R2+ R4 =10+5+5=20Ω R33＝R3+ R4 =10+5=15Ω R12＝R21＝－RG =-10Ω
I5
—
I2 R2 - I4 R4 - IG RG = 0 I3 R3 + I4 R4 - US = 0
网孔电流法（一）
能否选择一组数量更少的电流、电压变量分析电路? 所选变量必须具备以下性质：
完备性 这些变量求得以后，利用它们可以获得所有的
支路电压和电流。
独立性 如果是电流变量，应自动满足KCL；如果是电
网孔电流法（一）
(R1+ R2) im1-R2im2=uS1-uS2
- R2im1+ (R2 +R3) im2 =uS2 记 uSm1= uS1-uS2 uSm2= uS2
i1
i2
R1 im1R2
+
+
im2
3.2 网孔电流法
u13 un1
u23 un2
u12 un1 un2
2.节点的自电导与互电导 与电路中节点直接相连接的支路所有电导之和， 称为该节点的自电导，简称自导。电路中相邻节 点共有的电导，称为两个节点的互电导，简称互 导。相邻节点的互导相等。 各节点电压在自导中引起的电流总是流出该节点 的，因而自导总是正的；另一节点电压通过互导 引起的电流总是流入该节点的，因而互导总是负 的；两个节点之间没有电导时，互导为零。
3.网孔电流方程 在列写网孔方程时，原则上与支路电流法中列 写KVL方程一样，只是需要用网孔电流表示各 电阻上的电压，且当电阻中同时有几个网孔电 流流过时，应该把各网孔电流引起的电压都计 算进去。通常，选取网孔的绕行方向与网孔电 流的参考方向一致，然后列出网孔方程。
R11im1 R12im2 R13im3 uS11 R21im1 R22im2 R23im3 uS22 R i R i R i u 32 m2 33 m3 S33 31 m1
I
例2-19 电路如图2-38所示，试用网孔电流法求 支路电流 I、I2Ω、I4Ω及电压U。
解 标定网孔电流Im1、Im2、Im3的参考方向如 图所示。网孔3中有一个1A的理想电流源，因 而在网孔3的边界支路，故Im3=1A ，因而不需 要再列写网孔3的方程。按照网孔电流法的规 则，分别列出网孔1、网孔2的方程为： 网孔1 1 2 1 Im1 2Im2 Im3 2 网孔2 2Im1 2 4 1 Im2 4Im3 0 将Im3=1A代入，整理得到联立方程为
G2un1 G2 G3 un2 G2uS2 iS3
G11un1 G12un2 iS11 G21un1 G22un2 iS22
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
电路基础理论中关于网孔数目的计算方法
作者：陈建斌
来源：《科学与财富》2011年第05期
[摘要] 本文针对本校专科电路基础教材中网孔数目计算过程的空白，通过运用教材的基本定义，结合数学归纳或者总结归纳的方法，分析得出网孔数目的计算公式或规律。
以增强学生对电路基础课程的理解，达到良好的理论教学效果。
[关键词] 电路基础理论网孔数目 b-n+1
在电路基础课程的学习中，当我们介绍到2b方程：对具有b条支路n个结点的连通电路，可以列出n-1个线性无关的KCL方程和b-n+1个线性无关的的KVL方程时，很多同学对为什么是b-n+1个线性无关的KVL方程时提出疑问。
在这里的b-n+1其实是网孔数目。
因为KVL方程是针对回路或者闭合路径列出的，而要列出线性无关的KVL方程则直接由网孔列出就可以，而任何回路的KVL方程都可由此回路所包含的网孔的KVL方程相加得到，所以回路的KVL方程并不是线性无关的。
接下来我们分析网孔数目b-n+1是如何得来，即网孔数目的计算方法。
首先，我们先了解关于支路、结点、回路和网孔的定义。
特别说明：由于教材不同可能关于这四个名词的定义不一样，但计算结果是相同的。
本文定义采用普通高等教育“十五”国家规划教材·高职高专教育版·高等教育出版社·胡翔骏主编·《电路基础简明教程》。
支路：一个二端元件视为一条支路。
结点：电路元件的联接点。
（两结点间由理想导线相连，视为一个结点）
回路：由支路组成的闭合路径。
网孔：将电路画在平面上，内部不含有支路的回路。
接下来，假设支路有b条，结点有n个，对应网孔数目为M，我们先分析两种比较特殊的情况：
（1）因为b条支路就是b个二端元件，当这b个二端元件全部串联在一起时，结点数目最多，有b个，即n=b，如图1所示，此时网孔数M=1=b-b+1=b-n+1
（2）当此b个二端元件全部并联时，结点数目最少，n=2,如图2所示，此时网孔数M=b-1=b-2+1=b-n+1
综合（1）、（2）两种情况得出b以及n与b的关系，即b≧2且2≦n≦b(n,b∈N).那么，接下来介于（1）、（2）两种情况之间的其他情况呢？
我们可以用一个表来表示支路数b、结点数n和网孔数M之间的关系：
从上表中其实我们很容易发现一个规律：当n=2递增到n=b时，网孔数相应从M=b-1递减到M=1；那么n和M的和就是不变的，即n+M始终等于b+1，由此我们得出网孔数M=b-n+1。
以上我们对2b方程中关于可以列出b-n+1个线性无关的KVL方程就做了详细分析，对同学们理解2b方程有很重要的作用，也从而为后面关于支路电压/电流法和网孔/结点分析法打好坚实基础。
参考文献
[1]胡翔骏.电路基础简明教程[M].北京：高等教育出版社，2004（1）
[2]周长源.电路理论基础[M].北京：高等教育出版社，1996（2）■
注：本文中所涉及到的图表、注解、公式等内容请以PDF格式阅读原文。