(完整版)初一数学人教版(下册)与三角形有关的角练习题一(含答案)
与三角形有关的角练习题
与三角形有关的角练习题一、选择题：1．若一个三角形的三个内角互不相等,则它的最小角必小于( ）A.45B.60C.30D.12．下列命题中，不正确的为( ）A ．钝角三角形是斜三角形B ．在一个三角形中至多有一个内角不小于60C ．三角形的没有公共顶点的两个外角的和大于平角D ．三角形的外角中，最小的一个是钝角，那它一定是锐角三角形3．以下命题正确的是（ ）A.三角形三个外角的和是360 B ．三角形一个外角大于它的两个内角的和C 。
三角形的外角都不大于90D ．三角形中的内角没有大于120的4．下列说法正确的是（ ）A.一个钝角三角形一定不是等腰三角形，也不是等边三角形B ．一个等腰三角形一定是锐角三角形，或直角三角形C.一个直角三角形一定不是等腰三角形，也不是等边三角形D ．一个等边三角形一定不是钝角三角形，也不是直角三角形5．三角形的三个外角中，钝角的个数最少是（ )A ．3B ．2C ．1D ．06．如图，ABC ∆中，AD 是BC 边上中线，AE 是BD 边的中线,AF 是DC 边的中线,且AB<AC,则下列结论中错误的是（ ）A ．1>2>3>C ∠∠∠∠B ．BE=ED=DF=FCC ．1>4+5+C ∠∠∠∠D ．AE=AF7．锐角三角形中,两个锐角的和必大于（ )A ．120B ．110C ．100D ．908．如图，在△ADE 中，引线段EB 与EC ，下列各等式中，正确的是（ ）A ．A+1+7=D+3+6∠∠∠∠∠∠B ．1+5=2+7∠∠∠∠C ．6+A=2+7∠∠∠∠D ．A+5+7=2+8+6∠∠∠∠∠∠9．若一个三角形的三个外角的度数之比为2:3:4，则与之对应的三个内角的度数之比为 （ )A ．4:3：2 B ．3:2:4 C ．5:3：1 D ．3：1：510．如图，已知1=60,A+B+C+D+E+F ∠∠∠∠∠∠∠（ ）A ．360B ．540C ．240D ．28011．a ， b ，c 是ABC ∆的三边长，且22(a b)(b c)+=+，则ABC ∆一定是（ ） A ．等腰三角形 B ．直角三角形C 。
(完整word版)初一数学人教版(下册)三角形练习题一(含答案)
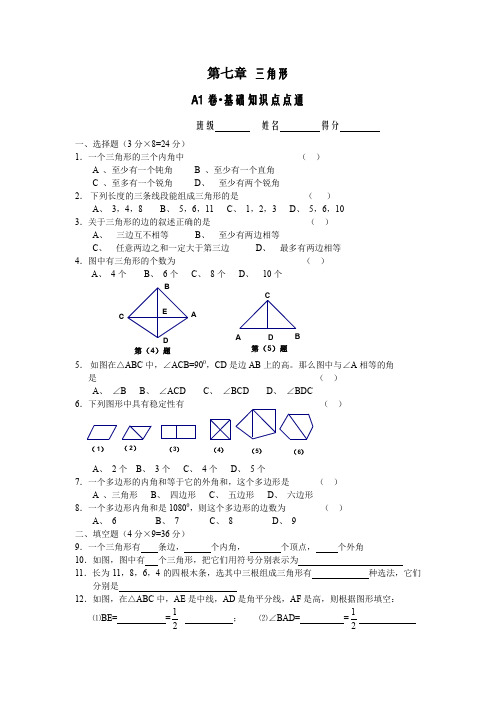
第七章三角形A1卷•基础知识点点通班级姓名得分一、选择题（3分×8=24分）1．一个三角形的三个内角中（）A 、至少有一个钝角B 、至少有一个直角C 、至多有一个锐角D、至少有两个锐角2．下列长度的三条线段能组成三角形的是（）A、3，4，8B、5，6，11C、1，2，3D、5，6，103．关于三角形的边的叙述正确的是（）A、三边互不相等B、至少有两边相等C、任意两边之和一定大于第三边D、最多有两边相等4．图中有三角形的个数为（）A、4个B、6个C、8个D、10个5．如图在△ABC中，∠ACB=900，CD是边AB上的高。
那么图中与∠A相等的角是（）A、∠BB、∠ACDC、∠BCDD、∠BDC6．下列图形中具有稳定性有（）A、2个B、3个C、4个D、5个7．一个多边形的内角和等于它的外角和，这个多边形是（）A 、三角形B、四边形C、五边形D、六边形8．一个多边形内角和是10800，则这个多边形的边数为（）A、6B、7C、8D、9二、填空题（4分×9=36分）9．一个三角形有条边，个内角，个顶点，个外角10．如图，图中有个三角形，把它们用符号分别表示为11．长为11，8，6，4的四根木条，选其中三根组成三角形有种选法，它们分别是12．如图，在△ABC中，AE是中线，AD是角平分线，AF是高，则根据图形填空：⑴BE= =21；⑵∠BAD= =21第（4）题EDCBA第（5）题DCBA（1）（2）（3）（4）（5）（6）⑶∠AFB= =900；13．在△ABC 中，若∠A=800，∠C=200，则∠B= 0， 若∠A=800，∠B=∠C ，则∠C= 014．已知△ABC 的三个内角的度数之比∠A ：∠B ：∠C=1：3：5，则∠B= 0，∠C= 015．如图，在△ABC 中，∠BAC=600，∠B=450，AD 是△ABC 的一条角平分线，则∠DAC= 0，∠ADB= 016．十边形的外角和是 0；如果十边形的各个内角都相等，那么它的一个内角是17．如图，∠1=∠2=300，∠3=∠4，∠A=800，则=x ，=y三、解下列各题18．对下面每个三角形，过顶点A 画出中线，角平分线和高（4分×3=12分）19．求出下列图中x 的值：（4分×3=12分）20．（8分）一个多边形的外角和是内角和的72，求这个多边形的边数第（10）题E D CBA第（12）题B第（15）题D CA800yx4321第（17）题E D CBA(1)C B A C B A(2)C B A (3)(1)x 0x 0(2)(3)4x ︒3x ︒3x ︒2x ︒21．在△ABC 中，∠A=21∠C=21∠ABC ， BD 是角平分线，求∠A 及∠BDC 的度数（8分）附加题（10分×2=20分）22.如图，已知∠1=∠2，∠3=∠4，∠A=1000，求x 的值。
七年级下册数学《三角形有关的角》例题
三角形有关的角有疑问的题目请发在“51加速度学习网”上，让我们来为你解答（）51加速度学习网整理一、知识回顾1、任何三角形的内角和都等于180°2、三角形的一个外角等于不相邻的两个内角之和。
3、三角形的外角和等于360°。
二、典型例题例1：一个三角形的三个内角中（）A．至少有一个钝角B．至少有一个直角C．至多有一个锐角D．至少有两个锐角分析：此题考查三角形内角和定理，较为容易．解答：根据三角形内角和定理，一个三角形的三个内角中至少有两个锐角．故选D．_________________________________________________________________________例2：已知在△ABC中，∠A=70°-∠B，则∠C等于（）A．35°B．70°C．110°D．140°分析：结合已知条件，根据三角形的内角和为180°求解．解答：∵∠A=70°-∠B，∴∠A+∠B=70°，∴∠C=180°-（∠A+∠B）=180°-70°=110°（三角形的内角和为180°）．故选C．_________________________________________________________________________例3：（2012•天门）如图，AB∥CD，∠A=48°，∠C=22°．则∠E等于（）A．70°B．26° C．36° D．16°分析：由AB∥CD，根据两直线平行，内错角相等，即可求得∠1的度数，又由三角形外角的性质，即可求得∠E的度数．解答：∵AB∥CD，∠A=48°，∴∠1=∠A=48°，∵∠C=22°，∴∠E=∠1-∠C=48°-22°=26°．故选B．______________________________________________________________________________ 例4：（2012•云南）如图，在△ABC中，∠B=67°，∠C=33°，AD是△ABC的角平分线，则∠CAD的度数为（）A．40° B．45° C．50° D．55°分析：首先利用三角形内角和定理求得∠BAC的度数，然后利用角平分线的性质求得∠CAD 的度数即可．解答：∵∠B=67°，∠C=33°，∴∠BAC=180°-∠B-∠C=180°-67°-33°=80°∵AD是△ABC的角平分线，∴∠CAD=1/2 ∠BAD=1/2 ×80°=40°故选A．______________________________________________________________________________例5：（1999•南昌）已知△ABC中，∠A：∠B：∠C=2：3：4，则这个三角形是（）A．锐角三角形B．直角三角形 C．钝角三角形D．等腰三角形分析：根据比例，设三个内角为2k、3k、4k，根据三角形的内角和定理求出最大角的度数．解答：根据题意，设∠A、∠B、∠C分别为2k、3k、4k，则∠A+∠B+∠C=2k+3k+4k=180°，解得k=20°，∴4k=4×20°=80°＜90°，所以这个三角形是锐角三角形．故选A．______________________________________________________________________________例6：（2012•肇庆）如图，已知D、E在△ABC的边上，DE∥BC，∠B=60°，∠AED=40°，则∠A的度数为（）A．100° B．90° C．80° D．70°分析：先根据平行线的性质求出∠C的度数，再根据三角形内角和定理求出∠A的度数即可．解答：∵DE∥BC，∠AED=40°，∴∠C=∠AED=40°，∵∠B=60°，∴∠A=180°-∠C-∠B=180°-40°-60°=80°．故选C．例7：（2009•铁岭）如图所示，已知直线AB∥CD，∠C=125°，∠A=45°，则∠E的度数为（）A．70° B．80° C．90° D．100°分析：首先根据两条直线平行，同位角相等，得∠BFE的度数；再根据三角形的一个外角等于和它不相邻的两个内角和求解．解答：∵AB∥CD，∠C=125°∴∠BFE=125°∴∠E=∠BFE-∠A=125°-45°=80°．故选B例8：（2008•聊城）如图，∠1=100°，∠2=145°，那么∠3=（）A．55°B．65° C．75°D．85°分析：由题可知，∠4=180°-∠1，∠5=180°-∠2，又因为∠3+∠4+∠5=180°，从而推出∠3=65°解答：∵∠1=100°，∠2=145°，∴∠4=180°-∠1=180°-100°=80°，∠5=180°-∠2=180°-145°=35°，∵∠3=180°-∠4-∠5，∴∠3=180°-80°-35°=65°．故选B．三、解题经验本节题目常常结合前面所学的知识来考查，我们要对三角形的内角和定理必须理解，感兴趣的同学可以把三角形拼成平行四边形来证明这个定理。
人教版初中数学七年级下册《三角函数》测试题(含答案)
人教版初中数学七年级下册《三角函数》测试题(含答案)1. 三角函数只适用于正三角形吗？答案：不仅适用于正三角形，还适用于普通三角形和任意角的三角形。
2. 在直角三角形ABC中，已知∠B=90°，AB=6cm，BC=8cm，求∠A和∠C的正弦、余弦、正切值。
答案：- 正弦值：sinA = AB/AC = 6/10 = 0.6，sinC = BC/AC = 8/10 = 0.8- 余弦值：cosA = BC/AC = 8/10 = 0.8，cosC = AB/AC = 6/10 = 0.6- 正切值：tanA = AB/BC = 6/8 = 0.75，tanC = BC/AB = 8/6 =1.333. 在任意三角形ABC中，已知∠A=30°，a=8cm，b=5cm，求∠B和∠C的正弦、余弦、正切值。
答案：- 正弦值：sinB = b/AC = 5/8.66 ≈ 0.577，sinC = c/AC = √3/2 ≈ 0.866- 余弦值：cosB = c/AC = √3/2 ≈ 0.866，cosC = a/AC = 4/8.66 ≈ 0.462- 正切值：tanB = b/a = 5/8 ≈ 0.625，tanC = c/a = √3/4 ≈ 0.8664. 已知sinA = 0.4，且A为锐角，求A的值。
答案：A = arcsin(0.4) ≈ 23.58°5. 已知∠A=60°，求cosA的值。
答案：cosA = cos(60°) = 0.56. 在任意三角形ABC中，已知a=6cm，b=8cm，c=10cm，求∠A、∠B、∠C的正弦、余弦、正切值。
答案：- 正弦值：sinA = a/BC = 6/10 = 0.6，sinB = b/AC = 8/10 = 0.8，sinC = c/AB = 10/8 ≈ 1.25- 余弦值：cosA = b/AB = 8/10 = 0.8，cosB = a/AC = 6/10 = 0.6，cosC = c/BC = 10/6 ≈ 1.67- 正切值：tanA = a/b = 6/8 = 0.75，tanB = b/a = 8/6 ≈ 1.33，tanC = c/a = 10/6 ≈ 1.67。
七年级下册数学三角形测试题(含答案)
第7章三角形一、选择题1．如果在一个顶点周围用两个正方形和n 个正三角形恰好可以进行平面镶嵌，则n 的值是（ ）．A ．3 B ．4 C ．5 D ．6 2．下面四个图形中，线段BE 是⊿ABC 的高的图是（ ）3．（20XX 年••福州市）已知三角形的两边长分别为4cm 和9cm ，则下列长度的四条线段中能作为第三边的是（ ） A ．13cmB ．6cmC ．5cmD ．4cm4．三角形一个外角小于与它相邻的内角，这个三角形是（ ） A ．直角三角形 B ．锐角三角形 C ．钝角三角形 D ．属于哪一类不能确定 5．如图，在直角三角形ABC 中，AC ≠AB ，AD 是斜边上的高， DE ⊥AC ，DF ⊥AB ，垂足分别为E 、F ，则图中与∠C （∠C 除外）相等的角的个数是（ ） A 、3个 B 、4个 C 、5个 D 、6个6．如图，将一副三角板叠放在一起，使直角的顶点重合于O ， 则∠AOC+∠DOB=（ ）A 、900B 、1200C 、1600D 、18007．以长为13cm 、10cm 、5cm 、7cm 的四条线段中的三条线段为边，可以画出三角形的个数是（ ）(A)1个 (B)2个 (C)3个 (D)4个8．给出下列命题：①三条线段组成的图形叫三角形 ②三角形相邻两边组成的角叫三角形的内角 ③三角形的角平分线是射线 ④三角形的高所在的直线交于一点，这一点不在三角形内就在三角形外 ⑤任何一个三角形都有三条高、三条中线、三条角平分线 ⑥三角形的三条角平分线交于一点，且这点在三角形内。
正确的命题有( )A.1个B.2个C.3个D.4个第5题图第6题图二、填空题9．如图，一面小红旗其中∠A=60°, ∠B=30°,则∠BCD= 。
10．为了使一扇旧木门不变形，木工师傅在木门的背面加钉了一根木条这样做的道理是___________________.11．把一副常用的三角板如图所示拼在一起，那么图中∠ADE 是 度。
人教版初中数学三角形经典测试题及答案
人教版初中数学三角形经典测试题及答案本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.March人教版初中数学三角形经典测试题及答案一、选择题1．如图，在菱形ABCD 中，点A 在x 轴上，点B 的坐标轴为()4,1, 点D 的坐标为()0,1， 则菱形ABCD 的周长等于（ ）A ．5B ．43C ．45D ．20【答案】C【解析】【分析】 如下图，先求得点A 的坐标，然后根据点A 、D 的坐标刻碟AD 的长，进而得出菱形ABCD 的周长.【详解】如下图，连接AC 、BD ，交于点E∵四边形ABCD 是菱形，∴DB ⊥AC ，且DE=EB又∵B ()4,1，D ()0,1∴E(2，1)∴A(2，0)∴AD=()()2220015-+-= ∴菱形ABCD 的周长为：45故选：C【点睛】本题在直角坐标系中考查菱形的性质，解题关键是利用菱形的性质得出点A 的坐标，从而求得菱形周长.2．如图，在ABC 中，AB AC =，30A ∠=︒，直线a b ∥，顶点C 在直线b 上，直线a 交AB 于点D ，交AC 与点E ，若1145∠=︒，则2∠的度数是（ ）A ．30°B ．35°C ．40°D ．45°【答案】C【解析】【分析】 先根据等腰三角形的性质和三角形内角和可得ACB ∠度数，由三角形外角的性质可得AED ∠的度数，再根据平行线的性质得同位角相等，即可求得2∠．【详解】∵AB AC =，且30A ∠=︒，∴18030752ACB ∠︒-︒==︒， 在ADE ∆中，∵1145A AED ∠∠∠=+=︒，∴14514530115AED A ∠∠=︒-=︒-︒=︒，∵//a b ，∴2AED ACB ∠∠∠=+，即21157540∠=︒-︒=︒，故选：C ．【点睛】本题考查综合等腰三角形的性质、三角形内角和定理、三角形外角的性质以及平行直线的性质等知识内容．等腰三角形的性质定理：等腰三角形两底角相等；三角形内角和定理：三角形三个内角的和等于180 ；三角形外角的性质：三角形的外角等于与它不相邻的两个内角之和；两直线平行，同位角相等．3．如图，已知AB∥CD，直线AB，CD被BC所截，E点在BC上，若∠1＝45°，∠2＝35°，则∠3＝（）A．65°B．70°C．75°D．80°【答案】D【解析】【分析】由平行线的性质可求得∠C，在△CDE中利用三角形外的性质可求得∠3．【详解】解：∵AB∥CD，∴∠C＝∠1＝45°，∵∠3是△CDE的一个外角，∴∠3＝∠C+∠2＝45°+35°＝80°，故选：D．【点睛】本题主要考查平行线的性质，掌握平行线的性质和判定是解题的关键，即①两直线平行⇔同位角相等，②两直线平行⇔内错角相等，③两直线平行⇔同旁内角互补，④a∥b，b∥c⇒a∥c．4．如图，11∥l2，∠1＝100°，∠2＝135°，则∠3的度数为()A ．50°B ．55°C ．65°D ．70°【答案】B【解析】【分析】 如图，延长l 2，交∠1的边于一点，由平行线的性质，求得∠4的度数，再根据三角形外角性质，即可求得∠3的度数．【详解】如图，延长l 2，交∠1的边于一点，∵11∥l 2，∴∠4＝180°﹣∠1＝180°﹣100°＝80°，由三角形外角性质，可得∠2＝∠3+∠4，∴∠3＝∠2﹣∠4＝135°﹣80°＝55°，故选B ．【点睛】本题考查了平行线的性质及三角形外角的性质，熟练运用平行线的性质是解决问题的关键．5．如图，在ABC 中，AB AC =，点E 在AC 上，ED BC ⊥于点D ，DE 的延长线交BA 的延长线于点F ，则下列结论中错误的是（ ）A ．AE CE =B ．12DEC BAC ∠=∠ C ．AF AE =D ．1902B BAC ∠+∠=︒ 【答案】A【解析】【分析】 由题意中点E 的位置即可对A 项进行判断；过点A 作AG ⊥BC 于点G ，如图，由等腰三角形的性质可得∠1=∠2=12BAC ∠，易得ED ∥AG ，然后根据平行线的性质即可判断B 项；根据平行线的性质和等腰三角形的判定即可判断C 项；由直角三角形的性质并结合∠1=12BAC ∠的结论即可判断D 项，进而可得答案． 【详解】解：A 、由于点E 在AC 上，点E 不一定是AC 中点，所以,AE CE 不一定相等，所以本选项结论错误，符合题意；B 、过点A 作AG ⊥BC 于点G ，如图，∵AB =AC ，∴∠1=∠2=12BAC ∠， ∵ED BC ⊥，∴ED ∥AG ，∴122DEC BAC ∠=∠=∠，所以本选项结论正确，不符合题意； C 、∵ED ∥AG ，∴∠1=∠F ，∠2=∠AEF ，∵∠1=∠2，∴∠F =∠AEF ，∴AF AE =，所以本选项结论正确，不符合题意；D 、∵AG ⊥BC ，∴∠1+∠B =90°，即1902B BAC ∠+∠=︒，所以本选项结论正确，不符合题意．故选：A ．【点睛】本题考查了等腰三角形的判定和性质、平行线的判定和性质以及直角三角形的性质等知识，属于基本题型，熟练掌握等腰三角形的判定和性质是解题的关键．6．下列说法不能得到直角三角形的（ ）A ．三个角度之比为 1：2：3 的三角形B ．三个边长之比为 3：4：5 的三角形C ．三个边长之比为 8：16：17 的三角形D ．三个角度之比为 1：1：2 的三角形 【答案】C【解析】【分析】三角形内角和180°，根据比例判断A 、D 选项中是否有90°的角，根据勾股定理的逆定理判断B 、C 选项中边长是否符合直角三角形的关系.【详解】A 中，三个角之比为1:2:3，则这三个角分别为：30°、60°、90°，是直角三角形； D 中，三个角之比为1:1:2，则这三个角分别为：45°、45°、90°，是直角三角形；B 中，三边之比为3:4:5，设这三条边长为：3x 、4x 、5x ，满足：()()()222345x x x +=，是直角三角形；C 中，三边之比为8:16:17，设这三条边长为：8x 、16x 、17x ，()()()22281617x x x +≠，不满足勾股定理逆定理，不是直角三角形故选：C【点睛】本题考查直角三角形的判定，常见方法有2种；（1）有一个角是直角的三角形；（2）三边长满足勾股定理逆定理.7．如图，□ABCD的对角线AC、BD交于点O，AE平分BAD交BC于点E，且∠ADC＝60°，AB＝12BC，连接OE．下列结论：①AE＝CE；②S△ABC＝AB•AC；③S△ABE＝2S△AOE；④OE＝14BC,成立的个数有（）A．1个B．2个C．3个D．4【答案】C【解析】【分析】利用平行四边形的性质可得∠ABC=∠ADC=60°，∠BAD=120°，利用角平分线的性质证明△ABE是等边三角形，然后推出AE=BE=12BC，再结合等腰三角形的性质：等边对等角、三线合一进行推理即可．【详解】∵四边形ABCD是平行四边形，∴∠ABC=∠ADC=60°，∠BAD=120°，∵AE平分∠BAD，∴∠BAE=∠EAD=60°∴△ABE是等边三角形，∴AE=AB=BE，∠AEB=60°，∵AB=12BC ， ∴AE=BE=12BC ， ∴AE=CE ，故①正确；∴∠EAC=∠ACE=30°∴∠BAC=90°，∴S △ABC =12AB•AC ，故②错误； ∵BE=EC ，∴E 为BC 中点，O 为AC 中点，∴S △ABE =S △ACE=2 S △AOE ，故③正确；∵四边形ABCD 是平行四边形，∴AC=CO ，∵AE=CE ，∴EO ⊥AC ，∵∠ACE=30°，∴EO=12EC ， ∵EC=12AB ， ∴OE=14BC ，故④正确； 故正确的个数为3个，故选：C ．【点睛】此题考查平行四边形的性质，等边三角形的判定与性质．注意证得△ABE 是等边三角形是解题关键．8．如图，四边形ABCD 和EFGH 都是正方形，点E H ，在ADCD ，边上，点F G ，在对角线AC 上，若6AB ，则EFGH 的面积是( )A．6 B．8 C．9 D．12【答案】B【解析】【分析】根据正方形的性质得到∠DAC＝∠ACD＝45°，由四边形EFGH是正方形，推出△AEF与△DFH是等腰直角三角形，于是得到DE 22EF，EF2AE，即可得到结论．【详解】解：∵在正方形ABCD中，∠D＝90°，AD＝CD＝AB，∴∠DAC＝∠DCA＝45°，∵四边形EFGH为正方形，∴EH＝EF，∠AFE＝∠FEH＝90°，∴∠AEF＝∠DEH＝45°，∴AF＝EF，DE＝DH，∵在Rt△AEF中，AF2＋EF2＝AE2，∴AF＝EF 2 AE，同理可得：DH＝DE＝22EH又∵EH＝EF，∴DE＝22EF＝22×22AE＝12AE，∵AD＝AB＝6，∴DE＝2，AE＝4，∴EH＝2DE＝22，∴EFGH的面积为EH2＝（22）2＝8，故选：B．【点睛】本题考查了正方形的性质，等腰直角三角形的判定及性质以及勾股定理的应用，熟练掌握图形的性质及勾股定理是解决本题的关键．9．如图，已知△ABC是等腰直角三角形，∠A＝90°，BD是∠ABC的平分线，DE⊥BC于E，若BC＝10cm，则△DEC的周长为（）A．8cm B．10cm C．12cm D．14cm【答案】B【解析】【分析】根据“AAS”证明ΔABD≌ΔEBD .得到AD＝DE，AB＝BE，根据等腰直角三角形的边的关系，求其周长.【详解】∵BD是∠ABC的平分线，∴∠ABD＝∠EBD.又∵∠A＝∠DEB＝90°，BD是公共边，∴△ABD≌△EBD (AAS)，∴AD＝ED，AB＝BE，∴△DEC的周长是DE＋EC＋DC＝AD＋DC＋EC＝AC＋EC＝AB＋EC＝BE＋EC＝BC＝10 cm.故选B.【点睛】本题考查了等腰直角三角形的性质，角平分线的定义，全等三角形的判定与性质. 掌握全等三角形的判定方法（即SSS 、SAS 、ASA 、AAS 和HL ）和全等三角形的性质（即全等三角形的对应边相等、对应角相等）是解题的关键．10．如图，正方体的棱长为6cm ，A 是正方体的一个顶点，B 是侧面正方形对角线的交点．一只蚂蚁在正方体的表面上爬行，从点A 爬到点B 的最短路径是（ ）A ．9B ．310C ．326+D ．12【答案】B【解析】【分析】 将正方体的左侧面与前面展开，构成一个长方形，用勾股定理求出距离即可．【详解】解：如图，AB=22(36)3310++= ．故选：B ．【点睛】此题求最短路径，我们将平面展开，组成一个直角三角形，利用勾股定理求出斜边就可以了．11．等腰三角形有一个是50°，它的一条腰上的高与底边的夹角是（）A．25°B．40°C．25°或40°D．50°【答案】C【解析】∵等腰三角形有一个是50°∴有两种可能①是三个角为50°、50°、80°；②是三个角为50°、65°、65°分情况说明如下：①当三个角为50°、50°、80°时，根据图①，可得其一条腰上的高与底边的夹角∠DAB=40°；②当三个角为50°、65°、65°，根据图②，可得其一条腰上的高与底边的夹角∠DAB=25°故故选：C① ②点睛：本题主要考查三角形内角和定理：三角形内角和为180°.12．如图，在平面直角坐标系中，已知点A（﹣2，0），B（0，3），以点A为圆心，AB 长为半径画弧，交x轴的正半轴于点C，则点C的横坐标介于（）A．0和1之间B．1和2之间C．2和3之间D．3和4之间【答案】B【解析】【分析】先根据点A ，B 的坐标求出OA ，OB 的长度，再根据勾股定理求出AB 的长，即可得出OC 的长，再比较无理数的大小确定点C 的横坐标介于哪个区间．【详解】∵点A ，B 的坐标分别为（﹣2，0），（0，3），∴OA ＝2，OB ＝3，在Rt △AOB 中，由勾股定理得：AB =∴AC ＝AB ，∴OC 2，∴点C 2，0），∵34<< ，∴122<< ，即点C 的横坐标介于1和2之间，故选：B ．【点睛】本题考查了弧与x 轴的交点问题，掌握勾股定理、无理数大小比较的方法是解题的关键．13．满足下列条件的是直角三角形的是（ ）A ．4BC =，5AC =，6AB =B ．13BC =，14AC =，15AB = C ．::3:4:5BC AC AB =D ．::3:4:5A B C ∠∠∠=【答案】C【解析】【分析】要判断一个角是不是直角，先要知道三条边的大小，用较小的两条边的平方和与最大的边的平方比较，如果相等，则三角形为直角三角形；否则不是．【详解】A ．若BC=4，AC=5，AB=6，则BC 2+AC 2≠AB 2，故△ABC 不是直角三角形；B.若13BC =，14AC =，15AB =，则AC 2+AB 2≠CB 2，故△ABC 不是直角三角形； C ．若BC ：AC ：AB=3：4：5，则BC 2+AC 2=AB 2，故△ABC 是直角三角形；D ．若∠A ：∠B ：∠C=3：4：5，则∠C ＜90°，故△ABC 不是直角三角形；故答案为：C ．【点睛】本题主要考查了勾股定理的逆定理，如果三角形的三边长a ，b ，c 满足a 2+b 2=c 2，那么这个三角形就是直角三角形．14．如图，在ABC ∆中，AB 的垂直平分线交AB 于点D ，交BC 于点E ．ABC ∆的周长为19，ACE ∆的周长为13，则AB 的长为（ ）A ．3B ．6C ．12D ．16【答案】B【解析】【分析】 根据线段垂直平分线的性质和等腰三角形的性质即可得到结论．【详解】∵AB 的垂直平分线交AB 于点D ，∴AE=BE ，∵△ACE 的周长=AC+AE+CE=AC+BC=13，△ABC 的周长=AC+BC+AB=19，∴AB=△ABC 的周长-△ACE 的周长=19-13=6，故答案为：B ．【点睛】本题考查了线段垂直平分线的性质：垂直平分线垂直且平分其所在线段；垂直平分线上任意一点，到线段两端点的距离相等．15．如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（）A．1个B．2个C．3个D．4个【答案】C【解析】【分析】【详解】要使△ABP与△ABC全等，必须使点P到AB的距离等于点C到AB的距离，即3个单位长度，所以点P的位置可以是P1，P2，P4三个，故选C.16．如图,已知AC=FE,BC=DE,点A,D,B,F在一条直线上,要利用“SSS”证明△ABC≌△FDE,还可以添加的一个条件是()A．AD=FB B．DE=BD C．BF=DB D．以上都不对【答案】A【解析】∵AC=FE，BC=DE，∴要利用“SSS”证明△ABC≌△FDE，需添加条件“AB=DF”或“AD=BF”.故选A.17．满足下列条件的两个三角形不一定全等的是()A．有一边相等的两个等边三角形B．有一腰和底边对应相等的两个等腰三角形C．周长相等的两个三角形D．斜边和一条直角边对应相等的两个等腰直角三角形【答案】C【解析】A.根据全等三角形的判定，可知有一边相等的两个等边三角形全等，故选项A不符合；B.根据全等三角形的判定，可知有一腰和底边对应相等的两个等腰三角形全等，故选项B 不符合；C.根据全等三角形的判定，可知周长相等的两个三角形不一定全等，故选项C符合；D.根据全等三角形的判定，可知斜边和直角边对应相等的两个等腰直角三角形全等，故选项B不符合.故本题应选C.18．△ABC中，AB=AC，∠A=36°，∠ABC和∠ACB的平分线BE、CD交于点F，则共有等腰三角形( ）A．7个B．8个C．9个D．10个【答案】B【解析】∵等腰三角形有两个角相等，∴只要能判断出有两个角相等就行了，将原图各角标上后显示如左下：因此，所有三角形都是等腰三角形，只要判断出有哪几个三角形就可以了.如右上图，三角形有如下几个：①，②，③；①+②，③+②，①+④，③+④；①+②+③+④；共计8个. 故选：B.点睛：本题考查了等腰三角形的判定与性质、三角形内角和定理以及三角形外角的性质，此题难度不大，解题的关键是求得各角的度数，掌握等角对等边与等边对等角定理的应用.19．如图，在△ABC 中，AB ＝AC ，点D 在AC 上，且BD ＝BC ＝AD ，则∠A 的度数为( )A ．30°B ．45°C ．36°D ．72°【答案】A【解析】∵AB=AC ，BD=BC=AD ，∴∠ABC=∠C=∠BDC ，∠A=∠ABD ，又∵∠BDC=∠A+∠ABD ，∴∠BDC=∠C=∠ABC=2∠A ，∵∠A+∠ABC+∠C=180°，∴∠A+2∠A+2∠A=180°，即5∠A=180°，∴∠A=36°.故选A.20．如图，在ABC ∆中，90C =∠，30B ∠=，以A 为圆心，任意长为半径画弧分别交AB 、AC 于点M 和N ，再分别以M 、N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，连结AP 并延长交BC 于点D ，则下列说法中正确的个数是（ ） ①AD 是BAC ∠的平分线；②ADC 60∠=；③点D 在AB 的垂直平分线上；④:1:3DAC ABC S S ∆∆=A ．1B ．2C ．3D ．4【答案】D【解析】【分析】 根据题干作图方式，可判断AD 是∠CAB 的角平分线，再结合∠B=30°，可推导得到△ABD 是等腰三角形，根据这2个判定可推导题干中的结论.【详解】题干中作图方法是构造角平分线，①正确；∵∠B=30°，∠C=90°，AD 是∠CAB 的角平分线∴∠CAD=∠DAB=30°∴∠ADC=60°，②正确∵∠DAB=∠B=30°∴△ADB 是等腰三角形∴点D 在AB 的垂直平分线上，③正确在Rt △CDA 中，设CD=a ，则AD=2a在△ADB 中，DB=AD=2a ∵1122DAC S CD AC a CD ∆=⨯⨯=⨯，13(CD+DB)22BAC S AC a CD ∆=⨯⨯=⨯ ∴:1:3DAC ABC S S ∆∆=，④正确故选：D【点睛】本题考查角平分线的画法及性质、等腰三角形的性质，解题关键是熟练角平分线的绘制方法.。
(完整word版)初一数学人教版(下册)三角形练习题一(含答案)
(完整word版)初一数学人教版(下册)三角形练习题一(含答案)亲爱的读者：本文内容由我和我的同事精心收集整理后编辑发布到文库，发布之前我们对文中内容进行详细的校对，但难免会有错误的地方，如果有错误的地方请您评论区留言，我们予以纠正，如果本文档对您有帮助，请您下载收藏以便随时调用。
下面是本文详细内容。
最后最您生活愉快 ~O(∩_∩)O ~第七章三角形A1卷•基础知识点点通班级姓名得分一、选择题（3分×8=24分）1．一个三角形的三个内角中（）A 、至少有一个钝角B 、至少有一个直角C 、至多有一个锐角D、至少有两个锐角2．下列长度的三条线段能组成三角形的是（）A、3，4，8B、5，6，11C、1，2，3D、5，6，103．关于三角形的边的叙述正确的是（）A、三边互不相等B、至少有两边相等C、任意两边之和一定大于第三边D、最多有两边相等4．图中有三角形的个数为（）A、4个B、6个C、8个D、10个5．如图在△ABC中，∠ACB=900，CD是边AB上的高。
那么图中与∠A相等的角是（）A、∠BB、∠ACDC、∠BCDD、∠BDC6．下列图形中具有稳定性有（）A、2个B、3个C、4个D、5个7．一个多边形的内角和等于它的外角和，这个多边形是（）A 、三角形B、四边形C、五边形D、六边形8．一个多边形内角和是10800，则这个多边形的边数为（）A、6B、7C、8D、9二、填空题（4分×9=36分）9．一个三角形有条边，个内角，个顶点，个外角10．如图，图中有个三角形，把它们用符号分别表示为11．长为11，8，6，4的四根木条，选其中三根组成三角形有种选法，它们分别是12．如图，在△ABC中，AE是中线，AD是角平分线，AF是高，则根据图形填空：⑴BE= =21；⑵∠BAD= =21第（4）题EDCBA第（5）题DCBA（1）（2）（3）（4）（5）（6）⑶∠AFB= =900；13．在△ABC 中，若∠A=800，∠C=200，则∠B= 0， 若∠A=800，∠B=∠C ，则∠C= 0 14．已知△ABC 的三个内角的度数之比∠A ：∠B ：∠C=1：3：5，则∠B= 0，∠C= 015．如图，在△ABC 中，∠BAC=600，∠B=450，AD 是△ABC 的一条角平分线，则∠DAC= 0，∠ADB= 016．十边形的外角和是 0；如果十边形的各个内角都相等，那么它的一个内角是 0 17．如图，∠1=∠2=300，∠3=∠4，∠A=800，则=x ，=y三、解下列各题18．对下面每个三角形，过顶点A 画出中线，角平分线和高（4分×3=12分）19．求出下列图中x 的值：（4分×3=12分）20．（8分）一个多边形的外角和是内角和的72，求这个多边形的边数第（10）题E D C BA第（12）题B第（15）题D CA800yx4321第（17）题E D CBA(1)CBACBA(2)CBA(3)(1)x 0x 0(2)(3)4x ︒3x ︒3x ︒2x ︒21．在△ABC 中，∠A=21∠C=21∠ABC ， BD 是角平分线，求∠A 及∠BDC 的度数（8分）附加题（10分×2=20分）22.如图，已知∠1=∠2，∠3=∠4，∠A=1000，求x 的值。
人教版七年级下第七章第二节三角形有关的角同步练习及答案
新世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。
版权所有@新世纪教育网7.2.2 三角形的外角(检测时间50分钟 满分100分)班级________ 姓名_________ 得分______一、选择题:(每小题3分,共18分)1.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( ) A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法确定2.如果三角形的一个外角和与它不相邻的两个内角的和为180°,那么与这个外角相邻的内角的度数为( )A.30°B.60°C.90°D.120°3.已知三角形的三个外角的度数比为2:3:4,则它的最大内角的度数为( ) A.90° B.110° C.100° D.120°4.已知等腰三角形的一个外角是120°,则它是( )A.等腰直角三角形;B.一般的等腰三角形;C.等边三角形;D.等腰钝角三角形 5.如图1所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE 等于( )A.120°B.115°C.110°D.105°F EDCA654321FECBA140︒80︒1(1) (2) (3)6.如图2所示,在△ABC 中,E,F 分别在AB,AC 上,则下列各式不能成立的是( )A.∠BOC=∠2+∠6+∠A;B.∠2=∠5-∠A;C.∠5=∠1+∠4;D.∠1=∠ABC+∠4 二、填空题:(每小题3分,共18分)1.三角形的三个外角中,最多有_______个锐角.2.如图3所示,∠1=_______.3.如果一个三角形的各内角与一个外角的和是225°,则与这个外角相邻的内角是____度.4.已知等腰三角形的一个外角为150°,则它的底角为_____.5.如图所示,∠ABC,∠ACB 的内角平分线交于点O,∠ABC 的内角平分线与∠ACB 的外角平分线交于点D,∠ABC 与∠ACB 的相邻外角平分线交于点E,且∠A=60°, 则∠BOC=_______,∠D=_____,∠E=________.6.如图所示,∠A=50°,∠B=40°,∠C=30°,则∠BDC=________.E O D C BA DCBA新世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
与三角形有关的角课时练
第一课时721与三角形有关的内角
4. 如图所示，/
1 + / 2+ / 3+ / 4的度数为(
) A100 °
B.180 °
C.360 ° 5. 如图所示，AB // CD, AD , BC 交于 0, / A=35 ° , / BOD=76
A. 31 °
B.35 °
C.41 °
D.76. 6. ______________________________________________________ 在△ ABC 中：(1)若/ A=80 °，/ B=60 °，则/ C= _________________________________
(2) 若/ A=50 °，/ B= / C ,则/ C= ____________
(3) 若/ A :/ B :/ C=1 : 2 : 3，则/ A= ____________ / B= ________ / C= _________
(4) 若/ A=80 °，/ B-/ C=40°，则/ C= ____________
2.在△ ABC 亠卄 1 中，若 Z A= Z B=-
2 Z C ,则Z C 等于（ ) A.45 °
B.60 °
C.90°
D.120 ° 3.一个三角形的内角中，至少有（ ) A 一个内角 B.两个内角 C. 一内钝角
D. 一个直角 D.无法确定 ，则/ C 的度数是（ A.75 ° B.60° C.65° D.55°
9.如图所示，AD 、AE 分别是△ ABC 的角平分线和高，若/ 求/ DAC 的度数.
第一课时答案:
1•在我们的生活中处处有数学的身影，请看图，折叠一张三角形纸
片, 把三角形的三个角拼在一起，就得到一个著名的几何定理，请你
写 出这一定理的结论：三角形的三个内角和等于 _____________ °
B=5
0 °
1.180;
2.C，提示：依据三角形内角和定理得,
3.B ;
4.C，提示：作如图辅助线，这样把/ 四个角的和转化为两个三角形的内角和，
即2X 180° =360 °
1/ C+ 1/ C+Z C=180 °，解得 / C=90 1、Z 2、/ 3、/ 4
5. C ，提示：T AB // CD ,•••/ D= / A=35 ° . / DOC=180 °
-Z BOD=180 ° -76 ° =104 在厶 COD 中，Z C=180° -Z D- Z DOC=180 ° -35° -104° =41 °;
6. (1) 40°; (2) 65°; (3) 30°, 60°, 90 ° (4) 30°
7.300°,提示：T Z 1 + Z 2=180° -30° =150 °,Z 3+ Z 4=180 ° -30° =150 ° ,
• Z 1+ Z 2+Z 3+ Z 4=150° +150° =300 ° ; 8.A
9•解：T Z B=50 ° ,Z C=70 ° ,
• Z BAC=60 °，又T AD 是厶ABC 的角平分线
1
•Z BAD= _ BAC 30 •又 T AE 是厶 ABC 的高
2
• Z BAE=180 ° - Z B- Z AEB=40 °,「.Z DAC= Z BAE- Z BAD=10 ° .
第二课时7.2.2三角形的外角
(1) 如图①，已知Z A=72 ° ,Z B=38 °，则Z ACD= _____________ .;
(2) 如图②已知 AC 丄BC Z CBD=148 °，则Z A= __________ ;
(3 )如图③，x = ________ _;
(4)如图④Z A = Z B= Z C= x ，则Z ACD= ____________ .;
2.如图所示，已知 AB // CD , Z A=55 ° ,Z C=20 °，则 Z P= ____________
A. Z 1 = Z 2+ Z 3 .
B. Z 1=2Z 2+ Z 3
C. Z 1=2 Z 2-Z 3
D. Z 1=180 ° - Z 2-Z 3 5如图所示，D 是厶ABC 边AC 上的一点，E 是BD 上的一点，Z 1,Z 2,Z A 之间的关系 描述正确的是(
) A. Z A vZ 1>Z 2
B. Z 2 >Z 1>Z A
C. Z 1>Z 2 >Z A
D.无法确定 6..若一噶三角形三个内角的度数之比为 1 : 2 : 3,则与之相邻的三个外角的度数之比为 ( )
A. 1 : 2 : 3
B. 3 : 2 :
1 C. 3 : 4 : A + Z B+ Z C+ Z D+ Z E= _______
AB // CD ，则( ) 1•根据图形填
空:
第1题图
3. 如图所示，Z
4. 如图所示，已
知 第3题图
第4题图
5 D. 5 : 4 : 3
7•—个零件的形状如图所示，按规定/
A 应等于90 °，/
B 和/
C 应分别是32°和21°, 检验工人量得/ BDC=148 ° 合格的理由• 8如图所示，在△ ABC 中，/ A=60 交点，求/ BHC 的度数• CE 的 ,B
D , C
E 分别是 第二课时答案： 1.( 1 ) 110°( 2) 58°( 3) 60°( 4) 120°; 2.35°; 3.180°,提示：因为/ 1= / B+ / D , / 2= / C+Z E ,所以/ A + / B+ / C+ / D+ / E= / A+ / 1 + Z 2=180 ° ; 4.A ，提示：因为 AB // CD ，所以Z ABD= Z 3,因此Z 1 = Z 2+ Z ABD= Z 2+ Z 3; 5.B ，提示：三角形的一个外角
大于与它不相邻的任何一个内角， 故选B ; 6.D ，提示：设三角形三个内角分别为 x ,2x ,3x , 则x 2x 3x 180，解得x 30，所以三角形三个内角分别为 30°, 60°, 90°,与之 相邻的三个外角的度数分别为 150°, 120°, 90°,所以选D ; 7. 解：如图，连接 AD 并延长至E , 则 Z CDE= Z C+ Z CAD , Z BDE= Z B 所以Z BDC= Z CDE+ Z BDE =Z C+ Z CAD+ Z B+ Z BAD=21 ° +32 所以这个零件不合格. 8. 解：因为BD , CE 分别是AC , AB 所以Z ABD=180 ° -Z ADB- Z A=180 ° Z BAD , +90° =143°工148° 上的高，所以Z ADB= -90 ° -60° =30 ° , 因此Z BHC= Z BEH+ Z ABD=90 ° +30 ° =120
c
Z BEH=90 ° ,。