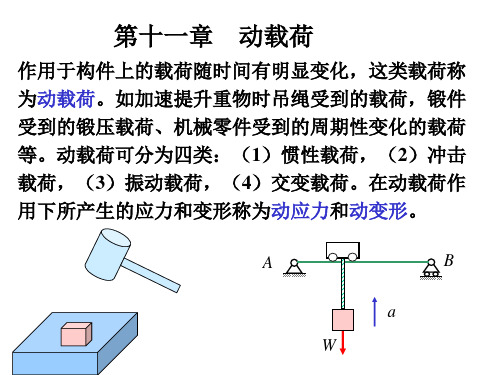
动载荷

动荷系数 K d
v2 g st
P d K d P st d K d st
d K d st
三、冲击响应计算
例 直径0.3m的木桩受自由落锤冲击，落锤重5kN,
求：桩的最大动应力。E=10GPa
解：①求静变形 stP E stLAW EA L 42m 5m ②动荷系数
Wv h=1m
K d11 2h st112 4 12 05 0201 .97
1
一、动载荷：
§10-1 基本概念
载荷不随时间变化（或变化极其平稳缓慢），构件各部
件加速度保持为零（或可忽略不计），此类载荷为静载荷。
载荷随时间急剧变化，构件的速度有显著变化，此类载
荷为动载荷。
二、动响应：
构件在动载荷作用下产生的各种响应（如应力、应变、位
移等），称为动响应。
实验表明：只要应力不超过比例极限 ,在动载荷下胡克定
1、起重机丝绳的有效横截面面积为A , [] =300MPa ,物体单位体 积重为 , 以加速度a上升，试校核钢丝绳的强度（不计绳重）。
解：①受力分析如图:
x
aa
L
Nd
mn
qst
x
qG
惯性力q：GgAa
Nd(qstqG)xA(x 1g a)
②动应力
d
Nd A
x(1a)
g
最大动应力
dmax L(1g a)Kdstmax
1.假设： ①冲击物为刚体； ②冲击物不反弹； ③不计冲击过程中的声、光、热等能量损耗（能量守恒）； ④冲击过程为线弹性变形过程。(保守计算)
2.动能 T ，势能 V ，变形能 U，冲击前、后，能量守恒： (冲击 )T 1V 前 1U 1T2V2U2(冲击 ) 后
最大冲击效应：冲击后的动能为零，T2=0
一个冲击力的变形能为U2=(1/2)PdΔd
3.动荷系数为Kd：
P d K d P st d K d st
d K d st
一、轴向自由落体冲击问题
冲击前： mg v
动能 T1 mv 2 / 2 势能 V1 mgh 变形能 U 1 0
冲击后：动能T2 0
势能 V2 mg d 变形能 U 2 Pd d /2
当温度降低到某一温度下时，材料在发生塑性变形之 前就因拉断而破坏，这就是材料的冷脆。而上述温度则称 为脆性转变温度或简称转变温度。
38
39
40
41
动荷:K 系 dff数 s dt11(v2g fs)t2h
(1)自由落 :Kd体 1
12h fst
(2)突然荷 :Kd载 2
例10.4
• 在水平平面内的AC杆绕通过A点的垂直轴以
匀角速 转动。杆的C端有一重为Q的集中
质量。如因发生故障在B点卡住而突然停止 转动，试求AC杆上的最大冲击应力。设AC 杆的质量可以不计。
律仍成立，且E静=E动。
三、动应力分类：
1.简单动应力： 加速度可以确定，采用“动静法”求解 。 2.冲击载荷： 速度在极短暂的时间内急剧改变，加速度
不能确定，采用“能量法”求之；
3.交变应力： 应力随时间作周期性变化，如疲劳问题。
4.振动问题： 求解方法很多。
§10-2 动静法的应用
• 惯性力的概念
• 在AB轴的B端有一个质量很大的飞轮。与
飞轮相比，轴的质量可以忽略不计。轴的 另一端A装有刹车离合器。飞轮的转速为 n=100r/min，转动惯量为Ix=0.5kN·m·s2。 轴的直径d=100mm。刹车时使轴在10秒内 均匀减速停止转动。求轴内最大动应力。
y
mt x
md
A
B
0
16
解：
0=—n3—0 =—3—100—0 =—103—rad/s
物体，试校核钢丝绳的强度。
Nd L q(1+a/g)
G(1+a/g)
解：①受力分析如图:
a Nd(GqL)(1g) ②动应力
dNAd1A(Gq
L)1(a) g
2.9 1 1 4 0 (5 1 03 0 2.5 5 6)0 1 ( 9 2 .8)
2M 14 P 3 a0 M 0P 强度a足够 9
结构（受冲击构件）受外力（冲击物） v 作用的时间很短，冲击物的速度在很短的 时间内发生很大的变化，甚至降为零，冲 击物得到一个很大的负加速度a，结构受到 冲击力的作用。
Qa
冲击物
受冲击 的构件
20
方法原理：能量法
( 机械能守恒 ）
在冲击物与受冲构件的接触区域内，应力状态异常复杂， 且冲击持续时间非常短促，接触力随时间的变化难以准确分 析。工程中通常采用能量法来解决冲击问题，即在若干假设 的基础上，根据能量守恒定律对受冲击构件的应力与变形进 行偏于安全的简化计算。
30
例10.4 解
T= —1 mv2 2
= —1 —Q (l)2
2g V=0
31
Ud=
—1 2
—d—2
st
Q
T = Ud
—1 2
—d—2
st
Q
=
—1 2
—Q g
(l)2
——d
st
=
(l)2
——
g st
32
d
=
—d st
st
=
Kd
st
Kd
=
——d
st
=
—(—l)2
g st
33
st的计算：
Q以静载方式作用于C端(仿佛在 重力场中)利用求弯曲变形的方 法求出C点的静位移
条件。 t
O D
qG
qG 解：①惯性力分析，见图１
qGAgan
AD2
2g
②内力分析如图2
图1
2Nd0 qGsinD 2dqGD
Nd 图2 Nd
D 2
an 2
NdqG2DA4gD22
③应力分析 ④强度条件
dNAd4Dg22gv2
d
v 2
g
v [ ] g
最大线速度：
vmax
[ ] g
例10.1
(2 )突然 h荷 0:, K 载 d2
二、不计重力的轴向冲击： v
mg
冲击前：
动能 T1 mv 2 / 2 势能 V1 0 变形能 U 1 0
冲击前后能量守恒，且
冲击后：
Pd KdPst (Pst mg) d Kdst
动能 T2 0 势能 V2 0 变形能 U 2 Pd d /2
12mv2 m2gKd2st
mg(h
fd
)
0
AC fd
B x 冲 击 后 T2 V2 U 2
00
1 2
Pd
fd
1 2
k
(
fd
)2
f
冲击前、后，能量守恒，所以：
1 2
Pst f st
(
fd )2
1 2
mg f st
(
fd )2
1 2m2v m(h gfd)2 m fst(gfd)2
fd(11(v2 gfs) t 2h)fstKdfst
式中Pd,d,d,d 分别表示动载荷，动应力，动应变和动位移；
Pst,st,st,s分t 别表示静载荷，静应力，静应变和静位移。
8
例 起重机钢丝绳长L=60m，有效横截面面积A=2. 9cm2 , 单位长重
量q=25. 5N/m , [] =300MPa , 以a=2m/s2的加速度提起重50kN 的
F=ma 牛顿第二定律 F-ma=0 F+(-ma)=0 达朗伯原理
4
动静法
达朗伯原理
处于不平衡状态的质点系，存在惯性力，惯性力的方向 与加速度方向相反，惯性力的数值等于质点的加速度与质量 的乘积。
只要在每一质点上加上惯性力，就可以把动力学问题在 形式上作为静力学问题来处理，这就是动静法。
一、直线运动构件的动应力
=—1—-—0 =- — rad/s2
t
3
y
mt x
md
A
B
0
17
md=-Ix
0.5(
)0.5 kN·m 33
T=mt=md0.35kN·m
y
mt x
A
md
B
0
18
最大扭转切应力为
tmax=
T
Wt
=
2.67106Pa=2.67MPa
y
mt x
A
md
B
0
19
§10-4 杆件受冲击时的应力和变形
•冲击问题的特点：
h
冲击前后能量守恒，且 Pd KdPst (Pst mg)
d Kdst
d mg
1 2m 2 v m (h g K d s) tm 2K g d 2 st
v2 /g2h Kd 1 1 st
△st:冲击物落点的静位移。
讨论：
Kd 1
1v2 /g2h st
(1)自由v 落 0:,体 K d11 2h st
O点旋转， 已知许用应力[] ，求转臂的截面面积（不计转臂
自重）。
FG
解：①受力分析如图:
惯性力：
O L
FGmna2Lm 2LG /g
②强度条件
F G/A
A
FG
2GL
(g)
例 设圆环的平均直径D、厚度t ，且 t«D，环的横截面面积为
A，单位体积重量为 ，圆环绕过圆心且垂直于圆环平面的轴以
等角速度旋转，如图所示，试确定圆环的动应力，并建立强度
③求动应力
f
6m
静应力：stW /A0.070 M 7P 4a
动应力： dKdst1.5 4M 1 Pa
四、 梁的冲击问题