第十一届华杯赛决赛试题及答案
(完整版)第11-17届初一华杯赛试题及答案
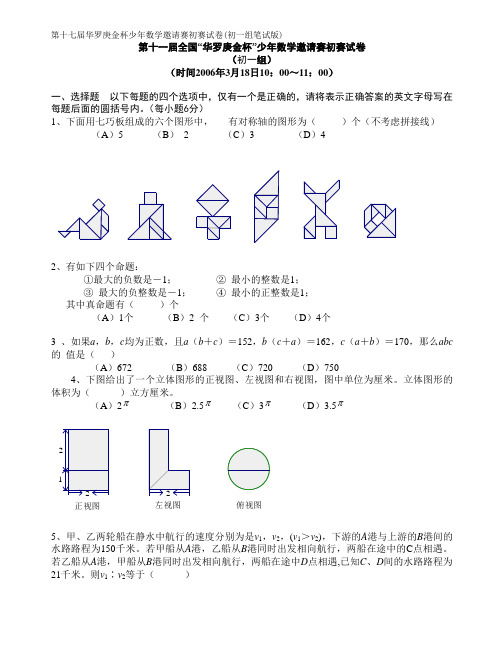
由上式和b >α,b=13,α=1,d=l所以,K=12,m和n有唯一解m=13n =156.
答:m=13n =156.
7、已知 ,则小于S的最大的整数是(0)
8.如图2,数轴上标有2n+1个点,它们对应的整数是:
为了确保从这些点中可以取出2006个,其中任何两个点之间的距离都不等于4,则n的最小值是(2005)
二.解答下列各题,要求写出简要过程
9、如图3,ABCD是矩形,BC=6cm,AB =10cm,AC和
BD是对角线.图中的阴影部分以CD为轴旋转一周,则阴影
②直角边为1的三角形有36×2=72(个);斜边长是2的三角形,1-6行依次有4+4+4+3+1+4=20(个),1-6列依次3+3+3+2+3+3=17(个),共20+17=37(个);直角边长是2的1-2行8个,2-3行6个,3-4行2个,4-5行8个,5-6行6个,共8+6+2+8+6=30(个);直角边长是3的1-3行4个,3-5行2个,4-6行4个,共4+2+4=10(个);斜边长是4的1-4行1个,2-5行2个,4-5行1个,共1+2+1=4(个);直角边长是4的3-6行2个。共72+37+30+10+4+2=155(个)
第十一届全国"华罗庚金杯"少年数学邀请赛
决赛试卷(初一组)
(红色字为参考答案)
(时间2006年4月22日10:00~l l :30〉
一、.填空
1、计算: ( )
华杯赛高中组试题及答案

华杯赛高中组试题及答案一、选择题(每题5分,共20分)1. 函数f(x)=x^2+2x+1的最小值是()。
A. 0B. 1C. 2D. 3答案:B解析:函数f(x)=x^2+2x+1可以写成f(x)=(x+1)^2,这是一个开口向上的抛物线,其最小值出现在顶点处,即x=-1时,f(-1)=1。
2. 已知数列{an}满足a1=1,an+1=2an+1,求a3的值是()。
A. 3B. 5C. 7D. 9答案:C解析:根据递推关系,a2=2a1+1=2*1+1=3,a3=2a2+1=2*3+1=7。
3. 已知三角形ABC的三边长分别为a、b、c,且满足a^2+b^2=c^2,判断三角形ABC的形状是()。
A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定答案:B解析:根据勾股定理的逆定理,若a^2+b^2=c^2,则三角形ABC为直角三角形。
4. 已知函数f(x)=x^3-3x,求f'(x)的值是()。
A. 3x^2-3B. 3x^2+3C. x^2-3D. x^2+3答案:A解析:对f(x)=x^3-3x求导,得到f'(x)=3x^2-3。
二、填空题(每题5分,共20分)5. 已知函数f(x)=x^2-4x+3,求f(2)的值是______。
答案:-1解析:将x=2代入函数f(x)=x^2-4x+3,得到f(2)=2^2-4*2+3=-1。
6. 已知等差数列{an}的首项a1=2,公差d=3,求a5的值是______。
答案:11解析:根据等差数列的通项公式an=a1+(n-1)d,得到a5=2+(5-1)*3=11。
7. 已知双曲线方程为x^2/a^2-y^2/b^2=1,其中a=2,b=1,求双曲线的渐近线方程是______。
答案:y=±x解析:双曲线的渐近线方程为y=±(b/a)x,代入a=2,b=1,得到y=±x。
8. 已知函数f(x)=sin(x)+cos(x),求f'(π/4)的值是______。
2011华杯赛决赛练习题10套

“华杯赛”决赛集训试题(一)一、填空题(每题10分,共80分)1、计算:18.25×1145 -1714 ÷(1-5459)=_______。
2、某实验员做实验,上午9时第一次观察,以后每隔4小时观察一次,当他第10次观察时,时针与分针的夹角为_______。
3、如图,A 是圆心,正方形的面积是10平方米,则圆的面积为_______。
4、一只方形水桶,高60厘米,其底面是边长50厘米的正方形,桶内盛水,水的深度是40厘米。
如将一个棱长为30厘米的正方体铁块放入桶内,水深将是_______厘米。
5、从1、2、……100这100个数中,每次取两个数,使其和大于100,共有_______种取法。
6、在分母小于10的分数中,有一个分数是最接近0.618的,那么这个分数是_______。
7、用1~9这9个数字各一次,组成一个两位完全平方数,一个三位完全平方数,一个四位完全平方数。
那么,其中的四位完全平方数最小是_______。
8、现有一块L 形的蛋糕如图所示,现在要求一刀把它切成3部分,因此只能按照如图的方式切,但不能斜着切或横着切。
要使得到的最小的那块面积尽可能大,那么最小的面积为______平方厘米。
二、简答题(每题10分,共40分)9、2002年北京召开的国际数学家大会,大会会标如图所示,它是由四个相同的直角三角形拼成的(直角边长为2和3)。
则大正方形的面积是多少?10、已知等腰三角形的一个内角为70度,求其它的内角度数。
11、服装店购进A 型和B 型两批服装,成本共2160元,A 型服装按25%的利润定价,B 型服装按10%的利润定价。
实际都按定价的90%打折出售,结果仍获利140.4元,那么A 型服装的成本价多少元?12、如图,四边形ABCD 中,E 为BC 的中点,AE 与BD 交于F ,且F 是BD 的中点,O 是AC ,BD 的交点,AF=2EF 。
三角形AOD 的面积是3平方厘米,求四边形ABCD 的面积。
第十一届华为杯全国研究生数学建模竞赛D题—国家二等奖

(由组委会填写)第十一届华为杯全国研究生数学建模竞赛学校青岛科技大学参赛队号10426019队员姓名1.王玉江2.陈桂兵3.严春梅(由组委会填写)第十一届华为杯全国研究生数学建模竞赛题目人体营养健康角度的中国果蔬发展战略研究摘要:水果和蔬菜是重要的农产品,主要为人体提供矿物质、维生素、膳食纤维。
因此,预测我国果蔬的消费与生产趋势,科学地规划与调整我国果蔬的中长期的种植模式,具有重要的战略意义。
针对问题一,首先选取需要研究的主要水果、蔬菜品种,以其总计含量分别达到各自总产量的90%为约束条件,采用多目标规划(产量最多、营养含量最高、种类最少)筛选出主要的水果、蔬菜品种(水果10种、蔬菜8种,结果见表4、表5)。
随后,查询2002至2010年主要品种的产量,通过两种方法(损耗率、进出口差量)计算人均消费量,用灰色预测GM(1,1)和曲线拟合两种模型预测未来人均消费量,并分别检验拟合效果、进行误差分析,发现基于损耗率估计消费量灰色预测的效果较理想。
所以以苹果为例,综合考虑损耗率和进出口量利用灰色预测模型估计其2010至2020年的人均消费量(见表9、表12),拟合出曲线图(见图2、图6),分析其发展趋势。
针对问题二,首先依据10种营养成分在主要果蔬产品中含量的相似性,运用Spss 软件对10种营养成分进行Q型聚类降维得6大类营养成分(结果见表12),每类营养成分都筛选出一个营养成分作为代表分别是膳食纤维、维生素A、维生素C、维生素E、钙、锌。
采用正态分布中间型模型计算每种营养成分年均实际摄入量关于标准摄入量的隶属度,隶属度越接近1表明实际摄入量越趋近于标准量,以此评价2014年的营养年摄入水平。
用维生素A、C、E隶属度的乘积量化维生素这一大类营养元素趋于健康的程度,同样对钙锌采取相同的措施作为矿物质的量化值,关于时间作图可知2014至2019年中国居民的营养健康状况趋于好转,2019至2020年趋于恶化。
华杯赛行程问题汇编(1-18届)

1。
(第一届华杯赛初赛第8题)早晨8点多钟有两辆汽车先后离开化肥厂向幸福村开去。
两辆车的速度都是每小时60千米。
8点32分的时候,第一辆汽车离开化肥厂的距离是第二辆汽车的三倍.到了8点39分的时候,第一辆汽车离开化肥厂的距离是第二辆汽车的2倍.那么,第一辆汽车是8点几分离开化肥厂的?2. (第一届华杯赛初赛第16题)有一路电车的起点站和终点站分别是甲站和乙站.每隔5分钟有一辆电车从甲站出发开往乙站,全程要走15分钟。
有一个人从乙站出发沿电车路线骑车前往甲站。
他出发的时候,恰好有一辆电车到达乙站。
在路上他又遇到了10辆迎面开来的电车,才到达甲站.这时候,恰好又有一辆电车从甲站开出。
问他从乙站到甲站用了多少分钟?3。
(第一届华杯赛决赛第12题)上午8点8分,小明骑自行车从家里出发,8分钟后,爸爸骑摩托车去追他,在离家4公里的地方追上了他,然后爸爸立刻回家,到家后又立刻回头去追小明,再追上他时候,离家恰好是8公里。
问这时是几点几分?4. (第一届华杯赛总决赛一试第13题)如下图,甲、乙、丙是三个站,乙站到甲、丙两站的距离相等。
小明和小强分别从甲、丙两站同时出发相向而行,小明过乙站100米后与小强相遇,然后两人又继续前进,小明走到丙站立即返回,经过乙站后300米又追上小强。
问甲、丙两站的距离是多少米?5。
(第一届华杯赛总决赛二试第4题)快、中、慢三辆车同时从同一地点出发,沿同一公路追赶前面的一个骑车人,这三辆车分别用6分钟、10分钟、12分钟追上骑车人,现在知道快车每小时走24千米,中车每小时走20千米,那么,慢车每小时走多少千米?6。
(第二届华杯赛初赛第2题)一个充气的救生圈(如右图).虚线所示的大圆,半径是33厘米.实线所示的小圆,半径是9厘米.有两只蚂蚁同时从A点出发,以同样的速度分别沿大圆和小圆爬行.问:小圆上的蚂蚁爬了几圈后,第一次碰上大圆上的蚂蚁?7. (第二届华杯赛决赛第11题)王师傅驾车从甲地开乙地交货.如果他往返都以每小时60公里的速度行驶,正好可以按时返回甲地。
历届华杯赛决赛试题剖析--第八讲(第十一届初赛).doc

历届华杯赛决赛试题剖析7华罗庚金杯少年数学邀请赛决赛试题(小学组)真题尝试1.如图所示,将一张正方形纸片先由下向上对折压平,再由右翻起向左对折压平, 得到小正方形ABCD,取AB的中点M和BC的中点N,剪掉ZXMBN,得五边形AMNCD。
则将折叠的五边形AMNCD纸片展开铺平后的图形是()。
3、奶奶告诉小明:“2006年共有53个星期日”。
聪敏的小明立到告诉奶奶:2007 年的元旦一定是()o (A)星期一(B)星期二(C)星期六(D)星期H4、如图,长方形ABCD中AB : BC=5 : 4。
位于A点的第一只蚂蚁按A-B-C-D-A的方向,位于C点的第二只蚂蚁按C-B-A-D-C的方向同时出发,分别沿着长方形的边爬行。
如果两只蚂蚁第一次在B点相遇,则两只蚂蚁第二次相遇在()边上。
(A) AB (B) BC (C) CD5、图中ABCD是个直角梯形(ZDAB=ZAB C=90°),以AD为一边向外作长方形ADEF, 其面积为6. 36平方厘米。
连接BE交AD于P,再连接PC。
则图中阴彩部分的面积是2. 2008006 共有-()个质因数。
(A) 4 (B) 5 (C) 6 (D) 7)平方厘米。
6、 五位同学扮成奥运会吉祥物福娃贝贝、晶晶、欢欢、迎迎和妮妮,排成一排表演 节目。
如果贝贝和妮妮不相邻,共有()种不同的排法。
(A )48 (B )72 (C ) 96 (D ) 120 二、A 组填空题7、 在算式第十一届+ 华杯赛小,汉字“第、十、一、届、华、杯、赛”代表1, 2, 3, 4, 5, 6, 7, 8, 9屮的7个数字,不同的汉字代表不同的数字,恰使得加法算式成立。
则“第、十、一、届、 华、杯、赛”所代表的7个数字的和等于 ________ 。
8、全班50个学生,每人恰有三角板或直尺中的一种,28人有直尺,有三角板的人 中,男生是14人,若已知全班共有女生31人,那么有直尺的女生有 ____________ 人。
华杯数论
华杯赛数论专辑A1.哥德巴赫猜想是说:“每个大于2的偶数都可以袤示成两个质数之和”。
问:168是哪两个两位数的质数之和,并且其中的一个的个位数字是1?【第六届华杯赛初赛试题】2.任意写一个两位数,再将它依次重复3遍成一个8位数.将此8位数除以该两位数所得到的商再除以9,问:得到的余数是多少?【第九届华杯赛初赛试题】3.将l999表示为两个质数之和:l999=口+口,在口中填入质数。
共有多少种表示法?【第七届华杯赛初赛试题】4.五个比0大的数它们两两的乘积是1,80,35,1.4,50,56,1.6,2,40,70这十个值,问这五个数中最大数是最小数的多少倍?【第07届华罗庚金杯少年数学邀请赛团体决赛口试试题】5.能将1,2,3,4,5,6,7,8,9填在3×3的方格表中(如下图),使得横向与竖向任意相邻两数之和都是质数吗?如果能,请给出一种填法:如果不能,请你说明理由.【第07届华罗庚金杯少年数学邀请赛团体决赛口试试题】6.将1,2,3,4,5,6,7,8,9九个数排成一行,使得第二个数整除第一个数,第三个数整除前两个数的和,第四个数整除前三个数的和,…,第九个数整除前八个数的和,如果第一个数是6,第四个数是2,第五个数是1.问排在最后的数是几?【第07届华罗庚金杯少年数学邀请赛团体决赛口试试题】7.能否找到自然数a和b,使a2=2002+b2.【第八届华杯赛复赛试题及解答】8.1到100所有自然数中与100互质各数之和是多少?【第九届华杯赛总决赛一试试题】9.a,b和c都是二位的自然数,a,b的个位分别是7与5,c的十位是1。
如果它们满足等式ab+c=2005,则a+b+c=( )。
【第十届华杯赛决赛试题】10.小于10且分母为36的最简分数共有多少个? 【第十届华杯赛口赛试题】11.构成自然数的所有数字互不相同,这些数字的乘积等于360。
求n的最大值。
【第十届华杯赛口赛试题】12.将两个不同的自然数中较大的数换成这两个数的差,称为一次操作,如对18和42可连续进行这样的操作。
(整理)第十一届全国“华罗庚金杯”少年数学邀请赛华杯赛初一组试卷附答案1
第十一届全国"华罗庚金杯"少年数学邀请赛决赛试卷(初一组) (红色字为参考答案)(时间2006年4月22日10:00~l l :30〉一、.填空 1、计算:243331(0.25)(2)3()5(2)168⎧⎫⎡⎤⎡⎤---⨯-÷⨯-+÷-=⎨⎬⎢⎥⎢⎥⎣⎦⎣⎦⎩⎭( 47 )2、当2m π=时,多项式31am bm ++的值是0,则多项式31452a b ππ++=( 5 )3、将若干本书分给几名小朋友,如果每人分4本书,就还余下20本书,如果每人分8本书,就剩有1名小朋友虽然分到了一些书,但是不足8本,则共有( 6 )名小朋友4、图l 中的长方形ABCD 是由四个等腰直角三角形和一 个正方形EFGH 拼成.己知长方形ABCD 的面积为120平方厘米,则正方形EFGH 的面积等于( 10 )平方厘米5、满足方程|||x-2006|-1|+8|=2006的所有x 的和为( 4012 )6、一个存有一些水的水池,有一个进水口和若干个口径相同的山水口,进水口每分钟进水3立方米.若同时打开进水口和三个出水口,池中水16分钟放完;若同时 打开进水口与五个出水口,池中水9分钟放完.池中原有水( 288 )立方米7、已知120052006123420052006(1)24816222k k k S +=-+-++-++-,则小于S 的最大的整数是( 0 )8.如图2,数轴上标有2n+1个点,它们对应的整数是:,(1),,2,1,0,1,2,,1,n n n n ------为了确保从这些点中可以取出2006个,其中任何两个点之间的距离都不等于4,则n 的最小值是( 2005 )图1图2n n-10-1-2-(n-1)-n二.解答下列各题,要求写出简要过程9、如图3,ABCD 是矩形,BC=6cm,AB =10cm,AC 和BD 是对角线.图中的阴影部分以CD 为轴旋转一周,则阴影 部分扫过的立体的体积是多少立方厘米?(z 取3.14) 解: ①设三角形BCO 以CD 为轴旋转一周所得到的立体的体积是S,S 等于高为10厘米,底面半径是6厘米的 圆锥的体积减去2个高为5厘米,底面半径是3厘米的圆 锥的体积. ②即:S=13×26×10×π-2×13×23×5×π=90π, 2S=180π=565.2(立方厘米).答:体积是565.2立方厘米. 10、将21个整数10,9,8,,3,2,1,0,1,2,3,,8,9,10------分为个数不相等的六组数,分别计算各组的平均值,那么这六个平均值的和最大是多少? 解:①分为个数不相等的6组,整数的个数分别为1、2、3、4、5、6. ②应当将数值大的分在整数个数少的组中.所以,可以如下分组:第一组10 第二组9 8 第三组7 6 5 第四组4 3 2 1 第五组0 -1 -2 -3 -4 第六组-5 -6 -7 -8 -9 -10③计算它们的平均值的和:109876543210123456789101171234562++++++----------+++++= 答:最大的和是1172。
奥数几何,数论,行程专题
宇光教育专题诊断——几何专题教师: 耿宏雷 所在学校: 联系电话:1. 下图是由9个等边三角形拼成的六边形,已知中间最小的等边三角形的边长是1,问:这个六边形的周长是多少? (第七届华杯赛初赛第6题)2. 如图:将三角形ABC 的BA 边延长1倍到D ;CB 边延长2倍到E ,AC 边延长3倍到F ,如果三角形ABC 的面积等于1,那么三角形DEF 的面积是_____。
(第一届迎春杯决赛第32题)3. 长方形草地ABCD 被分为面积相等的甲、乙、丙和丁四份(如下图),其中图形甲的长和宽的比是2:1,其中图形乙的长和宽的比是( ):( )。
(第八届华杯赛复赛第2题)4. 五环图由内圆直径为8,外圆直径为10的五个圆环组成,其中两两相交的小曲边四边形(阴影部分)的面积都相等。
已知五个圆环盖住的总面积是112.5,求每个小曲边四边形的面积(圆周率π取3.14)(第三届华杯赛复赛第15题)5.求图阴影部分的面积为_____平方厘米(取π为3)。
(第二届迎春杯决赛第40题)6.如下图,在一个正方体的两对侧面的中心各打通一个长方体的洞,在上下侧面的中心打通一个圆柱形的洞。
已知正方体边长为10厘米,侧面上的洞口是边长为4厘米的正方形,上下侧面的洞口是直径为4厘米的圆,求下图立体的表面积和体积?(π取3.14)(第七届华杯赛复赛第11题)7.有6个棱长分别是3cm,4cm,5cm的相同长方体,把它们的某些面染上红色,使得有的长方体只有一个面是红色的,有的长方体恰有两个面是红色的,有的长方体恰有三个面是红色的,有的长方体恰有四个面是红色的,有的长方体恰有五个面是红色的,还有一个长方体六个面都是红色,染色后把所有的长方体分割成棱长为1cm的小正方体,分割完毕后,恰有一面是红色的小正方体最多有几个?(第四届华杯赛决赛二试第4题)8.下图中的正方形被分为9个相同的小正方形,它们一共有16个顶点(共同的顶点算一个)。
以其中不在一条直线上的3个点为顶点,可以构成三角形。
(完整版)第11-17届初一华杯赛试题及答案
二、A组填空题
7.4/9设AB=2r则{πr^2/2-[π(r/3)^2/2+π(2r/3)^2/2]}/ (πr^2/2)=1-(1/9+4/9)=4/9
8.1.98原式=[2^2/(1×3)]×[3^2/(2×4)] ×[4^2/(3×5)] ×[5^2/(4×6)] ×[6^2/(5×7)] ×……×[98^2/(97×99)] ×[99^2/(98×100)]=2×99/100=1.98
(A) (B) (C) (D)
6、有一串数:1,22,,33,44,……,20042004,20052005,20062006。大明从左往右依次计算前面1003个数的末位数字之和,并且记为a,小光计算余下的1003个数的末位数字之和,并且记为b,则a-b=()。
(A)-3(B)3(C)-5(D)5
二、A组填空题(每小题8分)
4、下图给出了一个立体图形的正视图、左视图和右视图,图中单位为厘米。立体图形的体积为()立方厘米。
(A)2 (B)2.5 (C)3 (D)3.5
5、甲、乙两轮船在静水中航行的速度分别为是v1,v2,(v1>v2),下游的A港与上游的B港间的水路路程为150千米。若甲船从A港,乙船从B港同时出发相向航行,两船在途中的C点相遇。若乙船从A港,甲船从B港同时出发相向航行,两船在途中D点相遇,已知C、D间的水路路程为21千米。则v1∶v2等于()
2006
中,汉字“第、十、一、届、华、杯、赛”代表1~9中的9个数字,不同的汉字代表不同的数字,恰使得加法算式成立。则不同的填法共有;三位数华杯赛的最大可能值为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一届华杯赛决赛试题及解答
一、填空题
1、计算:÷126.3=()
2、如图是一个长方形,其中阴影部分由一副面积为1的七巧板拼成(如图b)。
那么这个长方形的面积是()
3、有甲、乙、丙、丁四支球队参加的足球循环赛,每两队都要赛一场,胜得3分,负者得0分,如果踢平,两队各得1分。
现在甲、乙、丙分别得了7分、1分和6分,已知甲和乙踢平,那么丁得()分。
4、图中,小黑格表示网络的结点,结点之间的连线表示它们有网线要联,连续标注的数字表示该段网线单位时间内可以通过的最大的信息量。
现在从结点A向结点B传递信息,那么单位时间内传梯的最大信息量是()。
5、先写出一个两位数62,接着在62右端写这两个数字的和8,得到628,再写末两位数字2和8的和10,得到62810,用上述方法得到一
个有2006位的整数:628101123…,则这个整数的数字之和是
()。
6、智慧老人到小明的年级访问,小明说他们年级共一百多名同学,老人请同学们按三人一行排队,结果多出一人,按五人一行排队,结果多出二人,按七人一行排队,结果多出一人,老人说我知道你们年级原人数应该是()人。
7、如图所示,点B是线段AD的中点,由A,B,C,D四个点所构成的所有线段的长度均为整数,若这些线段的长度之积为10500,则线段AB的长度是()。
8、100个非0自然数的和等于2006,那么它们的最大公约数最大可能值是()。
二、解答下列各题
9、如图,圆O的直径AB与CD互相垂直,AB=10厘米,以C为圆心,CA为半径画弧。
求月牙形ADBEA(阴影部分)的面积。
10、甲、乙、丙三只蚂蚁爬行的速度之比是8∶6∶5,它们沿一个圆圈从同一点同时同向爬行,当它们首次同时回到出发点时,就结束爬行。
问蚂蚁甲追上蚂蚁乙一共多少次(包括结束时刻)?
11、如图,ABCD是矩形,BC=6cm, AB=10cm,AC和BD是对角线,图中的阴影部分以C为轴旋转一周,则阴影部分扫过的立体的体积是多少立方厘米?(π取3.14)
12、将一根长线对折,再对折,共对折10次,得到一束线,用剪刀将这束线剪成10等份,问:可以得到不同长度的短线段各多少根?
三、解答下列各题
13、华罗庚爷爷在一首诗文中勉励青少年:
“猛攻若战是第一,熟练生出百巧来,勤能补拙是良训,一分辛劳一分才。
“
现在将诗文中不同的汉字对应不同的自然数,相同的汉字对应相同的自然数,并且不同汉字所对应的自然数可以排列成一串连续的自然数。
如果这个28个自然数的平均值是23,问“分”字对应的自然数的最大可能值是多少?
14、一根长为L的木棍,用红色刻度线将它分成m等份,用黑色刻度将它分成n等份(m>n)。
(1)设x是红色与黑色刻度线重合的条数,请说明:x+1是m和n的公约数;
(2)如果按刻度线将该木棍锯成小段,一共可以得到170根长短不等的小棍,其中最长的小棍恰有100根。
试确定m和n的值。
参考答案:
一、填空
1. 0.1
2.
3. 3
4. 17
5. 7018
6. 127
7. 5
8. 17
二、解答下列各题,要求写出简要过程
9解:①月牙形ADBEA(阴影部分)的面积=半圆的面积+△ABC的面积-扇形的面积
②月牙形ADBEA的面积==25(平方厘米).答:月牙形ADBEA的面积是25平方厘米。
10解:①甲乙丙三只蚂蚁的速度之比为8∶6∶5,所以,当它们首次
同时回到出发点时,甲运动8圈,乙运动6圈。
②蚂蚁甲比蚂蚁乙多
运动了1圈,就追上蚂蚁乙1次,所以,甲一共追上乙2次。
答:当三只蚂蚁爬行结束时,甲追上乙2次。
1l解:①设三角形BCO以CD为轴旋转一周所得到的立体的体积是s,S等于高为10厘米,底面半径是6厘米的圆锥的体积减去2个高为5
厘米,底面半径是3厘米的圆锥的体积。
②即:,
2S=180π=565.2(立方厘米)
答:体积是565.2立方厘米。
12解:
①10次对折后,得到的是1024条线并列的线束。
②用剪刀将得到的线束剪成10等分,除去两端,中间的8等分的线段都是较短的线段,共有8×1024根。
③另外,剪下的两端,其中,有一端,有2条短的线段。
余下
(2×1024-2)条线,每两条构成1条线段。
所以,较长的线段有1024-1=1023根,较短的线段共有8×1024+2=8194根。
答:较长的线段有1024-1=1023根,较短的线段共有8×1024+2=8194根。
三、解答下列各题,要求写出详细过程
13.解:①因为23×28=644,
②设这串连续自然数的起始的数是m,不同汉字所对应的自然数依次是:
m,m+1,…,m+23;设其中“分”字对应的自然数是m+x,“是”字对应m+a,“一”字对应m+b。
既然要求“分”字对应的自然数尽可能大,可以要求23≥X>a>b≥0。
诗文中“分、是”各出现2次,“一”出现3次,其他汉字只出现1次,则有
=644,
28m+276+(a+2b)+x=644,28m=368-x-(a+2b)
③,,但是,
23≥x,b≥0,a+b≥1+0,a+2b=a+b+b≥1.
所以,<35.29.
取m=12,x=23,a=9,b=0(或a=5,b=2或a=1,b=4),得到满足条件的解,其中“分”对应的自然数是35。
答:“分”对应的自然数的最大可能值是35。
14.解:①
同样,
② 由题设,,,
,
所以,,
,
即13+n是13×13的因数,13×13只有3个因数:1,13,.所以,
甲追上乙的位置(3分):③会判断丙在甲追上乙的时刻所爬行的距离(3分)。
即13+n是13×13的因数,13×13只有3个因数:1,13,13。
所以,
13+n=,n=-13=156,m=12。
求出正整m,n的另一方法:使,.
设m=Ka,n=Kb,(a,b)=1,代入上式,.
(b一a)和a,b都互质,一定整除K。
记d=是正整数,b>a则有:.
由上式和b>a,b=13,a=1,d=1。
所以,K=12,m和n有唯一解,
m=13,n=156。
符:m=13,n=156。
