奥数六年级千份讲义 225 11.第五讲几何立体部分

合集下载

奥数六年级千份讲义782西城综合分班考试班第五讲教师

第五讲应用题1．光明小学有学生900人，其中女生的47与男生的23参加了课外活动小组，剩下的340人没有参加。

这所小学有男、女生各多少人?【分析】由题意可知，女生可设为7x ，那么男生就是9007x -。

则可列方程得如下：13(9003)3403x x +-= 解得：70x =，则女生人数为：770490⨯=，男人人数为：900490410-=。

2．汽车从甲地开往乙地，第一小时走了全程的15多8千米，第二小时走了余下的路程的13少4千米，这是距乙地还有124千米，求甲、乙两地相距多少千米?【分析】由第一小时全程的15，第二小时走了余下的路程的13，可知走了：114(1)5315-⨯=。

那么全程就是：14(12484)(1)240515+-÷--=。

3．小红到商店买一盒花球，一盒白球，两盒球的数量相等，花球原价是2元钱3个，白球原价是2元钱5个。

新年优惠，两种球的售价都是4元钱8个，结果小红少花了5元钱，那么，她一共买了多少个球?【分析】由题意思可知，先前每个花球2233÷=元，每个白球2255÷=元；后来每个都是1482÷=。

因为数量相同，则买一个花球和一个白球比原来少21121()()322515---=。

所以一共买了157515÷=个球。

4．甲、乙两地出产同一种水果，甲地出产的水果数量每年保持不变，乙地出产的水果数量每年增真题模考加一倍，已知1990年甲、乙两地出产水果总数为98吨，1991年甲、乙两地总计出产水果106吨，则乙地出产水果的数量第一次超过甲地出产的水果数量是在年。

【分析】 1991年比1990年多出产水果106988-=(吨)，这是由于乙地出产数量增加一倍的缘故，这样就知道，乙地1990年出产8吨水果，甲地每年都出产98890-= (吨)水果。

乙地每年出产量翻番(增加一倍)，它的出产量依次是：8,16,32,64,128⋅⋅⋅ 6490，但12890因此，1994年乙地产量就能超过甲地。

六年级数学第5讲：立体几何

目录第5讲立体几何 (1)兴趣篇 (1)拓展篇 (6)超越篇 (10)第5讲立体几何兴趣篇1.一个长方体的长、宽、高分别为3厘米、2厘米、1厘米。

若它的棱长总和等于另一个正方体的棱长总和，则长方体与正方体的表面积之比是多少？长方体体积比正方体体积少多少立方厘米？÷=；【分析】该长方体的棱长总和为：()++⨯=；则正方体的边长为24122321424长方体的表面积为：()⨯+⨯+⨯⨯=，体积为：3216323121222⨯⨯=；正方体的表面积为：62224⨯⨯=⨯⨯=；体积为：2228所以长方体与正方体的表面积之比为：11:12，长方体的体积比正方体的体积少2立方厘米。

2.如图所示，将长为13厘米，宽为9厘米的长方形硬纸板的四角去掉边长为2厘米的正方形，然后沿虚线折叠成长方体容器。

这个容器的体积是多少立方厘米？如果四角去掉边长为3厘米的正方形呢？【分析】四个角都截去边长为2的正方形之后，长方体容器的长为1349-=，-=；宽为945其体积为95290⨯⨯=（立方厘米）。

如果四个角去的都是边长为3的正方形，则新形成的长方体的长为1367-=，-=，宽为963高为3，则新长方体的体积为73363⨯⨯=（立方厘米）。

3.用棱长是1厘米的小立方体拼成如图所示的立体图形。

这个图形的表面积是多少平方厘米？【分析】三视图法：从前往后看：7214⨯=；从左往右看：7214⨯=；从上往下看：9218⨯=；则这个图形的表面积为：14141846++=（平方厘米）。

4.（1）如图所示，将一个棱长为6的正方体从某个角切掉一个长、宽、高分别为4、3、5的长方体，剩余部分的表面积是多少？（2）如图所示，将一个棱长为5的正方体，从左上方切去一个长、宽、高分别为5、4、3的长方体，它的表面积减少了百分之几？【分析】（1）切去该长方体之后，整个表面积没有发生变化，则其表面积总和还为原表面积，为666216⨯⨯=平方厘米。

(完整word版)六年级奥数-第五讲.几何-立体部分.教师版

第五讲几何一一立体部分教学目标:对于小学几何而言，立体图形的表面积和体积计算，既可以很好地考查学生的空间想象能力，又可以具体考查学生在公式应用中处理相关数据的能力，所以，很多重要考试都很重视对立体图形的考查.知识点拨:、长方体和正方体如右图，长方体共有六个面（每个面都是长方形），八个顶点，十二条棱.①在六个面中，两个对面是全等的，即三组对面两两全等.（叠放在一起能够完全重合的两个图形称为全等图形. ）②长方体的表面积和体积的计算公式是：长方体的表面积：S长方体2（ab be ca）;长方体的体积：V长方体abc .③正方体是各棱相等的长方体，它是长方体的特例，它的六个面都是正方形. 如果它的棱长为a，那么：S正方体6a2, V正方体a3.、圆柱与圆锥立体图形表面积体积圆柱匕S圆柱侧面积2个底面积 2 n h 2 n2圆柱n hA /I'S圆锥侧面积底面积—n2n2360注：1是母线，即从顶点到底面圆上的线段长1 2V a锥体—n h3例题精讲:C如右图，在一个棱长为10的立方体上截取一个长为 8,宽为3, 高为2的小长方体，那么新的几何体的表面积是多少？我们从三个方向（前后、左右、上下）考虑，新几何体的表面积仍为原立方体的表面积：10 10 6 600.右图是一个边长为 4厘米的正方体，分别在前后、左右、上下各面的中心位置挖去一个边长 I 厘米的正方体，做成一种玩具.它的表面积是多少平方厘米？（图中只画出了前面、右面、上面挖去的正方体）原正方体的表面积是 4 4 696（平方厘米）.每一个面被挖去一个边长是1厘米的正方形，同时又增加了 5个边长是1厘米的正方体作为玩具的表面积的组成部分. 总的来看，每一个面都增加了 4个边长是1厘米的正方形. 从而，它的表面积是： 96 4 6 120平方厘米.在一个棱长为50厘米的正方体木块，在它的八个角上各挖去一个棱长为5厘米的小正方体，问剩下的立体图形的表面积是多少？对于和长方体相关的立体图形表面积，一般从上下、左右、前后 3个方向考虑.变化前后的表面积不变：50 50 615000（平方厘米）.F 图是一个棱长为 2厘米的正方体，在正方体上表面的正中，向下挖一个棱长为洞，接着在小洞的底面正中向下挖一个棱长为-厘米的正方形2小洞，第三个正方形小洞的挖法和前两个相同为 -厘米，那么4最后得到的立体图形的表面积是多少平方厘米？我们仍然从3个方向考虑•平行于上下表面的各面面积之和： 22 2 8（平方厘米）；左右方向、前后方向：2 2 4 16（平 1 1 方厘米），1 1 4 4（平方厘米）， 4 1（平方厘米），22114丄（平方厘米），这个立体图形的表面积为:444一个正方体木块，棱长是 1米，沿着水平方向将它锯成块，共得到大大小小的长方体24块，那么这24块长方体的表面积之和是多少?锯一次增加两个面，锯的总次数转化为增加的面数的公式为：锯的总次数 2增加的面数.【例1】【解析】【例2】【解析】【巩固】【解析】【例3】【解析】【例4】厂—丿O丿8 16 4 1 -29-（平方厘米）. 4 42片，每片又锯成 3长条，每条又锯成 4小1厘米的正方体小原正方体表面积：1 1 6 6（平方米），一共锯了（2 1）（3 1）（4 1） 6次， 6 112 6 18（平方米）.其中表面积最小的包装方法如图所示，表面积为 1034.【巩固】(2008年走美六年级初赛)一个表面积为56cm 2的长方体如图切成 27个小长方体，这27个小长方体__ 2表面积的和是 _________ cm .【解析】每一刀增加两个切面，增加的表面积等于与切面平行的两个表面积，所以每个方向切两刀后，表面积增加到原来的 3倍，即表面积的和为 56 3 168(cm 2).【例5】如图，25块边长为1的正方体积木拼成一个几何体，表面积最小是多少?【解析】当小积木互相重合的面最多时表面积最小 •设想27块边长为1的正方形积木，当拼成一个小积木，只有在两个角上各去掉一块小积木，或在同一个角去掉两块相邻的积木时，表面积不会增加，该几何体表面积为 54.【例6】要把12件同样的长a 、宽b 、高h 的长方体物品拼装成一件大的长方体，使打包后表面积最小，该如何打包？⑴当b 2h 时，如何打包？ ⑵当b 2h 时，如何打包？ ⑶当b 2h 时，如何打包？【解析】图2和图3正面的面积相同，侧面面积正面周长长方体长，所以正面的周长愈大表面积越大，图2的正面周长是 8h 6b ,图3的周长是12h 4b •两者的周长之差为 2 ( b 2h ).当b 2h 时，图2和图3周长相等，可随意打包；当 b 2h 时，按图2打包；当b 2h 时，按图3 打包•【巩固】要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体，表面积最小是多少?第一种按长宽高1 1 6拼接，重叠面有三种选择，共 3种包装方法•第二种按长宽高1 2 3拼接，有3个长方体并列方向的重叠面有三种选择，有2个长方体并列方向3 3 3的正方体时，表面积最小，现在要去掉【解析】考虑所有的包装方法，因为 6 12 3，所以一共有两种拼接方式:的重叠面剩下2种选择，一共有6种包装方法•其中表面积最小的包装方法如图所示，表面积为 1034.【例7】如图，在一个棱长为5分米的正方体上放一个棱长为 4分米的小正方体，求这个立体图形的表面积.7/我们把上面的小正方体想象成是可以向下“压缩”的， “压缩”后我们发现：小正方体的上面与大正方体上面中的阴影部分合在一起，正好是大正方体的上面 •这样这个立体图形的表面积就可以分成这样两部分：上下方向：大正方体的两个底面；四周方向（左右、前后方向）：小正方体的四个侧面，大正方体的四个侧面.上下方向：5 5 2 50 （平方分米）；侧面：5 5 4 100（平方分米），4 4 4 64（平方分米）.这个立体图形的表面积为：50 100 64 214（平方分米）.体紧贴在一起，则所得到的多面体的表面积是 ___________ 平方厘米.【解析】（法1）四个正方体的表面积之和为：（12 2232 52） 6 39 6234（平方厘米），重叠部分的面积为：123 （22 2 12）（32 22 12）（32 22 12）3 914 1440 （平方厘米）,所以，所得到的多面体的表面积为：234 40 194（平方厘米）.（法2）三视图法.从前后面观察到的面积为 52 32 22 38平方厘米，从左右两个面观察到的面积为52 32 34平方厘米，从上下能观察到的面积为扌25平方厘米.表面积为 38 34 252 194 （平方厘米）.【例9】把19个棱长为1厘米的正方体重叠在一起，按右图中的方式拼成一个立体图形•，求这个立体图形的表面积.【解析】【例8】（2008年“希望杯”五年级第2试）如图，棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方【解析】从上下、左右、前后观察到的的平面图形如下面三图表示•因此，这个立体图形的表面积为:上面2个左面 2个前面•上表面的面积为：9平方厘米，左表面的面积为：8平方厘米，前表面的面积为：10平方厘米•因此，这个立体图形的总表面积为：（9 8 10） 2 54 （平方厘米）•【巩固】用棱长是1厘米的立方块拼成如右图所示的立体图形，问该图形的表面积是多少平方厘米£ X._X、〈【解析】该图形的上、左、前三个方向的表面分别由 9、7、7块正方形组成.该图形的表面积等于（9 7 7） 2 46个小正方形的面积，所以该图形表面积为46平方厘米.【例10】有30个边长为1米的正方体，在地面上摆成右上图的形式，然后把露出的表面涂成红色.求被涂成红色的表面积.【例11】棱长是m 厘米（m 为整数）的正方体的若干面涂上红色，然后将其切割成棱长是1厘米的小正方体.至少有一面红色的小正方体个数和表面没有红色的小正方体个数的比为 13:12 ,此时m 的最小值是多少？【解析】 4 4 (1 2 3 4) 4 56(平方米).其中表面积最小的包装方法如图所示，表面积为1034.【解析】切割成棱长是1厘米的小正方体共有m3个，由于其中至少有一面是红色的小正方体与没有红色面的个数之比为13:12，而13 12 25，所以小正方体的总数是25的倍数，即m3是25的倍数，那么m是5的倍数.当m 5时，要使得至少有一面的小正方体有65个，可以将原正方体的正面、上面和下面涂色，此时至少一面涂红色的小正方体有 5 5 5 4 2 65个，表面没有红色的小正方体有125 65 60个，个数比恰好是13:12，符合题意•因此，m的最小值是5.【例12】有64个边长为1厘米的同样大小的小正方体，其中34个为白色的，30个为黑色的.现将它们拼成一个4 4 4的大正方体，在大正方体的表面上白色部分最多可以是多少平方厘米？【解析】要使大正方体的表面上白色部分最多，相当于要使大正方体表面上黑色部分最少，那么就要使得黑色小正方体尽量不露出来.在整个大正方体中，没有露在表面的小正方体有（4 2）3 8（个），用黑色的；在面上但不在边上的小正方体有（4 2）2 6 24 （个），其中30 8 22个用黑色.这样，在表面的4 4 6 96个1 1的正方形中，有22个是黑色，96 22 74（个）是白色，所以在大正方体的表面上白色部分最多可以是74平方厘米.【例13】三个完全一样的长方体，棱长总和是288厘米，每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数，给这三个长方体涂色，一个涂一面，一个涂两面，一个涂三面.涂色后把三个长方体都切成棱长为1厘米的小正方体，只有一个面涂色的小正方体最少有多少个？【解析】每个长方体的棱长和是288 3 96厘米，所以，每个长方体长、宽、高的和是96 4 24厘米.因为，每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数，所以，每个长方体的长、宽、高分别是9厘米、8厘米、7厘米.要求切割后只有一个面涂色的小正方体最少有多少个，则需每一个长方体按题意涂色时，应让切割后只有一个面涂色的小正方体最少•所以，涂一面的长方体应涂一个8 7面，有8 7 56个；涂两面的长方体，若两面不相邻，应涂两个8 7面，有8 7 2 112个；若两面相邻，应涂一个8 7 面和一个9 7面，此时有7 8 9 2 105个，所以涂两面的最少有105个；涂三面的长方体，若三面不两两相邻，应涂两个8 7面、一个9 7面，有7 8 8 9 4 147个；若三面两两相邻，有7 1 8 1 7 1 9 1 8 1 9 1 146个，所以涂三面的最少有146个.那么切割后只有一个面涂色的小正方体最少有56 105 146 307个.【例14】把一个大长方体木块表面上涂满红色后，分割成若干个同样大小的小正方体，其中恰好有两个面涂上红色的小正方体恰好是100块，那么至少要把这个大长方体分割成多少个小正方体？【解析】设小正方体的棱长为1,考虑两种不同的情况，一种是长方体的长、宽、高中有一个是1的情况，另一种是长方体的长、宽、高都大于1的情况.当长方体的长、宽、高中有一个是1时，分割后只有一层小正方体，其中有两个面涂上红色的小正方体是去掉最外层一圈的小正方体后剩下的那些. 因为有两个面涂上红色的小正方体恰好是100块，设100 a b，那么分成的小正方体个数为a 2b 2 1 ab 2 a b 4 2 a b 104，为了使小正方体的个数尽量少，应使 a b最小,而两数之积一定，差越小积越小，所以当a b 10时它们的和最小，此时共有10 2 10 2 144个小正方体.当长方体的长、宽、高都大于1时，有两个面涂上红色的小正方体是去掉8个顶点所在的小正方体后12条棱上剩余的小正方体，因为有两个面涂上红色的小正方体恰好是100块，所以长方体的长、宽、高之和是100 4 2 3 31.由于三个数的和一定，差越大积越小，为了使小正方体的个数尽量少，应该令312 2 27,此时共有2 2 27 108个小正方体.因为108 144，所以至少要把这个大长方体分割成 108个小正方体.□ 红 □ 红 □红□ _红□□ 红 □□ □ □ □ _红□其余四个面中，每个面的四个角上的方格不能再染成红色，至多能4个红色方格（见上中图）.因4个红色方格.最后.所以，红色方格最多有 ©I⑴⑴如图，每个角上三个方向的 3个方格必须染成不同的三种颜色，所以8个角上最多只能有 8个方格染成红色.⑵如图，阴影部分是首尾相接由 9个方格组成的环，这9个方格中只能有4个方格能染成同一种颜色（如果有5个方格染同一种颜色，必然出现相邻，可以用抽屉原理反证之：先去掉一个白格，剩下的然后两两相邻的分成四个抽屉，必然有一个抽屉中有两个红色方格），像这样的环，在正方体表面最多能找到不重叠的两道（关于正方体中心对称的两道），涉及的18个方格中最多能有8个可染成红色. ⑶剩下6 3 3 8 3 9 2 12个方格，分布在6条棱上，这12个格子中只能有6个能染成红色. 综上所述，能被染成红色的方格最多能有 8 8 6 22个格子能染成红色，第一种解法中已经给出 22 个红方格的染色方法，所以 22个格子染成红色是最多的情况.【例16】一个长、宽、高分别为21厘米、15厘米、12厘米的长方形•现从它的上面尽可能大的切下一个正方【例15】把正方体的六个表面都划分成 9个相等的正方形.用红、黄、蓝三种颜色去染这些小正方形，要求有公共边的正方形染不同的颜色，那么，用红色染的正方形最多有多少个？【解析】一个面最多有5个方格可染成红色（见左下图）.因为染有5个红色方格的面不能相邻，可以相对,所以至多有两个面可以染成 5个红色方格. ⑵体，然后从剩余的部分再尽可能大的切下一个正方体，最后再从第二次剩余的部分尽可能大的切下一个正方体，剩下的体积是多少立方厘米？【解析】本题的关键是确定三次切下的正方体的棱长•由于21:15:12 7:5:4，为了方便起见•我们先考虑长、宽、高分别为7厘米、5厘米、4厘米的长方体•因为7 5 4，容易知道第一次切下的正方体棱长应该是4厘米，第二次切时，切下棱长为3厘米的正方体符合要求•第三次切时，切下棱长为2厘米的正方体符合要求.那么对于原长方体来说，三次切下的正方体的棱长分别是12厘米、9厘米和6厘米，所以剩下的体【例17】有黑白两种颜色的正方体积木，把它摆成右图所示的形状，已知相邻标A的为黑色，图中共有黑色积木多少块？（有公共面）的积木颜色不同，积应是：21 15 12 12393631107 （立方厘米）•66【解析】分层来看，如下图（切面平行于纸面）共有黑色积木17块•【巩固】这个图形，是否能够由 1 1 2的长方体搭构而成？【解析】每一个1 1 2的长方体无论怎么放，都包含了一个黑色正方体和一个白色正方体，而黑色积木有17块，白色积木有15块，所以该图形不能够由1 1 2的长方体搭构而成•【巩固】有许多相同的立方体，每个立方体的六个面上都写着同一个数字（不同的立方体可以写相同的数字）先将写着2的立方体与写着1的立方体的三个面相邻，再将写着3的立方体写着2的立方体相邻（见左下图）•依这样构成右下图所示的立方体，它的六个面上的所有数字之和是多少？【解析】第一层如下图，第二层、第三层依次比上面一层每格都多1（见下图）•上面的9个数之和是27,由对称性知，上面、前面、右面的所有数之和都是27 •同理，下面的9个数之和是45,下面、左面、后面的所有数之和都是45.所以六个面上所有数之和是（27 45） 3 216 •【例18】（05年武汉明心杯数学挑战赛）如图所示，一个5 5 5的立方体，在一个方向上开有1 1 5的孔, 在另一个方向上开有2 1 5的孔，在第三个方向上开有 3 1 5的孔，剩余部分的体积是多少？表面积为多少？【解析】求体积：开了3 1 5的孔，挖去3 1 5 15，开了1 1 5的孔，挖去115 1 4;开了2 1 5的孔，挖去 2 1 5 （2 2） 6 , 剩余部分的体积是： 5 5 5 （15 4 6） 100 .（另解）将整个图形切片，如果切面平行于纸面，那么五个切片分别如图:求表面积：表面积可以看成外部和内部两部分.外部的表面积为 5 5 6 12 138，内部的面积可以分为前后、左右、上下三个方向，面积分别为 2 2 5 1 5 1 2 1 3 20、2 1 53 5 1 3 1 32、2 15 15 112 14，所以总的表面积为138 20 32 14 204.（另解）运用类似于三视图的方法，记录每一方向上的不同位置上的裸露正方形个数：前后方向：32上下方向：30 左右方向：40【总结】“切片法”：全面打洞（例如本题，五层一样），挖块成线（例如本题，在前一层的基础上，一条线一条线地挖），这里体现的思想方法是：化整为零，有序思考!【巩固】（2008年香港保良局第12届小学数学世界邀请赛）如图，原来的大正方体是由125个小正方体所构成的.其中有些小正方体已经被挖除，图中涂黑色的部分就是贯穿整个大正方体的挖除部分 •请问剩下的部分共有多少个小正方体？【解析】对于这一类从立体图形中间挖掉一部分后再求体积曾或小正方体数目）的题目一般可以采用“切片法”来做，所谓“切片法”，就是把整个立体图形切成一片一片的（或一层一层的），然后分别计算每一片或每一层的体积或小正方体数目，最后再把它们相加.采用切片法，俯视第一层到第五层的图形依次如下，其中黑色部分表示挖除掉的部分.1、2、3、4、5层剩下的小正方体分别有 22个、 11 11 6 22 72 （个）小正方体.【巩固】一个由125个同样的小正方体组成的大正方体，从这个大正方体中抽出若干个小正方体，把大正方体中相对的两面打通，右图就是抽空的状态•右图中剩下的小正方体有多少个？1 12 1 11 12 1 1 1 1 1 2 1 /12 2 2 2 2 2 22 2 22 21 1*21 尺12 2 2 2 2 / 1 21 1/ 1 2 1 1从图中可以看出，第 11个、11个、6个、22个,【解析】解法一：（用“容斥原理”来解）由正面图形抽出的小正方体有 5 5 25个，由侧面图形抽出的小正方体有5 5 25个，由底面图形抽出的小正方体有 4 5 20个，正面图形和侧面图形重合抽出的小正方体有1 2 2 1 2 2 8个，正面图形和底面图形重合抽出的小正方体有 1 3 2 2 7个，底面图形和侧面图形重合抽出的小正方体有 1 2 1 1 2 2 7个，三个面的图形共同重合抽出的小正方体有4个.根据容斥原理，25 25 20 8 7 7 4 52 ,所以共抽出了52个小正方体.125 52 73，所以右图中剩下的小正方体有73个.注意这里的三者共同抽出的小正方体是4个，必须知道是哪4块，这是最让人头疼的事.但你可以先构造空的两个方向上共同部分的模型，再由第三个方向来穿过“花墙” 这里，化虚为实的思想方法很重要.解法二：（用“切片法”来解）可以从上到下切五层，得：⑴从上到下五层，如图：请注意这里的挖空的技巧是：先认一种方向.比如：从上到下的每一层，首先都应该有第一层的空四块的情况，即如果挖第二层：第（1）步，把中间这些位置的四块挖走如图：第（2）步，把从右向左的两块成线地挖走. （请注意挖通的效果就是成线挖去），如图: 第（3）步，把从前向后的一块（请注意跟第二层有关的只是一块！）挖成线！如图:【例19】（2009年迎春杯高年级组复赛）右图中的⑴⑵⑶⑷是同样的小等边三角形，⑸⑹也是等边三角形且边长为⑴的2倍，⑺⑻⑼⑽是同样的等腰直角三角形，（11）是正方形•那么，以⑸⑹⑺⑻⑼⑽（11）为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的_________ 倍.其中左图是以⑴⑵⑶⑷为平面展开图的立体图形，是一个四个面都是正三角形的正四面体，右图以⑸⑹⑺⑻⑼⑽(11)为平面展开图的立体图形，是一个不规则图形，底面是(11),四个侧面是⑺⑻⑼⑽，两个斜面是⑸⑹. 对于这两个立体图形的体积，可以采用套模法来求，也就是对于这种我们不熟悉的立体图形，用一些我们熟悉的基本立体图形来套，看看它们与基本立体图形相比，缺少了哪些部分.由于左图四个面都是正三角形，右图底面是正方形，侧面是等腰直角三角形，想到都用正方体来套.对于左图来说，相当于由一个正方体切去 4个角后得到(如下左图，切去ABD"、CBDC i 、D i ACQ 、 B 1A C 1B);而对于右图来说，相当于由一个正方体切去2个角后得到(如下右图，切去 BACB i 、DACD 1).【解析】本题中的两个图都是立体图形的平面展开图,假设左图中的立方体的棱长为形的体积为：a 3丄a 2 a2右图中的立方体的棱长为 1 3-a ,3则以⑴⑵⑶⑷为平面展开图的立体图⑸ ⑺⑻ ⑹ (11) ⑼ ⑽1b ,以⑸⑹⑺⑻⑼⑽(11)为平面展开图的立体图形的体积为由于右图中的立方体的棱长即是题中正方形1的边长，是正三角形⑴的边长，通过将等腰直角三角形⑺分成的立方体的棱长是左图中的立方体的棱长的 2倍，即b 2a .那么以⑴⑵⑶⑷为平面展开图的立体图形的体积与以⑸⑹⑺⑻⑼⑽(11)为平面展开图的立体图形的体1 2 3 b — 2 b . 3 3而左图中的立方体的每一个面的对角线恰好4个相同的小等腰直角三角形可以得到右图中积的比为：1a 3：-b 3 [a 3：2 2a 3 1:16，也就是说以⑸⑹⑺⑻⑼⑽(11)为平面展开图的立体图形3 3 3 3的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的16倍.【例20】图⑴和图⑵是以正方形和等边三角形为面的立体图形的展开图，图中所有的边长都相同•请问：图⑴能围起来的立体图形的体积是图⑵能围起来的立体图形的体积的几倍？【解析】首先，我们把展开图折成立体图形，见下列示意图:对于这类题目，一般采用“套模法”，即用一个我们熟悉的基本立体图形来套，这样做基于两点考虑,一是如果有类似的模型，可以直接应用其计算公式；二是如果可以补上一块或者放到某个模型里面，那么可以从这个模型入手.我们把图⑴中的立体图形切成两半，再转一转，正好放进去！我们看到图⑴与图⑶的图形位置的微妙关系：11111 1丄丄1 1丄—，所以切掉8个角后的2 2 2 23 481 5体积是1 — 8 — •48 6 1再看图⑵中的正四面体，这个正四面体的棱长与图⑶中的每一条实线线段相等，所以应该用边长为-21由图⑷可见，图⑴这个立体的体积与图 ⑶这个被切去了 8个角后的立体图形的体积相等.假设立方体的1条边的长度是1,那么一个角的体积是图⑶1图⑷的立方体来套•如果把图⑵的立体图形放入边长为-的立方体里的话是可以放进去的.21这是切去了四个角后的图形，从上面的分析可知一个角的体积为一，所以图⑵的体积是：48---丄4丄，那么前者的体积是后者的 5丄20倍. 2 2 2 48 246 24【例21】如图，用高都是1米，底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体•问这个物体的表面积是多少平方米？（ n 取3.14）从上面看到图形是右上图，所以上下底面积和为2 3.14 1.52 14.13 （立方米），侧面积为2 3.14 （0.5 1 1.5） 1 18.84 （立方米），所以该物体的表面积是14.13 18.84 32.97（立方米）.【例22】有一个圆柱体的零件，高10厘米，底面直径是6厘米，零件的一端有一个圆柱形的圆孔，圆孔的直径是4厘米，孔深5厘米（见右图）•如果将这个零件接触空气的部分涂上防锈漆，那么一共要涂多少平方厘米？【解析】涂漆的面积等于大圆柱表面积与小圆柱侧面积之和，为6 26 n 10 n （一） 2 4 n 5 60 n 18n 20 n 98 n 307.72 （平方厘米）•2【例23】（第四届希望杯2试试题）圆柱体的侧面展开，放平，是边长分别为10厘米和12厘米的长方形，那么这个圆柱体的体积是立方厘米. （结果用n 表示）【解析】当圆柱的高是 12厘米时体积为(10\2 12n ( )12 2 n300 “（立方厘米）冗当圆柱的高是 12厘米时体积为,12 .2 “ n ( ) 102 n360 （立方厘米）•所以圆柱体的体积为300立方厘米 7t 7t或360立方厘米.【解析】1n【例24】如右图，是一个长方形铁皮，禾U用图中的阴影部分，刚好能做成一个油桶（接头处忽略不计），求这个油桶的容积.（n 3.14）XJ丿V ---------------- ——16.56m——- •【解析】圆的直径为：16.56 1 3.14 4（米），而油桶的高为2个直径长，即为：4 2 8（m），故体积为100.48立方米.【巩固】如图，有一张长方形铁皮，剪下图中两个圆及一块长方形，正好可以做成1个圆柱体，这个圆柱体的底面半径为10厘米，那么原来长方形铁皮的面积是多少平方厘米？（n 3.14）【解析】做成的圆柱体的侧面是由中间的长方形卷成的，可见这个长方形的长与旁边的圆的周长相等，则剪下的长方形的长，即圆柱体底面圆的周长为： 2 n 10 62.8（厘米），原来的长方形的面积为：（10 4 62.8）（10 2）2056（平方厘米）.【例25】把一个高是8厘米的圆柱体，沿水平方向锯去2厘米后，剩下的圆柱体的表面积比原来的圆柱体表面积减少12.56平方厘米•原来的圆柱体的体积是多少立方厘米？【解析】沿水平方向锯去2厘米后，剩下的圆柱体的表面积比原来的圆柱体表面积减少的部分为减掉的2厘米圆柱体的侧面积，所以原来圆柱体的底面周长为12.56 2 6.28厘米，底面半径为6.28 3.14 2 1厘米，所以原来的圆柱体的体积是n 12 8 8n 25.12（立方厘米）.【例26】一个圆柱体的体积是50.24立方厘米，底面半径是2厘米.将它的底面平均分成若干个扇形后，再截开拼成一个和它等底等高的长方体，表面积增加了多少平方厘米？（n 3.14）【解析】从图中可以看出，拼成的长方体的底面积与原来圆柱体的底面积相同，长方体的前后两个侧面面积与原来圆柱体的侧面面积相等，所以增加的表面积就是长方体左右两个侧面的面积.（法1）这两个侧面都是长方形，且长等于原来圆柱体的高，宽等于圆柱体底面半径.可知，圆柱体的高为50.24 3.14 224（厘米），所以增加的表面积为2 4 2 16（平方厘米）；（法2）根据长方体的体积公式推导. 增加的两个面是长方体的侧面，侧面面积与长方体的长的乘积就是长方体的体积.由于长方体的体积与圆柱体的体积相等，为50.24立方厘米，而拼成的长方体的长等于圆柱体底面周长的一半，为3.14 2 6.28厘米，所以侧面长方形的面积为50.24 6.28 8平方。

六年级奥数讲义必备专题第5讲.几何-立体部分.学生版

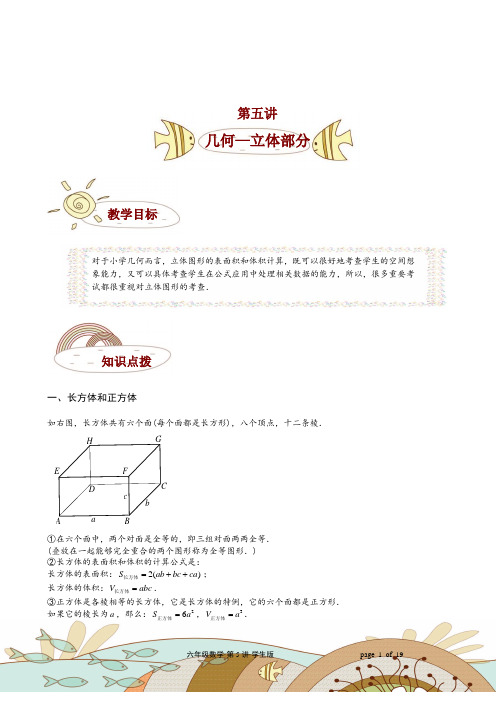
一、长方体和正方体如右图，长方体共有六个面(每个面都是长方形)，八个顶点，十二条棱．c b aHGFED CBA①在六个面中，两个对面是全等的，即三组对面两两全等． (叠放在一起能够完全重合的两个图形称为全等图形．) ②长方体的表面积和体积的计算公式是：长方体的表面积：2()S ab bc ca =++长方体；长方体的体积：V abc =长方体．③正方体是各棱相等的长方体，它是长方体的特例，它的六个面都是正方形．如果它的棱长为a ，那么：26S a =正方体，3V a =正方体．对于小学几何而言，立体图形的表面积和体积计算，既可以很好地考查学生的空间想象能力，又可以具体考查学生在公式应用中处理相关数据的能力，所以，很多重要考试都很重视对立体图形的考查．第五讲几何—立体部分教学目标知识点拨二、圆柱与圆锥立体图形表面积体积圆柱hr222π2πS rh r =+=+圆柱侧面积个底面积2πV r h =圆柱圆锥h r22ππ360nS l r =+=+圆锥侧面积底面积注：l 是母线，即从顶点到底面圆上的线段长 21π3V r h =圆锥体模块一：利用抽屉原理公式解题【巩固】在一个棱长为50厘米的正方体木块，在它的八个角上各挖去一个棱长为5厘米的小正方体，问剩下例题22例题精讲例题11如右图，在一个棱长为10的立方体上截取一个长为8，宽为3，高为2的小长方体，那么新的几何体的表面积是多少？右图是一个边长为4厘米的正方体，分别在前后、左右、上下各面的中心位置挖去一个边长l 厘米的正方体，做成一种玩具．它的表面积是多少平方厘米?（图中只画出了前面、右面、上面挖去的正方体）的立体图形的表面积是多少？【巩固】(2008年走美六年级初赛)一个表面积为256cm 的长方体如图切成27个小长方体，这27个小长方体表面积的和是 2cm ．例题44例题33下图是一个棱长为2厘米的正方体，在正方体上表面的正中，向下挖一个棱长为1厘米的正方体小洞，接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞，第三个正方形小洞的挖法和前两个相同为14厘米，那么最后得到的立体图形的表面积是多少平方厘米？一个正方体木块，棱长是1米，沿着水平方向将它锯成2片，每片又锯成3长条，每条又锯成4小块，共得到大大小小的长方体24块，那么这24块长方体的表面积之和是多少？25块积木【巩固】要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体，表面积最小是多少？例题77例题66例题55如图，25块边长为1的正方体积木拼成一个几何体，表面积最小是多少？要把12件同样的长a、宽b、高h的长方体物品拼装成一件大的长方体，使打包后表面积最小，该如何打包？⑴当b=2h时，如何打包？⑵当b<2h时，如何打包？⑶当b>2h时，如何打包？如图，在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体，求这个立体图形的表面积．【巩固】用棱长是1厘米的立方块拼成如右图所示的立体图形，问该图形的表面积是多少平方厘米?例题99例题88(2008年“希望杯”五年级第2试)如图，棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起，则所得到的多面体的表面积是_______平方厘米．把19个棱长为1厘米的正方体重叠在一起，按右图中的方式拼成一个立体图形.，求这个立体图形的表面积．例题1313例题1212例题1111例题1010有30个边长为1米的正方体，在地面上摆成右上图的形式，然后把露出的表面涂成红色．求被涂成红色的表面积．棱长是m 厘米（m 为整数）的正方体的若干面涂上红色，然后将其切割成棱长是1厘米的小正方体．至少有一面红色的小正方体个数和表面没有红色的小正方体个数的比为13:12，此时m 的最小值是多少?有64个边长为1厘米的同样大小的小正方体，其中34个为白色的，30个为黑色的．现将它们拼成一个444⨯⨯的大正方体，在大正方体的表面上白色部分最多可以是多少平方厘米？三个完全一样的长方体，棱长总和是288厘米，每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数，给这三个长方体涂色，一个涂一面，一个涂两面，一个涂三面．涂色后把三个长方体都切成棱长为1厘米的小正方体，只有一个面涂色的小正方体最少有多少个？A例题1717例题1616例题1515例题1414把一个大长方体木块表面上涂满红色后，分割成若干个同样大小的小正方体，其中恰好有两个面涂上红色的小正方体恰好是100块，那么至少要把这个大长方体分割成多少个小正方体？把正方体的六个表面都划分成9个相等的正方形．用红、黄、蓝三种颜色去染这些小正方形，要求有公共边的正方形染不同的颜色，那么，用红色染的正方形最多有多少个？一个长、宽、高分别为21厘米、15厘米、12厘米的长方形.现从它的上面尽可能大的切下一个正方体，然后从剩余的部分再尽可能大的切下一个正方体，最后再从第二次剩余的部分尽可能大的切下一个正方体，剩下的体积是多少立方厘米？有黑白两种颜色的正方体积木，把它摆成右图所示的形状，已知相邻(有公共面)的积木颜色不同，标A 的为黑色，图中共有黑色积木多少块？【巩固】这个图形，是否能够由112⨯⨯的长方体搭构而成？【巩固】有许多相同的立方体，每个立方体的六个面上都写着同一个数字(不同的立方体可以写相同的数字)先将写着2的立方体与写着1的立方体的三个面相邻，再将写着3的立方体写着2的立方体相邻(见左下图)．依这样构成右下图所示的立方体，它的六个面上的所有数字之和是多少?33223323322323111111【巩固】（2008年香港保良局第12届小学数学世界邀请赛）如图，原来的大正方体是由125个小正方体所构成的．其中有些小正方体已经被挖除，图中涂黑色的部分就是贯穿整个大正方体的挖除部分．请问剩下的部分共有多少个小正方体？第8题例题1818(05年武汉明心杯数学挑战赛)如图所示，一个555⨯⨯的立方体，在一个方向上开有115⨯⨯的孔，在另一个方向上开有215⨯⨯的孔，在第三个方向上开有315⨯⨯的孔，剩余部分的体积是多少？表面积为多少？【巩固】一个由125个同样的小正方体组成的大正方体，从这个大正方体中抽出若干个小正方体，把大正方体中相对的两面打通，右图就是抽空的状态．右图中剩下的小正方体有多少个？⑷⑶⑵⑴ ⑾⑽⑼⑻⑺⑹⑸例题2020例题1919（2009年迎春杯高年级组复赛）右图中的⑴⑵⑶⑷是同样的小等边三角形，⑸⑹也是等边三角形且边长为⑴的2倍，⑺⑻⑼⑽是同样的等腰直角三角形，⑾是正方形．那么，以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的倍．图⑴和图⑵是以正方形和等边三角形为面的立体图形的展开图，图中所有的边长都相同．请问：图⑴能围起来的立体图形的体积是图⑵能围起来的立体图形的体积的几倍？1110.511.5、例题2323例题2222例题2121如图，用高都是1米，底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体．问这个物体的表面积是多少平方米？(π取3.14)有一个圆柱体的零件，高10厘米，底面直径是6厘米，零件的一端有一个圆柱形的圆孔，圆孔的直径是4厘米，孔深5厘米(见右图)．如果将这个零件接触空气的部分涂上防锈漆，那么一共要涂多少平方厘米？(第四届希望杯2试试题)圆柱体的侧面展开，放平，是边长分别为10厘米和12厘米的长方形，那么这个圆柱体的体积是________立方厘米．(结果用π表示)16.56m【巩固】如图，有一张长方形铁皮，剪下图中两个圆及一块长方形，正好可以做成1个圆柱体，这个圆柱体的底面半径为10厘米，那么原来长方形铁皮的面积是多少平方厘米？(π 3.14=)10cm例题2626例题2525例题2424如右图，是一个长方形铁皮，利用图中的阴影部分，刚好能做成一个油桶(接头处忽略不计)，求这个油桶的容积．(π 3.14=)把一个高是8厘米的圆柱体，沿水平方向锯去2厘米后，剩下的圆柱体的表面积比原来的圆柱体表面积减少12.56平方厘米．原来的圆柱体的体积是多少立方厘米？一个圆柱体的体积是50.24立方厘米，底面半径是2厘米．将它的底面平均分成若干个扇形后，再截开拼成一个和它等底等高的长方体，表面积增加了多少平方厘米？(π 3.14=)8(单位：厘米)4106【巩固】一个酒精瓶，它的瓶身呈圆柱形(不包括瓶颈)，如图．已知它的容积为26.4π立方厘米．当瓶子正放时，瓶内的酒精的液面高为6厘米；瓶子倒放时，空余部分的高为2厘米．问：瓶内酒精的体积是多少立方厘米？合多少升？26【巩固】一个盖着瓶盖的瓶子里面装着一些水，瓶底面积为10平方厘米，(如下图所示)，请你根据图中标明的数据，计算瓶子的容积是＿＿＿＿＿＿．7cm4cm5cm例题2727(2008年”希望杯”五年级第2试)一个拧紧瓶盖的瓶子里面装着一些水(如图)，由图中的数据可推知瓶子的容积是_______ 立方厘米．(π取3.14)甲乙20cm 8cm100cm例题3131例题3030例题2929例题2828一个盛有水的圆柱形容器，底面内半径为5厘米，深20厘米，水深15厘米．今将一个底面半径为2厘米，高为17厘米的铁圆柱垂直放入容器中．求这时容器的水深是多少厘米？有甲、乙两只圆柱形玻璃杯，其内直径依次是10厘米、20厘米，杯中盛有适量的水．甲杯中沉没着一铁块，当取出此铁块后，甲杯中的水位下降了2厘米；然后将铁块沉没于乙杯，且乙杯中的水未外溢．问：这时乙杯中的水位上升了多少厘米？如图，甲、乙两容器相同，甲容器中水的高度是锥高的13，乙容器中水的高度是锥高的23，比较甲、乙两容器，哪一只容器中盛的水多？多的是少的的几倍？(2008年仁华考题)如图，有一卷紧紧缠绕在一起的塑料薄膜，薄膜的直径为20厘米，中间有一直径为8厘米的卷轴，已知薄膜的厚度为0.04厘米，则薄膜展开后的面积是平方米．【巩固】图为一卷紧绕成的牛皮纸，纸卷直径为20厘米，中间有一直径为6厘米的卷轴．已知纸的厚度为0.4毫米，问：这卷纸展开后大约有多长？CB A43【巩固】如图，直角三角形如果以BC 边为轴旋转一周，那么所形成的圆锥的体积为16π，以AC 边为轴旋转一周，那么所形成的圆锥的体积为12π，那么如果以AB 为轴旋转一周，那么所形成的几何体的体积是多少？ABC例题3333例题3232如图，ABC 是直角三角形，AB 、AC 的长分别是3和4．将ABC ∆绕AC 旋转一周，求ABC ∆扫出的立体图形的体积．(π 3.14=)已知直角三角形的三条边长分别为3cm ，4cm ，5cm ，分别以这三边轴，旋转一周，所形成的立体图形中，体积最小的是多少立方厘米？(π取3.14)O FABCDEOFABCDE【巩固】(2006年第十一届华杯赛决赛试题)如图，ABCD 是矩形，6cm BC =，10cm AB =，对角线AC 、BD相交O ．图中的阴影部分以CD 为轴旋转一周，则阴影部分扫出的立体的体积是多少立方厘米？DCB A O例题3535例题3434如图，ABCD 是矩形，6cm BC =，10cm AB =，对角线AC 、BD 相交O ．E 、F 分别是AD 与BC 的中点，图中的阴影部分以EF 为轴旋转一周，则白色部分扫出的立体图形的体积是多少立方厘米？(π取3)(人大附中分班考试题目)如图，在一个正方体的两对侧面的中心各打通一个长方体的洞，在上下底面的中心打通一个圆柱形的洞．已知正方体边长为10厘米，侧面上的洞口是边长为4厘米的正方形，上下底面的洞口是直径为4厘米的圆，求253015练习22练习11家庭作业（《小学生数学报》邀请赛）从一个棱长为10厘米的正方形木块中挖去一个长10厘米、宽2厘米、高2厘米的小长方体，剩下部分的表面积是多少？(写出符合要求的全部答案)一个酒瓶里面深30cm，底面内直径是10cm，瓶里酒深15cm．把酒瓶塞紧后使其瓶口向下倒立这时酒深25cm．酒瓶的容积是多少？(π取3)第2题练习55练习44练习31如右图所示，由三个正方体木块粘合而成的模型，它们的棱长分别为1米、2米、4米，要在表面涂刷油漆，如果大正方体的下面不涂油漆，则模型涂刷油漆的面积是多少平方米？(2008年第二届两岸四地”华罗庚金杯”少年数学精英邀请赛)一个圆柱体形状的木棒，沿着底面直径竖直切成两部分．已知这两部分的表面积之和比圆柱体的表面积大22008cm ，则这个圆柱体木棒的侧面积是________2cm ．(π取3.14) 如图，厚度为0.25毫米的铜版纸被卷成一个空心圆柱(纸卷得很紧，没有空隙)，它的外直径是180厘米，内直径是50厘米．这卷铜版纸的总长是多少米？5cm11cm备选33备选22备选11月测备选如右图，一个正方体形状的木块，棱长l米，沿水平方向将它锯成3片，每片又锯成4长条，每条又锯成5小块，共得到大大小小的长方体60块．那么，这60块长方体表面积的和是多少平方米?一个透明的封闭盛水容器，由一个圆柱体和一个圆锥体组成，圆柱体的底面直径和高都是12厘米．其内有一些水，正放时水面离容器顶11厘米，倒放时水面离顶部5厘米，那么这个容器的容积是多少立方厘米？(π3)如图，有一个边长为20厘米的大正方体，分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后，表面积变为2454平方厘米，那么挖掉的小立方体的边长是多少厘米？4cm12r r12h h备选11备选44一个圆柱体底面周长和高相等．如果高缩短4厘米，表面积就减少50.24平方厘米．求这个圆柱体的表面积是多少？(2009年”希望杯”一试六年级)如图，圆锥形容器中装有水50升，水面高度是圆锥高度的一半，这个容器最多能装水升．。

六年级奥数几何;第5讲;几何综合_二_;教师版

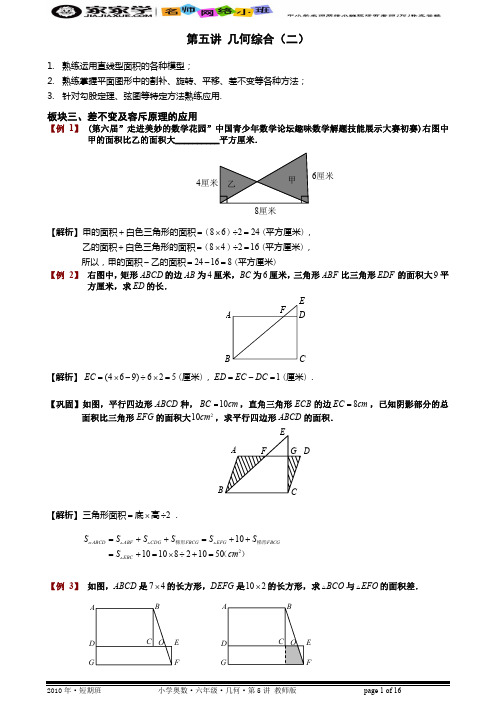
方法二：连接正方形 A 对角线(如右上图)，将 40 平方厘米的图形分成面积相等的两个梯形，而梯
形的上下底之和恰好是 20 厘米，所以梯形的高为 20 × 2 ÷ 20 = 2 (厘米)，即两个正方形的边长差，
由此可求出乙正方形的边长为(20 − 2)÷ 2 = 9 (厘米)，从而乙正方形的面积为 9 × 9 = 81(厘米 2)．
A
甲乙 D I JF
M
N H丙
B
E
C
【解析】因为 D 、 E 、 F 分别为三边的中点，所以 DE 、 DF 、 EF 是三角形 ABC 的中位线，也就与对应的边平行，根据面积比例模型，三角形 ABN 和三角形 AMC 的面积都等于三角形 ABC 的一半，即为 200．根据图形的容斥关系，有 SΔABC − S丙 = SΔABN + SΔAMC − SAMHN ，即 400 − S丙 = 200 + 200 − SAMHN ，所以 S丙 = SAMHN ．
【例 8】从一块正方形的玻璃板上锯下宽为 0.5 米的一个长方形玻璃条后，剩下的长方形的面积为 5 平方米，请问锯下的长方形玻璃条的面积等于多少？
0.5
5 5
5
0.5
0.5
5 5
2010 年·短期班
图a
图b
小学奥数·六年级·几何·第 5 讲教师版
page 3 of 16
【解析】我们先按题目中的条件画出示意图(如图 a )，我们先看图中剩下的长方形，已知它的面积为 5 平方米，它的长和宽相差 0.5 米，我们可以将这样形状的四个长方形拼成一个弦图(如图 b )．图 b 是一个大正方形，它的边长等于长方形的长和宽之和，中间的那个小正方形的边长，等于长方形的长和宽之差，即 0.5 米．所以中间的小正方形的面积为 0.5 × 0.5 = 0.25 平方米，那么大正方形的面积为 5 × 4 + 0.25 = 20.25 平方米．因为 4.5 × 4.5 = 20.25 ，所以大正方形的边长等于 4.5 米．所以原题中剩下的长方形的长与宽的和为 4.5 米，而长与宽的差为 0.5 米，所以剩下的长方形的长为： (4.5 + 0.5) ÷ 2 = 2.5 米，即原正方形的边长为 2.5 米．又知锯下的长方形玻璃条的宽为 0.5 米，于是可得锯下的长方形玻璃条的面积为 2.5 × 0.5 = 1.25 平方米．

奥数六年级千份讲义 25 1[1].学而思杯考前辅导

模块一、计算【例 1】（2008年学而思杯6年级1试第1题）计算：11111200820092010201120121854108180270++++= 。

【例 2】（2009年学而思杯6年级第6题）计算：1122426153577++++=____。

【例 3】（2008年学而思杯6年级第1题）计算：3413441344413444444441344444444412389275277527775277777777527777777775+⨯+⨯++⨯+⨯=。

【巩固】(第五届《小数报》数学竞赛初赛计算题第3题)计算：11111 123420 261220420 +++++【巩固】计算：1111111 315356399143195++++++学而思杯考前辅导【巩固】 111111212312100++++++++++【巩固】 234501(12)(12)(123)(123)(1234)(12349)(12350)++++⨯++⨯++++⨯+++++++⨯++++【巩固】 111111212312100++++++++++【巩固】 234501(12)(12)(123)(123)(1234)(12349)(12350)++++⨯++⨯++++⨯+++++++⨯++++【巩固】 (仁华学校入学测试题) 22222211111131517191111131+++++=------ .【巩固】计算：222222223571512233478++++⨯⨯⨯⨯【巩固】计算：222222222231517119931199513151711993119951++++++++++=----- ．【巩固】计算：222212350133********++++=⨯⨯⨯⨯．【巩固】11111 (......) 1200722006(2008)200622007120071111 (......) 20081200622005(2007)20061n nn n+++++-⨯⨯⨯-⨯⨯+++++⨯⨯⨯-⨯【巩固】1 2【例 4】（2009年学而思杯6年级第1题）a=10.8+10.98+10.998+10.9998+10.99998，的整数部分是。

六年级奥数专题-4几何五大模型——鸟头模型

几何五大模型——鸟头模型一两点都在边上：鸟头定理：（现出“鸟头模型”。

然后按一下出现一个鸟头，勾勒出鸟头的轮廓，出现如图的鸟头几何模型。

最后真实的鸟头隐去，只留下几何模型。

最后按一下，出公式。

）△ADE △ABC S AD ×AE =S AB ×ACE DC BA二一点在边上，一点在边的延长线上： △CDE △ABC S CD ×CE =S BC ×AC本讲要点例1如图，AD=DB ，AE=EF=FC ，已知阴影部分面积为5平方厘米，△ ABC的面积是平方厘米．例2例2 （1）如图在△ABC中，D、E分别是AB，AC上的点，且AD:AB=2:5, AE:AC=4:7,△ABC 的面积是16平方厘米，求△ABC的面积。

（2）如图在△ABC中，D在BA的延长线上，E在AC上，且AB:AD=5:2，AE:EC=3:2,△ADE 的面积是12平方厘米，求△ABC的面积。

已知△DEF 的面积为12平方厘米，BE=CE,AD=2BD,CF=3AF,求△ABC 的面积。

三角形ABC 面积为1，AB 边延长一倍到D ，BC 延长2倍到E ，CA 延长3倍到F ，问三角形DEF 的面积为多少？FE DC BA例4例3长方形ABCD 面积为120，EF 为AD 上的三等分点，G 、H 、I 为DC 上的四等分点，阴影面积是多大？如图，过平行四边形ABCD 内的一点P 作边AD 、BC 的平行线EF 、GH ，若PBD 的面积为8平方分米，求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米？例6例51. 如下左图，在ABC △中，D 、E 分别是BC 、AB 的三等分点，且ABC △的面积是54，求CDE △的面积。

2. 如图，长方形ABCD 的面积是1，M 是AD 边的中点，N 在AB 边上，且12AN BN．那么，阴影部分的面积等于．AB CD M N 图1家庭作业 B3. 如图以ABC △的三边分别向外做三个正方形ABIH 、ACFG 、BCED ,连接HG 、EF 、ID ，又得到三个三角形，已知六边形DEFGHI 的面积是77平方厘米，三个正方形的面积分别是9、16、36平方厘米，则三角形ABC 的面积是多少？IHG FE DC B A4.5. 如图，已知三角形ABC 面积为1，延长AB 至D ，使BD AB =；延长BC 至E ，使2CE BC =；延长CA 至F ，使3AF AC =，求三角形DEF 的面积。

六年级奥数-第五讲.几何-立体部分

第五讲几何——立体部分教学目标：对于小学几何而言，立体图形的表面积和体积计算，既可以很好地考查学生的空间想象能力，又可以具体考查学生在公式应用中处理相关数据的能力，所以，很多重要考试都很重视对立体图形的考查．知识点拨：一、长方体和正方体如右图，长方体共有六个面(每个面都是长方形)，八个顶点，十二条棱．c b aHGFED CBA①在六个面中，两个对面是全等的，即三组对面两两全等． (叠放在一起能够完全重合的两个图形称为全等图形．) ②长方体的表面积和体积的计算公式是：长方体的表面积：2()S ab bc ca =++长方体；长方体的体积：V abc =长方体．③正方体是各棱相等的长方体，它是长方体的特例，它的六个面都是正方形．如果它的棱长为a ，那么：26S a =正方体，3V a =正方体．二、圆柱与圆锥例题精讲：【例 1】如右图，在一个棱长为10的立方体上截取一个长为8，宽为3，高为2的小长方体，那么新的几何体的表面积是多少？【解析】我们从三个方向(前后、左右、上下)考虑，新几何体的表面积仍为原立方体的表面积：10⨯10⨯6=600．【例 2】右图是一个边长为4厘米的正方体，分别在前后、左右、上下各面的中心位置挖去一个边长l 厘米的正方体，做成一种玩具．它的表面积是多少平方厘米?（图中只画出了前面、右面、上面挖去的正方体）【解析】原正方体的表面积是4⨯4⨯6=96(平方厘米)．每一个面被挖去一个边长是1厘米的正方形，同时又增加了5个边长是1厘米的正方体作为玩具的表面积的组成部分．总的来看，每一个面都增加了4个边长是1厘米的正方形．从而，它的表面积是：96+4⨯6=120平方厘米．【巩固】在一个棱长为50厘米的正方体木块，在它的八个角上各挖去一个棱长为5厘米的小正方体，问剩下的立体图形的表面积是多少？【解析】对于和长方体相关的立体图形表面积，一般从上下、左右、前后3个方向考虑．变化前后的表面积不变：50⨯50⨯6=15000(平方厘米)．【例 3】下图是一个棱长为2厘米的正方体，在正方体上表面的正中，向下挖一个棱长为1厘米的正方体小洞，接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞，第三个正方形小洞的挖法和前两个相同为14厘米，那么最后得到的立体图形的表面积是多少平方厘米？【解析】我们仍然从3个方向考虑．平行于上下表面的各面面积之和：2⨯2⨯2=8(平方厘米)；左右方向、前后方向：2⨯2⨯4=16(平方厘米)，1⨯1⨯4=4(平方厘米)，12⨯12⨯4=1(平方厘米)，14⨯14⨯4=14(平方厘米)，这个立体图形的表面积为：816++4+1+14=1294(平方厘米).【例4】一个正方体木块，棱长是1米，沿着水平方向将它锯成2片，每片又锯成3长条，每条又锯成4小块，共得到大大小小的长方体24块，那么这24块长方体的表面积之和是多少？【解析】锯一次增加两个面，锯的总次数转化为增加的面数的公式为：锯的总次数⨯2=增加的面数．原正方体表面积：1⨯1⨯6=6(平方米)，一共锯了(2-1)+(3-1)+(4-1)=6次，6+1⨯1⨯2⨯6=18(平方米)．56cm的长方体如图切成27个小长方体，这27个小长方体【巩固】(2008年走美六年级初赛)一个表面积为2cm．表面积的和是2【解析】每一刀增加两个切面，增加的表面积等于与切面平行的两个表面积，所以每个方向切两刀后，表面积增加到原来的3倍，即表面积的和为2⨯=．563168(cm)【例5】如图，25块边长为1的正方体积木拼成一个几何体，表面积最小是多少？25块积木【解析】当小积木互相重合的面最多时表面积最小.设想27块边长为1的正方形积木，当拼成一个333⨯⨯的正方体时，表面积最小，现在要去掉2块小积木，只有在两个角上各去掉一块小积木，或在同一个角去掉两块相邻的积木时，表面积不会增加，该几何体表面积为54.【例6】要把12件同样的长a、宽b、高h的长方体物品拼装成一件大的长方体，使打包后表面积最小，该如何打包？⑴当b=2h时，如何打包？⑵当b<2h时，如何打包？⑶当b>2h时，如何打包？【解析】图2和图3正面的面积相同，侧面面积=正面周长⨯长方体长，所以正面的周长愈大表面积越大，图2的正面周长是8h+6b，图3的周长是12h+4b.两者的周长之差为2（b-2h）.当b=2h时，图2和图3周长相等，可随意打包；当b<2h时，按图2打包；当b>2h时，按图3打包.图3图2图1h ba【巩固】要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体，表面积最小是多少？【解析】考虑所有的包装方法，因为6=1⨯2⨯3，所以一共有两种拼接方式：第一种按长宽高1⨯1⨯6拼接，重叠面有三种选择，共3种包装方法.第二种按长宽高1⨯2⨯3拼接，有3个长方体并列方向的重叠面有三种选择，有2个长方体并列方向的重叠面剩下2种选择，一共有6种包装方法. 其中表面积最小的包装方法如图所示，表面积为1034.【例 7】如图，在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体，求这个立体图形的表面积．【解析】我们把上面的小正方体想象成是可以向下“压缩”的，“压缩”后我们发现：小正方体的上面与大正方体上面中的阴影部分合在一起，正好是大正方体的上面.这样这个立体图形的表面积就可以分成这样两部分：上下方向：大正方体的两个底面；四周方向(左右、前后方向)：小正方体的四个侧面，大正方体的四个侧面．上下方向：55250⨯⨯=(平方分米)；侧面：554100⨯⨯=(平方分米)，44464⨯⨯=(平方分米)．这个立体图形的表面积为：5010064214++=(平方分米)．【例 8】 (2008年“希望杯”五年级第2试)如图，棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起，则所得到的多面体的表面积是_______平方厘米．【解析】(法1)四个正方体的表面积之和为：2222+++⨯=⨯=(平方厘米)，(1235)6396234重叠部分的面积为：222222222⨯+⨯+++++++=+++=(平方厘米)，13(221)(321)(321)39141440所以，所得到的多面体的表面积为：23440194-=(平方厘米)．(法2)三视图法．从前后面观察到的面积为22253238++=平方厘米,从左右两个面观察到的面积为22+=平方厘米，从上下能观察到的面积为2525=平方厘米．5334表面积为()++⨯=(平方厘米)．3834252194【例9】把19个棱长为1厘米的正方体重叠在一起，按右图中的方式拼成一个立体图形.，求这个立体图形的表面积．【解析】从上下、左右、前后观察到的的平面图形如下面三图表示．因此，这个立体图形的表面积为：2个上面2+个左面2+个前面．上表面的面积为：9平方厘米，左表面的面积为：8平方厘米，前表面的面积为：10平方厘米．因此，这个立体图形的总表面积为：(9810)254++⨯=(平方厘米)．上下面左右面前后面【巩固】用棱长是1厘米的立方块拼成如右图所示的立体图形，问该图形的表面积是多少平方厘米?【解析】该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成．该图形的表面积等于(977)246++⨯=个小正方形的面积，所以该图形表面积为46平方厘米．【例10】有30个边长为1米的正方体，在地面上摆成右上图的形式，然后把露出的表面涂成红色．求被涂成红色的表面积．【解析】44(1234)456⨯++++⨯=(平方米)．【例11】棱长是m厘米（m为整数）的正方体的若干面涂上红色，然后将其切割成棱长是1厘米的小正方体．至少有一面红色的小正方体个数和表面没有红色的小正方体个数的比为13:12，此时m的最小值是多少?m个，由于其中至少有一面是红色的小正方体与没有红色面的【解析】切割成棱长是1厘米的小正方体共有3个数之比为13:12，而131225+=，所以小正方体的总数是25的倍数，即3m是25的倍数，那么m 是5的倍数．当5m=时，要使得至少有一面的小正方体有65个，可以将原正方体的正面、上面和下面涂色，此时至少一面涂红色的小正方体有5554265⨯+⨯⨯=个，表面没有红色的小正方体有1256560-=个，个数比恰好是13:12，符合题意.因此，m的最小值是5．【例12】有64个边长为1厘米的同样大小的小正方体，其中34个为白色的，30个为黑色的．现将它们拼成一个444⨯⨯的大正方体，在大正方体的表面上白色部分最多可以是多少平方厘米？【解析】要使大正方体的表面上白色部分最多，相当于要使大正方体表面上黑色部分最少，那么就要使得黑色小正方体尽量不露出来．在整个大正方体中，没有露在表面的小正方体有3-=(个)，用黑色的；在面上但不在边上的小(42)8正方体有2-=个用黑色．(42)624-⨯=(个)，其中30822这样，在表面的44696-=(个)是白色，所以在大⨯⨯=个11⨯的正方形中，有22个是黑色，962274正方体的表面上白色部分最多可以是74平方厘米．【例13】三个完全一样的长方体，棱长总和是288厘米，每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数，给这三个长方体涂色，一个涂一面，一个涂两面，一个涂三面．涂色后把三个长方体都切成棱长为1厘米的小正方体，只有一个面涂色的小正方体最少有多少个？【解析】每个长方体的棱长和是288396÷=厘米，所以，每个长方体长、宽、高的和是96424÷=厘米．因为，每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数，所以，每个长方体的长、宽、高分别是9厘米、8厘米、7厘米．要求切割后只有一个面涂色的小正方体最少有多少个，则需每一个长方体按题意涂色时，应让切割后只有一个面涂色的小正方体最少．所以，涂一面的长方体应涂一个87⨯面，有8756⨯=个；涂两面的长方体，若两面不相邻，应涂两个87⨯面，有872112⨯⨯=个；若两面相邻，应涂一个87⨯面和一个97⨯面，此时有()7892105⨯+-=个，所以涂两面的最少有105个；涂三面的长方体，若三面不两两相邻，应涂两个87⨯面、一个97⨯面，有()78894147⨯++-=个；若三面两两相邻，有()()()()()()718171918191146-⨯-+-⨯-+-⨯-=个，所以涂三面的最少有146个．那么切割后只有一个面涂色的小正方体最少有56105146307++=个．【例 14】把一个大长方体木块表面上涂满红色后，分割成若干个同样大小的小正方体，其中恰好有两个面涂上红色的小正方体恰好是100块，那么至少要把这个大长方体分割成多少个小正方体？【解析】设小正方体的棱长为1，考虑两种不同的情况，一种是长方体的长、宽、高中有一个是1的情况，另一种是长方体的长、宽、高都大于1的情况．当长方体的长、宽、高中有一个是1时，分割后只有一层小正方体，其中有两个面涂上红色的小正方体是去掉最外层一圈的小正方体后剩下的那些．因为有两个面涂上红色的小正方体恰好是100块，设100a b =⨯，那么分成的小正方体个数为()()()()221242104a b ab a b a b +⨯+⨯=+++=++，为了使小正方体的个数尽量少，应使()a b +最小，而两数之积一定，差越小积越小，所以当10a b ==时它们的和最小，此时共有()()102102144+⨯+=个小正方体．当长方体的长、宽、高都大于1时，有两个面涂上红色的小正方体是去掉8个顶点所在的小正方体后12条棱上剩余的小正方体，因为有两个面涂上红色的小正方体恰好是100块，所以长方体的长、宽、高之和是10042331÷+⨯=．由于三个数的和一定，差越大积越小，为了使小正方体的个数尽量少，应该令312227=++，此时共有2227108⨯⨯=个小正方体．因为108144<，所以至少要把这个大长方体分割成108个小正方体．【例 15】把正方体的六个表面都划分成9个相等的正方形．用红、黄、蓝三种颜色去染这些小正方形，要求有公共边的正方形染不同的颜色，那么，用红色染的正方形最多有多少个？【解析】一个面最多有5个方格可染成红色（见左下图）．因为染有5个红色方格的面不能相邻，可以相对，所以至多有两个面可以染成5个红色方格．红红红红红红红红红红红其余四个面中，每个面的四个角上的方格不能再染成红色，至多能染4个红色方格（见上中图）．因为染有4个红色方格的面也不能相邻，可以相对，所以至多有两个面可以染成4个红色方格．最后剩下两个相对的面，每个面最多可以染2个红色方格（见右上图）．所以，红色方格最多有52422222⨯+⨯+⨯=（个）．（另解）事实上上述的解法并不严密，“如果最初的假设并没有两个相对的有5个红色方格的面，是否其他的四个面上可以出现更多的红色方格呢？”这种解法回避了这个问题，如果我们从约束染色方格数的本质原因入手，可严格说明22是红色方格数的最大值．对于同一个平面上的格网，如果按照国际象棋棋盘的方式染色，那么至少有一半的格子可以染成红色．但是现在需要染色的是一个正方体的表面，因此在分析问题时应该兼顾棱、角等面与面相交的地方：⑴ ⑵ ⑶ ⑴如图，每个角上三个方向的3个方格必须染成不同的三种颜色，所以8个角上最多只能有8个方格染成红色．⑵如图，阴影部分是首尾相接由9个方格组成的环，这9个方格中只能有4个方格能染成同一种颜色(如果有5个方格染同一种颜色，必然出现相邻，可以用抽屉原理反证之：先去掉一个白格，剩下的然后两两相邻的分成四个抽屉，必然有一个抽屉中有两个红色方格)，像这样的环，在正方体表面最多能找到不重叠的两道（关于正方体中心对称的两道），涉及的18个方格中最多能有8个可染成红色． ⑶剩下633839212⨯⨯-⨯-⨯=个方格，分布在6条棱上，这12个格子中只能有6个能染成红色．综上所述，能被染成红色的方格最多能有88622++=个格子能染成红色，第一种解法中已经给出22个红方格的染色方法，所以22个格子染成红色是最多的情况．【例 16】一个长、宽、高分别为21厘米、15厘米、12厘米的长方形.现从它的上面尽可能大的切下一个正方体，然后从剩余的部分再尽可能大的切下一个正方体，最后再从第二次剩余的部分尽可能大的切下一个正方体，剩下的体积是多少立方厘米？【解析】本题的关键是确定三次切下的正方体的棱长.由于21:15:127:5:4=，为了方便起见.我们先考虑长、宽、高分别为7厘米、5厘米、4厘米的长方体.因为754>>，容易知道第一次切下的正方体棱长应该是4厘米，第二次切时，切下棱长为3厘米的正方体符合要求.第三次切时，切下棱长为2厘米的正方体符合要求．那么对于原长方体来说，三次切下的正方体的棱长分别是12厘米、9厘米和6厘米，所以剩下的体积应是：()33321151212961107⨯⨯-++=（立方厘米）.12129996663121263912【例 17】有黑白两种颜色的正方体积木，把它摆成右图所示的形状，已知相邻(有公共面)的积木颜色不同，标A 的为黑色，图中共有黑色积木多少块？A【解析】分层来看，如下图(切面平行于纸面)共有黑色积木17块.【巩固】这个图形，是否能够由112⨯⨯的长方体搭构而成？【解析】每一个112⨯⨯的长方体无论怎么放，都包含了一个黑色正方体和一个白色正方体，而黑色积木有17块，白色积木有15块，所以该图形不能够由112⨯⨯的长方体搭构而成.【巩固】有许多相同的立方体，每个立方体的六个面上都写着同一个数字(不同的立方体可以写相同的数字)先将写着2的立方体与写着1的立方体的三个面相邻，再将写着3的立方体写着2的立方体相邻(见左下图)．依这样构成右下图所示的立方体，它的六个面上的所有数字之和是多少?33223323322323111111【解析】第一层如下图，第二层、第三层依次比上面一层每格都多1(见下图)．765434565第三层654323454第二层第一层343212345上面的9个数之和是27，由对称性知，上面、前面、右面的所有数之和都是27．同理，下面的9个数之和是45，下面、左面、后面的所有数之和都是45．所以六个面上所有数之和是(2745)3216+⨯=．【例 18】 (05年武汉明心杯数学挑战赛)如图所示，一个555⨯⨯的立方体，在一个方向上开有115⨯⨯的孔，在另一个方向上开有215⨯⨯的孔，在第三个方向上开有315⨯⨯的孔，剩余部分的体积是多少？表面积为多少？【解析】求体积：开了315⨯⨯的孔，挖去31515⨯⨯=，开了115⨯⨯的孔，挖去11514⨯⨯-=；开了215⨯⨯的孔，挖去215(22)6⨯⨯-+=，剩余部分的体积是：555(1546)100⨯⨯-++=．(另解)将整个图形切片，如果切面平行于纸面，那么五个切片分别如图：得到总体积为：22412100⨯+=．求表面积：表面积可以看成外部和内部两部分．外部的表面积为55612138⨯⨯-=，内部的面积可以分为前后、左右、上下三个方向，面积分别为()22515121320⨯⨯+⨯-⨯-⨯=、 ()2153513132⨯⨯+⨯-⨯-=、()2151511214⨯⨯+⨯-⨯-=，所以总的表面积为138203214204+++=．(另解)运用类似于三视图的方法，记录每一方向上的不同位置上的裸露正方形个数：前后方向：32上下方向：30左右方向：40总表面积为()2323040204⨯++=．【总结】“切片法”：全面打洞(例如本题，五层一样)，挖块成线(例如本题，在前一层的基础上，一条线一条线地挖)，这里体现的思想方法是：化整为零，有序思考！【巩固】（2008年香港保良局第12届小学数学世界邀请赛）如图，原来的大正方体是由125个小正方体所构成的．其中有些小正方体已经被挖除，图中涂黑色的部分就是贯穿整个大正方体的挖除部分．请问剩下的部分共有多少个小正方体？第8题【解析】对于这一类从立体图形中间挖掉一部分后再求体积（或小正方体数目）的题目一般可以采用“切片法”来做，所谓“切片法”，就是把整个立体图形切成一片一片的（或一层一层的），然后分别计算每一片或每一层的体积或小正方体数目，最后再把它们相加．采用切片法，俯视第一层到第五层的图形依次如下，其中黑色部分表示挖除掉的部分．第1层第2层第3层第4层第5层从图中可以看出，第1、2、3、4、5层剩下的小正方体分别有22个、11个、11个、6个、22个，所以总共还剩下22111162272++++=（个）小正方体．【巩固】一个由125个同样的小正方体组成的大正方体，从这个大正方体中抽出若干个小正方体，把大正方体中相对的两面打通，右图就是抽空的状态．右图中剩下的小正方体有多少个？【解析】解法一：(用“容斥原理”来解)由正面图形抽出的小正方体有5525⨯=个，由侧面图形抽出的小正方体有5525⨯=个，由底面图形抽出的小正方体有4520⨯=个，正面图形和侧面图形重合抽出的小正方体有1221228⨯+⨯=个，底面图⨯+⨯+⨯=个，正面图形和底面图形重合抽出的小正方体有13227形和侧面图形重合抽出的小正方体有1211227⨯+⨯+⨯=个，三个面的图形共同重合抽出的小正方体有4个．根据容斥原理，252520877452-=，++---+=，所以共抽出了52个小正方体．1255273所以右图中剩下的小正方体有73个．注意这里的三者共同抽出的小正方体是4个，必须知道是哪4块，这是最让人头疼的事．但你可以先构造空的两个方向上共同部分的模型，再由第三个方向来穿过“花墙”．这里，化虚为实的思想方法很重要．解法二：(用“切片法”来解)可以从上到下切五层，得：⑴从上到下五层，如图：⑵或者，从右到左五片，如图：请注意这里的挖空的技巧是：先认一种方向．比如：从上到下的每一层，首先都应该有第一层的空四块的情况，即——如果挖第二层：第(1)步，把中间这些位置的四块挖走如图：第(2)步，把从右向左的两块成线地挖走．(请注意挖通的效果就是成线挖去)，如图：第(3)步，把从前向后的一块(请注意跟第二层有关的只是一块！)挖成线！如图：【例19】（2009年迎春杯高年级组复赛）右图中的⑴⑵⑶⑷是同样的小等边三角形，⑸⑹也是等边三角形且边长为⑴的2倍，⑺⑻⑼⑽是同样的等腰直角三角形，⑾是正方形．那么，以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的倍．⑷⑶⑵⑴⑾⑽⑼⑻⑺⑹⑸【解析】本题中的两个图都是立体图形的平面展开图，将它们还原成立体图形，可得到如下两图：其中左图是以⑴⑵⑶⑷为平面展开图的立体图形，是一个四个面都是正三角形的正四面体，右图以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形，是一个不规则图形，底面是⑾，四个侧面是⑺⑻⑼⑽，两个斜面是⑸⑹．对于这两个立体图形的体积，可以采用套模法来求，也就是对于这种我们不熟悉的立体图形，用一些我们熟悉的基本立体图形来套，看看它们与基本立体图形相比，缺少了哪些部分．由于左图四个面都是正三角形，右图底面是正方形，侧面是等腰直角三角形，想到都用正方体来套．对于左图来说，相当于由一个正方体切去4个角后得到(如下左图，切去1ABDA 、1CBDC 、111D AC D 、111B AC B )；而对于右图来说，相当于由一个正方体切去2个角后得到(如下右图，切去1BACB 、1DACD )．D 1C 1B 1A 1D CBAAB CDA 1B 1C 1D 1假设左图中的立方体的棱长为a ，右图中的立方体的棱长为b ，则以⑴⑵⑶⑷为平面展开图的立体图形的体积为：3231114233a a a a -⨯⨯⨯=，以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积为3231122233b b b b -⨯⨯⨯=．由于右图中的立方体的棱长即是题中正方形⑾的边长，而左图中的立方体的每一个面的对角线恰好是正三角形⑴的边长，通过将等腰直角三角形⑺分成4个相同的小等腰直角三角形可以得到右图中的立方体的棱长是左图中的立方体的棱长的2倍，即2b a =．那么以⑴⑵⑶⑷为平面展开图的立体图形的体积与以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积的比为：()33331212::21:163333a b a a =⨯=，也就是说以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的16倍．【例 20】图⑴和图⑵是以正方形和等边三角形为面的立体图形的展开图，图中所有的边长都相同．请问：图⑴能围起来的立体图形的体积是图⑵能围起来的立体图形的体积的几倍？图⑴ 图⑵ 【解析】首先，我们把展开图折成立体图形，见下列示意图：图⑴ 图⑵对于这类题目，一般采用“套模法”，即用一个我们熟悉的基本立体图形来套，这样做基于两点考虑，一是如果有类似的模型，可以直接应用其计算公式；二是如果可以补上一块或者放到某个模型里面，那么可以从这个模型入手．我们把图⑴中的立体图形切成两半，再转一转，正好放进去！我们看到图⑴与图⑶的图形位置的微妙关系：1和图3一致！60°图⑶ 图⑷由图⑷可见，图⑴这个立体的体积与图⑶这个被切去了8个角后的立体图形的体积相等．假设立方体的1条边的长度是1，那么一个角的体积是1111112222348⨯⨯⨯⨯=，所以切掉8个角后的体积是1518486-⨯=．再看图⑵中的正四面体，这个正四面体的棱长与图⑶中的每一条实线线段相等，所以应该用边长为12的立方体来套．如果把图⑵的立体图形放入边长为12的立方体里的话是可以放进去的．12这是切去了四个角后的图形，从上面的分析可知一个角的体积为148，所以图⑵的体积是：1111142224824⨯⨯-⨯=，那么前者的体积是后者的5120624÷=倍．【例 21】如图，用高都是1米，底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体．问这个物体的表面积是多少平方米？(π取3.14)1110.511.5【解析】从上面看到图形是右上图，所以上下底面积和为22 3.14 1.514.13⨯⨯=(立方米)，侧面积为2 3.14(0.51 1.5)118.84⨯⨯++⨯=(立方米)，所以该物体的表面积是14.1318.8432.97+=(立方米)．【例 22】有一个圆柱体的零件，高10厘米，底面直径是6厘米，零件的一端有一个圆柱形的圆孔，圆孔的直径是4厘米，孔深5厘米(见右图)．如果将这个零件接触空气的部分涂上防锈漆，那么一共要涂多少平方厘米？【解析】涂漆的面积等于大圆柱表面积与小圆柱侧面积之和，为266π10π()24π560π18π20π98π307.722⨯+⨯⨯+⨯=++==(平方厘米)．【例 23】 (第四届希望杯2试试题)圆柱体的侧面展开，放平，是边长分别为10厘米和12厘米的长方形，那么这个圆柱体的体积是________立方厘米．(结果用π表示)【解析】当圆柱的高是12厘米时体积为210300π()122ππ⨯⨯=(立方厘米)当圆柱的高是12厘米时体积为212360π()102ππ⨯⨯=(立方厘米)．所以圆柱体的体积为300π立方厘米或360π立方厘米．【例 24】如右图，是一个长方形铁皮，利用图中的阴影部分，刚好能做成一个油桶(接头处忽略不计)，求这个油桶的容积．(π 3.14=)【解析】圆的直径为：()16.561 3.144÷+=(米)，而油桶的高为2个直径长，即为：428(m)⨯=，故体积为100.48。

高斯小学奥数六年级上册含答案第25讲几何超越提高

第二十五讲几何超越提高本讲知识点汇总：一、常用的几何模型（请在下面的横线上写上适当的字母或数字）1．等高三角形：面积比等于底的比．2．共角三角形：3．沙漏模型：4．梯形中的比例关系：BC已知AB //CD ，则有==．D COAB____:____=____:____abS 2S1abA BCDE= ADEABCS S ⨯△△5．一般四边形中的比例关系：6．燕尾模型7．金字塔模型8．直角三角形；（1）勾股定理；（2）斜边上的中线是斜边的一半；（3）一个角为30°的直角三角形中，短直角边为斜边的一半；二、基本解题方法 1．求角度（1）n 边形内角和，外角和360°；（2）三角形中，一个外角等于不相邻的两个内角之和．2．求长度（1）面积反求；（2）比例关系；（3）勾股定理．3．求面积（1）公式法（2）面积关系法i 比例；ii 割补；iii 等积变换．()2180n -⨯︒已知DE//BC ，则：（1）ADDB =；（2）DEBC==．a b==（1）12S S =；（2）=ABDCBDS S △△．例1．如图，八边形的8个内角都是135°，已知，，，，求的长度．「分析」可以尝试把这个图形补成长方形，根据长方形对边相等解题．练习1、如图，一个六边形的6个内角都是120︒，其连续四边的长依次是2，10，10，3．求这个六边形的周长．例2．图中外侧的四边形是一个边长为10的正方形，「分析」大家还记得“弦图”解题法吗？练习2、如图，图中最大的长方形面积是27，最小的长方形面积是5，求阴影部分的面积．例3．如图，将边长为8和12的两个正方形并排放在一起，那么图中阴影部分的面积是多少？「分析」本题要用到“沙漏型”．练习3、如图，将边长为10和12的两个正方形并放在一起，那么阴影部分的面积是多少？HA 30FG = 10DE = 20BC = AB EF = 21010331012F10 B 20CA G30ED H例4．如图，△ABC 是等腰直角三角形，DEFG 是正方形，线段AB 与CD 相交于K 点．已知正方形DEFG 的面积是48，:1:3AK KB =，则△BKD 的面积是多少？「分析」本题会巧妙的运用“等高三角形”解题．练习4、如图，四边形ABCD 是一个梯形，四边形ACEB 是一个平行四边形．已知三角形BCE 的面积是18，三角形AOD 的面积是12，那么四边形ADEB 的面积是多少？例5．如图，边长为l 的正方形ABCD 中，，，三角形AEG 的面积是多少？「分析」这道题目需要做辅助线补成 “沙漏型”进行解题例6．如图，长方形ABCD 中，，，三角形DFG 的面积为2，长方形ABCD 的面积是多少？「分析」这道题目也需要做辅助线解题．:1:2DF FC =:2:3BE EC = CF FD = 2BE EC =CF D印加文明南美洲古代印第安人文明．印加为其最高统治者的尊号，意为太阳之子．15世纪起势力强盛，极盛时期的疆界以今秘鲁和玻利维亚为中心，北抵哥伦比亚和厄瓜多尔，南达智利中部和阿根廷北部，首都在秘鲁南部的库斯科．16世纪初由于内乱日趋衰落，1532年被西班牙殖民者灭亡．印加文明与玛雅文明、阿兹特克文明并称为“印第安三大古老文明”．具有殖民征服者和印加帝国王室成员双重身份的印卡·加西拉索·德拉维加，对16、17世纪西班牙征服南美洲印第安文明的过程有着独特的关照视角，并始终保持着对这场新旧文明冲突的矛盾立场．印加文明是在南美洲西部、中安第斯山区发展起来的又一著名的印第安古代文明．它的影响范围北起哥伦比亚南部的安卡斯马约河、南到智利中部的马乌莱河，全长4800公里，东西最宽处500公里，总面积达90多万平方公里，人口超过1000万．大体说来，它包括了现今厄瓜多尔山区、秘鲁山区部分，玻利维亚高原地区、半个智利和阿根廷西北部地区．印加帝国享有“美洲的罗马”之称，它以有一套完整的国家体系而闻名于世．印加国是一个奴隶制国家，奴隶主阶级包括印加王、王室贵族、高级官吏和祭司．他们不从事生产劳动，过着奢侈的生活．印加王被称为太阳之子，神的化身，拥有至高无上的权力，独揽国家一切政治、军事和宗教大权．为了维护自己的统治，印加王建立了以中央集权为中心的政治制度，他以斯科为中心，通过各级官吏，牢牢地控制着全国．除了政权机构外，印加奴隶主还拥有一支20万人的训练有素的常备军队，用其对外扩张，对内镇压反叛力量．印加帝国还建立了严厉的司法制度，用来维护奴隶主阶级的利益．为了巩固自己的统治，印加王还采取了一些文化和经济措施．例如，对于那些刚被征服的地区，强行推广克丘亚语．再者，在全国大兴道路和驿站建设，以库斯科为中心，修建了条条道路通京城的交通网，以利于对边远地区的控制．印加帝国的灭亡在1532年，最后一任印加帝国国王阿达华巴，被西班牙殖民侵略者弗朗西斯克·皮泽洛处以死刑，结束了400年以上繁荣的帝国历史．今日印加帝国最著名的遗址为建在马丘峰和华伊纳峰之间的马丘比丘．作业1．如图，在三角形ABC中，2AE EC=，BD DC=，已知三角形ABC面积是1，那么三角形ABO的面积是多少？2．图中是两个边长分别为8和12的正方形，那么阴影部分的面积是多少？3．如图，在五边形中有一个角为60°，别的角都是120°．这个五边形的周长是多少？4．如图，已知正方形ABCD的边长为20，E、F分别为AB及BC之中点．那么四边形BFGE的面积是多少？5．如图，在边长为20的正方形中，有一个四边形，那么阴影部分的面积是多少？ACBEO231ABE4第二十五讲几何超越提高例7．答案：20 详解：如图作出辅助线可补出一个长方形，且四个角补出四个等腰直角三角形．可知、．由可知、．所以、，又因为、，因此．例8．答案：53详解：如图可按图中粗虚线切割正方形，可知阴影部分的面积是正方形面积的一半加上中间小长方形面积的一半．例9．答案：43.2 详解：沙漏模型．例10．答案：12详解：等腰直角三角形的高和正方形的边长相等，所以两者的面积相等，根据沙漏有三角形DKB 和三角形AKC 的面积相等，而，所以三角形AKC 的面积是1份，三角形BKC 的面积是3份，三角形AKC 的面积是12，△BKD 的面积也是12．例11．答案：详解：延长AF ，构造沙漏模型，有，因此，所以，．41427277ADE S S =⨯=⨯=△阴 ::3:4DG GE AD EH == ::1:1AD CH DF FC == 27:1:3AK KB = 20HA = PG HP = CN DN = 10HA DN HP =-+ 10CN PG =+BM QF = AM QE = AB EF = 10HA AM HP DN QE ++=++2030BM CN PG QF ++=++ F 10 B20CA G30E D H N P QM 23例12．答案：72详解：延长DE 与AB 相交于H ，可得，．因此．可知．练习：练习1、答案：45简答：为便于描述，将六边形剩余两条边的长度分别设为a 和b ．如右图所示，将图形补成一个等边三角形，最上方的应该是一个边长为10的等边三角形，左下方则是一个边长为2的等边三角形，由此可得最大的等边三角形边长为2101022++=．这样221039a =--=，而222911b =--=．六边形边长就等于10102391145+++++=．练习2、答案：16简答：，．练习3、答案：简答：利用沙漏形可得阴影部分三角形的以12为高的底的长度为，所以，阴影面积为．练习4、答案：72简答：梯形ABCD 中三角形AOD 和BOC 面积相等，三角形ABC 和ECB 面积相等，所以，三角形AOB 的面积为6，根据等高三角形可得COD 的面积是24，四边形ADEB 的面积是．61212241872++++= 603601221111⨯÷=60113601111516+= ()275211-÷= 672ABCD ADF S S ==△ 612ADF GDF S S ==△△ 15:::1:533FG GA DF AH CD AB === ::3:2DC BH CE EB ==10210 3 10102 ab a a 2作业6．答案：0.4简答：连接OC ，由燕尾定理可知，且，所以且，因此．7．答案：38.4简答：应用沙漏模型确定顶点连线将大正方形的边分割出的两线段长度比．8．答案：14简答：如图分割图形即可．9．答案：80简答：延长CE 构造沙漏模型，得到DG 与GF 的长度比，进而求得三角形GFC 与三角形DFC 的面积比，即可求得三角形GFC 的面积，而三角形EBC 的面积易求，两面积相减即得所求．10．答案：112简答：如图虚线分割图形，可知阴影部分面积为大正方形面积的一半加上中间小长方形面积的一半．0.4ABO S =V 0.5ABD S =V :4:1ABO BOD S S =V V :::1:1ACD ABD COD BOC S S S S BD DC ===V V V V ::2:1ABO BOC S S AE EC ==V V 2311 32 2 236。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、长方体和正方体
如右图，长方体共有六个面(每个面都是长方形)，八个顶点，十二条棱．
①在六个面中，两个对面是全等的，即三组对面两两全等．
(叠放在一起能够完全重合的两个图形称为全等图形．)
②长方体的表面积和体积的计算公式是：
长方体的表面积：；
长方体的体积：．
③正方体是各棱相等的长方体，它是长方体的特例，它的六个面都是正方形．
【巩固】要把6件同样的长17、宽7、高的长方体物品拼装成一件大的长方体，表面积最小是多少？
【巩固】用棱长是1厘米的立方块拼成如右图所示的立体图形，问该图形的表面积是多少平方厘米?
如果它的棱长为，那么：，．
二、圆柱与圆锥
立体图形
表面积
体积
圆柱
圆锥
注：是母线，即从顶点到底面圆上的线段长
模块一：利用抽屉原理公式解题
【巩固】在一个棱长为50厘米的正方体木块，在它的八个角上各挖去一个棱长为5厘米的小正方体，问剩下的立体图形的表面积是多少？
【巩固】(2008年走美六年级初赛)一个表面积为的长方体如图切成27个小长方体，这27个小长方体表面积的和是．

奥数 六年级 千份讲义 225 11.第五讲 几何 立体部分

奥数六年级千份讲义782西城综合分班考试班第五讲教师

六年级数学第5讲： 立体几何

最新小学奥数之立体几何问题