小学奥数分数求和专题归纳与总结
六年级上册数学竞赛试题分数裂项求和方法总结_通用版
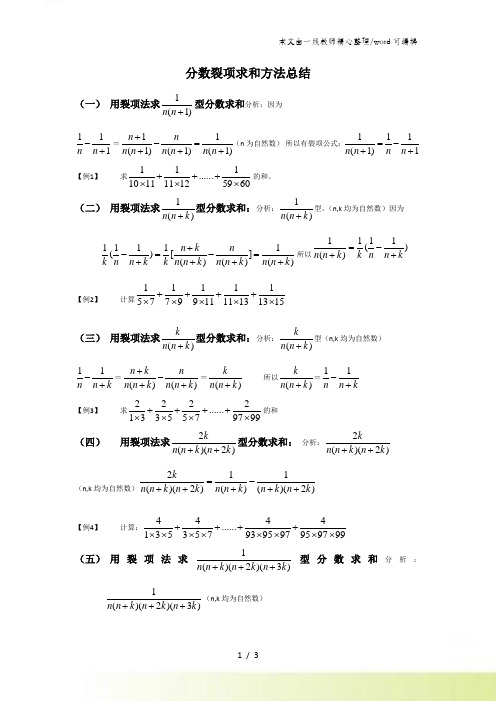
分数裂项求和方法总结(一) 用裂项法求1(1)n n +型分数求和分析:因为 111n n -+=11(1)(1)(1)n n n n n n n n +-=+++(n 为自然数) 所以有裂项公式:111(1)1n n n n =-++ 【例1】 求111 (101111125960)+++⨯⨯⨯的和。
(二) 用裂项法求1()n n k +型分数求和:分析:1()n n k +型。
(n,k 均为自然数)因为 11111()[]()()()n k n k n n k k n n k n n k n n k +-=-=++++所以1111()()n n k k n n k =-++【例2】 计算11111577991111131315++++⨯⨯⨯⨯⨯(三) 用裂项法求()k n n k +型分数求和:分析:()k n n k +型(n,k 均为自然数) 11n n k -+=()()n k n n n k n n k +-++=()k n n k + 所以()k n n k +=11n n k -+ 【例3】 求2222 (1335579799)++++⨯⨯⨯⨯的和 (四) 用裂项法求2()(2)k n n k n k ++型分数求和: 分析:2()(2)k n n k n k ++ (n,k 均为自然数)211()(2)()()(2)k n n k n k n n k n k n k =-+++++【例4】 计算:4444......135357939597959799++++⨯⨯⨯⨯⨯⨯⨯⨯ (五) 用裂项法求1()(2)(3)n n k n k n k +++型分数求和分析:1()(2)(3)n n k n k n k +++(n,k 均为自然数)【例5】 计算:111......1234234517181920+++⨯⨯⨯⨯⨯⨯⨯⨯⨯(六) 用裂项法求3()(2)(3)k n n k n k n k +++型分数求和: 分析:3()(2)(3)k n n k n k n k +++(n,k 均为自然数) 【例6】 计算:333 (1234234517181920)+++⨯⨯⨯⨯⨯⨯⨯⨯⨯ 【例7】计算:71+83+367+5629+6337+7241+7753+8429+883 【分析与解】解答此题时,我们应将分数分成两类来看,一类是把5629、6337、7241、7753这四个分数,可以拆成是两个分数的和。
小学奥数分数求和专题归纳与总结

分数求和分数求和的常用方法:1、公式法,直接运用一些公式来计算,如等差数列求和公式等。
2、图解法,将算式或算式中的某些部分的意思,用图表示出来,从而找出简便方法。
3、裂项法,在计算分数加、减法时,先将其中的一些分数做适当的拆分,使得其中一部分分数可以互相抵消,从而使计算简便。
4、分组法,运用运算定律,将原式重新分组组合,把能凑整或约分化简的部分结合在一起简算。
5、代入法,将算式中的某些部分用字母代替并化简,然后再计算出结果。
典型例题 一、公式法:计算:20081+20082+20083+20084+…+20082006+20082007分析:这道题中相邻两个加数之间相差20081,成等差数列,我们可以运用等差数列求和公式:(首项+末项)×项数÷2来计算。
20081+20082+20083+20084+…+20082006+20082007=(20081+20082007)×2007÷2=211003二、图解法: 计算:21 +41+81+161+321+641 分析:解法一,先画出线段图:从图中可以看出:21 +41+81+161+321+641=1-641=6463 解法二:观察算式,可以发现后一个加数总是前一个加数的一半。
因此,只要添上一个加数641,就能凑成321,依次向前类推,可以求出算式之和。
21 +41+81+161+321+641=21 +41+81+161+321+(641+641)-641=21 +41+81+161+(321+321)-641……=21×2-641 =6463 解法三:由于题中后一个加数总是前一个加数的一半,根据这一特点,我们可以把原式扩大2倍,然后两式相减,消去一部分。
设x=21+41+81+161+321+641①那么,2x=(21+41+81+161+321+641)×2 =1+21+41+81+161+321②用②-①得2x -x=1+21+41+81+161+321-(21 +41+81+161+321+641)x=6463所以,21 +41+81+161+321+641=6463三、裂项法 1、计算:21+61+121+201+301+……+901+1101 分析:由于每个分数的分子均为1,先分解分母去找规律:2=1×2,6=2×3,12=3×4,20=4×5,30=5×6,……110=10×11,这些分母均为两个连续自然数的乘积。
奥数里的分数应用原理总结

奥数里的分数应用原理总结1. 介绍奥数是指奥林匹克数学竞赛,是培养学生逻辑思维和数学能力的重要途径之一。
在奥数中,分数应用是一个重要的内容,我们来总结一下奥数里的分数应用原理。
2. 原理介绍分数是数学中的一种表示方法,表示一个整体被划分成若干部分的数。
在奥数中,分数应用主要包括四则运算、比较大小、化简、混合运算等。
2.1 四则运算分数的四则运算包括加法、减法、乘法和除法。
2.1.1 加法和减法两个分数相加或相减,需要满足相同的分母。
具体步骤如下: - 确定两个分数的分母是否相同,如果不同,先通分; - 将两个分数的分子进行对应的加法或减法运算; - 将运算结果的分子写在分数的上方,分母写在分数的下方。
2.1.2 乘法两个分数相乘,直接将两个分数的分子相乘,分母相乘。
具体步骤如下: - 将两个分数的分子相乘,将运算结果的分子写在分数的上方; - 将两个分数的分母相乘,将运算结果的分母写在分数的下方。
2.1.3 除法两个分数相除,可以将除法转化为乘法的形式。
具体步骤如下: - 将被除数的分子乘以除数的分母,将运算结果的分子写在分数的上方; - 将被除数的分母乘以除数的分子,将运算结果的分母写在分数的下方。
2.2 比较大小比较两个分数的大小,可以通过找到两个分数的公共分母进行比较。
具体步骤如下: - 确定两个分数的分母是否相同,如果不同,先通分; - 比较两个分数的分子的大小,如果分子相等,则比较分母的大小,分母越大,分数越小; - 如果分子不相等,比较两个分子的大小,分子越大,分数越大。
2.3 化简分数的化简是指将一个分数约分到最简形式。
具体步骤如下: - 找到分子和分母的最大公约数; - 将分子和分母分别除以最大公约数,得到最简分数。
2.4 混合运算混合运算是指分数与整数的组合运算,包括分数与整数的加减乘除等。
3. 实例分析下面通过一些实例来进一步理解奥数中分数应用的原理。
3.1 实例一:分数的四则运算假设有两个分数:1/3 和 2/5,我们来进行加法运算。
小学五年级奥数练习(分数的综合运算技巧详解 )

小学五年级奥数练习——分数地综合运算技巧详解(分数地复杂运算、分数地混合运算)一、知识点1.混合运算技巧在分数、小数地四则混合运算中,到底是把分数化作小数,还是把小数化作分数,这影响到运算过程地繁琐与简便程度,也影响到运算结果地精确度。
小数化成分数,或分数化成小数’,有如下几种技巧。
(1)在加减法中,有时遇到分数只能化成循环小数时’,不能把分数化成小数,此时要将包括循环小数在内地所有小数都化为分数;(2)在乘除法中,一般情况下,小数化成分数计算则比较简便;(3)一般情况下,在加减法中,分数化成小数比较方便;(4)在运算中,使用假分数还是带分数,需视情况而定;(5)在计算中经常用到除法’、比、分数、小数、百分数互相之间地变换,把这些常用地数互化成数表对学习非常重要。
2.复杂分数地运算注意点先找出分数线,确定分子部分和分母部分,然后这两部分分别进行计算,每部分地计算结果需要约分地要先约分,再改成“分子部分÷分母部分”地形式,最后求出结果。
3.比和比例地技巧化简比地方法:比地前项和后项同时乘以或除以相同地数(0除外’),最后地比值应写成最简整数比。
具体如下:(1)分数比:可以前项除以后项,在根据比值写出最’简单地整数比。
(2)小数比:可以先利用商不’变地性质将其转化为整数比,然后再化简;(3)整数比:可以根据商不变地性质或像分数约分(前后项同时除以它们’地最大公因数)那样进行化简;4.分数拆分从分母M 地约数中’任意找出两个m 和n ,有)()()()(11n m M n n m M m n m M n m M +++=++=B A 11+=;如10地约’数有:1,10,2,5。
如选1和2,有:)21(102)21(101)21(10)21(1101+++=++=151301+=;另外,a ,b ,c 为M 地约数:)()()()()(11c b a M c c b a M b c b a M a c b a M c b a M ++++++++=++++=5.循环小数循环小数与分数地互化,循环小数之间’简单地加、减法运算,涉及循环小数与分数地’运算主要利用运算定律进行简算。
六年级数学奥数第二讲 分数裂项巧求和

(10)+++…+
(11)+++…+
计算:(5)+++…+ 例4. 计算:+++…+
(6)+++…+
分析与解:是不是觉得本题和例3有些相似,但又不完全一样?例3 中每一个分数的分子都是4(两个自然数的差),而这道题中每一个分 数的分子都是1,可以直接将每一个分数写成两个分数相减的形式吗? 该怎么计算呢? 这就启发我们思考,能否将每一个分数的分子也变成两个自然数的 差呢?利用分数的基本性质是完全可以的。所以给原题乘4,为了使原 题的值不变,然后再除以4.即:
+++…+ =(+++…+)×4÷4 =(+++…+)÷4 =(—+—+—+…+—)÷4 =(—)÷4 =÷4 = 【举一反三】 计算: (7)+++…+
(8)+++…+
例5. 计算:+++…+ +++…+
分析与解:先算出每一个分数中的分母,再仔细观察每一个分 数,找出规律然后计算。
=+++…+ =+++…+ (分子分母同时乘以2) =(+++…+)×2 (利用乘法分配律,把分子的2同时 =(—)×2 提到括号外面) =×2= 【举一反三】 计算:(9)+++…+
【典型例题】 例1.计算:+++…++
小学六年级奥数运算部分的分数计算 (4页)

小学六年级奥数运算部分的分数计算 (4
页)
小学六年级奥数运算部分的分数计算
简介
本文档旨在帮助小学六年级学生进行奥数运算部分的分数计算。
以下将介绍几个常见的分数计算方法。
分数加法
分数加法是将两个或多个分数相加的运算。
要进行分数加法,
必须保持分母相同。
以下是一个示例:
1/4 + 2/4 = 3/4
分数减法
分数减法是将一个分数减去另一个分数的运算。
和分数加法一样,分母必须相同。
以下是一个示例:
3/4 - 1/4 = 2/4
分数乘法
分数乘法是将两个或多个分数相乘的运算。
分数乘法的规则很
简单,只需要将分子相乘得到新的分子,分母相乘得到新的分母。
以下是一个示例:
2/3 * 3/5 = 6/15
分数除法
分数除法是将一个分数除以另一个分数的运算。
分数除法的规
则是将第一个分数的分子乘以第二个分数的倒数。
以下是一个示例:3/4 ÷ 1/2 = 3/4 * 2/1 = 6/4
分数化简
分数化简是将分数转化为最简形式的运算,使分子和分母的公
约数最大化。
例如,将8/12化简为2/3。
将分数化简可以让计算更
简便明了。
总结
通过掌握分数加法、减法、乘法、除法和化简的方法,小学六年级学生可以更好地进行奥数运算部分的分数计算。
以上提供的方法是常见而简单的分数计算技巧,旨在帮助小学六年级的学生更好地理解和应用。
希望能对你有所帮助。
五年级奥数分数求和的技巧

五年级奥数分数求和的技巧
一、把十位数弄清楚
把学习数字的范围缩小到个位和十位数,再把十位数分类好,归类成小于等于6及大于6的两类。
二、个位数的求和运算
对于小于等于6的十位数,在个位上按常规方法做相应的运算,把加法按照数字从右往左从上到下依次排列,就可以更快地把个位数两两相加求和。
三、计算大于6的十位数
当十位数为7,8或者9时,我们可以把它们转换成一个十位数和一个个位数,分别进行记忆,然后把它们分别加上个位数,比如说7可以看做是6+1,8可以看做是6+2,9可以看做是6+3,然后再把6的分数和1、2、3的分数分别加起来就可以了。
四、综合利用技巧
我们可以先把小于等于6的十位数求和,然后把大于6的十位数把它们拆成十位数和个位数进行加减,最后综合处理,就可以较快地求出五年级奥数分数求和的结果了。
小学分数奥数题的知识点

小学分数奥数题的知识点在小学奥数的学习中,分数是一个非常重要的知识点。
通过学习和掌握分数的概念和运算规则,可以帮助学生建立数学思维,培养逻辑思维能力。
下面将介绍一些小学分数奥数题的常见知识点。
1. 分数的概念分数是表示一个数与单位整体的关系,由分子和分母两部分组成。
分子表示单位整体的份数,分母表示每份的份数。
例如,1/2表示一个整体分成两份,取其中的一份。
分数中的分子和分母都是整数,分母不能为零。
2. 分数的大小比较在比较两个分数的大小时,可以通过找出它们的公共分母,然后比较分子的大小来判断。
如果两个分数的分母相同,那么分子大的分数就更大;如果两个分数的分母不同,可以通过通分将它们的分母变为相同,再进行比较。
3. 分数的约分和通分对于一个分数,如果分子和分母有公共的因数,可以约去这个公共因数,得到一个与原分数相等的最简分数。
例如,4/8可以约分为1/2。
通分是指将两个或多个分数的分母改成相同的分母。
通分后,可以方便地进行分数的加减运算。
4. 分数的加减运算对于两个分数的加减运算,首先需要将它们的分母通分,然后再按照通分后的分母进行相应的加减操作。
最后再进行约分,得到最简分数。
5. 分数的乘法和除法两个分数的乘法可以直接将它们的分子相乘得到新分子,分母相乘得到新分母。
最后对新分数进行约分。
两个分数的除法可以将除数的分子和被除数的分母相乘得到新分子,除数的分母和被除数的分子相乘得到新分母。
同样地,最后对新分数进行约分。
6. 分数和整数的转换一个自然数可以看作是分母为1的分数,一个整数可以看作是分母为1的分数。
对于一个分数,如果分子和分母相等,那么它可以化简为1。
因此,分数和整数之间可以相互转换。
7. 分数的混合运算混合运算是指将分数与整数进行加减乘除的运算。
在混合运算中,可以先将分数转换为带分数表示,然后按照整数的加减乘除规则进行运算。
通过学习以上的知识点,可以帮助小学生在奥数题中灵活运用分数的概念和运算规则,提高解题能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分数求和分数求和的常用方法:1、 公式法,直接运用一些公式来计算,如等差数列求和公式等。
2、 图解法,将算式或算式中的某些部分的意思,用图表示出来,从 而找出简便方法。
3、 裂项法,在计算分数加、减法时,先将其中的一些分数做适当的 拆分,使得其中一部分分数可以互相抵消,从而使计算简便。
4、 分组法,运用运算定律,将原式重新分组组合,把能凑整或约分 化简的部分结合在一起简算。
5、 代入法,将算式中的某些部分用字母代替并化简,然后再计算出典型例题 、公式法:计算:2008 2008 2008 爲 …2006 20072008 2008分析:这道题中相邻两个加数之间相差盏8,成等差数列,我们可以运用等差数列求和公式:(首项+末项)X 项数+2来计算2008 2008 2008 2008 2008 2008=10031二、图解法:计算:1 + 1 + 1 +丄+丄+丄248163264分析:解法一,先画出线段图:12 3 4 2006 20071 2007+2008 2008X 2007 -21 11164)63 64122X— 1+11+1 +丄+丄一 4 8 16 32丄+丄+1632所以, + 1 + 1 +丄+ 丄 + 481632163 6464解法二:观察算式,可以发现后一个加数总是前一个加数的一半。
因 此'只要添上一个加数右,就能凑成 算式之和。
£ 64 63 64解法三:由于题中后一个加数总是前一个加数的一半, 根据这一特点, 我们可以把原式扩大2倍,然后两式相减,消去一部分设11 1 + 1+ 1+ 丄+丄 + 1①2 4 816 3264那么, 2 (1 + 1 1 + — 1 + 1 1 + — )X 224 8 1632 641 + —=1 +1+1+ 1+2481632②用②一①得132 ,依次向前类推,可以求出1 2 -1 2 -1 28 1 + 4 1+ 4+ — -+ 一16 3264+丄+ 丄+(1632 +丄+ (-+1632丄64从图中可以看出:扌+ 4 + 8 +16 + 32 + 64=1 -右=詈1 8 1 811+ -- ) 64 64 164 132 ' 643 5'35丿 2这些分母均为两个连续自然数的乘积。
治石刖。
这样将连加运算变成加减混合运算’中间分数互相抵消,只留下头和尾两个分数,给计算带来方便。
11 11 11 1 ++ - + + +…… + + 2 6 12 20 3090110=11 1 11 11111一++ + -------- 1 - -2 23349 10 10 11=113^=33_专。
所以’我们可以将题中的每一个加数都扩大倍后,再分裂成两个数的差进行简便计算。
9 3735 63 99143195 2551 11 X 丄=4 x(1 — - )X 」,1 3 3 21 1 1 1三、裂项法1、计算: 11111丄+丄+丄+丄+丄+261220301 1+ — + --90110分析: 由于每个分数的分子均为 1 ,先分解分母去找规律:2=1X 2, 6=2 X 3 , 12=3 X 4, 20=4 X 5,30=5 X6 ,……110=10 X 11 ,再变数型:因为^1 - 1,11 1_ 1 1 1 1 _1 ............ 623 2 3,12 34 34,2、计算:+1 5分析:因为2=11 5 + —29 331 1 45 9 5 9 ' 9 139 13 4 33 3711 9 13 4= 1 29 33 = 29 1 33, 1 1 + + - 1 55 9 9—+ —455 1 + 5_ 37)(1(1 (11+……13 —+13 + _ 9 1+1 1+9131 1+ +29 3333 37……+ 29 331 +29+)—433 37 1 +33333、计算:21 — 43 15分析:因为4 =4 X 1 =43 3 41=4 X — =4 1515111 2 12 3 1 2 3 412 3 100 4 1 1 111—=4 x 丄=4 X 丄=4 X( - - -)x-, 35 35 5 7 5 7 21 1 1 x =4 X ( — - — ) X -.15 17 15 17 2所以,先用裂项法求出分数串的和,使计算简便4 44 444 4 4 21 -3 15 35 63 99 143 195255 =21 —4 X (1 -1+1- -1+11 +…… •+丄一丄)X 13 355715172=21 -2 X (1 - 丄)17=19 -17 1 5 11 19 29 9701 98994、计算:—+ —+ — + — + — +……+ +2612203097029900分析:仔细观察后发现,每个加数的分子均比分母少1.这样可变形为:利用等差数列求和公式,或利用分数基本性质,变分母为两个数相乘。
丄=1-1= 1 -15=1 -1 =1 -1 口 = 1 1 =1 1 , 192 2 1 266 2 3 '1212 3 4 20=1 - -丄=1—19899 d=1 1 =11 -.然后再裂项相20 4 59900990099 100消。
1 ,5 , 11 ,19 + 29,9701-+ _ + — + +… + ■+ 2 6 12 20309702 99001 1 +(1 — 20)+……+(1 —融)4255 1 =4 X 」=42551 1=(1 - 2)+(1- 6) 1 1=1 X 99 —(丄 + 丄 + 2 6 —+丄2 2 3=99=99 1 1005、计算: =99丄+121 3+99001 1+ .... + )4 599 1001—+ ... + —3 41 2 3100分析:可以看出,第一项的分母为 1,第二项的分母为两个数相加,依此类推,最后一个分母是 100个数相加且都是等差数列。
这样,再裂项求和。
1+ ••…+---------- 1解法一:1 +1 2 1 2 3 1 2 3 4 1 2 3 1001111 2 1C (1 2) 2 2 2 2 12 2 3 2 3 4 1 =2 x(1 —丄) 101(1 3) 3 224 5(1 4) 422 100 101(1 100) 100 =1聖101 解法二:原式二1 2 2 (1 2) 2 (1 2 3) 2 (1 2 3 4)________ 1 22 (1 2 ……99 100)=2 2 =1 22 3 3 4 1 1=2 x(」—122 31=2 x(1 --------- )101 2100 101……一)100 101=1-991016、计算:+ …+98 99 100分析:可以把题中的每两个加数分解成两个分数之差:1 (丄丄)1 (丄丄)…… 123 212 23‘234 2 2334’1 1 1 1- -(————),此时,可消中间,留两头进行巧算。
98 99 100 2 98 9999 100原式=1 X (丄2 1 21 1 98 99 99 100 专x (=2 x (=4949 =19800九)+ 2 X (九1 12 1 1 2—+2 3 )99 1001 1+ ....+3 498 9999^)5 ,6 7I — — + +—2004 2004 2004 2004 2004 200420048, 9,10 1999 2000 , 2001 , 2002 — 十 十— .. ——十十2004 200420042004200420042004分析:算式中共有2002个分数,从第二个分数 丄开始依次往后数, 2004四、分组法:计算,1每四个分数为一组,到誥为止,共有500组,每组计算结果都是1 1 113 15 15 17 17 191【39】20022004 2004=2003=2004五、代入法:计算(珂分析:可以把算式中相同的一部分式子,设字母代替,可化繁为简,化难为易设111,1111,则2 3 4 2 3 4 5原式二(1) X B-(1) X A+ —A -=(热点习题计算:1、1 3 5 7 9 11 13 【1】49 49 49 49 49 49 492、1 1 1 1 丄丄丄 1 12 4 8 16 32 64 128 1283、1 1 1 11 1【§】2 6 12 20 30 42 70.原式20042004)+"20041020042004 2004199820041999 20002004 2004 2004+2004 2004+ 2001 )+ 2002+2004)+2004A 1 14、1988 1989 1989 1991 1 3 】1988 2009 57055611990 199112007 200812008 2009135 37 37 39151 13 41【1 —81 (12) (12) (1 2 3) (1 2 3) (1 2 3 4)6、2+ 3 6 5丄7丄 12 2011 — 3013丄【41 §】42 14 7、 1 5 11 19 2941 551 ■6-]2 6 12 20 30 42 5688、 4 16 36 64 100 144 196 256 ——3 15 35 63 99 143 195 255 9、1 5 7 9 11 13 15 17 19-- -6 12 20 30 42 56 72 90 【原式=12 3 3 + 4 4 5 5 6 62 3 3 4 4 5 5 6 6 =1 — (23 )+( 34 ) —(-2 3 2 33 4 3 44324 400 【10® ]323 399 21211107 7 8 8 9 9 10 10 11—— +7 7 8 8 9 9 10 10 11 4 5 )+ …-( 11) 5 4 5 10 1110 1111 11 1 1 1 1=1 —(丄丄)+(丄1)—(丄丄)+…一(丄 丄)3 2435 411 10 =1 —-丄=2】2 11 22 10、1 ___2 ___ 3_ 2002 2002 2002 5 67 8,9,10+ • + 200220022002 2002 2002 20024 20021998 1999 200020022002 2002 2001 +20022002 2002+…+ 1995 20021996+ 20021997 2002 【从第三个分数佥开始依次往后数,每8个分数为一组’到最后 为止,共有250组,一个分数哋 200223 20021 12 35) 1 13 1 2002 2002 11、(1 +1 15) x( 2每组计算结果都是0.所以,原式1 16)一(1+2(2【设 1 4- 2 12145,122 20 13 201 (1 1820【原式11112+2 丄+…2 1112 3 4 3)(1•+9 12原式X(1)—(6 63 12 3 44)(5 5 5 5)13、2 2001年是中国共产党建党 数。
