matlab 黄金分割法
机械优化设计

机械优化设计matlab优化设计程序学校:班级:学号:姓名:指导老师:一.进退法求最优点所在区间1.算例:函数:f=x(1)^3+x(2)^2-10*x(1)*x(2)+1;初始参数:x0=0,step=0.01,st=[0,0],sd=[1,1];2.编程代码:function [lb,ub]=jintuifa(x0,step0,st,sd)% lb为区间下限,up为区间上限% x0初始探测点,step0是初始探测步长,st初始搜索点,sd是初始搜索方向step=step0;f0=jintui(x0,st,sd);x1=x0+step0;f1=jintui(x1,st,sd);if f1<=f0while truestep=2*step;x2=x1+step;f2=jintui(x2,st,sd);if f1<=f2lb=x0;ub=x2;break;elsex0=x1;x1=x2;f0=f1;f1=f2;endendelsewhile truestep=2*step;x2=x0-step;f2=jintui(x2,st,sd);if f0<=f2lb=x2;ub=x1;break;elsex1=x0;x0=x2;f1=f0;f0=f2;endendendend%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=jintui(a,st,sd)f=objfun(st+a.*sd);end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=objfun(x)f=x(1)^3+x(2)^2-10*x(1)*x(2)+1;end3.运行结果二.黄金分割法求最求最优值1.eg:函数:f=x^2+2*x;初始参数:a=-3,b=5,e=0.0001;2.编程代码:function [ans,sp]=golden(a,b,e)%[a,b]初始区间,e为最小区间长度要求%ans为最优解,sp为所需迭代次数a(1)=a;b(1)=b;L=e;t(1)=a(1)+0.382*(b(1)-a(1));u(1)=a(1)+0.618*(b(1)-a(1));k=1;m(1)=feval('f1',t(1));n(1)=feval('f1',u(1));while(b(k)-a(k)>L)if(m(k)>n(k))a(k+1)=t(k);b(k+1)=b(k);t(k+1)=u(k);u(k+1)=a(k+1)+0.618*(b(k+1)-a(k+1));elsea(k+1)=a(k);b(k+1)=u(k);u(k+1)=t(k);t(k+1)=a(k+1)+0.382*(b(k+1)-a(k+1));endm(k+1)=feval('f1',t(k+1));n(k+1)=feval('f1',u(k+1));ans=feval('f1',t(k+1));k=k+1;endans=(a(k)+b(k))/2;sp=k-1;end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function y=f1(x)y=x^2+2*x;end3.运行结果三.无约束优化方法——坐标轮换法1.eg:函数:min f(x)=4*(x(1)-5)^2+(x(2)-6)^2;初始参数:初始点x为[8,9];2.编程代码:function [x,f]=lunhuan(x0)%输入初始点x0[8,9]%输出最优解点x,与最优解值fp=1;h=0.000001;x=x0;while(p>h)%做精度比较w=x(1);q=x(2);d1=[1,0];a1=golden('objfun',x,d1);%黄金分割法求最佳步长 x=x+a1*d1;d2=[0,1];a2=golden('objfun',x,d2);x=x+a2*d2;p=sqrt((x(1)-w)^2+(x(2)-q)^2);endf=objfun(x);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=objfun(x)%函数名f=4*(x(1)-5)^2+(x(2)-6)^2;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [lb,ub]=jintuifa(st,sd)%进退法函数x0=0;step0=0.000001;step=step0;f0=jintui(x0,st,sd);x1=x0+step0;f1=jintui(x1,st,sd);if f1<=f0while truestep=2*step;x2=x1+step;f2=jintui(x2,st,sd);if f1<=f2lb=x0;ub=x2;break;elsex0=x1;x1=x2;f0=f1;f1=f2;endendelsewhile truestep=2*step;x2=x0-step;f2=jintui(x2,st,sd);if f0<=f2lb=x2;ub=x1;break;elsex1=x0;x0=x2;f1=f0;f0=f2;endendendend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=jintui(a,st,sd)f=objfun(st+a.*sd);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function ans=golden(f_name,st,sd)[a,b]=jintuifa(st,sd); %进退法求最佳步长区间a(1)=a;b(1)=b;L=0.1;t(1)=a(1)+0.382*(b(1)-a(1));u(1)=a(1)+0.618*(b(1)-a(1));k=1;p=st+t(1)*sd;q=st+u(1)*sd;m(1)=feval(f_name,p);n(1)=feval(f_name,q);while(b(k)-a(k)>L)if(m(k)>n(k))a(k+1)=t(k);b(k+1)=b(k);t(k+1)=u(k);u(k+1)=a(k+1)+0.618*(b(k+1)-a(k+1));elsea(k+1)=a(k);b(k+1)=u(k);u(k+1)=t(k);t(k+1)=a(k+1)+0.382*(b(k+1)-a(k+1));endw=st+t(k+1)*sd;z=st+u(k+1)*sd;m(k+1)=feval(f_name,w);n(k+1)=feval(f_name,z);ans=feval(f_name,w);k=k+1;endt(k)=0;u(k)=0;m(k)=0;n(k)=0;p=[a',b',t',u',m',n'];ans=(a(k)+b(k))/2;end3.运行结果四.无约束优化方法——鲍威尔法1.eg:函数:min f(x)=4*(x(1)-5)^2+(x(2)-6)^2;初始参数:初始点x为[8,9],初始搜索方向[0,1],[1,0];2.编程代码:function [x,f]=powill(x0,d1,d2)%输入x0为初始点,d1,d2为两个线性无关向量for k=1:2w=x0(1);q=x0(2);a1=golden('objfun',x0,d1);x1=x0+a1*d1;a2=golden('objfun',x1,d2);x2=x1+a2*d2;d1=d2;d2=x2-x0;a3=golden('objfun',x2,d2);x3=x2+a3*d2;x0=x3;endx=x0;f=objfun(x);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=objfun(x)f=4*(x(1)-5)^2+(x(2)-6)^2;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [lb,ub]=jintuifa(st,sd)x0=0;step0=0.0001;step=step0;f0=jintui(x0,st,sd);x1=x0+step0;f1=jintui(x1,st,sd);if f1<=f0while truestep=2*step;x2=x1+step;f2=jintui(x2,st,sd);if f1<=f2lb=x0;ub=x2;break;elsex0=x1;x1=x2;f0=f1;f1=f2;endendelsewhile truestep=2*step;x2=x0-step;f2=jintui(x2,st,sd);if f0<=f2lb=x2;ub=x1;break;elsex1=x0;x0=x2;f1=f0;f0=f2;endendend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=jintui(a,st,sd)f=objfun(st+a.*sd);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function ans=golden(f_name,st,sd)[a,b]=jintuifa(st,sd);a(1)=a;b(1)=b;L=0.1;t(1)=a(1)+0.382*(b(1)-a(1));u(1)=a(1)+0.618*(b(1)-a(1));k=1;p=st+t(1)*sd;q=st+u(1)*sd;m(1)=feval(f_name,p);n(1)=feval(f_name,q);while(b(k)-a(k)>L)if(m(k)>n(k))a(k+1)=t(k);b(k+1)=b(k);t(k+1)=u(k);u(k+1)=a(k+1)+0.618*(b(k+1)-a(k+1));elsea(k+1)=a(k);b(k+1)=u(k);u(k+1)=t(k);t(k+1)=a(k+1)+0.382*(b(k+1)-a(k+1));endw=st+t(k+1)*sd;z=st+u(k+1)*sd;m(k+1)=feval(f_name,w);n(k+1)=feval(f_name,z);ans=feval(f_name,w);k=k+1;endend3.运行结果五.有约束优化方法——复合形法1.eg:函数:min f(x)=x1^2+x2^2-x1*x2-10*x1-4*x2+60 St:g1(x)=-x1≤0g2(x)=-x2≤0g3(x)=x1-6≤0g4(x)=x2-8≤0g5(x)=x1+x2-11≤02.编程代码:function fuhexing(n,b,h,xb1,xb2)%元素数n,初始可行点b,精度h,xb1横坐标上下界,xb2为纵坐标上下界if (rem(n,2)==0)k=n+n/2;elsek=n+(n+1)/2;end%取k值A=kexingdian(k,xb1,xb2,b');%确定可行点A=mubiao(A,n,k,h);%求出目标函数并排序比较,得出最优解End %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function A=mubiao(A,n,k,h)for i=1:kA(3,i)=objfun(A(:,i));endB=A';%根据目标函数值排序A=sortrows(B,3)';p=0;for j=1:kx=(objfun(A(:,j))-objfun(A(:,1)))^2;p=p+x;endo=sqrt(p/(k-1));%收敛条件if(o<h)%判断所求点是否为最优点disp('最优点为')xz(1)=A(1,1);xz(2)=A(2,1);disp(xz);disp('其函数值为')f=A(3,1);disp(f);elsexr=Xcpanduan(A,k,n,h,1.3);endend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function A=kexingdian(k,xb1,xb2,b)A=zeros(3,k);A(1,1)=b(1);A(2,1)=b(2);for i=2:kA(1,i)=xb1(1)+rand(1)*(xb1(2)-xb1(1));A(2,i)=xb2(1)+rand(1)*(xb2(2)-xb2(1));%产生j个顶点endt=0;for j=1:kif(A(1,j)+A(2,j)<=11&&A(1,j)<=6&&A(2,j)<=8)%判断是否有不可行点t=t+1;T(:,t)=A(:,j);endendif(t<k)%计算出可行点的中心位置xcxc=zhongxindian(T,t);endt=0;for j=1:k%利用中心点将原不可行点逼近为可行点while(A(1,j)+A(2,j)>11||A(1,j)>6||A(2,j)>8)A(:,j)=xc+0.5*(A(:,j)-xc);endendendx=x0;f=objfun(x);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function f=objfun(x)f= x1^2+x2^2-x1*x2-10*x1-4*x2+60;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function xc=Xcpanduan(A,k,n,h,a)for i=1:k-1T(:,i)=A(:,i);endxc=zhongxindian(T,k-1);%计算除最坏点以外的可行点中心坐标if(xc(1)+xc(2)<=11&&xc(1)<=6&&xc(2)<=8)%判断xc是否可行xr=Xrpanduan(xc,A,a,n,k,h);A(:,k)=xr;else%不可行时,即重新确定初始可行点fuhexing(n,h,A(:,1),xr);endend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function xc=zhongxindian(T,t)xc=[0;0;0];for i=1:txc=xc+T(:,i);endxc=xc/t;%求解中心点end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function xr=Xrpanduan(xc,A,a,n,k,h)xr=xc+a*(xc-A(:,k));while(xr(1)+xr(2)>11||xr(1)>6||xr(2)>8)%判断xr 是否可行若不可行,则持续迭代a=0.5*a;xr=xc+a*(xc-A(:,k));endxr=ercipanduan(a,xr,A(:,k),A,n,k,xc,h,xr);%可行时进入下一判断end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function xr=ercipanduan(a,p,b,A,n,k,xc,h,t)if(objfun(p)>=objfun(b))%判断反射点和最坏点函数值的大小if(a<=1e-10)A(:,k)=A(:,k-1);xr=Xcpanduan(A,k,n,h,a);disp(xr);elsea=0.5*a;xr=Xrpanduan(xc,A,a,n,k,h);%返回中心点判断,持续迭代endelseA(:,k)=p;%以反射点取代最坏点进行循环mubiao(A,n,k,h);xr=t;endend3.运行结果五.有约束优化方法——混合惩罚法1.eg:函数:min f(x)=(x(4)-x(1))^2+(x(5)-x(2))^2+(x(6)-x(3))^2;St:g1=x(1)^2+x(2)^2+x(3)^2-5;g2=(x(4)-3)^2+x(5)^2-1;g3=x(6)-8;g4=4-x(6);2.编程代码function [x,f]=hunhechengfa(x0,r0,c,h1,h2)k=1;z=0;A(:,1)=x0;r(1)=r0;while (z==0)k=k+1;x=lunhuan(x0,r(k-1));A(:,k)=x;r(k)=c*r(k-1);z=shoulian(A,r,h1,h2,k);if(z==1)break;endx0=x;enddisp('最优解点x=');disp(x);disp('最优值=');f=fhanshu(x);disp(f);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function z=shoulian(A,r,h1,h2,k)%判断收敛条件U=abs(objfun(A(:,k),r(k))-objfun(A(:,k-1),r(k-1))/obj fun(A(:,k-1),r(k-1)));V=0;for i=2:kV=V+(A(1,k)-A(1,k-1))^2;endV=sqrt(V);if(U<=h1&&V<=h2)z=1;elsez=0;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function p=objfun(x,r)%φ函数g1=x(1)^2+x(2)^2+x(3)^2-5;g2=(x(4)-3)^2+x(5)^2-1;g3=x(6)-8;g4=4-x(6);j=sqrt(r);u=r*(1/g1+1/g2+1/g3+1/g4);v=(g1^2+g2^2+g3^2+g4^2)/j;p=fhanshu(x)-u+v;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function f=fhanshu(x)%目标函数f=(x(4)-x(1))^2+(x(5)-x(2))^2+(x(6)-x(3))^2;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function x=lunhuan(x0,r)%轮换法p=1;h=0.01;d=zeros(6,6);a=zeros(6,1);x=x0;for i=1:6for j=1:6if(i==j)d(i,j)=1;endendendwhile(p>h)t=x;v=0;for k=1:6a(k)=golden(x,d(:,k),r);c=d(:,k);x=x-a(k)*c';v=v+(x(k)-t(k))^2;endp=sqrt(v);endend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function ans=golden(st,sd,r)%黄金分割法求最佳步长 [g,h]=jintuifa(st,sd,r);a(1)=g;b(1)=h;L=0.01;t(1)=a(1)+0.382*(b(1)-a(1));u(1)=a(1)+0.618*(b(1)-a(1));k=1;p=st+t(1)*sd';q=st+u(1)*sd';m(1)=objfun(p,r);n(1)=objfun(q,r);while(b(k)-a(k)>L)if(m(k)>n(k))a(k+1)=t(k);b(k+1)=b(k);t(k+1)=u(k);u(k+1)=a(k+1)+0.618*(b(k+1)-a(k+1));elsea(k+1)=a(k);b(k+1)=u(k);u(k+1)=t(k);t(k+1)=a(k+1)+0.382*(b(k+1)-a(k+1));endw=st+t(k+1)*sd';z=st+u(k+1)*sd';m(k+1)=objfun(w,r);n(k+1)=objfun(z,r);k=k+1;endans=(a(k)+b(k))/2;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=jintui(a,st,sd,r)%代入步长f=objfun(st+a.*sd',r);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [lb,ub]=jintuifa(st,sd,r)%进退法求最佳步长区间x0=0;step0=0.001;step=step0;f0=jintui(x0,st,sd,r);x1=x0+step0;f1=jintui(x1,st,sd,r);if f1<=f0while truestep=2*step;x2=x1+step;f2=jintui(x2,st,sd,r);if f1<=f2lb=x0;ub=x2;break;elsex0=x1;x1=x2;f0=f1;f1=f2;endendelsewhile truestep=2*step;x2=x0-step;f2=jintui(x2,st,sd,r);if f0<=f2lb=x2;ub=x1;break;elsex1=x0;x0=x2; f1=f0; f0=f2;endendend3.运行结果。
Matlab(R2009a版)_MATLAB简述

结束迭代;否则,转(5);
(5)若k=n则令:X(0)X(k1),转(2)开始新的一轮迭代,
否则转(6), (6)构造新的迭代方向:
k
f ( X ) (k1) 2 f (X (转k) )(23)
并令k=k+1,
S (.k 1 ) f( X (k 1 ))kS (k )
4-4 共轭梯度法
例题:用MATLAB使用共轭梯度法求解无约束优化问题,已知:
(2)产生中间插入点并计算其函数值
x1a0.38(b2a),f1f(x1) x2a0.61(b8a),f2f(x2) (3)比较函数值 f1和 f 2,确定区间的取舍:
若 f1 f2 ,则新区间 a,ba,x2
令 bx2,x2x 1,f2f1 记 N0 0
若 f1 f2 ,则新区间 a,bx1,b
➢编辑已有的M文件:
从MATLAB命令窗口的Flie菜单中选择
Open M-file命令。
21
函数文件
函数文件是另一种形式的M文件,每一个函数文 件都定义一个函数。Matlab提供的标准函数大部分 是由函数文件定义的。
函数文件的基本结构 函数文件由function语句引导,其基本结构为: function 输出形参表 = 函数名(输入形参表) 注释说明部分 函数体语句 其中,以function开头的一行为引导行,表示该M 文件是一个函数文件。 当输出形参多于一个时,应该用方括号括起来。
>> syms x; >> f=sin(x)+3*x^2; >> g=diff(f,x)
13
符号表达式的替换
用给定的数据替换符号表达式中的指定的符号变量
subs(f,x,a) 用 a 替换字符函数 f 中的字符变量 x a 是可以是 数/数值变量/表达式 或 字符变量/表达式
matlab编程实现二分法牛顿法黄金分割法最速下降matlab程序代码

matlab编程实现二分法牛顿法黄金分割法最速下降matlab程序代码二分法(Bisection Method)是一种寻找函数零点的数值计算方法。
该方法的基本思想是:首先确定一个区间[a, b],使得函数在这个区间的两个端点处的函数值异号,然后将区间逐步缩小,直到找到一个区间[a', b'],使得函数在这个区间的中点处的函数值接近于零。
以下是使用MATLAB实现二分法的示例代码:```matlabfunction [x, iter] = bisection(f, a, b, tol)fa = f(a);fb = f(b);if sign(fa) == sign(fb)error('The function has the same sign at the endpoints of the interval');enditer = 0;while (b - a) / 2 > tolc=(a+b)/2;fc = f(c);if fc == 0break;endif sign(fc) == sign(fa)a=c;fa = fc;elseb=c;fb = fc;enditer = iter + 1;endx=(a+b)/2;end```牛顿法(Newton's Method)是一种用于寻找函数零点的数值计算方法。
该方法的基本思想是:通过迭代来逼近函数的零点,每次迭代通过函数的切线来确定下一个近似值,直到满足收敛条件。
以下是使用MATLAB实现牛顿法的示例代码:```matlabfunction [x, iter] = newton(f, df, x0, tol)iter = 0;while abs(f(x0)) > tolx0 = x0 - f(x0) / df(x0);iter = iter + 1;endx=x0;end```黄金分割法(Golden Section Method)是一种用于寻找函数极值点的数值计算方法。
最优化方法实验

《最优化方法》实验报告实验序号:01 实验项目名称:线性规划及MATLAB应用《最优化方法》实验报告实验序号:02 实验项目名称:0.618黄金分割法的应用结果分析:根据以上结果可知,在区间[0,3]上,函数g(x)=x^3-2*x+1的最小值点在x=0.9271处,此时最小值为0。
第二题:P50 例题3.1程序:function [t,f]=golden3(a,b) %黄金分割函数的m文件t2=a+0.382*(b-a);f2=2*(t2)^2-(t2)-1;t1=a+0.618*(b-a); %按照黄金分割点赋值,更准确可直接算f1=2*(t1)^2-(t1)-1;while abs(t1-t2)>0.16; %判定是否满足精度if f1<f2a=t2;t2=t1;f2=f1;t1=a+0.618*(b-a);f1=2*(t1)^2-(t1)-1;elseb=t1;t1=t2;f1=f2;t2=a+0.382*(b-a);f2=2*(t2)^2-(t2)-1;endendt=(t1+t2)/2; %满足条件取区间中间值输出第四题:P64 T3程序:function [t,d]=newtow2(t0)t0=2.5;t=t0-(4*(t0)^3-12*(t0)^2-12*(t0)-16)/(12*(t0)^2-24*(t0)-12);k=1;T(1)=t;while abs(t-t0)>0.000005t0=t;t=t0-(4*(t0)^3-12*(t0)^2-12*(t0)-16)/(12*(t0)^2-24*(t0)-12); k=k+1;T(k)=t;endt1=t0;d=(t1)^4-4*(t1)^3-6*(t1)^2-16*(t1)+4;kTend运行结果:当x(0)=2.5当x(0)=3四.实验小结:1.通过这次实验,加深了对0.618法的理解。
2.在学习0.618法的过程中,又巩固了倒数、求解函数值等相关知识。
matlab实验黄金分割法

matlab实验黄金分割法黄金分割法(Golden Section Method)是一种用于解决最优化问题的数值计算方法。
在数学上,最优化问题可以表述为寻找某个函数的最小值或最大值。
而黄金分割法是一种无约束优化算法,常被用于一维函数的最优化问题。
在本文中,我们将介绍黄金分割法的原理,并通过Matlab实验来演示其应用。
黄金分割法的原理基于黄金分割比,即1:0.618。
黄金分割法通过将搜索区间不断缩小,直到满足指定的精度要求,最终找到函数的极值点。
下面我们将逐步介绍黄金分割法的步骤:1. 初始化:给定初始搜索区间[a, b],以及所需的精度要求ε。
2. 计算区间长度:计算区间长度L = b - a。
3. 计算划分点:计算第一个划分点x1 = a + 0.382L,以及第二个划分点x2 = a + 0.618L。
4. 计算函数值:计算在划分点x1和x2处的函数值f(x1)和f(x2)。
5. 更新搜索区间:比较f(x1)和f(x2)的大小关系,若f(x1) < f(x2),则新的搜索区间为[a, x2],否则为[x1, b]。
6. 判断收敛:如果L < ε,算法收敛,停止迭代;否则,返回步骤2。
接下来,我们将通过一个实例来演示黄金分割法在Matlab中的应用。
假设我们要优化以下函数:```matlabf(x) = x^2 + 5*sin(x)```首先,我们需要在Matlab中定义这个函数。
在命令窗口中输入以下代码:```matlabf = @(x) x^2 + 5*sin(x);```接下来,我们可以采用黄金分割法来最小化这个函数。
以下是Matlab代码的大致框架:```matlaba = 0;b = 10;epsilon = 0.001;L = b - a;x1 = a + 0.382*L;x2 = a + 0.618*L;while L >= epsilonf1 = f(x1);f2 = f(x2);if f1 < f2b = x2;elsea = x1;endL = b - a;x1 = a + 0.382*L;x2 = a + 0.618*L;end```以上代码中,我们使用了一个while循环来不断更新搜索区间和划分点,直到满足指定的精度要求。
求函数最大值黄金分割法matlab程序

黄金分割法是一种用于求解函数最大值的数值优化算法。
它利用黄金比例的特性,在搜索过程中逐步减小搜索范围,找到函数的最大值。
本文将介绍黄金分割法的原理和实现方法,并给出利用Matlab编写的程序示例。
一、黄金分割法的原理黄金分割法基于黄金比例的性质,即将一段线段分割成两部分,使整段线段与较短部分的比值等于较短部分与较长部分的比值。
利用这一特性,在搜索过程中逐步减小搜索范围,最终找到函数的最大值。
二、黄金分割法的实现1. 确定初始搜索范围:根据实际问题确定函数的定义域,确定搜索范围[a, b]。
2. 计算黄金分割点:根据搜索范围[a, b]计算黄金分割点x1和x2,使得搜索范围按照黄金比例减小。
3. 计算函数值:计算函数在x1和x2处的取值f(x1)和f(x2)。
4. 更新搜索范围:比较f(x1)和f(x2)的大小,确定新的搜索范围[a, b]。
5. 重复步骤2-4,直到满足收敛条件或达到迭代次数上限。
三、Matlab程序示例以下是利用Matlab编写的黄金分割法程序示例:```matlabfunction [x_opt, f_opt] = golden_section_method(f, a, b, tol, max_iter)phi = (1 + sqrt(5)) / 2; 黄金比例x1 = b - (b - a) / phi;x2 = a + (b - a) / phi;f1 = feval(f, x1);f2 = feval(f, x2);iter = 0;while (b - a) > tol iter < max_iterif f1 < f2a = x1;x1 = x2;f1 = f2;x2 = a + (b - a) / phi;f2 = feval(f, x2);elseb = x2;x2 = x1;f2 = f1;x1 = b - (b - a) / phi;f1 = feval(f, x1);enditer = iter + 1;endx_opt = (a + b) / 2;f_opt = feval(f, x_opt);end```四、结语黄金分割法是一种简单而有效的数值优化算法,可以用于求解函数的最大值。
Matlab习题及答案
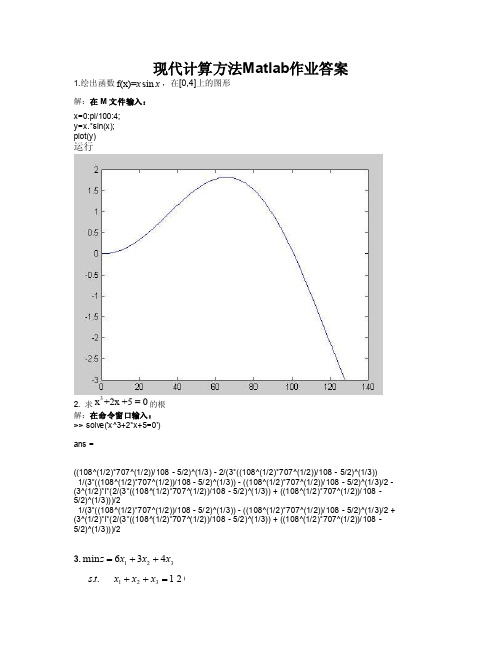
现代计算方法Matlab 作业答案1.绘出函数f(x)=sin x x ,在[0,4]上的图形解:在M 文件输入:x=0:pi/100:4;y=x.*sin(x);plot(y)运行2. 求3x +2x +5 = 0的根解:在命令窗口输入:>> solve('x^3+2*x+5=0')ans =((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3) - 2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3))1/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) - ((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)/2 -(3^(1/2)*i*(2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) + ((108^(1/2)*707^(1/2))/108 -5/2)^(1/3)))/21/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) - ((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)/2 +(3^(1/2)*i*(2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) + ((108^(1/2)*707^(1/2))/108 -5/2)^(1/3)))/23.321436min x x x z ++=120..321=++x x x t s301≥x5002≤≤x203≥x解:运用单纯形法计算此题,首先把约束条件化成标准形式:,,,,,205030120654321635241321≥=-=+=-=++x x x x x x x x x x x x x x x(1)在M 文件输入SimpleMthd 函数:function [x,minf] = SimpleMthd(A,c,b,baseVector)sz = size(A);nVia = sz(2);n = sz(1);xx = 1:nVia;nobase = zeros(1,1);m = 1;for i=1:nViaif (isempty(find(baseVector == xx(i),1)))nobase(m) = i;m = m + 1;else;endendbCon = 1;M = 0;while bConnB = A(:,nobase);ncb = c(nobase);B = A(:,baseVector);cb = c(baseVector);xb = inv(B)*b;f = cb*xb;w = cb*inv(B);for i=1:length(nobase)sigma(i) = w*nB(:,i)-ncb(i);end[maxs,ind] = max(sigma);if maxs <= 0minf = cb*xb;vr = find(c~=0 ,1,'last');for l=1:vrele = find(baseVector == l,1);if (isempty(ele))x(l) = 0;elsex(l)=xb(ele);endendbCon = 0;elsey = inv(B)*A(:,nobase(ind));if y <= 0disp('不存在最优解!');x = NaN;minf = NaN;return;elseminb = inf;chagB = 0;for j=1:length(y)if y(j)>0bz = xb(j)/y(j);if bz<minbminb = bz;chagB = j;endendendtmp = baseVector(chagB);baseVector(chagB) = nobase(ind);nobase(ind) = tmp;endendM = M + 1;if (M == 1000000)disp('找不到最优解!');x = NaN;minf = NaN;return;endend(2)在命令窗口输入:clear allA=[1 1 1 0 0 0;1 0 0 -1 0 0;0 1 0 0 1 0;0 0 1 0 0 -1];c=[6 3 4 0 0 0];b=[120;30;50;20];[xm,mf]=SimpleMthd(A,c,b,[3 4 5 6])xm =0 50 70mf =4304.计算下面函数在区间(0,1)内的最小值。
黄金分割法,进退法,基础原理及经过流程图

1黄金分割法的优化问题(1)黄金分割法基本思路:黄金分割法适用于[a , b]区间上的任何单股函数求极小值问题,对函数除要求“单谷”外不做其他要求,甚至可以不连续。
因此,这种方法的适应面非常广。
黄金分割法也是建立在区间消去法原理基础上的试探方法,即在搜索区间[a, b]内适当插入两点al, a2,并计算其函数值。
al, a2将区间分成三段,应用函数的单谷性质,通过函数值大小的比较,删去其中一段,是搜索区间得以缩小。
然后再在保留下来的区间上作同样的处理,如此迭代下去,是搜索区间无限缩小,从而得到极小点的数值近似解。
(2)黄金分割法的基本原理一维搜索是解函数极小值的方法之一,其解法思想为沿某一已知方向求目标函数的极小值点。
一维搜索的解法很多,这里主要采用黄金分割法(0.618法)。
该方法用不变的区间缩短率0.618代替斐波那契法每次不同的缩短率,从而可以看成是斐波那契法的近似,实现起来比较容易,也易于人们所接受。
rl=a+0,382(>-a) r2=a+0,618Cb-a) 如图班2户母4) 所以新区间为[a ,于2]以为新区间,继域求新的试点黄金分割法是用于一元函数f(x)在给定初始区间[a,b]内搜索极小点* *的一种方法。
它是优化计算中的经典算法,以算法简单、收敛速度均匀、效果较好而著称,是许多优化算法的基础,但它只适用于一维区间上的凸函数[6],即只在单峰区间内才能进行一维寻优,其收敛效率较低。
其基本原理是:依照“去劣存优”原则、对称原则、以及等比收缩原则来逐步缩小搜索区间[7]。
具体步骤是:在区间[a,b]内取点:al , a2把[a,b]分为三段。
如果f(a1)>f(a2),令a=a1,a1=a2,a2=a+r*(b-a);如果f(a1)<f(a2) ,令b=a2,a2=a1,a1=b-r*(b-a), 如果 | (b-a)/b | 和 | (y1-y2)/y2 | 都大于收敛精度e重新开始。
