天津市河西区2020-2021学年高二上学期期末考试数学试卷 Word版含解析
人教版2020-2021学年度上学期期末考试数学试卷(Word版 含解析)

人教版2020-2021学年度上学期期末考试数学试卷(全册)一、选择题(本大题共10小题,共30.0分)1.下列关于事件发生可能性的表述,正确的是( )A. 事件:“在地面,向上抛石子后落在地上”,该事件是随机事件B. 体育彩票的中奖率为10%,则买100张彩票必有10张中奖C. 在同批次10000件产品中抽取100件发现有5件次品,则这批产品中大约有500件左右的次品D. 掷两枚硬币,朝上的一面是一正面一反面的概率为 132.下列四个银行标志中,既是轴对称图形又是中心对称图形的是( ). A. B. C. D.3.关于 x 的一元二次方程 x 2−5x +2p =0 的一个根为 1 ,则另一根为( ).A. -6B. 2C. 4D. 14.下列关于二次函数 y =2x 2+3 ,下列说法正确的是( ).A. 它的开口方向向下B. 它的顶点坐标是 (2,3)C. 当 x <−1 时, y 随 x 的增大而增大D. 当 x =0 时, y 有最小值是35.如图,AB 为⊙O 的直径,点D 是弧AC 的中点,过点D 作DE ⊥AB 于点E ,延长DE 交⊙OO 于点F ,若AC = 12,AE = 3,则⊙O 的直径长为( )A. 10B. 13C. 15D. 166.某校食堂每天中午为学生提供A 、 B 两种套餐,甲乙两人同去该食堂打饭,那么甲乙两人选择同款套餐的概率为( )A. 12B. 13C. 14D. 237.如图,某幢建筑物从2.25米高的窗口A 用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点M 离墙1米,离地面3米,则水流下落点B 离墙的距离OB 是( )A. 2.5米B. 3米C. 3.5米D. 4米8.小明同学是一位古诗文的爱好者,在学习了一元二次方程这一章后,改编了苏轼诗词《念奴娇·哧壁怀古》:“大江东去浪淘尽,千古风流人物。
而立之年督东吴,早逝英年两位数。
天津市河西区2020至2021学年高二上学期期中数学试题及答案解析

则 PF PO 2 r 1 r 1 FO 4,
根据双曲线得定义可得圆心 P 在双曲线的一支上,
故选:B.
10.
6 7
【分析】
根据经过两点的直线的斜率公式,代入 A、B 两点的坐标加以计算,可得直线 l 的斜率.
17.在长方体 ABCD A1 B1C1 D1 中,点 E,F 分别在 BB1 ,DD1 上,且 AE A1B ,AF A1D .
(1)求证: A1C 平面 AEF;
(2)当 AD 3 ,AB 4 ,AA1 5时,求平面 AEF 与平面 D1B1BD 所成二面角的余弦值.
18.已知椭圆 C :
()
A. x2 y2 1 4 12
C. x2 y2 1 48 16
B. x2 y2 1 12 4
D. x2 y2 1 16 48
6.已知直线 l1 : x 2ay 1 0 与直线 l2 : (3a 1)x ay 1 0 平行,则 a ( )
A. 0
B. 0 或 1 6
C. 1 6
x2 a2
y2 b2
1(a
b 0 )的焦距为 2 ,离心率为
2. 2
(1)求椭圆 C 的标准方程;
(2)经过椭圆的左焦点 F1 作倾斜角为 60 的直线 l ,直线 l 与椭圆相交于 A , B 两点,
求线段 AB 的长.
试卷第 3页,共 3页
………○…………外…………○…………装…………○…………订…………○…………线…………○………… 学校:___________姓名:___________班级:___________考号:___________
天津市河西区2021届高三上学期期中考试数学试卷Word版含解析

【解析】
【分析】
分别给 进行取值,可计算求得 中元素,进而确定集合 ,得到结果.
【详解】当 或 或 时,
当 , 或 时, 或 ,
当 , 或 时, 或 ,
当 , 或 时, 或 ,
综上所述: ,共 个元素
故答案为:
【点睛】此题考查集合中元素个数的求解问题,关键是能够读懂描述法所表示的集合的含义,进而根据要求求得集合.
所以,当 时, .
(Ⅲ)依题意, ,即 .
记 ,那么 .
且 .
由 及(Ⅰ)得 .
由(Ⅱ)知,当 时, ,所以 在 上为减函数,
因此 .
又由(Ⅱ)知 ,故:
.
所以 .
【点睛】此题主要考查导数的运算、不等式证明、、综合分析问题和解决问题的能力.
14. ,且 ,那么 的最小值为______________.
【答案】64
【解析】
【分析】
根据根本不等式解得 取值范围,再结合等号确定最值取法.
【详解】 ,当且仅当 时取等号,所以 的最小值为
【点睛】在利用根本不等式求最值时,要特别注意等号取得的条件,否那么会出现错误.
15.如图,在 中, ,D,E分别边AB,AC上的点, 且 ,那么 ______________,假设P是线段DE上的一个动点,那么 的最小值为_________________.
点睛:此题主要考查了周期函数与对数函数的图象,数形结合是高考中常用的方法,考查数形结合,此题属于根底题;函数 和 图象交点的个数即函数 的零点个数,分别作出函数y=f〔x〕,y=log5|x-1|的图象,结合函数的对称性,利用数形结合法进行求解.
二、填空题〔本大题共6小题〕
10.集合 ,那么集合 中元素的个数是______.
天津市河西区新华中学2022-2023学年高二上学期期末考试化学试题

2021级高二年级第一学期期末学习情况反馈化学学科第I 卷(选择题)和第II 卷(非选择题)两部分,共100分,用时60分钟。
将自己的姓名、准考号填写在答题卡上。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷注意事项:1.每题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共28题,每题3分,共84分。
在每题列出的四个选项中,只有一项是最符合题目要求的。
1. 下列物质属于弱电解质的是( )A. 一水合氨B. 二氧化碳C. 消毒液D. 医用酒精 2. 下列溶液呈酸性的是( ) A. FeCl 3溶液 B. Na 2CO 3溶液 C. NaCl 溶液D. CH 3COONa 溶液3.某反应由两步反应A→B→C 构成,反应能量曲线如图,下列叙述正确的是( )A .两步反应均为吸热反应B . A→B 反应,反应条件一定要加热C .A 与C 的能量差为E 4D .三种化合物中C 最稳定 4.下列方程式书写正确的是( ) A .H 2S 的电离方程式:H 2S+H 2OH 3O ++HS -B .NaHCO 3在水溶液中的电离方程式:NaHCO 3=Na ++H ++CO 2-3C .23CO −的水解方程式:CO 2-3+2H 2OH 2CO 3+2OH -D .HS -的水解方程式:HS -+H 2O H 3O ++S 2-5.常温下,下列各组离子在给定溶液中一定能大量共存的是( ) A. =1012的溶液:SO 42-、Na +、S 2-、AlO 2- B. 含Na 2CO 3的溶液:K +、Cl -、NO 3-、Al 3+C. 水电离出来的c (H +)=10-13mol/L 的溶液:K +、S 2O 32--、SO 42--、Cl -D. 能使甲基橙变红色的溶液:Na +、Fe 2+、ClO -、NH 4+ 6. 向纯水中加入少量NaHSO 4,在温度不变时,溶液中( ) A .c (H +)c(OH −)减小 B .c (H +)增大C .水电离的c (H +)与c (OH -)的乘积增大D .c (OH -)增大7. 常温下,下列有关电解质溶液的说法正确的是( )A. 相同浓度的 HCOONa 和NaF 两溶液,前者的pH 较大,则K a(HCOOH) > K a(HF)B. 相同浓度的CH 3COOH 和CH 3COONa 两溶液等体积混合后pH 约为4.7,则溶液中c (Na +)>c (CH 3COO -) >c (H +)>c (OH -)C. FeS 溶于稀硫酸,而CuS 不溶于稀硫酸,则K sp(FeS)> K sp(CuS)D. 在1mol/L Na 2S 溶液中,c (S 2- )+c (HS -)+c (H 2S) = 0.5mol/L8. 常温下,体积相同、pH 相同的盐酸和醋酸两种溶液中,下列两者的量相同的是( ) A .电离程度 B .酸的物质的量浓度C .与Zn 反应开始时的反应速率D .与足量的Zn 反应产生H 2的量9.室温下,有两种溶液:①0.01 mol·L -1 NH 3·H 2O 溶液、②0.01 mol·L -1 NH 4Cl 溶液,下列操作可以使两种溶液中c (NH +4)都增大的是( ) A .通入少量HCl 气体 B .加入少量NaOH 固体 C .加入少量H 2OD .升高温度-+c(OH )c(H)10.某基态原子的价层电子的轨道表示式为,下列说法正确的是()A. 最外层有4个电子B. 有2种能量不同的电子C. 有8种运动状态不同的电子D. s电子的电子云轮廓图是哑铃形11.以下基态原子的价层电子排布式正确的是()A. Mn:1s22s22p63s23p63d54s2B. Zn:[Ar]3d104s2C. Cr:3d44s2D. Cu:3d104s112. 下列叙述正确的是()A. 某温度下,一元弱酸HA的K a越小,则NaA的K h(水解平衡常数)越大B. 铁管镀锡层局部破损后,铁管仍不易生锈C. 铜既可以发生析氢腐蚀又可以发生吸氧腐蚀D. ΔH>0,ΔS<0的反应在任何温度下均能正向自发进行13.下列说法中,不正确的是()A.键长与共价键的稳定性没有关系B.键能是衡量化学键稳定性的参数之一,键能越大,则化学键就越牢固C.键角是两个相邻共价键之间的夹角,说明共价键有方向性D.共价键是通过原子轨道重叠并共用电子对而形成的,所以共价键有饱和性14. 下列说法中正确的是()A. 需要加热才能发生的反应一定是吸热反应B. 放热反应在常温下一定很容易发生C. 吸热反应不加热不可能进行反应D. 反应是吸热还是放热是由反应物和生成物所具有的总能量的相对大小而决定的15.下列说法正确的是()A.100℃时水的pH≈6,呈中性B.饱和小苏打溶液中c(Na+) = c(HCO3−)C.室温下,加水稀释氨水,溶液中c(NH4+)×c(OH−)不变D.室温下,0.1 mol·L−1的氨水和0.1 mol·L−1NaOH溶液的pH相等16.生活中处处有化学,下列有关说法不正确的是()A.明矾水解时产生具有吸附性的胶体粒子,可杀菌消毒B.焊接时用NH4Cl溶液除锈与盐类水解有关C.草木灰与铵态氮肥不能混合施用与盐类水解有关D.生活中用电解食盐水的方法制取消毒液,与氧化还原有关17.BeCl2是共价分子,可以以单体、二聚体和多聚体形式存在,三者结构简式依次如图所示。
天津市河西区2024-2025学年高二上学期期中化学试卷

河西区2024~2025学年度第一学期高二年级期中质量调查化学试卷可能用到的相对原子质量:H 1 C 12 N 14 O 16 Mg 24本试卷分为第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)两部分。
第Ⅰ卷为第1页至第6页,第Ⅱ卷为第7页至第8页。
试卷满分100分。
考试时间60分钟。
第I卷(选择题共60分)第.1~10..1.个选项是最符合题目要求的............。
.........只有....4.分,..列出的四个选项中,....题,每题..在.每题1.下列变化过程中一定不存在化学能转化为热能的是A.干冰升华B.谷物酿酒C.木材燃烧D.鞭炮燃放2.下列日常生活情境与化学反应速率无关的是A.用较浓的白醋清洗水壶垢B.夏天将食物放在冰箱中冷藏C.糖果制作过程中添加着色剂D.面团加酵母粉放在温热处发酵3.下列事实,不能..用勒夏特列原理解释的是A.开启汽水瓶盖后,瓶中立刻泛起大量气泡B.对2HI(g)H2(g)+I2(g)平衡体系加压,气体颜色变深C.硫酸工业中,增大O2的浓度有利于提高SO2的转化率D.滴有酚酞的氨水溶液,适当加热溶液(忽略氨气挥发)后颜色变深4.下列有关反应2CO(g) = 2C(s)+O2(g) △H>0的推测正确的是A.低温下能自发进行B.高温下能自发进行C.任何温度下都不能自发进行D.任何温度下都能自发进行5.在10 L密闭容器内发生反应2A(g)+B(g)C(g),气体A在2 s内由8 mol/L变为6 mol/L,2 s内平均反应速率v(A)[单位均为mol/(L·s)]正确的是A.0.1 B.0.05 C.1 D.26.在密闭容器中,反应2X(g)+Y(g)3Z(g)达到平衡后,若将容器体积缩小一半,对反应产生的影响是A.v(正)减小,v(逆)增大B.v(正)增大,v(逆)减小C.v(正)和v(逆)都减小D.v(正)和v(逆)都增大7.已知:H 2(g)+F 2(g)=2HF(g) △H =-270 kJ/mol 。
天津市河西区2023-2024学年高二下学期期中考试数学试卷(含解析)
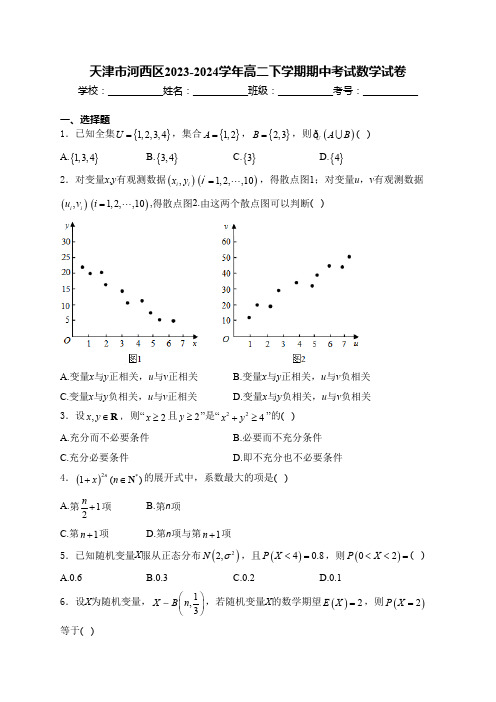
天津市河西区2023-2024学年高二下学期期中考试数学试卷学校:___________姓名:___________班级:___________考号:___________一、选择题1.已知全集,集合,,则( )A. B. C. D.2.对变量x ,y 有观测数据,得散点图1;对变量u ,v 有观测数据,得散点图2.由这两个散点图可以判断( )A.变量x 与y 正相关,u 与v 正相关B.变量x 与y 正相关,u 与v 负相关C.变量x 与y 负相关,u 与v 正相关D.变量x 与y 负相关,u 与v 负相关3.设,则“且”是“”的( )A.充分而不必要条件 B.必要而不充分条件C.充分必要条件D.即不充分也不必要条件4.的展开式中,系数最大的项是( )项B.第n 项C.第项D.第n 项与第项5.已知随机变量X 服从正态分布,且,则( )A.0.6B.0.3C.0.2D.0.16.设X 为随机变量,,若随机变量X 的数学期望,则等于( ){}1,2,3,4U ={}1,2A ={},32B =()U A B ð{}1,3,4{}3,4{}3{}4(),i i x y ()1,2,,10= i (),i i u v ()1,2,,10i = ,x y ∈R 2x ≥2y ≥224x y +≥()2*1()n x n +∈N 1+1n +1n +()22,N σ()40.8P X <=()02P X <<=1,3X B n ⎛⎫⎪⎝⎭()2E X =()2P X =7.某学习小组共有11名成员,其中有6名女生,为了解学生的学习状态,随机从这11名成员中抽选2名任小组组长,协助老师了解情况,A 表示“抽到的2名成员都是女生”,B表示“抽到的2名成员性别相同”,则( )8.的展开式中各项系数的和为2,则该展开式中常数项为( )A.-40 B.-20 C.20 D.409.用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( )A.243 B.252 C.261 D.279二、填空题10.的展开式中的系数为________.11.命题,的否定是________.12.已知,则________.13.含有3个实数的集合可表示为,又可表示为,则________.14.三位老师分配到4个贫困村调查义务教育实施情况,若每个村最多去2个人,则不同的分配方法有种________.15.某公司有甲、乙两家餐厅,小李第一天午餐时随机地选择一家餐厅用餐,如果第,则小李第二天去乙家餐厅的概率为________.三、解答题16.(1)证明:组合数性质;(2)计算:(用数字作答).17.已知集合,若()|P A B =512a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭822x y :p x ∀∈R 210x +>7270127(12)x a a x a x a x -=++++ 1357a a a a +++=,,1b a a ⎧⎫⎨⎬⎩⎭{}20,,a a b +20242024a b +=()1*1C C C ,m m n n n m n π-+=+∈N 2222234100C C C C ++++ {}23100A x x x =--≤(1),,求实数m 的范围;(2),,求实数m 的范围;(3),,求实数m 的范围.18.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(x 吨)与相应的生产能耗y (吨)标准煤的几组对照数据:(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程;(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?(参考:用最小二乘法求线性回归方程系数公式(参考数值:)19.某班主任对班级22名学生进行了作业量多少的调查,数据如下:在喜欢玩电脑游戏的12人中,有9人认为作业多,3人认为作业不多;在不喜欢玩电脑游戏的10人中,有4人认为作业多,6人认为作业不多.(1)根据以上数据填写列联表;关系?参考公式:B A ⊆{}121B x m x m =+≤≤-A B ⊆{}621B x m x m =-≤≤-B A ={}621B x m x m =-≤≤-ˆybx a =+ˆb=ˆy =-3 2.543546 4.566.53242526286⨯+⨯+⨯+⨯=+++=22⨯2K =参考数据:,,,.20.已知箱中装有4个白球和5个黑球,且规定:取出一个白球的2分,取出一个黑球的1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X 为取出3球所得分数之和.(Ⅰ)求X 的分布列;(Ⅱ)求X 的数学期望E(X).2( 2.072)0.15P K ≥=2( 2.706)0.10P K ≥=2( 3.841)0.05P K ≥=()2 5.0240.025P K ≥=参考答案1.答案:D解析:易知,则,故选:D.2.答案:C解析:变量x 与中y 随x 增大而减小,为负相关;u 与v 中,u 随v 的增大而增大,为正相关.3.答案:A解析:试题分析:若且,则,,所以,即;若,则如满足条件,但不满足且.所以“且”是“”的充分而不必要条件.故选A.4.答案:C解析:在的展开式中,第项的系数与第项的二项式系数相同,再根据中间项的二项式系数最大,展开式共有项,可得第项的系数最大,故选C.5.答案:B解析:由题意,随机变量X 服从正态分布,则正态分布曲线关于对称,又由,根据正态分布曲线的对称性,可得,所以,故选B.6.答案:A解析:因为,得,即.所以故选A 7.答案:A解析:由题意可知{}1,2,3A B = {}()4U A B = ð2x ≥2y ≥24x ≥24y ≥228x y +≥224x y +≥224x y +≥()2,2--2x ≥2y ≥2x ≥2y ≥224x y +≥()()2*1x n n +∈N 1r +1r +21n +1n +22,N σ()2x =(4)0.8P X <=(0)(4)1(4)0.2P X P X P X ≤=≥=-<=1(02)(0)0.50.20.32P X P X <<=-≤=-=()123E X n ==6n =16,3X B ⎛⎫ ⎪⎝⎭()2426112C 133P X ⎛⎫⎛⎫==⨯⨯-= ⎪ ⎪⎝⎭⎝⎭()2265211C C C P B +==()26211C C AB ==所以故选:A.8.答案:D解析:令得.故原式=.的通项,由得,对应的常数项,由得,对应的常数项,故所求的常数项为40,故选D 9.答案:B解析:由分步乘法原理知:用0,1,…,9十个数字组成的三位数(含有重复数字的)共有,组成无重复数字的三位数共有,因此组成有重复数字的三位数共有.10.答案:70解析:设的展开式中含的项为第项,则由通项知.令,解得,的展开式中的系数为.11.答案:,或,解析:全称量词命题的否定是存在量词命题,要注意否定结论,所以命题,的否定是:,故答案为:,12.答案:-1094解析:令,则,,()()()|P AB P A B P B ==1x =1a =5112x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭512x x ⎛⎫- ⎪⎝⎭521552155C (2)()C (1)2r r r r rr r r T x x x ----+=-=-521r -=2r =80=521r -=-3r =80=-91010900⨯⨯=998648⨯⨯=900648252-=822x y 1r +()811882222188C 1C rrr rr r r r r r T xy x y x y -----+--++⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭822r r -+-=4r =∴822x y ()4481C 70-=0x ∃∈R 2010x +≤x ∃∈R 210x +≤:p x ∀∈R 210x +>0x ∃∈R 2010x +≤0x ∃∈R 2010x +≤()7270127()12f x x a a x a x a x =-++++= 0127(1)1a a a a f ++++==- 701273(1)32187a a a a f a -++--==-=所以.故答案为:-109413.答案:1解析:因为有3个实数的集合可表示为,又可表示为,所以,即,则,即或,当时,集合为,与集合元素的互异性矛盾,故,,.故答案为:1.14.答案:60解析:若每个村去一个人,则有种分配方法;若有一个村去两人,另一个村去一人,则有种分配方法,所以共有60种不同的分配方法.解析:设“第1天去甲餐厅用餐“,“第1天去乙餐厅用餐”,“第2天去甲餐厅用餐”,“第2天去乙餐厅用餐”,根据题意得,则则由全概率公式得:,即1357(1)(1)10942f f a a a a --==-+++,,1b a a ⎧⎫⎨⎬⎩⎭{}2,0,a a b +a ≠0=0b =21a =1a =1a =-1a ={1,0,1}{1,1,0}1a =-0b =202420241a b +=34A 24=1234C A 36⨯=1A =1B =2A =2B =1122()()()()P A P B P A P B ====()21|A A =()21|P A B =21(|)P B A =()()()21211|P A B A B P B ==()214152P A B =⨯=()()()2112225|12P A B P B A P A ===()22|B A =21222121222()()()()(|)()(|)P B P A B P A B P A P B A P A P B A =+=+212113()252510P B =⨯+⨯=16.答案:(1)证明见解析;(2)166650解析:(1)证明:;(2)=.17.答案:(1);(2)(3)不存在满足题意的实数m解析:(1);当时,满足,则,解得:;当时,由得:,解得:;综上所述:实数m 的取值范围为.(2)由得:,解得:,即实数m 的取值范围为.(3),,方程组无解,不存在满足题意的实数m .18.答案:(1)见解析;(2);()()1!!!!(1)!C 1!C m m n n n n m n m m n m -+---++=()()()()()!1!1!!1!!1!!1!n n m n n m m n mm n m m n m m n m -+-++=+=-+-+-+()()11!!(1)C !(1)!!1!m n n n n m n m m n m +++===-+-+3223102222223223410044041300C C C C C C C C C C C =+++=+++++++ 22323310010010515100C C 10110099C C C 16665032C ⨯⨯==+++==+=⨯ (],3-∞[]3,4{}()(){}{}2310052025A x x x x x x x x =--≤=-+≤=-≤≤B =∅B A ⊆121m m +>-2m <B ≠∅B A ⊆12112215m m m m +≤-⎧⎪+≥-⎨⎪-≤⎩23m ≤≤(],3-∞A B ⊆62126521m m m m -≤-⎧⎪-≥-⎨⎪≤-⎩34m ≤≤[]3,4A B = 62215m m -=-⎧∴⎨-=⎩∴ˆ0.70.35yx =+(3)19.65吨解析:(1)把所给的四对数据写成对应的点的坐标,在坐标系中描出来,得到散点图如下;(2)由对照数据,计算得,,,,回归方程的系数为,,所求线性回归方程为;(3)由(2)的线性回归方程,估计生产100吨甲产品的生产能耗为(吨,吨,预测比技改前降低了19.65吨标准煤.19.答案:(1)答案见解析;(2)有关系解析:(1)根据题中所给数据,得到如下列联表:1(3456) 4.54x =⨯+++=1(2.534 4.5) 3.54y =⨯+++=4222221345686ii x==+++=∑413 2.543546 4.566.5iii x y==⨯+⨯+⨯+⨯=∑∴266.54 4.5 3.5ˆ0.7864 4.5b -⨯⨯==-⨯ 3.50.7 4.5ˆ0.35a =-⨯=∴ˆ0.70.35yx =+0.71000.3570.35⨯+=)9070.3519.65∴-=22⨯由(1)中的的列联表,可得,所以有充分的理由认为假设不成立,即认为喜欢玩电脑游戏与认为作业多少有关,这种判断出错误的概率不超过0.10.20.答案:(Ⅰ)见解析;解析:(Ⅰ)X 的可能取值有:3,4,5,6.故,所求X 的分布列为22⨯()220.10226943 2.7641 2.7061210139K K ⨯⨯-⨯=≈>=⨯⨯⨯3539C (3)C P X ===215439C C (4)C X ===125439C C (5)C P X ===3439C (6)C P X ===()51051345642211421E X ⨯+⨯+⨯+⨯==。
2023-2024学年天津市河西区高二上学期期中考试数学试卷+答案解析(附后)

2023-2024学年天津市河西区高二上学期期中考试数学试卷一、单选题:本题共9小题,每小题5分,共45分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.在空间直角坐标系中,已知点,给出下列4条叙述:①点P 关于x 轴的对称点的坐标是;②点P 关于yOz 平面的对称点的坐标是;③点P 关于y 轴的对称点的坐标是;④点P 关于原点的对称点的坐标是其中正确的个数是( )A. 3B. 2C. 1D. 02.空间四边形ABCD 中,,,,则等于( )A. B.C.D.3.过点的直线的斜率等于1,则m 的值为A. 1B.C. 2D. 4.若方程表示的曲线是圆,则实数a 的取值范围是( )A. B.C. D.5.已知过点的直线与圆相切,且与直线垂直,则( )A.B. 1C. 2D.6.若椭圆经过原点,且焦点分别为则其离心率为( )A. B.C.D.7.已知,是椭圆C 的两个焦点,过且垂直x 轴的直线交C 于A ,B 两点,且,则C 的方程为( )A.B.C.D.8.如图所示,在正方体中,棱长为1,E,F分别是BC,CD上的点,且,则与的位置关系是( )A. 平行B. 垂直C. 相交D. 与a值有关9.若是直线上的两点,那么间的距离为( )A. B. C. D.二、填空题:本题共6小题,每小题5分,共30分。
10.已知椭圆的焦距是2,则该椭圆的长轴长为__________.11.如图,隧道的截面是半径为4m的半圆,车辆只能在道路中心线一侧行驶,假设货车的最大宽度为am,那么要正常驶入该隧道,货车的限高为多少__________.12.已知直线和平面相交,设直线的方向向量与平面的法向量的夹角为,则直线与平面的夹角__________,用含的代数式表示__________用含的三角函数式表示13.已知点,和直线l:,动点在直线l上,则的最小值为__________.14.正方体的棱长为1,E,F分别为,CD的中点,则点F到平面的距离为__________.15.两相交圆与的公共弦所在的直线方程为__________,以公共弦为直径的圆的方程为__________.三、解答题:本题共5小题,共75分。
2020-2021学年天津市河西区九年级上学期数学期中试卷及答案

2020-2021学年天津市河西区九年级上学期数学期中试卷及答案一、选择题1. 在平面直角坐标系中,点关于原点对称的点的坐标为( )(2,0)A.B.(2,0)-(0,2)C.D. (0,2)-(2,2)-【答案】A【解析】【分析】根据点的坐标关于原点对称的方法可直接进行排除选项.【详解】解:点关于原点对称的点的坐标为.()2,0()2,0-故选:A .【点睛】本题主要考查点的坐标关于原点对称,熟练掌握点的坐标关于原点对称的方法是解题的关键.2. 下列四个图形中,既是轴对称图形,又是中心对称图形的是( )A. B.C. D.【答案】B【解析】【分析】直接根据轴对称图形与中心对称图形的定义进行判断即可【详解】解:A 、不是轴对称图形,是中心对称图形,故本选项不合题意;B 、既是轴对称图形,又是中心对称图形,故本选项符合题意;C 、是轴对称图形,不是中心对称图形,故本选项不合题意;D 、是轴对称图形,不是中心对称图形,故本选项不合题意.故选:B .【点睛】本题考查了轴对称图形与中心对称图形的定义,正确掌握知识点是解题的关键;3. 在抛物线y =x 2﹣4x﹣4上的一个点是( )A. (4,4)B. (3,﹣1)C. (﹣2,﹣8)D. (,12-) 74-【答案】D【解析】【分析】把各点的横坐标代入函数式,比较纵坐标是否相符,逐一检验.【详解】解:A 、x=4时,y=x 2-4x-4=-4≠4,点(4,4)不在抛物线上;B 、x=3时,y=x 2-4x-4=-7≠-1,点(3,-1)不在抛物线上;C 、x=-2时,y=x 2-4x-4=8≠-8,点(-2,-8)不在抛物线上;D 、x=时,y=x 2-4x-4=,点(,)在抛物线上. 12-74-12-74-故选D .【点睛】此题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.4. 二次函数的图象如图所示,则( )2y ax bx =+A. ,B. ,C. ,D. ,0a >0b >0a >0b <0a <0b >0a < 0b <【答案】D【解析】【分析】由抛物线的开口向下,得a<0,抛物线的对称轴在y 轴的左边,于是<0,所2b a-以b<0.【详解】解:如图,抛物线的开口向下,则, 0a <抛物线的对称轴位于y 轴的左侧,则a 、b 同号,即.0b <综上所述,,.0a <0b <故选:D .【点睛】本题考查了二次函数的图象与系数的关系,二次函数y=ax 2+bx+c 系数符号由抛物线开口方向,对称轴,抛物线与x 轴交点个数确定.5. 如图,⊙O 中,弦AB 、CD 相交于点P ,若∠A=30°,∠APD=70°,则∠B 等于( )A. 30°B. 35°C. 40°D. 50°【答案】C【解析】 分析:欲求∠B 的度数,需求出同弧所对的圆周角∠C 的度数;△APC 中,已知了∠A 及外角∠APD 的度数,即可由三角形的外角性质求出∠C 的度数,由此得解.解答:解:∵∠APD 是△APC 的外角,∴∠APD=∠C+∠A;∵∠A=30°,∠APD=70°,∴∠C=∠APD-∠A=40°;∴∠B=∠C=40°;故选C .6. 函数的图象与轴的交点坐标为( ). ()212y x =++y A.B. C. D.()0,2()1,2-()0,3()0,4【答案】C【解析】 【分析】代入x=0求出y 的值,即可得到答案.【详解】解:当x=0时,,()2123y x =++=∴函数的图象与y 轴的交点坐标为(0,3),()212y x =++故选:C .【点睛】本题考查二次函数图象上点的坐标特征,熟知图象上的点的坐标都满足函数关系式是解题的关键.7. 一个矩形的长比宽多2,面积是99,则矩形的两边长分别为( )A. 9和7B. 11和9C. D. , 1+1-1+1-+【答案】B【解析】【分析】设矩形的长为x ,则宽为,利用矩形的面积公式列方程即可解答(2)x -【详解】解:设矩形的长为x ,则宽为,则 (2)x -,(2)99x x -=解得,(舍去).111x =29x =-则,29x -=所以矩形的两边长分别为11和9,故选:B .【点睛】本题考查了一元二次方程的应用,解题关键是要读懂题目,根据题目给出的条件,找出合适的等量关系,列出方程,在求解.8. 如图,四边形ABCD 是的内接四边形,,则的度数是( )O 135B ∠=︒AOC ∠A.B. C. D.60︒70︒90︒180︒【答案】C【解析】【分析】 连接OA 、OC ,根据“圆内接四边形对角互补”可求得∠D 的度数,根据圆周角定理即可求得∠AOC.【详解】连接OA 、OC∵四边形ABCD 是的内接四边形,O 135B ∠=︒∴∠D=180°-∠B=45°∴∠AOC=2∠D=90°故选C【点睛】本题考查的是圆周角定理的相关推论,熟练的掌握“直径所对的圆周角是90度”及圆周角定理是关键.9. 抛物线与x 轴两交点间的距离是( )223y x x =--A. 4B. 3C. 2D. 1 【答案】A【解析】【分析】用十字相乘法将抛物线解析式进行因式分解,令,即可求出两个交点的横坐0y =标,从而求出交点间的距离.【详解】解:, 2(1)(3)23y x x x x +-=-=-当时0y =则,(1)(3)0x x +-=解得:,.11x =-23x =与x 轴的交点坐标为,.(1,0)-(3,0)则抛物线与x 轴两交点间的距离为.3(1)4--=故选:A .【点睛】本题考查抛物线与x 轴的交点坐标求法,令,解一元二次方程即可得到交点0y =的横坐标.10. 如图,将等边三角形放在平面直角坐标系中,A 点坐标,将绕点O 逆OAB ()1,0OAB 时针旋转60°,则旋转后点B 的对应点的坐标为( )B'A.B. C.D.12⎛- ⎝11,2⎛⎫- ⎪⎝⎭32⎛- ⎝12⎫⎪⎪⎭【答案】A【解析】【分析】过点B 作于H ,设交y 轴于J ,求出点B 的坐标,证明、关于BH OA ⊥BB 'B B 'y 轴对称,即可解决问题;【详解】解:如图,过点B 作于H ,设交y 轴于J .BH OA ⊥BB ',()10A ,Q ,1OA ∴=是等边三角形,,△AOB BH OA ⊥,, 1122OH AH OA ∴===BH ==,12B ⎛∴ ⎝,,60AOB BOB '∠=∠=︒ 90JOA ∠=︒,30BOJ JOB '∴∠=∠=︒,OB OB '= ,BB OJ '∴⊥,BJ JB '∴=,关于y 轴对称,B ∴B '∴, 12B ⎛'- ⎝故选:A .【点睛】本题考查了坐标与图形的性质,旋转变换,轴对称,等边三角形的性质等知识,解决问题的关键是理解题意,灵活运用所学知识;11. 如图,将△ABC 绕点B 顺时针旋转60°得△DBE,点C 的对应点E 恰好落在AB 延长线上,连接AD .下列结论一定正确的是( )A. ∠ABD=∠EB. ∠CBE=∠CC. AD∥BCD. AD =BC【答案】C【解析】 根据旋转的性质得,∠ABD=∠CBE=60°, ∠E=∠C,则△AB D 为等边三角形,即 AD =AB=BD,得∠ADB=60°因为∠ABD=∠CBE=60°,则∠CBD=60°,所以,∠ADB=∠CBD,得AD∥BC.故选C.12. 已知一元二次方程,有下列叙述: ()200++=≠ax bx c a ①若,则方程有两个不等实根;a 0>②若,方程的两根为,. 2b 4ac 0->1x =2x =③若,则方程没有实数根;240b ac -<④若,则抛物线的顶点在x 轴上.2b 4ac 0-=2y ax bx c =++其中,正确结论的个数是( )A. 1B. 2C. 3D. 4【答案】C【解析】【分析】根据一元二次方程根的判别式和抛物线的性质逐一求解即可;【详解】解:①若,时,方程有两个不等实根,故①错误,不符合题意;0a >0∆>②若,方程的两根为,,故②正确,240b ac ->1x =2x =符合题意;③若,则方程没有实数根,故③正确,符合题意;240b ac -<④若,抛物线和x 轴只有一个交点,故抛物线的顶点在x 轴240b ac -=2y ax bx c =++上,故④正确,符合题意.故选:C .【点睛】本题考查了一元二次方程根的判别式,熟练掌握根的判别式是解题的关键二.填空题(本大题共6小题,每小题3分,共18分)13. 方程的根是_________.22x =【答案】.x =【解析】【分析】【详解】,解得:x=.故答案为.22x =x =14. 若正方体的棱长为,表面积为,则与的关系式为________.x y y x 【答案】26y x =【解析】【分析】正方体有6个面,每一个面都是边长为x 的正方形,这6个正方形的面积和就是该正方体的表面积.【详解】解:∵正方体有6个面,每一个面都是边长为x 的正方形,∴表面积.26y x =故答案为:.26y x =【点睛】本题考查了列二次函数关系式,理解两个变量之间的关系是得出关系式的关键.15. 若平行四边形是圆内接四边形,则∠A 的度数为______.ABCD 【答案】90°【解析】【分析】由平行四边形的性质可得∠A=∠C,由圆的内接四边形的性质得到∠A+∠C=180°,由此可求得结果.【详解】解:∵四边形为平行四边形,ABCD ,A C ∴∠=∠∵四边形是圆内接四边形,ABCD ,180A C ∴∠+∠=︒,2180A ∴∠=︒,90A ∴∠=︒故答案为90°.【点睛】本题主要考查了平行四边形的性质,圆内接四边形的性质,熟记这两个性质是解决问题的关键.16. 如图,在半径为5的中,,则弦的长度为______.O 120AOB ∠=︒AB【答案】【解析】【分析】作OC⊥AB,根据垂径定理得到AC=BC=AB ,根据直角三角形的性质求出OC ,根据12勾股定理求出AC ,得到答案.【详解】解:作于C ,OC AB ⊥则, 12AC BC AB ==,,OA OB = 120AOB ∠=︒,30A ∴∠=︒, 1522OC OA ∴==由勾股定理得,, AC ==2AB AC ∴==故答案为:【点睛】本题考查的是垂径定理、圆心角、弧、弦的关系定理,正确作出辅助性、灵活运用定理是解题的关键.17. 如图,在中,,,将绕点C 顺时针旋转一Rt ABC 92ABC ∠=︒30ACB ∠=︒ABC 定的角度得到,点A 、B 的对应点分别是D 、E .当点E 恰好在上时,则DEC AC ADE ∠的度数为______.【答案】17° 【解析】【分析】由旋转的性质可得,,,92ABC DEC ∠=∠=︒CA CD =30ACB ACD ∠=∠=︒由等腰三角形的性质以及角的和差即可求解.【详解】∵将绕点C 顺时针旋转一定的角度得到,ABC DEC ,,,92ABC DEC ∴∠=∠=︒CA CD =30ACB ACD ∠=∠=︒为等腰三角形, ACD ∴CAD CDA ∴∠=∠ 180CAD CDA ACD ∠+∠+∠=︒ ,75CAD CDA ∴∠=∠=︒,927517ADE DEC DAC ∴∠=∠-∠=︒-︒=︒故答案为:17°.【点睛】本题考查了旋转的性质,等腰三角形的性质,掌握旋转的性质是本题的关键. 18. 如图,C 是线段上一动点,,都是等边三角形,M ,N 分别是,AB ACD △CBE △CD 的中点,若,则线段的最小值为______.BE 6AB =MN【解析】【分析】连接,根据等边三角形性质,得,再根据等腰三角形三线合一CN 60DCE ∠=︒性质,得,从而得;设,根据三角函数性质,计算得;再根据ECN ∠DCN ∠AC a =CN 勾股定理和二次函数的性质计算,即可得到答案 【详解】连接,CN∵和为等边三角形ACD △BCE ∴,, AC CD =BC CE =60ACD BCE B ∠=∠=∠=︒∴, 18060DCE ACD BCE ∠=︒-∠-∠=︒∵是的中点,N BE ∴,, CN BE ⊥302BCEECN BCN ∠∠=∠==∠︒∴, 90DCN DCE ECN ∠=∠+∠=∠︒设, AC a =∴ 12CM a =∵ 6AB =∴6BC a =-∴ cos )CN BCN BC a =∠⨯=-∴MN ===∴当时, 92a =MN【点睛】本题考查了等边三角形、等腰三角形、勾股定理、三角函数、二次函数的知识;解题的关键是熟练掌握等边三角形、等腰三角形、勾股定理、三角函数、二次函数的性质,从而完成求解.三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤推理过程) 19. (1)先填表,并在同一直角坐标系中画出二次函数和的图象; 2y x =()21y x =+x-3 -2 -1 0 1 2 32y x =__________________________________________()21y x =+____________ ______ ______ ______ ______ ______(2)分别写出它们顶点坐标.【答案】(Ⅰ)见解析;(2)二次函数的顶点坐标为,的顶点坐2y x =(0,0)2(1)y x =+标为 (1,0)-【解析】【分析】(1)列表,描点,连线画出图象即可; (2))根据二次函数图象即可写出顶点坐标; 【详解】解:(1)列表: x-3 -2 -1 0 1 2 32y x =941149()21y x =+ 41 0 14 9 16在同一直角坐标系中画出二次函数和的图象如图:2y x =()21y x =+(2)二次函数的顶点坐标为, 2y x =(0)0,的顶点坐标为; 2(1)y x =+(10)-△【点睛】本题考查了二次函数图象,利用描点法得出函数的图象,熟练掌握二次函数的性质是解题的关键;20. 如图,中,.ABC 90C ∠=︒(1)将绕点B 逆时针旋转90°,画出旋转后的三角形; ABC (2)若,.点A 旋转后的对应点为,求的长. 3BC =4AC =A 'A A '【答案】(1)见解析;(2)【解析】【分析】(1)利用旋转的性质画出点A 和点C 的对应点、,即可得到 A 'C 'BA C ''△(2)先利用勾股定理计算出AB=5,再利用旋转的性质得到,,5BA BA '==90A BA '∠=︒则可判断为等腰直角三角形,然后根据等腰直角三角形的性质求解 A BA '△【详解】解:(1)如图,为所作;BA C ''△(2)中,,,,ABC 90C ∠=︒ BC 3=AC 4=,5AB ∴===绕点B 逆时针旋转90°得到, ABC BA C ''△,, 5BA BA '∴==90A BA '∠=︒为等腰直角三角形, A BA '∴△.A A '∴==【点睛】本题考查了作图:旋转变换,勾股定理以及等腰三角形的判定和性质,熟练掌握旋转的性质是解题关键.21. 如图,的半径为,弦的长.O OA 50mm AB 50mm(Ⅰ)求的度数; OAB ∠(Ⅱ)求点O 到的距离.AB【答案】(Ⅰ);(Ⅱ) 60OAB ∠=︒【解析】【分析】(Ⅰ)连接OB ,根据等边三角形的判定定理得到为等边三角形,根据等边AOB 三角形的性质解答即可;(Ⅱ)过点O 作于C ,根据垂径定理求出AC ,根据勾股定理计算,得到答案; OC AB ⊥【详解】解:(Ⅰ)连接,OB,,50OA OB == 50AB =,OA OB AB ∴==为等边三角形,AOB ∴ ;60OAB ∴∠=︒(Ⅱ)过点O 作于C ,则, OC AB ⊥1252AC BC AB ===由勾股定理得,OC ==答:点O 到的距离为.AB 【点睛】本题考查了垂径定理,等边三角形的性质与判定,掌握相关的性质是解题的关键; 22. 二次函数(a ,b ,c 是常数)的自变量x 与函数值y 的部分对应值如下2y ax bx c =++表: x … -2 -1 0 1 2 … y…m-3-4-3…(Ⅰ)求这个二次函数的解析式; (Ⅱ)求m 的值;(Ⅲ)当时,求y 的最值(最大值和最小值)及此时x 的值.15x -≤≤【答案】(Ⅰ);(Ⅱ)m=5;(Ⅲ)x=1时,y 有最小值为-4,x=5时,y 2(1)4y x =--有最大值为12 【解析】【分析】(Ⅰ)利用待定系数法求函数解析式即可 (Ⅱ)直接将代入函数解析式即可求解2x =-(Ⅲ)利用表格中的数,在结合二次函数的增减性即可解答 【详解】解:(Ⅰ)设,2(1)4y a x =--将代入得,()0,3-2(1)4y a x =--,43a -=-解得,1a =∴这个二次函数的解析式为. 2(1)4y x =--(Ⅱ)当时,.2x =-2(21)45m =---=(Ⅲ)根据表格可知:函数的对称轴为,在对称轴左侧随的增大而减小,在对称1x =y x 轴右侧随的增大而增大,y x 自变量,15x -≤≤当时,y 有最小值为-4,∴1x =当时,y 有最大值为.∴5x =2(51)416412--=-=【点睛】本题考查了二次函数图像与性质及待定系数法求函数解析式,熟练掌握二次函数图像和性质是解题关键.23. 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,每个支干长出多少小分支? 若设每个支干长出x 个小分支.(Ⅰ)分析:根据问题中的数量关系,填表: ①主干的数目为______;②从主干中长出的支干的数目为______;(用含x 的式子表示) ③又从上述支干中长出的小分支的数目为______;(用含x 的式子表示) (Ⅱ)完成问题的求解.【答案】(Ⅰ)①1;②x;③;(Ⅱ)过程见解析,9个小分支 2x 【解析】【分析】(Ⅰ)根据主干为1及每个小支干长出个小分支即可得出个小问的结论 x (Ⅱ)根据主干支干数目支干数目支干数目,即可得出关于的一元二次方程,++⨯91=x 解方程取其正值即可【详解】解:(Ⅰ)根据题意得:①主干的数目为1; ②从主干中长出的支干的数目为x ;③又从上述支干中长出的小分支的数目为;2x故答案为:①1;②x;③; 2x (Ⅱ)依题意,得:, 2191x x ++=整理,得:,2900x x +-=解得:,(不合题意,舍去). 19x =210x =-所以每个支干长出9个小分支.【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题关键.24. 如图,已知平行四边形中,于点E ,以点B 为中心,取旋转角等于ABCD AE BC ⊥,把顺时针旋转,得到,连接.若,ABC ∠BAE △BA E ''V DA '60ADC ∠=︒50ADA '∠=︒.(Ⅰ)求的大小;DA E ''∠(Ⅱ)若延长和相交于点P ,求的大小? AE A E ''APA '∠(Ⅲ)连接,若,求的长度.PB AB a =PB【答案】(Ⅰ);(Ⅱ);(Ⅲ) 160︒60A PA '∠=︒PB =【解析】【分析】(Ⅰ)利用平行四边形的性质,得,180ADA DA B ''∠+∠=︒,再根据直角三角形两锐角互余,结合旋转的性质,可求出60ADC ABC ∠=∠=︒BA E ''∠的度数,进而可求出的度数DA E ''∠(Ⅱ)直接根据直角三角形中两锐角互余求解即可(Ⅲ)根据等腰三角形的性质,得,可证为直角三角形,30PA B PBA ''∠=∠=︒ABP △再利用三角函数解直角三角形即可求解【详解】解:(Ⅰ)∵四边形是平行四边形,ABCD ,,60ADC ABC ∴∠=∠=︒//AD BC, 180ADA DA B ''∴∠+∠=︒, 130DA B '∴∠=︒,AE BC ⊥ ,90AEB ∴∠=︒,30BAE =∴∠︒∵把顺时针旋转,得到,BAE △BA E ''V ,, 30BA E BAE ''∴∠=∠=︒AB A B '=;160DA E DA B BA E '''''∴∠=∠+∠=︒(Ⅱ),,90A EP '∠=︒ 30PA E '∠=︒;60A PA '∴∠=︒(Ⅲ)连接,PB,,30BAP ∠=︒ 90AEB =︒∠AB a =, 2AB BE ∴=, 2a BE ∴=AB A B '= , 22a aA E AB BE a BE ''∴=-=-== 30BA E BAP ''∠=∠=︒ 30PA B PBA ''∴∠=∠=︒ 60ADC ABC ∠=∠=︒90ABP ABC PBA '∴∠=∠+∠=︒,PB AB ∴⊥在中, ∴Rt ABP tan PBBAP AB∠=PBa=.PB ∴=【点睛】本题考查了平行四边形的性质,旋转的性质,直角三角形的性质,以及解直角三角形,灵活运用这些性质是解题关键.25. 如图,是等腰直角三角形,,,点P 是边上一动点,ABC 90A ∠=︒4BC =ABC 沿的路径移动,过点P 作于点D ,设,的面积为y .B AC →→PD BC ⊥BD x =BDP△(1)当时,求y 的值;1x =(2)在这一变化过程中,写出y 关于x 的函数解析式及x 的取值范围; (3)当x 取何范围时,(直接写出结果即可). 1322y <<【答案】(1);(2);(3)x 的取值范围为:12y =221x (0x 2)21x 2x(2x 4)2y ⎧≤≤⎪⎪=⎨⎪-+<≤⎪⎩或1x <<32x <<+【解析】【分析】(Ⅰ)是等腰直角三角形,则,则为等腰直角三ABC 45B C ∠=∠=︒PBD △角形,故,则,即可求解 BD PD x ==21122y BD PD x =⨯⨯=(Ⅱ)当点在上运动时,由(1)知,,当点在上运动时,P AB 212y x =P AB ,即可求解;2111(4)2222y BD PD x x x x =⨯⨯=⨯-=-+(Ⅲ)①当时,则,②当时,则,进而求解即02x ≤≤212y x =24x <<21x 2x 2y =-+可;【详解】解:(Ⅰ)是等腰直角三角形,则,ABC 45B C ∠=∠=︒因为PD⊥BC ,则为等腰直角三角形,PBD △故,BD PD x ==则, 21122y BD PD x =⨯⨯=当时,; 1x =12y =(Ⅱ)当点在上运动时,P AB 由(1)知,, 212y x =当点在上运动时,P AC 同理可得为等腰直角三角形,则, PDC △4CD BC BD x PD =-=-=则, 2111(4)2222y BD PD x x x x =⨯⨯=⨯-=-+故; 221x (0x 2)21x 2x(2x 4)2y ⎧≤≤⎪⎪=⎨⎪-+<≤⎪⎩(Ⅲ)①当时,02x ≤≤则, 212y x =当时,即,解得(舍去负值), 12y =21122y x ==1x =±当时,即,解得(舍去负值), 32y =21322y x ==x =故;1x <<②当时,24x <<则, 21x 2x 2y =-+当时,即=,解得: , 12y =21x 2x 2y=-+12)1222x x ==-舍去当时,即,解得: , 32y =213222x y x +=-=()1231x x ==,舍去故;32x <<+综上,x 的取值范围为:或.1x <<32x <<【点睛】本题是三角形的综合题,涉及到二次函数的基本性质、等腰三角形的性质、面积的计算等,要注意分类讨论,避免遗漏;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河西区2020—2021学年度第一学期高二年级期末质量调查数学试卷一、选择题:本大题共9小题,每小题4分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 数列1,-12,4-,14,…的一个通项公式为( ) A. 112n -⎛⎫-⎪⎝⎭B. 2n⎛- ⎝⎭C. ()112n n -⎛⎫-⎪ ⎪⎝⎭D. ()1112n n -+⎛-⎝⎭【答案】D 【解析】 【分析】可知该数列是一个以1为首项,2-为公比的等比数列,即可求出通项公式. 【详解】根据数列可知,该数列是一个以1为首项,所以该数列的通项公式为()()()11121+11111222n n n n n ----⎛⎛⎫⎛⨯-=-⨯-⨯=-⨯ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选:D.2. 设函数2()1f x x =-,当自变量x 由1变到1.1时,函数的平均变化率是( ) A. 2.1 B. 0.21 C. 1.21 D. 0.121【答案】A 【解析】 【分析】根据平均变化率的公式求解即可.【详解】 1.110.1x ∆=-=,22(1.1)(1) 1.11(11)0.21y f f ∆=-=---= 所以函数2()1f x x =-在区间[1,1.1]上的平均变化率为(1.1)(1)0.212.10.1y f f x x ∆-===∆∆.故选:A3. 已知数列{}n a 满足12a =,112n n a a -=-,则5a =( )A.65B.76C.54D.56【答案】A 【解析】 【分析】根据递推关系依次求出2345,,,a a a a 即可.【详解】12a =,112n n a a -=-,∴211322a a =-=,321423a a =-=,431524a a =-=,541625a a =-=. 故选:A.4. 记n S 为等差数列{}n a 的前n 项和,若4524a a +=,648S =,则{}n a 的公差为( ) A. 1 B. 2C. 4D. 8【答案】C 【解析】 【分析】根据等差数列的通项公式与求和公式,列出关于首项与公差的方程组,解方程组即可得到公差.【详解】设等差数列{}n a 的公差为d , 则45111342724a a a d a d a d +=+++=+=,611656615482S a d a d ⨯=+=+=, 联立11272461548a d a d +=⎧⎨+=⎩,解得4d =. 故选:C.【点睛】本题考查了等差数列通项公式与求和公式的简单应用,注意计算,属于基础题.5. 已知函数()y f x=,其导函数()y f x'=的图象如图,则对于函数()y f x=的描述正确的是()A. 在(),0-∞上为减函数B. 在0x=处取得最大值C. 在()4,+∞上为减函数D. 在2x=处取得最小值【答案】C【解析】分析:根据函数f(x)的导函数f′(x)的图象可知f′(0)=0,f′(2)=0,f′(4)=0,然后根据单调性与导数的关系以及极值的定义可进行判定即可.详解:根据函数f(x)的导函数f′(x)的图象可知:f′(0)=0,f′(2)=0,f′(4)=0当x<0时,f′(x)>0,f(x)递增;当0<x2时,f′(x)<0,f(x)递减;当2<x<4时,f′(x)>0,f(x)递增;当x>4时,f′(x)<0,f(x)递减.可知C正确,A错误;由极值的定义可知,f(x)在x=0处函数f(x)取到极大值,x=2处函数f(x)的极小值点,但极大值不一定为最大值,极小值不一定是最小值;可知B、D错误.故选C.点睛:由导函数图象推断原函数的性质,由f′(x)>0得增区间,由f′(x)<0得减区间,由f′(x)=0得到的不一定是极值点,需判断在此点左右f′(x)的符号是否发生改变.6. 我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯.”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层的灯数是()A. 1B. 2C. 3D. 6【答案】C【解析】 【分析】可知每一层灯数形成以2为公比的等比数列{}n a ,根据7381S =即可求出. 【详解】设顶层的灯数是1a ,则每一层灯数形成以2为公比的等比数列{}n a , 由题可得()7171238112a S -==-,解得13a =,故塔的顶层的灯数是3. 故选:C. 7. 函数()212cos x y e x x -+=-+的导数为( )A. ()()21222sin (21)cos x y ex x x x x -+⎡=-+--'⎣B. ()()21222cos (21)sin x y ex x x x x -+⎡⎤'=--+--⎣⎦C. ()()21222sin (21)cos x y e x x x x x -+⎡⎤'=--+--⎣⎦D. ()()21222cos (21)sin x y ex x x x x -+⎡⎤'=-+--⎣⎦【答案】B 【解析】 【分析】由导数运算法则可求出. 【详解】()212cos x y e x x -+=-+,()()()212212cos +cos x x e x x e x y x -+-+''⎡⎤-+-+'⎣∴⎦= ()()()2122122cos sin 2+1x x e x x e x x x -+-+=--+--+⋅-()()()2122cos +2+1si 2n x e x x x x x -+⎡⎤=--+--+⎣⎦()()21222cos (21)sin x e x x x x x -+⎡⎤=--+--⎣⎦.故选:B.8. 已知等比数列的首项为-1,前n 项和为n S ,若1053132S S =,则公比q =( )A. 2B. -2C.12D. 12-【答案】D 【解析】 【分析】根据等比数列前n 项和公式,可求得105,S S 表达式,结合题干条件,即可求得q 的值.【详解】当公比1q =时,1052S S =,不满足题意,当1q ≠时,101011q S q -=-,5511q S q-=-, 所以1051055131111321q S q q q S q--==+=--,解得12q =-, 故选:D9. 已知函数()ln ,111,14x x f x x x >⎧⎪=⎨+≤⎪⎩,()g x ax =则方程()()g x f x =恰有两个不同的实根时,实数a 的取值范围是( ). A. 10,e ⎛⎫ ⎪⎝⎭B. 11,4e ⎡⎫⎪⎢⎣⎭C. 10,4⎛⎤ ⎥⎝⎦D. 1,e 4⎛⎫ ⎪⎝⎭【答案】B 【解析】 【分析】作出函数()f x 与()g x 的图象,讨论交点个数可求出a 的取值范围. 【详解】作出函数()f x 的图象,见下图. 若()g x 与()ln 1y x x =>相切,求导得1y x'=,设切点为()00,x y ,则00ln y x =,切线斜率为01x ,即切线方程为:()0001ln y x x x x -=-,该切线过原点,则()00010ln 0x x x -=-,解得0e x =,此时1e a =,显然()1eg x x =与()f x 的图象只有一个交点,即方程()()g x f x =只有一个实根;若114ea ≤<,直线()g x 与()f x 的图象在1x ≤时无交点,在1x >时有2个交点,符合题意; 若104a <<,直线()g x 与()f x 的图象在1x ≤时有1个交点,在1x >时有2个交点,不符合题意;若0a ≤,直线()g x 与()f x 的图象在1x ≤时有1个交点,在1x >时无交点,不符合题意; 若1e>a ,,直线()g x 与()f x 的图象至多有一个交点,不符合题意. 所以只有114ea ≤<符合题意. 故选:B.【点睛】本题考查了方程的解与函数图象的关系,考查了曲线的切线方程的求法,利用数形结合的数学方法是解决本题的关键,属于难题.二、填空题:本大题共6小题,每小题5分,共30分.请将答案填在题中横线上.10. 在等差数列{}n a 中,n S 为其前n 项的和,若412S =,840S =,则16S =________. 【答案】144 【解析】 【分析】利用等差数列的前n 项和公式求出首项和公差,即可求解. 【详解】设等差数列的公差为d ,则4181434+122878+402S a d S a d ⨯⎧==⎪⎪⎨⨯⎪==⎪⎩,解得13,12a d ==,163161516+114422S ⨯∴=⨯⨯=.故答案为:144. 11. 函数ln ()x f x x=,其导函数为函数()'f x ,则()f e '=________. 【答案】0 【解析】 【分析】根据()f x 解析式,可求得()'f x 解析式,代入数据,即可得答案.【详解】因为ln ()(0)x f x x x=≠,所以2221ln (ln )ln 1ln ()x xx x x x x x f x x x x ⋅-''--'===, 所以21ln ()0ef e e-'==, 故答案:012. 已知数列{}n a 的通项公式21n a n n=+,n S 为其前n 项的和,则99S =________. 【答案】99100【解析】 【分析】根据数列{}n a 的通项公式21111n a n n n n ==-++,利用裂项相消法求解. 【详解】因为数列{}n a 的通项公式21111n a n n n n ==-++, 所以99111111991122399100100100S ⎛⎫⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 故答案:9910013. 函数3()3f x x x =-的单调递增区间是________. 【答案】()1,1- 【解析】 【分析】求出函数的导数,令()0f x '>即可求出.【详解】3()3f x x x =-,()233f x x '∴=-,令()0f x '>,即2330x ->,解得11x -<<,()f x ∴的单调递增区间是()1,1-.故答案为:()1,1-. 14. 已知数列{}n a 的通项公式为3217n n a n -=-,前n 项和为n S ,则n S 取得最小值时n 的值为_________. 【答案】8 【解析】 【分析】求出数列在n 的不同取值范围的正负判断出n S 的单调性可求出. 【详解】令30217n n a n -=≥-,解得3n ≤或172n ≥,∴当3n ≤时,0n a ≥,n S 单调递增,当47n ≤≤时,0n a <,n S 单调递减, 当8n ≥时,0n a >,n S 单调递增, 所以n S 取得最小值时n 的值为8. 故答案为:8.【点睛】本题考查数列前n 项和的最值的求法,解题的关键是根据数列的正负判断n S 的单调性.15. 将一个边长为6的正方形铁片的四角截去四个边长为x 的小正方形,做成一个无盖方盒.当方盒的容积V 取得最大值时,x 的值为_________. 【答案】1 【解析】 【分析】由题可得该方盒的容积()32424+36V x x x x =-,03x <<,利用导数判断其单调性可求出最值.【详解】由题可得03x <<,可知该方盒的底面是一个边长为62x -, 则该方盒的容积()()23262424+36V x x x x x x =-⋅=-,03x <<,()()()21248+361213V x x x x x '∴=-=--,则当()0,1x ∈时,()0V x '>,()V x 单调递增, 当()1,3x ∈时,()0V x '<,()V x 单调递减,∴当1x =时,()()max 116V x V ==,故当方盒的容积V 取得最大值时,x 的值为1. 故答案为:1.三、解答题:本大题共3小题,共34分.解答应写出文字说明,证明过程或演算步骤.16. 已知函数31()443f x x x =-+. (1)求()f x 的极值; (2)求()f x 在[]0,3上的最值. 【答案】(1)极大值为283,极小值为43-;(2)最大值为4,最小值为43-.【解析】 【分析】(1)求导,解对应的不等式,可得函数的单调性,从而可知函数的极值. (2)根据(1)的结果,再计算端点值,比较大小,即可得出最值. 【详解】(1)()31443f x x x =-+,()()()2422f x x x x =-=+-'令()0f x '=,解得2x =-或2x =,当x 变化时,()'f x ,()f x 的变化情况如下表:故当2x =-时,()f x 取得极大值,()2823f -=;当2x =时,()f x 取得极小值,()8428433f =-+=-;(2)由(1)可知()f x 的极大值为283,极小值为43-,又()04f =,()391241f =-+=,因为4143-<<,所以()f x 在[]0,3上的最大值为4,最小值为43-. 【点睛】思路点睛:本题考查利用导数求函数的极值与闭区间上的最值,设函数()f x 在[],a b 上连续,在(),a b 内可导,求()f x 在[],a b 上的最大值和最小值的步骤如下: ①求函数()y f x =在(),a b 内的极值;②将函数()y f x =)的各极值与端点处的函数值()(),f a f b 比较,其中最大的一个为最大值,最小的一个为最小值. 17. 已知函数()()ln 2xf x e x =-+.(1)求()f x 在()()0,0f 处的切线方程; (2)求证:()0f x >. 【答案】(1)11ln 22y x =+-;(2)证明见解析. 【解析】 【分析】(1)求出()f x 的导函数,由()0k f '=,可得答案.(2)求出()f x 的导函数,讨论出函数()f x 的单调性,得出其最小值,可证明. 【详解】(1)解:1()2xf x e x '=-+, 当0x =时,()102k f '==, 又()01ln 2f =-,所以切线方程为()11ln 22y x --=,即11ln 22y x =+-.(2)解:1()2x f x e x '=-+在区间()2,-+∞上单调递增, 又()10f '-<,()00f '>,故()0f x '=在区间()2,-+∞上有唯一实根0x ,且()01,0x ∈-,当()02,x x ∈-时,()0f x '<;当()0,x x ∈+∞时,()0f x '>,从而当0x x =时,()f x 取得最小值.由()00f x '=,得0012x e x =+,()00ln 2x x +=-, 故()()20000011()022x f x f x x x x +≥=+=>++. 【点睛】本题考查求函数在某点出的切线方程和利用导数证明不等式.解答本题的关键是由1()2x f x e x '=-+在区间()2,-+∞上单调递增,得出()0f x '=在区间()2,-+∞上有唯一实根0x ,从而得出()f x 的单调区,即()()20000011()22x f x f x x x x +≥=+=++,属于中档题. 18. 对于数列{}n a ,{}n b ,n S 为数列{}n a 是前n 项和,且1(1)n n n S n S a n +-+=++,111a b ==,132,n n b b n N *+=+∈.(1)求数列{}n a ,{}n b 的通项公式;(2)令2()(1)n n n a n c n b +=+,求数列{}n c 的前n 项和n T . 【答案】(1)2n a n =,1231n n b -=⋅-;(2)11525443n n n T -+=-⋅. 【解析】试题分析: (1)先根据和项与通项关系,将条件转化为项之间递推关系:121n n a a n +=++,再根据叠加法求数列{}n a 的通项公式;而求{}n b 通项公式,需变形构造一个等比数列{1}n b +,这是由于132n n b b +=+可变形得()1131n n b b ++=+,然后通过求等比数列通项公式,转化求{}n b 通项公式,(2)由于113n n n c -+=,所以利用错位相减法求和,求和时注意错位相减,减式中项的符号变化,合并时项数的确定,最后结果要除以1.q -试题解析:(1))因为()11n n n S n S a n +-+=++,所以121n n a a n +=++, 所以()()()112211n n n n n a a a a a a a a ---=-+-++-+ ()()212331n n =-+-+++ ()2112n n -+= 2n =,所以数列{}n a 的通项公式为2n a n =,由132n n b b +=+,可得()1131n n b b ++=+,所以数列{1}n b +是首项为112b +=,公比为3的等比数列,所以1123n n b -+=⋅,所以数列{}n b 的通项公式为1231n n b -=⋅-.(2)由(1)可得()21121233nn n n n n c n --++==⋅, 所以01221234133333n n n n n T --+=+++++ ①, 0013223341333333n n n n n T --⨯+=+++++ ②, ②-①得122111111111115253261613333322313n n n n n n n n n T ------+++⎛⎫=++++⋯+-=+-=- ⎪⋅⎝⎭-, 所以11525443n n n T -+=-⋅.。
