数据结构 第七章-图2.ppt
合集下载
第7章图_数据结构

v4
11
2013-8-7
图的概念(3)
子图——如果图G(V,E)和图G’(V’,E’),满足:V’V,E’E 则称G’为G的子图
2 1 4 3 5 6 3 5 6 1 2
v1 v2 v4 v3 v2
v1 v3 v4
v3
2013-8-7
12
图的概念(4)
路径——是顶点的序列V={Vp,Vi1,……Vin,Vq},满足(Vp,Vi1),
2013-8-7 5
本章目录
7.1 图的定义和术语 7.2 图的存储结构
7.2.1 数组表示法 7.2.2 邻接表 ( *7.2.3 十字链表 7.3.1 深度优先搜索 7.3.2 广度优先搜索 7.4.1 图的连通分量和生成树 7.4.2 最小生成树
*7.2.4 邻接多重表 )
7.3 图的遍历
连通树或无根树
无回路的图称为树或自由树 或无根树
2013-8-7
18
图的概念(8)
有向树:只有一个顶点的入度为0,其余 顶点的入度为1的有向图。
V1 V2
有向树是弱 连通的
V3
V4
2013-8-7
19
自测题
7. 下列关于无向连通图特性的叙述中,正确的是
2013-8-7
29
图的存贮结构:邻接矩阵
若顶点只是编号信息,边上信息只是有无(边),则 数组表示法可以简化为如下的邻接矩阵表示法: typedef int AdjMatrix[MAXNODE][MAXNODE];
*有n个顶点的图G=(V,{R})的邻接矩阵为n阶方阵A,其定 义如下:
1 A[i ][ j ] 0
【北方交通大学 2001 一.24 (2分)】
王道数据结构 第七章 查找思维导图-高清脑图模板
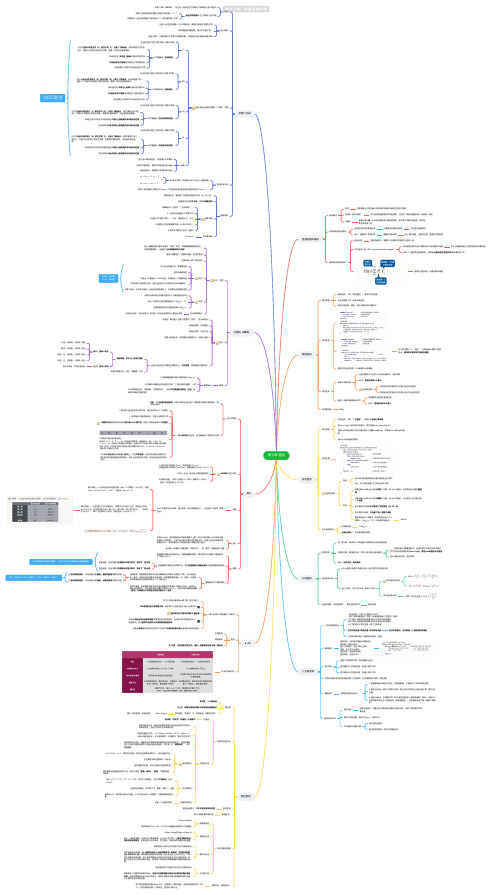
每次调整的对象都是“最小不平衡子树”
插入操作
在插入操作,只要将最小不平衡子树调整平衡,则其他祖先结点都会恢复平衡
在A的左孩子的左子树中插入导致不平衡
由于在结点A的左孩子(L)的左子树(L)上插入了新结点,A的平衡因子由1增
至2,导致以A为根的子树失去平衡,需要一次向右的旋转操作。
LL
将A的左孩子B向右上旋转代替A成为根节点 将A结点向右下旋转成为B的右子树的根结点
RR平衡旋转(左单旋转)
而B的原左子树则作为A结点的右子树
在A的左孩子的右子树中插入导致不平衡
由于在结点A的左孩子(L)的右子树(R)上插入了新结点,A的平衡因子由1增
LR
至2,导致以A为根的子树失去平衡,需要两次旋转操作,先左旋转再右旋转。
将A的左孩子B的右子树的根结点C向左上旋转提升至B结点的位置
本质:永远保证 子树0<关键字1<子树1<关键字2<子树2<...
当左兄弟很宽裕时,用当前结点的前驱、前驱的前驱来填补空缺 当右兄弟很宽裕时,用当前结点的后继、后继的后继来填补空缺
兄弟够借。若被删除关键字所在结点删除前的关键字个数低于下限,且与此结点 右(或左)兄弟结点的关键字还很宽裕,则需要调整该结点、右(或左)兄弟结 点及其双亲结点及其双亲结点(父子换位法)
LL平衡旋转(右单旋转)
而B的原右子树则作为A结点的左子树
在A的右孩子的右子树中插入导致不平衡
由于在结点A的右孩子(R)的右子树(R)上插入了新结点,A的平衡因子由-1
减至-2,导致以A为根的子树失去平衡,需要一次向左的旋转操作。
RR
将A的右孩子B向左上旋转代替A成为根节点 将A结点向左下旋转成为B的左子树的根结点
《数据结构图论部分》PPT课件
Page 4
2020/11/24
哥尼斯堡七桥问题
能否从某个地方出发,穿过所有的桥仅一次 后再回到出发点?
Page 5
2020/11/24
七桥问题的图模型
欧拉回路的判定规则:
1.如果通奇数桥的地方多于
C
两个,则不存在欧拉回路;
2.如果只有两个地方通奇数
桥,可以从这两个地方之一
A
B 出发,找到欧拉回路;
V4 是有向边,则称该图为有向图。
Page 9
2020/11/24
简单图:在图中,若不存在顶点到其自身的边,且同 一条边不重复出现。
V1
V2
V3
V4
V5
非简单图
V1
V2
V3
V4
V5
非简单图
V1
V2
V3
V4
V5
简单图
❖ 数据结构中讨论的都是简单图。
Page 10
2020/11/24
图的基本术语
邻接、依附
DeleteVex(&G, v); 初始条件:图 G 存在,v 是 G 中某个顶点。 操作结果:删除 G 中顶点 v 及其相关的弧。
Page 34
2020/11/24
InsertArc(&G, v, w); 初始条件:图 G 存在,v 和 w 是 G 中两个顶点。 操作结果:在 G 中增添弧<v,w>,若 G 是无向的,则还
Page 2
2020/11/24
• 知识点
– 图的类型定义 – 图的存储表示 – 图的深度优先搜索遍历和广度优先搜索遍历 – 无向网的最小生成树 – 拓扑排序 – 关键路径 – 最短路径
Page 3
数据结构第七章:图

例
a c G1
b d
vexdata firstarc adjvex next 1 4 ^ a 2 3 4 b c d 1 1 3 ^ ^ ^
19
7.3 图的遍历
深度优先遍历(DFS) 深度优先遍历
方法:从图的某一顶点 出发,访问此顶点; 方法:从图的某一顶点V0出发,访问此顶点;然后依 次从V 的未被访问的邻接点出发,深度优先遍历图, 次从 0的未被访问的邻接点出发,深度优先遍历图, 直至图中所有和V 相通的顶点都被访问到; 直至图中所有和 0相通的顶点都被访问到;若此时图 中尚有顶点未被访问, 中尚有顶点未被访问,则另选图中一个未被访问的顶 点作起点,重复上述过程, 点作起点,重复上述过程,直至图中所有顶点都被访 问为止。 问为止。
ω ij , 若(v i , v j )或 < v i , v j >∈ E(G) A[i, j ] = 0,其它
11
例
1 3
5
2
8 4 7 5 1 6 3 4 2
0 5 7 0 3
5 0 0 4 8
7 0 0 2 1
0 4 2 0 6
3 8 1 6 0
12
关联矩阵——表示顶点与边的关联关系的矩阵 表示顶点与边的关联关系的矩阵 关联矩阵
1
7.1 图的定义和术语
是由两个集合V(G)和E(G)组成的 组成的, 图(Graph)——图G是由两个集合 图 是由两个集合 和 组成的 记为G=(V,E) 记为
其中: 其中:V(G)是顶点的非空有限集 是顶点的非空有限集 E(G)是边的有限集合,边是顶点的无序对或有序对 是边的有限集合, 是边的有限集合
有向图——有向图 是由两个集合 有向图G是由两个集合 有向图 有向图 是由两个集合V(G)和E(G)组成的 和 组成的
北京理工大学数据结构图课件

A
B C D
第 5 页
E
7.1 图的定义与术语
3、无向图——无向图G是由两个集合V(G)和 E(G)组成的。 其中:V(G)是顶点的非空有限集。 E(G)是边的有限集合,边是顶点的 无序对,记为 (v,w) 或 (w,v),并且 (v,w)=(w,v)。
第 6 页
7.1 图的定义与术语
例如:
G2 = <V2,E2> V2 = { v0 ,v1,v2,v3,v4 } E2 = { (v0,v1), (v0,v3), (v1,v2), (v1,v4), (v2,v3), (v2,v4) }
V5
第 15 页
7.1 图的定义与术语
非 连 通 图
V0
V1
V2
V3
V0
V1 V3
V2
强连通分量
第 16 页
7.1 图的定义与术语
7、生成树
包含无向图 G 所有顶点的极小连通子图称为G生 成树。 极小连通子图意思是:该子图是G的连通子图, 在该子图中删除任何一条边,子图不再连通。
V0 V2 V3 V4 V3 连通图G1 V1 V0 V1 连通 所有顶点 V4 无回路
第 22 页
7.2 图的存储结构 3、有向图的逆邻接表 顶点:用一维数组存储(按编号顺序) 以同一顶点为终点的弧:用线性链表存储。
vexdata V0 V1 0 1 v0 v1 v2
v3
firstarc 3 0 0 ^ ^
V2
V3
2 3
^
^
2
章 类似于有向图的邻接表,所不同的是: 以同一顶点为终点弧:用线性链表存储
Boolean visited[MAX]; // 访问标志数组
B C D
第 5 页
E
7.1 图的定义与术语
3、无向图——无向图G是由两个集合V(G)和 E(G)组成的。 其中:V(G)是顶点的非空有限集。 E(G)是边的有限集合,边是顶点的 无序对,记为 (v,w) 或 (w,v),并且 (v,w)=(w,v)。
第 6 页
7.1 图的定义与术语
例如:
G2 = <V2,E2> V2 = { v0 ,v1,v2,v3,v4 } E2 = { (v0,v1), (v0,v3), (v1,v2), (v1,v4), (v2,v3), (v2,v4) }
V5
第 15 页
7.1 图的定义与术语
非 连 通 图
V0
V1
V2
V3
V0
V1 V3
V2
强连通分量
第 16 页
7.1 图的定义与术语
7、生成树
包含无向图 G 所有顶点的极小连通子图称为G生 成树。 极小连通子图意思是:该子图是G的连通子图, 在该子图中删除任何一条边,子图不再连通。
V0 V2 V3 V4 V3 连通图G1 V1 V0 V1 连通 所有顶点 V4 无回路
第 22 页
7.2 图的存储结构 3、有向图的逆邻接表 顶点:用一维数组存储(按编号顺序) 以同一顶点为终点的弧:用线性链表存储。
vexdata V0 V1 0 1 v0 v1 v2
v3
firstarc 3 0 0 ^ ^
V2
V3
2 3
^
^
2
章 类似于有向图的邻接表,所不同的是: 以同一顶点为终点弧:用线性链表存储
Boolean visited[MAX]; // 访问标志数组
数据结构(C语言版)_第7章 图及其应用

(1)创建有向图邻接表 (2)创建无向图的邻接表
实现代码详见教材P208
7.4 图的遍历
图的遍历是对具有图状结构的数据线性化的过程。从图中任 一顶点出发,访问输出图中各个顶点,并且使每个顶点仅被访 问一次,这样得到顶点的一个线性序列,这一过程叫做图的遍 历。
图的遍历是个很重要的算法,图的连通性和拓扑排序等算法 都是以图的遍历算法为基础的。
V1
V1
V2
V3
V2
V3
V4
V4
V5
图9.1(a)
图7-2 图的逻辑结构示意图
7.2.2 图的相关术语
1.有向图与无向图 2.完全图 (1)有向完全图 (2)无向完全图 3.顶点的度 4.路径、路径长度、回路、简单路径 5.子图 6.连通、连通图、连通分量 7.边的权和网 8.生成树
2. while(U≠V) { (u,v)=min(wuv;u∈U,v∈V-U); U=U+{v}; T=T+{(u,v)}; }
3.结束
7.5.1 普里姆(prim)算法
【例7-10】采用Prim方法从顶点v1出发构造图7-11中网所对 应的最小生成树。
构造过程如图7-12所示。
16
V1
V1
V2
7.4.2 广度优先遍历
【例7-9】对于图7-10所示的有向图G4,写出从顶点A出发 进行广度优先遍历的过程。
访问过程如下:首先访问起始顶点A,再访问与A相邻的未被 访问过的顶点E、F,再依次访问与E、F相邻未被访问过的顶 点D、C,最后访问与D相邻的未被访问过的顶点B。由此得到 的搜索序列AEFDCB。此时所有顶点均已访问过, 遍历过程结束。
【例7-1】有向图G1的逻辑结构为:G1=(V1,E1) V1={v1,v2,v3,v4},E1={<v1,v2>,<v2,v3>,<v2,v4>,<v3,v4>,<v4,v1>,<v4,v3>}
实现代码详见教材P208
7.4 图的遍历
图的遍历是对具有图状结构的数据线性化的过程。从图中任 一顶点出发,访问输出图中各个顶点,并且使每个顶点仅被访 问一次,这样得到顶点的一个线性序列,这一过程叫做图的遍 历。
图的遍历是个很重要的算法,图的连通性和拓扑排序等算法 都是以图的遍历算法为基础的。
V1
V1
V2
V3
V2
V3
V4
V4
V5
图9.1(a)
图7-2 图的逻辑结构示意图
7.2.2 图的相关术语
1.有向图与无向图 2.完全图 (1)有向完全图 (2)无向完全图 3.顶点的度 4.路径、路径长度、回路、简单路径 5.子图 6.连通、连通图、连通分量 7.边的权和网 8.生成树
2. while(U≠V) { (u,v)=min(wuv;u∈U,v∈V-U); U=U+{v}; T=T+{(u,v)}; }
3.结束
7.5.1 普里姆(prim)算法
【例7-10】采用Prim方法从顶点v1出发构造图7-11中网所对 应的最小生成树。
构造过程如图7-12所示。
16
V1
V1
V2
7.4.2 广度优先遍历
【例7-9】对于图7-10所示的有向图G4,写出从顶点A出发 进行广度优先遍历的过程。
访问过程如下:首先访问起始顶点A,再访问与A相邻的未被 访问过的顶点E、F,再依次访问与E、F相邻未被访问过的顶 点D、C,最后访问与D相邻的未被访问过的顶点B。由此得到 的搜索序列AEFDCB。此时所有顶点均已访问过, 遍历过程结束。
【例7-1】有向图G1的逻辑结构为:G1=(V1,E1) V1={v1,v2,v3,v4},E1={<v1,v2>,<v2,v3>,<v2,v4>,<v3,v4>,<v4,v1>,<v4,v3>}
第七章 图

vertex firstin firstout
顶点结点结构
顶点值域 指针域 指针域
tailvex headvex hlink
tlink
info
弧结点结构
弧尾结点 弧头结点 指针域 指针域 弧上信息
A B
C
在十字链表中容易求 得顶点的出度和入度
0 A
0 1
∧
2 0∧∧
1 B 2 C
2 1∧
0 2∧∧
图的遍历方法有两种: 深度优先搜索和广度优先搜索
7.3.1 深度优先搜索
按照深度方向搜索 ,它类似于树的先根遍历。 深度优先算法的基本思想是: (1)从图中某个顶点v0出发,首先访问v0。 (2)找出刚访问过的顶点vi的第一个未被访问 的邻接点,然后访问该顶点。重复此步骤,直 到当前的顶点没有未被访问的邻接点为止。 (3)返回前一个访问过的顶点,找出该顶点的 下一个未被访问的邻接点,访问该顶点。转2。
一、图的数组(邻接矩阵)存储表示 二、图的邻接表存储表示
三、有向图的十字链表存储表示 四、无向图的邻接多重表存储表示
一、图的数组(邻接矩阵)表示法
所谓邻接矩阵(Adjacency Matrix)的存 储结构,就是用一维数组存储图中顶点的信息, 用矩阵表示图中各顶点之间的邻接关系。假设 图G=(V,E)有n个确定的顶点,即V= {v0,v1,…,vn-1},则表示G中各顶点相邻关系为一 个n×n的矩阵
遍 历
DFSTraverse(G, v, Visit());
//从顶点v起深度优先遍历图G,并对每 //个顶点调用函数Visit一次且仅一次。
BFSTraverse(G, v, Visit());
//从顶点v起广度优先遍历图G,并对每 //个顶点调用函数Visit一次且仅一次。
顶点结点结构
顶点值域 指针域 指针域
tailvex headvex hlink
tlink
info
弧结点结构
弧尾结点 弧头结点 指针域 指针域 弧上信息
A B
C
在十字链表中容易求 得顶点的出度和入度
0 A
0 1
∧
2 0∧∧
1 B 2 C
2 1∧
0 2∧∧
图的遍历方法有两种: 深度优先搜索和广度优先搜索
7.3.1 深度优先搜索
按照深度方向搜索 ,它类似于树的先根遍历。 深度优先算法的基本思想是: (1)从图中某个顶点v0出发,首先访问v0。 (2)找出刚访问过的顶点vi的第一个未被访问 的邻接点,然后访问该顶点。重复此步骤,直 到当前的顶点没有未被访问的邻接点为止。 (3)返回前一个访问过的顶点,找出该顶点的 下一个未被访问的邻接点,访问该顶点。转2。
一、图的数组(邻接矩阵)存储表示 二、图的邻接表存储表示
三、有向图的十字链表存储表示 四、无向图的邻接多重表存储表示
一、图的数组(邻接矩阵)表示法
所谓邻接矩阵(Adjacency Matrix)的存 储结构,就是用一维数组存储图中顶点的信息, 用矩阵表示图中各顶点之间的邻接关系。假设 图G=(V,E)有n个确定的顶点,即V= {v0,v1,…,vn-1},则表示G中各顶点相邻关系为一 个n×n的矩阵
遍 历
DFSTraverse(G, v, Visit());
//从顶点v起深度优先遍历图G,并对每 //个顶点调用函数Visit一次且仅一次。
BFSTraverse(G, v, Visit());
//从顶点v起广度优先遍历图G,并对每 //个顶点调用函数Visit一次且仅一次。
数据结构(C语言版CHAP7(2)

V1
AOE网
a0
a7
V2 V6
a2 a3
V3
a5
a8
V4
V5
a1
V7 a 6 V 8 a4
结束
第 15 页
7.4
有向无环图的应用
为计算完成整个工程至少需要多少时间,需将每一子工程所需的时 间作为权值赋给AOE网的各边(就象哈夫曼树给结点赋权值一样)。 AOE网与关键路径部分,不作为课程要求。
V1
a0
V0
V1
V3
V4
V5
V6
结束
第 3 页
7.4
有向无环图的应用
2 AOE网( activity on edge net ) 用边表示活动,顶点表示事件的有向图称为AOE网。 事件发生表示以 该事件为起点的活动可以开始,以该事件为终点的活动已经结束。
a1 a2 a3 a4 a5 a6 分别表示例1中的7个子工程V0、V1、V2、V3、V4、V5、V6。a7 a8
结束
第 14 页
7.4
三 AOE网与关键路径
对工程人们关心两类问题:
有向无环图的应用
1)工程能否顺序进行,即工程流程是否“合理” 2)完成整项工程至少需要多少时间,哪些子工程是影响工程进度的关键 子工程? 为解决第二类问题,通常可用称为AOE网的有向图表示工程流程 用边表示活动,顶点表示事件。 事件发生表示以该事件为起点的活动可 以开始,以该事件为终点的活动已经结束。
结束
第 12 页
7.4
有向无环图的应用
4)拓扑排序算法 Status TopologicalSort(ALGraph G) { //有向图G采用邻接表存储结构。 //若G无回路,则输出G的顶点的一个拓扑序列并返回OK,否则ERROR。 FindInDegree(G, indegree); //求各顶点入度indegree[0..vernum-1] InitStack(S); For(i=0; i<G. vexnum; ++i) //建入度为0的顶点栈S indegree 0 0 if (! Indegree[i]) Push(S, i); //入度为0顶点的编号进栈 1 0 6 2 1 5 V3 3 2 4 4 2 3 V1 V4 V6 5 3 S.top 2 6 2 1 1 V2 V5 V7 S.base 0 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
} }/*DFSAL*/
8
7.3 图的遍历
在遍历时,对图中每个顶点至多调用一次DFS函数,因为 一旦某个顶点被标志成已被访问,就不再从它出发进行搜索。 因此,遍历图的过程实质上是对每个顶点查找其邻接点的过 程。其耗费的时间则取决于所采用的存储结构。
用邻接矩阵做图的存储结构时,查找各个顶点的邻接点所 需的时间为O(n2),其中n为图中顶点数。当以邻接矩阵做存 储结构时,深度优先搜索遍历图的时间复杂度为O(n2+n)。
7^
V0 V4
V2
V5
V6
V0 V1 V2 V3 V4 V7 V5 V6
V0 V1 V2 V3 V4 V7 V5 V6
12
void BFSTraverse(MGraph G)
7.3 图的遍历
/*从v出发,广度优先遍历连通图G*/
接点; 依此类推,直到图中所有访问过的顶点的邻接点 都被访问;
10
※求图G以V0为起点的的广度优先序列(设存储结构为邻 接矩阵)
V0,V1,V2, V3,V4,V7,V5,V6
VV0
VV1
V22
VV3
VV4
VV5
VV6
VV7
若图的存储结构为邻接表,则 访问邻接点的顺序不唯一,
深度优先序列不是唯一的
void DFS(Graph G, int v)
7.3 图的遍历
visited 0 0 10 20 30 40
……
{/* 从第v个顶点出发,递归地深度优先遍历图G*/
/* v是顶点在一维数组中的位置,假设G是非空图*/
visited[v] =1;
Visit(v); /*访问第v个顶点*/
for ( w=FirstAdjVex(G, v); w; w=NextAdjVex(G, v, w) )
当以邻接表做图的存储结构时,找邻接点所需时间为O(e), 其中e为无向图中边的数或有向图中弧的数。因此,当以邻 接表做存储结构时,深度优先搜索遍历图的时间复杂度为 O(n+e)。
9
7.3.2 广度优先遍历
7.3 图的遍历
图中某顶点v出发:
1)访问顶点v ;
2)访问v的所有未被访问的邻接点w1 ,w2 , …wk ; 3)依次从这些邻接点出发,访问它们的所有未被访问的邻
所有顶点间的最短路径问题; 5. 利用AOV网进行拓扑排序;利用AOE网求关键路径问题; 【掌 握】: 1. 掌握图的定义和术语; 2. 图的各种存储结构及其构造算法、在实际问题中的求解
效率。
2
7.3 图的遍历
7.3 图的遍历:从图的某顶点出发,访问图中所有顶点, 并且每个顶点仅访问一次。
图结构的遍历复杂性:
(4)在图结构中,一个顶点可以和其他多个顶点邻接,当 这样的顶点访问过后,考虑如何选取下一个要访问的顶点的 问题
3
图的遍历方法有深度优先遍历和广度优先遍历两种。 7.3.1 深度优先搜索 方法: (1)从图的某一顶点V0出发,访问此顶点; (2)依次从V0的未被访问的邻接点出发,深度优先遍历图, 直至图中所有和V0相通的顶点都被访问到。 若此时图中尚 有顶点未被访问,则另选图中一个未被访问的顶点作起点, 重复上述过程,直至图中所有顶点都被访问到。
4
※求图G以V0为起点的的深度优先序列(设存储结构为邻接 矩阵)
V0,V1,V3,V4,V7,V2,V5,V6,
VV0
VV1
VV2
VV3
VV44
VV5
VV6
VV7
若图的存储结构为邻接表,则 访问邻接点的顺序不唯一, 深度优先序列不是唯一的
5
深度优先遍历算法: 辅助数组:int visited[Max_Vertex_Num] ; 访问标志数组,全局变量,初始时所有分量 全为0,visited[v]=1表示顶点v已被访问.
if (!visited[w]) DFS(G, w);
/*对v的尚未访问的邻接顶点w递归调用DFS*/
} 6
在邻接表存储结构上实现深度优先搜索: void DFSTraverseAL(ALGraph G) /*深度优先遍历以邻接表存储的图G*/ {int i; for (i=0;i<G.vexnum; ++ i)
(1)在图结构中,没有一个“自然”的首结点,图中的任 意一个顶点都可以作为第一个被访问的结点
(2)在非连通图中,从一个顶点出发,只能访问它所在的 连通分量上的所有顶点,因此,还需考虑如何选取下一个出 发点以访问图中的其余连通分量
(3)在图结构中,如果有回路存在,那么一个顶点被访问 后,有可能沿回路又回到该顶点,考虑如何避免重复访问
visited[i]=0; /*标志数组初始化*/ for(i=0;i<G.vexnum;++i)
if (!visited[i]) DFSAL(G,i); /*Vi未访问过,从Vi开始DFS搜索*/
}
7.3 图的遍历7源自7.3 图的遍历void DFSAL(ALGraph G, int i) {/*从第v个顶点出发,递归地深度优先遍历图G*/
/* v是顶点的序号,假设G是用邻接表存储*/ EdgeNode *p; int w; visited[i] =1; Visit(i); /*访问第v个顶点*/ for (p=G.vertices[i].firstarc;p;p=p->nextarc)
{w=p->adjvex; /*w是v的邻接顶点的序号*/ if (!visited[w]) DFSAL(G, w); /*若w尚未访问, 递归调用DFS*/
∵ 先被访问的顶点,其 邻接点也要先被访问
∴设一队列保存已访问的 顶点
11
※ 在邻接表存储结构上的广度优先搜索
data firstarc
0 V0
1
adjvex next 2^
1 V1
0
3
4
2 V2
0
5
6^
3 V3
1^
4 V4
1
5 V5
2
6 V6
2
7 V7
1
7^ 6^ 5^ 4^
V1 V3
V7
Q
7.3 图的遍历
第7章 图
图是一种多对多的结构关系,每个元素可以有零个或多 个直接前趋;零个或多个直接后继。
2020/12/11
1
【重点掌握】: 1. 图的两种遍历方法:遍历的定义、深度优先搜索遍历和
广度优先搜索遍历的算法; 2. 应用图的遍历算法判断图的连通性及求图的生成树; 3. 用Prim、Kruskal算法求图的最小生成树; 4. 用Dijkstra算法求解单源最短路径问题;用Floyd算法求
8
7.3 图的遍历
在遍历时,对图中每个顶点至多调用一次DFS函数,因为 一旦某个顶点被标志成已被访问,就不再从它出发进行搜索。 因此,遍历图的过程实质上是对每个顶点查找其邻接点的过 程。其耗费的时间则取决于所采用的存储结构。
用邻接矩阵做图的存储结构时,查找各个顶点的邻接点所 需的时间为O(n2),其中n为图中顶点数。当以邻接矩阵做存 储结构时,深度优先搜索遍历图的时间复杂度为O(n2+n)。
7^
V0 V4
V2
V5
V6
V0 V1 V2 V3 V4 V7 V5 V6
V0 V1 V2 V3 V4 V7 V5 V6
12
void BFSTraverse(MGraph G)
7.3 图的遍历
/*从v出发,广度优先遍历连通图G*/
接点; 依此类推,直到图中所有访问过的顶点的邻接点 都被访问;
10
※求图G以V0为起点的的广度优先序列(设存储结构为邻 接矩阵)
V0,V1,V2, V3,V4,V7,V5,V6
VV0
VV1
V22
VV3
VV4
VV5
VV6
VV7
若图的存储结构为邻接表,则 访问邻接点的顺序不唯一,
深度优先序列不是唯一的
void DFS(Graph G, int v)
7.3 图的遍历
visited 0 0 10 20 30 40
……
{/* 从第v个顶点出发,递归地深度优先遍历图G*/
/* v是顶点在一维数组中的位置,假设G是非空图*/
visited[v] =1;
Visit(v); /*访问第v个顶点*/
for ( w=FirstAdjVex(G, v); w; w=NextAdjVex(G, v, w) )
当以邻接表做图的存储结构时,找邻接点所需时间为O(e), 其中e为无向图中边的数或有向图中弧的数。因此,当以邻 接表做存储结构时,深度优先搜索遍历图的时间复杂度为 O(n+e)。
9
7.3.2 广度优先遍历
7.3 图的遍历
图中某顶点v出发:
1)访问顶点v ;
2)访问v的所有未被访问的邻接点w1 ,w2 , …wk ; 3)依次从这些邻接点出发,访问它们的所有未被访问的邻
所有顶点间的最短路径问题; 5. 利用AOV网进行拓扑排序;利用AOE网求关键路径问题; 【掌 握】: 1. 掌握图的定义和术语; 2. 图的各种存储结构及其构造算法、在实际问题中的求解
效率。
2
7.3 图的遍历
7.3 图的遍历:从图的某顶点出发,访问图中所有顶点, 并且每个顶点仅访问一次。
图结构的遍历复杂性:
(4)在图结构中,一个顶点可以和其他多个顶点邻接,当 这样的顶点访问过后,考虑如何选取下一个要访问的顶点的 问题
3
图的遍历方法有深度优先遍历和广度优先遍历两种。 7.3.1 深度优先搜索 方法: (1)从图的某一顶点V0出发,访问此顶点; (2)依次从V0的未被访问的邻接点出发,深度优先遍历图, 直至图中所有和V0相通的顶点都被访问到。 若此时图中尚 有顶点未被访问,则另选图中一个未被访问的顶点作起点, 重复上述过程,直至图中所有顶点都被访问到。
4
※求图G以V0为起点的的深度优先序列(设存储结构为邻接 矩阵)
V0,V1,V3,V4,V7,V2,V5,V6,
VV0
VV1
VV2
VV3
VV44
VV5
VV6
VV7
若图的存储结构为邻接表,则 访问邻接点的顺序不唯一, 深度优先序列不是唯一的
5
深度优先遍历算法: 辅助数组:int visited[Max_Vertex_Num] ; 访问标志数组,全局变量,初始时所有分量 全为0,visited[v]=1表示顶点v已被访问.
if (!visited[w]) DFS(G, w);
/*对v的尚未访问的邻接顶点w递归调用DFS*/
} 6
在邻接表存储结构上实现深度优先搜索: void DFSTraverseAL(ALGraph G) /*深度优先遍历以邻接表存储的图G*/ {int i; for (i=0;i<G.vexnum; ++ i)
(1)在图结构中,没有一个“自然”的首结点,图中的任 意一个顶点都可以作为第一个被访问的结点
(2)在非连通图中,从一个顶点出发,只能访问它所在的 连通分量上的所有顶点,因此,还需考虑如何选取下一个出 发点以访问图中的其余连通分量
(3)在图结构中,如果有回路存在,那么一个顶点被访问 后,有可能沿回路又回到该顶点,考虑如何避免重复访问
visited[i]=0; /*标志数组初始化*/ for(i=0;i<G.vexnum;++i)
if (!visited[i]) DFSAL(G,i); /*Vi未访问过,从Vi开始DFS搜索*/
}
7.3 图的遍历7源自7.3 图的遍历void DFSAL(ALGraph G, int i) {/*从第v个顶点出发,递归地深度优先遍历图G*/
/* v是顶点的序号,假设G是用邻接表存储*/ EdgeNode *p; int w; visited[i] =1; Visit(i); /*访问第v个顶点*/ for (p=G.vertices[i].firstarc;p;p=p->nextarc)
{w=p->adjvex; /*w是v的邻接顶点的序号*/ if (!visited[w]) DFSAL(G, w); /*若w尚未访问, 递归调用DFS*/
∵ 先被访问的顶点,其 邻接点也要先被访问
∴设一队列保存已访问的 顶点
11
※ 在邻接表存储结构上的广度优先搜索
data firstarc
0 V0
1
adjvex next 2^
1 V1
0
3
4
2 V2
0
5
6^
3 V3
1^
4 V4
1
5 V5
2
6 V6
2
7 V7
1
7^ 6^ 5^ 4^
V1 V3
V7
Q
7.3 图的遍历
第7章 图
图是一种多对多的结构关系,每个元素可以有零个或多 个直接前趋;零个或多个直接后继。
2020/12/11
1
【重点掌握】: 1. 图的两种遍历方法:遍历的定义、深度优先搜索遍历和
广度优先搜索遍历的算法; 2. 应用图的遍历算法判断图的连通性及求图的生成树; 3. 用Prim、Kruskal算法求图的最小生成树; 4. 用Dijkstra算法求解单源最短路径问题;用Floyd算法求
