附录Ⅲ__简单荷载作用下梁的挠度和转角
材料力学(赵振伟)梁的弯曲变形2

3. 应用叠加原理的若干情况 1 ) 荷载的分解或重组
q m
q
L/2 L/2
L
F
q
q
m L/2 L/2
F
例
q0
EI
A 求图示自由端的挠度。
L2
L2
q0
L
w1
q0
w3
B
w2
L2
L2
w1
q0 L4 8EI
w2
q0 L 24
8EI
q0 L4 128EI
w3
B
L 2
q0 L 23
6EI
L 2
q0 L4 96EI
wA
w1
w2
w3
41q0 L4 384EI
2) 逐段刚化法
依据: 若结构可分为若干部分,且各部分在荷载作用下的 变形不是相互独立的,那么,结构中 A 点的位移是各个部 分在这一荷载作用下的变形在 A 点所引起的位移的叠加。
A EI a
变形刚体
F
F
Fa 2
B
C
a/2
wwww1122
B (F1, F2,, Fn ) B1(F1) B2 (F2 ) Bn(Fn )
yB (F1, F2,, Fn ) yB1(F1) yB2 (F2 ) yBn(Fn )
叠加法的特征: 1、梁在简单载荷作用下挠度、转角应为已知或有变形表可查; 2、叠加法适用于求梁个别截面的挠度或转角值。
分析和讨论
q
在下列不同的支承方 式中,哪一种刚度最高?
q
q
分析和讨论
q
梁由混凝土材料制成,如果横截面从左图改为右图,能 够改善强度吗?能够改善刚度吗?
梁的材料由普通钢改为优质钢,能够改善强度吗? 梁的材料由普通钢改为优质钢,能够改善刚度吗?
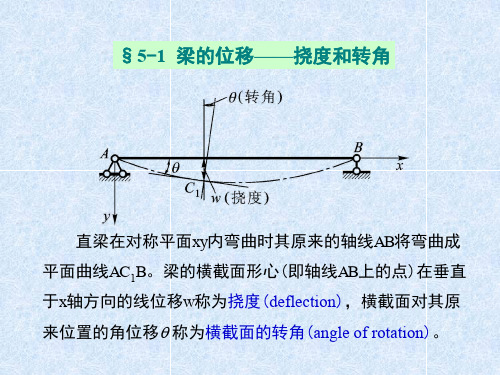
梁弯曲时的位移1梁的位移——挠度和转角2梁的挠曲线
x
a
3
x3
l2
b2
x
左、右两支座处截面的转角分别为
qA
q1
|x0
Fb l 2 b2 6lEI
Fabl b
6lEI
qB
q2
|xl
Fabl
6lEI
a
当a>b时有
qmax qB
Fabl a
6lEI
根据图中所示挠曲线的大致形状可知,最大挠度wmax 所在w 0 处在现在的情况下应在左段梁内。令左段梁的
22
2
挠曲线近似微分方程为
EIw M x q lx x2 2 以x为自变量进行积分得:
EIw
q 2
lx2 2
x3 3
C1
EIw
q 2
lx3 6
x4 12
C1x
C2
该梁的边界条件为 在 x=0 处 w=0, 在 x=l 处 w=0
悬臂梁和简支梁在简单荷载(集中荷载,集中力偶,分 布荷载)作用下,悬臂梁自由端的挠度和转角表达式,以及 简支梁跨中挠度和支座截面转角的表达式已在本教材的附 录Ⅳ中以及一些手册中给出。根据这些资料灵活运用叠加 原理,往往可较方便地计算复杂荷载情况下梁的指定截面 的挠度和转角。
从几何方面来看,平面曲线的曲率可写作
1
w
x 1 w2 3/2
式中,等号右边有正负号是因为曲率1/为度量平面曲线 (挠曲线)弯曲变形程度的非负值的量,而w"是q = w' 沿x方
《材料力学》课件5-3按叠加原理计算梁的挠度和转角

F
A
B
C 2 BF BM
M FL2
C
C 3 BF BM L2
C 3 C1 C 2 C 3
3 2 2 2 2 FL FL FL L L FL L FL FL2 1 2 1 1 2 1 2 2 L1 2 2 EI z1EI z1 2 EI z1 EI z1 3EI z 2 3EI z1
(d)
Me
Me
Me
Me
A
l 2
B
l 2
C
l 2
D
A
l 2
B
l 2
C
l 2
D
(a)
Me Me Me Me
A
l 2
B
l 2
C
l 2
D
A
l 2
B
l 2
C
l 2
D
(b)
(C)
Me
Me
A
l 2
B
l 2
C
l 2
D
AB,CD段弯矩为零,所以这两段保持直 线不发生弯曲变形。AB,BC,CD三段变 形曲线在交界处应有共切线。
q
B
EI z
A
c qc Fc
5qL4 qc 384 EI z
FL3 Fc 48EI z
C
l 2
l 2
q
A
B
5qL4 FL3 c 384 EI z 48EI z
C
EI z
l 2
F A
l 2
A qA FA
B
qL3 qA 24 EI z FL2 FA 16 EI z
按叠加原理计算梁的挠度和转角
按叠加原理计算梁的挠和转角

一、叠加原理的概念
当梁的变形微小,且梁的材料在线弹性范围内工作时, 梁的挠度和转角均与梁上的荷载成线性关系。在此情况下, 当梁上有若干荷载或若干种荷载作用时,梁的某个截面处 的挠度和转角就等于每个荷载或每种荷载单独作用下该截 面的挠度和转角的代数和。这就是计算梁的位移时的叠加 原理。
1
材料力学Ⅰ电子教案
悬臂梁和简支梁在简单荷载(集中荷载,集中力偶,分 布荷载)作用下,悬臂梁自由端的挠度和转角表达式,以及 简支梁跨中挠度和支座截面转角的表达式已在本教材的附 录Ⅳ中以及一些手册中给出。根据这些资料灵活运用叠加 原理,往往可较方便地计算复杂荷载情况下梁的指定截面 的挠度和转角。
2
材料力学Ⅰ电子教案
5ql 4 768 EI
0 5ql4 768 EI
qA
q A1 q A2
ql3 48 EI
ql3 384 EI
3ql3 128 EIBiblioteka qBq B1 q B2
ql3 48 EI
ql3 384 EI
7ql3 384 EI
7
材料力学Ⅰ电子教案
例题2 试按叠加原理求图a所示等直外伸梁其截面B的
上面求得的qB,由此引起的A端挠度w1=|qB|·a应叠加到图b
所示悬臂梁的A端挠度w2上去才是原外伸梁的A端挠度wA:
wA w1 w2
1 3
qa3 EI
a
2qa
8EI
4
7 qa4 12 EI
12
10
材料力学Ⅰ电子教案
qB
qBq
q BM
q2a3
24 EI
qa2 2a
3EI
1 3
qa3 EI
wD
梁的挠度
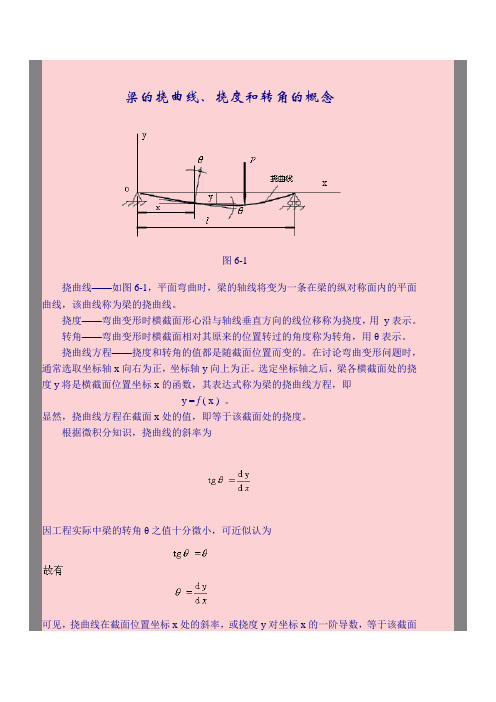
梁的挠曲线、挠度和转角的概念
图6-1
挠曲线——如图6-1,平面弯曲时,梁的轴线将变为一条在梁的纵对称面内的平面曲线,该曲线称为梁的挠曲线。
挠度——弯曲变形时横截面形心沿与轴线垂直方向的线位移称为挠度,用y表示。
转角——弯曲变形时横截面相对其原来的位置转过的角度称为转角,用θ表示。
挠曲线方程——挠度和转角的值都是随截面位置而变的。
在讨论弯曲变形问题时,通常选取坐标轴x向右为正,坐标轴y向上为正。
选定坐标轴之后,梁各横截面处的挠度y将是横截面位置坐标x的函数,其表达式称为梁的挠曲线方程,即
y = f ( x ) 。
显然,挠曲线方程在截面x处的值,即等于该截面处的挠度。
根据微积分知识,挠曲线的斜率为
因工程实际中梁的转角θ之值十分微小,可近似认为
可见,挠曲线在截面位置坐标x处的斜率,或挠度y对坐标x的一阶导数,等于该截面
的转角。
关于挠度和转角正负符号的规定:在如图6-1选定的坐标系中,向上的挠度为正,逆时针转向的转角为正。
《梁的挠度及转角 》课件

有限元分析
在现代工程分析中,有限元分析 是一种常用的方法来计算挠度和 转角。通过将梁离散化为有限个 小的单元,可以更精确地模拟梁
的变形和应力分布。
02
梁的挠度分析
静力挠度分析
静力挠度分析是指在静力载荷作 用下,对梁的挠度进行计算和分
析的过程。
静力挠度分析主要考虑梁的自重 、外部施加的均布载荷和集中载 荷等因素,通过计算得到梁的挠
温度转角分析
温度转角的大小取决于梁的材料、尺寸和温度变化等 因素。
单击此处添加正文,文字是您思想的提一一二三四五 六七八九一二三四五六七八九一二三四五六七八九文 ,单击此处添加正文,文字是您思想的提炼,为了最 终呈现发布的良好效果单击此4*25}
温度转角分析的目的是确定梁在温度变化下的变形程 度和转角大小,从而评估梁的耐热性能和稳定性。
5. 总结分析结果,提 出改进建议。
4. 将实测数据与理论 计算结果进行对比分 析;
案例分析结果与结论
结果
实测数据与理论计算结果基本一致, 证明了理论的正确性和实用性;
结论
梁的挠度和转角是结构安全的重要指 标,应加强监测和理论研究,以提高 结构的安全性和稳定性。
05
梁的挠度及转角优化设 计
优化设计方法与步骤案例二高层建筑中源自梁结构挠度及转角变 化案例三
大跨度钢结构的梁在风载作用下的 挠度及转角表现
案例分析方法与步骤
• 方法:理论计算与实测数据相结合
案例分析方法与步骤
步骤
1. 收集相关资料,了解工程概况和梁的结构特点 ; 2. 进行理论计算,预测梁的挠度和转角;
案例分析方法与步骤
3. 实地监测,获取梁 的实际挠度和转角数 据;
材料力学(土木类)第五章 梁弯曲时的位移(2)
3 3 3
利用叠加原理求图示弯曲刚度为EI的悬臂梁 例5-6 利用叠加原理求图示弯曲刚度为 的悬臂梁 自由端B截面的挠度和转角 截面的挠度和转角。 自由端 截面的挠度和转角。
F A l C EI l F D l B
原荷载可看成为图a和 两种荷载的叠加 两种荷载的叠加, 解:原荷载可看成为图 和 b两种荷载的叠加,对应 的变形和相关量如图所示。 的变形和相关量如图所示。
Fl θ C1 = 2 EI
2
3
由位移关系可得此时B截面的挠度和转角为: 由位移关系可得此时 截面的挠度和转角为: 截面的挠度和转角为
Fl 3 Fl 2 4 Fl 3 wB1 = wC1 + θ C1 ⋅ BC = + × 2l = 向下) (向下) 3EI 2 EI 3EI Fl θ B1 = θ C1 = 2 EI
q ( x) x 2 dθ B = dθ ( x) = dx 2 EI
范围对q(x)dx的作用进行叠加,相当于 的作用进行叠加, 在x=0, l范围对 范围对 的作用进行叠加 对上两式在前述范围内积分, 对上两式在前述范围内积分,即:
wB = ∫ d wB = ∫
0
l
l
0
11q 0 l q ( x ) x (3l − x ) dx = 6 EI 120 EI
上次课回顾: 上次课回顾:
1、度量梁变形的两个基本位移量:挠度和转角 度量梁变形的两个基本位移量: 2、挠曲线近似微分方程
EIw′′ = − M ( x )
3、挠曲线近似微分方程的积分 、
EIw ' ( x ) = ∫ ( − M ( x )) dx + C1
EIw ( x ) =
惯性矩截面系数弯矩图计算公式汇总
惯性矩、截面系数、弯矩图计算公式汇总附录1 截面图形的几何性质提要:不同受力形式下杆件的应力和变形,不仅取决于外力的大小以及杆件的尺寸,而且与杆件截面的几何性质有关。
当研究杆件的应力、变形,以及研究失效问题时,都要涉及到与截面形状和尺寸有关的几何量。
这些几何量包括:形心、静矩、惯性矩、惯性半径、极惯性矩、惯性积、主轴等,统称为“平面图形的几何性质”。
研究上述这些几何性质时,完全不考虑研究对象的物理和力学因素,作为纯几何问题加以处理。
平面图形的几何性质一般与杆件横截面的几何形状和尺寸有关,下面介绍的几何性质表征量在杆件应力与变形的分析与计算中占有举足轻重的作用。
附1.1 截面的静矩与形心任意平面几何图形如图1.1所示。
在其上取面积微元dA,该微元在yOz坐标系中的SSy=?zdA,Sz=?ydA坐标为z、y。
设静矩为,则有:AA图1.1 静矩的概念 (附1.1)静矩的量纲为长度的3次方。
由于均质薄板的重心与平面图形的形心有相同的坐标zC和yC。
则A?zC=?z?dA=Sy A———————————————————————————————————————————————由此可得薄板重心的坐标zC为zC=?AzdAA=SyA 同理有yC=Sz A?260? 材料力学所以形心坐标或zC=SyA,yC=SzA(附1.2)Sy=AzC,Sz=AyC由式(附1-2)得知,若某坐标轴通过形心轴,则图形对该轴的静矩等于零,即yC=0,Sz=0;zC=0,则Sy=0;反之,若图形对某一轴的静矩等于零,则该轴必然通过图形的形心。
静矩与所选坐标轴有关,其值可能为正,负或零。
如一个平面图形是由几个简单平面图形组成,称为组合平面图形。
设第i块分图形的面积为Ai,形心坐标为 yCi,zCi ,则其静矩和形心坐标分别为———————————————————————————————————————————————Sz=?AiyCi,Sy=?AizCii=1i=1nniCi(附1.3)SyC=z=A?Ayii=1nCi?Ai=1n,zC=SyA=?Azi=1nn(附1.4) ———————————————————————————————————————————————i?Ai=1i【例附1.1】求图1.2所示半圆形的Sy,Sz及形心位置。
2023大学_工程力学简明教程(景荣春著)课后习题答案下载
2023工程力学简明教程(景荣春著)课后习题答案下载工程力学简明教程(景荣春著)课后答案下载工程力学简明教程图书详细信息:印次:1-1装帧:平装印刷日期:-12-17工程力学简明教程(景荣春著):图书信息点击此处下载工程力学简明教程(景荣春著)课后答案工程力学简明教程(景荣春著):目录第1篇静力学第1章静力学公理和物体的受力分析51.1 静力学基本概念51.2 静力学公理61.3 约束和约束反力91.4 物体的受力分析13__小结18思考题19习题20第2章平面力系222.1 平面汇交力系222.1.1 平面汇交力系合成与平衡的几何法22 2.1.2 平面汇交力系合成与平衡的解析法25 2.2 力对点之矩282.3 平面力偶系292.4 平面任意力系352.4.1 力线平移定理352.4.2 平面任意力系的简化362.4.3 平面任意力系的平衡392.5 物体系统的平衡432.6 平面简单桁架的内力计算452.7 考虑摩擦的平衡问题482.7.1 滑动摩擦492.7.2 摩擦角与自锁现象512.7.3 考虑滑动摩擦的物体平衡问题52 __小结55思考题56习题58习题答案63第3章空间力系663.1 空间汇交力系663.2 力对点的矩和力对轴的矩693.3 空间力偶系723.4 空间任意力系743.5 重心78__小结83思考题84习题85习题答案87第2篇材料力学第4章材料力学的基本概念914.1 材料力学的任务914.2 变形固体的基本假设924.3 内力截面法和应力的概念934.4 位移与应变的概念964.5 杆件变形的基本形式97__小结100思考题101习题101习题答案103第5章拉伸、压缩与剪切1045.1 轴力及轴力图1055.2 轴向拉伸、压缩时的应力1075.2.1 轴向拉伸、压缩时横截面上的正应力107 5.2.2 轴向拉伸、压缩时斜截面上的应力110 5.3 轴向拉伸、压缩时材料的力学性能1125.3.1 轴向拉伸时材料的力学性能1125.3.2 轴向压缩时材料的力学性能1165.4 轴向拉伸、压缩时的强度计算1175.5 轴向拉伸、压缩时的变形1215.6 拉伸、压缩超静定问题1245.7 应力集中的概念1285.8 连接件的实用强度计算1295.8.1 剪切实用强度计算1305.8.2 挤压实用强度计算132__小结135思考题137习题138习题答案144第6章扭转1466.1 外力偶矩的计算扭矩及扭矩图147 6.2 薄壁圆筒的扭转1506.2.1 薄壁圆筒扭转时的切应力1506.2.2 切应力互等定理1526.2.3 剪切胡克定律1526.3 圆轴扭转时的应力和强度计算153 6.3.1 圆轴扭转时横截面上的切应力153 6.3.2 圆轴扭转时强度计算1566.4 圆轴扭转时的变形和刚度计算159 6.4.1 圆轴扭转时的变形1596.4.2 圆轴扭转时的刚度计算1596.5 圆轴扭转时的超静定问题162__小结163思考题165习题165习题答案167第7章弯曲1697.1 平面弯曲梁的.计算简图1717.2 梁的剪力与弯矩剪力图与弯矩图1727.2.1 剪力与弯矩1727.2.2 剪力方程与弯矩方程剪力图与弯矩图1767.2.3 剪力、弯矩和分布荷载集度间的微分关系181 7.2.4 按叠加原理作梁的弯矩图1877.2.5 平面刚架和曲杆的内力图1897.3 梁的正应力和强度计算1917.3.1 梁的正应力1917.3.2 梁的正应力强度条件1967.4 梁的切应力和强度计算2007.4.1 梁的切应力2007.4.2 梁的切应力强度计算2047.5 提高梁弯曲强度的措施2077.6 梁的变形和刚度计算2117.6.1 挠曲线近似微分方程2117.6.2 用积分法求梁的挠度和转角2137.6.3 用叠加法求梁的挠度和转角2197.6.4 梁的刚度计算和提高梁弯曲刚度的措施223 7.7 简单超静定梁224__小结227思考题229习题229习题答案238第8章应力状态和强度理论2408.1 应力状态的概念2408.2 二向应力状态2428.2.1 二向应力状态的解析法2428.2.2 二向应力状态的图解法2488.3 三向应力状态2528.4 广义胡克定律2548.5 强度理论及其应用2568.5.1 材料的破坏形式2568.5.2 常用的强度理论及其应用257__小结261思考题262习题263习题答案265第9章组合变形的强度计算2679.1 拉伸(压缩)与弯曲的组合2689.2 扭转与弯曲的组合2729.3 两相互垂直平面内的弯曲275__小结279思考题280习题281习题答案285第10章压杆稳定28610.1 压杆稳定的概念28610.2 细长压杆的临界力28810.2.1 两端铰支细长压杆的临界力28810.2.2 其他支座条件下细长压杆的临界力28910.3 压杆的临界应力及临界应力总图291 10.3.1 细长压杆的临界应力29110.3.2 临界应力总图29210.4 压杆的稳定计算29510.5 提高压杆稳定性的措施298__小结298思考题299习题300习题答案302附录A 截面的几何性质303A.1 形心与静矩303A.2 惯性矩和惯性积305A.3 平行移轴公式307A.4 主轴与主惯性矩的概念309思考题311习题311习题答案312附录B 梁在简单荷载作用下的变形314附录C 型钢表317表C-1 热轧等边角钢(GB 9787-1988)317 表C-2 热轧不等边角钢(GB 9788-1988)323 表C-3 热轧槽钢(GB 707-1988)328表C-4 热轧工字钢(GB 706-1988)331。
梁的挠度和转角
常数D表示起始截面的挠度×刚度(EI)
第八章 弯曲变形 /三、计算弯曲变形的两种方法
例题 一简支梁受力如图所示。试求 ( x), ( x) 和 , 。 A max F y 解: 1、求支座反力 x x C B A Fb Fa x FAy , FBy a b
L
L
L
2、分段列出梁的弯矩方程 AC段 (0 x a)
Fb( L2 b 2 ) A 0, 6 LEI
则由 解得:
C 1 x a
Fab(a b) 0( a b) 3LEI
0在AC段。
Fb 1 ( x ) [3x 2 ( L2 b 2 )] 0 6 LEI
x L2 b 2 3
D左 D右 连续条件: D左 D右 B左 B右
第八章 弯曲变形 /三、计算弯曲变形的两种方法
④积分常数的物理意义和几何意义
物理意义:将x=0代入转角方程和挠曲线方程,得 C 即坐标原点处梁的转角,它的 EI o EI倍就是积分常数C; 即坐标原点处梁的挠度的 EI倍就是积分常数D。 D EI o 几何意义:C——转角 D——挠度
第八章 弯曲变形 /三、计算弯曲变形的两种方法
例题:列出图示结构的边界条件和连续条件。
A 0 边界条件: A 0
连续条件:
B左 B右 B左 B右
第八章 弯曲变形 /三、计算弯曲变形的两种方法
例题:列出图示结构的边界条件和连续条件。
A 0 解:边界条件: A 0 C 0
答案 D
2、挠曲线的特征:光滑连续曲线(2)
FA=0 FB=0 MCD=const
A C D B
答案 D
