天文导航1
天文导航第2章 球面几何

17
天文导航原理及应用
2.2 球面三角
计算菲尔德和彼得堡之间小圆弧航 线的距离公式为:
在纬度53°23/N的圆弧周长=2πr,
其中,r = R cos AOC, AOC =
53°23´ = 53.3833°。 图中的红色弧ARB是这个圆周的一
部分,因此,
ARB = (160°.1667/360°)x2π
➢角的基本性质 1 球面三角形三角之和大于180Ο,小于540Ο。 2 球面三角形两角之和减去第三角小于180Ο。
➢边、角间的基本性质 边角存在对应关系,等边对等角;等角对等边;大边对大角。
13
天文导航原理及应用 2.3 球面三角
2.3.4 球面三角形的面积
球面S2 ( O , 1) 上球面三角形ABC 的面积为
原球面三角形与其极线三角形的关系
1 若一球面三角形是另一球面三角形的极线三角形,则这一球面三角 形也是前一球面三角形的极线三角形,即二者互为极线三角形。 2 极线三角形的边(角)与原球面三角形的角(边)互补。
12
天文导航原理及应用
2.3 球面三角
2.3.3 球面三角形的边角基本性质 ➢边的基本性质 1 球面三角形三边之和大于0Ο,小于360Ο。 2 球面三角形两边之和大于第三边,两边之差小于第三边。
cos AYB = (cos 36°.6167)2 + (sin 36°.6167)2 cos 160.1667° AYB = 71°.9663 = 71°58´ = 4318´.
因此菲尔德和彼得堡之间的大圆弧航线(黄色弧)距离是4318个海里,该
航线所需的时间为4318/500=8.636h=8h38m。
15
天文导航原理及应用
现代天文导航及其关键技术

现代天文导航及其关键技术一、本文概述Overview of this article随着科技的飞速进步和全球化的日益加深,天文导航作为一种古老而精确的导航技术,在现代社会中仍发挥着不可替代的作用。
天文导航不仅在海洋航行、空间探索等领域占据重要地位,而且在民用航空、卫星通信等方面也有着广泛的应用。
本文旨在全面介绍现代天文导航技术的发展现状、关键技术及其应用前景,以期为相关领域的研究者和实践者提供有价值的参考。
With the rapid progress of technology and the deepening of globalization, astronomical navigation, as an ancient and precise navigation technology, still plays an irreplaceable role in modern society. Astronomical navigation not only occupies an important position in fields such as ocean navigation and space exploration, but also has extensive applications in civil aviation, satellite communication, and other fields. This article aims to comprehensively introduce the current development status, key technologies, andapplication prospects of modern astronomical navigation technology, in order to provide valuable references for researchers and practitioners in related fields.文章首先将对天文导航的基本原理和历史发展进行简要回顾,以便读者对其有一个整体的认识。
航海基础知识有哪些

航海基础知识有哪些航海作为一种古老而神奇的技艺,在现代人的观念中或许已经略显陌生,但实际上,航海技术在现代社会中仍然扮演着至关重要的角色,不仅对于海洋贸易、渔业、旅游、军事等方面的发展起到了重要的推动作用,同时也在科技创新、环保、文化交流、国际关系等方面产生了重要影响。
因此,了解航海基础知识已经成为了一种必要的技能,接下来就让我们一起来了解一下吧。
一、导航术导航术是航海技术中最为基础的一项技能,其旨在通过观测天象、地球表面特征、气象等信息来确定船舶的位置和航向方向。
尽管现代船舶导航系统的应用已经相当普遍,但对于像渔民、航海员等地位的人来说,传统导航术依旧是必须掌握的技能。
常见的导航术有:1.天文导航术天文导航术是基于天文现象进行航海导航的一种方法。
通常通过观测太阳、月亮、恒星、行星等天体位置和变化,来测定船舶的经纬度和航向方向。
其中,最常见的是在夜间利用图谱来识别恒星、行星等,以此为依据来确定船舶的位置和航向方向。
2.地图导航术地图导航术是指利用地球表面实际情况和地图数据来测算船舶的位置和航向方向。
此种方法需要船员掌握对航行区域的了解,并具备解读和使用地图的技能。
3.气象导航术气象导航术是指利用天气预报和气象特征来推测船舶的位置和航向方向,特别是在大洋长途航行中需要掌握此项技能,以确保航行的安全性。
二、海图海图是船舶安全的第一道关卡。
海图主要分为近海航海图和远洋航海图,近海航海图包括港口、海湾、河口等领海范围内的海域,而远洋航海图则更关注海图的更新和完备性,细节更加丰富,其尺度通常为1:50,0000以上。
海图上的信息包括领海范围、水深、陆地和水下地形、海流、气压等气象特征等,对于船舶的安全和准确的船位测量非常重要。
三、航向确定航向是指船舶运行的方向,如何准确地测量得到船舶的航向方向也是航海技术中重要的一项。
常见的航向测量有:1.罗经测向法罗经是航海用的传统仪器之一,用于测量船舶的方向。
通过其中的钟表、罗经和陀螺仪等装置,罗经可以通过地球的磁场和引力确定船舶的方向,如此精密的测量方式也是其他方式无法取代的。
天文导航的原理及应用
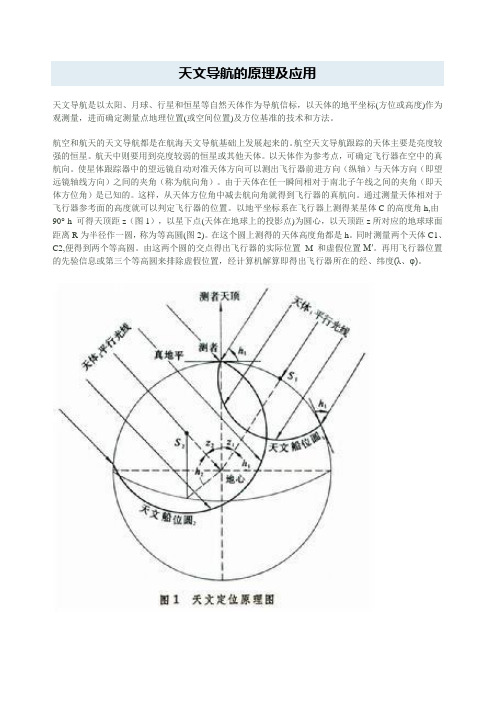
天文导航的原理及应用天文导航是以太阳、月球、行星和恒星等自然天体作为导航信标,以天体的地平坐标(方位或高度)作为观测量,进而确定测量点地理位置(或空间位置)及方位基准的技术和方法。
航空和航天的天文导航都是在航海天文导航基础上发展起来的。
航空天文导航跟踪的天体主要是亮度较强的恒星。
航天中则要用到亮度较弱的恒星或其他天体。
以天体作为参考点,可确定飞行器在空中的真航向。
使星体跟踪器中的望远镜自动对准天体方向可以测出飞行器前进方向(纵轴)与天体方向(即望远镜轴线方向)之间的夹角(称为航向角)。
由于天体在任一瞬间相对于南北子午线之间的夹角(即天体方位角)是已知的。
这样,从天体方位角中减去航向角就得到飞行器的真航向。
通过测量天体相对于飞行器参考面的高度就可以判定飞行器的位置。
以地平坐标系在飞行器上测得某星体C的高度角h,由90°-h 可得天顶距z(图1),以星下点(天体在地球上的投影点)为圆心,以天顶距z所对应的地球球面距离R为半径作一圆,称为等高圆(图2)。
在这个圆上测得的天体高度角都是h。
同时测量两个天体C1、C2,便得到两个等高圆。
由这两个圆的交点得出飞行器的实际位置M 和虚假位置M′。
再用飞行器位置的先验信息或第三个等高圆来排除虚假位置,经计算机解算即得出飞行器所在的经、纬度(λ、φ)。
天文导航的分类按星体的峰值光谱和光谱范围分,天文导航可分为星光导航和射电天文导航。
观测天体的可见光进行导航的叫星光导航,而接收天体辐射的射电信号(不可见光)进行导航的叫射电天文导航。
前者可解决高精度昼夜全球自动化导航定位,后者可克服阴雨等不良天气影响,通过探测射电信号进行全天候天文导航与定位。
根据跟踪的星体数,天文导航分为单星、双星和三星导航。
单星导航由于航向基准误差大而定位精度低,双星导航定位精度高,在选择星对时,两颗星体的方位角差越接近90°,定位精度越高。
三星导航常利用第三颗星的测量来检查前两次测量的可靠性,在航天中,则用来确定航天器在三维空间中的位置。
船用天文导航设备的技术特点与优势分析

船用天文导航设备的技术特点与优势分析引言:航海导航一直以来都是人类文明发展中的重要组成部分。
随着科技的进步和全球化的发展,船只导航设备的技术也在不断提升。
船用天文导航设备作为一种传统的导航方式,具有独特的技术特点和优势。
本文将对船用天文导航设备的技术特点与优势进行分析。
一、技术特点1. 天文观测精度高:船用天文导航设备是通过观测星体的位置和运动来进行航位推算的。
借助船载天文观测仪器,船只可以观测到恒星、行星和月球等天体的位置和方位,进而计算出船只的准确位置。
相比其他导航设备,船用天文导航设备的观测精度更高,可以达到较高的导航精度。
2. 不受电子干扰影响:在现代化的船舶上,电子设备广泛应用于各个领域,但是在某些情况下,电子设备可能会受到干扰导致工作不正常。
而船用天文导航设备则没有这个问题,它是基于天文观测的方式来进行导航,不受电磁波等电子干扰的影响,可以保证导航的稳定性和可靠性。
3. 独立性强:船用天文导航设备是一种独立的导航系统,不依赖于其他导航设备和基础设施。
即使在电子设备损坏或者通信中断的情况下,船只仍然可以凭借船用天文导航设备进行航位推算,确保船只的导航安全。
二、优势分析1. 完全无线化:相比其他导航设备,船用天文导航设备是完全无线化的。
船员只需要通过望远镜或者其他天文观测仪器观测星体的位置和方位,然后使用天文导航表进行计算,就可以得到船只的准确位置。
无需电子设备或者通信基站的支持,可以大大降低设备的维护和使用成本。
2. 抗干扰能力强:船用天文导航设备的导航结果不会受到电子设备和通信干扰的影响。
在海洋环境中,船只可能会遇到强电磁干扰或者通信中断的情况,而船用天文导航设备可以在这样的环境下正常工作,保证船只的导航安全。
3. 适应性强:船用天文导航设备适用于各种海洋环境和天气条件。
由于船只在航行中可能会遇到各种复杂的天气情况,如恶劣天气、强风浪等,这些情况可能会对其他导航设备产生影响。
而船用天文导航设备作为一种传统的导航方式,不会受到这些天气条件的限制,可以在各种复杂环境下正常工作。
天文导航的原理及应用
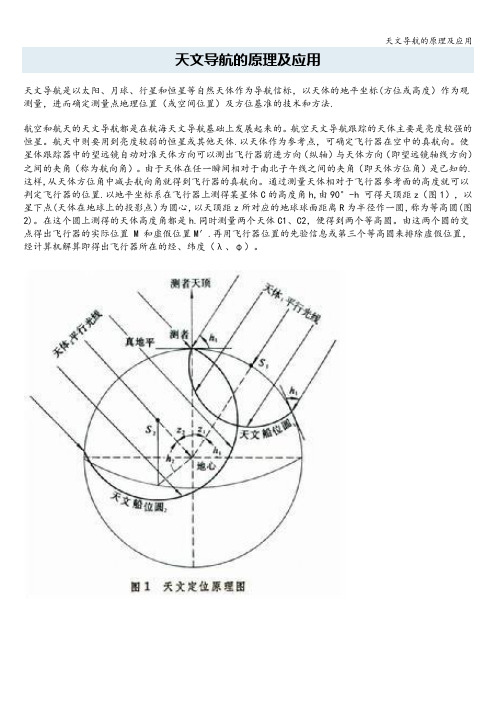
天文导航的原理及应用天文导航是以太阳、月球、行星和恒星等自然天体作为导航信标,以天体的地平坐标(方位或高度)作为观测量,进而确定测量点地理位置(或空间位置)及方位基准的技术和方法.航空和航天的天文导航都是在航海天文导航基础上发展起来的。
航空天文导航跟踪的天体主要是亮度较强的恒星。
航天中则要用到亮度较弱的恒星或其他天体.以天体作为参考点,可确定飞行器在空中的真航向。
使星体跟踪器中的望远镜自动对准天体方向可以测出飞行器前进方向(纵轴)与天体方向(即望远镜轴线方向)之间的夹角(称为航向角)。
由于天体在任一瞬间相对于南北子午线之间的夹角(即天体方位角)是已知的.这样,从天体方位角中减去航向角就得到飞行器的真航向。
通过测量天体相对于飞行器参考面的高度就可以判定飞行器的位置.以地平坐标系在飞行器上测得某星体C的高度角h,由90°-h 可得天顶距z(图1),以星下点(天体在地球上的投影点)为圆心,以天顶距z所对应的地球球面距离R为半径作一圆,称为等高圆(图2)。
在这个圆上测得的天体高度角都是h.同时测量两个天体C1、C2,便得到两个等高圆。
由这两个圆的交点得出飞行器的实际位置 M 和虚假位置M′.再用飞行器位置的先验信息或第三个等高圆来排除虚假位置,经计算机解算即得出飞行器所在的经、纬度(λ、φ)。
天文导航的分类按星体的峰值光谱和光谱范围分,天文导航可分为星光导航和射电天文导航。
观测天体的可见光进行导航的叫星光导航,而接收天体辐射的射电信号(不可见光)进行导航的叫射电天文导航。
前者可解决高精度昼夜全球自动化导航定位,后者可克服阴雨等不良天气影响,通过探测射电信号进行全天候天文导航与定位.根据跟踪的星体数,天文导航分为单星、双星和三星导航。
单星导航由于航向基准误差大而定位精度低,双星导航定位精度高,在选择星对时,两颗星体的方位角差越接近90°,定位精度越高。
三星导航常利用第三颗星的测量来检查前两次测量的可靠性,在航天中,则用来确定航天器在三维空间中的位置.仪器和系统航空常用的天文导航仪器有星体跟踪器、天文罗盘和六分仪等。
卫星天文导航自主定轨精度及误差分析

卫星天文导航自主定轨精度及误差分析季玮;白涛;武国强;林宝军【摘要】Using the star sensor and infrared earth sensor to observe starlight angular is the most project way to implement the satellite autonomous celestial navigation. But because of the external environment measurement error during the process of star sensor measurement. It will lead to the starlight angle has errors and finally cause the satellite orbit results inaccurately. To solve this problem, and combined with experimental data analysis, we ultimately determine the sensor system error is the main source of error which to cause the satellite autonomous celestial navigation orbit determination has the less accuracy. And using the least squares method to demarcate the sensor system error. To make more accurate observations, we use Kalman filter algorithm to eliminate noise of demarcate observations. Finally, using the actual satellite downlink data to validate this method and achieved good results.%通过星敏感器和红外地敏观测星光角距是目前实现卫星天文自主导航最为工程可行的方法,但由于星上敏感器在测量过程中不可避免的会引入外部环境测量误差,导致观测量星光角距存在偏差,最终会造成卫星定轨结果不精确.为解决这一问题,结合实验数据分析,最终确定了敏感器存在的系统误差是造成卫星天文导航定轨精度较低的最大误差源,并利用最小二乘方法对敏感器系统误差进行标定,将标定之后的观测量通过卡尔曼滤波算法进行噪声消除,使观测量更加准确.最后,利用星上实际下传数据对此方法进行验证,取得了良好的效果.【期刊名称】《电子设计工程》【年(卷),期】2017(025)015【总页数】5页(P90-93,97)【关键词】敏感器误差分析;静态地敏;天文导航;星光角距;星敏感器【作者】季玮;白涛;武国强;林宝军【作者单位】中国科学院上海微系统与信息技术研究所上海 200050;上海微小卫星工程中心上海 201203;上海微小卫星工程中心上海 201203;中国科学院光电研究院北京 100094;上海微小卫星工程中心上海 201203;中国科学院光电研究院北京 100094;上海微小卫星工程中心上海 201203;中国科学院光电研究院北京100094【正文语种】中文【中图分类】TN98天文导航是一种重要的卫星自主定轨方法[1-2],它仅需利用卫星自带的姿态敏感部件星敏感器、红外地平仪等,且不需要与外界进行任何的信息交互,是一种完全意义上的自主定轨方法。
星座与天文导航古老的星象解读现代航海

星座与天文导航古老的星象解读现代航海星座与天文导航:古老的星象解读现代航海导语:星座和天文导航是古老而又神秘的领域,其源远流长的历史承载了人类对天空的探索与想象。
本文将以宏观的视野,探讨星座和天文导航在古代航海中的重要性,并展示现代航海中对星座和天文导航的应用。
通过深入了解古代航海和现代航海的技术差异,我们能够更好地理解星座和天文导航如何在其中扮演着不可或缺的角色。
一、古代航海和星座导航古代航海者通过观测天空中的星座来导航,这是因为星座在不同的季节和纬度中的位置是相对稳定的。
根据星座的位置,航海者可以确定自己的位置和航向,并且推断出当前所处的纬度。
例如,“北极星”是北半球最重要的定位星座之一,航海者可以通过观察北极星的位置来确定自己的北方方向。
二、星座和传统航海导航系统在古代,人们开发了一套称为“星座导航系统”的技术,用于帮助航海者确定自己的位置和航向。
这种系统基于天体的观测,通过绘制和识别星座图案,来确定位置和方向。
例如,埃及人使用的星座导航系统就是一种非常精确的方式,通过观测特定星座的位置来导航。
三、星座和现代航海导航系统现代航海导航系统使用卫星定位和导航技术,相较于古代的星座导航系统,更加精确和便捷。
然而,星座和天文导航仍然被用于辅助现代导航系统,特别是在极地或出现GPS信号中断的情况下。
天体导航在航空和航海领域仍然是一项重要的技术。
例如,在极地地区的航行中,由于地球磁场的问题,GPS信号常常不可靠。
因此,航空器和船只需要依靠天文观测来确定自己的位置。
此外,星座和天文导航还在太空探索中发挥着重要作用,例如航天飞机和月球探测器的导航系统。
四、启示与展望星座和天文导航从古代发展到现代,一直在对人类探索和航海提供帮助。
无论在古代航海还是现代航海,导航都是一项至关重要的技术。
星座和天文导航通过观测和解读星象,为航海者提供了可靠的定位和导航方法,为他们的探索旅程提供了必要的支持。
在未来,随着科技的发展,星座和天文导航可能会继续演变和改进。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
隐蔽性好,可靠性高 作为天文导航基准的天体,
其空间运动规律不受人为破坏,不怕外界电磁波的 干扰,具有安全、隐蔽、生命力强等特点,从根本 上保证了天文导航系统最完备的可靠性
天文导航特点
适用范围大,发展空间广 天文导航不受地域、
空域和时域的限制,是一种在整个宇宙内处处适用 的导航技术,发展空间极其广阔。天文导航系统可 实现全球、昼夜、全天候、全自动导航 陆基台站,更不必向空中发射轨道运行体,设备简 单,工作可靠,不受别人制约,便于建成独立自主 的导航体制。因此,天文导航是一种难得的精确导 航定位与校准手段
• 天文年历中给出了太阳、月球、各大行星和 千百颗基本恒星在一年内不同时刻相对于不 同参考系的精确位置。
• 在航天器飞行过程中那些便于用星载设备进 行观察的自然天体就构成了天文导航的信标, 通过对信标观测所获得的数据进行处理后, 可获得航天器的所在位置。
航天器自主天文导航主要有两类方法:1, 纯天文几何解析方法;2,基于轨道动力学 的方法。
式中
rex [ Ac ] rey rez rmx rmy rmz
rmx 1 rmy cos * rzy
根据单位矢量 re和 rm ,可以化简上式
rex T [ Ac ][ Ac ] rmx cos * re rm rey rmy rex rez rey rzy rez cos * 1
如图所示,飞行器与近天体1(例如地球) 的单位位置矢量为 re ,近天体1与3颗导航恒
星的单位方向矢量为 s1 , s 2 , s3 ,A , A , A 的补角分 别为3次观测得到的3个量测量。可得到如 下方程:
1 2 3
恒星1
圆锥1
S1
航天器 S2 A1 Y 行星 R1 O X 圆锥3 A3 L1 S3 恒星3 A2 圆锥2 恒星2
§2.2天文导航中的位置面
位置面:当被测参数为常值时,飞行器可能位 置形成的曲面。 在任意时刻t要由测量装置提供足够多的 位置面才能进行空间定位。 天文导航的几何解析方法可归结为通过对 天体的测量获得位置面,通过位置面的组合 进行定位的方法。
对天体进行观测时的假设: 1、用来进行导航的天体,在观测时刻对已知 坐标系的位置可由天文年历查得;根据天体 与地球的距离分为近天体与远天体,太阳系 中的天体(太阳、行星、地球、月球)称为近天 体,并认为近天体是半径为已知的圆球,而 恒星则称为远天体。
re s1 cos A1 re s 2 cos A2 re s 3 cos A3
r
Z
同样可以得到飞行器与近天体2(例如月球)
的单位矢量 rm ,如果量测无误差,则这两条 位置线必相交于飞行器所在的位置。但由于 量测误差的存在,为了计算飞行器的坐标, 采用下面的计算方法:
这一几何描述也可用矢量公式表达。设i为 由近天体到恒星视线的单位矢量,这一矢 量的方向可由天文年历计算出来;r为近天 体到飞行器的位置矢量,r为未知量,由矢 量点乘关系可得位置面的数学描述为:
r i r cos A
其中A为已知的观测量。
近天体/飞行器/近天体
在图2.8中V为飞行器,P1、P2为两个近 天体,在t时刻由飞行器载仪表对P1和P2 进行天文测量,通过测量可求得P1与P2 间的夹角A。由几何关系可知,这时的位 置面是以两近天体连线为轴线,旋转通过 这两点的一段圆弧而获得的超环面,这段 圆弧的中心O在P1P2连线的垂直平分线 上,圆弧半径R与两近天体之间的距离rP 以及A的关系为
近天体/飞行器/远天体
在图中若V为飞行器,P为近天体,在t时刻 由飞行器载仪表对近天体和恒星进行天文测量, 通过测量可求得飞行器到近天体的视线与飞行 器到远天体的视线之间的夹角为A。
A 近天体 P V飞行器 A A i 恒星 A
位置面为圆锥 面,圆锥顶点在近天 体上,圆锥轴线为近 天体到恒星的视线方 向,圆锥的顶角为 (180度 – A)。
测量仪器:光学敏感器
天文导航常用传感器
地球敏感器---------地球辐射红外信息
太阳敏感器---------太阳可见光
星敏感器---------恒星可见光
天文导航特点
自主性强,无误差积累 天文导航以天体作为导
航基准,被动地接收天体自身辐射信号,进而获取 导航信息,是一种完全自主的导航方式,而且其定 位误差和航向误差不随时间的增加而积累,也不会 因航行距离的增大而增大
r Re 1re Rm 2 rm
式中,r
Hale Waihona Puke 为飞行器的位置矢量;Re , Rm 分别为 两个近天体的位置矢量;1 , 2 分别为飞行器 到近天体1和近天体2的位置矢量的模。
1re 2 rm Rm Re
写成矩阵形式为
rex r ey rez rmx xm xe 1 y y rmy m e 2 z m ze rmz
天文导航
1,概述
2,天文导航位置面的概念
3,基于纯天文几何解析法的天文导航原理
4,基于轨道动力学方程的天文导航原理
§2.1 概述
天文导航:以已知准确空间位置的自然天体
为基准,通过天体测量仪器被动探测天体位 置,经解算确定测量点所在载体的导航信息。
航天器天文导航是通过观测天体来测定飞行
中的航天器所在位置的技术。
dx dt v x dy v y dt dz v z dt 2 dv x x 1 J Re 7.5 z 1.5 F 2 x 3 2 dt r r r dv y y z2 Re 3 1 J 2 7.5 2 1.5 Fy r r r dt z z2 Re dv z dt r 3 1 J 2 r 7.5 r 2 4.5 Fz
系统状态方程简写为:
X (t ) f ( X , t ) w(t )
式中,状态矢量 X [ x
y
z vx
vy
v z ]T
误差矢量 w(t ) [0 0 0 Fx
Fy
Fz ]T
2,建立量测方程(观测方程)
在求解上述方程时,满足方程的解不是唯 一的,从几何上看,两个圆锥面的交线有两 条,这两条交线与超环面的交点也不是唯一 的,因而在求解时出现了模糊解问题。为解 决这一问题,通常是由于这些交点相距较远, 而根据飞行器运动的情况能知道飞行器在此 时刻的近似位置,在这些解中接近近似位置 的解,即为飞行器的实际位置。
地球卫星的轨道动力学模型为二体问题,
其天文导航系统的模型相对简单,我们 以地球卫星为例学习基于轨道动力学的 自主天文导航原理。 根据原理,自主天文导航包括三个部分: 1,建立系统的状态模型 2,建立量测模型 3,估计
1,建立系统的状态模型(状态方程)
系统状态模型即卫星轨道动力学模型
(2-1)
如果观测无误差,通过消元可以用式(2-1) 的任何两个分量决定 1和 。由于测量值不 可避免地存在误差,所以通常用最小二乘法 求出 1 和 ,即:
2 2
xm xe 1 ([ AcT ][ Ac ]) 1[ AcT ] ym ye 2 z m ze
设备简单,便于推广应用 天文导航不需要设立
天体是宇宙空间中各种星体的总称,天体包
括自然天体(恒星、行星、卫星、彗星、流 星等)和人造天体(人造地球卫星、人造行 星等)。 自然天体按人类难以干预的恒定的规律运动, 人们通过长期的观察与计算,掌握了自然天 体的运动规律,给出了按年度出版的反映自 然天体运动规律的天文年历。
掩星测量
位置面为圆柱体,圆柱体轴线与飞行器到恒星的视线方向 重合,并通过近天体中心,圆柱体直径等于近天体的直径。 这种测量只适用于末端导航。
由三次测量进行航天器天文定位
第1次—太阳/飞行器/恒星1, 得圆锥面A1; 第2次—太阳/飞行器/恒星2, 得圆锥面A2; 第3次—太阳/飞行器/地球; 得超环面A3。
2、认为光速和航天器与恒星的距离均为无穷
大; 3、按现有的技术条件,当飞行器运动状态产 生变化时,飞行器载仪表的测量能显示出变 化并能精确测量。
目前天文导航中用来确定位置面的可行 测量方法有:
近天体/飞行器/远天体的夹角测量; 近天体/飞行器/近天体夹角测量; 飞行器/近天体视角测量; 掩星测量。
基于轨道动力学的自主天文导航原理
根据航天器运行规律建立状态模型、以天文 观测信息建立量测模型,利用先进的估计方 法获得航天器的运动参数。
航天器自主天文导航系统模型存在确定性误 差和随机误差,无法准确建立导航系统的状 态模型,所以要获得高精度状态估值,必须 要用量测信息和先进的滤波方法对系统的状 态量即位置、速度等导航信息进行实时估计。
因为在航天器上观测到的两颗恒星之间的夹 角不会随航天器位置的改变而变化,而一颗 恒星和一颗行星中心之间的夹角则会随航天 器位置的改变而改变,该角度的变化才能够 表示位置的变化。因此要确定航天器的位置 信息,还需要观测近天体。通过观测近天体 中心和恒星视线矢量之间的夹角,可以确定 飞行器在观测时刻可能所在的位置,根据几 个不同位置面的组合,可以唯一确定飞行器 的位置 。
1 1 sin 2 * 2
1 cos *
cos rex 1 rmx
*
rey rmy
xm xe rez ym ye rmz z z m e
求出 1 和 2后,飞行器的位置坐标就可以由 式 r Re 1re Rm 2 rm 算出。
