哈工大电路习题答案第3章
电子电路第三章习题及参考答案
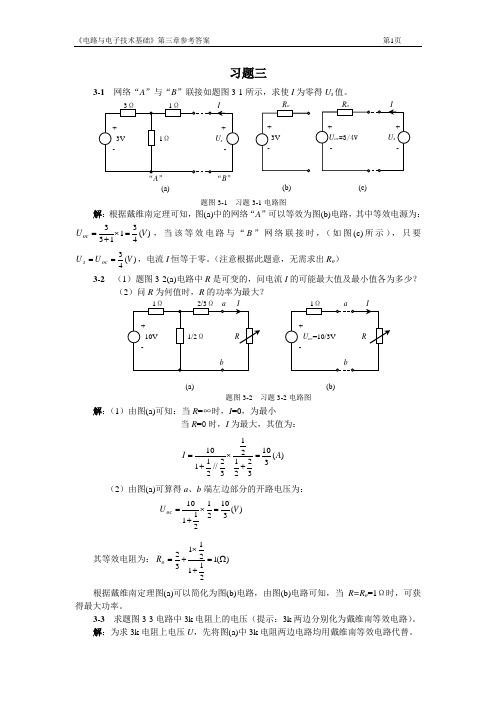
习题三3-1 网络“A ”与“B ”联接如题图3-1所示,求使I 为零得U s 值。
解:根据戴维南定理可知,图(a)中的网络“A ”可以等效为图(b)电路,其中等效电源为:)(431133V U oc =⨯+=,当该等效电路与“B ”网络联接时,(如图(c)所示),只要)(43V U U oc s ==,电流I 恒等于零。
(注意根据此题意,无需求出R o ) 3-2 (1)题图3-2(a)电路中R 是可变的,问电流I 的可能最大值及最小值各为多少? (2)问R 为何值时,R 的功率为最大?解:(1)由图(a)可知:当R =∞时,I =0,为最小当R =0时,I 为最大,其值为: )(31032212132//21110A I =+⨯+=(2)由图(a)可算得a 、b 端左边部分的开路电压为: )(3102121110V U oc =⨯+=其等效电阻为:)(121121132Ω=+⨯+=o R根据戴维南定理图(a)可以简化为图(b)电路,由图(b)电路可知,当R=R o =1Ω时,可获得最大功率。
3-3 求题图3-3电路中3k 电阻上的电压(提示:3k 两边分别化为戴维南等效电路)。
解:为求3k 电阻上电压U ,先将图(a)中3k 电阻两边电路均用戴维南等效电路代替。
“A ” “B ” (a)(b)(c)题图3-1 习题3-1电路图(a)(b)题图3-2 习题3-2电路图对于左边电路由弥尔曼定理有:)(1060//30//20)(20301601201302402012011Ω==-=++-=k R V U o oc对于右边电路由弥尔曼定理有:)(712040//60//60)(7240401601601402406048022Ω===++-=k R V U o oc 所以图(a)可以简化为图(b)电路,由图(b)很容易求得: )(4.5211338037120103207240V U ≈⨯=⨯+++=3-4 试求题图3-4所示的桥式电路中,流过5Ω电阻的电流。
【免费下载】哈工大数电答案

【3-1】 填空 1、与模拟信号相比,数字信号的特点是它的 离散 性。一个数字信号只有两种取值分
别表示为 0 和 1 。 2、布尔代数中有三种最基本运算: 与 、 或 和 非 ,在此基础上又派生出五种
基本运算,分别为与非、或非、异或、同或和与或非。 3、与运算的法则可概述为:有“0”出 0 ,全“1”出 1;类似地或运算的法则为
Y1 Y2 = ABD ABC CD
Y1 Y2 = AB C B D
Y1 Y2 = ABC D ABC BCD ACD
ABCD ABCD
ABCD ABCD
(8,9,10,13,14,15) BC BC D
d
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力根保通据护过生高管产中线工资敷艺料设高试技中卷术资配0料不置试仅技卷可术要以是求解指,决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高高与中中带资资负料料荷试试下卷卷高问总中题体资,配料而置试且时卷可,调保需控障要试各在验类最;管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下,安与要全过加,度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高;试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中,核资或对料者定试对值卷某,弯些审扁异核度常与固高校定中对盒资图位料纸置试,.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置,弯高尤曲中其半资要径料避标试免高卷错等调误,试高要方中求案资技,料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高,术料课中并中3试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术,管以术来架及避等系免多统不项启必方动要式方高,案中为;资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资,管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装,工置合作调理并试利且技用进术管行,线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确:指灵在导活分。。线对对盒于于处调差,试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷,术调应问试采题技用,术金作是属为指隔调发板试电进人机行员一隔,变开需压处要器理在组;事在同前发一掌生线握内槽图部内纸故,资障强料时电、,回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资,料料线试试缆卷卷敷试切设验除完报从毕告而,与采要相用进关高行技中检术资查资料和料试检,卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
哈工大模电答案第3章
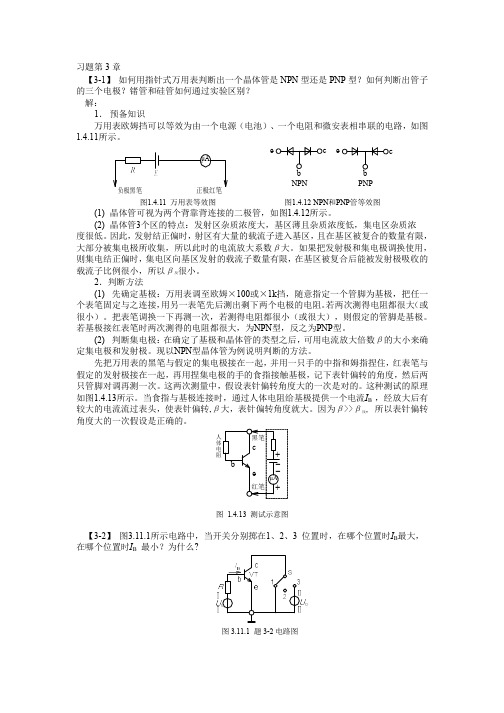
习题第3章【3-1】 如何用指针式万用表判断出一个晶体管是NPN 型还是PNP 型?如何判断出管子的三个电极?锗管和硅管如何通过实验区别? 解:1. 预备知识万用表欧姆挡可以等效为由一个电源(电池)、一个电阻和微安表相串联的电路,如图1.4.11所示。
μA正极红笔eeNPNPNP图1.4.11 万用表等效图 图1.4.12 NPN 和PNP 管等效图(1) 晶体管可视为两个背靠背连接的二极管,如图1.4.12所示。
(2) 晶体管3个区的特点:发射区杂质浓度大,基区薄且杂质浓度低,集电区杂质浓 度很低。
因此,发射结正偏时,射区有大量的载流子进入基区,且在基区被复合的数量有限,大部分被集电极所收集,所以此时的电流放大系数β大。
如果把发射极和集电极调换使用,则集电结正偏时,集电区向基区发射的载流子数量有限,在基区被复合后能被发射极吸收的载流子比例很小,所以β反很小。
2.判断方法(1) 先确定基极:万用表调至欧姆×100或×1k 挡,随意指定一个管脚为基极,把任一个表笔固定与之连接,用另一表笔先后测出剩下两个电极的电阻。
若两次测得电阻都很大(或很小)。
把表笔调换一下再测一次,若测得电阻都很小(或很大),则假定的管脚是基极。
若基极接红表笔时两次测得的电阻都很大,为NPN 型,反之为PNP 型。
(2) 判断集电极:在确定了基极和晶体管的类型之后,可用电流放大倍数β的大小来确定集电极和发射极。
现以NPN 型晶体管为例说明判断的方法。
先把万用表的黑笔与假定的集电极接在一起,并用一只手的中指和姆指捏住,红表笔与假定的发射极接在一起,再用捏集电极的手的食指接触基极,记下表针偏转的角度,然后两只管脚对调再测一次。
这两次测量中,假设表针偏转角度大的一次是对的。
这种测试的原理如图1.4.13所示。
当食指与基极连接时,通过人体电阻给基极提供一个电流I B ,经放大后有较大的电流流过表头,使表针偏转,β大,表针偏转角度就大。
哈工大电路理论基础课后习题答案(PDF精品)

答案2.1解:本题练习分流、分压公式。
设电压、电流参考方向如图所示。
(a) 由分流公式得:23A 2A 23I R Ω⨯==Ω+解得75R =Ω(b) 由分压公式得:3V 2V 23R U R ⨯==Ω+解得47R =Ω答案2.2解:电路等效如图(b)所示。
20k Ω1U +-20k Ω(b)+_U图中等效电阻(13)520(13)k //5k k k 1359R +⨯=+ΩΩ=Ω=Ω++由分流公式得:220mA 2mA 20k RI R =⨯=+Ω电压220k 40V U I =Ω⨯= 再对图(a)使用分压公式得:13==30V 1+3U U ⨯答案2.3解:设2R 与5k Ω的并联等效电阻为2325k 5k R R R ⨯Ω=+Ω(1) 由已知条件得如下联立方程:32113130.05(2) 40k (3)eqR U UR R R R R ⎧==⎪+⎨⎪=+=Ω⎩由方程(2)、(3)解得138k R =Ω 32k R =Ω 再将3R 代入(1)式得210k 3R =Ω答案2.4解:由并联电路分流公式,得1820mA 8mA (128)I Ω=⨯=+Ω2620mA 12mA (46)I Ω=⨯=+Ω由节点①的KCL 得128mA 12mA 4mA I I I =-=-=-答案2.5解:首先将电路化简成图(b)。
图 题2.5120Ω(a)图中1(140100)240R =+Ω=Ω2(200160)120270360(200160)120R ⎡⎤+⨯=+Ω=Ω⎢⎥++⎣⎦ 由并联电路分流公式得211210A 6A R I R R =⨯=+及21104A I I =-= 再由图(a)得321201A 360120I I =⨯=+由KVL 得,3131200100400V U U U I I =-=-=-答案2.6xRx(a-1)图2.6解:(a )设R 和r 为1级,则图题2.6(a)为2级再加x R 。
哈工大(威海)模电习题册(一)答案

第三章 多级放大电路一.解:(a )共射,共基 (b )共射,共射 (c )共射,共射 (d )共集,共基 (e )共源,共集 (f )共基,共集二.解:(1)R W 的滑动端在中点时A d 的表达式为beWc IOd )2( r R R u u A +-=∆∆=β(2)R W 的滑动端在最右端时I beW c C2C1O IbecC2I beW c C1)2( 2 2)( u r R R u u u u r R u u r R R u ∆⋅+-=∆-∆=∆∆⋅+=∆∆⋅+-=∆βββ所以A d 的表达式为beWc IOd )2( r R R u u A +-=∆∆=β比较结果可知,两种情况下的A d 完全相等;但第二种情况下的C21C u u ∆∆>。
三.解:R W 滑动端在中点时T 1管和T 2管的发射极静态电流分析如下:mA 517.02222e WBEQEE EQEE e EQ WEQ BEQ ≈-==+⋅+R R U V I V R I R I U + A d 和R i 分析如下:Ω≈++=-≈++-=Ω≈++=k 5.20)1(2972)1( k 18.5mV26)1(W be i Wbe cd EQbb'be R r R R r R A I r r ββββ四. 解:电路的共模输入电压u I C 、差模输入电压u I d 、差模放大倍数A d 和动态电压△u O 分别为V67.0672 mV 10mV 152Id d O becd I2I1Id I2I1IC -≈=∆-≈-==-==+=u A u r R A u u u u u u β由于电路的共模放大倍数为零,故△u O 仅由差模输入电压和差模放大倍数决定。
第五章 放大电路的频率响应一.解:(1)1be b s )(π21C r R R ∥+ 。
①;①。
(2)'s b bb'e b')]([21ππC R R r r ∥∥+ ;①;①,①,③。
第3章 习题解答 哈工大习题册
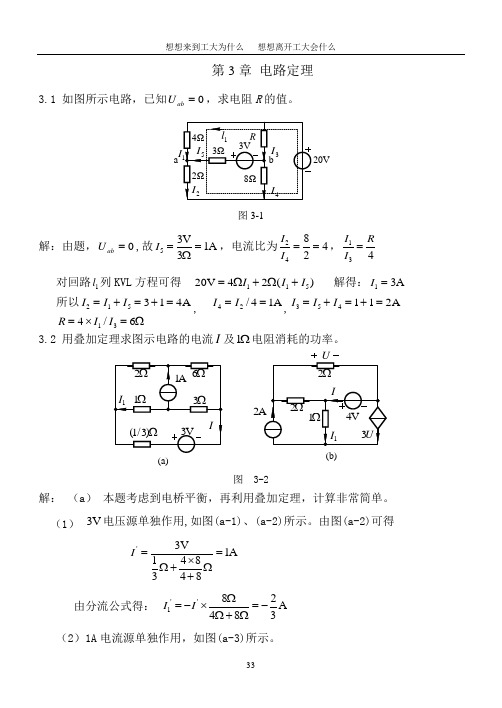
第3章 电路定理3.1 如图所示电路,已知0=ab U ,求电阻R 的值。
a图3-1解:由题,0=ab U ,故53V1A 3I ==Ω,电流比为24842I I ==,134I R I =对回路1l 列KVL 方程可得 11520V 42()I I I =Ω+Ω+ 解得:13AI =所以215314A I I I =+=+=, 42/41A I I ==,354112A I I I =+=+=134/6R I I =⨯=Ω3.2 用叠加定理求图示电路的电流I 及1Ω电阻消耗的功率。
(a)(b)2图 3-2解: (a ) 本题考虑到电桥平衡,再利用叠加定理,计算非常简单。
(1) 3V 电压源单独作用,如图(a-1)、(a-2)所示。
由图(a-2)可得'3V1A 148348I ==⨯Ω+Ω+由分流公式得: ''182A 483I I Ω=-⨯=-Ω+Ω(2)1A 电流源单独作用,如图(a-3)所示。
考虑到电桥平衡,0I ''=,133(1A)A 134I ''=-⨯=-+ (3)叠加:1A I I I '''=+=,11117/12A I I I '''=+=-2111 2.007WP I Ω=⨯=(a-1)(a-2)(a-3)(b )(1)4V 电压源单独作用,如图(b-1)所示。
24V 2V 22U Ω'=⨯=Ω+Ω,136A I U ''=-=-,125A I I I '''=+=- (2)2A 电流源单独作用,如图(b-2)所示。
'2I '(b-1)(b-2)222A 2V 22U Ω⨯Ω''=⨯=Ω+Ω,22/21A I U ''''== 对节点②列KCL 方程得1234A I U ''''=-=-对节点③列KCL 方程得235A I I U ''''''=-=- (3) 叠加 '"1116A 4A=10A I I I =+=---'"5A 5A=10A I I I =+=---2111100W P I Ω=⨯Ω=注释:不能用各独立源单独作用时电阻消耗的功率之和来计算电阻在电路中消耗的功率。
哈工大电路习题答案

哈工大电路习题答案哈工大电路习题答案在学习电路课程的过程中,我们经常会遇到各种各样的习题。
这些习题不仅能够帮助我们巩固所学的知识,还能够提高我们的解题能力。
然而,有时候我们可能会遇到一些难以解答的问题,这时候就需要一些参考答案来帮助我们。
下面,我将为大家提供一些哈工大电路习题的参考答案。
1. 电路基础习题1.1 电阻与电流关系题目:一个电阻为10欧姆的电路中,通过的电流为2安培,求电路中的电压是多少?答案:根据欧姆定律,电压等于电流乘以电阻,所以电压等于2安培乘以10欧姆,即20伏特。
1.2 串联电路题目:有两个电阻分别为5欧姆和10欧姆的电路,串联连接在一起,通过的电流为3安培,求电路中的总电阻是多少?答案:串联电路中的总电阻等于各个电阻之和,所以总电阻等于5欧姆加上10欧姆,即15欧姆。
1.3 并联电路题目:有两个电阻分别为5欧姆和10欧姆的电路,并联连接在一起,通过的电流为2安培,求电路中的总电阻是多少?答案:并联电路中的总电阻等于各个电阻的倒数之和的倒数,所以总电阻等于(1/5 + 1/10)的倒数,即6.67欧姆。
2. 电路分析习题2.1 戴维南定理题目:有一个电阻为10欧姆的电路,通过的电流为2安培,求该电路中的电压是多少?答案:根据戴维南定理,可以通过测量电阻两端的电压来求解。
由于电阻为10欧姆,电流为2安培,所以电压等于电阻乘以电流,即20伏特。
2.2 超节点法题目:有一个包含电流源和电阻的电路,其中一个节点既有电流源又有电阻,如何应用超节点法来简化电路分析?答案:超节点法是一种简化复杂电路分析的方法,可以将包含电流源和电阻的节点分解为两个节点,其中一个节点为电流源连接的节点,另一个节点为电阻连接的节点。
然后根据电流源和电阻之间的关系,可以求解出电路中的电流和电压。
3. 电路设计习题3.1 电路的功率计算题目:有一个电阻为10欧姆的电路,通过的电流为2安培,求该电路的功率是多少?答案:根据功率公式,功率等于电流的平方乘以电阻,所以功率等于2安培的平方乘以10欧姆,即40瓦特。
电路理论基础(哈尔滨工业大学陈希有第3版)3

u U = f2( I )
+ N1 I S=I
U = f1 (I ) i O I
置换定理的证明
U -
(c) 置换定理图示
说明: (1)置换定理要求置换后的电路有惟一解; 置换定理要求置换后的电路有惟一解; 置换定理要求置换后的电路有惟一解 (2)除被置换部分发生变化外,其余部分在置换前后必须保持完全相同; 除被置换部分发生变化外, 除被置换部分发生变化外 (3)若电路中某两点间电压为零,则可将量值为零的电压源接于该两点间, 若电路中某两点间电压为零,则可将量值为零的电压源接于该两点间, 若电路中某两点间电压为零 相当于将该两点短路;若电路中某支路电流为零, 相当于将该两点短路;若电路中某支路电流为零,则可将量值为零的电流 源串接于该支路,相当于将该支路断开。 源串接于该支路,相当于将该支路断开。
第3章 电路定理
提要 本章介绍电路理论中的几个常用定理。首先介绍置换定理; 本章介绍电路理论中的几个常用定理。首先介绍置换定理;然 后介绍齐性定理和叠加定理;它们是体现线性电路特点的重要定理, 后介绍齐性定理和叠加定理;它们是体现线性电路特点的重要定理,是 线性方程的齐次性和可加性在电路中的体现;其次介绍戴维南定理和诺 线性方程的齐次性和可加性在电路中的体现; 顿定理,它们是化简线性一端口电路的有效方法; 顿定理,它们是化简线性一端口电路的有效方法;最后介绍与基尔霍夫 定律同样适用的特勒根定理,并以此证明互易定理。 定律同样适用的特勒根定理,并以此证明互易定理。
0.5' I I' 2Ω U 'S 1 1Ω US2 IS (b) 1Ω + U' −
0.5" I I" 2Ω 1Ω + 1Ω (c) U" −
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答案3.1解:应用置换定理,将电阻R 支路用0.5A I =电流源代替,电路如图(b)所示。
I2对电路列节点电压方程:1212(1)0.5A 44n n I U U +Ω⨯-=-ΩΩ12116V(1)3 4.5 4.5n n U U -+Ω++⨯=ΩΩΩ0.5A I =解得11V n U =则12n UR I==Ω答案3.2解:(a ) 本题考虑到电桥平衡,再利用叠加定理,计算非常简单。
(1)3V 电压源单独作用,如图(a-1)、(a-2)所示。
(a-1)(a-2)由图(a-2)可得'3V1A 148348I ==⨯Ω+Ω+由分流公式得:''182A 483I I Ω=-⨯=-Ω+Ω(2)1A 电流源单独作用,如图(a-3)所示。
(a-3)考虑到电桥平衡,"0I =,在由分流公式得:"1131A A 134I =-⨯=-+(3)叠加:'"1A I I I =+= '"11117/12A I I I =+=-2111 2.007W P I Ω=⨯=(b )(1)4V 电压源单独作用,如图(b-1)所示。
'2I '(b-1)由图(b-1)可得,'24V2V (2+2)U Ω⨯==Ω'136A I U =-=- ''21'5A I I I =+=-(2)2A 电流源单独作用,如图(b-2)所示。
(b-2)''222A=2V 22U ⨯=Ω⨯+ "''2311A 2I I =⨯=对节点②列KCL 方程得,"""1132A 4A I U I +==对节点③列KCL 方程得,"""230I I U ++=解得"5A I =(3) 叠加'"1116A 4A=10A I I I =+=---'"5A 5A=10A I I I =+=---2111100W P I Ω=⨯Ω=答案3.3解 :利用叠加定理,含源电阻网络中的电源分为一组,其作用为'I,如图(b)所示。
S I 为一组,其单独作用的结果I '' 与S I 成比例,即:"S I kI =,如图(c)所示。
IIskI (a)(b)(c)+'"'S I I I I kI =+=+ (1)将已知条件代入(1)式得''04A 1A 2AI k I k ⎧=+⨯⎪⎨-=+⨯⎪⎩联立解得:'2A I =,12k =即:S 12A+2I I =-⨯将1A I =代入,解得S 6A I =答案3.4解:(1)125V U U ==时,电路对称,12n n U U =,可化简成图 (b)所示。
1U 2U (b)Ω41U 2U (a)对电路列节点电压方程,得1211(11)S 1.511n U U U ++⨯=+ΩΩ1 3.75V n U =o 11 2.5V (10.5)n U U Ω=⨯=+Ω(2)当123V U U =-=时,0.5Ω上电流为零,图(a)电路可化简成图(c)所示。
Ω41U 1U -(c)由分压公式得12114//4[()]3V 1(4//4)1U U U ΩΩ=--=Ω+ΩΩ+Ω解得o 12/2 1.5V U U ==(3)当18V U =,22V U =时,可看作1(53)V U =+,2(53)V U =-,即可视(a)、(b)电路所加激励之和。
应用叠加定理,o oo 2.5V 1.5V 4V U U U '''=+=+= 注释:差模或共模电压作用于对称电路时,可以采用简便计算方法;将一般电压分解成差模分量与共模分量代数和,再应用叠加定理也可简化计算。
答案3.5解:根据叠加定理,将图(a)等效成图 (b)与图 (c)的叠加。
I(b)2(c)由已知条件得S11S128W14V 2AI P U I '=== 28V U '= 112V U ''=22254W18V 3AS I S P U I ''=== 所以12S S I I 、共同作用时11126V U U U '''=+= 22226V U U U '''=+=每个电源的输出功率分别为S1S1152W I P I U == S2S2278W I P I U ==答案3.6解:应用戴维南定理或诺顿定理(1) 图(a)电路求开路电压和等效电阻,分别如图(a-1)和图(a-2)所示。
OC 3A 5(5V)10V U =⨯Ω+-=OCU +-i(a-1)(a-2)(a-3)图(b )电路等效过程如下:(b-1)OC(b-2)(b-3)OC 10A 540V 90V U =⨯Ω+= i 5R =Ω图(c )电路等效过程如下:OC U +-(c-1)5ΩiR (c-3)(c-2)OC 1A 510V 15V U =⨯Ω+= i 5R =Ω图(d )电路等效过程如下:OCiR (d-1)(d-2)(d-3)OC 10A 550V 100V U =⨯Ω+= i 5R =Ω图(e )电路等效过程如下:(e-1)iR (e-2)(e-3)图(f )电路等效过程如下:OCU +-iR (f-1)(f-2)(f-3)图(g )电路等效过程如下:1(g-1)1(g-2)i(g-3)图(h )电路等效过程如下:(h-3)(h-2)(h-1)OC U +-如果电路的等效内阻为非零的确定值,则电路既存在戴维南等效电路,又存在诺顿等效电路;如果电路的等效内阻为零,则只能等效成戴维南电路;如果电路的等效内阻为无穷大,则只能等效成诺顿电路。
答案3.7abab(a-1)(b-1)'解:(a)(1)求开路电压OC U开路时,对节点①由KCL ,20I I -+=,0I =开路电压OC 8V-10=8V U I =Ω(2)求等效电阻求i R 时8V 独立电压源置零,外加电压U ',如图(a-1)所示 。
由 KVL 得'10U I =-Ω对节点①由KCL 得,'2I I I I =-=''1010i U I R I I-Ω===-Ω(b)(1)求开路电压对节点①列KCL 方程211A I I =- (1)对回路1l 列KVL 方程得OC 1112108U I I I =-Ω+Ω=Ω (2)对回路2l :12101020V I I Ω-Ω= (3)将式(1)代入式(3),与式(2)联立,解得1 1.5A I = OC 12V U =(2)求等效电阻求i R 时将独立源置零,外加激励电流I 求ab 端口响应电压f U ,如图(b-1)所示。
由图(b-1)可知,112I I = (1)对回路1l 列KVL 方程'112108U I I I =-Ω+Ω=Ω (2)将式(1)代入式(2),得4i UR I ==Ω答案3.8解:将含源电阻网络化为戴维南等效电路,如图 (b)所示。
由此图求得:U +-U +-(b)OCi ()U U R R R=⨯+ (1) 将10R =Ω时,15V U =;20R =Ω,20V U =代入式(1),得OC iOC i 15V ()101020V ()2020U R U R ⎧=⨯Ω⎪+Ω⎪⎨⎪=⨯Ω⎪+Ω⎩联立解得:10i R =Ω 30V oc U =(1) 式可表示为30V()10U R R=⨯Ω+当30R =Ω时30V3022.5V (1030)U =⨯Ω=+Ω注释:一端口外接电路发生变化时,宜采用戴维南或诺顿定理进行分析。
答案3.9首先将开关右侧电路化简为戴维南等效电路,如图(b)所示,其开路电压为3V ,等效电阻为10ΩR 10Ω(b)开关断开时=13V U 得:OC i 13V 13V 3V1A 10U R --==Ω开关短接时=3.9A I 得:OC i 3V3.9A 10U I R =+=Ω联立求解得:OC 18V U = ,i 5R =Ω答案3.10解:将含源电阻网络等效为戴维南电路。
如图(b )所示。
负载电阻R 消耗的功率可表示为bU +-2OC i ()R U P R R R=⨯+ (1) 将已知条件分别代入(1)式,得2OC i2OC i ()1022.5W 10()2020W 20U R U R ⎧⨯Ω=⎪+Ω⎪⎨⎪⨯Ω=⎪+Ω⎩ 联立解得i 10R =Ω OC 30V U =当30R =Ω时22OC i 30V ()303016.9W 30(1030)R U P R ⎛⎫=⨯Ω=⨯Ω≈ ⎪+Ω+Ω⎝⎭答案3.11解:将图(a )电路化简如图(b )所示。
S I6(b)-+UOC62(62)S iI U U R Ω-=⨯Ω+Ω+代入两个已知条件:2A S I =时,0U =: OC 62A 12V U =Ω⨯=S 0I =时,2V U =-: OC i i 2V(8)8V+1A 2U R R -=-Ω+⨯=⨯Ω解得:OC 12V U = i 4R =Ω答案3.12解:(1)根据叠加定理和齐性定理,将电流I 写成一般表达式S I I I KI I '''''=+=+ (1)式中,SI KI '=是电流源单独作用时产生的电流;I ''是N 内独立电源作用产生的电流。
由已知条件得1.2mA 0K I ''=⨯+1.4mA 10mA K I ''=⨯+解得0.02K =, 1.2mA I ''= 代入式(1)得S 0.02 1.2mA I I =+所以当S 15mA I =时0.0215mA 1.2mA 1.5mA I =⨯+=(2)将22'左边等效成戴维南电路。
如图(b )所示U +-R Rb由(1)的计算结果得OC o ()(50100) 1.5mA 225mV U R R I =+=+Ω⨯=当R 改为Ω200时,OC o 225mV0.9mA (50200)U I R R ===++Ω答案3.13解:将开关S 左侧的电路化为最简等效电路。
3S (a)(b)6iR(c)ocU A由题意得(1)求开路电压OC U由图(a )可知,开路电压为3Ω电阻两端电压,即OC 35A=15V U =Ω⨯(2)求等效电阻i R将独立电压源置零,对3个2Ω电阻联接做星-三角变换。
电路如图 (b)所示。
()()i 3//6//6//62 1.5R =ΩΩΩΩ⨯=Ω亦可利用电桥平衡原理,电路如图 (c)所示,ab 间电位相等,等效电阻为i [(2//6)2]//3 1.5R =ΩΩ⨯Ω=Ω(3)开关闭合后电路如图(d )所示。
