哈工大电路原理基础课后习题
哈工大电路理论基础课后习题答案1

i2 3A 0.5A 2.5A
节点②:
i1 i2 i3 2.5A 2A 4.5A
对回路 l 列 KVL 方程:
10 i2 5 3A u 8V
得
u 32V 电压源发出的功率
P US 8V i1 8V 4.5A 36W
得
u2 280V
网络 N 吸收的功率
PN uN 3A 30W
电流源发出的功率
P iS u2 5A 1400W
注释:根据电流源的特性, 图中与电流源串联的电阻只影响电流源端电压或者说 只影响电流源提供的功率。 答案 1.11 解:设各元件电压电流方向如图所示。
i2 3A 0.5A 2.5A
i2 8A 3A 1A 2A 4A
① 1A
A
⑤
i2
3A
8A
i1
i3 ④ ② i4
2A
B
③ (b)
答案 1.5 解:如下图所示
5V i1
②
l3 1A
①
2A
l1 l2
7V
1A
i4
⑤ 1A ③
6V
l4 8V
i2
④
i3
(1)由 KCL 方程得 节点①:
i1 2A 1A 3A
①
i1 10 + 5A 5 u2 l2 10V l1 -
3A
50
N
25V
对节点①列 KCL 方程
i1 5A 3A 2A
对回路列 KVL 方程 回路 l1 :
i1 10 3A 5 uN 25V 10V
哈工大电路习题答案第6章

答案6.1解:将i和i3改写为余弦函数的标准形式,即2i4cos(t190)A4cos(t190180)A4cos(t10)A2i5sin(t10)A5cos(t1090)A5cos(t80)A3电压、电流的有效值为1002U70.7V,I1.414A12245I2.828A,I3.54A2322初相位10,100,10,80uiii123相位差1ui1010090u与i1正交,u滞后于i1;12ui10100u与i2同相;23ui10(80)90u与i3正交,u超前于i33答案6.2au10cos(t10)V.-822bU610arctg10233.1V,u102cos(t233.1)V-622-20.8cI0.220.8arctg20.889.4A,i20.8cos(t89.4)Am0.2dI30180A,i302cos(t180)A答案6.3解:(a)利用正弦量的相量表示法的线性性质得:UI111n,UIn22(b)磁通相量通常用最大值表示,利用正弦量的相量表示法的微分性质得:UjNmm(c)利用正弦量的相量表示法的线性性质与微分性质得:URIjLI答案6.4解:由KCL得电流i的振幅相量IIIIm1m2m3m(2100410580)A(0.347j1.973.939j0.6950.868j4.924)A526.86A电流i的瞬时值为i5cos(t26.86)A答案6.5解:电压表和电流表读数为有效值,其比值为阻抗模,即2()2/RLUI将已知条件代入,得22R(2π50L) 100V 15A22R(2π100L)100V 10联立方程,解得L13.7mH,R5.08答案6.6解:(a)RC串联电路中电阻电压与电容电压相位正交,各电压有效值关系为2222UU2U15040V30V电流i的有效值为IIC UXC30V103A(b)UXICC302A60VI R UR60V500.3ARC并联电路中电阻电流与电容电流相位正交,总电流有效值为22221.222.33IIIAACR(c)UXI301A30VCCC由U30VCUUXII2ALCLLX15L并联电容、电感上电流相位相反,总电流为III1ALC电阻电压与电容电压相位正交,总电压为:2230240250UUUVVCR答案6.7解:感抗XL L3210rad/s0.1H200容抗X C 11C36210rad/s510F100图(a)电路的相量模型如图(b)所示。
哈工大数字电路书后答案第4章
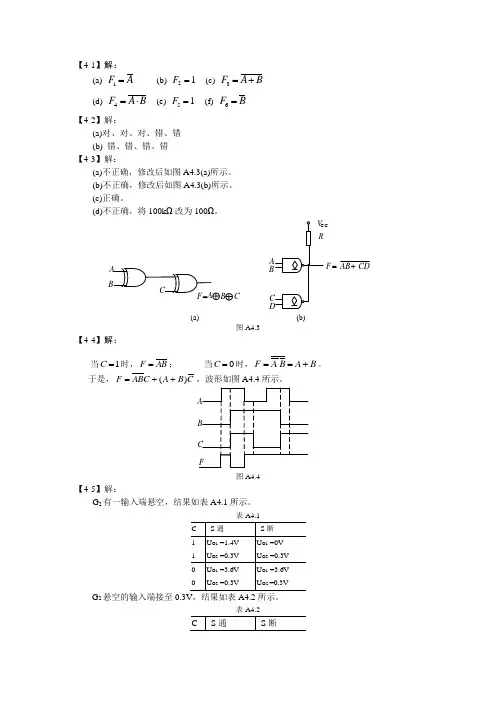
(a) 图 A4.3
(b)
【4-4】解: 当 C = 1 时, F = AB ; 当 C = 0 时, F = A B = A + B 。
于是, F = ABC + ( A + B )C ,波形如图 A4.4 所示。
图 .4
【4-5】解: G2 有一输入端悬空,结果如表 A4.1 所示。
表 A4.1 C 1 1 0 0 S通 UO1 =1.4V UO2 =0.3V UO1 =3.6V UO2 =0.3V S断 UO1 =0V UO2 =0.3V UO1 =3.6V UO2 =0.3V
1.4 V 1.4 V 1.4 V 1.4 V 1.4 V
0.3 V 0.3 V 0.3 V 0.3 V 0.3 V
【4-7】解: 电压表读数 V1=1.4V,V2=1.4V,V3=0.3V,V4=3V,V5=0.3V。 【4-8】解: 当 C=0 时, 输出端逻辑表达式为 F= A + B ; C=1 时, = A , 当 F 即, = A + B C + A C。 F 波形如图 A4.8 所示。
解答 问题 1.G1 悬空 2.波段开关 S 接到①端 3.波段开关 S 接到②端 4.波段开关 S 接到③端 5.波段开关 S 接到④端 表 A4.3 C=0 C=1 uO 万用表的读数 uO
万用表的读数 0.3 V 0.3 V 1.4 V 1.4 V 0.3 V
3.6 V 3.6 V 0.3 V 0.3 V 3.6 V
G2 悬空的输入端接至 0.3V,结果如表 A4.2 所示。
表 A4.2
C
S通
S断
1 1 0 0
UO1 =0.3V UO2 =3.6V UO1 =3.6V UO2 =3.6V
电路理论基础课后答案(哈工大陈希有)第9章
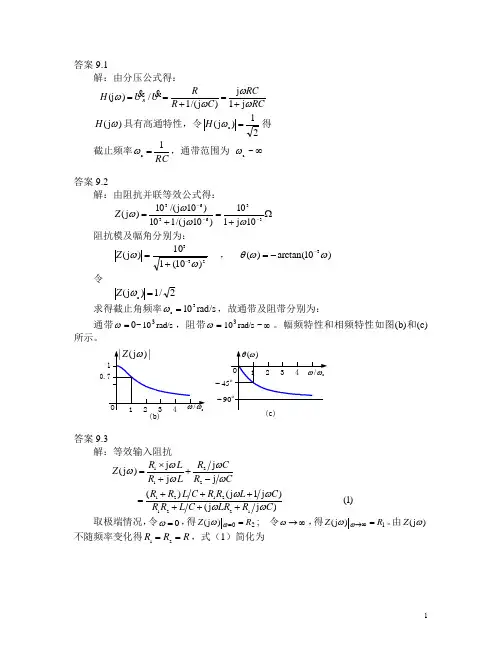
答案9.1解:由分压公式得:U U H R/)(j =ωRCRC C R R ωωωj 1j )j /(1+=+= )j (ωH 具有高通特性,令21)j (c =ωH 得截止频率RC1c =ω,通带范围为∞~c ω答案9.2解:由阻抗并联等效公式得:Ω+=+=---33636310j 110)10j /(110)10j /(10)j (ωωωωZ 阻抗模及幅角分别为:233)10(110)j (ωω-+=Z , )10arctan()(3ωωθ--= 令2/1)j (c =ωZ求得截止角频率rad/s 103c =ω,故通带及阻带分别为:通带=ω0~rad/s 103,阻带=ωrad/s 103~∞。
幅频特性和相频特性如图(b)和(c)所示。
(b)--答案9.3解:等效输入阻抗)1()j j ()j 1j ()(j j j j )j (122121212211C R LR C L R R C L R R C L R R CR CR L R L R Z ωωωωωωωωω++++++=-++⨯=取极端情况,令0=ω,得20)j (R Z ==ωω; 令∞→ω,得1)j (R Z =∞→ωω。
由)j (ωZ 不随频率变化得R R R ==21,式(1)简化为)j 1j ()j 1j (2)j 1j ()j 1j (2)j (22C L RC L R C L R CL RC L R C L R C L R C L R Z ωωωωωωωωω+++++=+++++= 由)j (ωZ 为实数得:CL R R C L R R C L =+=2,2 故当C L R R ==21时端口电流与端口电压的波形相似,此时C L Z =)j (ω。
答案9.4解: RC 并联的等效阻抗RCRC R C R Z RC ωωωj 1j /1j /+=+=RC RCZ L Z U U H +==ωωj /)j (12 RL LC RC L R R /j 11)j 1(j 2ωωωω+-=++= 幅频特性222)/()1(1)j (R L LC H ωωω+-=当0→ω时,1)j (=ωH ;当∞→ω时,0)j (=ωH所以它具有低通特性。
第9章习题解答哈工大习题册

第9章 线性动态电路暂态过程的复频域分析9.1根据定义求()()f t t t ε=和()e ()at f t t t ε-=的象函数。
解:(1)2020001e 1d e 1e d e )()(-s s t s stt t t s F stst stst =-=+-==∞-∞-∞-∞----⎰⎰ε (2)20)(20)(00)(1e)(1d e 1e d e )(e )(-ααααεααα+=+-=+++-==∞+-∞+-∞-∞-----⎰⎰s s ts s t t t t s F ts t s st st t9.2 求下列函数的原函数。
(a)6512)(2+++=s s s s F , (b) )2)(1(795)(23+++++=s s s s s s F , (c) 623)(2++=s s s F 。
解:(a) 6512)(2+++=s s s s F 3221+++=s A s A 3|31221-=++=-=s s s A , 3|31221-=++=-=s s s A所以 t t s s t f 321e 5e 3}3523{)(---+-=+++-=L(b))2)(1(795)(23+++++=s s s s s s F 212)2)(1(3221+++++=+++++=s A s A s s s s s 2|2311=++=-=s s s A 1|1321-=++=-=s s s A 所以 t t t t s s s L t f 21e e 2)(2)(}21122{)(----++'=+-++++=δδ(c)623)(2++=s s s F 22)5()1(5)5/3(++⨯=s , 查表得)5sin(e 53)(t t f t -= 9.3求图示电路的等效运算阻抗。
图题9.3解:由运算电路(略)求得端口等效运算阻抗为:11262241)3/(142)]3/(14[21)(22i ++++=++++=s s ss s s s s s Z , 112611430)(22++++=s s s s s Z i 9.4 图示电路,已知2S e ()t u t ε-=V ,求零状态响应u 。
第1章 习题解答 哈工大习题册

第一章 电路元件与电路基本定律1.1 图示电路,设元件A 消耗功率为10W ,求A u ;设元件B 消耗功率为-10W ,求B i ;设元件C 发出功率为-10W ,求C u 。
Au +-10V +-Cu +-(a)(b)(c)图 1.1解:(a)元件A 电压和电流为关联参考方向。
元件A 消耗的功率为A A A p u i =,则A A A 10W 5V 2Ap u i ===,真实方向与参考方向相同。
(b) 元件B 电压和电流为关联参考方向。
元件B 消耗的功率为B B B p u i =,则B B B 10W 1A 10Vp i u -===-,真实方向与参考方向相反。
(c) 元件C 电压和电流为非关联参考方向。
元件C 发出的功率为C C C p u i =,则C C C 10W 10V 1Ap u i -===-,真实方向与参考方向相反。
1.2 图示电路中,电容C = 2F ,电容电压()C u t 的波形如图所示。
(1)求电容电流()C i t ,并绘出波形图; (2)求电容功率表达式,并绘出功率波形图;(3)当t = 1.5s 时,电容是吸收功率还是放出功率?其值是多少?电容储能为多少?u +-图 1-2解:(1)有题可知电容电压的表达式为0201421202c t t t U t t t <⎧⎪<<⎪=⎨-<<⎪⎪>⎩又由电容的性质可知故当t<0时 i =0A0<t<1时1<t<2时 综上所述,可得到电容电流为:故电容电流波形如图1-2-1所示。
(2)电容上所消耗的功率为c c P U I = 当t<0时 0P = 当 0<t<1时 248P t t =⨯=当1<t<2时 4(42)816P t t =-⨯-=- 当t>2时 0P =故功率波形图如图1-2-2所示。
C i(3)t=1.5s 时电容两端电压为421V U t =-=,电容所消耗功率为21121122W CU J ==⨯⨯=由图中电压电流的参考方向可知电容是发出功率且发出功率为4W 。
哈工大电路理论基础课后习题答案3
UOC 35A=15V (2)求等效电阻 Ri
将独立电压源置零,对 3 个 2 电阻联接做星-三角变换。电路如图 (b)所示。
Ri 3 // 6 // 6 // 6 2 1.5
亦可利用电桥平衡原理,电路如图 (c)所示,ab 间电位相等,等效电阻为
等效电阻
Ri
US IS
10 11
又由已知条件得
U OC
(Ri
2)
I1
160 11
V
简化后的电路如图(c)所示。
所以当 R 4 时
I1
UOC R Ri
(160 /11)V (4 10 /11)
80 A 2.963A 27
将 I1 用电流源来置换,用叠加定理分析置换后的电路,即将 I 2 分解成 I2 I2 I2 。
4
(1) (2)
答案 3.8 解:将含源电阻网络化为戴维南等效电路,如图 (b)所示。由此图求得:
Ri
+
+
RU
U OC
-
-
(b)Leabharlann U ( UOC ) R(1)
Ri R
将 R 10 时,U 15V ; R 20 ,U 20V 代入式(1),得
15V 20V
( Ri (
U OC 10
U OC
) 10 ) 20
Ri 20
联立解得:
Ri 10 (1) 式可表示为
Uoc 30V
U ( 30V ) R 10 R
当 R 30 时
U 30V 30 22.5V (10 30)
注释:一端口外接电路发生变化时,宜采用戴维南或诺顿定理进行分析。
答案 3.9 首先将开关右侧电路化简为戴维南等效电路,如图(b)所示,其开路电压为 3V,
哈尔滨理工大学电路1-9章习题集答案解析
第一章(电路模型和定律)习题解答一、选择题1.KVL 和KCL 不适用于 D 。
A .集总参数线性电路;B .集总参数非线性电路;C .集总参数时变电路;D .分布参数电路2.图1—1所示电路中,外电路未知,则u 和i 分别为 D 。
A .0==i u uS ,; B .i u u S ,=未知;C .0=-=i u uS ,; D .i u u S ,-=未知3.图1—2所示电路中,外电路未知,则u 和i 分别为 D 。
A .S i i u =∞=, ;B .S i i u -=∞=, ;C .S i i u =未知, ; D .S i i u -=未知,4.在图1—3所示的电路中,按照“节点是三条或三条以上支路的联接点”的定义,该电路的总节点个数为 A 。
A .5个;B .8个;C .6个;D .7个5.在图1—4所示电路中,电流源发出的功率为 C 。
A .45W ;B .27W ;C .–27W ;D .–51W二、填空题1.答:在图1—5所示各段电路中,图A 中电流、电压的参考方向是 关联 参考方向;图B 中的电流、电压的参考方向是 非关联 参考方向;图C 中电流、电压的参考方向是 关联 参考方向;图D 中电流、电压的参考方向是 非关联 参考方向。
2.答:图1—6所示电路中的u 和i 对元件A 而言是 非关联 参考方向;对元件B 而言是 关联 参考方向。
3.答:在图1—7所示的四段电路中,A 、B 中的电压和电流为关联参考方向,C 、D中的电压和电流为非关联参考方向。
4.答:电路如图1—8所示。
如果10=R Ω,则10=U V ,9-=I A ;如果1=R Ω,则 10=U V ,0=I A 。
5.答:在图1—9 (a)所示的电路中,当10=R Ω时,=2u 50V ,=2i 5A ;当5=R Ω时,=2u 50V , =2i 10A 。
在图1—9 (b)所示的电路中,当R =10Ω时,2002=u V ,202=i A ;当5=R Ω时,1002=u V, 202=i A 。
电路基本理论课后答案(哈工大版)第10章
答案10.1解:0<t 时,电容处于开路,故V 20k 2m A 10)0(=Ω⨯=-C u 由换路定律得:V 20)0()0(==-+C C u u换路后一瞬间,两电阻为串联,总电压为)0(+C u 。
所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得:m A 5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解:0<t 时电容处于开路,电感处于短路,Ω3电阻与Ω6电阻相并联,所以A 3)363685(V45)0(=Ω+⨯++=-i ,A 2)0(366)0(=⨯+=--i i L V 24)0(8)0(=⨯=--i u C 由换路定律得:V 24)0()0(==-+C C u u ,A 2)0()0(==-+L L i i 由KVL 得开关电压:V 8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u 答案10.3解:0<t 时电容处于开路,0=i ,受控源源电压04=i ,所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C0>t 时,求等效电阻的电路如图(b)所示。
等效电阻Ω=++-==5)36(4i ii i i u R时间常数s 1.0i ==C R τ0>t 后电路为零输入响应,故电容电压为:V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为:V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4解:0<t 时电感处于短路,故A 3A 9363)0(=⨯+=-L i ,由换路定律得: A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。
(b)等效电阻Ω=+⨯+=836366i R ,时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应,故电感电流为A e 3e )0()(2/t t L L i t i --+==τ)0(≥t 电感电压V e 24d d )(21t L tiL t u --==)0(>tΩ3电阻电流为A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为:W 3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解:由换路定律得0)0()0(==-+L L i i ,达到稳态时电感处于短路,故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。
第3章 习题解答 哈工大习题册
第3章 电路定理3.1 如图所示电路,已知0=ab U ,求电阻R 的值。
a图3-1解:由题,0=ab U ,故53V1A 3I ==Ω,电流比为24842I I ==,134I R I =对回路1l 列KVL 方程可得 11520V 42()I I I =Ω+Ω+ 解得:13AI =所以215314A I I I =+=+=, 42/41A I I ==,354112A I I I =+=+=134/6R I I =⨯=Ω3.2 用叠加定理求图示电路的电流I 及1Ω电阻消耗的功率。
(a)(b)2图 3-2解: (a ) 本题考虑到电桥平衡,再利用叠加定理,计算非常简单。
(1) 3V 电压源单独作用,如图(a-1)、(a-2)所示。
由图(a-2)可得'3V1A 148348I ==⨯Ω+Ω+由分流公式得: ''182A 483I I Ω=-⨯=-Ω+Ω(2)1A 电流源单独作用,如图(a-3)所示。
考虑到电桥平衡,0I ''=,133(1A)A 134I ''=-⨯=-+ (3)叠加:1A I I I '''=+=,11117/12A I I I '''=+=-2111 2.007WP I Ω=⨯=(a-1)(a-2)(a-3)(b )(1)4V 电压源单独作用,如图(b-1)所示。
24V 2V 22U Ω'=⨯=Ω+Ω,136A I U ''=-=-,125A I I I '''=+=- (2)2A 电流源单独作用,如图(b-2)所示。
'2I '(b-1)(b-2)222A 2V 22U Ω⨯Ω''=⨯=Ω+Ω,22/21A I U ''''== 对节点②列KCL 方程得1234A I U ''''=-=-对节点③列KCL 方程得235A I I U ''''''=-=- (3) 叠加 '"1116A 4A=10A I I I =+=---'"5A 5A=10A I I I =+=---2111100W P I Ω=⨯Ω=注释:不能用各独立源单独作用时电阻消耗的功率之和来计算电阻在电路中消耗的功率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章习题1.1 图示元件当时间t<2s时电流为2A,从a流向b;当t>2s时为3A,从b流向a。
根据图示参考方向,写出电流的数学表达式。
1.2图示元件电压u=(5-9e-t/τ)V,τ>0。
分别求出t=0 和t→∞时电压u的代数值及其真实方向。
图题1.1 图题1.21.3 图示电路。
设元件A消耗功率为10W,求;设元件B消耗功率为-10W,求;设元件C发出功率为-10W,求。
图题1.31.4求图示电路电流。
若只求,能否一步求得?1.5 图示电路,已知部分电流值和部分电压值。
(1) 试求其余未知电流。
若少已知一个电流,能否求出全部未知电流?(2) 试求其余未知电压u14、u15、u52、u53。
若少已知一个电压,能否求出全部未知电压?1.6 图示电路,已知,,,。
求各元件消耗的功率。
1.7 图示电路,已知,。
求(a)、(b)两电路各电源发出的功率和电阻吸收的功率。
1.8 求图示电路电压。
1.9 求图示电路两个独立电源各自发出的功率。
1.10 求网络N吸收的功率和电流源发出的功率。
1.11 求图示电路两个独立电源各自发出的功率。
1.12 求图示电路两个受控源各自发出的功率。
1.13 图示电路,已知电流源发出的功率是12W,求r的值。
1.14 求图示电路受控源和独立源各自发出的功率。
1.15图示电路为独立源、受控源和电阻组成的一端口。
试求出其端口特性,即关系。
1.16 讨论图示电路中开关S开闭对电路中各元件的电压、电流和功率的影响,加深对独立源特性的理解。
第二章习题2.1 图(a)电路,若使电流A,,求电阻;图(b)电路,若使电压U=(2/3)V,求电阻R。
2.2 求图示电路的电压及电流。
2.3 图示电路中要求,等效电阻。
求和的值。
2.4求图示电路的电流I。
2.5 求图示电路的电压U。
2.6 求图示电路的等效电阻。
2.7 求图示电路的最简等效电源。
图题2.72.8 利用等效变换求图示电路的电流I。
(a) (b)图题2.82.9 求图示电路的等效电阻R。
2.10 求图示电路的电流和。
2.11列写图示电路的支路电流方程。
图题2.112.12 图示电路,分别按图(a)、(b)规定的回路列出支路电流方程。
图题2.122.13 用回路电流法求图示电路的电流I。
2.14 用回路电流法求图示电路的电流I。
图2.13 图2.142.15用回路电流法求图示电路的电流。
图题2.15 图题2.162.16 图示电路,列出回路电流方程,求 为何值时电路无解。
2.17 图示电路,分别按图(a)、(b)规定的回路列出回路电流方程。
图题2.172.18 图示电路中当以④为参考点时,各节点电压为U n1=7V,U n2=5V,U n3=4V,U n4=0。
求以①为参考点时的各节点电压。
2.19 图示电路中已知部分支路电压及节点①、③之间的电压,求各节点电压。
2.20用节点电压法求图示电路5A电流源发出的功率。
图题2.20 图题2.21 2.21 图示电路,用节点电压法求1A电流源发出的功率。
2.22 列出图示电路的节点电压方程。
2.23 列出图示电路的节点电压方程。
图题2.22 图题2.23 2.24 用改进节点电压法求图示电路的电流I。
图题2.242.25 列出图示电路的改进节点电压法方程。
图题2.25 图题2.262.26 用任意方法求图示电路的电流和。
2.27 求图示电路的输出电压。
图题2.27 图题2.282.28 求图示电路运算放大器的输出电流。
2.29 用节点分析法求图示电路的电压增益。
图题2.29 图题2.302.30 求图示电路的输出电压。
2.31 根据所学知识,设计一个4输入单输出的数模转换器(DAC),即输出电压与输入电压的关系为。
第三章习题3.1 图示电路,已知A,求电阻R。
3.2 用叠加定理求图示电路的电流I及电阻消耗的功率。
3.3 图示电路,当I S = 2A 时,I = -1A;当I S= 4A 时,I = 0。
若要使I = 1A,I S应为多少?3.4 图示电路具有对称性,为两个输入电压。
(1)若(称为共模输入),计算输出电压。
(2)若(称为差模输入),再计算输出电压。
(3)若,将输入电压分解成,求出后再利用(1)、(2)的计算结果求此时输出电压。
3.5图示电路中,N为无独立源二端口网络。
(1)当I S1 = 2A,I S2 = 0时,I S1输出功率为28W,且U2 = 8V;(2)当I S1 = 0,I S2 = 3A时,I S2的输出功率为54W,且U1=12V。
求当I S1=2A,I S2=3A 共同作用时每个电流源的输出功率。
3.6求图示各电路的戴维南等效电路或诺顿等效电路。
通过这些实例,研究哪些电路既存在戴维南等效电路,又存在诺顿等效电路,哪些电路只能具有一种等效电路。
试总结其规律。
3.7 求图示含受控源电路的戴维南与诺顿等效电路。
3.8 图中N为含独立源电阻网络,开关断开时量得电压,接通时量得电流求网络N的最简等效电路。
3.9 已知图示电路中时,其消耗的功率为22.5W;时,其消耗的功率为20W。
求时它所消耗的功率。
3.10图示电路N为线性含源电阻网络,已知当时,;时,。
求网络N的戴维南等效电路。
3.11图示电路中N为线性含源电阻网络,。
已知当时,;时,I=1.4mA,22'的输出电阻为。
(1)求当时,I为多少?(2)在时,将R改为200Ω,再求电流I。
3.12 图示电路中N为线性含源电阻网络。
已知当时,U=15V;R=20Ω时,U=20V。
求R=30Ω时,U=?3.13 图示电路,已知当开关S断开时,I = 5A 。
求开关接通后I = ?3.14 图示电路,已知当R=2Ω时,I1=5A,I2=4A。
求当R=4Ω时I1和I2的值。
3.15 图示电路,已知U=8V,R=12Ω。
求电流I和I1的值。
3.16 图示电路中,N为线性含源电阻网络。
已知时,;时,。
端戴维南等效电阻为。
求电流与电阻R的一般关系。
3.17 图示电路中N 为纯电阻网络,利用特勒根定理求出电流I。
3.18 图中N为互易性网络。
试根据图中已知条件计算电阻R。
3.19 用互易定理求图示电路电压U。
3.20 图示电路电流I可以写成I=K1U1+K2U2+K3U3+K4U4 。
试借助互易定理求各比例系数K i(i= 1,…,4 )。
第四章习题4.1 图示电路,已知(单位:V,A),。
求电流。
4.2图示电路,已知(单位:V,A)。
试求电压U。
4.3图示电路,已知(单位:A,V) ( U 1) ,(单位:A,V) (U2)。
求I1和U 1。
4.4 设图示电路中非线性电阻均为压控的,I1=f1(U1),I2=f2(U2)。
列出节点电压方程。
4.5设图示电路中非线性电阻均为流控的,U1=f1(I1),U2=f2(I2)。
列出回路电流方程。
4.6图示电路中非线性电阻的特性为U1=f1(I1)(流控的),I2=f2(U2)(压控的)。
试列出改进节点法方程。
4.7图示电路中两个非线性电阻的伏安特性为(单位:A,V),(单位:V,A)。
试列出求解U1及I2的二元方程组。
4.8图示电路,设(单位:A,V)。
试用牛顿-拉夫逊法求出电压U,要求准确到10 -3V。
4.9图示电路,设I=10 -4 (e 20U+e -20U)A。
试用牛顿-拉夫逊法求电压和电流,要求电压准确到10-3V。
初值分别为和。
4.10图示电路,设非线性电阻特性如图(b)所示。
试求电压U的值。
*4.11图题4.11(a)电路中两个非线性电阻的伏安特性分别如图(b)、(c)所示。
试求电流。
4.12图示电路中二极管特性近似用(单位:A,V)表示。
(1) 求U2与U1的关系。
(2) 10 电阻与二极管交换位置后,再求U2与U1的关系。
第五章习题5.1图(a)所示电容。
(1)设电压如图(b)所示,求出电流i。
(2)设电流如图(c)所示,且t=0 时已存有0.5C的电荷,求出t=3.5s时的电压u。
图题5.15.2图示电容网络,已知。
(1)求等效电容。
(2)设各电容原未充电,,求各电容储存的电场能量。
图题5.2 图题5.35.3 图示RC串联电路,设u C(0)=0,i(t)=I e-。
求在0<t<时间内电阻消耗的电能和电容存储的电能,并比较二者大小。
5.4 图示电路称为积分器(integrator),求输出电压与输入电压的关系。
5.5 图示电路称为微分器(differentiator),求输出电压与输入电压的关系。
图题5.4 图题5.55.6 已知图示电路中电容储能的变化规律为(t>0)。
试求t>0时的变化规律。
图题5.6 图题5.75.7已知图示电路中。
求控制系数。
5.8设图(a)所示电感中i(0)=1A,现在两端施加图(b)所示电压。
(1) 求时间t为何值时电流i为零。
(2) 求t=4s时电感上的磁链和存储的磁场能。
图题5.8 图题5.95.9 求图示电路中电压的最大绝对值。
5.10图(a)所示电感中,i(0)=0,周期电压u如图(b)。
求t=4s时电感电流值。
5.11 计算图示电路电容和电感各自储存的能量。
图题5.11 图题5.125.12 图示电路已知,。
求电压的变化规律。
5.13 求图示电路的等效电感。
5.14 图(a)所示互感为全耦合。
证明图(b)是它的等效电路,其中。
5.15 证明图(a)所示由电感组成的梯形电路与图(b)所示的含理想变压器电路相互等效,求出及变比n。
5.16图示电路中,要求u2=u1,变比n应为多少?5.17 图示电路,设。
求8Ω电阻消耗的功率。
5.18 求图示电路的等效电容。
第六章习题6.1 已知图示电路中V、A、A、A。
试写出电压和各电流的有效值、初相位,并求电压越前于电流的相位差。
6.2 写出下列电压、电流相量所代表的正弦电压和电流(设角频率为ω):(a)(b)(c)(d)30A6.3 下列各式中电压、电流、磁通、电荷均为同频率的正弦量,设角频率为ω。
试将各式变换为相量形式。
(a),(b)(c)6.4 用相量法计算图题6.1所示电路的总电流。
6.5 图示电路中正弦电流的频率为50Hz时,电压表和电流表的读数分别为100V和15A;当频率为100Hz时,读数为100V和10A。
试求电阻R和电感L。
6.6 图示各电路中已标明电压表和电流表的读数,试求电压和电流的有效值。
6.7 在图示电路中已知A,rad/s。
求各元件的电压、电流及电源电压,并作各电压、电流的相量图。
6.8 在图示电路中各元件电压、电流取关联参考方向。
设=1A,且取为参考相量,画出各电流、电压相量图,根据相量图写出各元件电压、电流相量。
6.9 已知图示电路中V,,,求。
6.10 已知图示电路中的感抗,要求。
