哈工大电路答案第12章
电子电路第十二章习题及参考答案
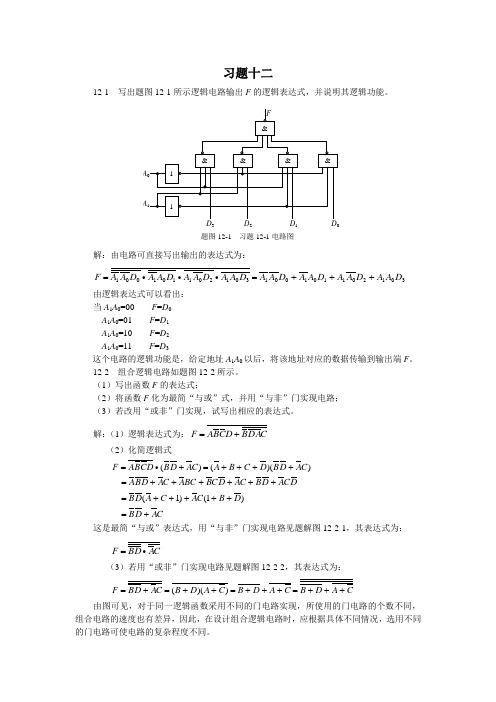
习题十二12-1 写出题图12-1所示逻辑电路输出F 的逻辑表达式，并说明其逻辑功能。
解：由电路可直接写出输出的表达式为：301201101001301201101001D A A D A A D A A D A A D A A D A A D A A D A A F +++==∙∙∙由逻辑表达式可以看出： 当A 1A 0=00 F =D 0 A 1A 0=01 F =D 1A 1A 0=10 F =D 2 A 1A 0=11 F =D 3这个电路的逻辑功能是，给定地址A 1A 0以后，将该地址对应的数据传输到输出端F 。
12-2 组合逻辑电路如题图12-2所示。
（1）写出函数F 的表达式；（2）将函数F 化为最简“与或”式，并用“与非”门实现电路； （3）若改用“或非”门实现，试写出相应的表达式。
解：（1）逻辑表达式为：C A D B D C B A F += （2）化简逻辑式CA DB D BC A C AD B D C A D B C A D C B BC A C A D B A C A D B D C B A C A D B D C B A F +=+++++=++++++=++++=+=∙)1()1())(()(这是最简“与或”表达式，用“与非”门实现电路见题解图12-2-1，其表达式为： C A D B F ∙=（3）若用“或非”门实现电路见题解图12-2-2，其表达式为： C A D B C A D B C A D B C A D B F +++=+++=++=+=))((由图可见，对于同一逻辑函数采用不同的门电路实现，所使用的门电路的个数不同，组合电路的速度也有差异，因此，在设计组合逻辑电路时，应根据具体不同情况，选用不同的门电路可使电路的复杂程度不同。
A A3210题图12-1 习题12-1电路图12-3 组合逻辑电路如题图12-3分析的结果，列成真值表的形式。
解：对于图12-3电路可以写出逻辑函数表达式为：ABCC AB C B ABC C A C B ABC C A F +=++==∙∙ =（AB ）⊙C真值表如右图所示，由真值表可以看出，该电路是实现AB 与C 的“同或”，及当AB 与C 的值相同时，电路输出为“1”，否则输出为“0”。
电路原理课后习题答案.
（d）（e）（f）
题1-4图
解（a）电阻元件，u、i为关联参考方向。
由欧姆定律u=Ri=104i
（b）电阻元件，u、i为非关联参考方向
由欧姆定律u=-Ri=-10i
（c）理想电压源与外部电路无关，故u=10V
（d）理想电压源与外部电路无关，故u=-5V
(e)理想电流源与外部电路无关，故i=10×10-3A=10-2A
电容电流
t=2 ms时
电容的储能为
7-20题7-20图所示电路，开关合在位置1时已达稳定状态，t=0时开关由位置1合向位置2，求t0时的电压 。
题7-20图
解：
用加压求流法求等效电阻
7-26题7-26图所示电路在开关S动作前已达稳态；t=0时S由1接至2，求t0时的 。
题7-26图
解：由图可知，t>0时
题4-5图
4-9求题4-9图所示电路的戴维宁或诺顿等效电路。
（a）
（b）
题4-9图
解：(b)题电路为梯形电路，根据齐性定理，应用“倒退法”求开路电压 。设 ，各支路电流如图示，计算得
故当 时，开路电压 为
将电路中的电压源短路，应用电阻串并联等效，求得等效内阻 为
4-17题4-17图所示电路的负载电阻 可变，试问 等于何值时可吸收最大功率？求此功率。
题2-1图
解：(1) 和 并联，其等效电阻 则总电流
分流有
(2)当
(3)
2-5用△—Y等效变换法求题2-5图中a、b端的等效电阻：（1）将结点①、②、③之间的三个9电阻构成的△形变换为Y形；（2）将结点①、③、④与作为内部公共结点的②之间的三个9电阻构成的Y形变换为△形。
题2-5图
解（1）变换后的电路如解题2-5图（a）所示。
电工与电子技术12章_陶桓齐_课后习题答案
第12章习题解答12-1 已知由与非门组成的基本RS触发器和输入端D R、D S的波形如题图12-1所示，试对应地画出Q和Q的波形，并说明状态“不定”的含义。
题图 12-1解：12.2 已知可控RS触发器CP、R和S的波形如题图12-2所示，试画出输出Q的波形。
设初始状态分别为0和1两种情况。
题图12-2解：12-3 在主从结构的JK触发器中，已知CP、J、K的波形如题图12-3所示，试画出Q端的波形。
设初始状态Q=0。
题图12-3解：12-4 维持阻塞型D触发器的输入D和时钟脉冲CP的波形如题图12-4所示，试画出Q端的波形。
设初始状态Q = 0。
题图12-4解：12-5 在T触发器中，已知T和CP的波形如题图12.5所示，试画出Q端的波形。
设初始状态Q= 0。
题图12-5解：12-6 写出题图12-6所示电路的逻辑关系式，说明其逻辑功能。
题图12-6解：逻辑关系为：Q D AQ BQ==+所以其功能为JK触发器。
12-7 如题图12-7所示的电路和波形，试画出D端和Q端的波形。
设初始状态Q= 0。
题图12-7解：12-8 将主从型JK触发器转换为T'触发器有几种方案？画出外部连线图。
解：12-9 电路如题图12-9所示。
画出Q0端和Q1端在六个时钟脉冲CP作用下的波形。
设初态Q=Q0= 0。
1题图12-9解：12-10 用题图12.10(a)所给器件构成电路，并在示波器上观察到如图12.10（b）所示波形。
试问电路是如何连接的？请画出逻辑电路图。
(a) (b)题图12-10解：12-11 已知如题图12.11(a)所示电路的各输入端信号如题图12-11(b)所示。
试画出触发器输出端Q0和Q1的波形。
设触发器的初态均为0。
(a) (b)题图12-11解：12-12 已知电路和时钟脉冲CP及输入端A的波形如题图12-12所示，试画出输出端Q、1Q 的波形。
假定各触发器初态为1。
(a) (b)题图12-12解：12-13 已知题图12-13(a)所示电路中输入A及CP的波形如题图12-13(b)所示。
哈工大微波技术12章答案
题 解第 一 章1-1 微波是频率很高，波长很短的一种无线电波。
微波波段的频率范围为8103⨯Hz~12103⨯Hz ，对应的波长范围为1m~0.1mm 。
关于波段的划分可分为粗分和细分两种。
粗分为米波波段、分米波波段、厘米波波段、毫米波波段、亚毫米波段等。
细分为Ka K Ku X C S L UHF 、、、、、、、…等波段，详见表1-1-2。
1-2 简单地说，微波具有下列特点。
（1） 频率极高，振荡周期极短，必须考虑系统中的电子惯性、高频趋肤效应、辐射效应及延时效应；（2） 波长极短，“反射”是微波领域中最重要的物理现象之一，因此，匹配问题是微波系统中的一个突出问题。
同时，微波波长与实验设备的尺寸可以比拟，因而必须考虑传输系统的分布参数效应；（3） 微波可穿透电离层，成为“宇宙窗口”；（4） 量子特性显现出来，可用来研究物质的精细结构。
1-3 在国防工业方面：雷达、电子对抗、导航、通信、导弹控制、热核反应控制等都直接需要应用微波技术。
在工农业方面，广泛应用微波技术进行加热和测量。
在科学研究方面，微波技术的应用也很广泛。
例如，利用微波直线加速器对原子结构的研究，利用微波质谱仪对分子精细结构进行研究，机载微波折射仪和微波辐射计对大气参数进行测量等等。
第 二 章2-1 解 ∵01011Z Z Z Z +-=Γ ∴)(82.811Ω=Z2-2 解图（a ）的输入阻抗021Z Z ab =； 图（b ）的输入阻抗0Z Z ab =；图（c ）的输入阻抗0Z Z ab =；图（d ）的输入阻抗052Z Z ab =； 其等效电路自绘。
2-3 解 ∵01011Z Z Z Z +-=Γ ∵e j j 4121)1(21π=+=Γ 2-4 解（1） ∵e j Z Z Z Z 40101122π=+-=Γ ∴83.511ρ11=Γ-Γ+= （2） ∵π2 =l β∴e e j l -j l 4π) β2(11022=Γ=Γϕ 2-5 解 ∵ljZ Z l jZ Z Z Z tg βtg β10010++= ∴)(39.673.8Ω+=j Z in)(24.6009.2201Ω+=j Z)(1005003Ω+=j Z2-6 证明∵)(00ββe e lj l j U U Γ+=-+ )(00ββ0e e l j l j Z U I Γ-=-+ 而I Z E I Z E U g 0-=-=∴e U E l j 0β2-+= 故2EU =+2-7 证明lZ j l j Z l jZ Z l jZ Z Z in tg β1tg βtg βtg β111001++=++= 而 ρ11min =Z ，对应线长为1min l 故 1min 11min 1tg β1tg βρ1l Z j l j Z ++= 整理得 1min 1min 1tg βρρtgβ1l j l j Z --=2-8 解 ∵38.001011=+-=ΓZ Z Z Z而给定的1Z 是感性复阻抗，故第一个出现的是电压腹点，即λ/4线应接在此处。
哈工大电路理论基础课后习题答案（PDF精品）
答案2.1解：本题练习分流、分压公式。
设电压、电流参考方向如图所示。
(a) 由分流公式得：23A 2A 23I R Ω⨯==Ω+解得75R =Ω(b) 由分压公式得：3V 2V 23R U R ⨯==Ω+解得47R =Ω答案2.2解：电路等效如图(b)所示。
20k Ω1U +-20k Ω(b)+_U图中等效电阻(13)520(13)k //5k k k 1359R +⨯=+ΩΩ=Ω=Ω++由分流公式得：220mA 2mA 20k RI R =⨯=+Ω电压220k 40V U I =Ω⨯= 再对图(a)使用分压公式得：13==30V 1+3U U ⨯答案2.3解：设2R 与5k Ω的并联等效电阻为2325k 5k R R R ⨯Ω=+Ω(1) 由已知条件得如下联立方程：32113130.05(2) 40k (3)eqR U UR R R R R ⎧==⎪+⎨⎪=+=Ω⎩由方程(2)、(3)解得138k R =Ω 32k R =Ω 再将3R 代入(1)式得210k 3R =Ω答案2.4解：由并联电路分流公式，得1820mA 8mA (128)I Ω=⨯=+Ω2620mA 12mA (46)I Ω=⨯=+Ω由节点①的KCL 得128mA 12mA 4mA I I I =-=-=-答案2.5解：首先将电路化简成图(b)。
图 题2.5120Ω(a)图中1(140100)240R =+Ω=Ω2(200160)120270360(200160)120R ⎡⎤+⨯=+Ω=Ω⎢⎥++⎣⎦ 由并联电路分流公式得211210A 6A R I R R =⨯=+及21104A I I =-= 再由图(a)得321201A 360120I I =⨯=+由KVL 得，3131200100400V U U U I I =-=-=-答案2.6xRx(a-1)图2.6解：（a ）设R 和r 为1级，则图题2.6(a)为2级再加x R 。
哈尔滨理工大学电路1-9章习题集答案解析
第一章(电路模型和定律)习题解答一、选择题1．KVL 和KCL 不适用于 D 。
A ．集总参数线性电路；B ．集总参数非线性电路；C ．集总参数时变电路；D ．分布参数电路2．图1—1所示电路中，外电路未知，则u 和i 分别为 D 。
A ．0==i u uS ,； B ．i u u S ,=未知；C ．0=-=i u uS ,； D ．i u u S ,-=未知3．图1—2所示电路中，外电路未知，则u 和i 分别为 D 。
A ．S i i u =∞=, ；B ．S i i u -=∞=, ；C ．S i i u =未知， ； D ．S i i u -=未知，4．在图1—3所示的电路中，按照“节点是三条或三条以上支路的联接点”的定义，该电路的总节点个数为 A 。
A ．5个；B ．8个；C ．6个；D ．7个5．在图1—4所示电路中，电流源发出的功率为 C 。
A ．45W ；B ．27W ；C ．–27W ；D ．–51W二、填空题1．答：在图1—5所示各段电路中，图A 中电流、电压的参考方向是 关联 参考方向；图B 中的电流、电压的参考方向是 非关联 参考方向；图C 中电流、电压的参考方向是 关联 参考方向；图D 中电流、电压的参考方向是 非关联 参考方向。
2．答：图1—6所示电路中的u 和i 对元件A 而言是 非关联 参考方向；对元件B 而言是 关联 参考方向。
3．答：在图1—7所示的四段电路中，A 、B 中的电压和电流为关联参考方向，C 、D中的电压和电流为非关联参考方向。
4．答：电路如图1—8所示。
如果10=R Ω，则10=U V ，9-=I A ；如果1=R Ω，则 10=U V ，0=I A 。
5．答：在图1—9 (a)所示的电路中，当10=R Ω时，=2u 50V ，=2i 5A ；当5=R Ω时，=2u 50V , =2i 10A 。
在图1—9 (b)所示的电路中，当R =10Ω时，2002=u V ,202=i A ；当5=R Ω时，1002=u V, 202=i A 。
【电工学期末考试习题】第12章 集成运算放大器 习题参考答案
第12章 集成运算放大器 习题参考答案一、填空题：1. 理想运放同相输入端和反相输入端的“虚短”指的是 同相输入端与反相输入端两点电位相等，在没有短接的情况下出现相当于短接时的现象。
2. 将放大器 输出信号 的全部或部分通过某种方式回送到输入端，这部分信号叫做 反馈 信号。
使放大器净输入信号减小，放大倍数也减小的反馈，称为 负 反馈；使放大器净输入信号增加，放大倍数也增加的反馈，称为 正 反馈。
放大电路中常用的负反馈类型有 并联电压 负反馈、 串联电压 负反馈、 并联电流 负反馈和 串联电流 负反馈。
3. 若要集成运放工作在线性区，则必须在电路中引入 负 反馈；若要集成运放工作在非线性区，则必须在电路中引入 开环 或者 正 反馈。
集成运放工作在线性区的特点是 输入电流 等于零和 输出电阻 等于零；工作在非线性区的特点：一是输出电压只具有 高电平、低电平两种稳定 状态和净输入电流等于 零 ；在运算放大器电路中，集成运放工作在 线性 区，电压比较器集成运放工作在 非线性 区。
4. 集成运放有两个输入端，称为 同相 输入端和 反相 输入端，相应有 同相输入 、 反相输入 和 双端输入 三种输入方式。
5. 放大电路为稳定静态工作点，应该引入 直流 负反馈；为提高电路的输入电阻，应该引入 串联 负反馈；为了稳定输出电压，应该引入 电压 负反馈。
6. 理想运算放大器工作在线性区时有两个重要特点是“虚短”和 “虚断” 。
三、选择题：（每小题2分，共16分）1.集成运算放大器能处理（ C ）。
A 、直流信号；B 、交流信号；C 、交流信号和直流信号。
2. 为使电路输入电阻高、输出电阻低，应引入（ A ）。
A 、电压串联负反馈；B 、电压并联负反馈；C 、电流串联负反馈；D 电流并联负反馈。
3. 在由运放组成的电路中，运放工作在非线性状态的电路是（ D ）。
A 、反相放大器；B 、差值放大器；C 、有源滤波器；D 、电压比较器。
哈工大电路原理基础课后习题
第一章习题1.1 图示元件当时间t<2s时电流为2A，从a流向b；当t>2s时为3A，从b流向a。
根据图示参考方向，写出电流的数学表达式。
1.2图示元件电压u=(5-9e-t/τ)V，τ>0。
分别求出t=0 和t→∞时电压u的代数值及其真实方向。
图题1.1 图题1.21.3 图示电路。
设元件A消耗功率为10W，求；设元件B消耗功率为-10W,求；设元件C发出功率为-10W，求。
图题1.31.4求图示电路电流。
若只求，能否一步求得？1.5 图示电路，已知部分电流值和部分电压值。
(1) 试求其余未知电流。
若少已知一个电流，能否求出全部未知电流？(2) 试求其余未知电压u14、u15、u52、u53。
若少已知一个电压，能否求出全部未知电压？1.6 图示电路，已知,,,。
求各元件消耗的功率。
1.7 图示电路，已知，。
求(a)、(b)两电路各电源发出的功率和电阻吸收的功率。
1.8 求图示电路电压。
1.9 求图示电路两个独立电源各自发出的功率。
1.10 求网络N吸收的功率和电流源发出的功率。
1.11 求图示电路两个独立电源各自发出的功率。
1.12 求图示电路两个受控源各自发出的功率。
1.13 图示电路，已知电流源发出的功率是12W，求r的值。
1.14 求图示电路受控源和独立源各自发出的功率。
1.15图示电路为独立源、受控源和电阻组成的一端口。
试求出其端口特性，即关系。
1.16 讨论图示电路中开关S开闭对电路中各元件的电压、电流和功率的影响，加深对独立源特性的理解。
第二章习题2.1 图(a)电路，若使电流A,，求电阻；图(b)电路，若使电压U=(2/3)V，求电阻R。
2.2 求图示电路的电压及电流。
2.3 图示电路中要求，等效电阻。
求和的值。
2.4求图示电路的电流I。
2.5 求图示电路的电压U。
2.6 求图示电路的等效电阻。
2.7 求图示电路的最简等效电源。
图题2.72.8 利用等效变换求图示电路的电流I。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
答案12.1解：分别对节点①和右边回路列KCL 与KVL 方程：Cq u u i i qi C L L R C C /===--==ψ将各元件方程代入上式得非线性状态方程：C q C q f f q/)/()(21=--=ψψ方程中不明显含有时间变量t ，因此是自治的。
答案12.2解：分别对节点①、②列KCL 方程： 节点①：=1i 321S 1/)(R u u i q--= 节点②：=2i 423212//)(R u R u u q--= 将)(),(222111q f u q f u == 代入上述方程，整理得状态方程：⎩⎨⎧+-=++-=)/())((/)(/)(/)(4343223112S 3223111R R R R q f R q f q i R q f R q f q答案12.3解：分别对节点①列KCL 方程和图示回路列KVL 方程得：⎩⎨⎧-=-=(2)(1) /323321u u R u i qS ψ 3u 为非状态变量，须消去。
由节点①的KCL 方程得：0413332432=-++-=++-R u u R u i i i i 解得)/()]()([)/()(433224114332413R R R f R q f R R R i R u u ++=++=ψ 将)(111q f u =、)(222ψf i = 及3u 代入式(1)、(2)整理得：⎩⎨⎧++-+-=+++-=Su R R R R f R R R q f R R R f R R q f q)/()()/()()/()()/()(4343224331124332243111ψψψ 答案12.4解：由KVL 列出电路的微分方程：=L u )(sin )(d d 3t R u Ri tS ωβψαψ+-=+-= 前向欧拉法迭代公式：)](sin )([31k k k k t R h ωβψαψψ+-+=+后向欧拉法迭代公式：)](sin )([1311++++-+=k k k k t R h ωβψαψψ梯形法迭代公式：)](sin )()(sin )([5.013131++++-+-+=k k k k k k t R t R h ωβψαωβψαψψ答案12.5解：由图(a)得：tu C u U t C t u Ci R R C R d d )(d dd d S -=-== (1) 由式(1)可知，当0>R i 时，0d d <t u R ，R u 单调减小；当0<R i 时，0d d >tuR ，R u 单调增加。
由此画出动态路径如图(b)所示。
V 3)0()0(S =-=++C R u U u响应的初始点对应P 。
根据动态轨迹，分段计算如下。
(1) AB 段直线方程为： 4+-=R R i u 。
由此得AB 段线性等效电路，如图(c)。
SU (c)U -+R u (d)由一阶电路的三要素公式得：V 4p =R u ，s 1-=τV )e 4(e )](0)(0[/p p t t R R R R u u u u -=-+=-++τ )0(1t t <<设1t t =时，动态点运动到A 点，即2e 41=-t ，求得s 693.02ln 1≈=t 。
(2) OA 段． 1t t >时，R u 将位于OA 段，对应直线方程R R i u =。
线性等效电路如图(d)。
由图(d)求得：)(1e 2t t R u --= V )(1t t >答案12.6解：0>t 时，由图(a)得R R i Ct u 1d d -=，0>R i R u 只能下降。
画出动态路径如图(b)所示。
响应的起始位置可以是A 或B 点。
(1) 设起始位置是A 点，响应的动态轨迹可以是A-O 或A-C-D-O ，其中C-D过程对应电流跳变。
(1.1) 设动态轨迹为A-O 。
非线性电阻在此段等效成Ω2 的线性电阻，响应电压为：t C t u 0.5e 2)(-= V )0(>t (1) (1.2) 设动态路径为A-C-D-O 。
(c) AC段等效电路(d) BC段等效电路AC 段的等效电路如图(c)所示。
由图(c)求得：V 2)0(=+C u ，V 3)(p =t u C ，s 1-=τ 由三要素公式得：)e 3(t C u -= V )0(t t << (2) 设1t 时刻到达C 点，即 1e 31=-t 解得 693.0≈t s 。
t t >时，动态轨迹位于DO 段，非线性电阻变成线性Ω2电阻，响应为)0.5(1e )(t t C t u --= V )(t t > (3) (2) 设起始位置为B 点，则设动态路径为B-C-D-O 。
位于BC 段时，线性等效电路如图(d)所示。
由图(d)求得V 1)(p -=t u C ，s 1=τt C t u -+-=e 31)(V )1'(0t t << (4)设1t '时刻到达C 点，即1e 311＝t -+- 解得 405.05.1ln 1≈='t s 。
CD 段对应电流跳变，瞬间完成。
1t t '>后动态轨迹进入DO 段，非线性电阻变成Ω2线性电阻。
响应为)'0.5(1)(t t C t u --=e V )'(t t > (5)上述式(1)、(2)与(3)、(4)与(5)是本题的三组解答。
答案12.7解：0t t ≤≤时，工作于OA 段，对应线性电感：iL ψ＝。
初始值0)0(=+ψ，特解R EL t p ⨯=1)(ψ，时间常数RL 1=τ 由三要素法，电路的零状态响应为：)e 1(e)]0()0([)()(111p p t L Rt L R L REt t --++-=-+=ψψψψ (1) 设1t 时刻到达A 点，即)e 1(1111t L RL RE--=ψ，解得111111111ln//ln ψψ-=-=∞∞i L i L R L R E L R E L R L t (2) 当t t >时， ψψ+=i L ，其中电感ii L --=∞∞ψψ。
对应上式的时间常数与强制分量分别是RL=τ，∞=∞=ψψψ)()(t p 故当t t >时的响应为21e))(1τψψψψt t t --∞∞-+=(答案12.8解：由图(a)电路得：V 3V 5.4636)0(=⨯+=-u当0>t 时，将除非线性电容以外的电路用戴维南电路等效，如图(c)所示。
其中等效电阻Ω==12//)6//3(i R 开路电压V 5.1OC =U 。
(1)10t t ≤≤时，电路工作在AB 段内，1112+=+=q C q u ，对应的线性等效电路如图(d)所示。
(c)(d)5.1-+u u(e)图 12.8V 3)0()0(==-+u u ，s 1=RC ＝τ，V 5.1)(p =t u 电路响应)V 1.5e 1.5(e )]0()0([)()(/p p t t u u t u t u --+++=-+=τ )(10t t ≤≤ 随着时间的延续，电压u 单调减小，设1t 时刻电压u 下降至A 点，即21.5e 1.51=+-t解得s 10.11≈t 。
(2) t t >时，工作在AO 段，u q 5.0=，此时电容等效为F 5.0的线性电容，如图(e)所示。
由图（e ）得时间常数及强制分量分别为：s 5.0'==RC τ，V 5.1)()(p ==∞=O C U u t u 电路响应：V ]e 5.05.1[e )]()([)()()(2')/(1p 1p 11t t t t t u t u t u t u ----+=--=τ答案12.9解：应用小信号分析法。
V 10S='u 单独作用时，电路的直流解为： A 01.0S0='=Ru I 。
(1) 动态电感H 06.06d d 00d ====I I i i L ψ。
小信号线性等效电路如图(b)所示。
0)0(=∆+i ，A 10)(3-=∞∆i ，s 106/5d -⨯==R L τ 根据三要素法求得：)(ε)e1(10)e1)((510613t i i t t L R d⨯----=-∞=∆∆ A (2)式(1)与式（2）相加得本题解答：A )](ε)e1(1001.0[)()(5106130t t i I t i t ⨯---+=∆+=答案12.10解：用小信号分析法求解。
（１）直流工作点V 4V 122120=⨯+=R R R U（２）动态电容F 104|d d 6d 0-=⨯==U u uq C（３）小信号电路如图（a ）所示，利用三要素公式求u ∆。
0)0(=∆+u ,V 3/1p =∆us 016.01041061261263d =⨯⨯⨯+⨯==-RC τ V )()e 1(31e )]0()0([5.62/p p t u u u u t t ετ--++-=∆-∆+∆=∆电路完全解答为)()e 1(3145.620t u U u t ε--+=∆+= V答案12.11解：用小信号分析法求解。
(1) 计算直流工作点。
直流电流源单独作用时，电容视为开路，如图(b)所示。
列KVL 方程得：05.0)(10000=++-U U I I S (1) 其中203010U I -=，代入式(1)得：010********=-+U U 解得：⎩⎨⎧-=)(V 39.1566.39V0舍去U (2) 动态电导S 10278.139.6102|d d 23d 0--=⨯=⨯⨯==U u uiG (2) 用复频域分析法计算阶跃响应。
复频域电路模型如图(c)所示。
-∆+)(s U /1.0(c)对图(c)列节点电压方程得：10/)](5.0/1.0[)()101(s U s s U G sC d ∆-=∆++解得42141063.1)1063.1(1000)(⨯++=⨯+=∆s A s A s s s U其中0614.021=-=A AV )()e 1(0614.0)(41063.1t t u t ε⨯--=∆ (3)式(2)与(3)相加得： V )]()e 1(0614.039.6[41063.1t u t ε⨯--+=答案12.12解：用小信号分析法求解。
(1) 计算直流工作点。
在S i 的直流分量作用时，电感视为短路，电容视为开路，如图(b)。
2I IdR 图题12.12(b)(c)0)2(1=+-⨯R L U I将2R R I U =代入上式得02=-+L L I I 20解得：⎩⎨⎧-=)舍去(A 2A10L I (1) A 1==L R I I , V 1==R C U U(2) 小信号等效电路为二阶动态电路，可用复频域分析法计算阶跃响应。