等差数列和求和基础训练

合集下载

等差数列基础练习题大全

等差数列基础练习题大全1、一个递增(后项比前项大)的等差数列，第28项比第53项________(多或少)______个公差。

2、一个递增(后项比前项大)的等差数列，第53项比第28项________(多或少)______个公差。

3、一个递增(后项比前项大)的等差数列，第55项比第37项________(多或少)______个公差。

4、一个递增(后项比前项大)的等差数列，第55项比第83项________(多或少)______个公差。

5、一个递增(后项比前项大)的等差数列，第28项比第73项________(多或少)______个公差。

6、一个递增(后项比前项大)的等差数列，第90项比第73项________(多或少)______个公差。

7、一个递增(后项比前项大)的等差数列，首项比第73项________(多或少)______个公差。

8、一个递增(后项比前项大)的等差数列，第87项比首项________(多或少)______个公差。

9、一个递减(后项比前项小)的等差数列，第18项比第32项________(多或少)______个公差。

10、一个递减(后项比前项小)的等差数列，第32项比第18项________(多或少)______个公差。

11、一个递减(后项比前项小)的等差数列，第74项比第26项________(多或少)______个公差。

12、一个递减(后项比前项小)的等差数列，第74项比第91项________(多或少)______个公差。

13、一个递减(后项比前项小)的等差数列，第29项比第86项________(多或少)______个公差。

14、一个递减(后项比前项小)的等差数列，第123项比第86项________(多或少)______个公差。

________(多或少)______个公差。

16、一个递减(后项比前项小)的等差数列，第76项比首项________(多或少)______个公差。

等差数列求和基础题

等差数列求和基础题一．选择题1. 等差数列{}n a 的前n 项和为n S ，若142,20,a S ==则6S = A.16 B.24 C.36 D.422. 设等差数列{}n a 的前n 项和为n S ,若111a =-,376a a +=-,则当n S 取最小值时,n 等于A.8B.7C.6D.93. 已知n S 是等差数列{}n a 的前n 项和，且63S =，1118S =，则9a 等于 A.3 B.5 C.8 D.154. 已知等差数列{a n }前n 项的和为S n , 233=a , S 3=9，则a 1= A.23 B.29C.-3D.6 5. 已知等差数列{}n a 中,256,15a a ==,若2n n b a =,则数列{}n b 的前5项和为 A. 90 B. 45 C. 30 D. 1866. 等差数列}{n a 的前n 项和为n S ，若119717,170a a a S ++=则的值为 A.10 B.20 C.25 D.307. 设等差数列｛a n ｝前n 项和为S n . 若a 1= -11,a 4+a 6= -6 ,则当S n 取最小值时，n 等于 A.6 B. 7 C.8 D.98. 设等差数列{}n a 的前n 项和为n S ，246a a +=，则5S 等于 A.10 B.12 C.15 D.309. 已知等差数列{}n a 满足244a a +=，3510a a +=，则它的前10项的和10S = A.138 B.135 C.95 D.2310. 记等差数列的前n 项和为n S ，若244,20S S ==，则该数列的公差d = A.2 B.3 C.6 D.711. 已知等差数列{}n a 中，26a =，515a =，若2n n b a =，则数列{}n b 的前5项和等于A.30B.45C.90D.18612. 设S n 是等差数列{a n }的前n 项和，若S 5 = S 9，则a 3:a 5 = A.5:9 B.9:5 C.3:5 D.5:3 13. 在等差数列}{n a 中，已知S 3=9，S 9=54，则}{n a 的通项n a 为 A.33-=n a n B.n a n 3= C.2+=n a n D.1+=n a n 14. 若等差数列}{n a 的前3项和93=S 且11=a ，则2a 等于 A.3 B.4 C.5 D.615. 等差数列{}n a 中，11a =，3514a a +=，其前n 项和100n S =，则n = A.9 B.10 C.11 D.1216. 等差数列{a n }的前n 项和为S n ，若等于则442,10,2S S S == A.12B.18C.24D.4217. 已知{}n a 是等差数列，1010a =，其前10项和1070S =，则其公差d = Ａ.23-Ｂ.13- Ｃ.13 Ｄ.2318. 在等差数列｛a n ｝中，若a 4+a 6 =12, S n 是数列｛a n ｝的前n 项和，则S 9的值为 A.48 B.54 C.60 D.6619. 一个只有有限项的等差数列,它的前5项的和为34,最后5项和为146,所有项的和为234,则它的第七项等于 A.22 B.21 C.19 D.1820. 已知数列{a n }的通项公式是a n =2n –49 (n ∈N )，那么数列{a n }的前n 项和S n 达到最小值时的n 的值是 A.23 B.24 C.25 D.2621. 已知等差数列{a n }中,a 2+a 8=8,则该数列前9项和S 9等于 A.18 B.27 C.36 D.45 22. 设S n 是等差数列{a n }的前n 项和,若S 7=35,则a 4= A.8B.7C.6D.523. 等差数列{}n a 中，n S 是前n 项和，且38S S =，7k S S =，则k 的值为 A.4B.11C.2D.1224. 等差数列{a n }中，若a 1＋a 4＋a 7＝39，a 3＋a 6＋a 9＝27，则前9项的和S 9等于 A.66 B.99 C.144 D.297 25. 等差数列{a n }中，a 1+a 2+…+a 50＝200，a 51+a 52+…+a 100＝2700，则a 1等于 A.－1221B.－21.5C.－20.5D.－2026. 等差数列｛a n ｝的前n 项和为S n ，若a 3+a 17=10，则S 19的值为 A.95 B.100 C.115 D.12527. 在等差数列}{n a 中，，，83125S S a =-=则前n 项和n s 的最小值为 A.80- B.76- C.75- D.74-28. 等差数列{a n }中，若a 3+ a 4+ a 5+ a 6+ a 7=450 则前9项和S 9=A.1620B.810C.900D.67529. 已知等差数列{}n a 的前n 项和为n S ，若5418a a =-，则8S 等于 A.144 B.72 C.54 D.36 30. 在等差数列{a n }中，前n 项和S n =36n －n 2，则S n 中最大的是 A.S 1 B.S 9 C.S 17 D.S 1831. 将含有k 项的等差数列插入4和67之间，结果仍成一新的等差数列，并且新的等差数列所有项的和为781，则k 的值为A.20B.21C..22D.2432. 设数列{}n a 是等差数列，且n S a a ,6,682=-=是数列 {}n a 的前n 项和，则 A.S 4<S 3 B.S 4==S 2 C.S 6<S 3 D.S 6=S 333. 已知等差数列前n 项和为S n ，若S 15<0,S 14>0,则此数列中绝对值最小的项为 A.第6项 B.第7项 C.第8项 D.第9项 34. 设等差数列{}n a 的前n 项和为n S ，已知20092007120102010,2,20092007S S a S =--==则 A.2008- B.2008 C.2010- D.201035. 已知等差数列{}n a 中，10795=-+a a a ，记n n a a a S +++= 21，则13S 的值为 A.130 B.260 C.156 D.16836. 已知等差数列{}n a 的前n 项和为n S ,且424a a -=，39S =,则数列{}n a 的通项公式为A.n a n =B.2n a n =+C.21n a n =-D.21n a n =+37. 等差数列{}n a 中，14739a a a ++=，36927a a a ++=，则数列{}n a 前9项和9S 等于 A.297 B.144 C.99D.6638. 等差数列{}n a 的前n 项和)3,2,1(⋅⋅⋅=n S n 当首项1a 和公差d 变化时，若1185a a a ++是一个定值，则下列各数中为定值的是A. 15SB. 16SC.17SD.18S39. 在公差为2的等差数列{}n a 中，如果前17项和为1734S =，那么12a 的值为 A. 2 B. 4 C. 6 D. 840. 已知等差数列30,240,18,}{49===-n n n n a S S S n a 若项和为的前，则n 的值为 A.18B.17C.16D.1541. 已知等差数列854,18,}{S a a S n a n n 则若项和为的前-== A.18 B.36 C.54 D.72 42. 设函数()f x =，类比课本推导等差数列的前n 项和公式的推导方法计算(4)(3)...(0)(1)...(4)(5)f f f f f f -+-++++++的值为A.2 B. 2 C.2 D. 243. 在等差数列｛a n ｝中，,3321=++a a a 165302928=++a a a ，则此数列前30项和等于 A.810 B.840 C.870 D.90044. 设数列}{n a 是递增等差数列，前三项的和为12，前三项的积为48，则它的首项为 A.1 B.2 C.4 D.645. 已知等差数列{}n a 的公差0<d ，若10,248264=+=⋅a a a a ，则该数列的前n 项和n S 的最大值为 A.50 B.45 C.40 D.3546. 等差数列{}n a 中，11a =,3514a a +=，其前n 项和100n S =,则n = A.9 B.10 C.11 D.1247. 若}{n a 是等差数列，首项01>a ，020082007>+a a ，020082007<⋅a a ，则使数列}{n a 的前n 项和n S 为正数的最大自然数n 是A.4013B. 4014C. 4015D. 401648. 设数列{n a }是等差数列，且n S a a ,6,682=-=是数列{n a }的前n 项和，则A.S 4<S 5B.S 4=S 5C.S 6<S 5D.S 6=S 549. 已知等差数列{}n a 的通项公式()211,2,3n a n n =-=，，记11T a =，1121122,,n n n n n n T a n T T a a n -+-++⎧⎪=⎨++⎪⎩为奇数,为偶数（2,3,n =），那么2n T =A.21n+ B.1162n - C.25 436n n n n ⎧⎨-+≠⎩，=1，，1D.232n n + 50. 已知数列2),1(2,}{a a S S n a n n n n 则且项和为的前-=等于A.4B.2C.1D.—251. 等差数列1062,}{a a a S n a n n ++若项和为的前为一个确定的常数，则下列各个和中，也为确定的常数的是A.S 6B.S 11C.S 12D.S 1352. 设n S 是等差数列{}n a 的前n 项和，若3163=S S 则=126S SA.310 B.13 C.81 D.9153. 已知等差数列{}n a 的前n 项和为n S ，若9S =18，n S =240，4n a -=30，则n 的值为 A.18 B.17 C.16 D.15 54. 若等差数列{}n a 的前5项和525S =，且23a =，则7a = A.12 B.13 C.14 D.1555. 已知{}n a 是等差数列，124a a +=，7828a a +=，则该数列前10项和10S 等于 A.64B.100C.110D.12056. 等差数列{a n }、{b n }的前n 项和分别为S n 、T n ，且3457-+=n n T S n n ，则使得nnb a 为整数的正整数n 的个数是 A.3 B.4 C.5 D.657. 数列{}n a 是公差为2-的等差数列，若509741=+++a a a ，则=++++99963a a a a A.－182 B.－82 C.－148 D.－7858. 设A ．B ．C 三点共线（该直线不过原点O ），数列{a n }是等差数列，S n 是该数列的前n 项和=a 1+a 200，则S 200=A.200B.100C.50D.30059. 一个等差数列共n 项，其和为90，这个数列的前10项的和为25，后10项的和为75，则项数n 为 A.14 B.16 C.18D.2060. 等差数列{a n }中，a 1>0，公差d <0, S n 为其前n 项和，对任意自然数n ，若点（n, S n ）在以下4条曲线中的某一条上，则这条曲线应是61. 已知等差数列{a n }前n 项和S n 有最大值且11011-<a a ，当S n 是最小正数时，n = A.17 B.18 C.19 D.20 62. 记等差数列{}n a 的前n 项和为n S ，若112a =，420S =，则6S = A.16B.24C.36D.4863. 设|a n |是等差数列，若a 2=3,a 7=13,则数列{a n }前8项的和为 A.128 B.80 C.64 D.5664. 已知等差数列}{n a 的前n 项和为S n ，若OC a OA a OB 20043+=，且A 、B 、C 三点共线（该直线不过原点O ），则S 2006 ＝A.1003B. 1004C. 2006D.2007 65. 等差数列{}n a 的前n 项和为n S ，若1697=+a a ，77=S ，则12a 的值是 A.15 B.30 C.31 D.6466. 已知数列{a n }、{b n }都是公差为1的等差数列，其首项分别为a 1、b 1，且a 1+b 1=5，a 1、b 1∈N *，设C n =a b （n ∈N *），则数列{C n }前10项和等于A.55B.70C.85D.10067. 已知,)1()1()1(22102nn nx a x a x a a x x x ++++=++++++ 若 ++21a an a n -=+-291，那么自然数n 的值为A. 3B.4C.5D.668. 已知等差数列{a n }的前n 项和为S n ，若m >1，m ∈N*，且21121,38m m m m a a a S -+-+==，则m 等于A.11B.10C.9D.869. 已知等差数列{a n }中, S n 是它的前n 项和，若S 16>0, S 17<0, 则当S n 取最大值时，n 的值为 A.16 B.9 C.8 D.10 70. 已知两个等差数列{}n a 和{}n b 的前n 项和分别为A n 和n B ，且7453n n A n B n +=+，则使得n na b 为整数的正整数n 的个数是A.2B.3C.4D.571. 设数列}{n a 是等差数列，且n S a a ,6,673=-=是数列}{n a 的前n 项和，则 A.54S S =B.56S S =C.64S S >D.56S S <72. 已知数列{－2n+25}，其前n 项和S n 达到最大值时，n 为A.10B.11C.12D.1373. 若n S 是等差数列{}n a 的前n 项和,其首项10a >,991000a a +>,991000a a ⋅<,则使0n S >成立的最大自然数n 是A.198B.199C.200D.20174. 设等差数列{}n a 满足81335a a =.且10a >.n S 为其前n 项之和.则n S 中最大的是 A.10S B.11S C.20S D.21S 75. 已知S n 是等差数列{a n }的前n 项和，且a 2＋a 4＋a 7＋a 15＝40，则S 13的值为 A.20 B.65C.130D.26076. 等差数列{}n a 的通项公式是12+=n a n ，其前n 项和为n S ，则数列⎭⎬⎫⎩⎨⎧n S n 的前10项和为A.75B.70C .120 D.10077. 在等差数列}{n a 中，若30,240,1849===-n n a S S ，则n 的值为 A.14B.15C.16D.1778. 在等差数列{}n a 中，若C a a a =++1383，则其前n 项和n S 的值等于5C 的是 A.15S B.17S C.8S D.7S79. 设{}n a 是等差数列，1359a a a ++=，69a =，则这个数列的前6项和等于Ａ.12Ｂ.24Ｃ.36Ｄ.4880. {}n a 是等差数列，10110,0S S ><，则使n a <0的最小的n 值是 A.5 B.6 C.7 D.881. 等差数列}{n a 的前n 项和为n S ，若10173=+a a ，则19S 的值是 A.55 B.95 C.100 D.不能确定 82. 在等差数列{a n }中，a 1>0,且3a 8=5a 13,则S n 中最大的是 A.S 21B.S 20C.S 11D.S 1083. 设S n 是等差数列前n 项的和，若9535=a a ,则59S S等于 A.1 B.－1 C.2D.2184. 已知等差数列{a n }的公差为正数，且a 3·a 7=－12,a 4+a 6=－4,则S 20为 A.180B.－180C.90D.－9085. 若{a n }是等差数列，首项a 1>0,a 2003+a 2004>0,a 2003·a 2004<0,则使前n 项和S n >0成立的最大自然数n 是 A.4005B.4006C.4007D.400886. 已知等差数列{}n a 中，247,15a a ==，则前10项的和10S ＝ A.100 B.210 C.380 D.400 87. 设S n 是等差数列｛a n ｝的前n 项和，若S 3S 6＝13，则S 6S 12＝A .310 B.13 C.18 D .1988. 设等差数列｛a ｝的前n 项的和为S n ，若a 1＞0，S 4=S 8，则当S n 取得最大值时，n 的值为 A.5 B.6 C.7 D.889. 已知等差数列｛a n ｝的前n 项和为S n ，若1O a B ＝200OA a OC ＋，且A 、B 、C 三点共线（该直线不过原点O ），则S 200＝A.100B. 101C.200D.201 90. 已知等差数列{a n }的前20项的和为100，那么a 7·a 14的最大值为 A.25 B.50 C.100 D.不存在91. 若某等差数列{a n }中，a 2+a 6+a 16为一个确定的常数，则其前n 项和S n 中也为确定的常数的是 A.S 17 B.S 15 C.S 8 D.S 792. 在等差数列{a n }中，a 10<0，a 11>0，且a 11>|a 10|，则{a n }的前n 项和S n 中最大的负数为 A.S 17B.S 18C.S 19D.S 2093. 等差数列}{n a 的公差为d ，前n 项的和为S n ，当首项a 1和d 变化时，1182a a a ++是一个定值，则下列各数中也为定值的是 A.S 7B.S 8C.S 13D.S 1594. 在等差数列{ a n }中，S 4 =1, S 8 =4,则a 17 + a 18 + a 19+ a 20 的值是 A ．7 B ．8 C ．9 D ．1095. 设a 1, a 2, a 3,……和b 1, b 2, b 3,……都是等差数列，且a 1=25, b 1=75,a 100＋b 100=100,则数列a 1＋b 1, a 2＋b 2,……的前100项的和是A.0B.100C.10000D.不确定96. 等差数列{a n }中，若前15项的和S 15=90，则a 8等于97. 已知S k 表示数列{a k }前k 项和,且S k + S k+1 = a k +1 (k ∈N*),那么此数列是 A ．递增数列 B ．递减数列 C ．常数列 D ．摆动数列 98. 设S n 是等差数列{a n }的前n 项和,若31a a =95,则59S S等于 A.-1 B.21C.1D.2 99. 等差数列{a n }中，a n -4=30,且前9项的和S 9=18，前n 项和为S n =240,则n 等于 A.15B.16C.17D.18100. 等差数列{a n }中，若a 10=10,a 19=100,前n 项和S n =0,则n 等于 A.7B.9C.17D.19参考答案（仅供参考） 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 D C A B A D A C C B C B D A B 16 17 18 19 20 21 22 23 24 25 26 27 2829 30C D B D B C D A B C A C BB D3132 33 34 35 36 37 38 39 40 41 42 43 44 45 AB C C A C C A D D D B B B B 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 B B B D A B A D B B B B B C C 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 C D C A A C B B C D A C A C C 76 77 78 79 80 81 82 83 84 85 86 87 8889 90 A B A B B B B A A B B A BA A 919293949596979899100B C C C C A C C A C。

等差数列求和练习题以及答案解析

等差数列求和练习题以及答案解析练题1已知等差数列的首项为5，公差为3，请求前10项的和。

解析根据等差数列求和公式：其中：a 是首项，d 是公差，n 是项数。

代入已知条件，得到：所以，前10项的和为245。

练题2一等差数列的首项为7，公差为2，已知前6项的和为90，请求这个等差数列的第7项。

解析可利用等差数列求和公式和已知条件来解答该问题。

根据等差数列求和公式：已知前6项的和为90，代入公式得到：90 = (6/2)(2a + (6-1)d)其中，a 是首项，d 是公差。

将已知条件代入方程中，得到：90 = 3(2a + 5d)进一步整理得到：2a + 5d = 30由已知条件可得到方程组：{a = 72a + 5d = 30}解方程组可得到 a = 7，d = 4。

根据等差数列的通项公式：其中，a 是首项，d 是公差，n 是项数。

代入已知条件，得到：an = a + (n-1)da7 = 7 + (7-1)4a7 = 7 + 6*4a7 = 7 + 24a7 = 31所以，该等差数列的第7项为31。

练题3已知等差数列的前15项的和为135，公差为1，请求该等差数列的首项。

解析可利用等差数列求和公式和已知条件来解答该问题。

根据等差数列求和公式：已知前15项的和为135，代入公式得到：135 = (15/2)(2a + (15-1)1)整理得到：270 = 15(2a + 14)进一步整理得到：2a + 14 = 18解方程可得到 a = 2。

所以，该等差数列的首项为2。

练题4一等差数列的首项为3，公差为4，已知该等差数列的前n项和为49n，请问 n 的值是多少？解析可利用等差数列的前n项和公式来解答该问题。

根据等差数列的前n项和公式：已知该等差数列的前n项和为49n，代入公式得到：49n = (n/2)(2a + (n-1)d)其中，a 是首项，d 是公差。

代入已知条件，得到：49n = (n/2)(2*3 + (n-1)*4)整理得到：49n = n(6 + 4n - 4)进一步整理得到：49n = n(4n + 2)解方程可得到 n = 7。

等差数列求和及练习题(整理).doc

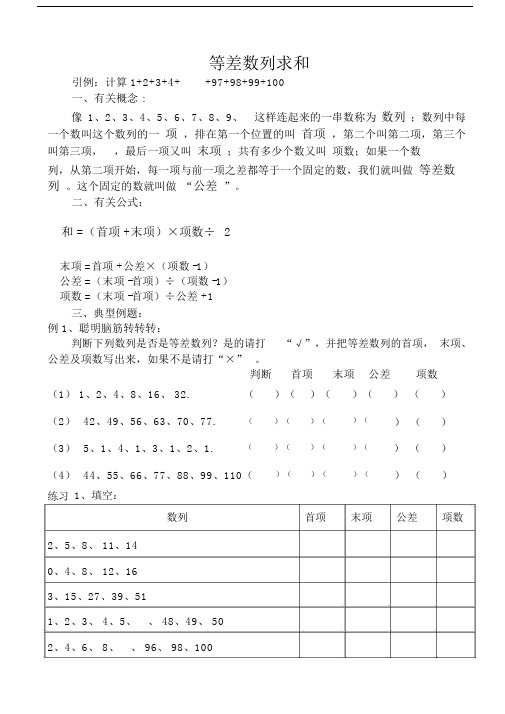
等差数列求和引例：计算 1+2+3+4++97+98+99+100一、有关概念 :像1、2、3、4、5、6、7、8、9、这样连起来的一串数称为数列；数列中每一个数叫这个数列的一项，排在第一个位置的叫首项，第二个叫第二项，第三个叫第三项，，最后一项又叫末项；共有多少个数又叫项数；如果一个数列，从第二项开始，每一项与前一项之差都等于一个固定的数，我们就叫做等差数列。

这个固定的数就叫做“公差”。

二、有关公式：和 =（首项 +末项）×项数÷ 2末项 =首项 +公差×（项数 -1）公差 =（末项 -首项）÷（项数 -1）项数 =（末项 -首项）÷公差 +1三、典型例题：例 1、聪明脑筋转转转：判断下列数列是否是等差数列？是的请打“√”，并把等差数列的首项，末项、公差及项数写出来，如果不是请打“×”。

判断首项末项公差项数（1） 1、2、4、8、16、 32.（）（）（）（）（）（2）42、49、56、63、70、77. （）（）（）（）（）（3）5、1、4、1、3、1、2、1. （）（）（）（）（）（4）44、55、66、77、88、99、110（）（）（）（）（）练习1、填空：数列首项末项公差项数2、5、8、 11、140、4、8、 12、163、15、27、39、511、2、3、 4、5、、 48、49、 502、4、6、 8、、 96、 98、100例 2、已知等差数列 1,8,15, , 78.共 12 项，和是多少？（博易 P27例 2）（看 ppt,推出公式）例 3、计算 1+3+5+7++35+37+39练习 2：计算下列各题（1）6+10+14+18+22+26+30 （3）1+3+5+7++95+97+99（2）3+15+27+39+51+63（4）2+4+6+8++96+98+100（3）已知一列数 4,6,8,10 ，，64，共有 31 个数，这个数列的和是多少？例 5、有一堆圆木堆成一堆，从上到下，上面一层有 10 根，每向下一层增加一根，共堆了 10 层。

等差数列前N项和(基础训练)

等差数列前N 项和〔根底训练〕1．在等差数列}{n a 中，836a a a +=，那么=9S 〔〕〔A 〕0 〔B 〕1 〔C 〕1- 〔D 〕以上都不对答案：A解析：66583a a a a a =+=+，05=a ，599a S =。

2．设n S 为等差数列}{n a 的前n 项和。

)6(144,324,3666>===-n S S S n n 。

那么n等于〔〕〔A 〕16 〔B 〕 17 〔C 〕 18 〔D 〕19 答案： B解析：216)144324(36)(6)(166=-+=+=-+-n n n a a S S S ， 361=+n a a ， 3242)(1=+=n n a a n S3、〔全国，8〕方程〔x2－2x+m 〕〔x2－2x+n 〕=0的四个根组成一个首项为41的等差数列，那么|m －n|等于〔〕A.1B.43C.21D.83 答案：C解析：设4个根分别为x1、x2、x3、x4，那么x1+x2=2，x3+x4=2，由等差数列的性质，当m+n=p+q 时，a x1为第一项，x2必为第4项，可得数列为41，43，45，47，∴m=167，n=1615.∴|m－n|=21.4、等差数列{}n a 的前n 项和为n S ，假设71310a a +=，那么19S 的值是〔〕.A 55 .B 95 .C 100 .D 无法确定答案:B解析：()()119713191919191095222a a a a S ++⨯====5、设n S 是等差数列{}n a 的前n 项和，假设735S =，那么4a =〔〕A ．8B ．7C ．6D ．5答案：D.解析：n S 是等差数列{}n a 的前n 项和，假设74735,S a == ∴ 4a =5。

6、｛an ｝是递增数列，且对任意n∈N*都有an=n2+λn 恒成立，那么实数λ的取值范围是〔〕A.(－27,+∞) B.(0,+∞) C.(－2,+∞) D.(－3,+∞)答案：D解析：由｛an ｝为递增数列得an+1－an=2n+1+λ＞0恒成立,即λ＞－2n －1在n≥1时恒成立，只需λ＞(－2n －1)max=－3。

等差数列前n项和基础训练题(有详解

等差数列前n 项和基础训练题（有详解)一、单选题1．已知等差数列{}n a 的前n 项和n S ，且3515S S ==，则7S =（） A ．4B ．7C ．14D ．722．已知数列{}n a 为等差数列，若84a =，则数列{}n a 的前15项和15S =( ) A ．12B ．32C ．60D ．1203．在等差数列{}n a 中，35a =则{}n a 的前5项和5S =（） A ．7B ．15C ．25D ．204．记为等差数列的前项和，若，，则的公差等于（） A ．-2B ．0C ．1D ．25．已知数列{}是等差数列，，则其前13项的和是（） A ．45B ．56C ．65D ．786．在等差数列{a n }中，a 3＋a 9＝27－a 6，S n 表示数列{a n }的前n 项和，则S 11＝( ) A ．18 B ．99 C ．198 D ．297 7．已知等差数列中，若，则它的前项和为（） A ．B ．C ．D ．8．已知等差数列的前项和为．若，，则A ．35B ．42C ．49D ．639．数列的前项和，当取最小值时的值为（） A ． B ． C ．D ．10．已知等差数列{a n }满足a 1+a 2+a 3+…+a 101=0，则有（） A ．a 1+a 101＞0 B ．a 2+a 100＜0 C ．a 3+a 99=0 D ．a 51=5111．若等差数列满足7890a a a ++>， 7100a a +<，则当{}n a 的前n 项和最大时， n 的值为（）A ．7B ．8C ．9D ．1012．若等差数列{}n a 的前n 项和n S 满足44S =， 612S =，则2S =（） A ．1-B ．0C ．1D ．3ns和为( )A.－45B.－50C.－55D.－66 14．等差数列 ,4,1,2-的前n 项和为（） A ．()4321-n n B ． ()7321-n n C ． ()4321+n n D ． ()7321+n n 15．数列{}n a 是等差数列，它的前n 项和可以表示为（）A ．C Bn An S n ++=2B ． Bn An S n +=2C ． C Bn An S n ++=2()0≠aD ． Bn An S n +=2()0≠a二、填空题16．已知等差数列{}n a 的前n 项和为n S ，若57915a a a ++=，则13S =________.17．已知数列{}n a 的前n 项和2n S n =，则4a =_______.18．已知等差数列{}n a 的前n 项和为n S ，3577,13,a a S ===_____；19．在等差数列{}n a 中，已知54a =，则129a a a +++=______.20．已知数列的前项和（），则此数列的通项公式为__________．21．已知数列{a n }的前n 项和S n ＝21n n --，则{a n }的通项公式a n ＝________. 22．等差数列中，，则数列前9项的和等于______________。

(完整版)等差数列基础练习题.docx

数列基础知识点和方法归纳1. 等差数列的定义与性质定义： a n 1 a n d （ d 为常数）， a n a 1n 1 d等差中项： x ， A ， y 成等差数列2Ax ya 1 a n nnn 1 前 n 项和Snna 1d22性质： a n 是等差数列（1）若 m n p q ，则 a ma n a p a q ；2. 等比数列的定义与性质定义：a n1q（ q 为常数， q0 ），an aqn 1a n.1等比中项： x 、 G 、 y 成等比数列G2xy ，或Gxy .na 1 ( q 1) 前项和：S n a 1qnn 1( q 1) （要注意！）1 q性质： a n 是等比数列（1）若 m np q ，则 a · aa · amnpq等差数列·基础练习题一、填空1.等差数列 8，5， 2，⋯的第 20___________.2.在等差数列中已知 a1=12, a6=27, d=___________3. 在等差数列中已知d 1，a7=8，a1=_______________ 34.等差数列 -10，-6，-2， 2，⋯前 ___的和是 545.数列 a n的前n和S n＝3n n2，a n＝___________二、9. 在等差数列a n中a3a1140 ， a4a5a6a7a8a9a10的（）A.84B.72C.60.D.4810. 在等差数列a n中，前 15 的和S1590 ， a8（）A.6B.3C.12D.412. 在等差数列a n中,若a3a4a5a6a7450 ， a2a8的等于（）A.45B.75C.180D.30014. 数列 3， 7，13， 21，31，⋯的通公式是（）A. C.a n4n1B. a n n3n2n 2 a n n2n1 D.不存在16.设等差数列a n的前n 项和公式是S n5n23n ，求它的前3项，并求它的通项公式17.如果等差数列a n的前4项的和是2，前 9 项的和是 -6，求其前 n 项和的公式。

等差数列基础训练

等差数列基础训练一，选择题（1）在等差数列{a n }中，已知a 4+ a 7+ a 10=17，a 4+ a 5+ a 6+…+ a 14=77。

若a k =13，则k=（）（A ）16 （B ）18 （C ）20 （D ）22（2）在等差数列{a n }中，已知a 1+ a 4+ a 7=45，a 2+ a 5+ a 8=39。

则a 3+ a 6+ a 9的值是（）（A ）24 （B ）27 （C ）30 （D ）33（3）在等差数列{a n }中，已知a 1+ a 13=3，那么它的前13项的和S 13等于（）（A ）39 （B ）20 （C ）19.5 （D ）18（4）已知{a n }是等差数列，则下列各不等式中正确的是（）（A ）a 3a 6<a 4a 5 （B ）a 3a 6≤a 4a 5 （C ）a 3a 6>a 4a 5 （D ）a 3a 6≥a 4a 5（5）在等差数列{a n }中，a 10<0,a 11>0,且a 11>|a 10|，S n 是前n 项和，则（）（A ） S 1，S 2，…S 10都小于零，S 11，S 12，…都大于零；（B ） S 1，S 2，…S 19都小于零，S 20，S 21，…都大于零；（C ） S 1，S 2，…S 5都小于零，S 6，S 7，…都大于零；（D ） S 1，S 2，…S 20都小于零，S 21，S 22，…都大于零；（6）在等差数列{a n }中,a 1=-5，它的前11项的平均值是5，若从中抽取1项，余下的10项的平均值是4，则抽取的是（）（A ）a 11 （B ）a 10 （C ）a 9 （D ）a 8（7）一个等差数列的前4项之和是40，最后4项之和是80，所有项之和是210，则项数n 是（）（A ）12 （B ）14 （C ）16 （D ）18（8）在等差数列{a n }中, a 3=2，则前5项的和等于（）（A ）10 （B ）16 （C ）20 （D ）32二，填空题（9）在等差数列{a n }中,满足3a 4=7a 7，且a 1>0，S n 是数列{a n }前n 项和，若S n 取得最大值，则n=（10）在数列{a n }和{b n }中，a 1=2，对任意自然数n ，3a n+1-a n =0，b n 是a n+1与a n 的等差中项，则{b n }的各项和是（11）在等差数列{a n }中,n n n nS S n n a a 22,1214则--==（12）在数列{a n }中,a 1=-20，a n+1=a n +4，则|a 1|+|a 2|+…+|a 20|= 三，解答题（13）已知两个等差数列{a n }和{b n }的前n 项和分别是S n 和T n ，且S n :T n =(2n+1):(3n-2)求99b a的值。

等差数列前n项和公式基础训练题(含详解)

；③ ；
④ ；此外，需注意裂项之后相消的过程中容易出现丢项或多项的问题，导致计算结果错误.
11．
【解析】
【分析】
根据得到，，计算得到答案.
【详解】
；，解得
故答案为：
【点睛】
本题考查了等差数列的通项公式和前项和，意在考查学生对于等差数列公式的灵活运用.
12．
【解析】
【分析】
利用来求的通项.
A．18B．36C．45D．60
7．设为等差数列，，为其前n项和，若，则公差（）
A． B． C．1D．2
8．等差数列的前项和为，已知，，则当取最大值时的值是（）
A．5B．6C．7D．8
9．已知是数列的前项和，且，则（）．
A．72B．88C．92D．98
10．设为等差数列的前项的和，，则数列的前2017项和为（）
所以，所以 .
故答案为： .
【点睛】
本题考查等差数列公差的计算，难度较易.已知等差数列中的两个等量关系，可通过构造方程组求解等差数列的公差，还可以通过等差数列的下标和性质求解公差.
20．已知数列{an}的前n项和为Sn=n2+3n+5，则an=______．
参考答案
1．A
【解析】
设 ,根据是一个首项为a,公差为a的等差数列，各项分别为a,2a,3a,4a. .
2．B
【解析】
【分析】
根据等差数列的性质，求出，再由前n项和公式，即可求解.
【详解】
∵ ，
∴ ，∴
∴由得，∴ .
故选:B.
【点睛】
本题考查等差数列性质的灵活应用，以及等差数列的前n项和公式，属于中档题.

等差数列与等比数列的求和问题综合练习题

等差数列与等比数列的求和问题综合练习题数列是数学中常见的一个概念，它包含了一系列按照某种规律排列的数字。

在数列中，等差数列和等比数列是两种常见的类型，它们之间存在着不同的求和方法。

本文将通过综合练习题的方式，详细探讨等差数列与等比数列的求和问题。

一、等差数列求和等差数列是指数列中相邻两项之间的差值保持恒定的数列。

首先，我们来看一个等差数列求和的例子。

例题1：已知等差数列的首项a1为3，公差d为4，求前10项的和S10。

解题思路：利用等差数列通项公式an = a1 + (n-1)d，其中an代表数列的第n 项。

首先计算出第10项的值a10 = a1 + (10-1)d = 3 + (10-1)4 = 3 + 9*4 = 3 + 36 = 39。

其次计算出前10项的和S10 = (a1 + a10) * n / 2 = (3 + 39) * 10 / 2= 42 * 10 / 2 = 210。

答案：前10项的和S10为210。

二、等比数列求和等比数列是指数列中相邻两项之间的比值保持恒定的数列。

下面我们来看一个等比数列求和的例子。

例题2：已知等比数列的首项a1为3，公比q为2，求前5项的和S5。

解题思路：利用等比数列通项公式an = a1 * q^(n-1)，其中an代表数列的第n 项。

首先计算出第5项的值a5 = a1 * q^(5-1) = 3 * 2^(5-1) = 3 * 2^4 = 3 * 16 = 48。

其次计算出前5项的和S5 = a1 * (1 - q^n) / (1 - q) = 3 * (1 - 2^5) / (1 - 2) = 3 * (1 - 32) / (1 - 2) = 3 * (-31) / (-1) = 93。

答案：前5项的和S5为93。

三、综合练习题接下来，我将给出一些综合训练题，涵盖了等差数列与等比数列的求和问题。

请你根据题意，独立思考并计算出答案。

练习题1：已知等差数列的首项a1为2，公差d为3，求前20项的和S20。

等差数列基础训练及答案解析

等差数列基础训练及答案解析等差数列基础训练(一)选择题：1．已知命题甲是“△ABC的一个内角B为60°”，命题乙是“△ABC的三个内角A、B、C成等差数列”，那么[ ]．A．甲是乙的充分条件，但不是乙的必要条件B．甲是乙的必要条件，但不是乙的充分条件C．甲是乙的充要条件D．甲既不是乙的充分条件，也不是必要条件2．已知数列{an}的前n项和为：①2n；②2n＋6；③n2；④n2-1；⑤n2＋2n；⑥n2＋n＋1；⑦n3；⑧0．在上述各数列中构成等差数列的有 [ ]．A．3个 B．4个C．5个 3．公差为d的等差数列的前n项和为Sn＝n(1-n)，那么 [ ]．A．d＝2，an＝2n-2B．d＝2，an＝2n＋2C．d＝-2，an＝-2n-2D．d＝-2，an＝-2n＋2[ ]．．6个DA．1001 B．1000C．999 D．9985．已知等差数列{an}中的前三项依次为a-1，a＋1，2a＋3，则此数列的通项公式为[ ]．A．an=2n-5B．an=2n-3C．an＝2n-1D．an=2n＋16．等差数列{an}，已知a3＋a11=10，则a6＋a7＋a8等于 [ ]．A．20 C．15 7．在等差数列{an}中，S5＝28，S10=36，则S15等于 [ A．24 B．18D．12．B．44] C．64 D．808．首项为18，公差为-3的等差数列，前n项和Sn取最大值时，n等于 [ ]．A．5或6 B．6C．7 D．6或79．在项数为2n＋1的等差数列中，所有奇数项的和与所有偶数项的和之比为 [ ]．10．在等差数列{an}中，am＝n，an＝m(n≠m)，则am＋n等于 [ ]．A．mn B．m＋nC．m2＋n2 D．011．在50和350之间，所有末位数字是1的整数之和是 [ ]A．5880 B．5684C．4877 D．456012．三角形三个边长组成等差数列，周长为36，内切圆周长为6π，则此三角形是[ ]．A．正三角形B．等腰直角三角形C．等腰三角形，但不是直角三角形D．直角三角形，但不是等腰三角形(二)填空题：13．已知1，4，7，10，?是等差数列，若(1)1＋4＋7＋?＋x＝477，则x＝_____；(2)(x＋1)＋(x＋4)＋(x＋7)＋?＋(x＋298)=15950，则x＝______；(3)在此数列的每相邻两项中间插入三项，使它们仍构成一个新的等差数列，则原数列的第10项，是新数列的第______项，新数列的第29项，是原数列的第_____项．14．在等差数列{an}中，感谢您的阅读，祝您生活愉快。

等差数列及其前n项和(分层练习)

等差数列及其前n 项和（分层练习）[基础训练]1．[2019全国卷Ⅰ]记S n 为等差数列{a n }的前n 项和．已知S 4＝0，a 5＝5，则( )A ．a n ＝2n －5B ．a n ＝3n －10C ．S n ＝2n 2－8nD ．S n ＝12n 2－2n答案：A 解析：解法一：设等差数列{a n }的首项为a 1，公差为d ，则⎩⎨⎧S 4＝4a 1＋4×32d ＝0，a 5＝a 1＋4d ＝5，解得⎩⎪⎨⎪⎧a 1＝－3，d ＝2.所以a n ＝－3＋(n －1)×2＝2n －5， S n ＝n (－3＋2n －5)2＝n 2－4n .故选A ．解法二：因为a 5＝5，S 5＝S 4＋a 5＝5＝5a 3，所以a 3＝1. 令n ＝3，则可验证A 正确，B 错误；令n ＝5，则可验证C ，D 错误．故选A ．2．[2020河南八所重点高中测评]已知{a n }为等差数列，a 1＋a 3＋a 5＝105，a 2＋a 4＋a 6＝99，则a 20＝( )A ．7B ．3C ．－1D ．1答案：D 解析：由{a n }是等差数列及a 1＋a 3＋a 5＝105，得3a 3＝105，即a 3＝35，由{a n }是等差数列及a 2＋a 4＋a 6＝99，得3a 4＝99，即a 4＝33，则公差d ＝a 4－a 3＝－2，则a 20＝a 3＋(20－3)d ＝35－34＝1.故选D ．3．[2020辽宁抚顺一模]在等差数列{a n }中，已知a 3＋a 10＝10，则数列{a n }的前12项和为( )A ．30B ．60C ．90D ．120答案：B 解析：S 12＝12(a 1＋a 12)2＝12(a 3＋a 10)2＝60. 4．[2020福建泉州期末]等差数列{a n }中，a 1＋a 4＋a 7＝39，a 3＋a 6＋a 9＝27，则数列{a n }前9项的和S 9等于( )A ．99B ．66C ．144D ．297答案：A 解析：由等差数列的性质，可得a 1＋a 7＝2a 4，a 3＋a 9＝2a 6，又∵a 1＋a 4＋a 7＝39，a 3＋a 6＋a 9＝27， ∴3a 4＝39,3a 6＝27，解得a 4＝13，a 6＝9， ∴a 4＋a 6＝22，∴数列{a n }前9项的和S 9＝9(a 1＋a 9)2＝9(a 4＋a 6)2＝9×222＝99. 故选A ．5．在等差数列{a n }中，若a 4＋a 6＋a 8＋a 10＋a 12＝240，则a 9－13a 11的值为( )A ．30B ．31C ．32D ．33 答案：C 解析：由等差数列的性质及a 4＋a 6＋a 8＋a 10＋a 12＝240，可得5a 8＝240，解得a 8＝48.设等差数列{a n }的公差为d ，则a 9－13a 11＝a 8＋d －13(a 8＋3d )＝23a 8＝32. 故选C ．6．[2020四川成都月考]已知等差数列{a n }的公差为d ，前n 项和为S n ，当首项a 1和d 变化时，a 2＋a 8＋a 11是一个定值，则下列各数也为定值的是( )A ．S 7B ．S 8C ．S 13D ．S 15 答案：C7．已知等差数列{a n }的前n 项和为S n ，且a 5＝8，S 3＝6，则a 9＝________. 答案：16 解析：设等差数列{a n }的首项为a 1，公差为d ，则⎩⎪⎨⎪⎧ a 1＋4d ＝8，3a 1＋3d ＝6，解得⎩⎪⎨⎪⎧a 1＝0，d ＝2，所以a 9＝a 1＋8d ＝16. 8．设等差数列{a n }的前n 项和为S n ，若a 1＝－11，a 4＋a 6＝－6，则当S n取最小值时，n 等于________．答案：6 解析：因为a 4＋a 6＝2a 1＋8d ＝－22＋8d ＝－6，解得d ＝2，所以S n ＝－11n ＋n (n －1)＝(n －6)2－36，当n ＝6时，S n 取最小值．9．[2020福建外国语中学调研]已知等差数列{a n }的公差d >0，前n 项和为S n ，且a 2·a 3＝45，S 4＝28.(1)求数列{a n }的通项公式；(2)若b n ＝S n n ＋c (c 为非零常数)，且数列{b n }也是等差数列，求c 的值．解：∵S 4＝28，∴(a 1＋a 4)×42＝28， ∴a 1＋a 4＝14，则a 2＋a 3＝14，又a 2·a 3＝45，公差d >0， ∴a 2<a 3，a 2＝5，a 3＝9，∴⎩⎪⎨⎪⎧ a 1＋d ＝5，a 1＋2d ＝9，解得⎩⎪⎨⎪⎧a 1＝1，d ＝4，∴a n ＝4n －3. (2)由(1)知，S n ＝2n 2－n ， ∴b n ＝S n n ＋c ＝2n 2－n n ＋c.∴b 1＝11＋c ，b 2＝62＋c ，b 3＝153＋c .又{b n }是等差数列，∴b 1＋b 3＝2b 2，即2×62＋c ＝11＋c ＋153＋c ，解得c ＝－12或c ＝0(舍去)．[强化训练]1．[2020河北衡水中学高考押题]已知数列{a n }是首项为1，公差为2的等差数列，数列{b n }满足a 1b 1＋a 2b 2＋a 3b 3＋…＋a n b n＝12n ，数列{b n }的前n 项和为S n ，则S 5的值为( )A ．－454B ．－450C ．－446D ．－442答案：B 解析：∵数列{a n }是首项为1，公差为2的等差数列，∴a n ＝1＋2(n －1)＝2n －1.∵数列{b n }满足a 1b 1＋a 2b 2＋a 3b 3＋…＋a n b n ＝12n ，∴当n ≥2时，a 1b 1＋a 2b 2＋…＋a n －1b n －1＝12n －1，两式相减可得a n b n ＝12n －12n －1，可得b n ＝(1－2n )·2n (n ≥2)．当n ＝1时，1b 1＝12，解得b 1＝2，不符合上式，∴b n ＝⎩⎪⎨⎪⎧2，n ＝1，(1－2n )2n，n ≥2，∴S 5＝2－3×22－5×23－7×24－9×25＝－450，故选B ．2．[2020河南洛阳高二期末]设等差数列{a n }满足(1－a 1 008)5＋2 016(1－a 1 008)＝1，(1－a 1 009)5＋2 016(1－a 1 009)＝－1，数列{a n }的前n 项和记为S n ，则( )A ．S 2 016＝2 016，a 1 008>a 1 009B ．S 2 016＝－2 016，a 1 008>a 1 009C ．S 2 016＝2 016，a 1 008<a 1 009D ．S 2 016＝－2 016，a 1 008<a 1 009答案：C 解析：构造函数f (x )＝x 5＋2 016x ，则f (x )是奇函数，且在R 上单调递增，依题意得f (1－a 1 008)＝－f (1－a 1 009)，又－f (1－a 1 009)＝f (a 1 009－1)，则f (1－a 1 008)＝f (a 1 009－1)，所以1－a 1 008＝a 1 009－1，即a 1 008＋a 1 009＝2，所以S 2 016＝a 1＋a 2 0162×2 016＝a 1 008＋a 1 0092×2 016＝2 016，排除B ，D ；由f (1－a 1 008)>f (1－a 1 009)，得1－a 1 008>1－a 1 009，所以a 1 008<a 1 009，故选C ．3．[2020湖北黄冈模拟]设等差数列{a n }的前n 项和为S n ，等差数列{b n }的前n 项和为T n ，若S n T n ＝2 018n －13n ＋4，则a 3b 3＝( )A ．528B ．529C ．530D ．531答案：D 解析：根据等差数列的性质：a n b n ＝S 2n －1T 2n －1得a 3b 3＝S 5T 5＝2 018×5－13×5＋4＝531.故选D ．4．设等差数列{a n }的前n 项和为S n ，且S 9＝18，a n －4＝30(n >9)，若S n ＝336，则n 的值为( )A ．18B ．19C ．20D ．21答案：D 解析：由题意得S 9＝9a 5＝18，解得a 5＝2，根据等差数列的性质，得S n ＝n (a 1＋a n )2＝n (a 5＋a n －4)2＝n2×(2＋30)＝336，解得n ＝21.5．[2020浙江台州期末]已知公差不为零的等差数列{a n }满足a 23＝a 1a 4，S n为数列{a n }的前n 项和，则S 3S 1的值为( )A ．94 B ．－94 C ．32D ．－32答案：A 解析：设等差数列{a n }的公差为d (d ≠0)，由a 23＝a 1a 4，得(a 1＋2d )2＝a 1(a 1＋3d )，整理得a 1d ＋4d 2＝0.因为d ≠0，所以a 1＝－4d ，所以S 3＝3a 1＋3d ＝－9d ，所以S 3S 1＝－9d －4d ＝94，故选A ．6．[2020广东湛江一模]若等差数列{a n }的前n 项和S n 有最大值，且a 11a 10<－1，那么使S n 取最小正值的项数n ＝( )A ．15B ．17C ．19D ．21答案：C 解析：由于S n 有最大值，所以d <0，因为a 11a 10<－1，所以a 11＋a 10a 10<0，所以a 10>0>a 11，且a 10＋a 11<0，所以S 20＝10(a 1＋a 20)＝10(a 10＋a 11)<0，S 19＝19a 10>0，又a 1>a 2>…>a 10>0>a 11>a 12>…，所以S 10>S 9>…>S 2>S 1>0，S 10>S 11>…>S 19>0>S 20>S 21>…，又S 19－S 1＝a 2＋a 3＋…＋a 19＝9(a 10＋a 11)<0，所以S 19为最小正值，故选C ．7．[2020河南郑州模拟]在等差数列{a n }中，a 1＝－2 018，其前n 项的和为S n ，若S 2 0132 013－S 2 0112 011＝2，则S 2 018＝________.答案：－2 018 解析：因为S n n ＝a 1＋12(n －1)d ，所以数列⎩⎨⎧⎭⎬⎫S n n 也成等差数列，由S 2 0132 013－S 2 0112 011＝2，得公差为1，因此S 2 0182 018＝S 11＋(2 018－1)×1＝－1，则S 2 018＝－2 018.8．[2020湖南长沙模拟]已知函数f (x )＝cos x (x ∈(0,2π))有两个不同的零点x 1，x 2(x 1<x 2)，且方程f (x )＝m 有两个不同的实根x 3，x 4(x 3<x 4)，若把这四个数按从小到大排列构成等差数列，则实数m 的值为________．答案：－32 解析：函数f (x )＝cos x (x ∈(0,2π))有两个不同的零点x 1，x 2(x 1<x 2)，所以x 1＝π2，x 2＝3π2，因为方程f (x )＝m 有两个不同的实根x 3，x 4，若把这四个数按从小到大排列构成等差数列，若m >0，则由余弦函数的图象知，x 3，π2，3π2，x 4构成等差数列，可得公差d ＝3π2－π2＝π，则x 3＝π2－π＝－π2<0，显然不可能；若m <0，则由余弦函数的图象知，π2，x 3，x 4，3π2构成等差数列，可得3d ＝3π2－π2，解得d ＝π3，所以x 3＝π2＋π3＝5π6，则m ＝cos x 3＝cos 5π6＝－32.9．设等差数列{a n }的前n 项和为S n ，若1≤a 4≤4,2≤a 5≤3，则S 6的取值范围是________．答案：[0,30] 解析：S 6＝6a 1＋6×52d ＝6a 1＋15d ，设S 6＝ma 4＋na 5＝m (a 1＋3d )＋n (a 1＋4d ) ＝(m ＋n )a 1＋(3m ＋4n )d ，则⎩⎪⎨⎪⎧ m ＋n ＝6，3m ＋4n ＝15，解得⎩⎪⎨⎪⎧m ＝9，n ＝－3，∴S 6＝9a 4－3a 5.又∵1≤a 4≤4,2≤a 5≤3，∴9≤9a 4≤36，－9≤－3a 5≤－6， ∴0≤9a 4－3a 5≤30，即0≤S 6≤30.10．[2020福建漳州模拟]已知数列{a n }满足na n －(n ＋1)·a n －1＝2n 2＋2n (n ＝2,3,4，…)，a 1＝6.(1)求证：⎩⎨⎧⎭⎬⎫a n n ＋1为等差数列，并求出{a n }的通项公式；(2)设数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和为S n ，求证：S n <512.(1)解：由na n －(n ＋1)a n －1＝2n 2＋2n (n ＝2,3,4，…)，a 1＝6，可得a nn ＋1－a n －1n＝2，又a 11＋1＝3，则⎩⎨⎧⎭⎬⎫a n n ＋1是首项为3，公差为2的等差数列，可得a n n ＋1＝3＋2(n －1)＝2n ＋1，则a n ＝(n ＋1)(2n ＋1)(n ∈N *)．(2)证明：由1(n ＋1)(2n ＋1)<12n (n ＋1)＝12⎝ ⎛⎭⎪⎫1n －1n ＋1，可得数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和S n ＝1a 1＋1a 2＋…＋1a n<16＋12×⎝ ⎛⎭⎪⎫12－13＋13－14＋…＋1n －1n ＋1 ＝16＋12⎝ ⎛⎭⎪⎫12－1n ＋1<16＋14＝512，即S n <512.。

等差数列求和练习

1.对以下数列求和11＋14＋17＋…＋101297＋293＋289＋…＋209193＋187＋181＋…＋1031＋3＋4＋6＋7＋9＋10＋12＋13＋…＋66＋67＋69＋702＋4＋8＋10＋14＋16＋20＋22＋…＋92＋94＋98＋1001000＋999－998＋997＋996－995＋…＋106＋105－104＋103＋102－1012. 在19和91之间插入5个数，使这7个数构成一个等差数列。

写出插入的5个数。

3. 在1000到2000之间，所有个位数字是7的自然数之和是多少？4.左下图是一个堆放铅笔的V形架，如果V形架上一共放有210支铅笔，那么最上层有多少支铅笔？5.有一堆粗细均匀的圆木，堆成右上图的形状，最上面一层有6根，每向下一层增加一根，共堆了25层。

问：这堆圆木共有多少根？6. 在上题中，如果最下面一层有98根，这堆圆木共有2706根，那么共堆了多少层？7. 用相同的立方体摆成右图的形式，如果共摆了10层，那么最下面一层有多少个立方体？8. 某剧院有25排座位，后一排比前一排多2个座位，最后一排有70个座位。

问：这个剧院一共有多少个座位？9.小明从1月1日开始写大字，第1天写了4个，以后每天比前一天多写相同数量的大字，结果全月共写了589个大字。

问：小明每天比前一天多写几个大字？10.一个七层书架放了777本书，每一层比它的下一层少7本书。

问：最上面一层放了几本书？11. 学校进行乒乓球选拨赛，每个参赛选手都要和其他所有选手各赛一场，一共进行了78场比赛。

问：有多少人参加了选拨赛？12. 编号为1～9的九个盒子中共放有351粒米，已知每个盒子都比前一号盒子多同样粒米。

如果1号盒子内放了11粒米，那么后面的盒子比它前一号的盒子多放几粒米？如果3号盒子内放了23粒米，那么后面的盒子比它前一号的盒子多几粒米？13. 某校排练体操，一圈套一圈地围成若干圈，从外向内各圈人数依次少4人。

等差数列基础训练(精选)

1. 设等差数列{}n a 的前n 项和为n S ，若972S =,则249a a a ++= .2. 若lg 2,lg(21),lg(23)x x-+成等差数列，则x = .3. 在等差数列{}n a 中31140a a +=，则45678910a a a a a a a -+++-+= .4. 已知数列{}n a 的前n 项为和n S ，点（n ，S n n ），在直线11122y x =+上．数列{}n b 满足 2120n n n b b b ++-+=（n ∈N *），且b 3＝11，前9项和为153．求数列{}n a ，{}n b 的通项公式.5.等差数列{}n a 中, 12318192024,78a a a a a a ++=-++=,则此数列前20项的和等于 .6. 数列{}n a 中，有()()12323...12n a a a na n n n ++++=++，试用n 表示n a = .7. 已知数列{}n a 的前n 项和为252+-=n n S n ,则数列{}n a 的前10项和为．8. 等差数列{}n a 的前n 项和为n S ，已知2110m m m a a a -++-=，2138m S -=,则m = ． 9. 在等差数列}{n a 中，,0,01110><a a 且||1011a a >，则在n S 中最大的负数为 .10. 在数列{n a }中，1a = 1，nn n a a a +=+221 ( n ∈N * )，则2010a 等于． 11. 已知等差数列}{n a 中，12497,1,16a a a a 则==+= .12. 设等差数列{}n a 的前n 项和为n S ，若39S =，636S =，则789a a a ++= .13．数列{}n a 中，12a =，121n n a a n +=+-，则其通项公式为=n a ．14．数列{}n a 中，)2(112,1,21121≥+===-+n a a a a a n n n ，则其通项公式为=n a ． 15.设{}n a 是公差不为零的等差数列，n S 为其前n 项和，满足222223457,7a a a a S +=+=求数列{}n a 的通项公式及前n 项和n S 分别为____________.16．已知数列的12++=n n S n ，则12111098a a a a a ++++=_____________.17. 已知数列{}n a 对任意的*p q ∈N ，满足p q p q a a a +=+，且26a =-，那么10a = .18．等差数列{}n a 的前n 项和为n S ，且53655,S S -=则4a = .19. 己知}{n a 为等差数列，122,3a a ==，若在每相邻两项之间插入三个数，使它和原数列的数构成一个新的等差数列，求：（1）原数列的第12项是新数列的第几项？（2）新数列的第29项是原数列的第几项？。

4.2.2 等差数列的前n项和(1)(基础练)

4.2.2 等差数列的前n 项和（1）基础练一、单选题1．在a 和b 之间插入10个数，使之成为等差数列，则插入的10个数的和为（）A ．()12a b +B ．()10a b +C ．()6a b +D ．()5a b +2．{}n a 是等差数列，124a a +=，7828a a +=，则该数列前10项和10S 等于（）A ．64B ．100C ．110D ．1203．n S 是等差数列{}n a 的前n 项和，如果10120s = ，那么110a a + 的值是（）A ．12B ．24C ．36D ．484．已知n S 为等差数列{}n a 的前n 项和，若254a a +=，7S =21，则7a 的值为（）A ．6B ．7C ．8D ．95．已知等差数列{}n a 的前n 项和为n S ，4S 40=，S 210n =，4S 130n -=，则n =（）A ．12B ．14C ．16D ．186．等差数列{}n a 的前n 项和记为n S ，若2415a a a ++的值为一个确定的常数，则下列各数中也是常数的是（）A ．7SB ．8SC ．13SD ．15S二、填空题7．在等差数列{}n a 中，69121530a a a a +++=，则前20项之和20S =______. 8．在50和350之间所有末位数是3的整数之和是______.9．等差数列{}n a 的第10项为23，第25项为-22，则12350...a a a a ++++=______．三、解答题10．设等差数列{}n a 的首项1a 及公差d 都为整数，前n 项和为n S 。

（1）若110a =，1498S =，求数列{}n a 的通项公式；（2）若16a ≥，110a >，1477S <，求所有可能的数列{}n a 的通项公式.参考答案1．【答案】D【解析】由题可知,该数列一共有12项，且112a a a b ==，,11221131067a a a a a a a a a b +=+=+=⋯=+=+，共6组,减去112a a +这一组,故插入的数之和(61)()5()S a b a b =-⨯+=+. 故选D 2．【答案】B【解析】设等差数列的公差为d ，由a 1+a 2=4，a 7+a 8=28，可得：111146728a a d a d a d ++=⎧⎨+++=⎩解方程组可得1a 1,d 2101109101002S a d ⨯∴=+=. 故选B 3．【答案】B【解析】()10110110512024S a a a a =+=∴+=故选B4．【答案】D【解析】依题意有1114472121a d a d a d +++=⎧⎨+=⎩解得132a d =-⎧⎨=⎩，故7163629a a d =+=-+⨯=. 故选D. 5．【答案】B【解析】依题意有()()()()411414640121024541302n n S a d n n S na d n n S n a d -⎧⎪=+=⎪-⎪=+=⎨⎪⎪--=-+=⎪⎩，解得14n =，故选B.6．【答案】C【解析】由于题目所给数列为等差数列，根据等差数列的性质，有()2415117318363a a a a d a d a ++=+=+=，故7a 为确定常数，由等差数列前n 项和公式可知()11313713132a a S a+⋅==也为确定的常数，故选C. 7．【答案】150【解析】由等差数列{}n a 的性质可得：912615120a a a a a a +=+=+，又69121530a a a a +++=，120=15a a ∴+，则该数列的前20项之和()1202020S =10151502a a +=⨯=．故填150． 8．【答案】5940【解析】50和350之间的所有末位数字是3的整数有53637383..343，，，，，构成一个首项为153a =，公差为10d =的等差数列,1(1)1043n a n d n a =+-=+,3431043n =+，解得30n =,根据等差数列前n 项和公式即30(53343)3059402S +⨯==故填5940 9．【答案】2059【解析】由题意可知，101923a a d =+=，2512422a a d =+=-，解得150a =，3d =-，所以()()5013533n a n n =+-⨯-=-.由5330n a n =-<，得533n >，又*n N ∈，所以从第18项开始数列的各项为负.而()()213103503222nn n S n n n-=+⨯-=-+.所以()123501217181950175017a a a a a a a a a a S S S +++⋅⋅⋅+=++⋅⋅⋅+---⋅⋅⋅-=--223103310321717505020592222⎡⎤⎡⎤⎛⎫⎛⎫=⨯-⨯+⨯--⨯+⨯= ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦故填205910．【答案】（1）222n a n =-；（2）12n a n =-和13n a n =-【解析】（1）由1498S =得121314a d +=，又111100a a d =+=，所以2d =-，120a =。

巩固练习_基础_等差数列及其前n项和

【巩固练习】一、选择题1.在等差数列{a n }中，a 1＝2，a 3＋a 5＝10，则a 7＝( )A ． 5B ．8C ． 10D ． 142．数列{a n }的通项公式a n ＝2n ＋5，则此数列( )A ．是公差为2的递增等差数列B ．是公差为5的递增等差数列C ．是首项为7的递减等差数列D ．是公差为2的递减等差数列 3.已知{a n }是等差数列，a 3＋a 11＝40，则a 6－a 7＋a 8等于( )A ．20B ．48C ．60D ．72 4.（2016年全国Ⅰ高考）已知等差数列{}n a 前9项的和为27，10=8a ，则100=aA.100B.99C.98D.975.（2015 新课标Ⅱ）设S n 是等差数列{a n }的前n 项和,若a 1+a 3+a 5=3,则S 5=（）A ．5B ．7C ．9D ．116. 设S n 是等差数列{a n }的前n 项和，若3613S S =，则612S S 等于( ) A.310 B.13C.18D.19 二、填空题7. 若等差数列{a n }满足a 7＋a 8＋a 9＞0，a 7＋a 10＜0，则当n ＝时，{a n }的前n 项和最大．8.在公差d=21的等差数列{a n }中，已知S 100=145，则a 1+a 3+a 5+……+a 99的值为_____. 9.把20分成四个数成等差数列，使第一项与第四项的积同第二项与第三项的积的比为2∶3，则这四个数从小到大依次为____________.10.已知数列{a n }的前n 项和S n ＝n 2－9n ，第k 项满足5<a k <8，则k ＝________.11. 在等差数列{a n }中，a 3＝7，a 5＝a 2＋6，则a 6＝________.三、解答题12.在等差数列{a n }中，a 3+a 4+a 5+a 6+a 7=450，求a 2+a 8.13．已知数列{a n }是等差数列，令221n n n a a b -=+，求证：{b n }也是等差数列.14．已知等差数列{a n }满足，S p =q ，S q =p ，(p≠q)，求S p+q .15．已知等差数列{a n }中，a 1＜0，S 9=S 12，求S n 何时取最小值.16. （2016 全国II 卷高考）等差数列{n a }中，34574,6a a a a +=+=. （Ⅰ）求{n a }的通项公式；（Ⅱ）设[]n n b a =，求数列{}n b 的前10项和，其中[]x 表示不超过x 的最大整数，如[0.9]=0,[2.6]=2.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

等差数列及等差数列求和
学习目标：
1.理解等差数列的概念以及性质。

2掌握等差数列的通项公式和前n 项和公式。

3能运用等差中项的性质解题，并能灵活运用等差数列的求和公式解题。

4了解等差数列求和公式的函数特征，并能运用之求前n 项和的最值。

知识要点梳理：
1等差数列的定义：如果一个数列从第2项起，每一项与它的前一项的差等于，这个数列就叫，用式子可表示为，则数列{}n a 叫做等差数列。

2等差数列的单调性。

公差时，数列为递增数列；公差时，数列为递减数列；当公差为时，数列为常数列，等差数列不会为摆动数列。

3等差数列的通项公式和前n 项和公式：
n a = 。

或n a = n s = = 。

前n 项和公式是用方法推导的。

已知n m a a 为等差数列的任意两项，
公差为d ，则d=
n
m a a n m -- （公差的计算：d =1--n n a a ）
4等差数列的性质。

若}{n a 为等差数列
（1）m,n,p,q ∈*
N ,当m+n=p+q,则。

⑵若公差为d ，则}{2n a 是，公差为。

⑶若}{n b 为等差数列，则}{n n b a +是。

（4）,,2
a b A a A b +=
⇔成等差数列则三个数成等差可设为，
四个数成等差可设为。

（5）若{}n a 的前n 项的和n s 则仍是等差数列。

（）若，是等差数列，为前项和，则
；
42121
a b S T n a b S T n n n n m m
m m =--
{}（）为等差数列（，为常数，是关于的常数项为
52
a S an bn a
b n n n ⇔=+0的
二次函数。

课后练习：一．选择题。

1若lg 2,lg(21),lg(23)x x -+成等差数列，则x 的值等于（） A.0 B. 2log 5 C. 32 D.0或32
2. 在等差数列{}n a 中31140a a +=，则45678910a a a a a a a -+++-+的值为（）
A.84
B.72
C.60 .
D.48 3 在等差数列{}n a 中，前15项的和1590S = ，8a 为（）
A.6
B.3
C.12
D.4
4. 等差数列{}n a 中, 12318192024,78a a a a a a ++=-++=,则此数列前20项的和等于
A.160
B.180
C.200
D.220
5. 在等差数列{}n a 中,若34567450a a a a a ++++=，则28a a +的值等于（）
A.45
B.75
C.180
D.300
6．设｛a n ｝（n ∈N *
）是等差数列，S n 是其前n 项的和，且S 5＜S 6，S 6＝S 7＞S 8，则下列结论错误．．
的是（） A.d ＜0 B.a 7＝0 C.S 9＞S 5
D.S 6与S 7均为S n 的最大值 7．若一个等差数列前3项的和为34，最后3项的和为146，且所有项的和为390，则这个数列有（）
A.13项
B.12项
C.11项
D.10项
8．设数列{a n }是递增等差数列，前三项的和为12，前三项的积为48，则它的首项是（） A.1 B.2 C.4 D.6
9．等差数列{a n }的前m 项和为30，前2m 项和为100，则它的前3m 项和为（） A.130 B.170 C.210 D.260
二填空题。

．
1. 等差数列8，5，2，…的第20项为___________.
2. 在等差数列中已知a 1=12, a 6=27,则d=___________
3. 在等差数列中已知13
d =-
，a 7=8，则a 1=_______________
4. 2
()a b +与2
()a b -的等差中项是________________- 5. 等差数列-10，-6，-2，2，…前___项的和是54 6. 正整数前n 个数的和是___________
7. 数列{}n a 的前n 项和2
3n S n n -＝，则n a ＝___________
8.设等差数列a 4=5，a 9=17， a 14= 。

9等差数列｛a n ｝，｛b n ｝的前n 项和分别为S n 与T n ，若
1
32+=
n n T S n
n ，则
9
9b a =
10．设数列｛a n ｝的通项为a n ＝2n －7（n ∈N *），则|a 1|＋|a 2|＋…＋|a 15|＝．三．解答题。

1.根据下列各题中的条件，求相应的等差数列{}n a 的有关未知数：（1）151,,5,66
n a d S ==-
=-求n 及n a ；（2）12,15,10,n n d n a a S ===-求及
2已知等差数列{a n }，a 5+a 6+a 7=15， a 5a 6a 7=45，求数列{a n }的通项公式．
3已知a 1=kc ，a 2=kc 2，a 3=kc 3，k>0，c>0。

求证lga 1，lga 2，lga 3成等差数列
4在项数为2n 的等差数列中，各奇数项之和为75，各偶数项之和为90，末项与首项之差为27，求n ．
5．已知等差数列{a n}，a1>0，S3=S11，该数列的前多少项之和最大?
6．等差数列{a n}的前n项和S n=m，前m项和S m=n(m>n)，求前m+n项和S m+n
7．已知数列{a n}的前n项和S n=3n2+n-1，求通项a n，并判断此数列是否为等差数列?。