第五章多组分系统热力学与相平衡
第五章 多组分系统热力学及相平衡
第五章 多组分系统热力学与相平衡主要公式及其适用条件1. 拉乌尔定律与亨利定律（对非电解质溶液）拉乌尔定律：A *A A x p p = 其中，*A p 为纯溶剂A 之饱和蒸气压，A p 为稀溶液中溶剂A 的饱和蒸气分压，x A 为稀溶液中A 的摩尔分数。
亨利定律： B B B B B B B c k b k x k p c,b,x,===其中，B p 为稀溶液中挥发性溶质在气相中的平衡分压，B B B c,b ,x ,k k ,k 及为用不同单位表示浓度时，不同的亨利常数。
2. 理想液态混合物定义：其任一组分在全部组成范围内都符合拉乌尔定律的液态混合物。
BB B x p p *=其中，0≤x B ≤1 , B 为任一组分。
3. 理想液态混合物中任一组分B 的化学势)ln((l)(l)B *B B x RT μμ+=其中，(l)*B μ为纯液体B 在温度T ﹑压力p 下的化学势。
若纯液体B 在温度T ﹑压力0p 下标准化学势为(l)0B μ，则有：m =+≈⎰*00BBB B (l)(l)(l)d (l)0p*,p μμV p μ 其中，m B (l)*,V 为纯液态B 在温度T 下的摩尔体积。
4. 理想液态混合物的混合性质① 0Δm i x =V；② 0Δm i x=H ； ③ B=-∑∑mix B BB BΔ()ln()S n Rxx ；④ S T Gm i x m i x ΔΔ-=5. 理想稀溶液① 溶剂的化学势：m =++⎰0A AA A(l )(l )l n ()(l )dp*,p μμR Tx V p 当p 与0p 相差不大时，最后一项可忽略。
② 溶质B 的化学势：)ln(ln((g)ln((g))ln((g)(g)(0BB 0BB B 0B 0BB B B b b RT )p b k RT μ)p b k RT μp p RT μμμb,b,++=+=+==溶质）我们定义：⎰∞+=+pp b,b,0pV μ)p b k RT μd ln((g)B 0B0B 0B(溶质)(溶质)同理，有：⎰⎰∞∞+=++=+pp x,x,pp c,c 00p V μpk RT μpV μ)p c k RT μd (溶质)(溶质)d (溶质)(溶质)B 0B 0B 0B B 0B00B ,0B)ln((g)ln((g)⎰⎰⎰∞∞∞++=++=++=p p x ,pp c,pp b,0pV x RT μp V c c RT μp V b b RT μμd ()ln()(d )()ln()(d )()ln(B B 0B B 0B 0BB 0B 0B B 溶质)溶质溶质溶质溶质(溶质)(溶质)注：（1）当p 与0p 相差不大时，最后一项积分均可忽略。
第05章 相平衡
第五章相平衡§5.1 引言相平衡是热力学在化学领域中的重要应用之一。
化工中很多分离提纯过程，例如精馏、吸收、结晶、萃取等，都涉及到物质在不同相中的分配，它们主要利用物质的挥发性或溶解度等方面的差异，以达到分离提纯的目的，相平衡亦可为此提供理论依据。
因此研究相平衡有着重要现实意义。
一、相（phase）体系内部物理和化学性质完全均匀的部分称为相。
相与相之间在指定条件下有明显的界面。
（1）气体，不论有多少种气体混合，只有一个气相。
（2）液体，按其互溶程度可以组成一相、两相或三相共存。
（3）固体，一般有一种固体便有一个相。
两种固体粉末无论混合得多么均匀，仍是两个相（固体溶液除外，它是单相）。
体系中相的总数用Φ表示。
二、相变物质从一个相流动到另一个相的过程，称为相变化，简称相变。
相变包括气化（boil）、冷凝（condensation）、熔化（melt）、凝固（freeze）、升华（sublimation）、凝华以及晶型转化等。
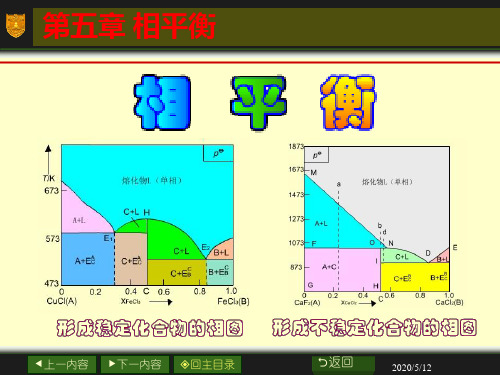
三、相图（phase diagram）将多相体系的状态随组成、温度、压力等强度性质的改变而发生的过程用图形表示，称为相图。
根据组成相的物态不同分为气-液相图、液-液相图和液-固相图。
根据用途不同可将相图分为温度-蒸汽压图（T－p图，P314 图5.1）、蒸汽压－组成图（p－x图，P318 图5.3）:恒定温度，研究P-x，y之间的关系。
称为压力组成图。
温度－组成图（T －x 图，P321 图5.5）:在恒定压力下表示二组分系统气-液平衡时温度与组成关系的相图。
研究T-x ，y 之间的关系。
和温度－蒸汽压－组成图（T －p －x 图，P322 图5.6），T-x-y ,x-y ,p-x-y 相图等。
四、自由度（degrees of freedom ）确定平衡体系的状态所必须的压力、温度和浓度等独立强度性质的数目称为自由度，用字母f 表示。
如果已指定某个强度性质，除该性质以外的其它强度性质数称为条件自由度，用*f 表示。
第五章 相平衡
b.同一相内物质间有浓度限制条件R′
5.3 相律
相律
例如：合成氨时系统内有N2,H2,NH3 N2+3H2=2NH3
Kp p p p
2 NH 3 3 N2 H 2
C= S-R C =S-R-R´ 5.3 相律
相律
C = S - R - R'
注意： (1)R---表示独立的化学平衡数。有时系统中可以 存在很多化学平衡，但是独立的并不多。
5.3 相律
相律
自由度(degree of freedom) 系统内独立可变因素的数目称为自由度，用字母f 表示。独立可变因素包括压力、温度和浓度等。
独立可变因素是指在一定范围内这些可变因素变 化时，不会引起相的改变，既不会使原有相消失， 也不会增加新的相。
5.3 相律
相律
相律(phase rule)
Φmin=1
fmin=0
(3)可求系统中最多相数Φ
max
5.3 相律
相律
例题(P336，习题4)：已知Na2CO3(s)和 H2O(l)可以生成三种水合物： Na2CO3· H2O(s)， Na2CO3· 7H2O(s)和 Na2CO3· 10H2O(s)，试求： (1) 在大气压力下，与Na2CO3水溶液和冰 平衡共存的水合盐的最大值； (2) 在298K时，与水蒸气平衡共存的水合 盐的最大值。
单组分系统的两相平衡
解：
p2 vap H m 1 1 (1) ln p1 R T1 T2 p2 34170J m ol1 1 1 ln 1 1 10.02kPa 8.314J m ol K 293K 303K p2 15.91kPa
5.1 引言
热力学相平衡
返回
2012-5-17
水的相图
OD 是AO的延长线，是过冷水和水蒸气的介稳平衡 线。因为在相同温度下，过冷水的蒸气压大于冰的蒸 气压，所以OD线在OB线之上。过冷水处于不稳定状 态，一旦有凝聚中心出现，就立即全部变成冰。 O点 是三相点（triple point），气-液-固三相 共存， F = 3, f = 0 。三 相点的温度和压力皆由 体系自定。 H2O的三相点温度为273.16 K，压力为610.62 Pa。
f ** = f − 2 指定了压力和温度，
上一内容
下一内容
回主目录
返回
2012-5-17
5.2
多相体系平衡的一般条件
在一个封闭的多相体系中，相与相之间可以有热 的交换、功的传递和物质的交流。对具有 F 个相体系 的热力学平衡，实际上包含了如下四个平衡条件： (1)热平衡条件：设体系有α , β , K ,F 个相，达到平衡 时，各相具有相同温度
上一内容 下一内容 回主目录
返回
2012-5-17
5.4 单组分体系的相图
单组分体系的相数与自由度
C =1
当 F =1
F =2 F =3
f +F = 3
单相 两相平衡 三相共存
f =2 f =1 f =0
双变量体系 单变量体系 无变量体系
单组分体系的自由度最多为2，双变量体系 的相图可用平面图表示。
*
上一内容
下一内容
回主目录
返回
上一内容
下一内容
回主目录
返回
2012-5-17
5.1 引言
相（phase） 体系内部物理和化学性质完全均匀 的部分称为相。相与相之间在指定条件下有明显 的界面，在界面上宏观性质的改变是飞跃式的。 体系中相的总数称为相数，用 F 表示。 气体，不论有多少种气体混合，只有一个气相。 液体，按其互溶程度可以组成一相、两相或三 相共存。 固体，一般有一种固体便有一个相。两种固体粉 末无论混合得多么均匀，仍是两个相（固体溶液 除外，它是单相）。
物理化学
多组分系统热力学与相平衡
（一）多组分系统热力学
引言 溶液（Solution）
广义的说两种或两种以上物质彼此以离子或分子状态均匀混 合所形成的系统称为溶液。 溶液可分为气态溶液、固态溶液和液态溶液。 根据溶液中溶质的导电性又可分为电解质溶液和非电解质溶液。 本章主要讨论液态的非电解质溶液。
溶剂（solvent）和溶质（solute） 如果组成溶液的物质原来有不同的状态，通常将液态 物质称为溶剂，气态或固态物质称为溶质。
由B B RT ln xB 得B / T B / T R ln xB
在压力、组成不变的条件下，上式对T求偏导数，得
B / T / T p, x
( [
B
/ T / T
p
B
T ] P , nB , nC T
)
G ( )T , P ,nc nB [ ] T { }P ,nB ,nC T
kx pB
kx pB
kx pB
3、拉乌尔定律与亨利定律的对比
对于二组分系统，在稀溶液范围内，一个符合亨利定律 另一个则必符合拉乌尔定律；反之也必然成立。这说明对于 同一溶液，拉乌尔定律及亨利定律适用的浓度范围是相同的。
§5.3 理想液态混合物
1、理想液态混合物的定义
若液态混合物中任一组分在全部浓度范围内都符合拉乌尔 定律，则该液态混合物称为理想液态混合物。 理想液态混合物中各组分分子的大小和物理性质相同；分子 之间的作用力完全相同，溶液中任一组分的分子所处的环境与 其纯组分时的环境完全相同。
l, T , p RT ln xB B l, T , p, xc B
简写成
B RT ln xB
第五章 多相平衡PhaseEquilibrium 物理化学课件
(2) 相律的推导
现设该独立变量为温度，则根据纯液态锌的克拉佩 龙－克劳休斯方程，p(Zn)=f (T)， 在一定温度下有确 定的p(Zn)，上面第一个方程表示如下的平衡
ZnO(s) + C(s) = Zn(g) +CO(g) 因其平衡常数在定温下为定值，有K1=p(Zn)·p(CO) 于是p(CO)有定值。再根据第二个化学平衡，其平衡 常数在定温下为另一定值K2=p(CO2)/p2(CO)，因此 p(CO2)也有定值。故一个强度变量的值可确定其它四 个强度变量的值，F=1，同样若先确定另一强度变量 的值，例如p(CO)为某值，同样可推论出其它强度变 量的值。
(2) 相律的推导
设有 S 种物质在 P 个相中， 描述一个相的状态要 T，p，(x1, x2, …xs)
(S–1)种独立变量 所以总变量数= P(S –1) + 2
(2) 相律的推导
在一个封闭的多相系统中，相与相之间可以有热的 交换、功的传递和物质的交流。对具有P个相系统的 热力学平衡，实际上包含了如下四个平衡条件： (1)热平衡条件：设系统有、Ⅱ······P 个相，达到平 衡时，各相具有相同温度
2c(NH3) = c(H2S) 但如果分解产物在不同相则不然，如反应：
CaCO3(s) = CO2(g) + CaO(s) c(CO2, g)和c(CaO, s)无关，则无浓度限制条件。 设浓度限制条件的数目为R′，则又有R′个关于浓度的 方程式。
(2) 相律的推导
化工热力学第五章 相平衡 ppt课件
汽液平衡计算类型
计算类型 泡点压力计算
(bubble point pres.)
泡点温度计算 (bubble point temp.)
露点压力计算 (dew point pres.)
均已被确定，但描述系统的平衡状态无须使用全部的变量，只要由相律 求得的自由度数的变量即可。因此相平衡问题在数学上是完全可解的， 这也是气液相平衡计算的主要任务，并进而进行各相的其它热力学性质 计算。
【例5-1】 试确定下述系统到达相平衡时的自 由度
（1）水的三相点， （2）水－水蒸汽平衡， （3）水－水蒸汽－惰性气体， （4）乙醇－水汽液平衡， （5）戊醇－水汽液平衡（液相分层）。
由此可见，对于一个典型的化工生产车间，无论是原料（混 合物）的预处理、物料的反应，还是产物与副产物的分 离，都需要用平衡性质来确定分离方法及其设备的结构 尺寸。
5.1 相平衡基础 5.2互溶体系的汽液平衡计算通式 5.3汽液平衡 5.4 汽液平衡数据的热力学一致性检验 5.5平衡、稳定性与液液平衡 5.6 其他类型的相平衡
解：根据相律的表达式，分别计算各个特定相平衡条件下的 自由度
(1) 对于水的三相点体系 C＝1（水）
＝3（三相－汽、
液、固）
自由度: F ＝1－3＋2＝0 这说明水的三相点是一
个无变量平衡状态。
(2) 对于水－水蒸汽平衡体系 C＝1（水）
＝2（两相－汽、液）
则自由度为 F ＝1－2＋2＝1
fˆi L
fi
0
L i
xi
i 1,2,3,L N
5.2.1 状态方程法（EOS法）
yiˆiV xiˆiL i 1,2,3,L N
5.2.2 活度系数（ i 法）
第五章多组分系统与相平衡问答题
第五章多组分系统与相平衡问答题（一、多组分系统热力学）1、什么叫理想混合物？理想混合物模型的微观特征是什么？什么叫理想稀溶液？理想稀溶液模型的微观特征是什么？2、固体糖可顺利溶解在水中，试比较固体糖的化学势与糖水中的化学势哪个高？3、重结晶制取纯盐的过程中，析出NaCl固体的化学势与母液中NaCl的化学势哪个高？4、马拉松运动员沿途准备的饮料应该是那一种A 白开水B 含适量的维生素的等渗饮料C 20%葡萄糖饮料D 高脂肪、高蛋白、高能量饮料5、298K，0.01mol/kg糖水的渗透压为∏1, 0.01mol/kg食盐水的渗透压为∏2，则∏1与∏2的关系如何？6、0.450克化合物溶于30克水中，（水的冰点降低常数k f=1.86），凝固点降低了0.150℃,该化合物的分子量是多少？7、在一恒温抽空得玻璃罩中，封入两杯液面相同的糖水（A）和纯水(B)，经历若干时间后，两杯液面的高度将如何变化？8、关于偏摩尔量，下面叙述不正确的是(A)偏摩尔量的数值可以是正数、负数和零。
(B)溶液中每一种广度性质都有偏摩尔量，而且都不等于其摩尔量。
(C)除偏摩尔吉布斯自由能外，其它偏摩尔量都不等于化学势。
(D)溶液中各组分的偏摩尔量之间符合吉布斯——杜亥姆关系式。
9、两只烧杯中各有1kg水，向A杯加入0.01mol蔗糖，向B杯内溶入0.01molNaCl，两只烧杯按同样速度冷却降温，则哪只烧杯先结冰？10、低压下影响亨利系数k的因素有哪些？11、如果在纯A(l)中加入B 物质，在何种条件下才会出现即使溶液的沸点升高又使溶液的凝固点降低的现象？12、在一定温度下，某理想稀溶液中溶质B的化学势可用下列方程表示：μB=μx,Bθ+RT ln(x B) = μb,Bθ+RT ln(b B/ bθ)= μc,Bθ+RT ln(c B/cθ)以上各μBθ的大小与物理意义是否相同？请说明原因。
13、A和B形成溶液，在定温定压条件下当组成发生变化时，若μA 增大，则μB必然减小，反之亦然，对吗？14、化学势的定义是什么？它和偏摩尔吉布斯函数、偏摩尔亥姆霍兹函数、偏摩尔焓、偏摩尔热力学能是否一回事。
物理化学：相平衡
相平衡是热力学在化学领域中的重要应用之一。研究 多相体系的平衡在化学、化工的科研和生产中有重要的 意义，例如：溶化、蒸馏、重结晶、萃取、提纯及金相 分析等方面都要用到相平衡的知识。
一、基本概念
第一节 相律
1、 相（phase） 体系内部物理和化学性质完全均匀的 部分称为相。相与相之间在指定条件下有明显的界面， 在界面上宏观性质的改变是飞跃式的。体系中相的总数 称为相数，用Φ表示。
三、自由度数（f）
自由度: 确定平衡体系的状态所必须的独立强度变量的
数目称为自由度，用字母 f 表示。这些强度变量通常是
压力、温度和浓度等。
以水为例〔注意是商量平衡态〕∶ a. 当φ=1时，例如液态水的T、p可在肯定范围内改变， φ不变 ∴ f=2 b. 当φ=2时，例如气－液平衡，指定p外，则Tb确定； 而指定T，则水有确定的平衡蒸气压p，∴ f=1 c. 当φ=3时，即气－液－固三相平衡共存时〔三相点〕，T、 p是确定的〔273.16K、6.1×102Pa、由水的性质所决定〕， ∴ f=0，如果变化T或p，则不可能三相共存〔即φ≠3〕。
一、水的相图 水的相图是依据实验绘制的。图上有：
水 的 相 图
(1) 气、液、固单相区∶f=1－1＋2=2
(2) 两相平衡线∶
f=1－2＋2=1
OC线∶气－液平衡
T与液态水的饱和蒸气压p蒸气的关系
或沸点Tb与p外的关系
OA线∶液－固平衡 凝固点Tf与p外的关系
OB线∶气－固平衡
T与冰的饱和蒸气压p蒸气的关系
dp/dT=ΔHm / T·ΔVm 此方程适合于任何纯物质的两相平衡
2、对于气－液或气－固两相平衡体系 近似处理∶a. 假设蒸气遵守理想气体状态方程
第五章多相平衡
2020/10/8
-- 5 --
2 物种数(number of substance)
系统中所含的的化学物质数成为“物种数”, 用 S 表示.
3 组分数(number of components)
能够表示系统中各相组成所需要的最少独立物 种数, 用C 表示.
即 C SR R '
R — 表示独立的化学平衡数目.
R’— 表示化学平衡中同一相浓度限制条件的个 数.
2020/10/8
-- 6 --
• 例: 由O2,C,CO,CO2组成体系,求体系的独立化学反应数R?
• 解: 对于由O2,C,CO,CO2组成体系,存在如下化学反应:
• 单组分的相变温度与压力之间存在一定的关系, 此 关系即为克劳修斯—克拉贝龙方程.
2020/10/8
-- 20 --
在 T、p 一定条件下, 纯物质两相平衡时有
当温度和压力微变T +dT、p +dp,则该物质在
两相的化学势分别微变至 d,d, 在达
到新的平衡时,由于
dd
2020/10/8
-- 21 --
•
NaCl = Na+ + Cl-
•
H2O = H+ + OH－
•
H2O+H2O = (H2O)2
•
• 物种: •
NaCl, Na+, Cl-, H2O, H+, OH-, (H2O)2… S=7
•
R= 3
(食盐,水的电离和水的缔合);
•
R’=2
第五章相平衡
第五章相平衡（Phase equilibrium）相平衡、热平衡和化学平衡是热力学在化学领域中的重要应用，也是化学热力学的主要研究对象。
相平衡研究对生产和科学研究具有重大的实际意义。
例如在化学研究和化学生产过程的分离操作中，经常会遇到各种相变化过程，如蒸发、冷凝、升华、溶解、结晶和萃取等，这些过程及到不同相之间的物质传递。
相平衡研究是选择分离方法、设计分离装置以及实现最佳操作的理论基础。
除了分离以外，相平衡及其基本理论还广泛应用于冶金、材料科学、地质矿物学、晶体生长等学科中，对这些部门的科研和生产有着重要的指导意义。
相平衡研究多相体系相变化规律，是热力学基本原理在化学领域中的重要应用。
“相律”是根据热力学原理推导出来的，以统一观点处理各种类型多相平衡的理论方法十分严谨明确。
它表明一个多相平衡体系的组分数、相数以及自由度之间的关系，可以帮助我们确定体系的平衡性质以及达平衡的必要条件。
然而，相律也有其局限性，它只能对多相平衡作定性描述。
可指明特定条件下平衡体系至多的相数以及为保持这些相数所必具的独立变量数。
但究竟是哪些相共存？哪些性质可作为独立变量以及它们之间的定量关系如何等问题，相律均无能为力。
这方面知识仍有待从实验中确定。
本章着重讨论各种相平衡体系所遵守的一个普遍规律----相律，以及各种基本类型的相图，具体分析体系的相平衡情况与温度、压力和组成等因素的关系，并举例说明其实际应用§5.1相律一、基本术语1、相：体系中物理性质和化学性质完全均匀的一部分称为相物质从一个相转移到另一个相的过程称为相变化过程，而相平衡状态就是相变化过程的极限，此时宏观上投有任何物质在相间传递。
此处“完全均匀”，是指体系中的物质在分子水平上的均匀混合的状态，此时即便是由多种物质构成的体系，但其物理性质和化学性质都达到了完全均匀的程度，用一般的仪器已分不出其界面了，形成一个均相体系。
多相体系中，相与相之间存在明显的界面，称为相界面。
第五章 相平衡
二元凝聚系统相图表示法：T－x图
一、二元凝聚系统相图的基本类型
1.具有一个低共熔点的简单二元系统相图
特点：两组分在液态时完全互溶，形成单相溶液； 固态时完全不互溶，二组分各自从液相中分别结 晶，组分间无化学作用，不生成新化合物。
⑴
相
图
分
析
G
H
相区：
aEb : 高温熔体的单相区 (液相区)
bEH : L B 两相平衡共存区
熔体(1600℃) 熔体 (1670℃)
α－石英
870℃
1470℃
α－鳞石英
α－方石英
1723℃ 熔融石英
573℃
163℃
180～270℃
急
冷
β－石英
β－鳞石英
β－方石英
石英玻璃
117℃ γ－鳞石英 同 级 转 变(慢)
同
类 转
(快)
变
SiO2相图
1、在573℃以下的低温，SiO2的稳定晶型为－石英，加热至573℃转变为高温型 的－石英，这种转变较快；冷却时在同一温度下以同样的速度发生逆转变。如 果加热速度过快，则－石英过热而在1600℃时熔融。如果加热速度很慢，则在 870℃转变为－鳞石英。
以 忽略压强的影响，相律中的“2”应为“1”。
3. 必须正确判断独立组分数、独立化学反应式、相数以及限 制条件数，才能正确应用相律。
4. 自由度只取“0”以上的正值。如果出现负值，则说明体系可 能处于非平衡态。
第二节 单元系统相图
单元系统中， c = 1
f=c–p+2=3–p
pmin=1 pmax=3
2. 介稳态 即热力学非平衡态，经常出现于硅酸盐系统中。
如： α－石英 870α℃－鳞石英 1470℃α－方石英
第五章多相体系—相平衡Heter...
第五章多相体系—相平衡Heterogeneous SystemPhase EquilibriumIntroduction: 多相体系的分离& 提纯第一节相律1.1 基本概念相：体系中物理性质与化学性质完全均匀的部分相数：一个体系所含相的数目，用符号P表示气体：一般只有一相；（P＝1）液体：完全互溶，只有一相；部分互溶，有几层就有几相；(P＝1，2，3……）固体：有几种固体就有几相。
固态溶液：“固溶体”（P＝1）相变化过程（相变）；相平衡状态；相界面独立组分数：形成一个热力学平衡体系所需要的最少物种数，简称组分数，用符号C 表示。
组分数＝物种数－独立的化学平衡数－独立的限制条件数C ＝S －R －R ´S ：物种数，即体系所含物质的数目R ：独立的化学平衡反应数R ´：独立的限制条件数，比如浓度，比例等例如，由NH 4Cl(s)、HCl(g)和NH 3(g)构成的体系，①体系的S=3②三种物质之间又存在化学反应NH 4Cl(s)＝HCl(g)+NH 3(g) R=1③若该混合物是由NH 4Cl(s)分解而得，则体系中HCl(g)与NH 3(g)的浓度比保持1:l ，即存在关系式y HCl = y NH 3，则R'=1因此：由NH 4Cl(s)分解而得到的混合物，C=3-1-1=1，该体系为单组分体系独立组分数：形成一个热力学平衡体系所需要的最少物种数，简称组分数，用符号C表示。
组分数＝物种数－独立的化学平衡数－独立的限制条件数C＝S －R－R´S：物种数，即体系所含物质的数目R：独立的化学平衡反应数R´：独立的限制条件数，比如浓度，比例等例如：N2+3H2= 2NH3高温、催化剂存在时S = 3, R = 1, R´= 0, 则：C=3-1-0 = 2 （双组分系统）高温、催化剂存在且N2：H2＝1 : 3 时S = 3, R = 1, R´= 1, 则：C=3-1-1 = 1 （单组分系统）自由度数：确定和保持平衡状态所需的独立改变的变量的数目，称为自由度数，用F 表示。
多组分系统热力学
多组分系统热力学
多组分系统热力学是研究多个组分构成的系统的热力学行为的科学。
在多组分系统中，各个组分之间可能会相互作用，从而影响整个系统的热力学性质。
多组分系统热力学的研究内容包括：
1.热力学第一定律：能量守恒定律，即在一个封闭系统中，能量不
能被创造或消除，只能从一种形式转化为另一种形式。
2.热力学第二定律：熵增定律，即在一个封闭系统中，熵（即系统
的混乱程度）只能增加，不能减少。
这意味着，系统总是朝着熵增的方向演化，而不是熵减的方向。
3.相平衡：研究在给定的温度和压力下，不同物质之间是如何平衡
的。
4.化学平衡：研究在给定的温度和压力下，化学反应是如何平衡的。
5.热力学第三定律：绝对零度不能达到原理，即任何物质在绝对零
度下的熵均为零。
这些定律和原理对于理解多组分系统的热力学行为非常重要。
在化学工程、材料科学、生物工程等领域中，多组分系统热力学被广泛应用于研究复杂系统的热力学性质和行为。
第五章 热力学在相平衡体系中的应用43
步冷曲线：表现为一平台
29
c）相图分析
30
d)物系点 a，P 点的变化
a，P 点的步冷曲线
31
3.生成固溶体的二组分体系
固溶体：固体溶液，两组分的原子、分子大 小相当，晶体结构相似，可以互相 替代晶格中的位置
特点：a）为一相，存在浓度 b）与固体混合物不同 分类：完全互溶固溶体 部分互溶固溶体
（2）相图的绘制 配制不同组成的样品
做步冷曲线 拐点和平台的温度 T，标在 T-X 图上 相点连线——绘制出相图 a）做 5 个样品的步冷曲线 含 Cd：0%，20%，40%，70%，100% 相应的拐点：A，C，D，E，F，G，H
14
b）在步冷曲线右边，T-X 坐标 c）将不同的拐点和平台的 T 标在 T-X 图上 d）对多点做性质分析，连线得相图
2
WB OA W AB
W A OB W AB
说明：a）即力学中的杠杆原理
b）只适用于两相平衡 X：摩尔分数或质量百分数
W：总摩尔数或总质量
3
4.完全不互溶双液系 如：水-氯苯体系，汞-水体系 两组分间没有相互溶解，每个组分的蒸汽压 等于其单独存在时的蒸汽压 体系的总蒸汽压 P=P*A+P*B 即 P > P*A, P > P*B
3.杠杆规则（原理）
设：TO 时物系点 O 的 重量 W，组成为 X 相点：A：WA，X A B：WB，XB
1
由质量守恒原理：
XW=XAWA+XB WB W=WA+WB X（ WA+WB ）=X AWA+XB WB WA（X-X A）=WB（XB-X）
即：WAOA=WBOB WA OB W A OB 1 1 WB OA WB OA W A WB OB OA WB OA
第五章多组分系统热力学与相平衡
第五章 多组分系统热力学与相平衡（一）主要公式及其适用条件1、拉乌尔定律 A *A A x p p =式中*A p 是与溶液在同一温度下纯A 液体的饱和蒸气压。
此式适用于理想液态混合物中的任一组分或理想稀溶液中的溶剂A 。
2、亨利定律 B B ,B x k p x =式中k x ,B 为溶液的组成用摩尔分数x 表示时溶质B 的亨利系数，其值与溶质、溶剂的性质及温度有关。
亨利定律也可以c B 、b B 等表示，但相应的亨利系数的大小和单位皆不相同。
此式只适用于理想稀溶液中的性质。
3、理想液态混合物中任一组分B 的化学势表示式 B B B ln x RT +=O μμ在理想液态混合物的温度下，p =p O =100kPa 的纯B(l)的状态定为B 的标准态，相应的化学势O B μ称为B 的标准化学势。
4、理想稀溶液化学势的表示式（1）溶剂A A A A ln x RT +=O μμ温度为T 、p =p O =100kPa 下，纯（A ）的状态定为溶剂的标准状态。
（2）溶质B B ,B B ln x RT x +=O μμ)/ln(B ,B O O +=c c RT c μ=)/ln(B ,B O O +b b RT b μ同一种溶质B 在温度T 、p =p O =100kPa 下，用不同的组成表示化学势时，标准状态不同，O B μ不同，但B μ为定值。
5、稀溶液的依数性（1）蒸气压降低 B *A A *A *A A /)(/x p p p p p =-=∆式中x B 为溶质B 的摩尔分数。
此式适用于只有A 和B 两个组分形成的理想液态混合物或稀溶液中的溶剂。
（2）凝固点降低 ∆T f = K f b B式中O ∆=A m,fus A 2*f f /)(H M T R K ，称为溶剂A 的凝固点降低常数，它只与溶剂A 的性质有关。
此式适用于稀溶液且凝固时析出的为纯A(s)，即无固溶体生成。
（3）沸点升高 ∆T b = K b b B式中O ∆=A m,vap A 2*/)(H M T R K b b ，称为沸点升高常数，它只与溶剂的性质有关。
大学物理化学知识整理
第一章 理想气体1、理想气体：在任何温度、压力下都遵循P Ｖ=ｎRT 状态方程的气体。
2、分压力:混合气体中某一组分的压力。
在混合气体中，各种组分的气体分子分别占有相同的体积(即容器的总空间)和具有相同的温度。
混合气体的总压力是各种分子对器壁产生撞击的共同作用的结果。
每一种组分所产生的压力叫分压力,它可看作在该温度下各组分分子单独存在于容器中时所产生的压力B P 。
P y P B B =,其中∑=BBB B n n y 。
分压定律:∑=BB P P道尔顿定律：混合气体的总压力等于与混合气体温度、体积相同条件下各组分单独存在时所产生的压力的总和。
∑=BB V RT n P )/(3、压缩因子ＺＺ=)(/)(理实m m V V 4、范德华状态方程 RT b V V ap m m=-+))((2 nRT nb V Van p =-+))((22５、临界状态（临界状态任何物质的表面张力都等于０)临界点C ——蒸气与液体两者合二为一，不可区分,气液界面消失； 临界参数：(1)临界温度c T ——气体能够液化的最高温度。
高于这个温度,无论如何加压 气体都不可能液化;(2)临界压力c p ——气体在临界温度下液化的最低压力； （3)临界体积c V ——临界温度和临界压力下的摩尔体积。
６、饱和蒸气压:一定条件下，能与液体平衡共存的它的蒸气的压力。
取决于状态，主要取决于温度,温度越高，饱和蒸气压越高。
7、沸点:蒸气压等于外压时的温度。
８、对应状态原理——处在相同对比状态的气体具有相似的物理性质。
对比参数：表示不同气体离开各自临界状态的倍数 (１)对比温度c r T T T /= (2)对比摩尔体积c r V V V /= (3）对比压力c r p p p /= ９、rr r c r r r c c c T Vp Z T V p RT V p Z =⋅=10、压缩因子图:先查出临界参数,再求出对比参数r T 和r p ,从图中找出对应的Z 。
物理化学第五章(例题在课件尾部)
3、自由度及自由度数 (1)自由度：描述相平衡体系所必须指定的最少独立变量。 (2)自由度数F：描述相平衡物系中所必须指定的最少独立变量 数目。如T、P、各相浓度等。 或：在不引起旧相消失和新相生成的前提下，物系(体系)可 以在一定范围内自由变动的强度性质数目。 4、相律 (1)相律定义：解决相平衡物系中F,P,C之间相互关系的规律。
其中3=2－1,所以不是独立的； 为此：S=5，R=2 ③R＇独立浓度限制条件数，对每个独立反应而言
R＇求算方法
如:CaCO3(s)= CaO(s)+ CO2(g),
C+
参加反应各物质处于不同相时,R ' 0; 参加反应物质中有2种或以上物质处于同 一相,且浓度自始至终严格按反应方程式 计量系数反应者,R ' 1, 否则R ' 0
ξ5—2拉乌尔定律和亨利定律
1.拉乌尔定律
(1)定义：定温下，稀溶液中溶剂A的蒸气压PA等于纯溶剂蒸气压
与溶剂的摩尔分数xA的乘积或溶剂蒸气压降低值( 溶剂蒸气压之比等于溶液中溶质的量分数。 (2)公式： 或 )与纯
注意: PA若溶质不挥发,则PA为溶液蒸气压;若溶质挥发,则PA为溶 剂A在气相中的蒸气分压,该定律仅适用于较稀溶液(或理想稀溶
a)当P=1时，F为最大，Fmax=C+1，确定画相图座标数。 b)当F=0时，P为最大，Pmax=C+2，确定最多共存相数。 c)当F<0时,系统处于非平衡态。
ξ5—9单组分系统相平衡
1、水的相图（单组分系统的相图） （1）相图制备依据
描述由实验数据把多相物系状态随温度，压力，等变量变化关系
的图形叫相图。我们讨论的单组分物系为真空纯水，即C=1，令 F=0时，则Pmax=C+2=1+2=3；令P=1时，则Fmax=C-P+2=2；故单组分或（不定积分式） NhomakorabeaP
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
def
cB ＝nB /V
单位mol/L
4 质量摩尔浓度 质量摩尔浓度: 溶液中溶质B的量和溶剂的质量的比。
def
bB ＝nB / mA
单位mol/kg
§5-2 拉乌尔定律和亨利定 律
1 拉乌尔定律
稀溶液中溶剂A的蒸气压pA 等于同温度下纯溶剂的饱和蒸 气压与溶液中溶剂A的摩尔分数xA,的乘积。
pA pA xA
p
B(l)
B(l)
Vm,B(l)dp
p
代入
B(l)
B(1)
RT ln x
得到理想液态混合物中组分
B
的化学
势与组成的关系为：
p
B(l) B(l) RT ln xB Vm*,B(l)dp
p
在一般情况下，p 与 p 相差不大，所以可近似写作：
B(l) B(l) RT ln xB
2 理想液态混合物的混合性质
则溶剂A在T，p
下化学势： 当有多种溶质时：
A A RTM AbB
A A RTM A bB
B
2 溶质的化学势
稀溶液中的电解质符合亨利定律，以挥发性的气体溶质为 例，并推广至挥发性的溶质。
在一定的T，p下，溶液中溶质 B 的化学势 B（溶质）与气相 中 B 的化学势 B(g)相等。若认为气相为理想气体 ，有：
B(溶质)
B(g)
B(g)
RT ln( pB
/
p
)
将亨利定律代入
B(溶质)
B(g)
RT ln(kx,B /
p
) RT ln(xB)
x,B T, p RT ln(xB)
该式和溶剂的化学势具有相同的形式，式中x,B(T, p)是T, p
的函数，一定温度和压力下有定值，但它不是纯溶质的化学势 而是在xB=1,且服从亨利定律的那个状态的化学势，实际上并不
所谓“理想液态混合物的混合性质”是指，在恒温恒压下， nB 摩尔纯液体 B 与 n c摩尔纯液体 C 形成组成为 xB的理想液 态混合物的过程中，系统热力学性质 V，H，S，G等的变化。
以下讨论，虽然以两组分理想混合物为例，但其结论对于 形成多组分混合物也是适用的。
(1) 混合过程的mixV = 0 由dG＝－SdT＋Vdp和化学势定义知
第五章 多组分系统热力学 与相平衡
（一）多组分系统热力学
多组分多相体系
气态混合物
多组分体系
混合物 液态混合物 （√）
多组分单相体系
(两种或两种 以上的物质)
固态混合物
溶液
液态溶液 （√） 固态溶液
混和物: 各组分选用同样的标准态和方法加以研究 溶 液: 组成区分为溶质和溶剂，用不同的标准态和方法加以研究
溶剂分子或溶质分子周围都是溶剂分子。
1 溶剂的化学势
若在一定温度T 下，与理想稀溶液平衡的气体为理想气体混 合物，因溶剂A遵循拉乌尔定律,所以其化学势和理想混合物 中任一组分B 的化学势完全相同。
A
A
RT
ln
xA
在p和p 相差 不大时
p
RT ln x A
A
( ) A
B(l)
B(l)
V m,B(l)
若亨利定律写作 pB=kc,BcB,溶质化学势可以近似写作：
B(溶质)
c,B
RT
ln(cB ) c
溶质标准态为温度 T，压力p 下，体积摩尔浓度 cB = c = 1 moldm-3,而且符合理想稀溶液的溶质。该态亦为假想态。
pB 标准态 kb,B
(p p )
pB 标准态 kc,B
(p p )
A
b
乌尔定律。
2.亨利定律 在一定温度下和平衡状态下，稀溶液中挥发性溶质 B (即
所溶解的气体)在气相中分压pB与其在溶液中组成成比例。
pB kx,B xB
也可以以量浓度和质量摩尔浓度来表示组成
pB kc,B cB pB kb,B bB
式中k为亨利系数，其数值取决于T, p以及溶质和溶剂的性 质， 溶液组成的表示法不同，亨利系数的单位不同。kx,B, kb,B 和kc,B的单位分别是Pa, Pa·mol-1 ·kg和 Pa·mol-1 ·m3。
混合过程的体积变化为：
mixV
nB VB nC VC
nB
V m,B
nC
V m,C
0
即在恒温、恒压下，由纯液体形成理想液态混合物时，系统 体积不变。
(2)混合热等于零： mix H = 0.
将 B(l)
B(1)
RT
ln x除以T
后，在恒压、组成不变的条件
下对T 求偏导数：
B /T
亨利定律适用条件：
(1) pB 指挥发性溶质在液面上的分压力。若有几种气体同时溶解 于同一个溶剂，在总压不大时，亨利定律能分别适用于每种气体。
(2)溶质气相和液相中的分子形态必须相同，例如HCl，在气相中 为HCl分子，在苯中也为HCl分子，所以对HCl的苯溶液，可应用 亨利定律。但HCl在水中电离，所以对HCl的水溶液，不可应用 亨利定律。
bB B
A
c
溶质组成用b和c表示时，溶质的标准态示意图
cB B
§5-5 稀溶液的依数 性
所谓稀溶液的依数性,指稀溶液的： 1）溶质不挥发时，溶剂的蒸气压下降； 2）溶质不析出时，溶剂的凝固点降低； 3）溶质不挥发时，沸点升高； 4）渗透压增加。
这些量仅与稀溶液中溶质质点数有关，而与溶质本性无关， 故称之为依数性。
Bl Bg
将蒸汽相看作理想气体的混合物
B(l)
B(g )
B(g)
RT
ln
pB p
将拉乌尔定律代入
B(l)
B(g )
B(g)
RT
ln
p B p
RT
ln
x
对于 xB= 1 的纯液体 B，其饱和蒸气压为 pB ，所以同温度
下纯液体的化学势为：
* B(l)
B(g)
RT
ln
pB* p
pB
则纯液态混合物种任一组分的化学势为
溶液很稀： 溶剂分子主要是A-A分子间 的相互作用力 溶质分子处于溶剂的包围中完 全受A-B分子间的相互作用力
对溶剂分子: 稀溶液中各个A分子溢出液面的能力和纯溶剂 相同，但由于单位面积上 A 分子所占液面上的分子的总分数 由纯态时的 1，下降到 溶液态的 xA 。所以单位面积上溶剂
A 的蒸发速率按比例下降 pA xA
kx,B
实线代表实际蒸汽压和组成
的关系
kx,A
pA kx ,A xA
实线下面的虚线代表按拉乌
pB
尔定律计算的蒸汽压曲线
pA
pB pB xB 实线上面的虚线代表按亨利
定律计算的蒸汽压曲线
pA pA xA
A
xB
B
B在A中的稀溶液
A在B中的稀溶液
A、B两种液体在一定温度下 混合成溶液。
由图可见拉乌尔定律和亨利 定律适用的浓度范围是相同 的；即溶剂符合拉乌尔定律 溶质则符合亨利定律，反之 依然。
1 摩尔分数
§5-1 组成表示方 法
摩尔分数 x 或 y：物质 B 的物质的量与混合物(溶液) 总的物质的量的比。
def
xB 或yB ＝nB / nB xB 1 B
2 质量分数
质量分数: 物质 B 的质量与混合物(溶液) 总的质量比。
def
wB ＝mB / mB B
wB 1
B
3 物质的量浓度 物质的量浓度: 溶液中溶质B的量和溶液总体积的比。
T
p,x
B / T R ln xB
T
p,x
B / T
T
p,x
由吉布斯－杜亥姆方程
G T
T
p
H T2
知：
HB
H* m,B
所以混合过程的焓变化为：
mixH
nB HB nC HC
nB
H m,B
nC
H m,C
0
即在恒温、恒压下，由纯液体形成理想液态混合物时，系统焓 不变，即混合热为零。
由 mixG mix H T mix S 得到
mixG RT nB ln xB nC ln xC
因为 xB < 1，所以 mixG < 0 ；因为是恒温恒压非体积 功为零，所以过程自发。
§5-4 理想稀溶液中溶剂与溶质的化学 势
定义：理想稀溶液指的是溶质的相对含量趋于零的溶 液。在
这种溶液中，溶质分子间的距离非常远，几乎每一个
B
p
T ,x
VB;
B
p
T ,x
V* m,B
在恒温、恒组成的条件下，将 B(l)
B(1)
RT
ln
x
对p
求偏导数
B
p
T ,x
B
p
T ,x
VB
V* m,B
即理想液态混合物中任一组分的偏摩尔体积等于该组分的 纯态在该温度压力下的摩尔体积。
(3)混合过程的 mix S > 0.
由dG = -SdT＋Vdp知
B
T
p,x
SB;
B
T
p,x
Sm ,B
将 B(l)
B(1)
RT
ln x在恒压、组成不变的条件下对T
求偏
导数：
B
T
p,x
B RT ln xB
T
p,x
B
T
p,x
R
ln
xB
SB
S* m,B
§5-3 理想液态混合 物
定义：液态混合物在全部浓度范围内都符合拉乌尔定律称为 理想液态混合物
从分子的角度来看，理想液态混合物中各组分物理性质相近， 异种分子间的相互作用力，与它们混合前，各自处于纯态时 的同种分子间的相互作用力相同。