多相多组分系统热力学
南京大学物理化学(第五版)04章_多组分系统热力学
(
Gm p
)T
Vm
对多组分系统,把 Gm 换为 B ,则摩尔体积变为偏
摩尔体积 VB 。
化学势与温度的关系
(
B
T
)
p
,nB
,
nc
[ T
G ( ) ] T , p,nc p,nB ,nc nB
[ nB
G ( T ) p,nB ,nc ]T , p,nc
(S) [ nB ]T , p,nc
nk 0
dnk
k
n1Z1 n2 Z2 nk Zk nBZB B=1
偏摩尔量的加和公式
k
Z= nB ZB
B=1
这就是偏摩尔量的加和公式,说明系统的总 的容量性质等于各组分偏摩尔量的加和。
例如:系统只有两个组分,其物质的量和偏 摩尔体积分别为 n1,V1 和 n2 ,V2 ,则系统的总体积为:
(1)热力学能
设系统中有 1, 2,3, , k 个组分
所含的量分别为 n1, n2, , nk
U U (S,V , n1, n2, , nk )
化学势的定义
U U (S,V , n1, n2, , nk )
其全微分为
dU
U ( S )V ,nB dS
(
U V
)
S
,nB
dV
k U B1 ( nB )S ,V ,nc(cB) dnB
如果转移是在平衡条件下进行,则
dG 0 又
dnB dnB
所以 (B B )dnB 0
化学势在相平衡中的应用
(B B )dnB 0
因为 dnB 0 所以
B B
组分B在α,β两相中,达平衡的条件是该
物理化学电子教案第四章
2021/11/9
偏摩尔量的数值随混合物的组成变化
在温度、压力恒定下,混合物的组成发生变化 时,各组分偏摩尔量变化的相互依赖关系。
2021/11/9
同除以总摩尔数n 增202大1/11与/9 减小的比例与混合物中两组分的物质的量成反比
2021/11/9
对混合物中任 一组分B取偏 导数
2021/11/9
2. 多组分多相系统的热力学基本方程
G=∑G() A=∑A() H=∑H() U=∑U()
2021/11/9
G=∑G(), S=∑S(), V=∑V()
3. 化学势判据及其应用举例
2021/11/9
3. 化学势判据及其应用举例
亥姆霍兹函数判据
(dT 0,dV 0, W ' 0)
2021/11/9
§4.2 化学势
化学势的定义:混合物中组分B的偏摩尔吉布斯函数
B
( G nB
)T , p,nc
保持温度、压力和除B以外的其它组分不变,体系的
Gibbs自由能随 nB的变化率称为化学势,所以化学势 就是偏摩尔Gibbs自由能。
化学势在判断相变和化学变化的方向和限度方面有重 要作用。
多组分系统的组成表示法
溶质B的浓度表示法 (1)物质的摩尔分数 xB
溶质B物质的量与溶液总物质的量之比
(2)质量摩尔浓度bB
溶质B的物质的量除以溶剂A的质量
(3)物质的摩尔浓度cB
溶质B的物质的量除以溶液的体积
(4)质量分数wB
溶质B的质量与溶液总质量之比
def
xB
nB
ni
bB def
nB mA
25℃,100kPa
多组分系统

第四章 多组分系统热力学及其在溶液中的应用§4.1 引 言1.基本概念1)多组分系统:由两种或两种以上物质所组成的系统。
(多组分系统可以是单相的也可以是多相的。
)2)混合物:由两种或两种相互均匀混合而构成的系统。
(可以是气相、液相或固相) 3)溶 液(1)定义:由两种或两种以上物质在分子级别呈均匀混合而成的系统。
(2)溶液组分命名:溶质,溶剂。
(3)分类:(1)固态溶液、液态溶液。
(2)电解质溶液、非电解质溶液。
(4)应注意问题:形成溶液后,一般溶质、溶剂受力 情况与纯组分受力情况不同,所以对它们研究方法是不同的。
2.溶液中物质受力情况溶剂-溶剂 f 11 ,溶质-溶质 f 22 ,溶剂-溶质 f 12。
1) 纯态: 溶质 f 22 溶剂 f 11 2) 稀溶液: 溶质 f 22 溶剂 f 11 3) 中等浓度: 溶质 f 22,f 12 溶剂 f 12, f 11 4) 高浓度: 溶质 f 22 溶剂 f 12 3.受力变化同热效应关系1) 放热2) 吸热3) 不吸热不放热§4.2 多组分系统的组成表示法1.组成表示法1)B 的质量浓度:单位体积混合物中所含B 的质量。
1211,22f f f >121122,f f f <121122f f f ==()B B m Vρ=单位 与T 有关2)B 的质量分数:单位质量混合物中所含B 的质量。
单位为1,与T 无关3)B 的浓度:单位体积混合物中所含B 的物质的量。
单位 或 同T 有关。
4)B 的摩尔分数( 或):组分B 的物质的量与混合物中总物质的量的比值。
单位为1,与T 无关液体用 ,气体用5)溶质B 的质量摩尔浓度:每千克溶剂中所含溶质的物质的量。
单位 与T 无关。
6)溶质B 的摩尔比:单位物质的量的溶剂中所含溶质的物质的量。
单位为1,与T 无关。
2.常用的浓度表示法之间的关系 1) 与 的关系:若取1000 g 溶剂对稀溶液 2) 与 关系:-3kg m ⋅B B W w W =B Bn c V =-3mol m ⋅-3mol dm ⋅B x B y B B n x n=B x By ()BB A n m m =⋅-1mol kg BB A n r n =B x B m B BB A B n n x n n n ==+∑AB B A B BB A10001000m x m m M M m M ==++∑∑A B 1000M m <<∑B AB 1000m M x =B x BC A B B BW W c M ρρ=-=-∑∑AB B B B A AB B B B B BB A A c c c M x W c M c M c M c c M M ρρ===--+++∑∑∑∑∑()B AB A B Bc M x c M M ρ=+-∑若溶液很稀则3) 同 的关系: 取 取若溶液很稀则 若 取 对水§4.3 偏摩尔量1.偏摩尔量的定义 1. 问题的引出对简单均相系统 ,要描述其状态,只需要两个状态性质(T 、p )就可以了。
化学势与热力学基本方程

对于某些过程,比如未达到平衡的化学变化,如果限定其不 做非体积功,那么根本就不存在可逆方式,总是不可逆的, 但实际上有可能通过设计原电池让化学变化可逆进行。
1.可逆性判据
以吉氏函数可逆性判据为例: dGT , p,W 0 0
dG S ( )dT ( ) V ( )dp( )
( i
3-3 化学势与热力学 基本方程
1.均相多组分系统的热力学基本方程
G G(T , p, n1, n2 , , nK )
G
G
K G
dG
T
p,nj
dT
p
T ,nj
dp
i1
ni
T , p,nji
dni
G
G
T
p,nj
dT
p
T ,nj
dp
K i 1
δV ( ) ( 2, , )独立变化 p(1) p(2) p( ) p
δni( ) ( 2,
, )独立变化
(1) i
(2) i
δx (k)独立变化
( i
k
)
i
0;
k 1,
,R
i
上述四条就是多相平衡的必要条件。
( ) i
i
化学位的含义:
用导热柔软膜将两相分开,在膜上刺一小孔,系统将
Gi
dni
i
def
Gi
G ni
T , p,nji
K
G ni i i1
H G TS
n K
i1 i i
TS
U H pV
n K
i1 i i
TS
pV
A U TS
n K
i1 i i
第四章多组分系统热力学2

物化习题第四章多组分系统热力学一判断题1、在101.3Kpa下,往纯水中加入少量NaCl,与纯水比较,此稀溶液沸点升高。
()2、偏摩尔量集合公式Z=∑nBzB,m适用条件是恒温过程。
()恒温恒压过程3、Henry系数Kx,B只与溶剂溶质性质有关,而与温度无关。
()温度不同,亨利系数不同。
温度升高,系数升高。
4、沸点升高系数Kb的数值与溶剂、溶质的性质有关,且与温度有关。
()Kb的量仅与溶剂的性质有关5.、若A分子和B分子之间的相互作用力,与A,B各自处于纯态时分子之间的相处作用力相同,混合后,则有⊿Hmin=0.( )6、标准就态是认为规定的某些特定状态。
()7、理想溶液中,各种微粒间的相互作用力可忽略不计。
()处于凝聚态的分子,其分子间的距离很小,分子间的相互作用力和分子的体积均不能忽略。
8、一切纯物质的凝固点都随外压的增大而上升。
()9、稀溶液的非典一定比纯溶剂的沸点高。
()在同一外压条件下10、在相同温度和压力下,相同质量摩尔浓度的葡萄糖和食盐水的渗透压不相同。
()Ⅱ=CbRT,溶液的渗透压的大小只由溶液中的溶质的浓度决定,而与溶质的本性无关。
11、摩尔分数和质量摩尔浓度与温度无关,而物质的量浓度与温度有关()12、在相平衡中,若各相中均有组分B,则组分B在个相中的化学势一定相等。
()系统处于相平衡,由于系统任一组分B在其存在的每个相中的化学势相等。
13、溶剂中融入挥发性溶质,肯定会引起溶液的蒸汽压升高。
()14、二组分理想液态混合物的总蒸汽压大于任一组分的蒸汽压。
()处于中间态。
15、只有广度性质才有偏摩尔量。
( )16、凡是自由能降低的过程一定都是自发过程。
()17、拉乌尔定律和亨利定律既适合于理想溶液,也适合于稀溶液。
()18、偏摩尔量因为与浓度有关,因此它不是一个强度性质。
()19、某一体系达平衡时,熵最大,自由能最小。
()20、在一个多组分溶液中,只有溶质才有偏摩尔量。
()21、封闭系统中,由状态1经定温、定压过程变化到状态2,非体积功W′>△G和△G﹤0,则此过程一定能发生。
多组分系统热力学及其在溶液中的应用2

多组分系统热力学及其在溶液中的应用2在前面的讨论中,我们所涉及到的系统均为纯物质系统或组成恒定的系统。
但在实际上常见的却是多组分系统或变速成系统。
本章将就多组分系统的热力学问题进行讨论。
在正式讨论之前,先将多组分系统进行分类:①按研究的方法分:多组分系统可有单相和多相之分。
本章将讨论多组分系统单相系统。
多组分单相系统由两种或两种以上的物质以分子大小相互均匀混合而成的均匀系统当对均匀系统中各组分现用相同的标准和同样方法研究时,称之为混合物;当对均匀系统中各组分加以区别,选用不同的标准和不同的方法(例如:将系统中的组分分为溶剂(A)和溶质(B))研究时,称之为溶液。
②按聚集状态分:分为气态溶液或混合物、液态溶液或混合物、固态溶液或混合物本章讨论的对象主要是液态系统,包括液态溶液和液态混合物。
③按导电性能分:对于溶液中溶质,按其导电性能可分为电解质溶液和非电解质溶液,本能力讨论非电解质溶液。
④按规律性分:理想混合物理想稀溶液混合物{溶液{真实混合物真实溶液本章讨论的主要对象为混合物和稀溶液,适当介绍一些真实溶液。
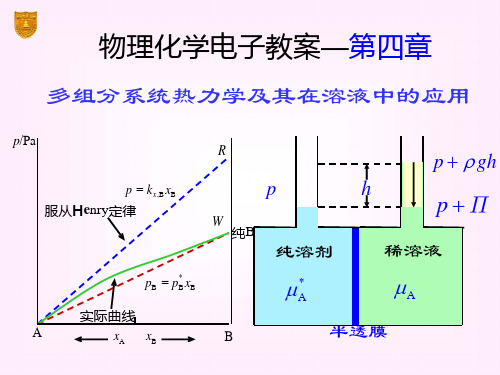
1.物质B的物质的量分数(物质B的摩尔分数):某BnB某B=────∑B某B=1∑BnB2.物质B的物质的质量分数:WBmBWB=────∑BWB=1∑BmB3.物质B的量浓度:CB/mol·m-3nBcB=───V4.物质B的质量摩尔浓度:mB/mol·kg-1nBmB=───W剂1.拉乌尔定律在一定温度下,纯液体A有一定的蒸汽压p某A,若向液体A加入溶质B,实验表明这是溶剂A的蒸汽压会下降。
法国化学家拉乌尔归纳多次的实验结果得出如下结论:“定温下稀溶液内溶剂的蒸汽压等于同温度下纯溶剂的蒸汽压乘它在溶液内的摩尔分数”。
即pA=p某A某A推导:设溶液由二个组分构成:A-溶剂B-溶质向溶剂A加入溶质B由实验知pA<p某A即Δp=(p某A-pA)>0且某B↑→Δp↑所以Δp∝某B由于构成稀溶液,加入的溶质较少,溶剂A分子电动势受力环境没有什么改变,只是单位体积溶液中A分子的数量减少了,使气相中ρA下降,而导致pA亦下降,也就是说加入B的数量越多,ρA下降越多,pA的下降也越大,这样,Δp仅与加入溶质B的数量有关,而与其本性无关了。
第1节 多组分多相平衡

一 描述相平衡系统状态的独立变量
4 自由度f :
描述相平衡系统确定状态所需要的独立的强度变量 (T、p、xi)的数目称为自由度数,用 f 表示。
这些变量可在有限的范围内任意改变,
不消失旧相也不产生新相。
根据代数定理,n个方程能限制或者关联n个变量,所以相平 衡系统中非独立变量的数目就是独立方程式的数目。因此,
指定温度为1000 K ,所求自由度为条件自由度, P=2
因此
f *= C -P+1= 2 - 2 + 1= 1
f* =1 的意义可理解为,在1000 K时,只要反应系统的 p 一经确定, 则两相中各组分的物质的量分数可由化学反应的平衡常数求出。
例4-3 P91
【例】 CaCO3(s)在高温上分解为CaO(s)和CO2(g)。现在一定 压力的CO2气中加热CaCO3(s),加热过程中在一定温度范围 内CaCO3(s)不会分解,根据相律解释这一实验事实。 解 N = 3 ; 有一个平衡的化学反应式,R = 1; 分解产物CaO(s)和CO2(g)不在同一相内,R' = 0 。 C = 3-1-0 = 2 , 其相律表达式为 f = C-P+2= 4 -P 现在 CO2(g)的压力一定,其自由度为条件自由度,
(2) 在给定条件下反应 N2(g)+3H2(g)=2NH3(g) 达到平衡。系统中 有几个独立的平衡化学反应式,就有几个物种数不独立,R 即为 几。N =3、R =1、R’ = 0 , C = N-(R+R’ ) = 2 (3) 在(2)条件下限制进料比[N2]∶[H2]=1∶3 ,如果同一相 中两种物质的数量保持一定的比例,就构成一个浓度限制条件。 有几个独立浓度限制条件,就可以减少几个描述系统的相的组成 的物种数。N =3、R =1、R’ =1 , C = 3-1-1 = 1 。
多组分

系统中不同组分XB变化有无规律?
——Gibbs-Duhem方程
dV nAdVA VAdnA nC dVC VC dnC
在恒T,p下,将物质的量分别为dnA和dnC的A,C两物质加入由A,C组 成的均相液态混合物中,则:
dV VAdnA VC dnC
T , nB
G p T , nB T , p , nC
T , p , nC
例1:恒T、p下,1molA (l)和2molB (l)混合, 混合物的体积为140cm3。现混合物中加入 0.0001mol(极少量) A (l)后,测得混合物 体积增加0.002cm3,求该T、p下A (l)和 B (l)的偏摩尔体积。
解:
0.002 VA 20cm3 m ol1 0.0001
VA 2VB 140cm3
140 20 VB 60cm3 m ol1 2
§4.2 化学势
混合系统中组分B的偏摩尔吉布斯函数GB称为 定义: 化学势 。符号:B 定义式:
B Gm ※纯组份的化学势等于该组份的摩尔吉布斯函数:
∵ dG B (a ) B ( ) dnB 0 B (a ) B ( )
dnB
a a相,B
恒温恒压下,相变化朝着化学势减小的方向自发进行。
T,p B(a ) B( )
B (a ) B ( ) α→β自发 B (a ) B ( ) 相平衡 B (a ) B ( ) β→α自发
nAdVA ncdVc 0
xAdVA xcdVc 0
分析: 若dVA > 0 → dVC < 0;由VA变化求VC变化 → VA、VC变化非独立,相互制约
