第四章 正弦交流电xue
合集下载
第四章 正弦交流电路
江苏江大苏学大电学工电电工子电教子研室
正弦交流电路
可以证明同频率正弦波运算后，频率不变。
如： u 1 u2
u u1 u2
2U 1 sin t 1 2U 2 sin t 2
2U1 sin t 1 2U2 sin t 2
2U sin t
前两种不便于运算，所以引入相量表示法。
江苏江大苏学大电学工电电工子电教子研室
正弦交流电路
正弦量的相量表示法
概念 ：一个正弦量的瞬时值可以用一个旋转的有向线
段在纵轴上的投影值来表示。
u Um sin t
ω
Um
t
U 有向线段长度 =
m
有向线段与横轴夹角 = 初相位
有向线段以角速度 ω 按逆时针方向旋转
称电压超前电流，或电流滞后电压
江苏江大苏学大电学工电电工子电教子研室
正弦交流电路
ψu ψi 0
电压滞后电流
ui i
u
电流超前电压
ψu ψi 90
电流超前电压 90
ui u i
O
ωt
O
ωt
90°
ψu ψi 0
电压与电流同相
ψu ψi 180
正弦交流电的优越性： 便于传输； 便于运算； 有利于电器设备的运行； .....
江苏江大苏学大电学工电电工子电教子研室
正弦交流电路
4.1 正弦交流电的基本概念
一、 正弦量
电路中凡随时间按正弦规律周期性变化的电压和电流 等称为正弦量，如图中电流，数学表达式为，波形如图
i Im sin t i
2
3.只有正弦量才能用相量表示，非正弦量不可以。
第4章 正弦交流电的基本概念
1
第4章 正弦交流电的基本概念
4.1 4.2 4.3 引言 正弦交流电的三要素 正弦电量的相量表示法
4.4 正弦交流电路中的元件
2
4.1 引 言
电路中的电量有周期性变化和非周期性变化两类。我们
把波形的大小和方向随时间作正弦周期性变化的电量称为正 弦交流电，如图4.1所示。
图4.1 正弦交流电
同理，电压相量的最大值表示为
U e jj U j U m m m
电流和电压的有效值相量表示为
(4.14)
I U
I m 2 U
m
I m e jj 2 2
I e jj Ij U e jj Uj
(4.15)
U m e jj
2
(4.16)
18 【例4.1】 已知
本、最重要的电量形式，其应用非常广泛。正弦交流电也可
简称交流电。
4
4.2 正弦交流电的三要素
4.2.1 变化的快慢
正弦交流电变化的快慢可用三种方式表示。 1. 周期T 交流电量往复变化一周所需的时间叫一个周期，用字母T表 示，单位是秒(s)，如图4.1所示。 2. 频率f 每秒内波形重复变化的次数称为频率，用字母f表示，单位 是赫兹(Hz)。频率和周期互为倒数，即
(4.9)
(4.10)
即正弦量的最大值等于有效值的 2 倍。 有效值是一个非常重要的概念，所有用电设备铭牌上标注 的都是有效值。
14
4.3 正弦电量的相量表示法
由于复数可用来表示矢量，矢量可用来表示正弦量，因
而复数也就可以表示正弦量。为了与一般的复数及表示空间 矢量的复数相区别，我们把表示正弦时间函数的复数叫做相 量，并用在大写字母上方加点表示。 设正弦电量是i=Im sin(ωt+j)，现在讨论复数指数函数 Imej(ωt+j)的展开式: Imej(ωt+j)=Im[cos(ωt+j)+j sin(ωt+j)] =Im cos(ωt+j)+jImsin(ωt+j)
第4章 正弦交流电的基本概念
4.1 4.2 4.3 引言 正弦交流电的三要素 正弦电量的相量表示法
4.4 正弦交流电路中的元件
2
4.1 引 言
电路中的电量有周期性变化和非周期性变化两类。我们
把波形的大小和方向随时间作正弦周期性变化的电量称为正 弦交流电，如图4.1所示。
图4.1 正弦交流电
同理，电压相量的最大值表示为
U e jj U j U m m m
电流和电压的有效值相量表示为
(4.14)
I U
I m 2 U
m
I m e jj 2 2
I e jj Ij U e jj Uj
(4.15)
U m e jj
2
(4.16)
18 【例4.1】 已知
本、最重要的电量形式，其应用非常广泛。正弦交流电也可
简称交流电。
4
4.2 正弦交流电的三要素
4.2.1 变化的快慢
正弦交流电变化的快慢可用三种方式表示。 1. 周期T 交流电量往复变化一周所需的时间叫一个周期，用字母T表 示，单位是秒(s)，如图4.1所示。 2. 频率f 每秒内波形重复变化的次数称为频率，用字母f表示，单位 是赫兹(Hz)。频率和周期互为倒数，即
(4.9)
(4.10)
即正弦量的最大值等于有效值的 2 倍。 有效值是一个非常重要的概念，所有用电设备铭牌上标注 的都是有效值。
14
4.3 正弦电量的相量表示法
由于复数可用来表示矢量，矢量可用来表示正弦量，因
而复数也就可以表示正弦量。为了与一般的复数及表示空间 矢量的复数相区别，我们把表示正弦时间函数的复数叫做相 量，并用在大写字母上方加点表示。 设正弦电量是i=Im sin(ωt+j)，现在讨论复数指数函数 Imej(ωt+j)的展开式: Imej(ωt+j)=Im[cos(ωt+j)+j sin(ωt+j)] =Im cos(ωt+j)+jImsin(ωt+j)
第四章 正弦交流电路习题参考答案
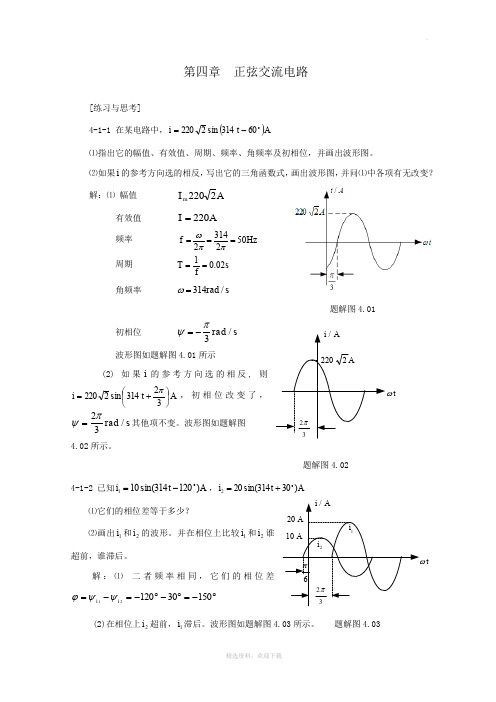
tωAi /A222032πtωAi /A 2032π6πA102i 1i 第四章 正弦交流电路[练习与思考]4-1-1 在某电路中，()A t i 60 314sin 2220-=⑴指出它的幅值、有效值、周期、频率、角频率及初相位，并画出波形图。
⑵如果i 的参考方向选的相反，写出它的三角函数式，画出波形图，并问⑴中各项有无改变？ 解：⑴ 幅值 A I m 2220有效值 A I 220= 频率 3145022f Hz ωππ=== 周期 10.02T s f== 角频率 314/rad s ω=题解图4.01 初相位 s rad /3πψ-=波形图如题解图4.01所示(2) 如果i 的参考方向选的相反, 则A t i ⎪⎭⎫ ⎝⎛+=32 314sin 2220π，初相位改变了，s rad /32πψ=其他项不变。
波形图如题解图 4.02所示。
题解图4.02 4-1-2 已知A )120314sin(101 -=t i ，A )30314sin(202 +=t i⑴它们的相位差等于多少？⑵画出1i 和2i 的波形。
并在相位上比较1i 和2i 谁超前，谁滞后。
解：⑴ 二者频率相同，它们的相位差︒-=︒-︒-=-=1503012021i i ψψϕ (2)在相位上2i 超前，1i 滞后。
波形图如题解图4.03所示。
题解图4.03+1+j1m I ∙2m I ∙mI ∙︒60︒30︒1.234-2-1 写出下列正弦电压的相量V )45(sin 2201 -=t u ω，)V 45314(sin 1002+=t u 解：V U ︒-∠=∙4521101 V U ︒∠=∙4525024-2-2 已知正弦电流)A 60(sin 81+=t i ω和)A 30(sin 62-=t i ω，试用复数计算电流21i i i +=，并画出相量图。
解：由题目得到Aj j j j I I I m m m ︒∠=+=-++=︒-︒+︒+︒=︒-∠+︒∠=+=∙∙∙1.231093.32.9)32.5()93.64()30sin 630cos 6()60sin 860cos 8(30660821 所以正弦电流为)A 1.23(sin 101+=t i ω题解图4.04 相量图如题解图4.04所示。
电工学课件(收藏版)-正弦交流电路
频率 f 的单位为1/s，称为Hz(赫兹)。我国工业用电的频率为 50Hz→工频。
3)初相(位)φi (initial phase angle)
正弦量在 t = 0 时刻的相位，称为正弦量的初相位，简称初
相。即
( t i ) t0 i
初相的单位用弧度或度表示，通常取| φi |≤1800。它与计时零
若 0，则称 u 超前 i ( 或称 i 滞后 u )。 若 0，则称 u 滞后 i ( 或称 i 超前 u )。 若 0，则称 u 和 i 同相。 若 | | ，则称 u 和 i 反相。 若 | | / 2，则称 u 和 i 正交。
同频率正弦量的相位差可通过观察波形确定，在同一个周期内 两个波形的极大值(或极小值)之间的角度值(≤1800)，即为两者 的相位差。超前者先达到极值点。初相位与计时零点的选取有关， 而相位差与计时零点的选取、变动无关。
面上把该复数逆（顺）时针旋转π。
二、正弦量的相量表示
在线性电路中，如果激励是正弦量，则电路中各支路的电压 和电流的稳态响应将是同频率的正弦量。如果电路有多个激励 且都是同一频率的正弦量，则根据线性电路的叠加性质可知， 电路全部稳态响应都将是同一频率的正弦量。处于这种稳定状 态的电路称为正弦稳态电路，又称正弦电流电路。
则必须有
F1 F2
Re[F1] Re[F2 ] ，Im[ F1] Im[ F2 ]
或必须有 | F1 || F2 | ，arg( F1 ) arg( F2 )
例1. 547 10 25 ? 解: 547 10 25 (3.41 j3.657) (9.063 j4.226)
3/2； i滞后（落后） u于/2, 不说 i 领先（超前） u于
3/2。
电子电工学 第四章知识点
di U XL u L dt I u i ωL
U jω C I
U 1 I jω C
单一参数正弦交流电路的分析计算小结
电路 电路图 基本 参数 (参考方向) 关系 阻抗 i 设 + u i
电压、电流关系 瞬时值 有效值
功 相量图 相量式
率
有功功率 无功功率
(2) 平均功率(有功功率)P：瞬时功率在一个周期内的平均值
P 1 T
P 单位:瓦（W）
T
0
p dt
1 T
T
0
u i dt
1 T
T
0
UI (1 cos2 ω t )d t UI
二、 电感元件的交流电路 1. 电压与电流的关系 设： i
2 I sin ω t d( I msinω t ) uL 2 Iω L sin(ω t 90) 2 U sin( ω t 90) dt
XL
I 0 I i 2 I si n ω t 可得： 根据： U U 90 Iω L 90 u 2 I ω L sin ( ω t 90 )
则：
U U I I
90 jL
电感电路复数形式的欧姆定律
jI ωL I (jX ) U L
220 U 45 V？ 2
• j45
1.已知：
3.已知：
复数 j30 I 4e A
4 2 sin (ω t 30 )A ？
瞬时值
有效值
45 Um 220 e V？
4.已知：
10 60A 2.已知： I
i 10 sin ( ω t 60 )A ？
北京科技大学电工技术课件第4章
该用电器最高耐压低于电源电压的最大值，所 以不能用。
（4-10）
§4.1.3 正弦波特征量之三 —— 初相位
i 2I sin t
（t ）：正弦波的相位角或相位。
：
t
=
0
时的相位，称为初相位或初相角。
i
t
180
说明： 给出了观察正弦波的起点或参考点，
常用于描述多个正弦波相互间的关系。
位
滞 后
2 1
i2
1 2 0
t i1 滞后于 i2
1 2 180
（4-13）
两种正弦信号的相位关系
同
相 位
2
1
i1
i2
t
1 2
反
相
位
1 2
i1
i2 1 2
t 180
（4-14）
例 已知： i sin1000t 30
幅度： 频率：
Im 1A
I 1 0.707A 2
1000 rad/s
Im
i Im sin t
t
特征量:
I m ： 电流幅值（最大值）
： 角频率（弧度/秒）
： 初相角
（4-5）
§4.1.1 正弦波特征量之一 —— 频率与周期
i
t
T
描述变化周期的几种方法：
1. 周期 T：变化一周所需的时间 单位：秒，毫秒…
2. 频率 f：每秒变化的次数 单位：赫兹，千赫兹 ...
f 1000 159 Hz 2 2
初相位： 30
（4-15）
在近代电工技术中，正弦量的应用是十分广 泛的。在强电方面：电流的产生和传输。在弱电 方面：信号源。
正弦量广泛应用的原因
1、可利用变压器将正弦电压升高或降低。
（4-10）
§4.1.3 正弦波特征量之三 —— 初相位
i 2I sin t
（t ）：正弦波的相位角或相位。
：
t
=
0
时的相位，称为初相位或初相角。
i
t
180
说明： 给出了观察正弦波的起点或参考点，
常用于描述多个正弦波相互间的关系。
位
滞 后
2 1
i2
1 2 0
t i1 滞后于 i2
1 2 180
（4-13）
两种正弦信号的相位关系
同
相 位
2
1
i1
i2
t
1 2
反
相
位
1 2
i1
i2 1 2
t 180
（4-14）
例 已知： i sin1000t 30
幅度： 频率：
Im 1A
I 1 0.707A 2
1000 rad/s
Im
i Im sin t
t
特征量:
I m ： 电流幅值（最大值）
： 角频率（弧度/秒）
： 初相角
（4-5）
§4.1.1 正弦波特征量之一 —— 频率与周期
i
t
T
描述变化周期的几种方法：
1. 周期 T：变化一周所需的时间 单位：秒，毫秒…
2. 频率 f：每秒变化的次数 单位：赫兹，千赫兹 ...
f 1000 159 Hz 2 2
初相位： 30
（4-15）
在近代电工技术中，正弦量的应用是十分广 泛的。在强电方面：电流的产生和传输。在弱电 方面：信号源。
正弦量广泛应用的原因
1、可利用变压器将正弦电压升高或降低。
电工2第四章 正弦交流电
2
频率不变
U (U 1 cos 1 U 2 cos 2 ) (U 1 sin 1 U 2 sin 2 )
tg
1
U 1 sin 1 U 2 sin 2 U 1 cos 1 U 2 cos 2
幅度变化
15
相位变化
u u1 u2 2U1 sin t 1 2U 2 sin t 2 2U sin t
7
2、角频率： 反映正弦量变化的快慢。
t
T
角频率（ω）：每秒变化的弧度。 单位：弧度/秒( rad/s ) 频率（f）：每秒变化的次数。 单位：赫兹( HZ )，千赫兹( KHZ ) ... 周期（T）：变化一周所需的时间。 单位：秒( s )，毫秒( ms )...
8
T、f、 之间的关系：
0
I
I 10 2 45 0
j45
I m 10 e
45 0
？
实数有效值
100 50 0 已知：I
最大值
I m 2 I 100 2
0
则： 100 sin ( t 50 ) i
？
25
复数的运算：加、减、乘、除法。
设： A1= a1+j b1 = r1∠ 1
幅度变化 频率不变 相位变化
综上：
同频率正弦波相加，其结果仍是该频率下的 正弦波。 正弦量的波形图及三角函数式表示法比较直 观，但用于运算很繁琐！ 启示：在讨论同频率正弦波时，只要知道幅度与 16 初相位即可。
4.2
一、相量图
复数平面 实 轴 Im
正弦电量的相量表示法
ω 旋转矢量
O ωt
0
Re
频率不变
U (U 1 cos 1 U 2 cos 2 ) (U 1 sin 1 U 2 sin 2 )
tg
1
U 1 sin 1 U 2 sin 2 U 1 cos 1 U 2 cos 2
幅度变化
15
相位变化
u u1 u2 2U1 sin t 1 2U 2 sin t 2 2U sin t
7
2、角频率： 反映正弦量变化的快慢。
t
T
角频率（ω）：每秒变化的弧度。 单位：弧度/秒( rad/s ) 频率（f）：每秒变化的次数。 单位：赫兹( HZ )，千赫兹( KHZ ) ... 周期（T）：变化一周所需的时间。 单位：秒( s )，毫秒( ms )...
8
T、f、 之间的关系：
0
I
I 10 2 45 0
j45
I m 10 e
45 0
？
实数有效值
100 50 0 已知：I
最大值
I m 2 I 100 2
0
则： 100 sin ( t 50 ) i
？
25
复数的运算：加、减、乘、除法。
设： A1= a1+j b1 = r1∠ 1
幅度变化 频率不变 相位变化
综上：
同频率正弦波相加，其结果仍是该频率下的 正弦波。 正弦量的波形图及三角函数式表示法比较直 观，但用于运算很繁琐！ 启示：在讨论同频率正弦波时，只要知道幅度与 16 初相位即可。
4.2
一、相量图
复数平面 实 轴 Im
正弦电量的相量表示法
ω 旋转矢量
O ωt
0
Re
电工技术第四章
+
+
O
能量交换大小——无功功率Q
2 t t
无功功率：
Q UI
XCI2
1
C
I2
U2 XC
CU 2
单位：乏或千乏(Var、KVar )
R
u、i同相
L
u比i超前90
Um U R Im I U IR
I U
Um Im
U I
L
XL
U jLI jX LI
U
I
P UI I 2R U 2 R
i
+ uR R
+ uL L
+ uC C
2、相量
U R RI
U L jX L I
U U R U L U C
RI jX LI jXC I
IR j( X L XC ) IZ
U C jXC I
Z R j( X L XC ) R jX 阻抗
电阻 电抗
注意：U U R U L UC
90 )
5、瞬时功率 p ui UI sin2t
平均功率 P 1
t
pdt 0
（有功功率） T 0
不消耗功率，只能量交换，
u、i
i
u
O
p
+
&#率Q
无功功率——瞬时功率最大值
Q UI
LI 2
X LI 2
U2
L
U2 XL
单位：乏或千乏(Var、KVar )
Z
Z
U I
U u I i
U I
u
i
有效值关系
Z U I
u i
相位关系
4、相量图
U L U L U C
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
【答】不是，应从研究它们的频率、大小和 相位着手。
1
4.2.2判断下列各式的正误：
i
u R
i
u X X
i
C
u X
X
L
U I R
U I
C
U I
L
U I R
U I
X
U I
C
X
L
2
4.2.3判断下列各式错在哪里： (a)i 10 sin(t 30) A 10 30
1 1 1 796.2 6 C 2fC 2 50 4 10 U 2200 （ ）I 1 0.2890 A jX C 796.2 90 XC i 0.28 2 sin(314t 90 )A
i u
（2）U I ( jX C ) 0.1 60 796.2 90 79.62 150 V u 79.62 2 sin( 314 t 150 )V
（1） i 7 2 sin tA I 70 A U I jX I jL I j 2fL
L
70 (2 50 100 103 )90 219.890 V u 219.8 2 sin(314t 90 )V
3A
4A
R
L
C
A1
的读数（ 5 ）A
A5 A4
的读数（ 4 ）A
的读数（ 8 ）A
7
课堂讨论
(3)
L
V1
6V
V2
(4)
R
V2
8V
13 V
V1
L C
20 V 8V
V3
C
V1
V3 V4
的读数（ 2 ）V
V2
(5)
2 6V
V1
的读数（ 5 ）V
2
V2
1
1
V2
的读数（4.8）V
8
课堂讨论
4.2 如图所示电路，已知开关 S 闭合前后电流表的 读数不变。(1) 分析 XL 与 XC 的大小关系； (2) 试问开关 S 闭合前后，电路的性质是否发生变化？
U 2060V
(a )i 10si n( t 30) A
3
i
u L
4.3.1 在图示的电感元件的正弦交流电中， L=100mH, f=50Hz,(1)已知 i 7 2 sin t A，求电压u (2)已知 U 127(30) V，求 I ，并画出相量图
U 127 30 （2）I 4 120 A jX L 31.490 i 4 2 sin(314t 120 )A
4
4.3.2 在图示的电容元件的正弦交流电中， C=4 F, f=50Hz，(1)已知 u 220 2sin t ( 60 V，求电流i；（2）已知 I 0.1 ) A ， 求 U ，并画出相量图
课堂讨论
4.4 判断下列各式的正确性。 (1) U1 = 180 30o V = 180 2 sin ( t＋30o ) V （ ） o (2) i = 10sin( t－30o ) A = 10 e －j30 A （ ） o (3) U = 220 e －30 V（ ） (4) I2 = 4 0o A （ ） (5) uR =RiR （ ） (12) 如下图 (6) uL = XLiL （ ） ） u = u1＋u2＋u3 （ (7) Z = R＋XL＋XC （ ） U = U1＋U2＋U3 （ ） (8) UC = XCIC （ ） u u u ＋ 1 － ＋ 2－ ＋ 3－ (9) u = Z i （ ） Z1 Z2 Z3 (10) U = Z I （ ） ＋ u － (11) U = Z I （ ）
11
课堂讨论
4.5 图示正弦电路中，Z = ( 40 + j 30 ) ，XL = 10 ，有效值 U2 = 200 V， 则总电压的有效值 U 为 ( b )。
＋ jXL ＋ U2 Z －
U
－
a. 178.9 V b. 226 V c. 120 V
I
U 2 200 4A Z 50
设I 40 A 则：U U1 U 2 I jX L IZ 40 (40 j 30 j10) 160 245 V U 160 2 226V
5
4.3.3 图示电路中，设 i 2sin 6280t mA，试分析电流 在R和C两个支路之间的分配，并估算电容器两端电压的 有效值。 i 1 1
XC
C
6280 50 10
6
3.18
I 2 0 A I U U R R 1000 I C U U X C 3.18 2 I R I C 2 I 2 U 20 4.47V
9
课堂讨论
4.3 如图所示电路，(1) 如果 Z1 = R1，则 Z2 为何 种性质的参数，总电流表的读数达到最大值 I1max？且 I1max = ？(2) 如果 Z1 = jXC，则 Z2 为何种性质的参数时， 总电流表的读数达到最小值 I1min？且 I1min = ？ A1 I3 I1
13
课堂讨论
4.7 在 R、L 并联的正弦交流电路中，R = 40 ， XL = 30 ，电路的无功功率 Q = 480 var， 则视在功 率 S 为 ( c )。 a. 866 V· A b. 800 V· A c. 600 V· A
如果串联？
S=800VA
30 串联：Z 40 j 30 arctan 36.87 40 Q 480 Q S sin S 800VA sin 0.6 480 40 j 30 360 j 480 并联：Z arctan 25 53.13 360 40 j 30 25 25 Q 480 Q S sin S 600VA sin 0.8
14
4.8 如下图示，已知 220 ,U 1超前于U 90，超前于I 30, U V 求U 1和U 2。
U1
I
பைடு நூலகம் U
U1
30
90
90
30
U
Z1
U2
I
U2
V U 1 127 U 1 U 2 sin 30 V V U U 2 cos30 220 U 2 254
A2 A3
3A Z1 Z2
5A
5
3
即3 5 I1 5 3
I2
答案： (1) Z2 = （ R2 ） I1max = （ 8 ）A (2) Z2 = （ jXL ） I1min = （ 2 ）A
三角形：两边之和大于 第三边，两边之差小于 第三边 时，I1有最大值 (1)当边3和边5在同一直线的同一方向 I1max 3 5 8 时，I1有最小值 (2)当边3和边5在同一直线的相反方向 I1min 5 3 2 10
(b) I 545 A (c)U 2060V 20 2 sin(t 60)V
【答】（a）式中
是瞬时表达式，
是相量表达式，二者不等；（b）式中I为有效值， 是相量，二者不等；（c）式中 是相量表达式， 是瞬时值表达式，二者不等。 10 30
545 A
20 2 sin( t 60)V
12
4.6 已知某交流电路的端电压和电流分别为： u = 311sinωt V， i = 45sin (ωt＋45o) A，由此可知该电 路的性质为（ c ）交流电路。 a. 电阻性 b. 电感性 c. 电容性
311 U 2 0 V I 45 45 A 2 u i 0 45 -45 容性
A
1A
R XL XC S
I
U U R j( X L X C ) Z
U I Z U、I不变 Z 不变 Z R 2 ( X L X C )2
答案： X L X C 不变 (1) XC = （ 2 ） XL (2) S 闭合前电路的性质为（电容性 ）。 X L X C X L S 闭合后电路的性质为（ 电感性 ）。 X C 2 X L
4.2.1 在下列几种表示正弦交流电路基尔霍夫定律的公式 中，哪些是正确的？哪些是不正确的？ (a ) i 0, u 0;
(b) I 0, U 0; (c ) I 0, U 0;
【答】(a)和（c）是正确的，（b）不正确。
4.1.1分析计算正弦交流电时是否也与直流电一样是从研究它们的 大小和方向着手？
-jXc
15
4.9 下图是一移相电路，如 C 0.01F , 输入电压 果
u1 2 sin 6280 , 今欲使输出电压 2 在相位上 tV u 前移60，问应匹配多大的电阻 ? 此时输出电压 R 的有效值U 2 等于多少？
U 2 R同相位 的初相位是60 I I U 10 Z 60 I60 I Z R jX C Z 且X C 1 15.9 K C XC 60 arctg R 9.2 K R
2
i
C
u1 R
u2
16
Z R 2 X C 18.37K U 2 U1 R 0.5V Z
R=1K
IC
+ U -
C=50 F
I
I R jX C R IC
IR
U
6
第4章 正弦交流电路
课堂讨论
4.1 如图所示电路，已知一些电流表或电压表的 读数，求另外一些电流表或电压表的读数。 (1)