近似数
近似数
3202 1872
1960
2000
2000
最高位的下一位的数比5小,最高位上的数不变。 最高位的下一位的数比5大,最高位上的数加1。
最高位是百,近似数常常是整百。
说出下列数的近似数: 588 120 600 100 400 230 709 391 613 906 200 700 400 600 900
407 897
680
900
700
最高位的下一位的数比5小,最高位上的数不变。 最。
说出下列数的近似数: 2781 3089 3000 3000 6000 哪种近似数更容易记住? 2800 3100 6200 4800 8900 2780 只有一个数不 3090 是“0”的近似 数最容易记住 4810 8930
6203 4809
8928
5000
9000
最高位的下一位的数比5小,最高位上的数不变。 最高位的下一位的数比5大,最高位上的数加1。
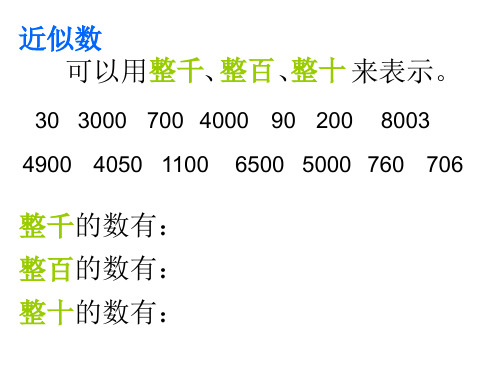
近似数 整百 、 整十 来表示。 可以用整千、
30 3000 700 4000 90 200 8003
4900 4050 1100
6500 5000 760 706
整千的数有:
整百的数有:
整十的数有:
最高位是千,近似数常常是整千。
说出下列数的近似数: 4008 1002 4000 1000 3000 6200 7098 6870 4005 9753 6000 7000 7000 4000 10000
近似数及其计算方法

近似数及其计算方法江苏省泗阳县李口中学沈正中一、求近似数的三种方法1.四舍五入法这是一种最常用的求近似数的方法,就是看确定保留数位的下一位数字,比5小的(即0、1、2、3、4),就把这个数字以及后面的所有数字舍去;如果这个数字比4大(即5、6、7、8、9),就把这个数字以及后面的所有数字舍去后,向前一位进一。
如64.96283,保留到万分位写为64.9628,即64.96283≈64.9628(以下类推),保留到千分位写作64.963,保留到百分位写作68.96,保留到十分位写作64.0,保留到整数写作64。
由此可以看出:“四舍”时,近似数比准确值小,“五入”时,近似数比准确值大。
在实际生活中,有时把一个数的留存数位确认后,只要下一位数字或后面的数字存有不以0的(即1、2、3、……、9),都必须向前一位入一。
例如:同学们同时回去独木舟,每只船上最多可载7个同学,17个同学至少须要几只船?17÷7≈2.4,就是说17个同学须要2只船还余3人,这3人还须要一只船,所以一共须要3只船。
即17÷7=≈3(只)。
由此可知:用进一法获得的对数数总比精确值大。
在实际生活中,有时把一个数的保留数位确定后,不管下一位数字或后面的数字是几(即0、1、2、3、……、9),都不要向前一位进一。
例如:用一根5m米短水管制成一批27cm长相同规格的水管,可以制成多少根?500÷27=≈18(根)由此可知:Weinreb尾法获得的对数数总比精确数大。
二、近似数的四则混合运算1.对数数的加减法在一般情况下,近似数相加减的和或差精确到哪一位,与已知数中精确度最低的一个相同,计算法则:(1)确认结果准确至哪一个数位(与已知数中精确度最高那个数准确数位相同);(2)把已知数中的其它数,四舍五入到已知数中精确度最低那个数数位的下一位;(3)展开排序,并且把配得的数的末位数字四舍五入。
【例1】求近似数25.4、0.456、8.738和56的和。
近似数和近似值

近似数、近似值
同实际数相接近的一个数,称为近似数.例如,某省有3800万人,“3800万”就是该省人口数的近似数.因为一个省的人口,有出生、有死亡,经常有变动,很难得到一个准确的实际数.
近似等于精确值的值,称为近似值.例如,除法运算的商,求至某位上四舍五入,所得到的值,都是这个商的近似值,如果是四舍,则所得的值称为过剩近似值.
不足近似值﹤精确值﹤过剩近似值
由此可知,近似数指的是根据实际情况,不可能得到或很难得到的一个不甚准确的数.而近似值是对精确值而言的,这个精确值是可能得到的.。
近似数

近似数导学案学习目标:1、了解近似数与有效数字的概念,能按精确度的要求取近似数,能根据近似数的不同形式确定其精确度和有效数字。
2、体会近似数在生活中实际应用。
重点:近似数的求法,精确度有效数的确定难点:精确度及有效数字的确定一、自主学习:1、回顾四舍五入法取近似值如:π≈3 (精确到个位)π≈3.1 (精确到0.1或精确到十分位)π≈3.14 (精确到或精确到)π≈(精确到万分位或精确到)2、近似数(1)生活中有的量很难或没有必要用准确数表示,而是用一个有理数近似地表示出来,我们称这个有理数为这个量的近似数。
如长江的长约为6300㎞,这里的6300㎞就是近似数。
因此,我们把接近准确数而不等于准确数的数,叫做这个数的近似数或近似值。
(2)304.35精确到个位的近似数为。
(3)精确度是指近似数与准确数的。
一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位,保留两位小数,精确到0.01,精确到百分位等说法的含义相同。
按括号要求取近似数①12341000(精确到万位)②2.715万(精确到百位)(4)有效数字:在四舍五入后的近似数中,从一个数的左边起,到末位数字止,所有的数字都是这个数的。
例1:近似数0.03050,最前面的两个0不是有效数字,而3后面的0和5后面的0都是这个数的有效数字。
用科学记数法表示的近似数a×10n,有效数字只与a有关,如3.12×510的有效数字为3,1,2。
当近似数后面有单位时,有效数字与单位无关,只与单位前面的数有关,如2.35万,有三个有效数字为2,3,5。
所以按照有效数字个数的要求对一个数取近似数,如:1.804(保留两个有效数字)的近似值为1.8。
例2:下列由四舍五入得到的近似数,它们精确到哪一位,有几个有效数字?①0.01020 ②1.20 ③1.50万④-2.30×410例3:用四舍五入法,按括号要求取近似值①607500 (保留两个有效数字)②0.030549 (保留三个有效数字)注意例2中③和④的精确度的确定:对于a×10n精确度由还原后的数字a的末位数字所在的数位决定;对于含有文字单位的近似值,精确度也是由还原后的数字中近似数的末位数字所在的位数决定的。
近似数

1、我们班级的人数是 中女生有 ,男生有
,其 。
2、量一量数学课本的长度约 是 ,宽度约 是 。
1、准确数和近似数:
观察上面两题中的数字,它们之 间有什么区别?
• 与实际完全符合的数是准确数. • 与实际非常接近的数是近似数. • 测量的结果,往往是近似数。除了测量, 还常常会遇到或用到近似数,如,我国 的陆地面积约为960万平方公里,小明 的年龄为12岁,这里的960、12都是近 似数。
【说明】 进一法:不论精确位后的数 如何,只要比0大,就进一;去尾法:不 论精确位后的数如何,一律舍去。
【方法点拨】
一般地,一个近似数四舍五入到某一 位,就说这个近似数精确到那一位。 例如,小明的身高为1.70米,1.70这 个近似数精确到百分位。
下列由四舍五入法得到的近似数 ,各精确到哪一位?
(1) 132.4
(2) 0.0572
十分位
万分位 百位
(3) 2.40 万
王平与李明测量一根钢管的长,王平测 得长是0.80米,李明测得长是0.8米。两人 测量的结果是否相同?为什么?
(3)130542 (精确到千位)
注意:精确到十位及其以上位数时, 首先用科学计数法表示,再1.50与近似数 1.5相同吗?近似数1.50末尾 的0能否去掉不写?
某校学生 320 人外出参观,已 有65名学生坐校车出发,现还需要 几辆45座的大巴? 要把一根100cm长的圆柱形 钢材截成6cm的一段一段做零件 。最多可以截得几段?
2、关于精确度问题:
近似数的近似程度是精确度。 我们都知道:Л= 3.1415926…… 计算中我们需对Л取近似数。 如果结果只取整数,那么按四舍五入的法则应为 3,就叫做精确到个位(或精确1); 如果结果取1位小数,那么应为3.1,就叫做精确 到0.1(或精确到十分位); 如果结果取2位小数,那么应为3.14,就叫做精 确到0.01(或精确到百分位); ……
近似数

典例分析:
例2、用四舍五入法,按括号中的要求对下列 各数取近似数。 (1)64.8 (精确到个位) (2)0.34082 (精确到0.001) (3)0.9541 (精确到十分位) (4)130542 (精确到千位) (5)2345817 (精确到万位) (6)160400 (保留两个有效数字) (7)2150783 (保留4个有效数字)
情景导入:
生活中,我们会接触到形形色色的数字,有些要求准 确无误,有些则不需要完全符合实际。 例如: (1)一小时等于60分钟。 (2)珠穆朗玛峰的海拔高度约为8844米。 (3)一次数学考试中,有4个人得100分。 (4)小明的身高约为151cm,体重为43千克。 在这些例子中,哪些数据是准确无误的?哪些数 据是接近实际的?你能找出来吗?
本节课你学会了什么? 有哪些收获?
思考:
(1)小明的身高为1.60米,可是在记录时 体育委员记成了1.6米,请你利用这堂课所 学的知识进行分析,你认为正确吗? (2)若6尺布可做一件上衣,则9尺布能做 多少件这样的上衣? (3)若每条船能坐3个人,则10个人需要 几条船?
能力提升
1、小亮打算把自己的房间美化一下, 在墙壁上涂彩色颜料,他测量了房间墙 壁长16米,高2.5米,然后到商店来选 购涂料,一桶涂料可涂6.5平方米,你 能帮小亮计算一下,需要购买几桶这种 彩色涂料?
典例分析:
(1)64.8 ≈ 65 (2)0.34082 ≈0.341 (3)0.9541 ≈ 1.0 5 1 . 31 10 (4)130542 ≈ (5)2345817 ≈ 2.35106 (6)160400 ≈ 1.6 105 (7)2150783 ≈ 2.151106
求近似数有哪几种方法?

求近似数有哪几种方法?
求近似数有哪几种方法?一般有3种:
1.四舍五入法这是最常用的求近似数的方法。
当省略的尾数的最高位上的数是4或比4小的时候,就把尾数舍去;当省略的尾数最高位上的数是5或比5大时,把尾数去掉后,要向前一位进1。
举例(45000≈5万,612000≈61万)
2.进一法在实际生活中,有时把一个数的尾数省略后,不管尾数最高位上的数是几,都要向它的前一位进一。
用进一法得到的近似数总比准确值大。
举例(45000≈5万,612000≈62万)
3.去尾法在实际生活中,有时把一个数的尾数省略后,不管尾数最高位上的数字是几,都不要向它的前一位进一。
用去尾法得到的近似数总比准确值小。
举例(45000≈4万,612000≈61万)。
二年级关于近似数的说明

近似数都有以下特点:1、取的近似数要方便计算。
2、近似数要取整千、整百、整十的数。
3、近似数不唯一。
现在最难理解的是第三点。
举例说明:1、两位数取近似数(四舍五入)其实我到是觉得,四舍五入也不难理解,讲明白了反而有助于孩子估数。
两位数取近似数,原则上按四舍五入,如,36≈40,42≈40,35≈40。
但是,估算时,仍可以具体情况具体分析,如,45+36≈?按四舍五入法,是90,但孩子们可能觉得,如果把45中的5舍去,结果“80”更接近准确数“81”,这样更好。
2、三位数取近似数(取整百或整百整十的数)分为以下几种情况:?a、十位上是8、9或0、1,不管个位上是几,都可以取整百的数,如,382≈400,991≈1000,209≈200,318≈300。
(这种情况实际上是从十位向百位的四舍五入,鼓励用此方法,方便估算)。
有些同学觉得,如果取整百整十的数其结果会更接近近似数,于是把个位向十位四舍五入,变成:382≈380,991≈990,,209≈210,318≈320,这样也很好。
但是,如果要取整百整十的数,就取最接近准确数的那个,比如,382不要估成390,要按四舍五入法去取。
特别说明的是,像九百九十几这样的数,干脆直接约成1000。
b、十位上是3——7的数,取整百整十的数,严格按照四舍五入,如,371?≈?370,567??≈570。
3、四位数取近似数(取整千或整千整百的数)同理,百位上是0、1或8、9,则可以取整千的数,如:3098≈3000,2156≈2000,3849≈4000,3912≈4000。
根据具体情况取整千整百也行,如3098≈其他情况要严格按照从十位向百位四舍五入,如,3789≈3800,2643≈2600.(实际上,像2643这种情况,估成2700也可以,几十个数对于上千的数来说,舍掉或进上去,都无所谓。
但为了让孩子们不迷惑,所以我就这样规定了。
)需要说明的是,四位数不要估成整千整百整十的数,比如,8952不能估成8950,没意义,可以估成8900,也可以直接估成9000.像9992,直接估成10000。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
近似数一个数与准确数相近(比准确数略多或者略少些),这一个数称之为近似数,如:我国的人口无法计算准确数目,但是可以说出一个近似数.比如说我国人口有13亿,13亿就是一个近似数.一个近似数四舍五入到哪一位,那么就说这个近似数精确到哪一位,从左边第一个不是0的数字起到精确的数位止的所有数止。
如:我国的人口无法计算准确数目,但是可以说出一个近似数.比如说我国人口有15亿,15亿就是一个近似数.近似数的四则计算加法和减法在通常情况下,近似数相加减,精确度最低的一个已知数精确到哪一位,和或者差也至多只能精确到这一位。
示例例如,一个同学去年体重30.4千克,今年体重比去年增加了3.18千克。
求今年体重时要把这两个近似数加起来。
因为30.4只精确到十分位,比3.18的精确度(精确到百分位)低,所以加得的和最多也只能精确到十分位。
为了容易看出计算结果的可靠程度,我们在竖式中每一个加数末尾添上一个“?”,用来表示被截去的数字。
30.4?+ 3.18 33.5?可以看到,因为第一个加数从百分位起的数就不能确定,所以加得的和从百分位起数字也不能确定。
近似数的加减一般可按下列法则进行:(1)确定计算结果能精确到哪一个数位。
(2)把已知数中超过这个数位的尾数“四舍五入”到这个数位的下一位。
(3)进行计算,并且把算得的数的末一位“四舍五入”。
例1 求近似数2.37与5.4258的和。
先把5.4258“四舍五入”到千分位,得5.426,再做加法。
2.37 +5.426 7.796 把7.796“四舍五入”到百分位,得7.80。
例2 求近似数0.075与0.001263的差。
先把0.001263“四舍五入”到万分位。
0.075 -0.0013 0.0737 把0.0737“四舍五入”到千分位,得0.074。
例3 求近似数25.3、0.4126、2.726的和。
25.3 0.41 + 2.73 28.44 把28.44“四舍五入”到十分位,得28.4。
在通常情况下,近似数相乘除,有效数字最少的一个已知数有多少个有效数字,积或者商也至多只能有同样多个有效数字。
例如,近似数9.04和4.3相乘,从竖式中看到,积里只有前两位数字是确定的,就是说只能有两位有效数字。
这和第二个因数的有效数字的个数相同。
9.0 4 ?×4.3 ?????? 2 7 1 2 ? 3 6 1 6 ? 3 8.?????近似数的乘除一般可按下列法则进行(1)确定结果有多少个有效数字。
(2)把已知数中有效数字的个数多的四舍五入到只比结果中需要的个数多一个。
(3)进行计算,并且把算得的数“四舍五入”到应有的有效数字的个数。
例4 求247.65与0.32的积。
把247.65“四舍五入”到个位。
2 4 8 ×0.3 2 4 9 6 7 4 4 7 9.3 6 把79.36“四舍五入”到个位,得79。
例5 求近似数7.9除以24.78的商。
7.9÷24.78≈7.9÷24.8≈0.318≈0.32混合运算近似数的混合运算,可按运算顺序和近似数的计算法则分步计算,但中间运算的结果要比最后结果多取一位数字。
例6 计算3.054×2.5-57.85÷9.21。
3.054×2.5-57.85÷9.21 ≈3.05×2.5-57.85÷9.21 ≈7.63-6.28≈1.4 根据已知数据,最后运算的结果要取两位数字,因此,中间运算的结果要取三位数字!近似数和有效数字与实际数字比较接近,但不完全符合的数称之为近似数。
对近似数,人们常需知道他的精确度。
一个近似数的近确度通常有以下两种表述方式用四舍五入法表述。
一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位。
另外还有进一和去尾两种方法。
用有效数字的个数表述。
有四舍五入得到的近似数,从左边第一个不是零的数字起,到末位数字为止的数所有数字,都叫做这个数的有效数字。
有效数对于一个近似数,从左边第一个不是0的数字起,到精确到的位数止,所有的数字都叫做这个数的有效数字1.有效数字中只应保留一位欠准数字,因此在记录测量数据时,只有最后一位有效数字是欠准数字。
2.在欠准数字中,要特别注意0的情况。
0在非零数字之间与末尾时均为有效数;在小数点前或小数点后均不为有效数字。
如0.078和0.78与小数点无关,均为两位有效数字。
506与220均为三位有效数字。
3.л等常数,具有无限位数的有效数字,在运算时可根据需要取适当的位数。
(1)实验中的数字与数学上的数字是不一样的.如数学的8.35=8.350=8.3500, 而实验的8.35≠8.350≠8.3500. (2)有效数字的位数与被测物的大小和测量仪器的精密度有关.如前例中测得物体的长度为7.45cm,若改用千分尺来测,其有效数字的位数有五位. (3)第一个非零数字前的零不是有效数字. (4)第一个非零数字以及之后的所有数字(包括零)都是有效数字. (5)当计算的数值为lg或者pH、pOH等对数时,由于小数点以前的部分只表示数量级,故有效数字位数仅由小数点后的数字决定。
例如lgx=9.04为2位有效数字,pH=7.355为三位有效数字。
(6)当特别地,当第一位有效数字为8或9时,因为与多一个数量级的数相差不大,可将这些数字的有效数字位数视为比有效数字数多一个。
例如8.314是五位有效数字,96845是六位有效数字. (7)单位的变换不应改变有效数字的位数.因此,实验中要求尽量使用科学计数法表示数据.如100.2m可记为0.1002km.但若用cm和mm作单位时,数学上可记为10020cm和100200mm,但却改变了有效数字的位数,这是不可取的,采用科学计数法就不会产生这个问题了..舍入规则1.当保留n位有效数字,若第n+1位数字≤4就舍掉。
2.当保留n位有效数字,若第n+1位数字≥6时,则第n位数字进1。
3.当保留n位有效数字,若第n+1位数字=5且后面数字为0时,则第n位数字若为偶数时就舍掉后面的数字,若第n位数字为奇数时加1;若第n+1位数字=5且后面还有不为0的任何数字时,无论第n位数字是奇或是偶都加1。
如将下组数据保留一位小数45.77=45.8。
43.03=43.0。
0.26647 = 0.3。
10.3500 = 10.4。
38.25=38.2。
47.15=47.2。
25.6500 = 25.6。
20.6512 = 20.7 有效数字就是一个数从左边第一个不为0的数字数起到精确的数位止,所有的数字(包括0,科学计数法不计10的N次方),称为有效数字。
简单的说,把一个数字前面的0都去掉,从第一个正整数到精确的数位止所有的都是有效数字了。
如:0.0109,前面两个0不是有效数字,后面的109均为有效数字(注意,中间的0也算)。
3.109*10^5(3.109乘以10的5次方)中,3 1 0 9均为有效数字,后面的10的5次方不是有效数字5200000000,全部都是有效数字。
0.0230,前面的两个0不是有效数字,后面的230均为有效数字(后面的0也算)1.20有3个有效数字1100.024有7个有效数字2.998*10^4(2.998乘以10的4次方)中,保留3个有效数字为3.00*10^4 对数的有效数字为小数点后的全部数字,如lg x=1.23有效数字为2.3,lg a=2.045有效数字为0、4.5,pH=2.35有效数字为3.5。
整体遵循四舍六入五成双的方法计算规则1.加减法以小数点后位数最少的数据为基准,其他数据修约至与其相同,再进行加减计算,最终计算结果保留最少的位数。
例:计算50.1+1.45+0.5812= 修约为:50.1+1.4+0.6=52.12. 乘除法以有效数字最少的数据为基准,其他有效数修约至相同,再进行乘除运算,计算结果仍保留最少的有效数字。
例:计算0.0121×25.64×1.05728= 修约为:0.0121×25.6×1.06= 计算后结果为:0.3283456,结果仍保留为三位有效数字。
记录为:0.0121×25.6×1.06=0.328 例:计算2.5046×2.005×1.52= 修约为:2.50×2.00×1.52= 当把1.13532×10⒑保留3个有效数字时,结果为1.14×10⒑运算中若有π、e等常数,以及√2.1/2等系数,其有效数字可视为无限,不影响结果有效数字的确定。
一般来讲,有效数字的运算过程中,有很多规则.为了应用方便,本着实用的原则,加以选择后,将其归纳整理为如下两类.一般规则(1)可靠数字之间运算的结果为可靠数字. (2)可靠数字与存疑数字,存疑数字与存疑数字之间运算的结果为存疑数字. (3)测量数据一般只保留一位存疑数字. (4)运算结果的有效数字位数不由数学或物理常数来确定,数学与物理常数的有效数字位数可任意选取,一般选取的位数应比测量数据中位数最少者多取一位.例如:π可取=3.14或3.142或3.1416……;在公式中计算结果不能由于"2"的存在而只取一位存疑数字,而要根据其他数据来决定. (5)运算结果将多余的存疑数字舍去时应按照"四舍六入五凑偶"的法则进行处理.即小于等于四则舍;大于六则入;等于五时,根据其前一位按奇入偶舍处理(等几率原则).例如,3.625化为3.62,4.235则化为4.24.(1)有效数字相加(减)的结果的末位数字所在的位置应按各量中存疑数字所在数位最前的一个为准来决定.例如30.4 26.65 + 4.325 - 3.905 34.725 22.745 取30.4+4.325=34.7,26.65-3.905=22.74. (2)乘(除)运算后的有效数字的位数与参与运算的数字中有效数字位数最少的相同. 由此规则(2)可推知:乘方,开方后的有效数字位数与被乘方和被开方之数的有效数字的位数相同. (3)指数,对数,三角函数运算结果的有效数字位数由其改变量对应的数位决定.例如:中存疑数字为0.08,那么我们将的末位数改变1后比较,找出发生改变的位置就能得知. (4)有效数字位数要与不确定度位数综合考虑. 一般情况下,表示最后结果的不确定度的数值只保留1位,而最后结果的有效数字的最后一位与不确定度所在的位置对齐.如果实验测量中读取的数字没有存疑数字,不确定度通。
