第28招 三角函数值大小比较
专题28 锐角三角函数(解析版)

专题28 锐角三角函数知识点一:锐角三角函数 1.三角函数定义在Rt △ABC 中,若∠C=90°A sin A ac ∠==的对边斜边A cos A bc ∠==的邻边斜边A tan A A ab∠==∠的对边的邻边A cot A A ba ∠==∠的邻边的对边2.同角三角函数的关系(1)平方关系:22sin cos 1A A += (2)商数关系:sin tan cos A A A =cos cot sin A A A = (3)倒数关系:tan cot 1A A ⋅=3.互为余角的三角函数关系sin(90)cos A A ︒-=,cos(90)sin A A ︒-=tan(90)cot A A ︒-=,cot(90)tan A A ︒-=或者:若∠A+∠B=90°,则sinA=cosB ,cosA=sinB ,tanA=cotB ,cotA=tanB 4. 特殊角的三角函数值5.锐角三角函数的增减性(0°--90°)(1)锐角的正弦值(或正切值)随着角度的增大而增大,随着角度的减小而减小。
(2)锐角的余弦值(或余切值)随着角度的增大而减小,随着角度的减小而增大。
6.锐角三角函数的取值范围0≤sin α≤1,0≤cos α≤1,tan α≥0,cot α≥0. 知识点二:解直角三角形 1.直角三角形中边角关系在直角三角形ABC 中,如果∠C=90°,∠A ,∠B ,∠C 所对的边分别为a ,b ,c ,那么(1)三边之间的关系为222a b c +=(勾股定理) (2)锐角之间的关系为∠A+∠B=90° (3)30°角所对直角边等于斜边的一半。
(4)直角三角形斜边上的中线等于斜边的一半。
(5)边角之间的关系为:(三角函数定义) 2.其他有关公式 (1)1sin 2S ab C ∆==1sin 2bc A =1sin 2ac B (2)Rt △面积公式:1122S ab ch == (3)直角三角形外接圆的半径2cR =,内切圆半径2a b c r +-=结论:直角三角形斜边上的高ab h c= 3.实际问题中术语的含义 (1)仰角与俯角在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角。
新人教版九年级数学下册《28章 锐角三角函数 28.1特殊角的三角函数值及用计算器求角的三角函数值》教案_7

28.1 锐角三角函数 第3课时 特殊角的三角函数值学习目标1. 重点:运用三角函数的知识,自主探索,推导出30°、 45°、60°角的三角函数值.2. 难点:熟记三个特殊锐角的三角函数值,并能准确地加以运用.导学过程一、情境导入问题1:一个直角三角形中,一个锐角的正弦、余弦、正切值是怎么定义的? sin ∠A= cos ∠A= tan ∠A= 变式训练:1.说出角B 的三角函数. sin ∠B= cos ∠B= tan ∠B=2. 互余的两角之间的三角函数关系:若∠A +∠B =90°,则sin A cos B ,cos A sin B , tan A · tan B = . 考点小测1.如果把一个直角三角形的各边长都扩大为原来的3 倍,那么它的各锐角的余弦值( ) A .扩大为原来的3倍 B .缩小为原来的 C .不变D .以上都不对2.(2018·孝感)如图,在Rt △ABC 中, ∠C =90°, AB =10,AC =8,则sin A 等于( ) A .35 B .45 C .34 D .433.(2016·广东)如图,在平面 直角坐标系中,点A 的坐标为(4,3),那么cos α的值是( )A .34B .43C .35D .454.(2015·丽水)如图,点A 为∠α边上的任意一点,过点A 作AC ⊥BC 于点C ,过点C 作CD⊥AB 于点D ,下列用线段比表示cos α的值,错误的是( )A .BD BCB .BC ABC .AD AC D .CD AC二、合作探究1.cos 3023322︒(天津中考)的值等于( )A.B. C.1 D.2.(2018.1322︒大庆中考)2cos60等于( )A.1B.C.D.问题2:两块三角尺中有几个不同的锐角?各是多少度?设每个三角尺较短的边长为1,分别求出这几个锐角的正弦值、余弦值和正切值.思考:30°角的三角函数值分别是多少?思考:60°角的三角函数值分别是多少?思考:45°角的三角函数值分别是多少? 归纳结果 30° 45° 60° siaA cosA tanA三、讲授新课例3:求下列各式的值.(1)cos 260°+sin 260°. (2)cos 45sin 45︒︒-tan45°.练习:23.(60cos 60tan 45_____︒+︒-︒=大庆中考)计算:sin4.求下列各式的值:(1)1-2 sin30°cos30°(2)3tan30° - tan45°+2sin60°(3) 三、讲授新课41()906,3,. (2) (2) AO OB AO=3OB .Rt ABC C AB BC A α∆∠=︒=∠例()如图1,在中,,求的度数如图,是圆锥的高,是底面半径,,求的度数()()=︒30sin ()()=︒30cos ()()()()==︒30tan ()()=︒60sin ()()=︒60cos ()()____60tan ==︒()()()()==︒45sin ()()()()==︒45cos ()()____45tan ==︒︒︒︒⨯+60tan )30sin 30(cos 224.(2018.,2tan 1,sin ,ABC A B A B ABC ∆∠∠==∆南关校级一模)在中,都是锐角,对最确切的判断是( )A.等腰三角形 B.等腰直角三角形C.直角三角形 D.锐角三角形2.90721.Rt ABC C BC AC A B ∆∠=︒==∠∠在中,,,,求,的度数 练习:5.(2014·本溪)在△ABC 中,∠B =45°,cos A =12,则∠C 的度数是________.216.sin (tan 1)02________αβαβαβ-+-=+=(酒泉中考)已知,均为锐角,且满足 则度四、强化训练五、知识梳理(1)特殊角的三角函数值:30° 45° 60° sin α 12 22 32 cos α 32 22 12 tan α3313(2)若角α为锐角,则随角α的增大,正弦(sin α) ______, 余弦(cos α) ______,正切(tan α) ______. (3)若角α为锐角,则_____<sin α <______, _____>cos α >_____ , tan α >_____. 重难点突破策略(1)锐角三角函数的基本计算和求锐角大小,准确记忆特殊角的三角函数值是关键.(2)解决与三角函数有关的问题需要有基本图形------直角三角形。
人教版数学九年级下册28.1.3特殊角的三角函数值及用计算器求锐角三角函数值课件

1、sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。 例5 (1)如图,在Rt△ABC中,∠C=90°,
591 398 351 (1)cos260°+sin260° 正弦值和正切值随A的增大而增大,余弦值随A的增大而减小 例3 填空:比较大小 设两条直角边长为a,则斜边长= 解:过点C作CD⊥AB于点D 解:过点C作CD⊥AB于点D 先转化, 30°36′ =30.
另一条直角边长= 2a2 a2 3a
sin30 a 1
30°
2a 2
cos30 3a 3 2a 2
tan30 a 3 3a 3
sin60 3a 3 2a 2
60°
cos60 a 1 2a 2
tan60 3a 3 a
设两条直角边长为a, 则斜边长= a2 a2 2a
sin45 a 2 2a 2
人教版九年级数学第二十八章 锐角三角函数
28.1.3 特殊角的锐角三角函数及用
科学计算器求锐角的三角函数值
回顾锐角三角函数
B sin AA斜 的边 对 B A边 C Ba c
斜边c
∠A的对边a
cos AA的邻 A边 C b 斜边ABc
A
∠A的邻边b
C
tan AA邻 的 边 对 边B AC Ca b
1、sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。 842 5,tanB=0.
1、sinA、cosA是在直角三角形中定义 627 5,sinB=0.
1、你能得出互为余角的两个锐角A、B正切值的关系吗? 例4 求下列各式的值:
第二十八章 锐角三角函数(单元总结)-2021学年九年级数学下册(人教版)(解析版)
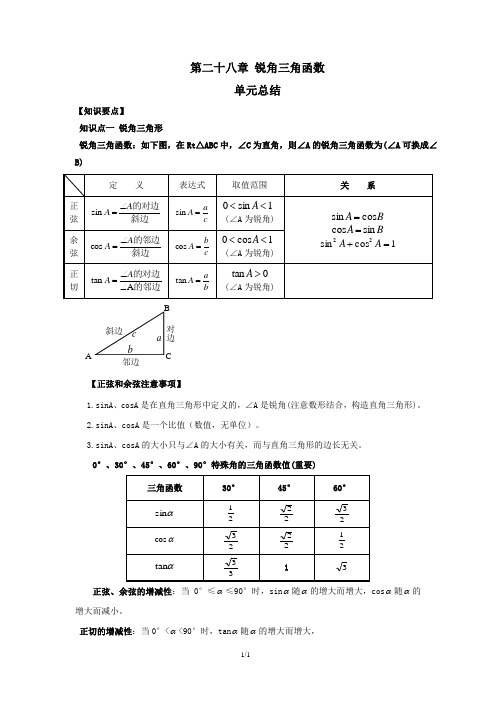
第二十八章 锐角三角函数单元总结【知识要点】 知识点一 锐角三角形锐角三角函数:如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B)【正弦和余弦注意事项】1.sinA 、cosA 是在直角三角形中定义的,∠A 是锐角(注意数形结合,构造直角三角形)。
2.sinA 、cosA 是一个比值(数值,无单位)。
3.sinA 、cosA 的大小只与∠A 的大小有关,而与直角三角形的边长无关。
0°、30°、45°、60°、90°特殊角的三角函数值(重要)正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
正切的增减性:当0°<α<90°时,tan α随α的增大而增大,对边邻边C知识点二 解直角三角形一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形. 直角三角形五元素之间的关系: 1. 勾股定理()2. ∠A+∠B=90°3. sin A==4. cos A= =5.tan A= =【考查题型】考查题型一 正弦典例1.(2020·陕西西安市·西北工业大学附属中学九年级期中)如图,在54⨯的正方形网格中,每个小正方形的边长都是1,ABC ∆的顶点都在这些小正方形的顶点上,则sin BAC ∠的值为( )A .43B .34C .35D .45【答案】D 【分析】过C 作CD AB ⊥于D ,首先根据勾股定理求出AC ,然后在Rt ACD ∆中即可求出sin BAC ∠的值.【详解】如图,过C 作CD AB ⊥于D ,则=90ADC ∠︒,∴AC =222234=+=+AC AD CD =5. ∴4sin 5CD BAC AC ∠==. 故选D . 【点睛】本题考查了勾股定理的运用以及锐角三角函数,正确作出辅助线是解题的关键.变式1-1.(2018·西城区·北京四中九年级期中)如图,在Rt ABC ∆中,90C =∠,10AB =,8AC =,则sin A 等于( )A .35B .45C .34D .43【答案】A 【解析】分析:先根据勾股定理求得BC=6,再由正弦函数的定义求解可得. 详解:在Rt △ABC 中,∵AB=10、AC=8, ∴2222=108=6AB AC --,∴sinA=63105BC AB ==. 故选:A .点睛:本题主要考查锐角三角函数的定义,解题的关键是掌握勾股定理及正弦函数的定义.变式1-2.(2019·山东淄博市·九年级期中)如图,在Rt△ABC中,∠C=90°,sin A=45,AC=6cm,则BC的长度为()A.6cm B.7cm C.8cm D.9cm 【答案】C【详解】已知sinA=45BCAB=,设BC=4x,AB=5x,又因AC2+BC2=AB2,即62+(4x)2=(5x)2,解得:x=2或x=﹣2(舍),所以BC=4x=8cm,故答案选C.考查题型二余弦典例2.(2020·福建省泉州市培元中学九年级期中)如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC等于()A 5B25C5D.23【答案】B【详解】由格点可得∠ABC所在的直角三角形的两条直角边为2,4,222425+=∴cos∠25525=.故选B .变式2-1.(2016·辽宁铁岭市·九年级期末)在ABC 中,C 90∠=,AB 6=,1cosA 3=,则AC 等于( ) A .18 B .2C .12D .118【答案】B 【分析】根据三角函数的定义,在直角三角形ABC 中,cosA =ACAB,即可求得AC 的长. 【详解】解:∵在△ABC 中,∠C =90°,∴cosA =ACAB , ∵cosA =13,AB =6,∴AC =123AB =,故答案选:B . 【点睛】本题考查了解直角三角形中三角函数的应用,解题的关键是要熟练掌握直角三角形中边角之间的关系.变式2-2.(2019·山东滨州市·九年级期末)如图,在平面直角坐标系中,点M 的坐标为M (5,2),那么cosα的值是( )A 5B .23C 25D 5【答案】D 【分析】如图,作MH⊥x轴于H.利用勾股定理求出OM,即可解决问题.【详解】解:如图,作MH⊥x轴于H.∵M(5,2),∴OH=5,MH=2,∴OM=22(5)2+=3,∴cosα=5 OHOM=,故选:D.【点睛】本题考查解直角三角形的应用,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.考查题型三正切典例3.(2020·广东深圳市·深圳中学八年级期中)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为()A.12B.1 C3D3【答案】B【分析】连接BC,由网格求出AB,BC,AC的长,利用勾股定理的逆定理得到△ABC为等腰直角三角形,即可求出所求. 【详解】 如图,连接BC ,由网格可得AB=BC=5,AC=10,即AB 2+BC 2=AC 2, ∴△ABC 为等腰直角三角形, ∴∠BAC=45°, 则tan ∠BAC=1, 故选B .【点睛】本题考查了锐角三角函数的定义,解直角三角形,以及勾股定理,熟练掌握勾股定理是解本题的关键.变式3-1.(2018·江苏苏州市·九年级期末)如图,在等腰Rt ABC ∆中,90C ∠=︒,6AC =,D 是AC 上一点,若1tan 5DBA ∠=,则AD 的长为( ).A .2B .3C .2D .1【答案】A 【解析】分析:本题考查等腰直角三角形的性质及解直角三角形.解题的关键是作辅助线,构造直角三角形,运用三角函数的定义建立关系式然后求解. 解析:如图,作DE ⊥AB 于E .∵tan ∠DBA==,∴BE=5DE .∵△ABC 为等腰直角三角形,∴∠A=45°,∴AE=DE .∴BE=5AE ,又∵AC=6,∴AB=6,∴AE+BE=AE+5AE=6,∴AE=,∴在等腰直角△ADE中,由勾股定理,得AD=,AE=2.故选A.变式3-2.(2020·河北唐山市·九年级期末)如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若2tan5BAC∠=,则此斜坡的水平距离AC为()A.75m B.50m C.30m D.12m 【答案】A【分析】根据BC的长度和tan BAC∠的值计算出AC的长度即可解答.【详解】解:因为2tan5BCBACAC=∠=,又BC=30,所以,3025AC=,解得:AC=75m,所以,故选A.【点睛】本题考查了正切三角函数,熟练掌握是解题的关键.考查题型四特殊角的三角函数值典例4.(2018·南昌市期末)点M(-sin60°,cos60°)关于x轴对称的点的坐标是( )A.(32,12) B.(-32,-12)C.(312) D.(-123【答案】B 【详解】∵点(-sin60°,cos60°)即为点(312),∴点(-sin60°,cos60°)关于y 3,12).变式4-1.(2019·山东淄博市·九年级期中)下列式子错误的是()A.cos40°=sin50°B.tan15°•tan75°=1C.sin225°+cos225°=1 D.sin60°=2sin30°【答案】D【详解】试题分析:选项A,sin40°=sin(90°﹣50°)=cos50°,式子正确;选项Btan15°•tan75°=tan15°•cot15°=1,式子正确;选项C,sin225°+cos225°=1正确;选项D,sin60°=3,sin30°=12,则sin60°=2sin30°错误.故答案选D.变式4-2.(2018·河北唐山市·九年级期末)如果△ABC中,sin A=cos B=22,则下列最确切的结论是()A.△ABC是直角三角形B.△ABC是等腰三角形C.△ABC是等腰直角三角形D.△ABC是锐角三角形【答案】C【解析】因为sin A=cos B 2,所以∠A=∠B=45°,所以△ABC是等腰直角三角形. 故选C.考查题型五同角的三角函数典例5.(2018·山东潍坊市·九年级期末)在Rt△ABC中,∠C =90°,sinA=45,则cosB的值等于( )A.35B.45C.34D5【答案】B 【解析】在Rt△ABC中,∠C=90°,∠A+∠B=90°,则cos B=sin A=45.故选B.点睛:本题考查了互余两角三角函数的关系.在直角三角形中,互为余角的两角的互余函数变式5-1.(2018·浙江台州市·九年级期末)在Rt △ABC 中,cosA= 12,那么sinA 的值是( )A .2B .2C .3D .12【答案】B 【分析】利用同角三角函数间的基本关系求出sinA 的值即可. 【详解】:∵Rt △ABC 中,cosA=12 ,∴ =2, 故选B . 【点睛】本题考查了同角三角函数的关系,以及特殊角的三角函数值,熟练掌握同角三角函数的关系是解题的关键.变式5-2.(2018·湖南岳阳市·九年级期末)在Rt ABC 中,C 90∠=,如果4cosA 5=,那么tanA 的值是( ) A .35B .53C .34D .43【答案】C 【分析】本题可以利用锐角三角函数的定义求解. 【详解】解:∵在Rt △ABC 中,∠C=90°,∴cosA=b c ,tanA=ab ,a 2+b 2=c 2. ∵cosA=45,设b=4x ,则c=5x ,a=3x .∴tanA=a b =3344x x =. 故选C.【点睛】利用锐角三角函数的定义,通过设参数的方法求三角函数值.考查题型六 解直角三角形典例6.(2020·东北师大附中明珠学校九年级期中)如图,两根竹竿AB 和AD 斜靠在墙CE 上,量得∠ABC=α,∠ADC=β,则竹竿AB 与AD 的长度之比为( )A .tan tan αβB .sin sin βαC .sin sin αβD .cos cos βα【答案】B【分析】在两个直角三角形中,分别求出AB 、AD 即可解决问题;【详解】在Rt △ABC 中,AB=AC sin α, 在Rt △ACD 中,AD=AC sin β, ∴AB :AD=AC sin α:AC sin β=sin sin βα, 故选B .【点睛】 本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是学会利用参数解决问题. 变式6-1.(2020·山东枣庄市·九年级期末)如图,在ABC ∆中,144CA CB cosC ==,=,则sinB 的值为( )A .10B .15C .6D .10 【答案】D【分析】过点A 作AD BC ⊥,垂足为D ,在Rt ACD ∆中可求出AD ,CD 的长,在Rt ABD ∆中,利用勾股定理可求出AB 的长,再利用正弦的定义可求出sinB 的值.【详解】解:过点A 作AD BC ⊥,垂足为D ,如图所示.在Rt ACD ∆中,1CD CA cosC ⋅==,2215AD AD CD ∴=-=;在Rt ABD ∆中,315BD CB CD AD =﹣=,=,22BD AD 26AB ∴=+=,AD 10sin AB B ∴==. 故选:D .【点睛】考查了解直角三角形以及勾股定理,通过解直角三角形及勾股定理,求出AD ,AB 的长是解题的关键.变式6-2.(2019·辽宁沈阳市·九年级期末)如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A 处看乙楼楼顶B 处仰角为30°,则甲楼高度为( )A.11米B.(36﹣153)米C.153米D.(36﹣103)米【答案】D【分析】分析题意可得:过点A作AE⊥BD,交BD于点E;可构造Rt△ABE,利用已知条件可求BE;而乙楼高AC=ED=BD﹣BE.【详解】解:过点A作AE⊥BD,交BD于点E,在Rt△ABE中,AE=30米,∠BAE=30°,∴BE=30×tan30°=103(米),∴AC=ED=BD﹣BE=(36﹣103)(米).∴甲楼高为(36﹣103)米.故选D.【点睛】此题主要考查三角函数的应用,解题的关键是熟知特殊角的三角函数值.考查题型七利用解直角三角形相关知识解决实际问题典例7.(2019·河南许昌市·九年级期末)如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B 处的求救者后,又发现点B 正上方点C 处还有一名求救者.在消防车上点A 处测得点B 和点C 的仰角分别是45°和65°,点A 距地面2.5米,点B 距地面10.5米.为救出点C 处的求救者,云梯需要继续上升的高度BC 约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,2≈1.4)【答案】云梯需要继续上升的高度BC 约为9米.【分析】过点A 作AM EF ⊥于点M ,AD BC ⊥于点D ,在Rt ABD ∆中,求得AD 的长;在Rt ACD ∆中,求得CD 的长,根据BC=CD-BD 即可求得BC 的长.【详解】过点A 作AM EF ⊥于点M ,AD BC ⊥于点D ,∵CN EF ⊥ ,∴90AMN MND ADN ∠=∠=∠=︒,∴四边形AMND 为矩形.∴ 2.5DN AM ==米.∴10.5 2.58BD BN DN =-=-=(米),由题意可知,45BAD ∠=︒,65CAD ∠=︒,∵AD BC ⊥,∴90ADB ∠=︒,在Rt ABD ∆中,tan BD BAD AD ∠=, ∴88tan tan45BD AD BAD ===∠︒(米). 在Rt ACD ∆中,tan CD CAD AD∠=, ∴tan 8tan658 2.116.8CD AD CAD =⋅∠=︒≈⨯=(米).∴16.888.89BC CD BD =-≈-=≈(米).答:云梯需要继续上升的高度BC 约为9米.【点睛】本题考查解直角三角形﹣仰角俯角问题,添加辅助线,构造直角三角形,建立直角三角形模型是解决问题的关键.变式7-1.(2018·江苏无锡市·九年级期末)如图,为了测量出楼房AC 的高度,从距离楼底C 处603米的点D (点D 与楼底C 在同一水平面上)出发,沿斜面坡度为i=1:3的斜坡DB 前进30米到达点B ,在点B 处测得楼顶A 的仰角为53°,求楼房AC 的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈43,计算结果用根号表示,不取近似值).【答案】153+【分析】如图作BN ⊥CD 于N ,BM ⊥AC 于M ,先在RT △BDN 中求出线段BN ,在RT △ABM 中求出AM ,再证明四边形CMBN 是矩形,得CM=BN 即可解决问题.【详解】如图作BN ⊥CD 于N ,BM ⊥AC 于M .在RT △BDN 中,BD=30,BN :ND=13,∴BN=15,DN=153,∵∠C=∠CMB=∠CNB=90°,∴四边形CMBN是矩形,∴CM=BM=15,BM=CN=603153453-=,在RT△ABM中,tan∠ABM=43 AMBM=,∴AM=603,∴AC=AM+CM=15603+.【点睛】构造适当的直角三角形,并应用锐角的三角函数,正确理解坡比的概念.变式7-2.(2018·山西晋中市期末)“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)【答案】高、低杠间的水平距离CH 的长为151cm .【解析】分析:利用锐角三角函数,在Rt △ACE 和Rt △DBF 中,分别求出AE 、BF 的长.计算出EF .通过矩形CEFH 得到CH 的长.详解:在Rt △ACE 中,∵tan ∠CAE=CE AE, ∴AE=()15515521tan tan82.47.5CE cm CAE =≈≈∠︒ 在Rt △DBF 中,∵tan ∠DBF=DF BF, ∴BF=()23423440tan tan80.3 5.85DF cm DBF =≈=∠︒. ∵EF=EA+AB+BF≈21+90+40=151(cm )∵CE ⊥EF ,CH ⊥DF ,DF ⊥EF∴四边形CEFH 是矩形,∴CH=EF=151(cm ).答:高、低杠间的水平距离CH 的长为151cm .点睛:本题考查了锐角三角函数解直角三角形.题目难度不大,注意精确度.。
三角函数线的定义三角函数线怎么画三角函数线比较大小

一、三角函数线比较大小(1)正弦线、余弦线、正切线都是有向线段,利用它们的数量来表示三角函数值,是数形结合的典型体现。
三角函数线表示三角的函数值的符号规定如下:正弦线MP、正切线AT方向与y轴平行,向上为正,向下为负;余弦线OM在x轴上,向右为正,向左为负。
(2)作三角函数线时,所用字母一般都是固定的,书写顺序也不能颠倒。
特别要注意正切线必在过A(1,0)的单位圆的切线上(其中二、三象限角需作终边的反向延长线)。
(3)对于终边在坐标轴上的角,有时三角函数线退化为一个点,有时又为整个半径。
当角α的终边在y轴上时,角α的正切线不存在。
(4)当时,正弦线、余弦线、正切线与角α并不是一一对应的。
一般地,每一个确定的MP、OM、AT都对应两个α的值。
三、三角函数线的定义:1.设任意角α的顶点在原点O,始边与x轴的正半轴重合,终边与单位圆相交于点P(x,y),过P点作x轴的垂线,垂足为M,过点A(1,0)作单位圆的切线,2.设它与角α的终边或其反向延长线相交于点T,则有向线段MP、OM,AT分别叫做角α的正弦线,余弦线,正切线,即:sinα=MP,cos α=OM,tanα=AT,如下图:3. 注:线段长度表示三角函数值大小,线段方向表示三角函数值正负。
4.设任意角α的顶点在原点O,始边与x轴的正半轴重合,终边与单位圆相交于点P(x,y),过P点作x轴的垂线,垂足为M,过点A(1,0)作单位圆的切线,5.设它与角α的终边或其反向延长线相交于点T,则有向线段MP、OM,AT分别叫做角α的正弦线,余弦线,正切线,即:sinα=MP,cos α=OM,tanα=AT,如下图:注:线段长度表示三角函数值大小,线段方向表示三角函数值正负。
28.2-3-锐角的三角函数值及其计算

sinA=0.9816
键,
和第
显示结果
sin-10.9816 =78.99184039
cosA=0.8607
cos-10.8607 =30.60473007
tanA=0.1890 tanA=56.78
tan-10.1890 =10.70265749
tan-156.78 =88.99102049
A
同角之间的三角函数关系.
B
c
a
┌
b
C
300
450
450 ┌ 600 ┌
2.三角函数的计算 (1)运用计算器计算由已知锐角求它的三角函数值; (2)会用计算器根据已知的三角函数值求出相应的角度; (3)初步掌握解直角三角形知识的应用.
课后作业
《五中三模》九年级下册P6~7的《基础闯 关》、《三年模拟》、《五年中考》为必做, 其它选做;做完自己批改订正. 预习本章第4、5节.
第二十八章 直角三角形的边角关系
28.2~3 锐角的三角函数值及其计算
复习引入
锐角三角函数定义
直角三角形中边与角的关系:锐角三角函数.
在直角三角形中,若一个锐角确定,那么这个角的对边,邻边
和斜边之间的比值也随之确定.
sin A a , cos A b ,
c
c
B
sin B b , cosB a ,
(2)cos600+tan600;
3 2 sin 450 sin 600 2 cos 450;
2
4 2 sin 2 300 cos2 600 2 cos2 450.
2
2.一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向 两边摆动时,摆角恰好为600,且两边摆动的角度相同, 求它摆至最高位置时与其摆至最低位置时的高度之 差(结果精确到0.01m).
利用单位圆比较三角函数值的大小

2012-04教学实践一、高中教材中设置算法的重要性从算法的历史文化背景看,在中国古代数学中蕴含着丰富的算法内容和思想,出现了许多著名的数学著作,如《九章算术》《周髀算经》《黄帝九章算经细草》《详解九章算法》等。
中国在算法上还取得了许多伟大的成就,如最早采用“十进制”计数法;最早论述了最小公倍数;最早得出有六位准确数字的π值;最早提出联立一次方程的解法。
在国外数学中,最早就有了欧几里德的辗转相除法,牛顿的切线法求方程的近似解,这些都是很典型的算法。
从《普通高中数学课程标准》看,国家已将算法作为新内容加入到了中学数学的必修部分。
其中提到“学生将在义务教育阶段初步感受算法思想的基础上,结合对具体数学实例的分析,体验程序框图在解决问题中的作用;通过模仿、操作、探索,学习设计程序框图表达解决问题的过程;体会算法的基本思想以及算法的重要性和有效性,发展有条理的思考与表达的能力,提高逻辑思维能力。
”算法已成为中学数学的核心内容,贯穿着中学数学的主线,是我国新课程改革的重大成果之一。
从对学生的发展看,把算法引入到高中数学课程,首先是认同了算法的教育意义。
算法有利于培养学生的逻辑思维能力;有利于学生理解古代数学文化的精髓;有利于提高他们的编程能力和对计算机的应用能力;有利于传承和发扬我国古代数学。
二、算法内容简介下面以人教A 版高中数学必修3教材为例简单谈一下自己的看法。
《算法初步》这一章总共分为三部分,一是算法与程序框图,教材通过解二元一次方程组,引入了算法的概念,并介绍了如何用自然语言描述算法,并通过程序框图引出三种基本逻辑结构:顺序结构、条件结构和循环结构。
二是基本算法语句,介绍了赋值语句、输入输出语句、条件语句和循环语句,其中循环语句又分直到型(Until )和当型(While )两种循环语句结构,它们之间的互相转化问题。
三是算法案例,介绍了三个具体案例:欧几里德辗转相除法及浅析高中数学新内容《算法初步》文/杜丽桃摘要:从设置算法的重要性,高中教材中的算法内容简介,算法体现的思想价值以及对算法重点内容的反思几个方面对高中数学新内容《算法初步》进行了探究和认识。
九年级下册数学第28章《锐角三角函数》知识点梳理

九年级数学下册第28章《锐角三角函数》知识点梳理一.知识框架
二.知识概念
1.Rt△ABC中
(1)∠A的对边与斜边的比值是∠A的正弦,记作sinA=∠A的对边斜边
(2)∠A的邻边与斜边的比值是∠A的余弦,记作cosA=∠A的邻边斜边
(3)∠A的对边与邻边的比值是∠A的正切,记作tanA=∠A的对边∠A的邻边
(4)∠A的邻边与对边的比值是∠A的余切,记作cota=∠A的邻边∠A的对边
2.特殊值的三角函数:
本章内容使学生了解在直角三角形中,锐角的对边与斜边、邻边与斜边、对边与邻边、邻边与对边的比值是固定的;通过实例认识正弦、余弦、正切、余切四个三角函数的定义。
并能应用这些概念解决一些实际问题。
的解,将其定义扩展到复数系。
】。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【反馈检测 2 答案】B
【反馈检测
2
详细解析】函数
y
sin
x
在区间 [
,
] 为单调递增函数,在区间[
,
3
] 为单调递增函数,
22
22
5
由
4
sin 5
sin 4
,由
sin( ) sin( ) ,故 A,C 错误; y tan x 在
7 72
7
7
56
5
6
区间[ , ] 为单调递增函数, tan 15 tan(2 ) tan( ) ,
22
8
8
8
由 tan( ) tan( ) ,即 tan(15 ) tan( ) ,故 B 正确;
87
8
7
8
7
cos( 3 ) cos 3 cos( 3 ) cos 2 0,
5
5
5
5
cos( 9 ) cos 0 ,所以有 cos( 3 ) cos( 9 ) ,故 D 错误,综上所述,选 B.
形。
2、三角函数线
(1)由于 sin MP ,所以 MP 就叫角 的正弦线.正弦线的起点在垂足,终点在角的终边与单位圆的
交点.
Hale Waihona Puke (2)由于 cos OM ,所以 OM 就叫角 的余弦线.余弦线的起点在原点,终点在垂足. (3)由于 tan AT ,所以 AT 就叫角 的正切线.正切线的起点在单位圆与 x 轴正半轴的交点 A, 终点在过点 A 的切线与角 的终边或反向延长线的交点.
5
5
5
【反馈检测 1】设 a= sin 24 ,b= cos( 39 ) ,c= tan( 43 ) ,则( )
5
10
12
A.a>b>c B.b>c>a C.c>b>a D.c>a>b
方法二
函数的单调性比较法
使用情景
一般三角函数可以化成同名三角函数.
解题步骤
先利用三角函数诱导公式把它们化成同名三角函数,再利用三角函数的单调性解答.
2
sin(x) sin x, 奇函数
当 x 2k k 时,
ymax 1;当 x 2k
k
时,
ymin
1.
2
cos(x) cos x, 偶函数
既无最大值,也无最小值
tan(x) tan x, 奇函数
在
2k
2
, 2k
2
k 上是增函数;在
2k
2
,
2k
3 2
k 上是减函数. 对称中心 k , 0k
【例 2】 下列关系式中正确的是( )
A. sin110 sin1680 cos100
B. sin1680 sin110 cos100
C. sin110 cos100 sin1680
D. sin1680 cos100 sin110
【点评】由于要比较的对象只有正弦和余弦,所以可以通过诱导公式把它们统一化成正弦,再利用正 弦函数的单调性解答. 学.科.网
【解析】 a
sin 3
sin
2
2
,则
是第一象限的锐角,根据三角函数线,所以 b
a c ,故选 A.
5
5
5
【点评】(1)本题中由于有正弦、余弦和正切,且角 (0, ) ,所以选择三角函数线比较大小比较方便.
(2)本题中 a sin 3 , 化简成 a sin 3 sin 2 ,这样三个角相同利用三角函数线比较更简洁.
3、三角函数值大小的比较常用的方法是三角函数线和单调性两种方法.
【方法讲评】
方法一
三角函数线比较法
使用情景
一般直接比较困难或者三角函数里面有正切.
解题步骤
一般通过画三角函数线比较大小.
【例 1】设 a sin 3 , b cos 2 , c tan 2 , 则( )
5
5
5
A. b a c
B. b c a C. a b c D. a c b
【知识要点】
1、 正弦函数y余弦si函n x数, 正切函数y cos x,
性质
y sin x
y tan x 的图象与性质 y cos x
y tan x
图象
定义域 值域 最值 周期性 奇偶性
单调性
对称性
R
1,1
R
1,1
x
x
k
2
,k
R
当
x
2k
2
k
时,
ymax
1;当
x
2k
2
k 时, ymin 1.
4
4
5
4
【反馈检测 2】下列不等式中,正确的是( )
A. sin 5 sin 4 B. tan 15 tan( ) C. sin( ) sin( ) D. cos( 3 ) cos( 9 )
7
7
8
7
5
6
5
4
高中数学常见题型解法归纳及反馈检测第 28 讲: 三角函数值大小比较参考答案
【反馈检测 1 答案】C
2k , 2k k
在
上是
2k , 2k
增函数;在
k 上是减函数.
在
k
2
,
k
2
k 上是增函数.
对称中心
k
2
,
0
k
对称中心
k 2
,
0
k
x k k 对称轴 x k k ,既是中
对称轴
2
,
心对称又是轴对称图形。
既是中心对称又是轴对称图
无对称轴,是中心对称但不 是轴对称图形。
