奇异值分解
奇异值分解的一些特性以及应用小案例

奇异值分解的一些特性以及应用小案例一、奇异值分解的特性1.唯一性:对于任意一个矩阵A,它的奇异值分解是唯一的。
也就是说,任意两个不同的SVD分解结果之间,只有奇异向量的顺序和奇异值的正负可能不同。
2.矩阵的逆和伪逆:对于一个非奇异矩阵A,它的逆可以通过对SVD 分解后的三个矩阵进行逆乘得到,即A的逆等于VΣ⁺U^T,其中Σ⁺是Σ的逆矩阵的转置。
当A是一个奇异矩阵时,可以用伪逆来表示它的逆。
3.奇异值与特征值的关系:对于一个方阵A,它的SVD分解与特征值分解存在一定的关联。
A的非零奇异值的平方等于A的非零特征值,而U 和V中的列向量分别是A的左特征向量和右特征向量。
二、奇异值分解的应用案例1.图像压缩:在图像处理中,SVD可以用于对图像进行压缩。
将图片矩阵进行SVD分解后,可以利用奇异值的特性,选择数值较大的奇异值,然后将较小的奇异值设为0,以达到降低图像质量的目的。
这样就可以减少图像所需的存储空间,同时避免图像失真过大。
2.推荐系统:在推荐系统中,SVD可以用于对用户和物品之间的隐含关系进行建模。
将用户-物品评分矩阵进行SVD分解,得到用户特征矩阵和物品特征矩阵,然后可以通过计算用户特征向量和物品特征向量之间的相似度,来预测用户对未评分物品的喜好程度,从而实现个性化的推荐。
3.语言模型:在自然语言处理中,SVD可以用于构建词向量的模型。
通过对大量文本数据进行SVD分解,可以得到一个降维后的向量空间,每个词语对应一个向量。
这些向量可以捕捉到不同词语之间的语义关系,例如可以用向量表示"男人"-"女人"的关系,从而进行词义相似度计算、文本分类、情感分析等任务。
以上是奇异值分解的一些特性以及应用案例的简要介绍。
奇异值分解具有唯一性、与特征值分解有一定的关系,可以用于矩阵的逆和伪逆计算。
在实际应用中,SVD被广泛用于图像压缩、推荐系统和语言模型等领域。
通过对SVD的理解和应用,可以在相关领域中提供强大的分析和建模能力。
奇异值分解

奇异值分解奇异值分解是线性代数中一种重要的矩阵分解,在信号处理、统计学等领域有重要应用。
定义:设A为m*n阶矩阵,AHA的n个特征值的非负平方根叫作A的奇异值。
记为σi(A)。
如果把AHA的特征值记为λi(A),则σi(A)=λi(AHA)^(1/2)。
定理:(奇异值分解)设A为m*n阶复矩阵,则存在m阶酉阵U和n阶酉阵V,使得:A = U*S*V’其中S=diag(σi,σ2,……,σr),σi>0 (i=1,…,r),r=rank(A)。
推论:设A为m*n阶实矩阵,则存在m阶正交阵U和n阶正交阵V,使得A = U*S*V’其中S=diag(σi,σ2,……,σr),σi>0 (i=1,…,r),r=rank(A)。
说明:1、奇异值分解非常有用,对于矩阵A(m*n),存在U(m*m),V(n*n),S(m*n),满足A = U*S*V’。
U和V中分别是A的奇异向量,而S是A的奇异值。
AA'的正交单位特征向量组成U,特征值组成S'S,A'A的正交单位特征向量组成V,特征值(与AA'相同)组成SS'。
因此,奇异值分解和特征值问题紧密联系。
2、奇异值分解提供了一些关于A的信息,例如非零奇异值的数目(S的阶数)和A的秩相同,一旦秩r确定,那么U的前r列构成了A的列向量空间的正交基。
关于奇异值分解中当考虑的对象是实矩阵时: S对角元的平方恰为A'A特征值的说明. (对复矩阵类似可得)从上面我们知道矩阵的奇异值分解为: A=USV, 其中U,V是正交阵(所谓B为正交阵是指B'=B-1, 即B'B=I), S为对角阵.A'A=V'S'U'USV=V'S'SV=V-1S2V上式中, 一方面因为S是对角阵, S'S=S2, 且S2对角元就是S的对角元的平方. 另一方面注意到A'A是相似与S2的, 因此与S2有相同特征值.注:下面的符号和上面的有差异,注意区分SVD步骤:1、求AHA或AAH2、求AHA或AAH的特征值及特征向量x1,x2,...xr, r个特征值组成3、U=(x1,x2,...xr)地4、V1=AU1Δr-1,取V2与其正交,则V=(V1,V2)则n阶复方阵U的n个列向量是U空间的一个标准正交基,则U是U距阵.一个简单的充分必要判别准则是方阵U的转置共扼距阵乘以U 等于单位阵,则U是U距阵正交向量组的性质定义1Euclid空间V的一组两两正交的非零向量叫做V的一个正交向量组.若正交向量组的每一个向量都是单位向量,这个正交组就叫做一个标准正交向量组.设V是一个n维Euclid空间.若V中n个向量α1,α2,…,αn构成一个正交组,则由定理9.2.1知道这n个向量构成V的一个基.这样的一个基叫做V的一个正交基.若V的一个正交基还是一个标准正交向量组,则称这个基是V的一个标准正交基。
奇异值分解原理

奇异值分解原理
奇异值分解(Singular Value Decomposition,SVD)是一种矩阵分解技术,它可以将一个矩阵分解为三个矩阵的乘积,这三个矩阵分别是左奇异矩阵,奇异值矩阵和右奇异矩阵。
奇异值分解的主要应用之一是矩阵的减少,这种减少可以用来减少矩阵的计算复杂度,以及减少需要存储的内存大小。
奇异值分解的另一个主要应用是降维,它可以将原始数据集中的特征映射到较低维度的特征空间,从而能够去除噪声和保留最重要的特征。
这样做的好处是减少计算量和节省内存,同时还能提高计算机的运行效率。
此外,奇异值分解还可以用于机器学习中的特征提取和特征抽取,它可以将原始数据的高维特征映射到较低维特征空间,从而提取出最重要的特征,并减少噪声的影响。
总之,奇异值分解是一种非常有用的数学工具,可以用于减少矩阵计算复杂度,减少内存大小,降维,特征提取以及特征抽取等任务。
它可以有效地帮助我们解决许多数据分析问题,因此被广泛应用于许多机器学习领域。
矩阵的奇异值分解

非对称矩阵分解
非对称矩阵的特征值分解
对于非对称矩阵,其特征值可能是复数,因此不能直接进行实数域上的特征值分 解。但是,可以通过引入复数域上的特征向量和特征值,将非对称矩阵分解为复 数域上的特征向量矩阵和特征值矩阵的乘积。
非对称矩阵的奇异值分解
对于任意实非对称矩阵,都可以进行奇异值分解,即$A = USigma V^T$,其中 $U$和$V$是正交矩阵,$Sigma$是对角矩阵,对角线上的元素是$A$的奇异值。 非对称矩阵的奇异值分解在数据降维、图像处理等领域有广泛应用。
通信信道均衡策略
信道均衡原理
在通信系统中,信道均衡是一种用于补偿信道失真、提高通信质量的技术。奇异值分解可用于信道均衡中的信道 矩阵分解,从而实现对信道特性的准确估计和补偿。
基于奇异值分解的信道均衡算法
利用奇异值分解对信道矩阵进行分解,根据得到的奇异值和左右奇异向量设计均衡器,实现对信道失真的有效补 偿。
3
个性化推荐
结合用户历史行为数据和相似度计算结果,为用 户推荐与其兴趣相似的物品或服务。
05 奇异值分解在信号处理和 通信中应用
信号降噪与重构技术
基于奇异值分解的信号降噪
利用奇异值分解能够将信号分解为多个独立成分的特点,对含噪信号进行降噪处理,提高信号质量。
信号重构技术
通过保留奇异值分解得到的主要成分,对信号进行重构,实现信号的压缩和恢复。
特殊类型矩阵分解
正定矩阵的Cholesky分解
对于正定矩阵,可以进行Cholesky分解,即$A = LL^T$,其中$L$是下三角 矩阵。Cholesky分解在求解线性方程组、最优化问题等场景中具有重要作用。
稀疏矩阵的分解
对于稀疏矩阵,可以采用特定的分解方法,如LU分解、QR分解等,以便更有效 地进行存储和计算。这些分解方法在数值计算、科学计算等领域有广泛应用。
奇异值分解与特征值分解的比较分析(Ⅰ)

奇异值分解与特征值分解是线性代数中两个重要的矩阵分解方法。
它们在数据分析、信号处理、图像压缩等领域都有着广泛的应用。
本文将对这两种分解方法进行比较分析,探讨它们的优缺点及适用范围。
一、奇异值分解(SVD)奇异值分解是一种将一个矩阵分解成三个矩阵的方法,即将一个m×n的矩阵A分解为U、Σ和V三个矩阵的乘积,其中U是一个m×m的酉矩阵,Σ是一个m×n的对角矩阵,V是一个n×n的酉矩阵。
奇异值分解有着许多优点,比如对于任意的矩阵A,都存在奇异值分解。
并且,对于奇异值分解的性质有许多重要的应用,比如在矩阵压缩和降维、矩阵逆的计算等方面。
二、特征值分解(EVD)特征值分解是一种将一个方阵分解成三个矩阵的方法,即将一个n×n的方阵A分解为P、Λ和P-1三个矩阵的乘积,其中P是一个n×n的可逆矩阵,Λ是一个n×n的对角矩阵,P-1是P的逆矩阵。
特征值分解也有着诸多优点,比如对于对称矩阵来说,特征值分解是唯一的,而且特征值分解在对称矩阵的对角化、矩阵对称化等方面有着重要的应用。
三、奇异值分解与特征值分解的比较分析1. 计算复杂度在计算复杂度方面,特征值分解的计算复杂度通常比奇异值分解高。
特征值分解需要解特征值问题,而奇异值分解只需要进行奇异值分解,因此在计算复杂度上,奇异值分解更加高效。
2. 适用范围特征值分解对于对称矩阵有着很好的适用性,而奇异值分解对于任意矩阵都有着适用性。
因此,在实际应用中,奇异值分解的适用范围更广。
3. 稳定性在矩阵的微小扰动下,特征值分解的结果可能会有较大的变化,而奇异值分解对于矩阵的微小扰动具有更好的稳定性。
因此在数值计算中,奇异值分解更加稳定可靠。
四、结论奇异值分解与特征值分解是两种重要的矩阵分解方法,它们在不同的领域有着不同的应用。
在计算复杂度、适用范围和稳定性等方面,奇异值分解相对于特征值分解具有更多的优势。
奇异值分解
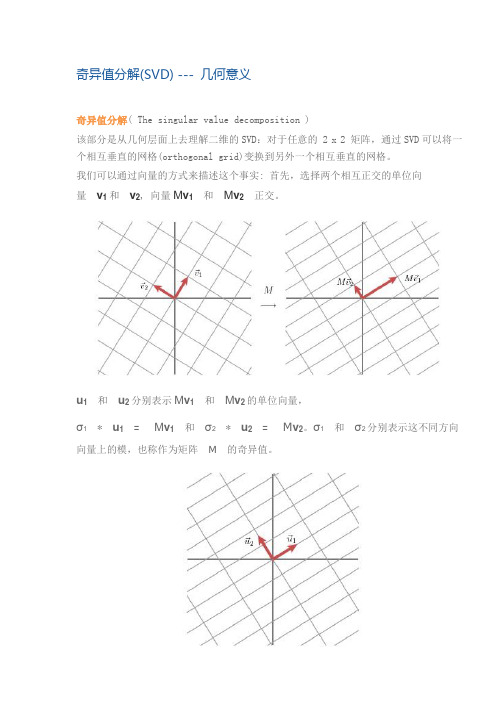
奇异值分解(SVD) --- 几何意义奇异值分解( The singular value decomposition )该部分是从几何层面上去理解二维的SVD:对于任意的 2 x 2 矩阵,通过SVD可以将一个相互垂直的网格(orthogonal grid)变换到另外一个相互垂直的网格。
我们可以通过向量的方式来描述这个事实: 首先,选择两个相互正交的单位向量v1 和v2, 向量M v1和M v2正交。
u1和u2分别表示M v1和M v2的单位向量,σ1* u1= M v1和σ2* u2= M v2。
σ1和σ2分别表示这不同方向向量上的模,也称作为矩阵M的奇异值。
这样我们就有了如下关系式M v1= σ1u1M v2= σ2u2我们现在可以简单描述下经过M线性变换后的向量x 的表达形式。
由于向量v1和v2是正交的单位向量,我们可以得到如下式子:x = (v1x) v1 + (v2x) v2这就意味着:M x = (v1x) M v1 + (v2x) M v2M x = (v1x) σ1u1 + (v2x) σ2u2向量内积可以用向量的转置来表示,如下所示v x = v T x最终的式子为M x = u1σ1v1T x + u2σ2v2T xM = u1σ1v1T + u2σ2v2T上述的式子经常表示成M = UΣV Tu 矩阵的列向量分别是u1,u2 ,Σ是一个对角矩阵,对角元素分别是对应的σ1和σ2,V 矩阵的列向量分别是v1,v2。
上角标T表示矩阵V 的转置。
这就表明任意的矩阵M是可以分解成三个矩阵。
V 表示了原始域的标准正交基,u 表示经过M 变换后的co-domain的标准正交基,Σ表示了V 中的向量与u 中相对应向量之间的关系。
(V describes an orthonormal basis in the domain, and U describes an orthonormal basis in the co-domain, and Σ describes how much the vectors in V are stretched to give the vectors in U.)如何获得奇异值分解?( How do we find the singular decomposition? ) 事实上我们可以找到任何矩阵的奇异值分解,那么我们是如何做到的呢?假设在原始域中有一个单位圆,如下图所示。
奇异值分解定理

奇异值分解定理奇异值分解(Singular Value Decomposition,简称SVD)是线性代数中一种重要的矩阵分解方法,常用于数据分析、信号处理、图像压缩等领域。
SVD的定理表明,任何矩阵都可以分解成三个矩阵的乘积,其中一个矩阵是正交矩阵,另外两个矩阵是对角矩阵,且对角线上的元素称为奇异值。
奇异值分解定理的数学概念比较复杂,需要一定的线性代数基础。
下面将对奇异值分解定理进行详细解释。
给定一个m行n列的实数矩阵A,假设rank(A)为r.那么存在两个实数方阵U(m×r)和V(n×r),使得:A = UΣV^T其中,U的每一列是A^TA的特征向量,V的每一列是AA^T的特征向量,Σ是一个对角矩阵,对角线上的元素称为奇异值。
奇异值分解定理的证明比较复杂,这里只给出一个简要的证明思路。
假设A的列向量为{a1, a2, ..., an},它们构成了一个n维向量空间的一组基。
我们可以将这组基转化为标准正交基,得到一组正交矩阵U和V。
然后我们可以通过对U和V进行一些数学操作,得到UΣV^T形式的矩阵。
最后,我们可以证明这个矩阵确实满足奇异值分解定理的要求。
奇异值分解定理在数据分析中有广泛的应用。
例如,在推荐系统中,我们可以通过SVD将用户对物品的评分矩阵分解,得到用户和物品的特征矩阵,从而进行个性化推荐。
在语音识别中,我们可以通过SVD将语音信号分解成一组基本声音的叠加,从而实现语音信号的降噪和特征提取。
在图像压缩中,我们可以通过SVD将图像分解成一组基本的图像模式,从而实现图像的降噪和压缩。
奇异值分解定理的应用不仅局限于上述领域,还可以应用于信号处理、图像处理、文本处理等其他领域。
通过奇异值分解,我们可以将复杂的问题转化为简单的线性代数运算,从而大大简化问题的求解过程。
然而,奇异值分解也有一些限制。
首先,奇异值分解是一种数值方法,对计算精度要求较高。
其次,奇异值分解的计算复杂度较高,对于大规模矩阵的分解可能会很耗时。
第15章 奇异值分解

• 实际应用中提到矩阵的奇异值分解时,通常指截断奇异值分解。
截断奇异值分解
例
• 矩阵A的秩为3,
• 若取k=2,则其截断奇异值分解是
几何解释
• 从线性变换的角度理解奇异值分解, m x n 矩阵A表示从n维空间Rn到 m维空间Rm的一个线性变换,
坐标系的旋转或反射变换U,得到向量
。
• 原始空间的标准正交基,
经过坐标系的旋转变换VT、 坐标轴的缩放变换刃、 坐标系的旋转变换U, 得到和经过线性变换A等价的结果。
例
• 给定一个2阶矩阵
• 其奇异值分解为
例
• 观察基于矩阵A的奇异值分解将R2的标准正交基
• 进行线性转换的情况 • 首先,VT表示一个旋转变换,将标准正交基e1, e2旋转,得到向
• 的奇异值分解
例
• (1)求ATA的特征值和特征向量
• 得到齐次线性方程组
例
• 该方程有非零解的充要条件是
• 解此方程,得矩阵ATA的特征值
和
。
• 将特征值代入线性方程组,得到对应的单位特征向量
例
• (2)求正交矩阵V • 构造正交矩阵V
• (3)求对角矩阵
• 奇异值为
和
• 构造对角矩阵
例
• (3)求 m x n 对角矩阵
• 计算A的奇异值
• 构造 m x n 矩形对角矩阵 ,主对角线元素是奇异值,其余 元素是零
奇异值分解的计算
• (4) 求m阶正交矩阵U • 对A的前r个正奇异值,令 • 得到 • 求AT的零空间的一组标准正交基
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
地球物理系反演报告
实验一奇异值分解计算广义逆G+
专业:地球物理学
姓名:
学号:
指导教师:邵广周
实验一 奇异值分解计算广义逆G +
一、基本原理
对于任意的n m ⨯方程组:b Ax =
其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=mn m n a a a a A
1
111
⎥⎥
⎥⎦
⎤
⎢⎢⎢⎣⎡=n x x x 1 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=m b b b 1 如果n m =,只要n 方阵A 非奇异,就有逆阵1-A ,从而得到解b A x 1-=。
然而,对于n m ≠的一般情况,A 是长方阵,就没有通常的逆阵。
不过它仍然可以有相应于特定方程类型的几种形式的广义逆矩阵,其中适于任何情况的广义逆叫做Penrose 广义逆,记为+A 。
于是,方程的解可以为:
b A x +=
由奇异值分解(SVD )可以将A 分解为:
T V U A ∑=
其中U ,V 分别为m ,n 阶正交阵
⎥
⎥⎥⎥⎥⎥⎥⎥⎦⎤
⎢⎢⎢⎢⎢
⎢⎢⎢⎣
⎡=∑00
1
r
σσ 这样A 的广义逆+A 可表示为:
T U V A 1-+∑=
其中
⎥⎦⎤⎢⎣⎡∑=∑--0001
1
r
⎥⎥⎥⎦⎤⎢⎢⎢⎣
⎡=∑---1111r r
σσ
这样我们可以看出,完成A 的奇异值分解后,求解A 的广义逆就变得很简单,从而可以方便地求出方程组的最小二乘解。
下面我们说明对矩阵进行奇异值分解的方法和步骤。
通常情况下我们考虑m>n 时矩阵A 的奇异值分解,因为当m<n 时,可以将n-m 行补零使其成为方阵后再进行分解。
这样我们就将矩阵A 的奇异值分解分为两大步,若干小步如下:
一、用Householder 变换将A 约化为双对角矩阵。
具体步骤如下:
1. 以A 的第1列作为v ,取i=1,按下列式子构造Householder 矩阵Q 式中i H 为Q ,为了方便以后的说明我们还用i H 表示
2
/122
)
(1)(12
)(22
)(),,,,0,0(),,,)(,,0,0()
1(∑=++==+=-
=m
i k k i T m i i i T m i i i i i i
T i i i v v
v v v v v v v v sign v u u u u I H 其中,
2. 将Q 1左乘A 得到矩阵Q 1 A ,并以Q 1 A 的第1行作为v ,取i=2,按(1)式构造Householder 矩阵H 2, 右乘Q 1A 得到Q 1A H 2。
3. 取Q 1A H 2的第2列为v ,i=2,按(1)式构造Householder 矩阵Q 2,左乘Q 1A H 2,得到Q 2 Q 1A H 2,并将计算Q 2 Q 1将其存入Q 1。
4. 取Q 2 Q 1A H 2的第2行为v ,i=3,按(1)式构造Householder 矩阵H 3,右乘Q 2 Q 1A H 2,得到Q 2 Q 1A H 2 H 3,并将H 2 H 3存入H 2。
5. 依次类推,计算出Q n Q n-1…Q 1AH 2 H 3…H n-1为双对角矩阵,并将Q n Q n-1…Q 1存入到Q 1中,H 2 H 3…H n-1存入到H 2 中。
Q n Q n-1…Q 1AH 2 H 3…H n-1为双对角矩阵记为:
⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎢
⎢⎢⎢⎢⎣
⎡=-00
01
3
22
1
n n n B βγβγβγβ 需要注意的是:当n m =时,只计算到Q n-1…Q 1AH 2 H 3…H n-2
二、用原点位移QR 算法进行迭代,计算所有的奇异值,并最终结合(一)计算出出U 和V 。
1. 按下式列旋转矩阵H 0
⎥⎥
⎥
⎥⎥
⎥⎦
⎤
⎢⎢⎢⎢⎢⎢⎣⎡-=110 c s s c H (2)
式中
()
(
)
[]
2
/121
2
2
2
1
21222121222
122112
2212142
121//-----+--+-+++==-=+===n n n n n n n n n n r r
s r c γ
γγβγβγβγβσγβξσβξξξξξ
并将计算BH 0
2. 按下式构造列旋转矩阵并计算Q 1 BH 0
⎥⎥
⎥
⎥⎥
⎥⎦
⎤⎢⎢⎢⎢⎢⎢⎣⎡-=11
1 c s s c Q
3. 构造列旋转矩阵并计算Q 1 BH 0H 1以及H 0H 1
⎥⎥
⎥⎥
⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-=1111 c s s c H
4. 构造列旋转矩阵并计算Q 2 Q 1 BH 0H 1以及Q 2 Q 1
⎥⎥
⎥⎥
⎥⎥⎥⎥⎦
⎤
⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-=1112 c s s c Q
5. 按类似(3),(4)的方法构造列旋转矩阵,并计算相应的新矩阵Q i …Q 2 Q 1
BH 0H 1…H i-1,直到i=n ,并记1211Q Q Q Q n =,1101
1-=n H H H H ,110121
11-==n n H H BH Q Q Q Q B ,即1111
1BH Q B = 6. 判断B 1的次对角线元素是否在误差范围内可以认为是0,若是则分解完毕,若否,则将B 1作为上面的B 重复步骤1,2,3,4,5,6。
直到B k 可以近
似看作是对角阵。
即:1
1111-----=k k k k k k H B Q B
记112211Q Q Q Q k k --=,112211--=k k H H H H
则B k 的对角线元素就是矩阵A 的奇异值,即T V U A ∑=中的∑已经求得,从上面的过程中我们可以将A 按下面的式子进行分解:
21HH QB Q A k =
对比T V U A ∑=,k T T B H H V Q Q U =∑==,,21,这样我们就完成了矩阵A 的奇
异值分解,由于U 和V 都是正交阵,我们能够得到A 的广义逆+A ,从而可以根据下列公式计算方程组的最小二乘解:
b A x +=
二、程序设计及结果分析
1、本次实验给的是109⨯的方程组:b Ax =,具体数值如下:
1001001001601001001016001001001
1611100000023000111000
260000
0011
1291.414000 1.4140000.41438.4850000.4140000.414
037.0713⎡⎤⎡⎤⎡⎤
⎢⎥⎢⎥⎢⎥⎢
⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢
⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥
⎢⎥⎢⎥⎢⎥=⎢
⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥
⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎣
⎦⎣⎦⎣⎦
⎥⎥⎥ 其中,计算精度为:000001.0=EPS 。
2、计算结果
123456789 1.000350.999651.000002.000352.000001.999652.999293.000353.00035x x x x x x x x x ⎡⎤⎡⎤
⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥
⎣
⎦⎣⎦
3、结果分析
由以上结果分析可知,奇异值分解对求解欠定矩阵是很有用的。
计算结果与
真实模型值相符。
且误差较小。
可见,奇异值分解对于求解奇异矩阵还是很有用的,具有很
好的可行性,其结果也符合方程组。
通过本次实验,我对奇异值分解
有了更进一步的理解,了解了其基本原理及具体求解步骤。
