运筹学应用问题举例
简单的运筹学实际应用案例

简单的运筹学实际应用案例运筹学(Operations Research)是一门研究如何有效利用有限资源进行决策的学科,它通过数学、统计学和经济学等方法,帮助管理者做出最佳决策。
下面将介绍几个简单的运筹学实际应用案例。
1.生产线优化假设一公司拥有多条生产线,每条生产线对应不同的产品。
公司希望通过优化生产线的调度,以达到最大的产出和利润。
运筹学可以通过数学模型和算法,对生产线进行优化调度。
例如,可以使用线性规划模型来确定每条生产线的产量和调度,以最大化总利润;也可以使用整数规划模型来考虑生产线的限制和约束条件。
2.物流网络设计一家物流公司需要设计其物流网络,以最小化成本并满足客户对快速物流的需求。
运筹学可以通过数学模型和算法,帮助物流公司优化物流网络的设计。
例如,可以使用网络流模型来确定货物在物流网络中的最佳路线和节点,以最小化总运输成本;也可以使用线性规划模型来决定在不同节点上的仓库和货物库存量,以满足客户的需求。
3.航班调度问题一家航空公司需要制定最佳航班调度计划,以最大化航班利润并排除延误风险。
运筹学可以通过数学模型和算法,帮助航空公司优化航班调度。
例如,可以使用线性规划模型来决定不同航班的起降时间和机型,以最大化航班利润;也可以使用排队论模型来评估航班的延误风险,并制定相应的调度策略。
4.人员调度问题一家超市需要制定最佳的员工调度计划,以最大化服务质量和节约人力成本。
运筹学可以通过数学模型和算法,帮助超市优化员工调度。
例如,可以使用整数规划模型来决定不同时间段需要多少员工,并考虑员工的技能匹配和工作时间的合理安排;也可以使用模拟仿真方法来评估不同调度策略的效果,并做出相应的决策。
以上是几个简单的运筹学实际应用案例,运筹学在实际生产和管理中有着广泛的应用。
通过数学模型和算法的应用,可以帮助企业优化资源配置、提高效率和决策质量,从而实现最佳的经济效益。
运筹学实例 含解析

案例1. 工程项目选择问题某承包企业在同一时期内有八项工程可供选择投标。
其中有五项住宅工程,三项工业车间。
由于这些工程要求同时施工,而企业又没有能力同时承担,企业应根据自身的能力,分析这两类工程的盈利水平,作出正确的投标方案。
有关数据见下表:表1 可供选择投标工程的有关数据统计工程类型 预期利润/元 抹灰量/m 2混凝土量/ m 3砌筑量/ m 3住宅每项 50011 25 000 280 4 200 工业车间每项 80 000480 880 1 800 企业尚有能力108 0003 68013 800试建立此问题的数学模型。
解:设承包商承包X 1项住宅工程,X 2项工业车间工程可获利最高,依题意可建立如下整数模型:目标是获利最高,故得目标函数为21X 80000X 50011z Max +=根据企业工程量能力限制与项目本身特性,有约束:利用WinSQB 建立模型求解:1080002X 4801X 25000≤+3680X 880X 28021≤+13800X 1800X 420021≤+为整数,;,2121X X 3X 5X ≤≤综上,承包商对2项住宅工程,3项车间工程进行投标,可获利最大,目标函数Max z=340022 元。
案例2. 生产计划问题某厂生产四种产品。
每种产品要经过A,B两道工序加工。
设该厂有两种规格的设备能完成A工序,以A1 ,A2表示;有三种规格的设备能完成B工序,以B1 ,B2,B3 表示。
产品D可在A,B任何一种规格的设备上加工。
产品E可在任何规格的A设备上加工,但完成B工序时只能在B1设备上加工。
产品F可在A2及B2 ,B3上加工。
产品G可在任何一种规格的A设备上加工,但完成B工序时只能在B1 ,B2设备上加工。
已知生产单件产品的设备工时,原材料费,及产品单价,各种设备有效台时如下表,要求安排最优的生产计划,使该厂利润最大?设设产品设备有效台时1 2 3 4A1 A2 B1 B2 B357647109812111068108601110000400070004000原料费(元/件)单价(元/件)0.251.250.352.000.502.800.42.4解:设Xia(b)j为i产品在a(b)j设备上的加工数量,i=1,2,3,4;j=1,2,3,得变量列表设备产品设备有效台时Ta(b)j1 2 3 4A1 A2 B1 B2 B3X1a1X1a2X1b1X1b2X1b3X2a1X2a2X2b1X3b2X3b3X3a1X3a2X3b1X3b2X3b3X4a1X4a2X4b1X4b2X4b3601110000400070004000原料费Ci (元/件) 单价Pi (元/件) 0.25 1.25 0.352.00 0.50 2.80 0.4 2.4其中,令X 3a 1,X 3b 1,X 3b 2,X 3b 3,X 4b 3=0 可建立数学模型如下: 目标函数: ∑∑==-=4121)](*[Maxi j iaj Ci Pi X z=1.00*(X 1a 1+X 1a 2)+1.65*(X 2a 1+X 2a 2)+2.30* X 3a 2+2.00*( X 4a 1+X 4a 2)约束条件:利用WinSQB 求解(X1~X4,X5~X8,X9~X12,X13~X17,X18~X20分别表示各行变量):4,3,2,1X21j 31==∑∑==i X j ibjiaj2,1T X 41iaj=<=∑=j Taj i iaj 3,2,141=<=∑=j TbjT Xi ibj ibj2,1;4,3,2,10X iaj ==>=j i 且为整数32,1;4,3,2,10X ibj ,且为整数==>=j i 0X X X X X 4b33b33b23b13a1=====综上,最优生产计划如下:设备产品1 2 3 4A1 A2 B1 B2 B3774235004004008732875目标函数zMax=3495,即最大利润为3495案例3. 高校教职工聘任问题 (建摸)由校方确定的各级决策目标为:P 1 要求教师有一定的学术水平。
运筹学案例集

运筹学案例集常州宝菱重工机械有限公司孔念荣收集整理运筹学的一些典型性应用•合理利用材料问题:如何在保证生产的条件下,下料最少•配料问题:在原料供应量的限制下,如何获取最大收益•投资问题:从投资项目中选取最佳组合,使投资回报最大•产品生产计划:合理利用人力、物力、财力等,使获利最大•劳动力安排:用最少的劳动力来满足工作的需要•运输问题:如何制定最佳调运方案,使总运费最少一、生产计划问题案例1(2-4)、某工厂用A、B、C、D四种原料生产甲、乙两种产品,生产甲和乙所需各种原料的数量以及在一个计划期内各种原料的现有数量见下表所示。
又已知每单位产品甲、乙的售价分别为400元和600元,问应如何安排生产才能获得最大收益?已知生产单位产品所需的设备台时及A、B两种原材料的消耗、资源的限制,如下表:问题:工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多?案例3(2-25)、某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量,数据如下表所示。
问题:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产品的铸造中,由本公司铸造和由外包协作各应多少件?案例4(2-28)、永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品,均要经过A、B两道工序加工。
设有两种规格的设备A1、A2能完成A工序;有三种规格的设备B1、B2、B3能完成B 工序。
Ⅰ可在A、B的任何规格的设备上加工;Ⅱ可在任意规格的A设备上加工,但对B工序,只能在B1设备上加工;Ⅲ只能在A2与B2设备上加工,数据如下表所示。
问题:为使该厂获得最大利润,应如何制定产品加工方案?案例5、某造纸厂用原材料白坯纸生产原稿纸、笔记本和练习本三种产品。
该厂现有工人100人,每月白坯纸供应量为3万公斤。
已知工人的劳动生产率为:每人每月生产原稿纸30捆,或生产日记本30打,或练习本30箱。
运筹学案例集

运筹学案例集常州宝菱重工机械有限公司孔念荣收集整理运筹学的一些典型性应用•合理利用材料问题:如何在保证生产的条件下,下料最少•配料问题:在原料供应量的限制下,如何获取最大收益•投资问题:从投资项目中选取最佳组合,使投资回报最大•产品生产计划:合理利用人力、物力、财力等,使获利最大•劳动力安排:用最少的劳动力来满足工作的需要•运输问题:如何制定最佳调运方案,使总运费最少一、生产计划问题案例1(2-4)、某工厂用A、B、C、D四种原料生产甲、乙两种产品,生产甲和乙所需各种原料的数量以及在一个计划期内各种原料的现有数量见下表所示。
又已知每单位产品甲、乙的售价分别为400元和600元,问应如何安排生产才能获得最大收益?已知生产单位产品所需的设备台时及A、B两种原材料的消耗、资源的限制,如下表:问题:工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多?案例3(2-25)、某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量,数据如下表所示。
问题:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产品的铸造中,由本公司铸造和由外包协作各应多少件?案例4(2-28)、永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品,均要经过A、B两道工序加工。
设有两种规格的设备A1、A2能完成A工序;有三种规格的设备B1、B2、B3能完成 B 工序。
Ⅰ可在A、B的任何规格的设备上加工;Ⅱ可在任意规格的A设备上加工,但对B工序,只能在B1设备上加工;Ⅲ只能在A2与B2设备上加工,数据如下表所示。
问题:为使该厂获得最大利润,应如何制定产品加工方案?案例5、某造纸厂用原材料白坯纸生产原稿纸、笔记本和练习本三种产品。
该厂现有工人100人,每月白坯纸供应量为3万公斤。
已知工人的劳动生产率为:每人每月生产原稿纸30捆,或生产日记本30打,或练习本30箱。
运筹学产品配套问题应用题

运筹学产品配套问题应用题
1.工地派48人去控土和运输如果每人每天垩均挖土5方或运土3方;那么应该怎样合理规划人员,正好能使挖出的土及时运走?
2.一套仪器由一个A部件和三个B部件构成.用10m钢材可以做40个A部件或240个B部件,现要用6m钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
3.用铁皮做罐头盒,每张铁皮可制作盒身16个或制作盒底43个,一个盒身与两个盒底配成一套罐头盒。
现有100张白铁皮,用多少张制盒身,多少张制盒底,才能使做出的盒身和盒底配套,又能充分利用铁皮?
4.某车间每天能生产甲种配件120个,或者乙种零件100个。
甲、乙两种零件分别取3个、2个才能配成一套。
要在30天内生产最多的成套产品,问怎样规划甲、乙两种零件的天数?
5.服装厂用355米布做成人服装和儿童服装,成人服装每套平均用布3.5米,儿童服装每套平均用布1.5米。
现已做了80套成人服装,用余下的布还可以做几套儿童服装?。
运筹学在工业领域的应用案例

运筹学在工业领域的应用案例运筹学是一门研究如何通过数学模型和优化方法来解决实际问题的学科。
它广泛应用于工业领域,帮助企业提高生产效率、优化资源利用以及优化决策。
本文将以一些实际案例来展示运筹学在工业领域的应用。
案例一:物流调度在现代物流中心,卡车调度是一个重要而复杂的问题。
一家物流企业面临着如何合理安排卡车的运输路线以及如何将货物分配给不同的卡车的问题。
运筹学通过建立数学模型和优化算法,可以帮助企业快速找到最佳的调度方案。
通过考虑货物的重量、体积、运输距离等因素,运筹学能够帮助企业节省时间和成本,提高物流效率。
案例二:生产计划在工业生产中,合理的生产计划对企业的运营至关重要。
运筹学可以通过建立生产计划的数学模型,考虑原材料、人力资源、设备利用率等因素,制定最优的生产计划。
这种方法可以帮助企业合理安排生产任务、减少生产成本,并确保产品按时交付。
案例三:库存管理有效的库存管理对于企业的正常运营非常重要。
过多的库存会增加企业的成本,而库存不足则会导致订单无法及时完成。
运筹学可以利用数学模型和优化算法,预测需求并制定合理的库存策略。
通过运筹学的方法,企业可以实时调整库存水平,减少库存成本,同时确保生产进度和客户需求之间的平衡。
案例四:供应链优化供应链优化是一个复杂的问题,涉及到多个环节和多个参与者之间的协调。
运筹学可以帮助企业建立供应链的数学模型,考虑供应商、生产商、分销商等各个环节的需求和约束,通过优化算法找到最佳的供应链配置方案。
通过运筹学的方法,企业可以提高供应链的响应速度和灵活性,降低整体成本,提供更好的服务。
案例五:设备维护与优化在工业领域,设备的维护和优化是保证生产连续性和降低成本的关键。
运筹学可以利用数据分析和模型建立,制定设备的维护计划和优化方案。
通过预测设备故障、制定维护策略和排班方案,运筹学可以帮助企业降低设备故障率,最大限度地提高设备利用率,进而提高生产效率和降低成本。
综上所述,运筹学在工业领域有着广泛的应用。
2.6-运筹学应用实例汇总
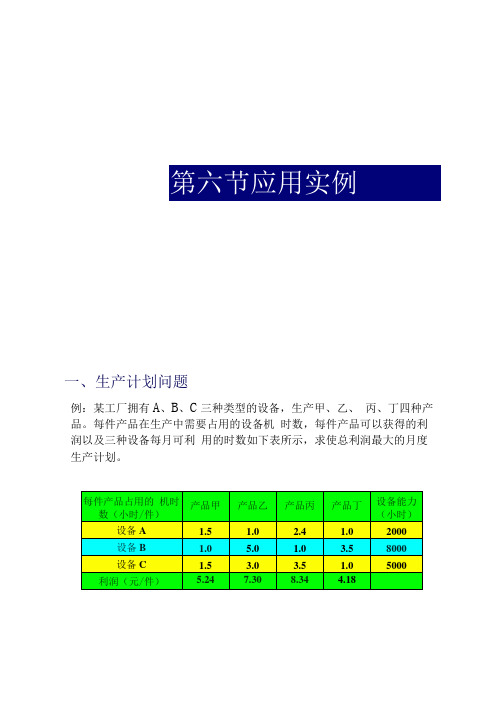
一、生产计划问题例:某工厂拥有A、B、C三种类型的设备,生产甲、乙、丙、丁四种产品。
每件产品在生产中需要占用的设备机时数,每件产品可以获得的利润以及三种设备每月可利用的时数如下表所示,求使总利润最大的月度生产计划。
建模思路■用线性规划制订使总利润最大的生产计划。
■设变量X1为第i种产品的生产件数(i=1, 2, 3, 4),目标函数z为相应的生产计划可以获得的总利润。
在加工时间以及利润与产品产量成线性关系的假设下,可以建立如下的线性规划模型:建模max z= 5.24X1 +7.30x2 +8.34x3 +4.18x4目标函数1.5Xj +1.0x2+2.4X3+1.0X4<2000LOX1 +5.0X2+1.0X3+3.5X4<8000 约束条件1・5X] +3.0X2+3.5X3+1.0X4<5000Xp X2, X3, X4 >0 变量非负约束练习:某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量。
数据如下表。
问:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产品的铸造中,由本公司铸造和由外包协作各应多少件?甲 .乙丙资源限制铸造工时(小时/件)51078000机加工工时(小时/件)64812000装配工时(小时/件)32210000自产铸件成本(兀/件)354外协铸件成本(兀/件)56一机加工成本(元/件)213装配成本(元/件)322产品售价(元/件)231816解:设孙孙寺分别为三道工序都由本公司加工的甲、乙、丙三种产品的件数,同,幅分别为由外协铸造再由本公司加工和装配的甲、乙两种产品的件数。
求占的利润:利润二售价-各成本之和产品甲全部自制的利润产品甲铸造外协,其余自制的利润产品乙全部自制的利润产品乙铸造外协,其余自制的利润产品丙的利润可得到毛(i = 1,2, 3,4,5)的利润分别为15、10、7、13、9=23-(3+2+3)=15 =23-(5+2+3)=13 =18-(5+1+2)=10 =18-(6+1+2)=9 =16-(4+3+2)=7通过以上分析,可建立如下的数学模型:目标函数:Max 15百+ 10电+ 7两+ 13题+ 9不约束条件:5为+ 10西+ 7玛<80006为+ 4出+ 8^ + 6々+ 4不3百+ 2X2 + 2均+ 3局+ 2不毛,演,传,演,与12000 10000二、混合配料问题例:某工厂要用四种合金T1, T2, T3和T4为原料,经熔炼成为一种新的不锈钢G。
运筹学运输问题生活案例

运筹学运输问题生活案例运筹学是一门研究如何在有限资源下做出最佳决策的学科,其中运输问题是其中一个重要的应用领域。
下面我将从多个角度给出一些关于运筹学运输问题的生活案例。
1. 物流配送,物流公司面临着如何合理安排货物的运输路线和运输方式的问题。
运筹学可以通过优化算法来确定最佳的配送路线,以最小化成本和时间。
例如,一个快递公司可以利用运筹学方法来确定每辆送货车的最佳路线,以便在最短的时间内将包裹送达目的地。
2. 交通拥堵,城市交通拥堵是一个普遍存在的问题。
运筹学可以帮助城市交通管理部门优化交通流量,减少拥堵。
例如,通过调整交通信号灯的配时,可以最大程度地减少交叉口的等待时间,提高交通效率。
3. 航空航班调度,航空公司需要合理安排航班的起降时间和航线,以最大程度地利用飞机资源并提高乘客的满意度。
运筹学可以通过航班调度算法来帮助航空公司做出最佳决策。
例如,考虑到飞机的燃油消耗、乘客的转机需求和机场的容量限制等因素,可以确定最佳的航班起降时间和航线。
4. 供应链管理,供应链中的物流运输是一个重要的环节。
运筹学可以帮助企业优化供应链中的物流运输安排,以最小化库存成本和运输成本。
例如,通过运筹学方法,可以确定最佳的运输路径和运输模式,以确保产品按时到达目的地,同时最大程度地降低成本。
5. 城市垃圾收集,城市垃圾收集也是一个需要合理安排的运输问题。
通过运筹学方法,可以确定最佳的垃圾收集路线和收集车辆的分配,以最小化运输成本和提高垃圾收集的效率。
以上是一些关于运筹学运输问题的生活案例。
运筹学在各个领域都有广泛的应用,通过优化算法和决策模型,可以帮助解决各种运输问题,提高效率,降低成本。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
注: 本题结果不唯一, 例如还有如下的解.
星期一 星期二 星期三 星期四 星期五 星期六 星期日 200 200 200 200 200 200 200 7 0 6 2 4 0 3 0 1 1 1 1 1 0 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 0 4400 12 15 16 14 16 18 19 12 15 12 14 16 18 19
首先,问题可以自然地按时间分为五个阶段。
第一 年 第二 年 第三 年 第四 年 第五 年
5 6
5 6
5 6
5 6
5 6
7 8
7 8
7 8
7 8
7 8
第一 年
第二 年
2
第三 年
4
第四 年
5
第五 年
8
5
9 7 8
5
8
5
2
5
1
5 6
4
6
2 5
4
6
4 9
8
6
5 6
2
6
8 4
1
7 8
4 7
5
7 8
8 1 9
x3 x4 x5 x6 12 二、 x3 x4 x5 x6 x7 15 三、 x4 x5 x6 x7 x1 12 四、 x5 x6 x7 x1 x2 14 五、 x6 x7 x1 x2 x3 16 六、 x7 x1 x2 x3 x4 18 日、 x1 x2 x3 x4 x5 19
星期一 星期二 星期三 星期四 星期五 星期六 星期日
例(动态投资问题)宏银公司承诺为某建设项目资 金管理。该项目可以在2002年底筹得所需要的贷款, 而工程所需要的资金为: 2003年—100万元,2004年—150万元,2005年— 120万元,2006年—110万元。 为了有效地使用所筹得的资金,在满足每年的资金 需求的情况下,可以将多余的资金用于以下的投资 项目:
(1)于2003年初购买A种债券,期限3年,到期后 可以得到140%的回报;
(2)于2003年初购买B种债券,期限2年,到期可 获125%的回报; (3)于2004年初购买C种债券,期限2年,到期后 可以得到130%的回报; (4)于每年初将任意数额的多余资金存入银行, 期限1年,到期利率为4%
问题是宏银公司应如何选择这些投资项目,使得 2002年底筹集的贷款额最小。
求解结果
星期一 星期二 星期三 星期四 星期五 星期六 星期日 星期一 星期二 星期三 星期四 星期五 星期六 星期日 200 200 200 200 200 200 200 3 4 6 2 4 0 3 0 1 1 1 1 1 0 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 0 4400 16 15 12 14 16 18 19 12 15 12 14 16 18 19
一、 x2
3.变量非负约束:
xi 0且为整数, i 1,2,...,7
目标函数:总费用最小,总费用与使
用的总人数成正比。由于每个人必然在
且仅在某一天开始休息,所以总人数等
于
x
i 1
7
i
模 型
min 200 xi
i 1 7
x2 x3 x4 x5 x6 12 x x x x x 15 3 4 5 6 7 x4 x5 x6 x7 x1 12 x1 x2 x5 x6 x7 14 s.t. x1 x2 x3 x6 x7 16 x1 x2 x3 x4 x7 18 x1 x2 x3 x4 x5 19 x 0且为整数, i 1,2,...,7 i
1万元收益 2万元收益 3万元收益 4万元收益 实际投入 可投入 各项目收益 总收益
A 15 28 40 51 x 1 4 15 60
B 13 29 43 55 y 0 3 0
C 11 30 45 58 z 3 3 45
例 某公司正在研究确定某种新产品今后五年的销售 价格,根据调查,由于各种因素的影响,对该产品 的销售,今后可能有四种价格,按此四种价格销售 每件产品的预期利润见表
利用Excel可以得到最优解为(单位:万元):
x 418.8022 y1 144.2308 y 2 y3 0, , , w1 78.57143 w2 96, w3 0 ,
变量 x y1 y2 目标 1 0 变量的值 418.8022 144.2308 约束 1 -1 约束 1.04 约束 约束
y3 0 0 -1 1.04
w1 0 0 0 78.57143 -1 -1 1.04
w2 0 96 -1 1.25 1.4
w3 0 418.8022 0 100 -1 150 120 1.3 110
100 150 120 110
注:在建立此类型数学模型时若需要决策变量取整数,约束条 件用大于等于号比用等于号要好。此时若采用过于苛刻的约束 条件,很可能就得不到可行解;要获得可行解可能需要约束条 件一定的松弛度。
8
4 3
8
第二阶段的优化
第一 年 第二 年
2 4 2 5 4 7 5 7 5 4
第三 年
4 8 4 9 8 1 9 1 9 8
第四 年
5 2
第五 年
8 1
5 9
9 7 8
5 11 6 13 7 13 8 15
5 6 7 8
5 6 5 7 6
5 6 7 8
8 4
5 6 7 8
6 7 7 8 8 6
2
8 4 1 3 4
5 6 7 8
6 7 7 8 8 6
1
4
6
3
第四阶段的优化
第一 年 第二 年
2 4 2 5 4 7 5 7 5 4
第三 年
4 8 4 9 8 1 9 1 9 8
第四 年
5 2 5 6 5 7 6 7 6 2
第五 年
8 1 8 4 1 3 4 3 4 1
5 9
9 7 8
5 11 6 13 7 13 8 15
记2002年底筹集的贷款总数为x。
记2003,2004,2005存入银行的余款分别为y1, y2, y3。 记购买债券A,B,C的投资额分别为w1, w2, w3。 则该问题的目标函数为:min x 约束条件为各年的所需资金限制 2003:可以使用的资金为x-y1-w1-w2;所需资金100万 元 2004:可以使用的资金为1.04y1-y2-w3;所需资金150 万元 2005:可以使用的资金为1.04y2+1.25w2-y3;所需资 金120万元 2006:可以使用的资金为1.04y3+1.40w1+1.30w3;所 需资金110万元
模 型 假 设
• 每天工作8小时,不考虑夜班的情况; • 每个人的休息时间为连续的两天时间; • 每天安排的人员数不得低于需求量, 但可以超过需求量
问 题 分 析
因素:不可变因素:需求量、休息时间、单位费用; 可变因素:安排的人数、每人开始工作的时间、总 费用; 方案:确定每天工作的人数,由于连续休息2天,当 确定每个人开始休息的时间就等于知道工作的时间, 因而确定每天开始休息的人数就知道每天开始工作 的人数,从而求出每天工作的人数。 变量:第i天开始休息的人数 x i , i 1, 2,...,7 约束条件 : 1.每人休息时间2天。 2. 每天工作人数不低于需求量,第i天工作的人数 就是除了该天在休息的所有人,即除了第i-1天及第i 天开始休息的人以外的所有人,所以有约束:
故所求模型为
min x x y1 w1 w2 100 1.04 y1 y2 w3 150 1.04 y2 1.25w2 y3 120 1.04 y3 1.40w1 1.30w3 110 x, y1 , y2 , y3 , w1 , w2 , w3 0
1
6
1 3 4
4
6
7
3
第三阶段的优化
第一 年 第二 年
2 4 2 5 4 7 5 7 5 4
第三 年
4 8 4 9 8 1 9 1 9 8
第四 年
5 2 5 6 5 7 6 7 6 2
第五 年
8 1
5 9
9 7 8
5 11 6 13 7 13 8 15
5 17 6 21 7 24 8 16
5 6 7 8
在下面的计算中假设各阶段投资的项目依次是A、B、 C。
k=4,f4(x4)=0 k=3,0≤d3≤x3,x4=x3-d3
k=2,0≤d2≤x2,x3=x2-d2
k=1,0≤d1≤x1,x2=x1-d1
最优解为
x1=4, d1*=1, x2=x1-d1=3, d2*=0, x3=x2-d2*=3, d3=3, x4=x3-d3=0,
9
7 8
5 7 6
6
7 8
1 3 4
4
7 8
65 717来自3第一阶段的优化
第一 年 第二 年
2
第三 年
4
第四 年
5
第五 年
8
5 9
9 7 8
5
8
5
2
5
1
5 6 7
4
2 5 4 7 5 7 5 4
6 7 7 8
6 7
4 9 8 1
8
6 7
5 6
2
6 7
8 4
