力学中的计算方法(方程求根)
数值计算方法方程求根

数值计算⽅法⽅程求根数值计算⽅法实验报告实验内容:⽅程求根实验室:专业班级:学号:姓名:2.⽤MATBAB软件,⽤⼆分法求⽅程f(x)=x^3+4*x^2-10=0在区间[1,2]内根的近似值,为使误差不超过10^-5时所需要的⼆分次数。
function bisection_time(tolerance)a=1;b=2;k=0;while(abs(b-a)>tolerance)c=(a+b)/2;fa=a^3+4*a^2-10;fb=b^3+4*b^2-10;fc=c^3+4*c^2-10;if((fa==0)|(fc==0))disp(k);elseif(fa*fc<0)b=c;k=k+1;elseif(fc*fb<0)a=c;k=k+1;elseif(fb==0)disp(k);endendsoluntion=(a+b)/2;disp(soluntion);disp(k);运⾏结果1.36523176.取x0=1.5,⽤⽜顿迭代法求f(x)=x^3+4*x^2-10=0的跟的近似值function new(tolerance)x0=1.5;k=0;a=x0^3+4*x0^2-10;b=3*x0^2+8*x0;x1=x0-a/b;while(abs(x0-x1)>tolerance)x0=x1;k=k+1;a=x0^3+4*x0^2-10;b=3*x0^2+8*x0;x1=x0-a/b;enddisp(x1);disp(k);运⾏结果1.3652338.弦割法求⽅程f(x)=x^3-3*x^2-x+9=0在区间[-2,-1]内的⼀个实根近似值Xk,使|f(x) |<=10^-5. function xuange(k)x0=-2;x1=-1;t=0;a=x1^3-3*x1^2-x1+9;b=x0^3-3*x0^2-x0+9;x2=x1-a*(x1-x0)/(a-b);while(abs(x1-x0)>k)x0=x1;x1=x2;a=x1^3-3*x1^2-x1+9;b=x0^3-3*x0^2-x0+9;x2=x1-a*(x1-x0)/(a-b);t=t+1;enddisp(x1);disp(t)运⾏结果-1.52510269.⽤艾特肯算法求⽅程f (x )=x^3+4*x^2+10=0在区间[1,2]内的根的近似值(取X0=1.5,g (x )=410x ,精确到|Xk+1-Xk|<=10^-5,并与第2,3,6题的相应结果进⾏⽐较。
计算方法 4方程求根的迭代法

是所求方程(5―1)的根x。
我们把每次二分后的有根区间(ak,bk)的中点
1 xk ( ak bk ) 2
作为所求根x的近似值,这样获得一个近似根的序列
x0,x1,x2,…,xk,… 该序列必以根x为极限,即
lim xk x
k
1 x xk (bk ak ) bk 1 ak 1 2
表 5―1
§2
迭代法的基本思想是 : 首先将方程 (5―1) 改写成某 种等价形式,由等价形式构造相应的迭代公式,然后选取 方程的某个初始近似根x0,代入迭代公式反复校正根的 近似值,直到满足精度要求为止。迭代法是一种数值计 算中重要的逐次逼近方法。 例如,求方程 x3-x-1=0
在x=1.5附近的一个根(用六位有效数字计算)。
为下列等价形式 x=g(x) 然后按(5―7)构造迭代公式 (5―7)
xk 1 g ( xk ), k 0,1,2,
从给定的初始近似根 x0 出发 , 按迭代公式 (5―8) 可
以得到一个数列 x0,x1,x2,…,xk,… 若这个数列{xk}有极限,则迭代公式(5―8)是收敛 的。此时数列的极限
x y g(x ) g( y ) q x y
* * * * *
*
因为q<1,所以上式矛盾,故必有
x y
亦即方程在(a,b)内有唯一的根。
再考虑迭代公式 x k+1=g(xk) , 由李普希茨条件 k=0,1,2,…
xk 1 x g ( xk ) g ( x ) qk x0 x
收敛。
②对于收敛的迭代过程,误差估计式(5―11)说明迭代值的 偏差|xk-xk-1|相当小,就能保证迭代误差|x-xk|足够小。
方程求根(计算方法)

高斯像(2)
高斯像(3)
高斯像(4)
第二章 方程求根
§2.2 二分法
§2.2 二分法
❖ 定义:如果函数f(x)在区间[a,b]上连 续,且f(a)f(b)<0,则方程在区间[a,b]上 一定有实根,[a,b]叫方程的有根区间。
【注记】f(a)f(b)<0只保证有实根, 但并不保证根是 唯一, 即不保证是单根, 也不排斥f(a)f(b)>0时在[a,b] 上有根的情形。即,f(a)f(b)<0对于在[a,b]上有实根 是充分的, 但不必要;f(a)f(b)<0对于在[a,b]上有唯 一单实根不充分也不必要。如图所示:
§2.1 问题的提出
• 有多种数值算法可以求解非线性方程, 我们在本章将学习其中得几种,它们是:
✓ 二分法(bisection method) ✓迭代法(iteration method) ✓牛顿法(Newton method) ✓牛顿下山法(Newton downhill method)。
牛顿(1)
§2.1 问题的提出
➢ 扫描流程
§2.1 问题的提出
【历史注记】人们很早就探索了高次方程的数值解 的求法。巴比伦泥板中有平方表和立方表,利用它 们可以解某些特殊的二次和三次方程。中国古人相 当系统地解决了求高次方程数值解的问题,《九章 算术》以算法形式给出了二次方程及正系数三次方 程正根的具体计算程序;7世纪王孝通也给出了求 三次方程正根的数值解法;11世纪贾宪在《黄帝九 章算法细草》中创“开方作法本源图”,用“立成 释锁法”解三次和三次以上高次方程, 同时他又提 出一种更为简便的“增乘开方法”;13世纪秦九韶 在《数书九章》中的“正负开方术”最后完成,提 供了一个用算筹布列解任何次数字方程的可行算法。
计算方法实验:方程求根

实验一 方程求根一、实验目的用不同方法求任意实函数方程f (x )=0在自变量区间[a ,b]内或某一点附近的实根,并比较方法的优劣性。
二、实验方法 (1)二分法对方程f (x )=0在[a ,b]内求根。
将所给区间二等分,在二分点x=(b-a)/2处判断是否f (x )=0。
若是,则有根x=(b-a)/2;否则继续判断是否f(a)·f(b)<0,若是,则令b=x ,否则令a=x 。
重复此过程,直至求出方程f(x)=0在[a ,b]内的近似根为止。
(2)迭代法将方程f (x )=0等价变换为x=φ(x )的形式并建立相应的近似根为止。
(3)牛顿法设已知方程f (x )=0的一个近似根x 0,则函数f (x )在点x 0附近可用一阶泰勒多项式p 1(x )=f (x 0)+f ’(x 0)(x-x 0)来近似,因此方程f (x )=0可近似表示为f (x 0)+f ’(x 0)(x-x 0)=0。
设f ’(x 0)≠0,则 x=x 0-f (x 0)/’f (x 0)取x 作为原方程新的近似根x 1,然后再将x 1作为x 0代入上式。
迭代公式为 x k+1=x k -f (x k )/f ’(x k )三、实验内容1)在区间[0,1]内用二分法求方程e x +10x-2=0的近似根,要求误差不超过0.5×10-3。
2)取初值x0=0,用迭代公式x k+1=(2-e x k )/10,(k=0,1,2,…)求方程e x + 10x-2=0的近似根,要求误差不超过0.5×10-3。
3)取初值x 0=0用牛顿迭代法求方程e x + 10x-2=0的近似根,要求误差不超过0.5×10-3。
四、实验程序 (1)二分法(2)迭代法(3)牛顿法五、实验结果(仅供参考)(1)x11=0.09033 (2)x5=0.09052 (3)x2=0.09052六、结果分析由上面的对二分法、迭代法、牛顿法三种方法的三次实验结果,我们可以得出这样的结论:二分法要循环k=10次,迭代法要迭代k=4次,牛顿法要迭代k=2次才能达到精度为0.5×10-3的要求,而且方程e x+10x-2=0的精确解经计算,为0.0905250,由此可知,牛顿法和迭代法的精确度要优越于二分法。
计算方法-方程求根实验
实验四 方程求根实验一. 实验目的(1)深入理解方程求根的迭代法的设计思想,学会利用校正技术和松弛技术解决某些实际的非线性方程问题,比较这些方法解题的不同之处。
(2)熟悉Matlab 编程环境,利用Matlab 解决具体的方程求根问题。
二. 实验要求用Matlab 软件实现根的二分搜索、迭代法、Newton 法、快速弦截法和弦截法,并用实例在计算机上计算。
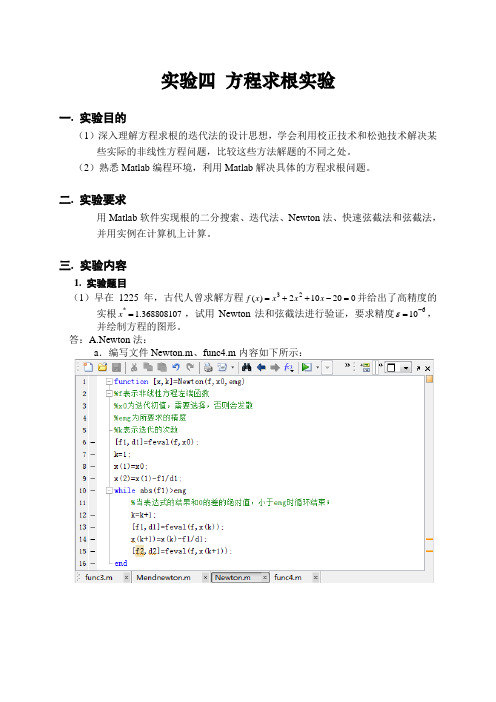
三. 实验内容1. 实验题目(1)早在1225年,古代人曾求解方程020102)(23=-++=x x x x f 并给出了高精度的实根368808107.1*=x ,试用Newton 法和弦截法进行验证,要求精度610-=ε,并绘制方程的图形。
答:A.Newton 法:a .编写文件Newton.m 、func4.m 内容如下所示:b.运行,如下所示A为矩阵,由上面可知,对于初值为5,运行7次即可得到所需的精度,验证结果为古人给出的解释正确的;c.作图,编写下面的文件photo1.m.然后运行即可:注意下面中的x矩阵即为刚才计算出来的x系列,k为迭代的次数:a.编写文件Chord.m内容如下所示:b.运行结果如下所示:由上表可知,在精度为10^-6时有7位有效数字,古人的结果还是正确的c.作图,在上面运行后,即运行newton法时写的photo1.m文件即可出现图像:可以看到图中两条曲线基本重合; (2)取5.00=x ,用迭代法求方程x e x -=的根,然后用Aitken 方法加速,要求精度为结果有4为有效数字。
答:a. 编写文件func7.m 和Aiken.m ,内容如下所示:b .运行:具有四位有效数字 (3)用快速弦截法求解方程01)(=-=x xe x f ,要求精度为610-=ε,取6.05.010==x x ,作为开始值,并绘制1)(-=x xe x f 的图形。
答:对照可知,书本后面的程序已经正确,运行即可:下面为快速弦截法的主程序文件:函数文件如下:运行如下:作图,编写下面的文件:运行该文件就可以y=x*exp(x)-1函数和插值函数的图:可以看到两条直线基本重合在一起了,扩大图片可以看到两条直线是不重合的:2. 设计思想要求针对上述题目,详细分析每种算法的设计思想。
计算方法2_方程求根

习题2
2.1 试构造迭代收敛的公式求解下列方程:
(1)4
sin cos x x x +=
; (2)x x 24-=。
2.2 方程0123=--x x 在5.1=x 附近有根,把方程写成三种不同的等价形式: (1)211x x +=,对应迭代公式2111k
k x x +=+; (2)231x x +=,对应迭代公式3211k k x x +=+;
(3)112-=x x ,对应迭代公式1
11-=+k k x x 。
判断以上三种迭代公式在5.10=x 的收敛性,选一种收敛公式求出5.10=x 附近的根到4位有效数字。
2.3 已知)(x x ϕ=在[a,b]内有一根*x ,)(x ϕ在[a,b]上一阶可微,且13)(],,[<-'∈∀x b a x ϕ,试构造一个局部收敛于*
x 的迭代公式。
2.4 设)(x ϕ在方程)(x x ϕ=根*x 的邻近有连续的一阶导数,且1)(*<'x ϕ,证明迭代公式)(1k k x x ϕ=+具有局部收敛性。
2.4 )5()(2-+=x x x αϕ,要使迭代法)(1k k x x ϕ=+局部收敛到5*=x ,
则α的取值范围是______________。
2.5 用牛顿法求方程0742)(2
3=---=x x x x f 在[3,4]中的根的近似值(精确到小数点后两位)。
2.6 试证用牛顿法求方程0)3()2(2=+-x x 在[1,3]内的根2*=x 是线性收敛的。
2.7 应用牛顿法于方程03
=-a x , 导出求立方根3a 的迭代公式,并讨论其收敛性。
方程求根

迭代法—算例分析2
例如:求方程 f ( x) x3 x 1 0 在x0 1.5 附近的根 x*
22
§2.2
迭代法—算例分析2
例如:求方程 f ( x) x3 x 1 0 在x0 1.5 附近的根 x*
3 解:将方程改写为 xk 1 x , k 1
由此建立迭代公式: xk 1 3 xk 1 (k 0,1, 2, ) 计算结果如下表
f (1)<0, f (2)>0 记 I0=[1,2] , x0 =(1+2)/2=1.5
因为 f (x0) f (1)>0 得 I1=[1.5, 2] , x1 =(1.5+2)/2=1.75
f (x1) f (1.5)<0 得 …….
I2=[1.5, 1.75] , x2 =(1.5+1.75)/2=1.625
if B A 0 where else x1 2 x2 2 x3 2 where
( B 2 A3 | B |)1 / 3 ;
A cos( a , 3 3 2 a A cos( ) , 3 3 4 a A cos( ) , 3 3 arccos( B / A3 / 2 ) ; )
二分法
求 f (x) = 0 的根
原理:若 f C[a, b],且 f (a) ·f (b) < 0,则 f 在 (a, b) 上必有一根。
y
f (x)
a
x*
b
x
称[a, b]为方程的有根区间。
7
§2.1
二分法—算法构造
a x a1
b2 x* x
b
给定有根区间 [a, b] ( f(a) ·f(b) < 0) 和 精度 或 1. 令 x = (a+b)/2 2. 如果 b – a < 或 f (x) < , 停机,输出 x 3. 如果 f (a) f (x) < 0 , 则令 b = x,否则令 a = x, 返回第1步 用二分法求根,通常先给出 f (x) 草图以确定根的大概位置。
化工计算方法-2-方程求根

an2 解: 范德华方程 p 2 (V nb) nRT V • 将上式改写成为迭代公式并代入数据
V nRT 49.2948 nb 0.0742 2 2 2 p an / V 9.33 16.68 / V
2 0.0821 300.2 5.2833 L 9.33
故f(x)在点x0附近可近似为 f ( x) f ( x0 ) f ( x0 )( x x0 ) 0 如令 f ( x 0 ) 0
f ( x0 ) x x0 f ( x0 )
15
•例题2-5 用迭代法求以下方程在1.5 附近的 根,要求精度10-5。
f ( x) x 3 x 1 0
解:选择迭代格式 (1)
x
3
x 1
1. 直接迭代法计算步骤 2. (1)给定初值x0、收敛精度和最大迭代次数,令计数器i=0 3. (2)判断i 是否大于n,如果是,输出信息,中止计算,否 则令i=i+1; 4. (3) 用迭代格式进行迭代计算; 5. (4)判断迭代结果是否满足收敛判据 ,如果满足,中止计 算并输出结果,否则返回到步骤(2)
a
x1
x2
x3
x4
x5
x b
• 将[a,b]分割成小区间,保证每一区间只有一个实根
• 从a开始搜索根。先检查小区间内是否有根,无根转向下一 区间;有根则用二分法求出 • 依次对每一区间进行搜索和检查,直至求出全部实根。 4
2.1.2 应用举例 例 题2-1 求方程 f ( x) x 3 x 1 0 在区间(1,1.5)内的实 根,要求精度为10-5 。
2.2 直接迭代法(简单迭代)
f ( x) 0
y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ˆK x
Fixed-Point Iteration ( x K 1 x K ) 2 xK x K 2 x K 1 x K 2
y=x
x0 , x1 g( x0 ), x2 g( x1 ), ˆ 0 , x3 g( x2 ), x ˆ 1 , x4 g( x3 ), x ... ...
0 f ( x*) f ( x0 ) f ( x0 )( x * x0 ) y
x* x0
f ( xk ) x k 1 x k f ( x 线性 /* linear */ k)
f ( x0 ) f ( x0 )
x*
x
x0
只要 f C1,每一步迭代都有 xk x * , f ’( xk ) 0, 而且 lim k 则 x*就是 f 的根。
1 | x k 1 x k | | x * xk | 1 L
L | x1 x0 | | x * xk | 1 L
k
( k = 1, 2, … )
且存在极限
lim
k
x * x k 1 g x * x * xk
Fixed-Point Iteration
1 | x k 1 x k | ? ④ | x * xk | 1 L | x k 1 x k | | x * x k | | x * x k 1 | | x * x k | L | x * x k | | x k 1 x k | 来 Lk 可用 | x1 x0 | ? ⑤ | x * xk | 1 L 控制收敛精度
Bisection Method
When to stop?
a x a1 x*
x2 b
b
x k 1 x k ε1
或
f ( x ) ε2
不能保证 x 的精 度
2
x* x
Bisection Method
误差 分析: ab ba x |x x*| 第1步产生的 1 2 有误差 1 2
ˆ x
( x1 x 0 ) 2 ˆ x0 x x 0 2 x1 x 2
牛顿法 /* Newton - Raphson Method */
原理:将非线性方程线性化 —— Taylor 展开 /* Taylor’s expansion */ 取 x0 x*,将 f (x)在 x0 做一阶Taylor展开: f ( ) f ( x ) f ( x0 ) f ( x0 )( x x0 ) ( x x0 )2, 在 x0 和 x 之间。 2! 将 (x* x0)2 看成高阶小量,则有:
证明:① g(x) 在[a, b]上存在不动点?
令 f ( x ) g( x ) x
f ( x ) 有根
a g( x ) b
f ( a ) g ( a ) a 0 , f ( b ) g( b) b 0
② 不动点唯一?
~ g( x ~ ),则 反证:若不然,设还有 x ~ ) g(ξ ) ( x * x ~ ), 在 x * 和 x ~ 之间。 ~ g( x*) g( x x* x ~ )(1 g(ξ )) 0 ~ ( x* x 而 | g(ξ ) | 1 x* x
Bisection Method
例1:求方程 f(x)=x3-x-1=0 在区间(1,1.5)内的 根。要求误差不超过0.005
解 (1)这里a=1,b=1.5, ∵ f(1)*f(1.5)<0 ∴区间(1,1.5)内必有根存在。 (2) b k a
2 ε 0.005
lnb a ln ε k
3 f ( x ) x 3 x 1 0 在 (1, 2) 的实根。 例:求
如果用
x
| g( x ) | | x 2 | 1 K 现令 ( x ) (1 K ) x Kg( x ) (1 K ) x ( x 3 1) 3 2 2 K 0 希望 | ( x ) | | 1 K Kx | 1 ,即 2
Fixed-Point Iteration
改进、加速收敛 /* accelerating convergence */
待定参数法: 若 | g’(x) | 1,则将 x = g(x) 等价地改造为
x x Kx Kg( x ) (1 K ) x Kg( x ) ( x ) 求K,使得 | ( x ) | | 1 K Kg( x ) | 1
Newton - Raphson Method
证明:Newton’s Method 事实上是一种特殊的不动点迭代
其中 g( x ) x
g ( x*)
f ( x) ,则 f ( x )
f ( x*) f ( x*) 0 1 收敛 2 f ( x*)
由 Taylor 展开: 在单根 /*simple root */ f ( k ) 0 f ( x*) f ( xk ) f ( xk )( x * xk ) ( x * xk )2 附近收敛快
例:用切线法求方程的根。 xex-1=0 x
xk e 解: xk 1 xk 1 x k
k
取x0=0.5 迭代结果如表所示
| xk 1 xk | 收敛条件:
Newton - Raphson Method
定理 (收敛的充分条件)设 f C2[a, b],若
(1) f (a) f (b) < 0;(2) 在整个[a, b]上 f ”不变号且 f ’(x) 0;
P(x1, x2)
ˆ K 比x K 收敛得nsen 加速:
x0 , x1 g( x0 ), x2 g( x1 ), ˆ 0 , x1 g( x ˆ 0 ), x2 g( x1 ), x ˆ ˆ , ... ... x
0
x x1 x* x2 x0
1 3 ( x 1) g( x ) 进行迭代,则在(1, 3
2)中有
在 (1, 2) 上可取任意 2 K 0 ,例如K = 0.5,则对
x 1
应 x 3 x 1 ( x 3 1) 即产生收敛序列。
2 6
3
埃特金(Aitken) 加速: 一般地:
y y = g(x)
第 k 步产生的 xk 有误差 |xk x*|
ba 2k
对于给定的精度 ,可估计二分法所需的步数 k :
ba ε k 2 k
lnb a ln ε
ln 2
①简单; ② 对f (x) 要求不高(只要连续即可) .
①无法直接求复根及偶重根 ② 收敛慢
注:用二分法求根,最好先给出 f (x) 草 图以确定根的大概位置。 或用搜索程序,将[a, b]分为若干小 区间,对每一个满足 f (ak)· f (bk) < 0 的区 间调用二分法程序,可找出区间[a, b]内 的多个根,且不必要求 f (a)· f (b ) < 0 。
方程求根
非线性方程求根
/* Solutions of Nonlinear Equations */
求 f (x) = 0 的根 二分法 /* Bisection Method */
原理(介值定理): 若 f (x)C[a, b],且 f (a) · f (b) < 0,则 f 在 (a, b) 上 必有一根。
| x k 1 x k | | g ( x k ) g ( x k 1 ) | | g ( ξ k )( x k x k 1 ) |
k L | x k xL | ...... L | x1 x0 | k 1 越 小 收敛越快
⑥ lim
k
lim
③ 当k 时, xk 收敛到 x* ?
| x * xk | | g( x*) g( xk 1 ) | | g(ξ k 1 ) | | x * xk 1 |
L | x * xk 1 | ...... Lk | x * x0 | 0
Fixed-Point Iteration
basically are OhSo yeah? Whowe tells done! can’t believe you that I the method it’s so simple! is convergent? What’s the problem?
Fixed-Point Iteration y p1 p0 y=x y=g(x) y p0 y=x
k
x * x k 1 g ( ξ k )( x * x k ) lim g ( x*) k x * xk x * xk
x * x k 1 g x * ? x * xk
注:定理条件非必要条件,可将[a, b]缩小,定义局部收 敛性:若在 x* 的某 领域 B = { x | | x x* | } 有 gC1[a, b] 且 | g’(x*) | < 1,则由x0B 开始的迭代 收敛。即调整初值可得到收敛的结果。
x0 y x1 x* y=x x x0 y y=g(x) p0 x* y=g(x)
p1 y=g(x) x1 y=x x
p0 p1 x1 x0 x*
x x0 x*
p1
x
x1
Fixed-Point Iteration
定理
考虑方程 x = g(x), g(x)C[a, b], 若
( I ) 当 x[a, b] 时, g(x)[a, b]; ( II ) 0 L < 1 使得 | g’(x) | L < 1 对 x[a, b] 成立。 则任取 x0[a, b],由 xk+1 = g(xk) 得到的序列 x k k 0 收敛 于g(x) 在[a, b]上的唯一不动点。并且有误差估计式:
