投影面平行线
2-2 点、线、面的投影特性

2-2 点、线、面的投影特性一、点的投影1、点的三面投影点是组成物体最基本的几何元素。
如图2-9所示,在三投影面体系中,由空间点A(x,y,z)分别向三投影面作正投影,得其三面投影a(x,y)、a′(x,z)、a″(y,z),即过点A分别作三投影面的垂线,其垂足即为点A的三面投影;展开H面和W面,得到点A的三视图:a 、a′长对正,a′、a″高平齐,a 、a″宽相等,如图2-10所示。
图2-9 点的三面投影图2-10 点的三视图例1 :已知空间点B的两面投影b ,b′,如图2-11所示,求其第三面投影b″。
分析:空间点B的三面投影b 、b′、b″符合“长对正,高平齐,宽相等”的投影规律。
作图: b′与b″高平齐,b与b″宽相等,则其交点即为b″。
图2-11 求点的第三面投影图2-12 求点的三面投影例2 :已知空间点D(5,4,3),如图2-12所示,求其三面投影。
分析:空间点D的三面投影分别为d(x,y)、d′(x,z)、d″(y,z),且符合“长对正,高平齐,宽相等”的投影规律。
作图:分别在三投影轴上取x1=5,y1=4,z1=3,按“长对正,高平齐,宽相等”的投影规律分别作直线段,交点即为空间点D的三面投影(d 、d′、d″)。
2、两点的相对位置空间两点的相对位置是指空间两点间前后、左右、上下的位置关系。
两点在空间的相对位置可以根据两点的坐标值来判定,如图2-13所示。
X坐标确定两点的左右位置关系。
X坐标值大的点在左;Y坐标确定两点的前后位置关系。
Y坐标值大的点在前;Z坐标确定两点的上下位置关系。
Z坐标值大的点在上。
图2-13 两点的相对位置故A点在B点的右,后,上方,即B点在A点的左,前,下方。
3、重影点及其可见性判断若空间两点在某一投影面上的投影重合,则称这两点为该投影面的重影点。
此时,这两点位于同一投射线上,且有两个坐标的值分别相等,不等值的坐标之大小可以确定重影点的可见性,即X、Y、Z坐标值大的点分别位于左方、前方、上方,为可见点,如图2-14所示。
第二章 直线的投影
2.已知直线 AB 平行直线 CD,试完成直线
例:已知直线AB平行直线CD,试完成直线AB
AB 和 CD 的三面投影。 和CD的三面投影。
题解: c′〝
c
NEW
c
c
b
点C的投影在直线的同面投影上,并 符合点的投影规律。
二、D点不在 直线AB上。
a A d b a b
NEW
a b
D
d
B
d
例:判断点M是否在直线CD 上 解法1:
NEW
点M的投影不符合点在直线上的投影规律, 故M点不在直线CD上。
例:判断点M是否在直线CD 上
直线 水 平 线
直观图
投影图
投影特征 1、水平投影ab 反映实长 及直线的倾角β 和γ 。 2、正面投影a b //o x轴, 侧面投影a"b "//oy w 轴,且 均短于实长。 1、正面投影e f 反映实长 及直线的倾角α 和γ 。 2、水平投影ef //o x轴,侧 面投影e"f "//oz 轴,且均 短于实长。 1、侧面投影e"f" 反映实 长及直线的倾角α 和β 。 2、水平投影e f//oy H 轴,正 面投影e f //oz 轴,且均 短于实长。
• 1. 直线上的点,其投影必在该直线的同面投影上。 • 2. 直线上的点,分割线段之比,在投影后保持不变。
三.直线上的点 (一) 直线上点的投影特性
点C在直线上 AB上
1.直线上的点,
其投影必在该 直线的同面投 影上。
2.直线上的点,
投影的基本知识

X
Yw
b a
(2)投影面垂直线的投影
投影面垂直线在空间与一个投影面垂直,与另 两个投影面平行。 投影面垂直线分为:铅垂线、正垂线、侧垂线 三种。 投影面垂直线的投影特点为:一个投影积聚为 点,另两个投影垂直于相应的投影轴,且反应 实长。
投影面垂直线的投影图
(3)投影面平行线的投影
影子与投影区别
投影的分类
根据投射中心与投影面位置的不同,投影可分 为两大类:中心投影和平行投影。 中心投影:投射线都是由投射中心发出的,这 种投影方法称为中心投影法。由此得到的投影 图称为中心投影图。 平行投影:投射中心距投影面为无限远时,所 有投射线成为平行线,这种投影方法称为平行 投影法,由此得到的投影图称为平行投影图。
(1)两直线平行
投影特点:两直线在空中平行,则其各同面投 影平行。
(2)两直线相交
投影特点:两直线在空间相交,则其各同面投 影必相交,且交点符合点的投影规律
求相交两直线
(3)两直线交叉
投影特点:两直线在空间既不平行也不相交。
两直线交叉
平面的投影
用几何元素表示平面
各种位置平面的投影
如图
正投影特性
类似性:当直线或平面与投影面倾斜时,其 投影为缩短的线段或缩小的平面。
A B C b aA bA c A BA
a H
H`
正投影特性
全等性:当直线或平面与投影面平行时,其投影 反映实长或实形。
A B
C
a
b
a
b
H
H
c
正投影特性
积聚性:当直线或平面与投影面垂直时,其 投影积聚成一点或一直线。
第二章 投影的基本知识
第二篇投影制图第二章投影的基本知识【学习目的】掌握正投影的基本原理,掌握三视图的形成及其投影规律,掌握点、线、面的投影特性。
【学习要点】投影的基本特性;物体的三视图的绘制;点、线、面的投影特性。
第一节投影方法一、投影的概念(一)投影法的概念在日常生活中,我们看到在太阳光或灯光照射物体时,在地面或墙壁上出现物体的影子,这就是一种投影现象。
投影法与自然投影现象类似,就是投影线通过物体向选定的投影面投射,并在该面上得到图形的方法,用投影法得到的图形称作投影图或投影,如图2-1所示。
图2-1 投影的产生产生投影时必须具备的三个基本条件是投影线、被投影的物体和投影面。
需要注意的是,生活中的影子和工程制图中的投影是有区别的,投影必须将物体的各个组成部分的轮廓全部表示出来,而影子只能表达物体的整体轮廓,并且内部为一个整体如图2-2所示。
(a)影子 (b)投影图2-2 投影与影子的区别二、 投影法分类根据投影线与投影面的相对位置的不同,投影法分为两种。
(一) 中心投影法投影线从一点出发,经过空间物体,在投影面上得到投影的方法(投影中心位于有限远处),如图2-3所示。
图2-3 中心投影法缺点:中心投影不能真实地反映物体的大小和形状,不适合用于绘制水利工程图样。
优点:中心投影法绘制的直观图立体感较强,适用于绘制水利工程建筑物的透视图。
(二) 平行投影法投影线相互平行经过空间物体,在投影面上得到投影的方法(投影中心位于无限远处),称为平行投影法。
平行投影法根据投影线与投影面的角度不同,又分为正投影法和斜投影法,如图2-4所示。
(a )为斜投影法,(b )为正投影法。
(b)(a)图2-4 平行投影法优点:正投影法能够表达物体的真实形状和大小,作图方法也较简单,所以广泛用于绘制工程图样。
正投影法斜投影法在以后的章节中,我们所讲述的投影都是指的正投影。
三、投影的特性(一)真实性平行于投影面的直线段或平面图形,在该投影面上的投影反映了该直线段或者平面图形的实长或实形,这种投影特性称为真实性,如图2-5所示。
画法几何制图—平面投影及相对位置

② 若两投影面垂直面相互平行,
则它们具有积聚性的那组投影
必相互平行。
a
b c d
c d
b
b d
a c
e
d
b
ac
e
e f
f e
f h h
f
//
三峡大学
44
2 . 判 例别 判下 断列 下平 列面 两与 平平 面 面是 是否 否平 平行 行。
a )
b ) 举例
平行
不平行
三峡大学
45
二、相交问题(重点与难点)
三峡大学
22
例2:在平面ABC内作一条水平线,使其到H面 的距离为10mm。
a
10
m
n
c
b
b
c
n m
a
唯一解!
三峡大学
23
⒉ 平面上取点
若点在平面内的任一直线上,则此点一定在该平面上。 即:点在线上,则点在面上。
三峡大学
24
面上取点的方法:
首先面上取线
先找出过此点而又在平面内的一条直线作为辅助 线,然后再在该直线上确定点的位置。
铅垂面(⊥H) 正垂面(⊥V) 侧垂面(⊥W)
水平面(//H) 正平面(//V) 侧平面(//W)
与三个投影面都倾斜 一般位置平面
三峡大学
9
1) 投影面垂直面的投影
铅垂面
V PB
c
a
a
W
b
A
a b
H
C PH c
a c
b 投影特性:
1. abc积聚为一条线, 与OX、 OYH的夹角反映、角; 2 .abc、 abc为ABC的类似形;
1’ b’
投影面平行线设计教学课件

直线投影-投影面平行线
直线投影-投影面平行线
本节关键词: 一平行 二倾斜 三条线 四实长
直线投影-投影面平行线
本节关键词:
一平行(平行一个投影面) 二倾斜(倾斜另外两个面) 三条线(水平线、正平线、侧平线) 四实长(在所平行的投影面反映实长)
直线投影-投影面平行线
随堂练习: 投影面平行线有什么投影特点?
教材:《水利工程制图》
课题:投影面平行线
直线投影-投影面平行线
概念解读: 平行于一个投影面,同时倾斜于其他
两个投影面的直线称投影面平行线
直线投-投影面平行线
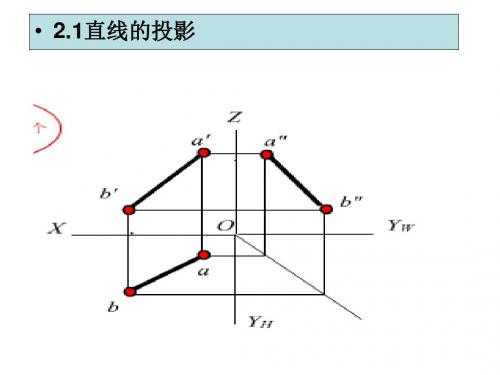
投影面平行线:平行于一个投影面,同时倾斜于其他两个投影面的直 线称投影面平行线。图3-12中AB∥V面,倾斜于(∠)H面及面,它 的正面投影a″b″反映实长及其于H、W面的倾角α 、γ (直线与其相应 投影的夹角即直线对相应投影面的倾角,它于H、V、W面的倾角分 别用α βγ 表示)。因Ya=Yb,所以ab∥OX,a″b″∥OZ。
直线投影-投影面平行线
本节重点部分 投影面平行线共有三种投影面平行线: 平行于水平投影面(H面)的直线:水平线 平行于正立投影面(V面)的直线:正平线 平行于侧立投影面(W面)的直线:侧平线
直线投影-投影面平行线
水平线:H(俯视)
直线投影-投影面平行线
正平线:V(主视)
直线投影-投影面平行线
知识点拓宽: ( )一个投影面的平面称为投影面平行面. A.平行于 B.垂直于 C.倾斜于 D.相交于
谢谢各位! 敬请批评指正!
各种位置直线的投影特性
各种位置直线的投影特性按照直线对三个投影面的相对位置,可以把直线分为三类:一般位置直线、投影面平行线、投影面垂直线。
后两类直线又称为特殊位置直线。
1.一般位置直线—与三个投影面都倾斜的直线一般位置直线的投影特性如下(图3-10):1)三面投影都倾斜于投影轴。
2)投影长度均比实长短,且不能反映直线与投影面倾角的真实大小。
直线对H、V、W的倾角分别用α、β、γ表示。
投影面平行线——平行于一个投影面,倾斜于另外两个投影面的直线(1)投影面平行线又可分为三种:平行于V面的直线叫正平线;平行于H面的直线叫水平线;平行于W面的直线叫侧平线。
图3-11 正平线的投影特性(2)正平线的投影特性(图3-11):1)直线平行于V面,则V面投影与直线本身平行且等长,a'b'=AB;2)正平线上各点到V面的距离即Y坐标都相等,则a b∥OX, a"b"∥OZ。
3)AB与H面的倾角为α,由于AB平行V面,所以AB与V面的倾角为0。
又因为AB ∥a'b',a b∥OX轴,所以,a'b'与OX轴的夹角为α,同理a'b'与OZ轴的夹角即为AB与W面的倾角γ。
表3-1为投影面平行线的投影特性。
表3-1 投影面平行线的投影特性名称轴测图投影图投影特性正平线(1)a'b'=AB, 反映α、γ角(2)a b//OX轴, a"b"//OZ轴水平线(1) cd=CD ,反映β、γ角(2)c'd'//OX轴, c"d"//O YW轴侧平线(1) e"f"=EF, 反映α、β角(2)e'f'//OZ轴,ef//O YH轴投影面平行线的投影特性:1.直线在与其平行的投影面上的投影,反映该线段的实长和与其他两个投影面的倾角2.直线在其他两个投影面上的投影分别平行于相应的投影轴,且比线段的实长短投影面垂直线——垂直于一个投影面,平行于另外两个投影面的直线1)投影面垂直线又可分为三种:垂直于V面的直线叫正垂线;垂直于H面的直线叫铅垂线;垂直于W面的直线叫侧垂线。
第三讲平面和直线投影特性
平行于侧面的直线称为侧平线
二、直线的投影分析
3.投影面垂直线 投影特性: (1)在所垂直的 投影面上投影积 聚为一点。 (2)其他两个投 影面上的投影反 映实长,且分别 垂直于相应的投 影轴。
垂直于水平面的直线称为铅垂线
二、直线的投影分析
3.投影面垂直线 投影特性: (1)在所垂直的 投影面上投影积 聚为一点。 (2)其他两个投 影面上的投影反 映实长,且分别 垂直于相应的投 影轴。
一、正投影的特性
二、点、线、面的投影特性
一、正投影法的基本特性
1.真实性:当直线、曲线或平面平行于投影面时, 直线或曲线反映实长,平面反映真实形状。
2.积聚性: 当直线、曲面或平面垂直于投影面时, 直线积聚成一点,曲面或平面积聚成曲线或直线。
3.类似性:当直线、曲线或平面倾斜于投影面时, 直线或曲线投影仍为直线或曲线,但小于实长。平面应 小于真实投影大小,与原平面外形类似。
垂直于正面的平面称为正垂面
三、平面的投影分析
3.投影面垂直面 投影特性: (1)在所垂直的投 影面内投影积聚 为一段斜线。 (2)其他两个投影 面上的投影均为 缩小的类似形。
垂直于侧面的平面称为侧垂面
投影举例: 根据物体的 立体图,画出其 三视图。
平行于水平面的平面称为水平面
三、平面的投影分析
2.投影面平行面 投影特性: (1)在所平行 的投影面上投 影反映实形。 (2)其他两个 投影面上的投 影积聚为直线, 且分别平行于 相应的投影轴。
平行于正面的平面称为正平面
三、平面的投影分析
2.投影面平行面 投影特性: (1)在所平行 的投影面上投 影反映实形。 (2)其他两个 投影面上的投 影积聚为直线, 且分别平行于 相应的投影轴。
4-5投影原理-线的投影
1.投影面垂直线的投影
在三投影面体系中,当直线垂直于某一个 A
投影面时,则必同时平行于另两个投影面,
这样的直线称为投影面垂直线。 共有三种投影面垂直线: 直线⊥投影面 H:铅垂线 B
P
a( b )
直线⊥投影面 V:正垂线
直线⊥投影面 W:侧垂线
(1)铅垂线— 垂直于水平投影面的直线
z a
a
A
b
a
b
b
a
X
O
YW
B
b
a
a b 投影特性:1.ab OX ; ab OYW 2. ab=AB 3.反映、 角的真实大小
b
YH
(2)正平线—只平行于正面投影面的直线
Z b a B b
b
a
a
b a
O
A
X
YW
a
b
a
b YH
2.4 线的投影
一、直线在单一投影面上的投影
A C D B P
a( b )
E F
P c
P
e
f
d
• 直线垂直于投影面:直线在该投影面上的投影积聚为点 • 直线平行于投影面:直线在该投影面上的投影反映实长 • 直线倾斜于投影面:直线在该投影面上的投影缩短
二、直线在三投影面体系中的投影
直线与投影面夹角的规定名称
(1). 求直线的实长及对 水平投影面的倾角角
AB
|zA-zB|
|zA-zB|
ab
|zA-zB |
AB
AB |zA-zB| ab
直线的投影
2.投影面垂直线
正垂线
立 体 及 其 三 视 图
投 影 轴 测 图
直 线 投 影 图
直线的投影
铅垂线
侧垂线
投影特性: 在所垂直的
投影面上的投影 积聚为一点;
另外两个投 影反映实长,且 垂直于相应的轴。
直线的投影 二、直线对投影面的各种相对位置及投影特性
3.一般位置直线 对三个投影面都是倾斜的直线称为一般位置直线。
特殊位置直线在三面投影中能直接显示其真长及对投影面的倾角,而一般位 置直线则不能。
用直角三角形法求一般位置直线的真长和倾角。
ΔABD为直角三角形,
其中AB为实长,AD=ab,α
为AB对H面的倾角,BD=Bb-
Db=b'bX- a'aX=ΔZ(直 线段AB两端点的Z坐标差)。
D
因此,已知AB投影,可以
通过ab和ΔZ作辅助直角三
角形求出AB及α角。
直线的投影 三、用直角三角形法求直线的真长及对投影面的倾角
特殊位置直线在三面投影中能直接显示其真长及对投影面的倾角,而一般位 置直线则不能。
用直角三角形法求一般位置直线的真长和倾角。
D
直线的投影 三、用直角三角形法求直线的真长及对投影面的倾角
特殊位置直线在三面投影中能直接显示其真长及对投影面的倾角,而一般位 置直线则不能。
在两直线交叉垂直时,也同样具有上述特性。
直线的投影 六、一边平行于投影面的直角的投影
例5: 如图a所示,求点A到直线BC的距离AK。
分析:由图可知BC∥V面,而AK⊥BC,故根据直 角投影定理可得:a′k′⊥b′c′。
图a
用直角三角形法求AK的实长
投影。投影用粗实线绘制。
直线的投影
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.水平投影平行Y轴。
投影面平行线
名称
铅垂线(⊥H面)
正垂线(⊥V面)
侧垂线(⊥W面)
直
观
图
投
影
图
投
影
特
点
1.水平投影积聚为一点。
2.正面投影和侧面投影都平行于Z轴,并反映实长。
1.正面投影积聚为一点。
2.水平投影和侧面投影都平行于Y轴,并反映实长。
1.侧面投影积聚为一点。2.正面投影和平投影都平行于X轴,并反映实长。
名称
水平线(∥H面)
正平线(∥V面)
侧平线(∥W面)
直
观
图
投
影
图
投
影
特
点
1.水平投影反映实长,与X轴夹角为β,与Y轴夹角为α。
2.正面投影平行X轴。
3.侧面投影平行Y轴。
1.正面投影反映实长,与X轴夹角为α,与Z轴夹角为γ。
2.水平投影平行X轴。
3.侧面投影平行Z轴。
1.侧面投影反映实长,与Y轴夹角为α,与Z轴夹角为β。
投影面垂直线
