射影几何公理
射影定理概念

射影定理的概念在数学中有两种不同的表述,分别对应于初等几何和代数几何两个不同领域。
1. 初等几何中的射影定理:
在平面几何中,尤其是直角三角形的背景下,射影定理(也称为欧几里得定理)表述为:在直角三角形ABC中,如果C是直角,则直角边AB上的高CD满足以下关系:
- CD² = AD × BD
- 同时,每一条直角边与其在斜边上的射影之间的乘积等于斜边的平方,即:
- AC × BC = AB²
换句话说,直角三角形斜边上的高是两直角边在斜边投影的比例中项,并且任意一直角边与它在斜边上的投影和斜边本身的长度之间也满足比例中项的关系。
2. 代数几何中的射影定理:
在更抽象的代数几何框架下,射影定理通常涉及射影空间和射影变换。
射影几何研究的是几何图形在无穷远点集合加入后的性质,以及这些图形经过投影变换后保持不变的特性。
例如,在代数几何中讨论射影
簇或射影变种时,射影定理可能指代将一个环上的代数集分解为其理想部分和闭点集的过程,这种分解有助于将复杂的代数问题转化为更容易处理的几何问题。
总结来说,射影定理在不同的数学分支中具有不同的意义,但都体现了射影思想的核心——通过投影操作来揭示几何对象间的深刻内在联系。
几何学中的射影定理和相似三角形——几何知识要点

几何学中的射影定理和相似三角形——几何知识要点几何学是研究空间和形状的学科,其中射影定理和相似三角形是其中重要的概念和定理。
本文将介绍这两个知识点,并探讨它们在几何学中的应用。
一、射影定理射影定理是几何学中的重要定理之一,它描述了两条平行线与一条横截线所形成的射影关系。
射影定理可以用于求解平行线之间的距离、角度和比例等问题。
射影定理的几何表述如下:当一条横截线与两条平行线相交时,它们所形成的对应的线段长度相等。
换句话说,射影定理说明了平行线与横截线之间的相似关系。
射影定理的应用非常广泛。
在建筑设计中,我们常常需要确定建筑物的高度、宽度等尺寸,射影定理可以帮助我们通过测量建筑物的阴影长度来确定其实际尺寸。
在地理测量中,射影定理也可以用于确定高山的高度、河流的宽度等。
二、相似三角形相似三角形是指具有相同形状但大小不同的三角形。
相似三角形之间存在一种特殊的比例关系,即对应边的比例相等。
相似三角形的判定条件有两种:AAA判定和AA判定。
AAA判定是指两个三角形的对应角度相等,而AA判定是指两个三角形的两个对应角度相等且对应边成比例。
相似三角形的性质有很多。
首先,相似三角形的对应角度相等,对应边成比例。
其次,相似三角形的周长和面积之间也存在一定的比例关系。
另外,相似三角形的高度、中线、角平分线等也成比例。
相似三角形在几何学中的应用非常广泛。
例如,在地图上测量两座建筑物之间的距离时,我们可以利用相似三角形的性质来计算。
此外,在工程设计中,相似三角形也可以用于计算物体的尺寸、角度等。
总结:几何学中的射影定理和相似三角形是非常重要的知识点。
射影定理描述了平行线与横截线之间的射影关系,可以用于求解距离、角度和比例等问题。
相似三角形是具有相同形状但大小不同的三角形,其对应边成比例。
相似三角形的性质有很多,可以用于计算距离、尺寸和角度等。
这些知识点在实际应用中具有广泛的用途,对于几何学的学习和应用都具有重要意义。
通过学习射影定理和相似三角形,我们可以更好地理解和应用几何学知识,提高解决实际问题的能力。
射影几何初步.doc
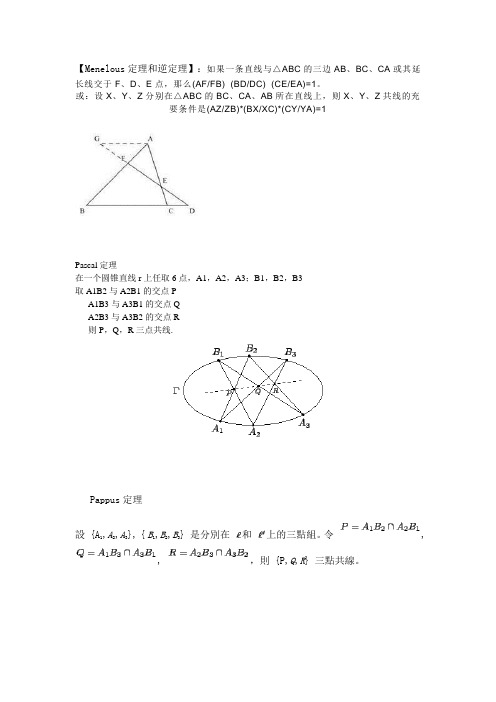
【Menelous定理和逆定理】:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1Pascal定理在一个圆锥直线r上任取6点,A1,A2,A3;B1,B2,B3取A1B2与A2B1的交点PA1B3与A3B1的交点QA2B3与A3B2的交点R则P,Q,R三点共线.Pappus定理,A2,A3}, { B1,B2,B3} 是分別在和上的三點組。
令,設 {A, ,則 {P,Q,R} 三點共線。
帕斯卡六边形定理:内接于二次曲线的六边形的三双对边的交点共线。
Ceva定理:在△ABC内任取一点O,直线AO、BO、CO分别交对边于D、E、F,则(BD/DC)*(CE/EA)*(AF/FB)=1 在△ABC内任取一点O,西姆松定理:过三角形外接圆上异于三角形顶点的任意一点作三边的垂线,则三垂足共线。
(此线常称为西姆松线)西姆松定理的逆定理若一点在三角形三边所在直线上的射影共线,则该点在此三角形的外接圆上。
托勒密定理:圆内接凸四边形两对对边乘积的和等于两条对角线的乘积Desargues(德沙格)定理:如果两个三角形的对应顶点的连线相交于一点, 则对应边的交点必定是共线的Desargues逆定理如果两个三角形的对应边的交点是共线的, 则对应顶点的连线必相交于同一点布立安香定理(Brianchon) 非退化的二次曲线的外切六点形的三对对顶点的连线必交于同一点。
布立安香逆定理如果一个六点形的三对对顶点的连线交于一点, 则这个六点形必为某一条二次曲线的外切六点形。
射影几何学

射影几何学射影几何是研究图形的射影性质,即它们经过射影变换后,依然保持不变的图形性质的几何学分支学科。
一度也叫做投影几何学,在经典几何学中,射影几何处于一种特殊的地位,通过它可以把其他一些几何学联系起来。
发展简况十七世纪,当笛卡儿和费尔马创立的解析几何问世的时候,还有一门几何学同时出现在人们的面前。
这门几何学和画图有很密切的关系,它的某些概念早在古希腊时期就曾经引起一些学者的注意,欧洲文艺复兴时期透视学的兴起,给这门几何学的产生和成长准备了充分的条件。
这门几何学就是射影几何学。
基于绘图学和建筑学的需要,古希腊几何学家就开始研究透视法,也就是投影和截影。
早在公元前200年左右,阿波罗尼奥斯就曾把二次曲线作为正圆锥面的截线来研究。
在4世纪帕普斯的著作中,出现了帕普斯定理。
在文艺复兴时期,人们在绘画和建筑艺术方面非常注意和大力研究如何在平面上表现实物的图形。
那时候,人们发现,一个画家要把一个事物画在一块画布上就好比是用自己的眼睛当作投影中心,把实物的影子影射到画布上去,然后再描绘出来。
在这个过程中,被描绘下来的像中的各个元素的相对大小和位置关系,有的变化了,有的却保持不变。
这样就促使了数学家对图形在中心投影下的性质进行研究,因而就逐渐产生了许多过去没有的新的概念和理论,形成了射影几何这门学科。
射影几何真正成为独立的学科、成为几何学的一个重要分支,主要是在十七世纪。
在17世纪初期,开普勒最早引进了无穷远点概念。
稍后,为这门学科建立而做出了重要贡献的是两位法国数学家——笛沙格和帕斯卡。
笛沙格是一个自学成才的数学家,他年轻的时候当过陆军军官,后来钻研工程技术,成了一名工程师和建筑师,他很不赞成为理论而搞理论,决心用新的方法来证明圆锥曲线的定理。
1639年,他出版了主要著作《试论圆锥曲线和平面的相交所得结果的初稿》,书中他引入了许多几何学的新概念。
他的朋友笛卡尔、帕斯卡、费尔马都很推崇他的著作,费尔马甚至认为他是圆锥曲线理论的真正奠基人。
射影几何学

在射影几何学中,把无穷远点看作是“理想点”。
通常的直线再加上一个无穷点就是无穷远直线,如果一个平面内两条直线平行,那么这两条直线就交于这两条直线共有的无穷远点。
通过同一无穷远点的所有直线平行。
德国数学家克莱因(图)在爱尔朗根大学提出著名的《爱尔朗根计划书》中提出用变换群对几何学进行分类在引入无穷远点和无穷远直线后,原来普通点和普通直线的结合关系依然成立,而过去只有两条直线不平行的时候才能求交点的限制就消失了。
由于经过同一个无穷远点的直线都平行,因此中心射影和平行射影两者就可以统一了。
平行射影可以看作是经过无穷远点的中心投影了。
这样凡是利用中心投影或者平行投影把一个图形映成另一个图形的映射,就都可以叫做射影变换了。
射影变换有两个重要的性质:首先,射影变换使点列变点列,直线变直线,线束变线束,点和直线的结合性是射影变换的不变性;其次,射影变换下,交比不变。
交比是射影几何中重要的概念,用它可以说明两个平面点之间的射影对应。
在射影几何里,把点和直线叫做对偶元素,把“过一点作一直线”和“在一直线上取一点”叫做对偶运算。
在两个图形中,它们如果都是由点和直线组成,把其中一图形里的各元素改为它的对偶元素,各运算改为它的对偶运算,结果就得到另一个图形。
这两个图形叫做对偶图形。
在一个命题中叙述的内容只是关于点、直线和平面的位置,可把各元素改为它的对偶元素,各运算改为它的对偶运算的时候,结果就得到另一个命题。
这两个命题叫做对偶命题。
这就是射影几何学所特有的对偶原则。
在射影平面上,如果一个命题成立,那么它的对偶命题也成立,这叫做平面对偶原则。
同样,在射影空间里,如果一个命题成立,那么它的对偶命题也成立,叫做空间对偶原则。
研究在射影变换下二次曲线的不变性质,也是射影几何学的一项重要内容。
如果就几何学内容的多少来说,射影几何学;仿射几何学;欧氏几何学,这就是说欧氏几何学的内容最丰富,而射影几何学的内容最贫乏。
比如在欧氏几何学里可以讨论仿射几何学的对象(如简比、平行性等)和射影几何学的对象(如四点的交比等),反过来,在射影几何学里不能讨论图形的仿射性质,而在仿射几何学里也不能讨论图形的度量性质。
射影定理数学

射影定理数学全文共四篇示例,供读者参考第一篇示例:射影定理是数学中一个非常重要的定理,它涉及到向量空间的一个关键概念——射影。
射影定理给出了一个向量在子空间上的投影,使得投影向量和原向量之间的误差最小。
让我们来回顾一下向量空间和子空间的概念。
向量空间是由一组向量组成的集合,满足一定的代数运算规则,比如加法和数乘。
子空间是向量空间的一个子集,同时也是一个向量空间。
二维平面上的一条直线就是一个子空间。
在实际问题中,我们常常需要将一个向量投影到一个子空间上。
这样做的一个重要原因是,子空间可能是我们能处理的一个更简单的空间,或者是一个我们感兴趣的具体问题所在的空间。
射影定理就是给出了如何在子空间上进行向量投影的方法。
射影定理的表述如下:设W是n维向量空间V的一个子空间,对于任意一个向量v\in V,存在唯一的向量w\in W,使得v和w之间的误差向量(v-w)与W中的任意向量u\in W垂直。
也就是说,v-w与u 的内积等于零。
利用这个性质,我们可以给出向量v在子空间W上的投影P(v)。
投影P(v)定义为与v最接近的W中的向量,使得误差向量(v-P(v))与W中的任意向量垂直。
我们也可以通过计算投影矩阵P来求得投影向量P(v),投影矩阵P满足P^2 = P且Pv = P(v)。
射影定理的一个重要应用是在最小二乘问题中的使用。
在最小二乘问题中,我们希望找到一个向量x,使得Ax尽可能接近b,其中A是一个矩阵,b是一个向量。
将最小二乘问题表示为A\hat{x} = P(b),其中\hat{x}是问题的解,P(b)是b在A的列空间上的投影。
通过射影定理,我们可以得到最小二乘问题的一个解析解。
这个解析解可以帮助我们更快地求解最小二乘问题,避免了需要迭代计算的过程。
射影定理还有很多其他应用,比如图像处理中的特征提取、数据挖掘中的维数约简等。
通过射影定理,我们可以更好地理解向量空间中的投影问题,从而应用到各种实际问题中。
射影定理

百科名片射影定理直角三角形射影定理(又叫欧几里德(Euclid)定理):直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
公式如图,Rt△ABC中,∠ABC=90°,AD是斜边BC上的高,则有射影定理如下:(1)(BD)^2;=AD·DC,(2)(AB)^2;=AD·AC ,(3)(BC)^2;=CD·AC 。
等积式(4)ABXBC=BDXAC (可用面积来证明)射影射影就是正投影,从一点到过顶点垂直于底边的垂足,叫做这点在这条直线上的正投影。
一条线段的两个端点在一条直线上的正投影之间的线段,叫做这条线段在这直线上的正投影,即射影定理。
直角三角形射影定理的证明(注:公式较多,难免出现乱码,请见谅)证明:射影定理简图(几何画板)一、在△BAD与△BCD中,∠A+∠C=90°,∠DBC+∠C=90°,∴∠A=∠DBC,又∵∠BDA=∠BDC=90°,∴△BAD∽△CBD,∴AD/BD=BD/CD,即BD²=AD·DC。
其余类似可证。
(也可以用勾股定理证明)注:由上述射影定理还可以证明勾股定理。
有射影定理如下:AB²=BD·BC,AC²=CD·BC 。
两式相加得:AB²+BC²=AD·AC+CD·AC =(AD+CD)·AC=AC²,即AB²+BC²=AC²(勾股定理结论)。
二、已知:三角形中角A=90度,AD是高.用勾股证射影:因为AD^2=AB^2-BD^2=AC^2-CD^2,所以2AD^2=AB^2+AC^2-BD^2-CD^2=BC^2-BD^2-CD^2=(BD+CD)^2-(BD^2+ CD^2)=2BD*CD.故AD^2=BD*CD.运用此结论可得:AB^2=BD^2+AD^2=BD^2+BD*CD=BD*(BD+CD)=BD*BC,AC^ 2=CD^2+AD^2=CD^2+BD*CD=CD(BD+CD)=CD*CB.综上所述得到射影定理。
射影几何课程中的基本数学思想

ΞΞΞ射影几何课程中的基本数学思想徐 天 长( 安庆师范学院 数学系, 安徽 安庆 246011)摘 要: 基本数学思想隐藏于知识和技能之中, 需要经过提炼和总结才能获得。
射影几何课程中的基本数学思想可归纳为五个方面。
关键词: 射影空间; 对偶原理; 变换群; 不变性中图分类号: O 185 文献标识码: A 文章编号: 1007- 4260 ( 2001) 03- 0032- 02数学思想往往隐藏于数学知识和技能之中, 需要经过提炼和总结才能获得, 因而不易为人们所注 意。
在射影几何课程中包含哪些基本的数学思想? 本文将从五个方面进行探讨。
1 在射影空间无通常元素与无穷远元素之分的思想 在射影几何中无穷远元素应该认为是实有其物, 而且应该与通常元素同等对待。
它们之间没有任何本质上的区别, 都是射影空间的有机组成部分。
虽然在初等几何里, 也经常引用无穷远元素, 但是在 那里使用它实质上只是限制在几何事实的特别的文字表达方式上。
例如说把圆柱当做有无穷远顶点的 圆锥, 不说是直线平行而说它们交于无穷远点。
因为在欧氏空间里, 实际上没有所谓无穷远元素。
当我 们比较一下初等几何与射影几何的研究对象时, 就会明显地看出上述所谈差别的原因, 因为初等几何 的主要内容是研究图形的度量性质。
如线段的长度, 两直线间的夹角, 图形的面积等等。
而在射影几何 中, 由于图形的度量性质不是其研究对象, 而只研究点线结合关系的命题, 所以上面提到的无穷远元素和通常元素之间的差异就失去了力量。
另外, 在中心投影下, 无穷远元素和通常元素之间可以相互转变。
如图 1 所示, Π1 上一族平行的的直线, 它们相交于 Π1 上的无穷远点 S ∞, 在 Π上的象却不是平行直线束, 而是构成以 S 为中心的直线束。
这足以说明, 在中心投影下, 无穷远点与通常点之间并没有本质上的差别。
射影几何与初等几何一样也有它自己的公理化体系,如果不从欧氏几何出发而使用近代公理法来定义射影空图 1 间, 则根本不会有无穷远元素这样的东西掺杂其中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
射影几何公理
摘要:
1.射影几何公理的概述
2.射影几何公理的基本概念
3.射影几何公理的推导与证明
4.射影几何公理的应用
5.射影几何公理的重要性
正文:
射影几何公理是射影几何的基础理论,它是研究射影空间中的点、线、面及其相关性质的数学工具。
射影几何公理主要包括以下几个方面:
1.射影空间:射影空间是一个向量空间,其中的加法运算满足齐次性。
射影空间中的点可以看作是向量,线可以看作是向量空间中的直线,面可以看作是向量空间中的平面。
2.射影映射:射影映射是从一个射影空间到另一个射影空间的映射,它保持向量之间的加法运算。
射影映射可以将射影空间中的点、线、面映射到另一个射影空间中,从而研究它们之间的关系。
3.射影几何公理:射影几何公理是描述射影空间中点、线、面及其相关性质的一组公理。
射影几何公理包括以下三条基本公理:
(1) 齐次公理:射影空间中的加法运算满足齐次性。
(2) 投影公理:对于射影空间中的任意直线和点,存在唯一的直线与该直线平行且经过该点。
(3) 线性组合公理:对于射影空间中的任意三个点,它们的线性组合可以表示为射影空间中的任意一点。
通过以上三条基本公理,可以推导出射影几何中的一系列定理和性质。
射影几何公理在几何学、物理学、计算机图形学等领域都有广泛应用。
4.射影几何公理的应用:射影几何公理在许多领域都有重要应用,例如在计算机图形学中,利用射影几何公理可以简化图形的表示和计算;在物理学中,射影几何公理可以用于描述光的传播和折射等现象;在几何学中,射影几何公理为研究空间几何问题提供了一种有效的方法。
5.射影几何公理的重要性:射影几何公理是射影几何的理论基础,它为研究射影空间中的点、线、面及其相关性质提供了一种统一的理论框架。
