高等数学随堂讲义由平行截面面积求体积
已知平行截面面积求立体的体积:图形、动画、计算

四川大学数学学院 徐小湛
July 1, 2012
切片法 3
例 1立 体 以 f(x ) x 2 1 和 g (x ) x 4 1 ( 3 x 3 ) 之 间 的 区 域 为 底 ,
1 0
1 5 0
在 x 处 的 垂 直 于 x 轴 的 截 面 是 一 个 高 H 3 的 等 腰 三 角 形 。
3
3 2 1 01 5 0 1 2 5
3
-3230x21100x432709 dx125
f:=x->(3/2)*(x^2/10+x^4/150+2): a:=-3:b:=3: Integrate(f(x),x=a..b)=integrate(f(x),x=a..b);
四川大学数学学院 徐小湛
July 1, 2012
切片法 5
现在来求这个立体的体积
截面面积 A(x) 1 3 [ f (x) g (x)]
2 3 x2 x4 ( 2) 2 10 150
立 体 体 积 V 3A ( x ) d x 33 (x 2 x 4 2 ) d x 2 7 0 9
切片法 1
已知平行截面的面积求体积
(切片法)
h蜀ttp南://xu竹xzm海
四川大学数学学院 徐小湛
July 1, 2012
切片法 2
用数学软件Maple作了有关动画 这些动画生动地显示了立体的形成过程
计算了一些立体的体积
g(x) x4 1 150
x
y
f (x) x2 1 10
四川大学数学学院 徐小湛
July 1, 2012
切片法 4
动画的Maple程序
数学分析10.2由平行截面面积求体积

第十章 定积分的应用 2 由平行截面面积求体积定义:设Ω为三维空间中的一立体,它夹在垂直于x 轴的两平面x=a 与x=b 之间(a<b). 称Ω为位于[a,b]的立体. 若在任意一点x ∈[a,b]处作垂直于x 轴的平面,它截得Ω的截面面积显然是x 的函数,记为A(x), x ∈[a,b],并称之为Ω的截面面积函数.公式1:设截面面积函数A(x)是[a,b]上的一个连续函数,对[a,b]作分割T :a=x 0<x 1<…<x n =b. 过各分点作垂直于x 的平面x=x i , i=1,2,…,n ,它们把Ω切割成n 个薄片. 设A(x)在每个小区间△i =[x i-1,x i ]上的最大, 最小值分别为M i 与m i ,那么每一薄片的体积△V i 满足 m i △x i ≤△V i ≤M i △x i . 于是Ω的体积V=∑=n1i i V △满足∑=n1i iix△m ≤V ≤∑=n1i i i x △M . 因为A(x)连续,从而在[a,b]上可积,所以当T 足够小时,能使i n1i i x △ω∑==∑=n1i i i i x )△m -(M <ε,ε为任意小的正数.∴V=∑=→n 1i i 0T M lim △x i (或∑=→n 1i i 0T m lim △x i )=∑=→n1i 0T A lim (ξi )△x i . 其中A(ξi )=M i (或m i ). ∴V=⎰ba A(x )dx.例1:求由两个圆柱面x 2+y 2=a 2与z 2+x 2=a 2 所围立体的体积.解:如图取该立体的第一卦限,即81部分.对任一x 0∈[0,a],平面x=x 0与这部分立体的截面是正方形,边长为:202x a -,即A(x)=a 2-x 2, x ∈[0,a]. ∴V=8⎰a 0A(x )dx=8⎰-a22)x (a dx=316a 3.例2:求由椭球面222222cz b y a x ++=1所围立体(椭球)的体积.解:以平面x=x 0(|x 0|≤a)截椭球面,得椭圆:⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-220222222a x 1c z a x 1b y =1.∴截面面积函数为:A(x)=πbc ⎪⎪⎭⎫ ⎝⎛-22a x 1, x ∈[-a,a]. ∴V=⎰aa -A(x )dx=⎰⎪⎪⎭⎫ ⎝⎛-aa -22a x 1πbc dx=34πabc.注:当a=b=c=r 时,就等于球的体积34πr 3.定理:设ΩA ,ΩB 为位于同一区间a,b 的两个立体,其体积分别V A ,V B .若在[a,b]上它们的截面面积函数A(x)与B(x)皆连续,且A(x)=B(x)则V A =V B .公式2:设f 是[a,b]上的连续函数,Ω是由平面图形0≤|y|≤|f(x)|, a ≤x ≤b 绕x 轴旋转一周的旋转体,则截面面积函数为A(x)=π[f(x)]2, x ∈[a,b]. ∴旋转体Ω的体积为:V=π⎰ba2[f(x )]dx.例3:试用公式2导出圆锥体的体积公式.解:设正圆锥的高为h ,底圆半径为r ,则有0≤|y|≤hrx, x ∈[0,h].∴V=π⎰⎪⎭⎫⎝⎛h02x h r dx=31πr 2h.例4:求由圆x 2+(y-R)2≤r 2 (0<r<R)绕x 轴旋转一周所得环状立体体积.解:圆的上下半圆分别为:y=f(x)=R+22x r -;y=g(x)=R-22x r -, |x|≤r. ∴圆环体截面面积函数为:A(x)=π[f(x)]2-π[g(x)]2=4πR 22x r -, x ∈[-r,r]. ∴V=2⎰-r022x r πR 4dx=8πR ⎰-r022x r dx= 2π2r 2R.习题1、如图所示,直椭圆柱体被通过底面短轴的斜平面所截,试求截得楔形体的体积.解:如图所示建立直角坐标系,则椭圆柱面的方程为:16y 100x 22+=1, 斜面的方程为Z=2x.用平面x=t 截这个立体,得一长方形,其边长为:8100t 12-和2t.∴A(x)=82x 100x 12⋅-=4x 100x 12-, x ∈[0,10].∴截得楔形体的体积为:V=⎰-1002100x 1x 4dx=3400.2、求下列平面曲线绕轴旋转所围成立体的体积: (1)y=sinx, 0≤x ≤π, 绕x 轴;(2)x=a(t-sint), y=a(1-cost) (a>0), 0≤t ≤2π, 绕x 轴; (3)r=a(1+cos θ), (a>0), 绕极轴;(4)2222b y a x +=1, 绕y 轴. 解:(1)V=π⎰π02x sin dx=2π2.(2)V=π⎰2π22cost)-(1a d[a(t-sint)]=πa3⎰2π3cost)-(1dt=5a 3π2.(3)r=a(1+cos θ), (a>0)是心脏线,而心脏线极轴之上部分的参数方程为: x=a(1+cos θ)cos θ; y=a(1+cos θ)sin θ, (0≤θ≤π) ∴V=|π⎰π322y dx|-|π⎰π32π2y dx|=|π⎰+π222θsin ) cos θ(1a da(1+cos θ)cos θ|=πa3⎰+++π2333) cos θ2θ)(1θcos sin 2θcosθsin 2θ(sin d θ=38πa 3.(4)y=b 22a x 1-, ∴V=πb 2⎰⎪⎪⎭⎫ ⎝⎛-a a -22a x 1dx =34a b 2π.3、已知球半径为r ,验证高为h 的球缺体积V=πh 2(r-3h) (h ≤r). 证:球缺体积可看作曲线y=22x R -,R-h ≤x ≤R 绕x 轴旋转而得, V=π⎰Rh-R 2y dx=π⎰-Rh-R 22)x (R dx=πh 2(r-3h). 得证.4、求曲线x=Rcos3t, y=Rsin3t, (R>0)所围平面绕x轴旋转所得立体体积.解:V=π⎰RR-2y dx=π⎰0π62tsinR dRcos3t=3πR3⎰π027ttcossin dt=10516πR3.5、导出曲边梯形0≤y≤f(x), a≤x≤b绕y轴旋转所得立体的体积公式为:V=2π⎰bax f(x)dx.证:曲边梯形绕y轴旋转,在x处的截面图形为一圆柱的侧面,其面积为:A(x)=2πx·f(x), a≤x≤b. 所围立体体积为:V=⎰baA(x)dx=2π⎰b a x f(x)dx. 得证.6、求0≤y≤sinx, 0≤x≤π所示平面图形绕y轴旋转所得立体体积. 解法1:曲线y=sinx可分成两部分:x=arcsiny, x=π-arcsiny, 0≤y≤1. 用y=t截这个立体,其截面面积为:A(t)=π[(π-arcsint)2- (arcsint)2]=π3-2π2arcsint.即面积函数为A(y)=π3-2π2arcsiny.∴V=⎰123arcsiny)2π-(πdy=2π2.解法2:利用第5题的结论可得:V=2π⎰πx sinx dx=2π2.。
由平行截面面积求体积
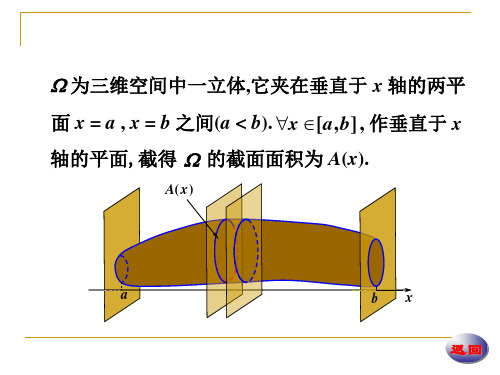
[ xi1, xi ] 上 A( x) 的最大、最小值分别为 Mi , mi , 则第 i 个小薄片的体积 ΔVi 满足
于是
mi Δxi ΔVi Mi Δxi ,
n
nБайду номын сангаас
n
miΔ xi V ΔVi MiΔxi .
i 1
i 1
i 1
当 T 0 时,
n
b
n
b
Mi xi
A( x)dx,
因此
A( x)
f
2 2
(
x)
f12( x) 4
R
r2 x2 ,
从而
r
V 8 R
r 2 x2dx 2 2r 2R.
0
例3 求由区域 ( x, y) | 0 x 1 , x y 2 x2
绕 y 轴旋转一周所得立体的体积. y
解 旋转体由曲线
2
x
y,
y [0,1]
2 y , y [1, 2]
所以 A( x) a2 x2 , x [0,a]. 于是求得
V
8V1 8
9 0
a2 x2
dx 16 a3. 3
以下讨论旋转体的体积.
设 f 是 [a,b] 上连续函数, 是由平面图形
A {( x, y) 0 | y | | f ( x) | , a x b}
绕 x 轴旋转一周所得的旋转体,则 A( x) π f 2 ( x) , x [a,b],
V π b f 2 ( x)dx. a
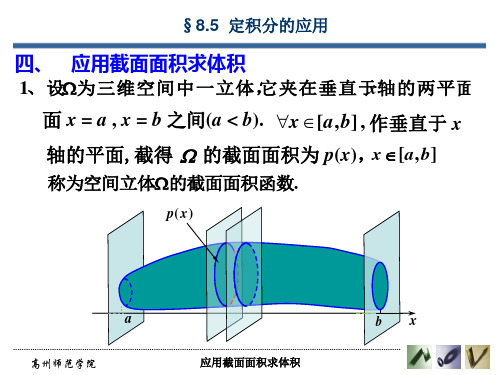
例2 求由圆 x2 ( y R)2 r2 (0 r R) 绕 x 轴
旋转一周所得环状立体的体积.
y
r
解 x2 ( y R)2 r2 的上下半圆分别为
应用截面面积求体积
a
左半圆的方程为x 2 ( y ) b a 2 y 2
环体的体积为:
o
a
b
x
V 1 ( y )dy 2 ( y )dy
a 2 a 2 a a
[(b a 2 y 2 )2 (b a 2 y 2 )2 ]dy
a a
e 1
高州师范学院
应用截面面积求体积
§8.5 定积分的应用
若由两条连续曲线 f ( x ), y g( x)以及x a, x b y
围成的平面区域绕 x轴旋转,则旋转体的体 积为
y
V f ( x )dx g ( x )dx
b 2 b 2
y = f ( x)
[ f 2 ( x ) g 2 ( x )]dx
高州师范学院
应用截面面积求体积
§8.5 定积分的应用
2、旋转体
一般地,如果旋转体是由连续曲线 y f ( x ) 、直 线 x a 、 x b 及 x 轴所围成的曲边梯形绕 x 轴 旋转一周而成的旋转体,其体积为:
y
y f ( x)
y
y f ( x)
o a b
x
o
a
x
b
x
V p( x )dx a
a
高州师范学院
应用截面面积求体积
b
x
§8.5 定积分的应用
设P( x )在[a, b]连续.
x [a, b], 截面面积函数是p( x ).设“厚度”是dx,
则体积微元为 所以,体积
dv p( x )dx
b b a a
v dv p( x )dx
平行截面面积求体积

例2 求由圆 x2 ( y R)2 r 2 (0 r R) 绕 x 轴
旋转一周所得环状立体的体积.
y
r
解 x2 ( y R)2 r2 的上下半圆分别为
R
y f2(x) R r2 x2,
O
x
y f1( x) R r 2 x2 .
因此
A( x)dx.
a
i 1
i 1
因此
b
V A( x)dx.
a
例1 求由两个圆柱面 围立体的体积.
x2 y2 a2 与 z2 x2 a2 所
z
a
x
a x0
O
a
y
解 先求出立体在第一卦限的体积V1. x0 [0,a] ,
x x0 与立体的截面是边长为 a2 x02 的正方形,
所以 A( x) a2 x2 , x [0,a]. 于是求得
A( x)
f
2 2
(
x)
f12( x) 4
R
r2 x2 ,
从而
r
V 8 R
r 2 x2dx 2 2r 2R.
0
例3 求由区域 ( x, y) | 0 x 1 , x y 2 x2
绕 y 轴旋转一周所得立体的体积. y
解 旋转体由曲线
2
x
y,
y [0,1]
2 y , y [1, 2]
围成的曲边三角形绕极轴旋转一周所得旋转体的
体积公式.
作业: P246:1,2(2,4),4,5,6
[ xi1, xi ] 上 A( x) 的最大、最小值分别为 Mi , mi ,
则第 i 个小薄片的体积 Vi 满足
mi xi Vi Mi xi ,
10.2由平行截面面积求体积讲解
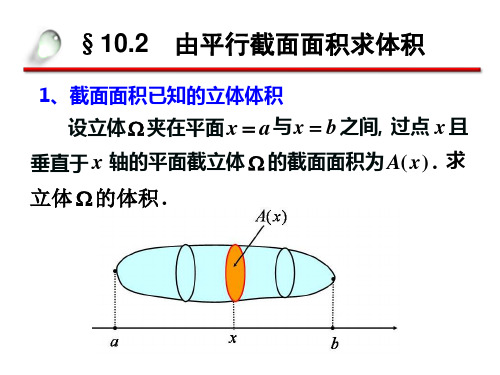
例6、求 y sin x(0 x ) 与 x 轴围成的图形绕 y
轴旋转所成旋转体的体积 .
作
业
习题10-2:2(1)(3)、6
2
体积:
V g 2 ( y )dy .
c
d
x y 例3、求椭圆 2 2 1 绕 x 轴一周所成旋转体体积. a b
2
2
2 2 2 求圆 x ( y R ) r (0 r R) 绕 x 轴 例 4、
旋转一周所得环状立体的体积.
y
r
R
O
x
例5、求由区域 {( x , y ) | 0 x 1, x y 2 x }
体积
V A( x )dx .
a
b
例1、求由两个圆柱面 x y a 与 z x a
2
2
2
2
2
2
所围立体的体积.
z
a
O
x
a
x0
a
y
例2、设一平面经过半径为 a 的圆柱体的底面中心,
且与底面夹角为 , 求这个平面截圆柱体所得 立体的体积 .
a
2、旋转体的体积 旋转体:平面图形绕它所在平面内的一条直线旋转 一周所成的立体. 情形1:0 y f ( x ), a x b 绕x 轴旋转一周
2
绕 y 轴旋转一周所得立体的体积 .
y
2
1
O
1
x
曲边梯形 0 y f ( x ), a x b 绕 y 轴 旋转一周的旋转体体积=?
x : 柱壳半径
f ( x ) : 柱壳高度
x x
x : 柱壳厚度
V 2xf ( x )x
由平行截面面积求体积华东师大数学分析ppt课件
(2)绕y轴旋转的旋转体体积可看作平面图OABC与OBC
分别绕y轴旋转构成旋转体的体积之差.
Vy
2a
0
2a
2
x
x 2 ( y )dy 0
1 ( y ) dy
2
y
2a
O
x x2 ( y )
x x1 ( y )
a
a ( t sin t ) a sin tdt a 2 ( t sin t ) 2 a sin tdt
a
球的体积
2b 2 2
1 2 a 4 2
ab
2 (a x x ) |0
a
3
3
4 2
a b
(2) 同理可得 V y
3
= 3
b
a x
o
a x
-a
-b
b
y
o
-a
-b
a x
例9 求摆线x=a(t-sint),y=a(1-cost)的一拱与y=0所围成
的图形分别绕x轴、y轴旋转构成旋转体的体积.
−
球的体积
= 3
二、旋转体的体积
1、旋转体概念: 就是由一个平面图形绕这平面内一条直线旋
转一周而成的立体.这直线叫做旋转轴.
圆柱
o
oa
y
y
y
b x
圆台
圆锥
bx
o
x
2、绕x轴
由连续曲线 y = f(x), x = a , x=b ,及 x 轴围成的平面图形绕 x
y
轴旋转所生成的旋转体的体积:
2
平行截面面积为已知的立体的体积
平行截面面积为已知的立体的体积立体几何是数学中一个非常重要的分支,其研究的对象是三维空间内的图形、体形和其相互之间的关系,是现代科学发展中必不可少的基础知识。
在立体几何中,平行截面面积为已知的立体的体积是一个非常重要的问题,也是学生在立体几何中需要掌握的一项基本知识。
一、概念平行截面面积为已知的立体的体积,表示的是在某一平面上所截得的平行截面面积均已知的空间图形的体积。
该问题主要涉及的是体积计算方法和空间几何方程的解法。
二、立体的表示在立体几何中,立体通常用多个平面组成的多边形进行表示。
对于三角形、四边形等基本图形,可以通过将它们叠放或旋转而构成不同的立体图形。
通过这些基本图形的不同组合,我们可以得到各种不同形状和大小的立体图形,例如长方体、正方体、棱锥、棱柱等。
除此之外,还有一些比较复杂的立体图形,如球体、圆锥、圆柱等。
这些图形的体积计算方法需要结合相应的几何公式才能求得。
例如,对于一个球体,其体积可以由其半径r来计算:V=4/3πr³其中π为圆周率,大约为3.14159。
对于其他几何体,也都有相应的体积计算方法,需要通过学习掌握。
三、平行截面的体积计算对于平行截面面积为已知的立体,通常情况下我们可以采用分形法,将其分割成若干个小体积,分别计算得到最终的体积。
其具体的计算过程和方法如下:1. 将已知的图形分割成若干个小图形,每一部分都是由若干个平行截面构成的。
2. 对于每个小图形,可以根据其平行截面面积进行求解,得到小图形的体积。
3. 将所有小图形的体积加起来,即可得到原图形的体积。
在计算过程中,需要注意的是,每个小图形体积的计算需要结合相应的几何公式。
例如,对于一个圆锥体积的计算,其体积可以由其底面面积S和高h来计算:V=1/3Sh四、解题方法对于平行截面面积为已知的立体体积计算,解题方法包括以下几个方面:1. 确定平行截面的位置和数量。
2. 根据平行截面面积和截面位置,将图形分成若干个小立体。
已知平行截面面积求立体的体积:图形、动画、计算
四川大学数学学院 徐小湛
July 1, 2012
切片法 6
例 2立 体 以 圆 x2y2R 2为 底 , 在 x处 的 垂 直 于 x轴 的 截 面 是 一 个 高 为 h的 等 腰 三 角 形 。
y
x2 y2 R2
x
g(x) x4 1 150
x
y
f (x) x2 1 10
四川大学数学学院 徐小湛
July 1, 2012
切片法 4
动画的Maple程序
with(plots): f:=x->x^2/10+1: g:=x->-x^4/150-1: a:=-3:b:=3:H:=3: xzou:=spacecurve([x,0,0],x=a-1..b+1,thickness=3,color=black): yzou:=spacecurve([0,y,0],y=a-1..b+1,thickness=3,color=black): base:=plot3d([x,y,0],x=a..b,y=g(x)..f(x),color=grey,style=patchnogrid): quxianf:=spacecurve([x,f(x),0],x=a-1..b+1,thickness=3,color=red): quxiang:=spacecurve([x,g(x),0],x=a-1..b+1,thickness=3,color=red): K:=50:for i from 0 to K do xi:=a+i*(b-a)/K: sanjiaoxing[i]:=spacecurve([[xi,g(xi),0],[xi,f(xi),0],[xi,(f(xi)+g(xi))/2,H],[xi,g(xi),0]],thickness=3,color=blue): sanjiaoban[i]:=plot3d([xi,y,z],y=(f(xi)+g(xi))/2-(f(xi)-g(xi))/2*(1-z/H)..(f(xi)+g(xi))/2+(f(xi)-g(xi))/2*(1z/H),z=0..H,color=yellow,style=patchnogrid): qumian1[i]:=plot3d([x,f(x)+(-f(x)+g(x))/2*t,H*t],t=0..1,x=a..xi,color=green): qumian2[i]:=plot3d([x,g(x)+(f(x)-g(x))/2*t,H*t],t=0..1,x=a..xi,color=green)od: sanjiaoxing:=display(seq(sanjiaoxing[i],i=0..K),insequence=true): sanjiaoban:=display(seq(sanjiaoban[i],i=0..K),insequence=true): qumian1:=display(seq(qumian1[i],i=0..K),insequence=true): qumian2:=display(seq(qumian2[i],i=0..K),insequence=true): display(xzou,yzou,base,quxianf,quxiang,sanjiaoban,sanjiaoxing,qumian1,qumian2,scaling=constrained);
高等数学第10章第2节由平行截面面积求体积
§ 2 由平行截面面积求体积
(一)一般体积公式:
设一几何体夹在x =a 和x =b (a<b )这两个平行平面之间,用垂直于X 轴的平面去截此几何体,设载面与X 轴交点为(x ,0),可得的截面面积为S (x ),如果S(x)是[a,b]上的(R )可积函数,则该几何体的体积V 等于:()b
a V S x dx =⎰.
例 1 求两圆柱
222222,a z x a y x =+=+
所围的立体体积
例2求底面积为S ,高为h 的斜柱体的体积V .
例3、求由椭球面222
2221x y z a b c
++=所围的几何体体积.(a,b,c>0) (二)旋转体的体积
设y =y(x)于[a,b](R )可积,曲线y =y(x),a ≤x ≤b ,绕x 轴产生旋转体的截面积为S(x)=2()y x π,则
V 旋体=2()b
b
a a S x dx y dx π=⎰⎰ 例4、求底半径为r ,高为h 的圆锥体的体积V .
例5求由圆)0()(222R r r R y x <<≤-+1绕x 轴所产生的旋转体体积.
作业:P246 2(2)(4), 3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a
O
x
a
x0
a
y
的体积V1 . x0 0, a , 解 先求出立体在第一卦限
x x0 与立体的截面是边长为 a x 的正方形,
2 2 0
所以A( x ) a 2 x 2 , x [0, a]. 于是求得
16 3 V 8V1 8 (a x )dx a . 0 3 以下讨论旋转体的体积.
数学分析 第十章 定积分的应用
§2 由平行截面面积求 体积
由平行截面面积求体积
A( x )
为三维空间中一立体,它夹在垂直于 x 轴的两平 面 x = a , x = b 之间(a < b). x [a , b] , 作垂直于 x
轴的平面,截得 的截面面积为 A(x).
a
b
x
若A(x) 在 [a , b] 上连续, 则 的体积为
于是
m Δ x
i 1 i b i i a
n
i
V ΔVi M i Δxi .
i 1 i 1
n
n
当 T 0 时,
M x
i 1
n
A( x )dx ,
b a
m x
i 1 i
n
i
A( x )dx .
a
b
因此
V A( x ) dx .
例1 求由两个圆柱面 x 2 y 2 a 2 与 z 2 x 2 a 2 所 围立体的体积.
4 π u sin udu 4 π sin 2 udu
0 0
π
π
分部积分
2
π 2
4 π 8 π sin 2 udu = 4 π 2 8 π 1 π 0 2 2
π 关于 对称 2
(利用“偶倍奇 零”)
说明
y
xxdx
柱面面积 柱壳体积
2π
2
0
a ( t sin t )a 2 (1 cos t ) 2 d t
y O
y πa
2πa
Vx
2πa 0
π y 2 dx 2
π 2 2
πa 0
π y 2 dx
x
2 π a (1 cos t ) a (1 cos t ) dt
0 3 π 3
3 π 6
利用对称性
t t 2 π a (1 cos t ) d t 16 π a sin d t ( 令 u ) 0 0 2 2 π 5 3 1 3 2 6 3 2 3 32 π a sin u du 32 π a 5 π a 0 6 4 2 2
2 π a ( t sin t ) a 2 (1 cos t ) 2 d t
0
2π
t 8 π a ( t sin t )sin dt 0 2 t 令u 2
3 2π 4
16 π a
4 (2 u sin 2 u )sin u du 0 π 令v u 2 π 2 16 π a 3 π (2v π sin 2v )cos 4 v d v 3
a
2
*若曲线 C 由极坐 标方程 r r ( ), [ , ] 表示,其 中 0 π.试求由曲线 C 和射线 ,
围成的曲边三角形绕极轴旋转一周所得旋转体的
体积公式.
例8 证明曲边扇形 旋转而成的体积为 证 先求 上微曲边扇形
绕极轴Leabharlann r r ( )d d r
r
r
绕极轴旋转而成的体积
体积元素
O
故
V π π
1 0
x dy x 2dy
2 1 2
2
O
1
x
1 0
3 y y 2dy (2 y )dy π 1 3
1
y2 2 7 π 2 y π. 2 1 6 0
例4 计算由椭圆 成的椭球体的体积. 解 方法1 利用直角坐标方程
b
x
ax
则
V 2 π y 2 d x 2 π ab 2 sin 3 t dt
0
a
2 2 π ab 3 4 π ab 2 3
2
4 3 特别当b = a 时, 就得半径为a 的球体的体积 π a . 3
例5 计算摆线
的一拱与 y=0
所围成的图形分别绕 x 轴, y 轴旋转而成的立体体积. 解 绕 x 轴旋转而成的体积为
a 2 2
设 f 是 [a , b] 上连续函数, 是由平面图形
A {( x , y ) 0 | y | | f ( x ) | , a x b}
绕 x 轴旋转一周所得的旋转体, 则
A( x ) π f 2 ( x ) , x [a, b],
V π f 2 ( x )dx .
y 2a
绕 y 轴旋转而成的体积为
π
x x2 ( y )
O
π a 2πa x x x1 ( y )
注意上下限 ! π a 2 ( t sin t ) 2 a sin t d t 2π π 2 π a ( t sin t ) 2 a sin t dt
πa
3
因此 A(x ) f 22 (x ) f12 (x ) 4R r 2 x 2 ,
从而
V 8 R
r
0
r 2 x 2 dx 2 2 r 2 R.
例3 求由区域 ( x, y ) | 0 x 1 , x y 2 x 2 绕 y 轴旋转一周所得立体的体积. y 解 旋转体由曲线 2 y [0,1] y, x 2 y , y [1,2] 1 和 y 轴所围平面图形绕 y 轴旋转一周而得.因此
2
π
奇函数
偶函数
例6 设
在 x≥0 时为连续的非负函数,且
形绕直线 x=t 旋转一周所成旋转体体积, 证明:
y
证 利用柱壳法
f ( x)
d V 2 π ( t x ) f ( x )d x
则
V ( t ) 2 π( t x ) f ( x )d x
0 t t 0 t 0
t
O
x
所围图形绕 x 轴旋转而
y O
b
x
ax
则 V 2 a π y 2 dx
0
2
(利用对称性)
b a 2 2 π 2 ( a x 2 )d x a 0 b2 2 1 3 a 4 2π 2 a x x π ab 2 a 3 0 3
方法2
利用椭圆参数方程
y O
解 垂直 x 轴的截面是椭圆
c
2
y b 2 (1
它的面积为
z 2 2 x ) c (1 a2
2
x2 a2
)
1
O
b x
a
因此椭球体体积为
3 a 4 x x V 2 π bc (1 a 2 )d x 2 πbc x 2 πabc 0 3a 0 3 特别当 a = b = c 时就是球体体积 .
a b
例2
求由圆 x ( y R) r (0 r R) 绕 x 轴
2 2 2
旋转一周所得环状立体的体积. 解 x 2 ( y R)2 r 2 的上下半圆分别为
y f2 ( x) R r 2 x 2 ,
y
r
R
O
x
y f1 ( x ) R r 2 x 2 .
2 π t f ( x )d x 2 π x f ( x )d x
故
t x xdx
V ( t ) 2 π f ( t )
V ( t ) 2 π f ( x )d x 2 π tf ( t ) 2 π tf ( t )
0
例7 计算由曲面
所围立体(椭球体)
的体积.
V A( x )dx .
a
b
后退
前进
目录
退出
证 设T : a x0 x1 xn b 是 [ a , b ] 的一分割, [ xi 1 , xi ] 上 A( x ) 的最大、最小值分别为 M i , mi ,
则第 i 个小薄片的体积 ΔVi 满足
mi Δxi ΔVi M i Δxi ,
2π 0
0
( t sin t ) 2 sin t dt
注
注
2π 0
( t sin t ) 2 sin t d t
( 令 u t π)
( t 2 sin t 2t sin 2 t sin 3 t )dt
0 π
2π
2 2 2 ( u 2 π u π )sin u 2( u π )sin u π sin 3 u d u
