第4章-2(阻抗与导纳)

合集下载

微波技术原理第4章微波网络基础

若已知归一化阻抗矩阵，就可求出散射矩阵。反之，若知道散射矩阵，也可求出归一化阻抗矩阵。
7. 互易网络和无损网络的散射矩阵的性质
根据广义散射矩阵的定义得到：
(1) 互易网络的 [z]为对称矩阵，即 [z ]=[z ]T 。可见，互易网络的散射矩阵是对称矩阵 [S]=[S]T 。
(2) 无损网络各端口的总输入能量等于总输出能量。
第4章微波网络基础
微波系统中除了传输线外，还有各种各样的微波元件或接头等非均匀区域。因为这些非均匀区域的形状不规则，在其中的微波传输规律很复杂。因此，要想通过求解麦克斯韦方程组得出其中的传输规律是不可能的。
实际上，我们并不需要知道微波在其中的传输规律，而只需知道这些非均匀区与外电路连接的端口特性。所以通常将其等效为一个网络，称为微波网络。
微波网络的端口及其参考面举例
对于单模传输系统，微波网络的端口数 = 被等效区域与外电路的接口数目 = 参考面的数目。
§4.3 微波网络的端口特性参量
1. 阻抗矩阵和导纳矩阵
V
2
I-2
V+2 I+2
I-3 V-3 I+3 V+3
I+1
V+1
I-1
V-1
I-N
I+N
V-N
V+N
2. 微波网络的互易性
从无耗网络的各个端口输入的总能量为 0。
互易网络的阻抗矩阵是对称的，因此，既互易又
无耗的网络满足：
（实部为0）
这说明，互易无耗网络的阻抗矩阵元为纯电抗。
例1 求下图的两端口网络的Z参量
ZA
ZB
端口1，V1
ZC
V2，端口2
根据定义：

阻抗与导纳

+
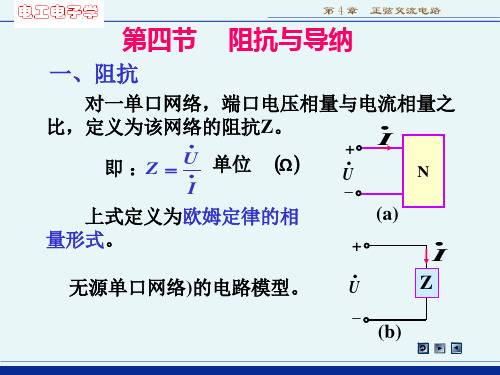
X L = ωL = 314 × 254 × 10 = 79.8Ω 1 1 XC = = = 39.8Ω −6 ωC 314 × 80 × 10
−3
Z = R + j( X L − X C ) = 30 + j(79.8 - 39.8)
= ( 30 + j40) = 50∠53.1o Ω
ɺ U 220∠20o ɺ I= = = 4.4∠ − 33.1o A Z 50 ∠53o
1 Z= Y
或
1 Y= Z
1、极坐标形式Z、Y之间的等效互换、极坐标形式、之间的等效互换形式 1 Z= 1 Y 即： ϕ 若 Z = Z ∠ϕ 则 Z∠ = Y∠ ′ ϕ ϕ = −ϕ′ 2、直角坐标形式Z、Y间的等效互换、直角坐标形式、间的等效互换形式 (1) 已知 Z=R+jX
1 则 Y = =G+ jB ： Z
2
2
Z
ϕ
X
R
阻抗三角形
ɺ U ∵ = Z ɺ I ɺ U ɺ ∴ ɺ = ZI =( R+jX) I
•
+
•
I
U
_
N
ɺ ɺ ɺ ɺ = RI +jXI =UR+UX
UR 与 I 同相
•
•
π UX 与 I 相差 2
•
•
•
I
+
U
U UX ϕ UR
•
•
UX I
•
•
R
jX
•
U
+ ɺ _ UR +
ϕ
UR
_
ɺ UX _
2
+ U – +U – ɺ1 ɺ + U – ɺ

阻抗和导纳

§8.2 正弦稳态分析(阻抗和导纳) 阻抗和导纳基本要求：
阻抗、导纳的概念阻抗角、导纳角的概念感性、容性的概念
1
§8.2 正弦稳态分析(阻抗和导纳)
在正弦稳态情况下，口电压相量与口电流相量之比称策动点阻抗或驱动点阻抗（简称阻抗）
Z ( j)
Um Im
Um Im
e j(u i )
1/ jC
IS
I1
I2
R1
R2 U0
U 01

R2 I 2

R1R2 R1 R2
1 jC
IS
9083.16
u01
2[90sin(t 83.16 )]
11
§8.2 正弦稳态分析(相量法)
②当=10rad/s时
U 02

R2 I 2

R1

R1R2
R2

1 j10C
IS

57639.8
Y ( j)
Im Um
Im Um
e j(i u )
Im Um
i
u
I
Y Y Y cosY j Y sin Y
G jB
U
其中 Y 导纳的模 Y 导纳角，约定 90 剟Y
G 电导，B 电纳。对同一端口，在同一频率下
90
Y1 Z
jB G
3
§8.2 正弦稳态分析(阻抗和导纳)
7
§8.2 正弦稳态分析(阻抗和导纳)
阻抗不同于正弦量的复数表示，它不是一个相量，而是一个复数计算量。
• 对同一端口来说 R 1
G
X1 B
Y1 1
R jX
Z R jX (R jX )(R jX )

微波工程-第4章微波网络分析

2Z0d 0.694 Z0d Z0a
电阻与耗散功率有关
4 Wm We I
2
电抗与储能有关
* 端口阻抗和反射系数的奇偶性
Z R jX Z 0 1 1
j
T=
波导模式的波阻抗——与传输线的形状、材料、频率和模式有关
Et 1 120 Zw H t Yw e Z TE or Z TM TEM quasi-TEM TE or TM
U , H
需满足条件三：人为指定特征阻抗（三种定义原则） 1. 特征阻抗等于波阻抗（特定模式的波阻抗） 2. 特征阻抗等于1
特性之间的关系时，可以采用类似于低频时的网络理论对微波传输线或元器件进行分析。
取定参考面 ti ，参考面以内是不均匀的，参考面以外是均匀传输线；将参考面以内的不均匀性等效成 N 端口网络；将参考面以外的均匀传输线等效成双导线。
微波工程基础第四章微波网络分析
微波工程基础第四章微波网络分析非TEM模的等效电压和电流（没有唯一解!!!）
I1 0
Z12
V1 I2

I1 0
V2 ZC ZC Z21 I2 ZB Z C
V1 S11 V2 S 21 SN1 VN
S12 S 22 SN 2
S1N V1 S2 N V2 S NN VN
Y0 iY0 j
P
n 1
N
n
0
单位矩阵——只有对角线上元素为1，其余元素均为0 * 广义散射矩阵与归一化阻抗矩阵的关系
S Z U

节点导纳和阻抗矩阵

Z ii—节点i的自阻抗或输入阻抗
Z ij—节点i和j之间的互阻抗
∑ Zij I j = Vi
j =1
n
—节点方程第i行
≠ 0, 如果令 I k
=V 则有 Z ik I k i
= I 0 j
或
1, 2,..., n, j ≠ k ) (j=
V Z ik = i I k
0, j ≠ k I = j
Z1q Z 2q Z iq Z pq Z qq
阻抗矩阵中对应于网络原有部分的全部元素保持原有数值不变
Z qq = ziq + Z ii
2. 追加连枝
叠加原理和替代定理
= Z I V i i1 1 + Z i 2 I 2 + + Z ik ( I k − I km ) + + Z im ( I m + I km ) + + Z ip I p =
YZ j = e j
Zj
ej
物理意义：当节点j注入单位电流，其余节点的注入电流都等于零时，网络各节点的电压在数值上就同阻抗矩阵的第j列的对应元素相等。
Y = LDU
LF = e j fi = =F DH UZ = H j
n
i< j 0 1 i j = i −1 l f i> j − ∑ k = j ik k
三、节点导纳矩阵的修改
根据原始节点导纳矩阵和修改的网络接线方式，快速形成修改后的节点导纳矩阵
(0) Y y + ii ik Y = − yik
− yik yik

阻抗和导纳

2006-1-1
！
3
阻抗和导纳(3)
İ
+
V
N0
−
İR
+
V
jX
−
İ + V G jB
−
İ + 或V
−
Z=R+jX
İ + 或V
−
Y=G+jB
图5.11 二端无源网络及其串联与并联等效电路
2006-1-1
！
4
阻抗和导纳(4)
在串联等效电路中，若X > 0，即ΨZ > 0，则电路具有电感特性，呈现感性；若X < 0，即ΨZ < 0，则电路具有电容特性，呈现容性。在并联等效电路中，若B > 0，即ΨY > 0，则电路具有电容特性，呈现容性；若B < 0，即ΨY < 0，则电路具有电感特性，呈现感性。
例电路如图5.10(a)所示。请问其等效阻抗和等效导纳。
解由于已知端电流为、端电压为，则
Z
V I
16
245 40
4
245 4 j4()
Y
I V
40 16 245
2 45 1 j 1 (S)
8
88
2006-1-1
！
5
阻抗和导纳(5)
并可按照图5.11画出其等效电路，且可以看出，该电路呈感性。当然，该例题也可直接根据电路的相量模型，写出等效阻抗为
这里，G为电Y导分VI量、VI B为(Ψ电i Ψ纳v分) 量G、 jΨB Y 为Y 导纳Y 角。
(5.27)
可以看出，对于同一网络有 |Z| = 1/|Y| 和 ΨZ = −ΨY的关系存在。根据式(5.26)和式(5.27)可知，一个二端无源网络可以等效为一个电阻与一个电抗串联或一个电导与一个电纳并联的形式，如图5.11所示。

电路中的阻抗与导纳

电路中的阻抗与导纳电路中的阻抗（Impedance）和导纳（Admittance）是电学中非常重要的两个概念。

阻抗是电路对交流电（AC）的抵抗能力，和电阻（Resistance）一样，单位是欧姆（Ohm），但是阻抗是一个复数。

导纳是电路对交流电的导电能力，和电导（Conductance）一样，单位是西门子（Siemens），也是一个复数。

1. 阻抗的定义和计算阻抗是电路对交流电的阻力，包括电容（Capacitance）、电感（Inductance）和电阻三种形式。

以电容为例，如果向电容放入交流电，首先会充电，然后在自身两极之间建立电场，导致电流的变化速度越来越慢，最后达到平衡状态。

因此，电容对交流电的阻力，和电流的相位差为90度。

电容的阻抗可以用以下公式计算：Z_c = 1/ jωC其中，Z_c 是电容的阻抗，j是虚数单位，ω是角频率（radians per second），C是电容的电容值（Farads）。

同理，电感的阻抗为：Z_l = jωL其中，Z_l 是电感的阻抗，L是电感的感抗值（Henries）。

电阻的阻抗为：Z_r = R其中，Z_r是电阻的阻抗，R是电阻的阻值（Ohms）。

将三种元件的阻抗按照欧姆定律叠加，可以得到整个电路的阻抗。

2.导纳的定义和计算导纳是对阻抗的倒数，“导纳”这个词在中文中的用法并不广泛，可能大家比较熟悉“电导”这个词，但是它们的意思是类似的。

导纳的计算方法如下：Y = 1/Z其中，Z是电路的阻抗，Y是电路的导纳。

导纳的好处在于，它更适合于串联和并联电路的计算。

将电路分解成元件，然后按照电路图的框架计算总的导纳，可以很方便地计算整个电路的电流和电压。

通过计算单元件的导纳，我们可以得到电路的传输特性，从而更好地理解电路的工作原理。

3.阻抗和导纳的应用阻抗和导纳在电路设计中有广泛的应用。

在RF电路中，阻抗匹配是非常重要的，它可以让信号在电路中以最大功率传输，从而减小反射损耗。

阻抗与导纳

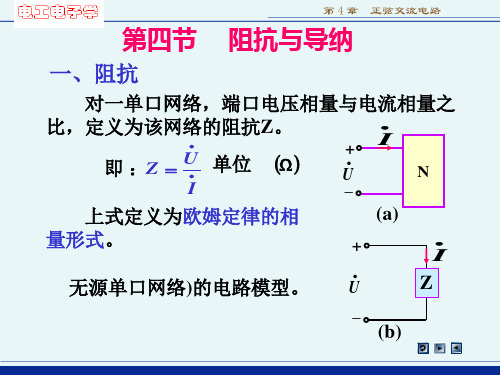
Z12 Z 23 Z2 Z12 Z 23 Z 31
Z 23 Z 31 Z3 Z12 Z 23 Z 31
使用以上公式时注意以下几点：
熟记基本元件的阻抗和导纳。同一元件或同一端口的阻抗和导纳互为倒数。
一般来讲，以上各公式中的阻抗和导纳用各自的模表示时，各等式不成立。例： Z Z1 Z 2 Z 3 Z n 和电阻电路中的分压、分流公式相同，在使用时，要注意符号与参考方向的关系。
o
C
注意： U U U U R L C
例2 如图所示电路。已知R1=3、 R2=8， o u 220 2 sin( 314 t 10 )V XC=6 、XL=4 ，求：各支路电流及总电流的瞬时值表达式。 I i 解: U 22010 o V
Z1 R1 jX L 3 j4 Z 2 R2 jX c 8 j6
3
Z R j( X L X C ) 30 j(79.8 - 39.8)
(30 j40) 5053.1o
22020o U o I 4.4 33 . 1 A o Z 5053
u R – + u u L – + u – C –
R L C
+ i1 u
。
2 1 I I
R1
XL
i2
R2
Xc
+
U
R1
R2
22010o 22010o U – – 1 I Z1 3 j4 553o 44 43 o A 相量模型 o o U 220 10 220 10 o 2 I 22 47 A o Z2 8 j6 10 37 o i 44 2 sin( 314 t 43 )A 1 o o I 1 I 2 44 43 2247 A I o

5.4阻抗与导纳及其等效变换

5．4 阻抗与导纳及其等效变换一、阻抗1．阻抗的定义及表示形式如下图(a)所示的单口无源线性两端网络N 0，设端口电压为2sin()u u U t ωϕ=+，对应的相量.u U U ϕ=∠，端口电流为2sin()i i I t ωϕ=+，对应的相量.i I I ϕ=∠。

则其端口电压相量与电流相量之比定义为该网络的阻抗Z ，即..()u i U UZ Z I Iϕϕϕ==∠-=∠ 由上式可得 u i U Z Iϕϕϕ⎫=⎪⎬⎪=-⎭说明：（1）Z 是一个复数，所以又称为复阻抗，Z 是阻抗的模，ϕ为阻抗角，它是电压与电流的相位差。

复阻抗的图形符号与电阻的图形符号相似，如上图(b)所示。

复阻抗的单位为Ω。

（2）阻抗Z 用代数形式表示时，可写为：j Z R X =+R ：Z 的实部，称为阻抗的电阻分量，单位：Ω，R 一般为正值；X ：Z 的虚部，称为阻抗的电抗分量，单位：Ω，X 的值可能为正，亦可能为负。

阻抗的代数形式与极坐标形式之间的互换公式：22arctan Z R X X R ϕ⎫=+⎪⎬=⎪⎭cos sin R Z X Z ϕϕ=⎫⎪⎬=⎪⎭由阻抗Z 的代数形式可知，由于R 一般为正值，所以有π2ϕ≤，且R 、X 和Z 三者之间的关系可用一个直角三角形表示，如上图（c ）所示。

2．阻抗的性质由于阻抗Z Z ϕ=∠而arctan XRϕ=，电路结构、参数或频率不同时，阻抗角ϕ可能会出现三种情况：（1）0ϕ>（即0X >）时，称阻抗的性质为感性，电路为感性电路；（2）0ϕ=（即0X =）时，称阻抗性质为电阻性，电路为阻性电路；（3）0ϕ<（即0X <）时，称阻抗性质为容性，电路为容性电路。

3．单口无源网络的串联等效电路由.......R X (j )j U Z I R X I R I XI U U ==+=+=+，可知.R U 与.I 同相位，.X U 与.I 相差π2。

第4章电力网络的数学模型

' ii

Y

Байду номын сангаас

Y
nn
Y
ki

Y ik Y kk
Y
1k
Ykk=yik，Yik=Yki=-yik，Yii’= Yii+Yii， Yii=yik 第j行、第j列的其它元素都为零，其余元素不变。 (2)在原有网络的节点i、j之间增加一支路：
Y i 1Y j 1 Y11 (1 ) I Y i 1 I ; Ii 1 Y11

式中
Y
(1 ) ij
Y ij

对方程式再作一次消元，其系数矩阵便演变为
Y11 (1 ) (1 ) Y 23 Y 2 n (2) (2) Y 33 Y 3 n (2) (2) Y n 3 Y nn Y1 n
I I
i
1 0, k 1,2, , n, k i
U

i
j
U
i
j
k
代入方程组有：
Z
ii
U
I
i
1
i
由此可见，当节点i上注入一单位电流，而其余的各节点均开路（即Ik=0）时，节点i上的电压即是自阻抗Zii的值（物理意义）。用数学式可表示为：
Z
ii

U i I i I
综上所述，阻抗矩阵有以下特点：
1. 与YB阵一样，ZB矩阵也是对称阵，且阶数相同；
2. 一般来说，ZB时满矩阵，不是稀疏阵；
3. 一般来说，，即ZB具有对角占优的特点， Z Z 这对迭代计算有利；

电路基础原理理解电路中的阻抗与导纳

电路基础原理理解电路中的阻抗与导纳电路是现代社会中常见的组成部分之一，我们在日常生活中经常会接触到各种电子设备和电路。

要深入理解电路的运作原理，了解阻抗和导纳的概念是非常重要的。

一、什么是阻抗和导纳？阻抗（Impedance）是指电路对交流电信号的阻碍程度，它由电阻、电感和电容三个因素共同构成。

阻抗一般用符号Z表示，单位是欧姆（Ω）。

阻抗分为实部和虚部，实部表示电路中的电阻，虚部表示电路中的电感和电容。

导纳（Admittance）是阻抗的倒数，表示电路对电流的容纳性。

导纳一般用符号Y表示，单位是西门子（S）。

导纳也有实部和虚部的分别，实部表示电路中的电导，虚部表示电路中的电纳。

二、阻抗与导纳的计算方法在交流电路中，阻抗和导纳的计算方法与直流电路中的电阻和电导类似。

对于纯电阻电路，阻抗与电阻数值相等，导纳与电导数值相等。

对于纯电感电路，阻抗由电感的大小、电路频率以及电感的内阻确定。

电感的阻抗为XL = 2πfL ，其中f表示频率，L表示电感值。

导纳为Y = 1 / Z 。

对于纯电容电路，阻抗由电容的大小、电路频率以及电容的内阻确定。

电容的阻抗为XC = 1 / (2πfC) ，其中C表示电容值，f表示频率。

导纳同样为Y = 1 / Z 。

三、阻抗与导纳的应用1. 阻抗与导纳的概念和计算方法在电路设计和分析中发挥着重要作用。

了解电路中的阻抗和导纳，可以帮助我们分析电路中的能量传输和功率流动情况，为电路的优化和设计提供指导。

2. 阻抗与导纳的概念也适用于通信领域。

在无线通信中，了解阻抗和导纳有助于我们理解信号在天线和传输线上的传播情况，从而提高通信质量和传输速率。

3. 阻抗与导纳的概念还可以应用于音响系统设计和音频信号处理中。

通过对扬声器和音频设备中的阻抗和导纳进行分析，可以优化音质和提升音频系统的性能。

四、总结阻抗和导纳是电路基础原理中的重要概念，它们的理解在电路设计和分析过程中具有重要的意义。

无论是在通信领域、音响系统设计还是电子设备开发中，了解阻抗和导纳的概念和计算方法都能够为我们提供更大的发展空间和创新的可能性。

射频电路设计_第4章_单端口网络和多端口网络(厦)

例题4．5 求解7形网络的4删参量矩阵 — 求解下面图中所示7形网络的朋cD参量矩阵：解：这个问题可以采用两种不同的方法求解。第1种方法是直接应用ABCD 参量矩阵元素的定义。按照前一例题的方法计算短阵元素。另一种方法是利
表4．1以两端口网络ABCD参量的形式总结了6种最常用的电路结构。根据这6种基本模型，大多数复杂电路都可以通过这些基本网络的适当搭配构成。
第四章单端口网络和多端口网络
主要内容：建立基本网络的输入、输出关系给出网络连接的规则介绍基于功率波关系的散射参量（S参量）
4.1 基本定义 4.2 互联网络 4.3 网络特性及其应用 4.4 散射参量
4.1基本定义
基本规则：不管单端网络还是N端网络，电流的脚标指明它
流入的相应网络端口；电压的脚标指明测量该电压的相应网络端口。如图
4.4 散射参量
4.4 散射参量
六、S参量的推广
4.4 散参量
4.4 散射参量
4.4 散射参量
七、散射参量的测量
常用的方法是采用矢量网络分析仪。如图
4.4 散射参量
4.4 散射参量
但负载的不理想，必然带来误差
4.4 散射参量
4.4 散射参量
4.3网络特性及其应用
一、网络参量之间的换算关系
由于电路结构的特殊性，有时需要在不同网络参量之间进行转换．以便得到特定的输入、输出特性表达式。例如，低频晶体管参数通常以h参量的形式给出，然而，当晶体管与其他网络级连时，ABCD参量也许是更合适的形式。所以，将h参量和ABCD 参量相互转换可以大大简化问题的难度。 1、从已知的A参量矩阵导出ABCD参量矩阵由定义式(4．11)，A元素可以表示为：
整个网络的ABCD参量矩阵等于各个网络ABCD参量矩阵的乘积。

阻抗与导纳

阻抗与导纳
阻抗与导纳
1. 阻抗: 无源二端网络端口上
电压相量与电流相量之比。

用极坐标来表示阻抗，可以写成
其中：z：阻抗模，φZ：阻抗角，R：电阻（分量〕，X：电抗（分量〕
阻抗模、电阻分量、电抗分量和阻抗角的关系可以用一个三角形来表示
当无源二端网络中同时含有电阻和电抗元件时，端口电压电流的相位差（阻抗角φZ）在-90°与+90°之间变化。

φZ>0：电压导前电流：N0为感性。

φZ<0：电压落后电流：N0为容性。

2．导纳：无源二端网络端口上电流相量与电压相量之比。

其中：G：电导分量，B：电纳分量
3．阻抗与导纳的关系
同一对端口
阻抗与导纳串并联
阻抗串联时：
阻抗并联时：
基本元件的阻抗与导纳
电阻元件的阻抗和导
纳为纯电阻，电感和
电容元件的阻抗和导
纳分别为纯电抗和纯
电纳。

电路的相量模型
将电路中电流，电压用相量表示；将基本元
件用它们的阻抗或导纳来标出，得到的电路
模型称为相量模型。

1、电感符号：L ，单位：h（亨特）感抗单位：Ω（欧姆）
2、电容符号：C ，单位：f（法拉）容抗单位：Ω（欧姆）
3、阻抗符号：Z，单位：Ω（欧姆）
4、导纳符号：Y，单位：s（西门子）。

《射频通信电路设计》第四章

Y Z
1
导纳矩阵与阻抗矩阵的关系
《射频通信电路》刘长军
4.1.2 阻抗矩阵和导纳矩阵
两端口射频网络的阻抗矩阵[Z] 和导纳矩阵[Y]
v1 Z11 i1 v2 Z , Z 22 i2 Z
i1 0
i2 0
v1 Z12 i2
i1 0
v2 Z , Z 21 i1

1
2
0 1
1 A AA AB AC jC 1
0 1 1 0
j L 1 jC 1 2
0 1
1 2 LC2 j L 3 2 j C C j LC C 1 LC 2 1 2 1 1
Y12
v2 0
i1 v2

v1 0
i1 Z 21i1 Z 22 i2
v1 0
Z 22 Z 1 Y11 22 Z Z11 Z 22 Z12 Z 21 Z Z11 21 Z12 Z 22
Y12
Z 1 12 Z11 Z Z 21 Z 22 Z12
《射频通信电路》刘长军
4.3.2 网络分析的应用
《射频通信电路》刘长军
4.3.2 网络分析的应用
1 1 1 YF R 1 1
cos l ATL j 1 sin l Z0
jZ 0 sin l cos l
Y Y ' Y ''
《射频通信电路》刘长军
4.2.3 网络的级联
i1 iA1 , v1 v A1 i2 iB 2 , v2 vB 2
iA 2 iB1 , v A 2 vB1

电路第4章-2(阻抗与导纳)

i + i1 u –
& I
R1
i2
R2
Xc
+
& U
R1
& I1
R2
& I2
XL
–
jXL - jX C
相量模型
解:
& U = 220∠10o V
1 1 1 = = = 0.2∠ − 53o S Y1 = R1 + jX L 3 + j4 5∠53o
1 1 1 Y2 = = = = 0.1∠37 o S R2 − jX C 8 − j6 10∠ − 37 o
U Um | Z |= = I Im
ϕ z = θu − θi
电压滞后电流， ϕ z < 0 电压滞后电流，容性电压电流同相， ϕ z = 0 电压电流同相，阻性
4.3.2 用阻抗法分析串联电路
相量模型将所有元件以相量形式表示：相量模型
C → − jX C 的阻抗
R R的阻抗
i + uR － R L － uC C (a) RLC 串联电路
Z = R + j( X L − X C )
5
1 ) = 5 + j (2 × 10 × 6 × 10 − 5 −6 2 × 10 × 0.001× 10
−3
= 5 − j 3.8 = 6.28∠ − 37.2° kΩ
ϕ z < 0 ，电路呈容性。
如果几个理想元件相串联几个理想元件相串联时，阻抗的模和幅角几个理想元件相串联可由以下三角形求出：
& & I1 = Y1U = 0.2∠ − 53o × 220∠10o = 44∠ − 43o A & & I 2 = Y2U = 0.1∠37o × 220∠10o = 22∠47o A

阻抗与导纳圆图

2

tan 1
RL2
2 X LZ0

X
2 L

Z02
二、圆图的基本构成
阻抗圆图是表示在复平面上的反射系数和归一化阻抗轨迹图，包括两个曲线坐标系统和四簇曲线。
1、反射系数曲线坐标（极坐标）：等反射系数模值圆反射系数相角射线
2、归一化阻抗曲线坐标：等归一化电阻圆等归一化电抗圆
1、反射系数曲线坐标
电流反射系数与导纳的关系
两个公式在形式上是完全相同的，所以导纳
圆图与阻抗圆图在图形坐标的数值、符号和曲线形状上是相同的，可以把阻抗圆图当作导纳圆图来使用，但是图上各点所代表的物理含义要作不同的解释。
1、导纳圆图的特点
jb' B 0.5
B0
容性
B 1
G 0.5
G 1
(0,0)
电压波腹 Rmax=S
上半圆阻抗为感抗，下半圆阻抗为容抗；
单位圆为纯电抗；
实轴为纯电阻；
实轴的右半轴为电压波腹，左半轴为电压波节；
匹配点、开路点和短路点。
三、导纳圆图
(z ') Z (z ') 1 Z (z ') 1
电压反射系数与阻抗的关系
'(z ') Y (z ') 1 Y (z ') 1
令 (z ') 2 e j a jb
可得
2a b2 Байду номын сангаас 2 且 2 1
等反射系数模值圆的方程
jb
||=0.5 S=3
j
||=1, =0
开路点
a
1
1
||=1, = 短路点

电力系统分析第4章习题答案

第四章思考题及习题答案4-1 节点导纳矩阵是如何形成的？各元素的物理意义是什么？节点导纳矩阵有何特点？答：节点导纳矩阵的对角元素称为自导纳，在数值上等于与该节点相连支路的导纳之和，其物理意义是：在该节点施加单位电压，其他节点全部接地时，由该节点注入网络的电流。

节点导纳矩阵的非对角元素称为互导纳，互导纳在数值上等于节点i 和ji Y j 之间支路导纳的负值，其物理意义是：在节点施加单位电压，其他节点全部接地时，经节点i j 注入网络的电流。

节点导纳矩阵有以下特点：其阶数等于电力网络中除参考节点之外的节点数；是稀疏矩阵；是对称矩阵；易于形成和修改。

4-2 节点阻抗矩阵中各元素的物理意义是什么？它有何特点？答：节点阻抗矩阵的对角元素称为自阻抗，其物理意义是：在该节点注入单位电流，其他节点全部开路时，该节点的电压值。

节点阻抗矩阵的非对角元素称为互阻抗，其物理意义是：互阻抗等于节点i 注入单位电流，其他节点全部开路时，节点ji Z j 的电压值。

节点导纳矩阵有以下特点：其阶数等于电力网络中除参考节点之外的节点数；是满矩阵；是对称矩阵；形成和修改较困难。

4-3 电力系统潮流计算中节点是如何分类的？答：电力系统进行潮流计算时，节点是可分为三类：（1）PQ 节点：给定节点的有功功率i P 和无功功率，待求节点电压幅值和相位角i Q i U i δ。

（2）PV 节点：给定节点的有功功率i P 和电压幅值，待求无功功率和电压的相位角i U i Q i δ。

（3）平衡节点（V δ节点）：给定节点电压幅值和电压相位角，待求节点的注入功率。

4-4 电力系统中变量的约束条件是什么？答：常用的约束条件有：（1）电压数值的约束：各节点电压幅值应限制在一定的范围之内，即； max .min .i i i U U U ≤≤（2）发电机输出功率的约束：电源节点的有功功率和无功功率应满足和；max .min .Gi Gi Gi P P P ≤≤max .min .Gi Gi Gi Q Q Q ≤≤（3）电压相角的约束：系统中两个节点之间的相位差应满足maxji j i ij δδδδδ−≤−=。

第4章-2(阻抗与导纳)

微波技术原理 第4章 微波网络基础

阻抗与导纳

阻抗和导纳

微波工程-第4章微波网络分析

节点导纳和阻抗矩阵

阻抗和导纳

电路中的阻抗与导纳

阻抗与导纳

5.4阻抗与导纳及其等效变换

第4章 电力网络的数学模型

电路基础原理理解电路中的阻抗与导纳

射频电路设计_第4章_单端口网络和多端口网络(厦)

阻抗与导纳

《射频通信电路设计》第四章

电路第4章-2(阻抗与导纳)

阻抗与导纳圆图

电力系统分析第4章习题答案

微波技术原理第4章微波网络基础

第4章电力网络的数学模型