第六章 时序逻辑电路-2
第6章_时序逻辑电路 课后答案

第六章 时序逻辑电路【题 6.3】 分析图P6.3时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,说明电路能否自启动。
Y图P6.3【解】驱动方程:11323131233J =K =Q J =K =Q J =Q Q ;K =Q ⎧⎪⎨⎪⎩ 输出方程:3YQ =将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+11313131n 12121221n+13321Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q +⎧=+=⎪=+=⊕⎨⎪=⎩ 电路能自启动。
状态转换图如图A6.3【题 6.5】分析图P6.5时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图。
A 为输入逻辑变量。
图A6.3Y图P6.5【解】驱动方程: 1221212()D AQ D AQ Q A Q Q ⎧=⎪⎨==+⎪⎩输出方程: 21Y AQ Q =将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+112n+1212()Q AQQ A Q Q ⎧=⎪⎨=+⎪⎩ 电路的状态转换图如图A6.51图A6.5【题 6.6】 分析图P6.6时序电路的逻辑功能,画出电路的状态转换图,检查电路能否自启动,说明电路能否自启动。
说明电路实现的功能。
A 为输入变量。
AY图P6.6【解】驱动方程: 112211J K J K A Q ==⎧⎨==⊕⎩输出方程: 1212Y AQ Q AQ Q =+将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+111n+1212QQ Q A Q Q ⎧=⎪⎨=⊕⊕⎪⎩ 电路状态转换图如图A6.6。
A =0时作二进制加法计数,A =1时作二进制减法计数。
01图A6.6【题 6.7】 分析图P6.7时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,说明电路能否自启动。
Y图P6.7【解】驱动方程: 001023102032013012301;;;J K J Q Q Q K Q J Q Q K Q Q J Q Q Q K Q==⎧⎪=•=⎪⎨==⎪⎪==⎩ 输出方程: 0123Y Q Q Q Q =将驱动方程带入JK 触发器的特性方程后得到状态方程为:*00*1012301*2023012*3012303()Q ()Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q⎧=⎪=++⎪⎨=++⎪⎪=+⎩ 设初态Q 1Q 3Q 2Q 1 Q 0=0000,由状态方程可得:状态转换图如图A6.7。
第6章 时序逻辑电路

J 和 K 接为互反,相当于一个D触发器。时钟相连 是同步时序电路。
电路功能: 有下降沿到来时,所有Q端更新状态。
2、移位寄存器 在计算机系统中,经常要对数据进行串并转换,移 位寄存器可以方便地实现这种转换。
左移移位寄存器
•具有左右移位功能的双向移位寄存器
理解了前面的左移移位寄存器,对右移移位寄存器 也就理解了,因位左右本身就是相对的。实际上,左右 移位的区别在于:N触发器的D端是与 Q N+1相连,还是 与Q N-1相连。
第六章 时序逻辑电路
如前所述,时序逻辑电路的特点是 —— 任一时刻 的输出不仅与当前的输入有关,还与以前的状态有关。
时序电路以触发器作为基本单元,使用门电路加以 配合,完成特定的时序功能。所以说,时序电路是由组 合电路和触发器构成的。
与学习组合逻辑电路相类似,我们仍从分析现成电 路入手,然后进行时序逻辑电路的简单设计。
状态化简 、分配
用编码表示 给各个状态
选择触发器 的形式
确定各触发器 输入的连接及 输出电路
NO 是否最佳 ?
YES
设计完成
下面举例说明如何实现一个时序逻辑的设计:
书例7-9 一个串行输入序列的检测电路,要求当序
列连续出现 4 个“1”时,输出为 1,作为提示。其他情 况输出为 0。
如果不考虑优化、最佳,以我们现有的知识可以很
第二步: 状态简化
前面我们根据前三位可能的所有组合,设定了 8 个
状态A ~ H,其实仔细分析一下,根本用不了这么多状态。
我们可以从Z=1的可能性大小的角度,将状态简化为
4 个状态:
a
b
c
d
A 000
B 100
D 110
数字电子技术基础-第六章_时序逻辑电路(完整版)

T0 1
行修改,在0000 时减“1”后跳变 T1 Q0 Q0(Q3Q2Q1)
为1001,然后按
二进制减法计数
就行了。T2 Q1Q0 Q1Q0 (Q1Q2Q3 )
T3 Q2Q1Q0
50
能自启动
47
•时序图 5
分 频
10 分 频c
0
t
48
器件实例:74 160
CLK RD LD EP ET 工作状态 X 0 X X X 置 0(异步) 1 0 X X 预置数(同步) X 1 1 0 1 保持(包括C) X 1 1 X 0 保持(C=0) 1 1 1 1 计数
49
②减法计数器
基本原理:对二进 制减法计数器进
——74LS193
异步置数 异步清零
44
(采用T’触发器,即T=1)
CLKi
CLKU
i 1
Qj
j0
CLKD
i 1
Qj
j0
CLK0 CLKU CLKD
CLK 2 CLKU Q1Q0 CLK DQ1Q0
45
2. 同步十进制计数器 ①加法计数器
基本原理:在四位二进制 计数器基础上修改,当计 到1001时,则下一个CLK 电路状态回到0000。
EP ET 工作状态
X 0 X X X 置 0(异步)
1 0 X X 预置数(同步)
X 1 1 0 1 保持(包括C)
X 1 1 X 0 保持(C=0)
1 1 1 1 计数
39
同步二进制减法计数器 原理:根据二进制减法运算 规则可知:在多位二进制数 末位减1,若第i位以下皆为 0时,则第i位应翻转。
Y Q2Q3
第6章-时序逻辑电路
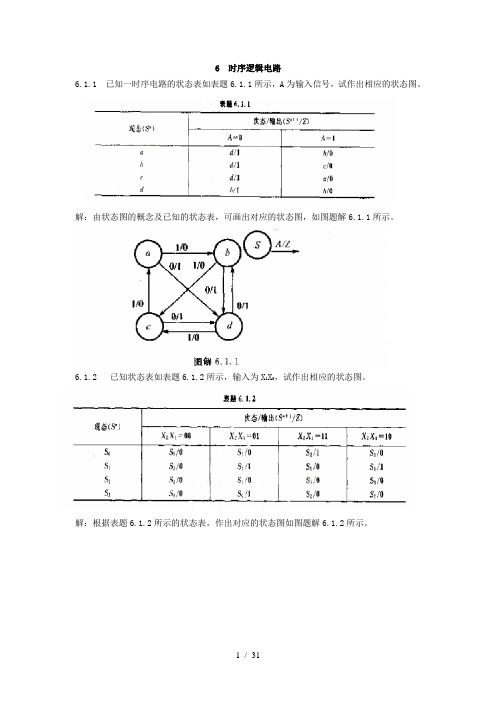
6 时序逻辑电路6.1.1 已知一时序电路的状态表如表题6.1.1所示,A为输入信号,试作出相应的状态图。
解:由状态图的概念及已知的状态表,可画出对应的状态图,如图题解6.1.1所示。
6.1.2已知状态表如表题6.1.2所示,输入为X1X0,试作出相应的状态图。
解:根据表题6.1.2所示的状态表,作出对应的状态图如图题解6.1.2所示。
6.1.3已知状态图如图题6.1.3所示,试列出它的状态表。
解:按图题6.1.3列出的状态表如表题解6.1.3所示。
6.1.5 图题6.1.5所示是某时序电路的状态图,设电路的初始状态为01,当序列A=100110(自左至右输入)时,求该电路输出Z的序列。
解:由图题6.1.5所示的状态图可知,当初态为01,输入信号的序列A=100110时,该时序电路将按图题解6.1.5所示的顺序改变状态,因而对应的输出序列为Z=011010。
6.1.6已知某时序电路的状态表如表题6.1.6所示,输入A,试画出它的状态图。
如果电路的初始状态在b,输入信号A一次是0、1、0、1、1、1、1,试求出其相应的输出。
解:根据表题6.1.6所示的状态表,可直接画出与其对应的状态图,如图题解6.1.6(a)当从初态b开始,依次输入0、1、0、1、1、1、1信号时,该时序电路将按图题解6.1.6(b)所示的顺序改变状态,因而其对应的输出为1、0、1、0、1、0、1。
6.2 同步时序逻辑电路的分析6.2.1 试分析图题6.2.1(a)所示时序电路,画出其状态表和状态图。
设电路的初始状态为0,试画出6.2.1(b)所示波形作用下,Q和Z的波形图。
解:由所给电路图可写出该电路的状态方程和输出方程,分别为1n nQ A QZAQ+=⊕=其状态表如表题解6.2.1所示,状态图如图题解6.2.1(a)所示,Q和Z的波形图如图题解6.2.1(b)所示。
6.2.2 试分析图题6.2.2(a)所示时序电路,画出其状态表和状态图。
数字电子技术第6章 时序逻辑电路

RD—异步置0端(低电平有效) 1 DIR—右移串行输入 1 DIL—左移串行输入 S0、S1—控制端 1 D0D1 D2 D3—并行输入
《数字电子技术》多媒体课件
山东轻工业学院
4、扩展:两片74LS194A扩展一片8位双向移位寄存器
《数字电子技术》多媒体课件
山东轻工业学院
例6.3.1的电路 (P276) 74LS194功能 S1S0=00,保持 S1S0=01,右移 S1S0=10,左移 S1S0=11,并入
(5)状态转换图
《数字电子技术》多媒体课件
山东轻工业学院
小结
1、时序逻辑电路的特点、组成、分类及描述方法; 2、同步时序逻辑电路的分析方法; 课堂讨论: 6.1,6.4
《数字电子技术》多媒体课件
山东轻工业学院
6.3 若干常用的时序逻辑电路
寄存器和移位寄存器 时序 逻辑电路 计数器 顺序脉冲发生器 序列信号发生器
移位寄存器不仅具有存储功能,且还有移位功能。 可实现串、并行数据转换,数值运算以及数据处理。 所谓“移位”,就是将寄存器所存各位数据,在每个移 位脉冲的作用下,向左或向右移动一位。
2、类型: 根据移位方向,分成三种:
左移 寄存器 (a) 右移 寄存器 (b) 双向 移位 寄存器 (c)
《数字电子技术》多媒体课件
学习要求 :
* *
自学掌握
1. 掌握寄存器和移位寄存器的概念并会使用; 2. 掌握计数器概念,熟练掌握中规模集成计数器74161 和74160的功能,熟练掌握用160及161设计任意进制计 数器的方法。
《数字电子技术》多媒体课件
山东轻工业学院
6.3.1寄存器和移位寄存器
一、寄存器
寄存器是计算机的主要部件之一, 它用来暂时存放数据或指令。
第六章 时序电路

二、时序逻辑电路的分类:
按 动 作 特 点 可 分 为
同步时序逻辑电路
所有触发器状态的变化都是在 同一时钟信号操作下同时发生。
异步时序逻辑电路
触发器状态的变化不是同时发生。
按 输 出 特 点 可 分 为
米利型时序逻辑电路(Mealy)
输出不仅取决于存储电路的状态,而且还 决定于电路当前的输入。
Q2 Q1 Q0
/Y
/0 /0 000→001→011 /1↑ ↓/0
CP Q0 010 Q1 Q2 Y
/0 101 /1 (b) 无效循环
100←110←111 /0 /0 (a) 有效循环
有效循环的6个状态分别是0~5这6个十进制数
字的格雷码,并且在时钟脉冲CP的作用下,这6个
状态是按递增规律变化的,即: 000→001→011→111→110→100→000→… 所以这是一个用格雷码表示的六进制同步加法 计数器。当对第6个脉冲计数时,计数器又重新从 000开始计数,并产生输出Y
Q=0时
LED亮
RD Q0 Q1 D1 Q2 D2 D3 Q3 S1
DIR D0 D1D2D3S0 DIL CLK +5V
74LS194
DIR D0
S0 DIL CLK +5V
清0按键 1秒
S1=0,S0=1
CLK 右移控制
本节小结:
寄存器是用来存放二进制数据或代
码的电路,是一种基本时序电路。任何
画状态转换图
Q3Q2Q1 /Y
000
/1 /1 111
/0
001
/0
010
/0
011 /0
第6章 时序逻辑电路-习题答案
第六章 时序逻辑电路6-1 分析题图6-1所示的同步时序电路,画出状态图。
题图6-1解: 11221211n n n n J K Q T Q Z Q Q ====,,,,11111111212n n n n nn n nQ J Q K Q Q Q Q Q Q +=+=+=+122212n n n n Q T Q Q Q +=⊕=⊕,状态表入答案表6-1所示,状态图如图答案图6-1所示。
答案表6-1答案图6-16-2 分析题图6-2所示的同步时序电路,画出状态图。
题图6-2 解:按照题意,写出各触发器的状态方程入下:11J K A ==,21n J Q =,21K =,1212n n nQ Q Q +=,111n n Q A Q +=⊕状态表入答案表6-2所示,状态图如图答案图6-2所示。
答案表6-2答案图6-2Q 2n Q 1n Q 2n+1 Q 1n+1 Z0 0 0 1 1 0 1 1 0 1 1 1 1 1 0 0 0 0 0 1A Q 2n Q 1n Q 2n+1 Q 1n+1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 1 1 0 0 0 1 0 1 1 0 0 1 0 0CLK D 1D 2D 3Q 3Q 2Q 1Q 2Q 3Q 1Q 1Q 2Q 3&6-3分析题图6-3所示的同步时序电路,画出状态图。
题图6-3解:按照题意,写出各触发器的状态方程入下:1112213232131n n n nn J K T J K Q Q T J Q Q K Q ========1,,, 133********n n n n n n n nQ J Q K Q Q Q Q Q Q +=+=+ 1222132n n n n nQ T Q Q Q Q +=⊕=⊕ 1111111n n n n Q T Q Q Q +=⊕=⊕=答案表6-3答案图6-36-4 在题图6-4所示的电路中,已知寄存器的初始状态Q 1Q 2Q 3=111。
数字逻辑设计第6章 时序逻辑电路习题与解答
L’/C 为 1 时,装入无效,161 对输入的 CLK 进行计数。 L’/C 为 1 或为 O 时,装入有效,而装入值为 D3=Q2,D2=Q1,D1=Q0,D0=串 行输入数据,所以该电路的功能将数据左移,低位补的是串行输入数据。 6-11 试分析图 6-74 的计数器在 C=1 和 C=0 时各为几进制计数器?
第 6 章 习题
6-1 说明时序电路和组合电路在逻辑功能和电路结构上有何不同?
题 6-1 答:
逻辑功能上,时序电路任一时刻的输出不仅取决于当时的输入,而且与电路 的原状态有关。
结构上的特点有两点: (1)时序电路中包含存储元件,通常由触发器构成。 (2)时序电路的存储元件的输出和电路输入之间存在着反馈连接。
Q2Q1Q0
000
/0
/1
001
/0
010
/0
101
/0
100
/0
011
由状态转换图可画出 Q2Q1Q0 和输出 F 的状态卡诺图如下:
Q1Q0 Q2 00 01 11 10
00
0
10
Q1Q0
Q2
00
01 11 10
00
10
0 10
11 0 X X
(a)Q2 卡诺图
Q1Q0 Q2 00 01 11 10
6-3 试分析图 6-69 所示时序逻辑电路的逻辑功能,写出电路的驱动方程、状态 方程和输出方程,画出电路的状态转换图。
F
FF0
DQ >C 1 Q
CLK
FF1
DQ >C 1 Q
图 6-69
题 6-3 解:根据图 6-69 可写出如下驱动方程:
第六章时序逻辑电路
CLK异0为步计计数数输器入与端、同Q步0为计输数出器端比,二,进具制有计如数下器 特点: CLK* 1电为计路数简输单入;端、Q3为输出端,五进制计数器 CLK* 1速与Q度0慢相连;、CLK0为输入端、Q3为输出端,十进制计数器
四、任意进制计数器的构成方法 设已知计数器的进制为N,要构成的任意进制计数
圆圈表示电路的各个状态,箭头表示状态表示的方向, 箭头旁注明转换前的输入变量取值和输出值
三、状态机流程图(SM图) 采用类似于编写计算机程序时使用的程序流程图的形
式,表示在一系列时钟脉冲作用下时序电路状态的流程以及 每个状态下的输入和输出。
四、时序图 在输入信号和时钟脉冲序列作用下,电路状态、
输出状态随时间变化的波形图。
电路在某一给定时刻的输出
取决于该时刻电路由的触输发入器保存 还取决于前一时刻电路的状态
时序电路: 组合电路 + 触发器
电路的状态与时间顺序有关
例:串行加法器电路
利用D触发器 把本位相加后 的进位结果保 存下来
时序电路在结构上的特点:
(1)包含组合电路和存储电路两个组成部分
(2)存储输出状态必须反馈到组合电路的输入端,与输入 信号共同决定组合逻辑电路的输出
串行进位方式以低位片的进位输出信号作为高位片的时 钟输入信号;
并行进位方式以低位片的进位输出信号作为高位片的 工作状态控制信号(计数的使能信号),两片的CLK同时接 计数输入信号。
二、异步计数器
B、减法计数器
二、异步计数器
B、减法计数器
根据T触发器的翻转规律即可画出在一系列CLK0脉冲信号 作用下输出的电压波形。
2、异步十进制计数器
J K端悬空相当于接逻辑1电平 将4位二进制计数器在计数过程中跳过从1010到1111这6个状态。
数字电路逻辑设计 第六章2
(一)反馈清零法
74160是模10计数器,要实现模853计数,须用三片74160级联。 ⑴先设计模1000计数器: M = M1×M2 ×M3=10 × 10 × 10=1000 ☆ 利用各片间进位信号快速传递方法,组成计数模值为1000计数器。 ⑵ 用异步清0法,使计数器计数脉冲输入到第853个脉冲时产整体置0 信号 使计数器返回到初始状态0000。 计数范围:
画出逻辑图如图
D2 D1 D0 CTT D3 CTP CTRDIV16 CO CT161 CR
LD
1
Q 3 Q2 Q 1 Q 0
0
0
&
O
0
(二)同步预置法
例:用四位同步二进制计数器74161设计余3BCD码计数器。
解:余3BCD码计数器的状态转移图如图所示
0011 1100
LD Q3Q2
画出逻辑图
&
1 CTP CR CTT 1
74161(1)
D0D1D2D3
Q0Q1Q2Q3 CO
CTP CTT
CR
74161(2)
D0D1D2D3
Q0Q1Q2Q3 CO
LD
LD
CP
(二)同步预置法
方法三、整体同步反馈置数: (利用进位输出作为置数译码信号) 计数范围196-255,当计数器计到255时,CO=1,使 两片74161置数控制端 /LD=0,下一个CP到来时置数。 预置输入=256-60=196 (196)10=(11000100)2 低位片预置数:0100 高位片预置数:1100
工作波形图: 5 6 7 8
9
10
6.5采用中规模集成器件设计任意进制计数器
1. M<N,N为单片计数器的最大计数值
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
若用非门连接,则正常输出。
M----大于N的素数(不能分解成N1*N2 )
整体置零方式:
将两片N进制计数器接成一个N*N(大于M )进制的计数器 在计数器为M状态(第M+1个状态)时译出异步置零信号 RD =0,将两片N进制计数器同时置零。
整体置数方式:
将两片N进制计数器接成一个N*N(大于M )进制的计数器
2、连接方式与特点 1)同步CP方式。
2)用低位的进位信号控制高位的功能转换端, 高位仅在 EP=ET=C1=1 的时间内计数。 3、进制 M 高位、低位各自能输出10个稳定状态:M = 10×10 = 100 高位的C 端是此计数器的进位输出端,进位信号为Y=1。
计数规律
计数脉冲序 号 电 路 状 态 进位输出C
0110 1011 状态转换图
0111
& 或者 & Q0 Y Y C Q3 Q2 Q1 Q0 CP< 0 0 0 1 0 0 1 RD 74LS160 EP 0 0 0 LD D3 D2 D1 D0 ET 0 0 1 0 0 1 1 1 1 1110 0 LD=0 /0 /0 1000 1001 0000 0001 /1 1010 0101 /0 0100 /0 (Q3Q2Q1Q0 / Y) 1100 1101
第六章
时序逻辑电路
任意进制计数器的构成方法
中规模集成计数器
前面介绍的同步(74160、74161、74190、 74191等)和异步计数器是组成中规模集成计数器 的基础。 包括二进制计数器、十进制计数器;有加法计 数器、加/减计数器(可逆计数器)等,它们通常都 具有计数、保持、预置数、清零(置零)等功能。
设:计数器的最大计数模值为N,若要得到一个模值为M (< N)的计数器,则只要在N进制计数器的顺序计数过程中,设法 跳过( N - M)个状态,只在M个状态循环计数即可。
1、反馈归0法---适用于有置零输入端的计数器,
如: 74160和74161
异步归零(如74160) 工作原理:
与计数脉冲CLK没有任何关系,只要异步清零计数端RD 出现 清零信号,计数器便立刻被清零。
整体置零方式、整体置数方式----M为素数,不 能分解成两数乘积
M=N1*N2
将一个N1进制计数器和一个N2进制计数器连接(串 行进位方式或并行进位方式)起来,构成M进制计数器。 例:用两片同步十进制计数器74160接成百进制计数器。 串行进位方式:用低位片的进位输出信号C接入高位片 的 时钟输入信号CLK。 并行进位方式:用低位片的进位输出信号C接入高位片的 工作状态使能控制信号EP/ET;两片的CLK输入端接在一 起作为计数输入信号。
例2 两片之间用非门连接的原理 74LS160是CP↑作用的计数器,若片间连接不用非门,则: 9 10 9 10 CP … CP …
Q0 Q1
1
0 0 1
0 0
Q0 Q1
1
0 0 1
0 0 0 0
低 位
Q2
Q3 C1
0
0
低 位
Q2
Q3 C1
高位 Q0 …
1
1
高位 Q0 …
0
1
第9个CP过后,电路输出 (1 ,1001),出错。
Y
1 1111 0010 /0 0011
例1的时序图: CP
0 Q0 1 2 3 4 5 6
例2的时序图: CP t
0 Q0 1 2 3 4 5 6
t 1 0 1 0 0 0
1 00
0 Q1
0 Q2
t
t
0 10 1 10
0 Q1
0 Q2 0 Q3 0
t
t
0 Q3 0
t t
t t
t t
0 00 或: 2Q0 Y=Q
1
1
解: 1、连接方式与特点 异步CP方式。(1)片Y’端的进位信号是(2)片的时钟。 (1)片是10进制, (即:两片之间是10进制)。 当两片计数到0001、0010状态时,电路整体清零。 Y 端是此计数器的进位输出端,进位信号为Y=0。
1
EP
ET D3 D2 D1 D0 C
EP
ET
D3 D2 D1 D0
C
74160(1)
Q3 Q2 Q1 Q0
RD
LD
74160(2)
Q3 Q2 Q1 Q0
RD
LD
计数 输入
1 CLK CLK
1
&
G1
&
进位输出
G2
用两片同步十进制计数器74160接成二十九进制计数器
整体置零方式
异步置零
注意:计数过程中,第(2)片74160不出 现1001状态,因而它的C端不能给出进位信号。 而且,门G1输出的脉冲时间极短,也不宜做进 位输出信号。 置零法可靠性差,而且还要另加译码电路 才能得到需要的进位输出信号。
X 0
X X
X X
X X
1 1
1
1 1
1
0 X
1
1 0
1
保持(包括C) 保持(C=0)
计数
任意进制计数器的构成方法
问题:已有的是N进制计数器,要得到的是M (任意正整数)进制计数器。
方法: 反馈置零法获得M进制计数器
反馈置数法获得M进制计数器
讨论:分 M<N 和 M>N 两种情况进行
M<N 的情况
0 0 0 0 1 1 1 1 0 0 0 0 0 …… 0 0 0 …… 0 0 1 1 0 0 1 1 0 0 0 0 1 0 0 0
Q0
0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 …. 1 0 0 ……
例2
试用两片74LS160构成百进制计数器。(串行进位) 为何用非门?
0
0
Y Y
0
Y=Q 或: 2
进位端的输出波形同左。
0
例3
用74LS160够成六进制,置入1001。
状态转换表 连线图 Q3 Q2 Q1 Q0 & 进位输出 0 0 0 0 0 0 0 1 Y 0 0 1 0 C Q3 Q2 Q1 Q0 CP< 0 0 1 1 LD 74LS160 EP 0 1 0 0 RD D3 D2 D1 D0 ET 跳 0 1 0 1 过 0 1 1 0 1 0 0 1 状 0 1 1 1 LD=0 态 1 0 0 0 置入 /0 /0 1 0 0 1 0001 0000 0010 Y=C=1 /0 /0 /0 状态转换图 1001 0100 0011 (Q3Q2Q1Q0 / Y) (检查自启动情况略)
1
1110
1111 Q3Q2Q1Q0
0000
0001
0010
0011
1001
0100
1101
1000
0111
0110
0101
1100
1100
1100
74160利用同步置数接成六进制计数器电路状态转换图
M>N的情况
用多片N进制计数器组合起来,构成M进制计数器。
各片之间的连接方式可分为:
串行进位方式、并行进位方式----M=N1 * N2
1010 1011 0110 状态转换图 3Q2Q1Q0 / Y) (Q /1 0101 1100 /0 /0 0100 /0 0011 1101
置零信号随着计数器 被置零而立刻消失, 如果有的触发器复位 速度慢有可能导致输 出错误
例1的时序图: CP
0 Q0 1 2 3 4 5 6
t
1 00
在选定的某一状态下译出 LD =0信号,将两个N进制计数 器同时置入适当的数据,跳过多余的状态,获得M进制计数器。
整体置零方式
首先,将两片74160以并行进位方式连成一个 百进制计数器.
计数器从0000状态开始计数,计入29个脉冲 时( S29 ) ,门G1译码立刻将两片74160同时 置零,得到二十九进制计数器。
0 Q1
0 Q2
t
t
0 10 1 10
0 Q3 0
t t
t
0 00 或: 2Q0 Y=Q
Y Y
0
Y=Q 或: 2
0
2、反馈置数法---适合于具有预置数功能的计数器
如:74160、74161和74LS190、74LS191
S0
Si
S i +1
置数操作可以在 任意状态下进行。
SN -1
Si+2 SN -2 SN -3 Sj Sj -1
Si S i +1
Si+2
N-M 个状 态
Sj
Sj -1
同步置数
利用第M个状态译码,使 LD=0,等下一个CP脉冲过后,电 路回到第一个循环状态。第M个状态为稳态。 例2: 用74LS160构成六进制计数器,置入0000。 连线图
状态转换表
CP 0 1 2 3 4 5 6 Q3 0 0 0 0 0 0 0 Q2 0 0 0 0 1 1 0 Q1 0 0 1 1 0 0 0
例1 试用两片74LS160构成百进制计数器。(并行进位) 1、连接线路 Y C Q3 Q2 Q1 Q0 EP (2) LD 74LS160 ET RD D3 D2 D1 D0 CP C Q3 Q2 Q1 Q0 EP< (1) LD 74LS160 ET RD D3 D2 D1 D0 CP 1
CP
1、连接线路 Y
C Q3 Q2 Q1 Q0 CP< 74LS160 EP LD (2) RD D3 D2 D1 D0 ET
1
C Q3 Q2 Q1 Q0 CP< 74LS160 EP LD (1) RD D3 D2 D1 D0 ET
