吉林省延边市长白山第一高级中学2021-2022高二数学上学期学科竞赛试题
吉林省长白山2022学年高中数学 全册综合素质检测 新人教A版必修2
2综合素质检测时间120分钟，满分150分。
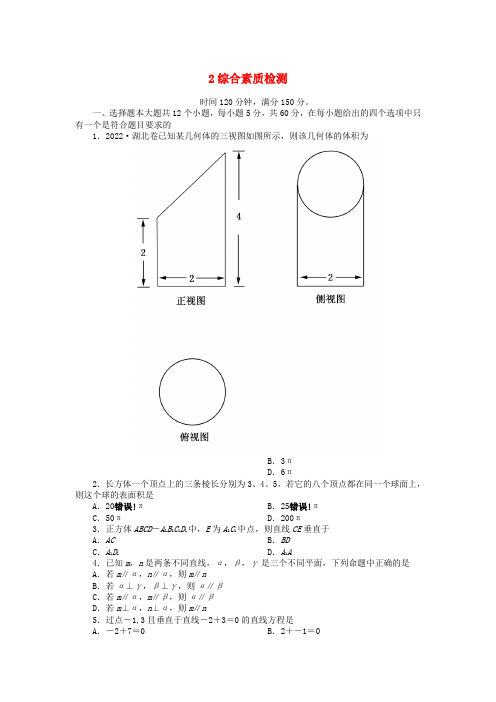
一、选择题本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的1．2022·湖北卷已知某几何体的三视图如图所示，则该几何体的体积为B．3πD．6π2．长方体一个顶点上的三条棱长分别为3、4、5，若它的八个顶点都在同一个球面上，则这个球的表面积是A．20错误!πB．25错误!πC．50πD．200π3．正方体ABCD－A1B1C1D1中，E为A1C1中点，则直线CE垂直于A．AC B．BDC．A1D1D．A1A4．已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是A．若m∥α，n∥α，则m∥nB．若α⊥γ，β⊥γ，则α∥βC．若m∥α，m∥β，则α∥βD．若m⊥α，n⊥α，则m∥n5．过点－1,3且垂直于直线－2＋3＝0的直线方程是A．－2＋7＝0 B．2＋－1＝0C．－2－5＝0 D．2＋－5＝06．若1C1C1C1C1C2a2a1C1C，n相交或异面，所以A不正确；B、C中还可能α，β相交，所以B、C不正确．很明显D正确．5[答案] B[解析] 设所求直线方程为－2－＋m＝0，则－2×－1－3＋m＝0，所以m＝1，即－2－＋1＝0，故直线方程为2＋－1＝06[答案] A[解析] 设圆心为C1,0，则AB⊥C1C1C1C－2,4在圆C上，所以切线的方程为－2－2－2＋4－1－1＝25，即4－3＋20＝1平行，所以－错误!＝错误!，即a＝－4，所以直线1的方程是－4＋3－8＝0，即4－3＋8＝＝错误!故选D11[答案] C[解析] 令a＝0，a＝1，得方程组错误!解得错误!所以C－1,2．则圆C的方程为＋12＋－22＝5，即2＋2＋2－4＝012[答案] B[解析] 如图，设A1,1，错误!＝|，为所求轨迹上任一点，则由题意知1＋||＝错误!，化简得2＝2||＋116[答案] 6 －2[解析] 由题设知直线1，2的交点为已知圆的圆心．由错误!得错误!所以－错误!＝－3，D＝6，－错误!＝1，E＝－217[解析]∵直线过2a2a N，DN，∵M是AE的中点，∴MN∥BE，∵△ABD是等边三角形，∴DN⊥AB由∠BCD＝120°知，∠CBD＝30°，所以∠ABC＝60°＋30°＝90°，即BC⊥AB，所以ND∥BC，所以平面MND∥平面BEC，故DM∥平面BEC21[解析] 1∵AB边所在直线的方程为－3－6＝0，且AD⊥AB，∴AD＝－3又∵点T－1,1在直线AD上，∴AD边所在直线的方程为－1＝－3＋1．即3＋＋2＝02由错误!解得点A的坐标为0，－2，因为矩形ABCD两条对角线的交点为M2,0．所以M为矩形ABCD外接圆的圆心．又|AM|＝错误!＝2错误!，则矩形ABCD外接圆的方程为－22＋2＝822[解析] 1证明：如图所示，取AB中点G，连CG、FG∵EF＝FB，AG＝GB，∴FG綊错误!EA又DC綊错误!EA，∴FG綊DC∴四边形CDFG为平行四边形，故DF∥CG∵DF⊄平面ABC，CG⊂平面ABC，∴DF∥平面ABC2证明：∵EA⊥平面ABC，∴AE⊥CG又△ABC是正三角形，∴CG⊥AB∴CG⊥平面AEB又∵DE∥CG，∴DF⊥平面AEB∴平面AEB⊥平面BDE∵AE＝AB，EF＝FB，∴AF⊥BE∴AF⊥平面BED，∴AF⊥BD3解：延长ED交AC延长线于G′，连BG′由CD＝错误!AE，CD∥AE知，D为EG′的中点，∴FD∥BG′又CG⊥平面ABE，FD∥CG∴BG′⊥平面ABE∴∠EBA为所求二面角的平面角．在等腰直角三角形AEB中，易求得∠ABE＝45°。
吉林省延边市长白山第一高级中学2022-2022学年高二生物上学期学科竞赛试题
吉林省延边市长白山第一高级中学2022-2022学年高二生物上学期学科竞赛试题时间：90 分钟分值：100 分一、单选题（本题共40个小题，其中1-20每小题1分，21-40每小题2分，共60分）1．下列不属于人体内环境的组成成分是（）A．Ca2+B．纤维蛋白原C．血红蛋白D．淋巴因子2．人体内环境的稳态不包括（）A．组织液温度的相对稳定B．线粒体基质中pH的相对稳定C．血浆渗透压的相对稳定D．血浆中各种化学成分的相对稳定3．下列与生物节律有关的结构是（）A．大脑皮层B．脑干C．小脑D．下丘脑4．下列哪项不是兴奋传导和传递的区别（）A．方式不同 B．方向不同 C．结构不同D．一个需要ATP，—个不需要5．研究甲状腺激素对蝌蚪发育的影响宜采用（）A．摘除法B．植入法C．饲喂法D．注射法6．糖尿病的主要症状是（）A．少饮、少食、少尿、消瘦B．多饮、少食、多尿、消瘦C．多饮、多食、多尿、消瘦D．少饮、多食、少尿、消瘦7．下列关于人体神经调节的叙述，正确的是（）A．调节方式是反射 B．不受激素影响 C．不存在信息传递 D．能直接消灭入侵病原体8．下列关于寒冷环境下体温调节的叙述正确的是（）A．皮肤血管舒张 B．汗液的分泌增加 C．甲状腺素分泌量增加 D．生长激素分泌增加9．大量饮用清水会导致尿液生成速率加快，原因是（）A．血浆渗透压增加 B．抗利尿激素分泌减少C．肾小管重吸收作用增强 D．细胞内液电解质流失10．结核杆菌感染人体并侵入细胞后会引起结核病，体内接触该靶细胞并导致其裂解的免疫细胞是( )A．浆细胞B．T淋巴细胞C．B淋巴细胞D．效应T细胞11．乙肝疾病（病毒）流行时，对进出某地区的人群进行体温测量的作用是（）A．发现易感人群 B．保护易感人群 C．控制传染源D．切断传播途径12．下列不属于艾滋病的主要传播途径是（）A．血液传播B．胎盘传播C．空气传播D．体液传播13．下列与免疫失调无关的疾病是（）A．皮肤荨麻疹 B．类风湿性关节炎 C．艾滋病 D．苯丙酮尿症14．不食不洁生水和生贝壳类海产品是防止霍乱发生的有效措施之一，可推断霍乱弧菌的传播方式是（）A．空气传播B．接触传播C．媒介物传播D．病媒传播15．预防细菌或病毒感染最有效的方法是接种疫苗，疫苗本质上属于（）A．抗原 B．抗体 C．淋巴因子D．抗原受体16．如图所示，用不透水的云母片插入燕麦幼苗的胚芽鞘尖端部分，并以右侧单侧光照其尖端，培养一段时间后，胚芽鞘的生长情况是（）A．向光(右)弯曲生长 B．向左弯曲生长C．不弯曲但直立生长 D．不弯曲也不生长17．生长素类似物在生产实践中通常不会用于（）A．解除顶端优势 B．培育无子番茄 C．促进插条生根 D．疏花疏果18．进行种群密度的取样调查时不宜采用的做法是（）A．样方内各年龄段的植物均需统计B．选取多种植物为调查对象C．计算各样方内的平均值D．随机选取大小相等的若干块方形地块为样方19．下列不属于种群特征的是（）A．种群密度B．年龄组成C．物种丰富度D．个体的均匀分布20．群落演替是一个长期而复杂的过程，下列有关群落演替说法错误的是（）A．光裸的岩石上发生的演替中地衣往往是群落演替的先驱物种B．自然条件下随着群落演替的进行，物种丰富度一般增加C．随着科技的发展，人类可任意改变群落演变的速度、方向和演替程度D．决定群落演替的根本原因存在于群落内部，外界环境变化也常成为引发演替的条件21．树林里多数鸟类在树冠筑巢、栖息，啄木鸟在树干上寻找食物，环颈雉在灌木层和地面活动，这种现象反映了（）A．群落的垂直结构 B．群落的水平分布 C．群落的物种组成 D．群落的物种丰富度22．下列有关生态系统成分的叙述，不正确的是（）A．自养生物都属于生产者，都可以进行光合作用，把无机物转变成有机物B．动物不都是消费者，其中食草动物为初级消费者C．分解者都是腐生生物，都是生态系统不可缺少的成分D．非生物的物质和能量是指土壤、阳光、水分、空气、热能等23．下列关于人体细胞外液的叙述，不正确的是（）A．人体的细胞外液即内环境B．细胞外液的化学成分中有葡萄糖、无机盐、激素、尿素等物质C．细胞外液主要成分之间的关系途径之一可表示为组织液→淋巴→血浆D．小肠壁的肌细胞可以不通过细胞外液从肠道直接吸收葡萄糖24．**研究人员发现了一个有趣的现象，肥胖可能与大脑中多巴胺的作用有关，多巴胺是一种重要的神经递质，在兴奋传导中起着重要的作用。
长白山一高高二数学第三章综合素质能力检测及备选题库
第三章综合素质能力检测及讲评备选练习一、选择题（本大题共12个小题,每小题5分，共60分，在每小题给出的四个选项中，只有一项是符号题目要求的．）1．a、b∈R,下列命题正确的是( )A．若a＞b，则a2＞b2B．若|a｜＞b，则a2＞b2C．若a＞|b｜，则a2＞b2D．若a≠｜b｜，则a2≠b22．设M＝2a（a－2)＋7，N＝(a－2）(a－3），则有( ）A．M＞N B．M≥NC．M＜N D．M≤N3．不等式x2－2x－5＞2x的解集是( )A．｛x｜x≥5或x≤－1｝B．{x｜x＞5或x＜－1}C．{x|－1＜x＜5}D．{x|－1≤x≤5}4．若a＞b＞0，全集U＝R,A＝{x｜ab＜x＜a｝，B＝｛x｜b＜x＜错误!}，则(∁U A）∩B为（）A ．{x ｜b ＜x ≤错误!｝B ．{x ｜错误!＜x ＜错误!}C ．{x ｜b ＜x ＜错误!｝D ．｛x |x ＜错误!或x ≥a ｝5．不等式x ＋(a －1）y ＋3＞0表示直线x ＋(a －1）y ＋3＝0( ）A ．上方的平面区域B ．下方的平面区域C ．当a ＞1时表示上方的平面区域，当a ＜1时表示下方的平面区域D ．当a ＜1时表示上方的平面区域,当a ＞1时表示下方的平面区域6．已知方程x 2＋2x ＋2a ＝0和x 2＋2(2－a ）x ＋4＝0有且只有一个方程有两个不相等的实根，则实数a 的取值范围是（ )A ．a ＜12或a ＞4B ．0≤a ＜错误!或a ＞4C ．0＜a ≤错误!或a ≥4D 。
错误!＜a ≤47．已知a ＞0，b ＞0，m ＝错误!＋错误!，n ＝错误!＋错误!，p ＝错误!,则m 、n 、p 的大小顺序是（ ）A ．m ≥n ＞pB ．m ＞n ≥pC ．n ＞m ＞pD ．n ≥m ＞p8．(2011·福州模拟）设f (x ）＝3ax －2a ＋1，若存在x 0∈（－1,1),使f(x0）＝0，则实数a的取值范围是( ）A．－1＜a〈错误!B．a＜－1C．a＜－1或a＞错误!D．a＞错误!9．不等式（x＋5）(3－2x)≥6的解集是( ）A。
2021-2022年高二数学竞赛试卷含答案
13．（本小题满分 20 分）
已知椭圆的中心在坐标原点，左顶点，离心率，为右焦点，过焦点的直线交椭圆于、两点（不
同于点）．
（Ⅰ）求椭圆的方程；
（Ⅱ）当时，求直线 PQ 的方程；
（Ⅲ）判断能否成为等边三角形，并说明理由．
13．解：（Ⅰ）设椭圆方程为 (a>b>0) ，
由已知
∴
-----------------------------------------2 分
)(
x0
2
x1
)
x02
x1
( x02
1)2 4
x02
∵，∴ ．解得．
∴直线 PQ 方程为，即或． ----------12 分
解法二： 椭圆右焦点．当直线的斜率不存在时，，不合题意．
设直线方程为，
--------------------------------------5 分
由 得 3 4k 2 x2 8k 2x 4k 2 12 0 ． ①
.
3．定义两种运算：，，则函数为（ ）
（A）奇函数 （C）奇函数且为偶函数
（B）偶函数 （D）非奇函数且非偶函数
3．A． f (x) 22 x2 22 x2 22 x2 (x [2, 2]) .
(2 x)2 2 | 2 x | 2
x
4．圆周上按顺时针方向标有 1，2，3，4，5 五个点，一只青蛙按顺时针方向绕圆从一个点跳
∴ 5 x 2 ( y 1) 2 其表示双曲线上一点（x,y)到定点（0,-1)与定直线 x-2y+3=0 之比为常数 e=, m | x2y3| 5
又由 e>1,可得 0<m<5.
7．直线 ax+by-1=0(a,b 不全为 0),与圆 x2+y2=50 有公共点，且公共点的横、纵坐标均为整数，
2021-2022年高二数学上学期竞赛期中试题理
2021-2022年高二数学上学期竞赛期中试题理一、选择题：本题共12小题，每小题5分，共60分。
1、设集合2A B x x x m==-+=，若，则（）{1,2,4},{|40}A． B. C. D.2、设，则“是“”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3、某几何体的三视图如图所示，则该几何体的体积为（）A. B.C． D.4、将的图象向左平移个单位，则所得图象的函数解析式为（）A. B. C. D.5、设点是所在平面内一点，且，则等于（）A. B. C. D.6．设，若是的等比中项，则的最小值为（）A. 8B.C. 4D. 17、若，则（）A. B. C. 1 D.8、下面程序执行后输出的结果是（）A. 4B.C.D.9、在棱长为的正方体中随机地取一点P ，则点P 与正方体各表面的距离都大于的概率为( )A. B. C. D.10、若偶函数在上单调递增， ()()3224log 3,log 5,2a f b f c f ⎛⎫=== ⎪⎝⎭，则满足（ ）A. B. C. D.11、已知函数211()sin sin (0)222x f x x ωωω=+->，，若在区间内没有零点，则的取值范围是（ ）A B C. D.12、数列满足，则数列的前60项和为（ ）A 3690B 3660C 1845D 1830二、填空题：本题共4小题，每小题5分，共20分。
13、已知是夹角为的两个单位向量，，，若，则的值为 。
14、已知实数 满足30102x y x y x +-≥⎧⎪-+≥⎨⎪≤⎩，则的最小值为_______________。
15、在中，内角的对边分别为，且满足222sin sin sin sin sin A B A B C ++=，则的取值范围为______________。
16、已知函数2||,()24,0x x mf x x mx m x ≤⎧=⎨-+>⎩，其中，若存在实数，使得关于的方程有三个不同的根，则的取值范围是______________。
2021年高二数学上学期竞赛试题 文
2021年高二数学上学期竞赛试题 文一、选择题(本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的）1、已知等差数列的首项为3，公差为2，则的值等于 ( )A ．1B ．14C ．15D ．162、ABC 中，AB =，，C =75则BC= ( )A ．3B ．C ．2D ．3+3、若，则下列不等式中，正确的不等式有 ( )① ② ③ ④A.1个B.2个C.3个D.4个4、已知等差数列中，前n 项和为S ，若+=6，则S 11= ( )A ．12B ．33C ．66D ．995、对于任意实数a ，b ，c ，d ，以下四个命题中①ac 2>bc 2，则a >b ；②若a >b ，c >d ，则；③若a >b ，c >d ，则；④a >b ，则>其中正确的有( )A ．1个B ．2个C ．3个D ．4个6、已知等比数列，若+=20，+=80，则+等于( )A ．480B ．320C ．240D ．1207、在ABC 中，角A 、B 、C 的对边分别是a 、b 、c ，若，则角B 的值为 ( )A ．B ．C ．或D ．或8、已知等比数列中，则其前3项的和的取值范围是( )A ．B ．C ．D ． 9、下列函数中，最小值为4的是（ ）A ．B ．C ．D ．10、数列满足a 1=1，，则使得的最大正整数k 为( )A ．5B ．7C ．8D ．10二、填空题(本大题共5个小题，每小题5分，共25分，将答案填在题后的横线上)11、在中，，那么A ＝_____________。
12、已知某等差数列共有10项，其奇数项之和为15，偶数项之和为30，则公差为 。
13、已知B A m m B m m A m ,,1,1,1则设--=-+=>之间的大小关系是 。
14、已知数列是一个公差不为0等差数列，且a 2=2，并且成等比数列，则=_____ ___。
吉林省长白山一高2021 2021学年上学期高二数学必修5第二章数列综
吉林省长白山一高2021 2021学年上学期高二数学必修5第二章数列综吉林省长白山一高2021-2021学年上学期高二数学必修5第二章数列综吉林长白山第一中学2022-2022第一学期高二数学必修5第二章数列综合素质能力检测试题一、多项选择题（本主题共有12个子题，每个子题得5分，共60分。
在每个子题给出的四个选项中，符号题只需要一个选项。
）1．(2021～2021河南汤阴县一中高二期中)等比数列{an}中，a7a11A20=6，A4+A14=5，然后a=（）10232a。
3或2B 3311c。
2d。
3或-22。
如果已知等比序列{an}的前n项之和为Sn，A1=1，并且满足Sn，Sn+2，Sn+1形成等差序列，则A3等于（）11a.2b．－211c.4d．－43．(2021辽宁理，6)在等差数列{an}中，已知a4＋a8＝16，则该数列前11项和s11＝()a、 58b.88c.143d.1764．已知－1，a1，a2,8成等差数列，－1，b1，b2，b3，－4成等A1A2比率序列，那么B的值是（）2a、－5b.555c．－2d.25.在算术序列{an}中，A1=-8，前16项的平均值为7。
如果提取了一个项目，其余15个项目的平均值为7.2，则提取的项目为（）a．第7项b．第8项c．第15项d．第16项6．(2021新课标全国理，5)已知{an}为等比数列，a4＋a7＝2，a5a6=-8，然后是a1+A10=（）a．7b．5c．－5d．－77．(2021北京朝阳区期末)已知数列{an}的前n项和为sn，且sn=2an-2，则A2等于（）a．4b．2c．1d．－2第1页共8页金太阳新课程标准资源网8．某工厂去年产值为a，计划今后5年内每年比上年产值增加10%，则从今年起到第5年，这个厂的总产值为()a、 1.14ab.1.15ac.11×（1.15－1）ad.10（1.16－1）a9．一个等差数列共有10项，其中奇数项的和为26，偶数项的和为15，则这个数列的第6项是()a、 3b。
2021-2022年高二数学上学期竞赛期中试题文
2021-2022年高二数学上学期竞赛期中试题文总分：150分 时间：120分钟一.选择题（每小题5分，共60分）1．已知集合，，则（ ）A. B. C. D.2．下列函数中，既是偶函数又是上的增函数的是A. B. C. D.3．若，则则的值等于 （ ）A. B. C. D.4．《九章算术》是我国古代的数学名著，书中有如下问题：“今有五人分五钱，令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分钱，甲、乙两人所得与丙、丁、戊三人所得相同，且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱？”（“钱”是古代的一种重量单位）.这个问题中，甲所得为A.钱B.钱C.钱D.钱5．若的内角满足，则（ ）A. B. C. D.6．已知实数c b a c b a ,,,23tan 123tan 2,25sin 21,24sin 24cos 2222则︒-︒=︒-=︒-︒=的大小关系为（ ）A. B. C. D.7．设是等比数列的前项和， ，则 的值为（ ）A. B. C. 或 D.8．若把函数的图象向右平移个单位后所得图象关于坐标原点对称，则的最小值为（ ）A. B. C. D.9．三棱锥及其正视图和侧视图如下图所示，且顶点均在球的表面上，则球的表面积为（ ）A ．B ．C ．D ．10．下列命题中,正确命题的个数为（ ）①若,则或”的逆否命题为“若且,则；②函数的零点所在区间是；③是的必要不充分条件A ．B ．C ． D.11．若圆上有且只有两个点到直线的距离等于，则半径的取值范围是( )A. B. C. D.12． 已知平面平面，，点，直线，直线，直线，则下列四种位置关系中，不一定成立的是（ ）A. B. C. D.二、填空题（共4题，每小题5分，共20分）13．已知实数，满足⎪⎩⎪⎨⎧<-->+->++02306203y x y x y x 则的最小值为_______14．若关于的不等式对任意恒成立，则实数的取值范围是_________15．已知实数成等差数列，且公差为；成等比数列，且的最小值为16．在中，已知 60,2,1=∠==A AC AB ，若点满足，且，则实数的值为______________三、解答题（本题共6题，共70分）17．（本小题10分）已知函数()sin 14f x x x π⎛⎫=+- ⎪⎝⎭． （1）求的值；（2）求在区间上的最大值和最小值．18．（本小题12分）已知函数．（1）求不等式的解集；（2）若关于的不等式有解，求实数的取值范围．19．（本小题12分）如图，已知四棱锥中，底面为菱形，平面，为上任意一点．（1）证明：平面平面；（2）试确定点的位置，使得四棱锥的体积等于三棱锥体积的4倍．20．（本小题12分）数列满足.（1）证明是等比数列，并求数列的通项公式；（2）已知符号函数⎪⎩⎪⎨⎧<-=>=0,10,00,1)sgn(x x x x 设，求数列的前项和.21．（本小题12分）漳州市博物馆为了保护一件珍贵文物，需要在馆内一种透明又密封的长方体玻璃保护罩内充入保护液体.该博物馆需要支付的总费用由两部分组成：①罩内该种液体的体积比保护罩的容积少立方米，且每立方米液体费用元；②需支付一定的保险费用，且支付的保险费用与保护罩容积成反比，当容积为立方米时，支付的保险费用为元.（1）求该博物馆支付总费用与保护罩容积之间的函数关系式；（2）求该博物馆支付总费用的最小值.22．（本小题12分）已知圆22:2430C x y x y ++-+=．（1）若圆的切线在轴和轴上的截距相等，求此切线的方程．（2）从圆外一点向该圆引一条切线，切点为， 为坐标原点，且有，求使得取得最小值的点的坐标．答案：1.B2.B3.C4.B5.D6.B7.C8.A9．A10.C11．A12.A13.-5；14.；15.6；16.1或17. （Ⅰ）因为sin 1442f πππ⎛⎫=- ⎪⎝⎭（Ⅱ）()sin 14f x x x π⎛⎫=+- ⎪⎝⎭sin +cos 122x x x ⎛⎫=⋅- ⎪ ⎪⎝⎭ 22sin cos 2cos 1x x x =+-因为， 所以所以 故124x π⎛⎫-≤+≤ ⎪⎝⎭ 当即时， 有最大值当即时， 有最小值18. 解：（Ⅰ）不等式f （x ）＜8，即|2x+3|+|2x ﹣1|＜8，可化为①或②或③，…解①得﹣＜x ＜﹣，解②得﹣≤x≤，解③得＜x ＜，综合得原不等式的解集为{x|-}．（Ⅱ）因为∵f（x ）=|2x+3|+|2x ﹣1|≥|（2x+3）﹣（2x ﹣1）|=4，当且仅当﹣≤x≤时，等号成立，即f （x ）min =4，…又不等式f （x ）≤|3m+1|有解，则|3m+1|≥4，解得：m≤﹣或m≥1．19. （Ⅰ）证明：∵平面，平面，∴，又∵底面为菱形，∴，，平面，平面，∴平面，又平面，∴平面平面．（Ⅱ）若四棱锥的体积被平面分成两部分，则三棱锥的体积是整个四棱锥体积的，设三棱锥的高为，底面的面积为，则，由此得，故此时为的中点．20 （Ⅰ）因为， 所以，所以数列是公比为，首项为的等比数列. 故，即.（Ⅱ）()()()21,sgn {21,n n n n n n b a a n +=⋅=-为偶数为奇数 数列的前项和 ()()()()()23991001002121212121S =-+++-+⋯+-++ 23100101222222=+++⋯+=-.21. 解：（Ⅰ）由题意设支付的保险费用，把， 代入，得.则有支付的保险费用（）故总费用()800080005000.5500250y x x x x=-+=+-，（ ）（Ⅱ）因为 2503750= 当且仅当且，即立方米时不等式取等号，所以，博物馆支付总费用的最小值为3750元.22. 解：（1）圆，所以圆心．①切线过原点，由题知，此时切线斜率必定存在，设．则，解得或．②切线不过原点，设，则，解得或．综上所述：切线方程为或或．（2）因为，且，即()()22221111122x r x y +=++--，整理得，则，所以222222211111339||252520PM PO x y y y y ⎛⎫⎛⎫==+=-+=-+ ⎪ ⎪⎝⎭⎝⎭．当时， ，此时．综上所述为时， 最小，最小值为．20734 50FE 僾26707 6853 桓5+26623 67FF 柿23859 5D33 崳-24028 5DDC 巜 36361 8E09 踉37701 9345 鍅28855 70B7 炷23051 5A0B 娋h35915 8C4B 豋。
长白山一高高二数学全册综合素质能力检测
必修5全册综合能力检测一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符号题目要求的．) 1．等差数列｛a n}中，a1＋a4＋a7＝39，a2＋a5＋a8＝33,则a5＋a8＋a11的值为（)A．30 B．27C．9 D．152．在△ABC中,B＝45°，C＝60°,c＝1，则最短边的边长等于（）A。
错误!B。
错误!C。
错误!D。
错误!3．不等式f(x)＝ax2－x－c>0的解集为{x｜－2〈x<1｝,则函数y ＝f(－x)的图象为( )4．已知数列｛a n｝，满足a n＋1＝错误!，若a1＝错误!,则a2012＝( ）A.错误!B．2C．－1 D．15．已知△ABC中，b＝30,c＝15，∠C＝29°,则此三角形解的情况是( ）A．一解B．两解C．无解D．无法确定6．用钢管制作一个面积为1m2，形状为直角三角形的铁支架框，有下列四种长度的钢管供选择，较经济（够用，又耗材最少）的是( )A．4。
6m B．4。
8mC．5m D．5。
2m7．公差不为零的等差数列的第1项、第6项、第21项恰好构成等比数列,则它的公比为（)A.错误!B．－错误!C．3 D．－38．已知Ω＝{(x，y)｜x＋y≤6，x≥0，y≥0｝，A＝{(x，y)｜x≤4,y≥0，x－2y≥0},若向区域Ω内随机投一点P,则点P落在区域A内的概率为（)A。
错误!B。
错误!C.错误!D。
错误!9．设a，b∈R,a2＋2b2＝6，则a＋b的最小值是( )A．－2 2 B．－错误!C．－3 D．－错误!10．钝角△ABC的三边长为连续自然数,则这三边长为( ）A．1,2,3 B．2，3,4C．3,4，5 D．4,5,611．(2012·福建文，11)数列｛a n｝的通项公式a n＝n cos nπ2，其前n项和为S n，则S2012等于（）A．1006 B．2012C．503 D．012．在R上定义运算⊕:x⊕y＝x（1－y)，若不等式(x－a)⊕(x＋a)〈1对任意实数x成立，则（）A．－1〈a<1 B．0〈a<2C．－错误!〈a〈错误!D．－错误!<a<错误!二、填空题（本大题共4个小题，每个小题4分，共16分．将正确答案填在题中横线上）13．等比数列{a n｝和等差数列｛b n}中,a5＝b5,2a5－a2a8＝0,则b3＋b7＝________.14．（2011·四川资阳模拟）在△ABC中,∠A＝错误!,BC＝3,AB＝6，则∠C＝________。
吉林省2021-2022年高二上学期数学期末考试试卷(I)卷
吉林省2021-2022年高二上学期数学期末考试试卷（I）卷姓名:________ 班级:________ 成绩:________一、单选题 (共9题；共18分)1. （2分）在等比数列{an}中，a4a10=9，则a7=（）A . 3B . ﹣3C . ±3D . ±22. （2分） (2020高二上·农安期末) 一质点沿直线运动，如果由始点起经过t秒后的位移s与时间t的关系是，那么速度为零的时刻是（）A . 1秒末B . 2秒末C . 3秒末D . 2秒末或3秒末3. （2分）在数列{an}中，已知a1 = 2，，则a4等于（）A . 4B . 11C . 10D . 84. （2分）等差数列｛an}的前n项和为Sn ，且S3=6,a3=0，则公差d等于（）A . -1B . 1C . -2D . 25. （2分）(2016·安徽模拟) 已知，则（）A . f（2）＞f（e）＞f（3）B . f（3）＞f（e）＞f（2）C . f（3）＞f（2）＞f（e）D . f（e）＞f（3）＞f（2）6. （2分） (2019高二上·吴起期中) 正项等比数列{ }中，若a1＋a2＝1，a3＋a4＝9，那么公比q等于A . 3B . 3或－3C . 9D . 9或－97. （2分） (2019高二上·惠州期末) 若是函数的导函数，则的值为（）A . 1B . 3C . 1或3D . 48. （2分）函数的图象上存在不同的三点到原点的距离构成等比数列，则以下不可能成为该等比数列的公比的数是（）A .B .C .D .9. （2分） (2019高一上·杭州期中) 对于函数，恰存在不同的实数，使，则（）A .B .C .D .二、填空题 (共6题；共6分)10. （1分） (2020高二上·河东期末) 等差数列中，，则的值为________．11. （1分） (2017高二上·靖江期中) 如图，直线l是曲线y=f（x）在x=4处的切线，则f（4）+f′（4）的值为________．12. （1分）(2020·浙江) 已知数列{an}满足an＝，则S3＝________．13. （1分） (2017高二下·黄山期末) 函数y=x3+x的递增区间是________．14. （1分）(2017·衡阳模拟) 已知，数列的前n项和为Sn ，数列{bn}的通项公式为bn=n﹣8，则bnSn的最小值为________．15. （1分） (2019高二下·深圳月考) 函数在[0,3]上的最小值为________.三、解答题 (共3题；共30分)16. （10分） (2019高二下·宁夏月考) 已知函数f（x）=x2（x-1）．（1）求函数f（x）的单调区间；（2）求f（x）在区间[-1，2]上的最大值和最小值．17. （10分） (2020高二下·宁波期中) 已知函数（1）若，求证：（2）若，恒有，求实数的取值范围.18. （10分） (2018高一下·四川期末) 已知等差数列的前项和为，且，在等比数列中， .（Ⅰ）求及；（Ⅱ）设数列的前项和为，求 .参考答案一、单选题 (共9题；共18分)答案：1-1、考点：解析：答案：2-1、考点：解析：答案：3-1、考点：解析：答案：4-1、考点：解析：答案：5-1、考点：解析：答案：6-1、考点：解析：答案：7-1、考点：解析：答案：8-1、考点：解析：答案：9-1、考点：解析：二、填空题 (共6题；共6分)答案：10-1、考点：解析：答案：11-1、考点：解析：答案：12-1、考点：解析：答案：13-1、考点：解析：答案：14-1、考点：解析：答案：15-1、考点：解析：三、解答题 (共3题；共30分)答案：16-1、答案：16-2、考点：解析：答案：17-1、第11 页共13 页答案：17-2、考点：解析：答案：18-1、第12 页共13 页考点：解析：第13 页共13 页。
吉林省延边市长白山第一高级中学学年高二化学上学期学科竞赛试题
吉林省延边市长白山第一高级中学2022-2022学年高二化学上学期学科竞赛试题时间：90分钟 分值：100分可能用到的相对原子质量：C-12 O-16 H-1 N-14 Na-23 Cl-35.5 Ag-108 Br-80 S-32 I-127一、单项选择题1.室温时,向含有AgCl 和AgBr 固体的悬浊液中参加少量的NaBr 固体,以下各项中增大的是( )A.c (Ag +)B. ()()c Cl c Br --C.c (Cl -)D. ()()()c Ag c Br c Cl +--⋅ 2.pH=1的HA 、HB 两溶液各10mL,分别加水稀释至1000mL,其pH 变化关系如下图,以下说法正确的选项是( )A.HA 一定是强酸,HB 一定是弱酸B.稀释后,HA 溶液的酸性比HB 溶液的酸性弱C.向上述10mL HA 溶液中参加10mL pH=13的NaOH 溶液,溶液中有c (Na +)>c (A -)>c (OH -)>c (H +)D.当a=3时,HA 、HB 两溶液起始浓度相等3.以下说法正确的选项是( )A.CO(g)的燃烧热:ΔH =-283.0kJ ·mol -1,那么2CO 2(g)2CO(g)+O 2(g)反响的ΔH =-566.0kJ ·mol -1B.NaOH(aq)+HCl(aq)NaCl(aq)+H 2O(l) ΔH =-57.3kJ ·mol -1,那么含40.0g NaOH 的稀溶液与稀醋酸完全中和,放出57.3kJ 的热量C.2C(s)+2O 2(g)2CO 2(g) ΔH =a;2C(s)+O 2(g)2CO(g) ΔH =b,那么a>b D.C(石墨,s)C(金刚石,s) ΔH >0那么石墨比金刚石稳定4.相同温度下,根据三种酸的电离常数,以下判断正确的选项是( )酸HX HY HZ 电离常数K/(mol·L -1) 9×10-7 9×10-6 1×10-2A.相同温度下,HX 的电离常数会随浓度变化而改变B.反响HZ+Y -=HY+Z -能发生C.HZ 属于强酸,HX 和HY 属于弱酸D.三种酸的强弱关系:HX>HY>HZ5.硫及其化合物的转化关系如下图(反响条件已省略),以下说法正确的选项是( )A.ΔH 1=ΔH 2+ΔH 3B.图中涉及的反响均为化合反响C.途径①发生氧化复原反响,H 2O 2既被氧化又被复原D.假设ΔH 1<ΔH 2+ΔH 3,那么2H 2O 2(aq)2H 2O(l)+O 2(g)为吸热反响6.以下事实不能用勒夏特列原理解释的是( )A.溴水中有以下平衡Br 2+H 2OHBr+HBrO,当参加硝酸银溶液后,溶液颜色变浅 B.合成氨反响(正反响为放热反响),为提高氨的产率,理论上应采取降低温度的措施 C.反响CO(g)+NO 2(g)CO 2(g)+NO(g),达平衡后,升高温度体系颜色变深 D.对于2HI(g)H 2(g)+I 2(g),达平衡后,缩小容器体积可使体系颜色变深 7.室温下,有pH 均为9、体积均为10mL NaOH 溶液和CH 3COONa 溶液,以下说法正确的选项是( )A.两种溶液中的c (Na +)相等B.两溶液中由水电离出的()c OH -之比为-9-51010C.分别加水稀释到100mL 时,两种溶液的pH 依然相等D.分别与同浓度的盐酸反响,pH=7时消耗的盐酸体积相等8.近年来,我国北京等地出现严重雾霾天气,据研究,雾霾的形成与汽车排放的CO 、NO 2等有毒气体有关。
高二数学上学期学科竞赛试题
延边长第一高级中学2021-2021学年高二数学上学期学科竞赛试题时间是：120分钟 分值：150分 一、选择题〔每一小题5分，一共60分〕1．命题:(1,),23x p x ∀∈+∞> ，那么p ⌝ 是〔 〕 A.(1,),23x x ∀∈+∞ B.(,1],23x x ∀∈-∞ C.00(1,),23x x ∃∈+∞ D.00(,1],23x x ∃∈-∞2．23:,522:≥=+q p ,那么以下判断中，错误的选项是 〔 〕A ．p 或者q 为真，非q 为假B ． p 或者q 为真，非p 为真C ．p 且q 为假，非p 为假D ． p 且q 为假，p 或者q 为真 3．“x y =〞是“||||x y =〞的〔 〕条件 A ．充要 B ．充分不必要C ．必要不充分D ．既不充分也不必要4. 过椭圆2241x y +=的一个焦点1F 的直线与椭圆交于,A B 两点，那么A 与B 和椭圆的另一个焦点2F 构成的2ABF ∆的周长为〔 〕A. 2B. 4C. 8D. 5．m ，n 为两条不同的直线，α，β为两个不同的平面，对于以下四个命题： ①m α⊂，n ⊂α，m β，n βαβ⇒ ②n m ∥，n m αα⊂⇒③αβ，m α⊂，n m n β⊂⇒ ④m α∥，n mn α⊂⇒其中，真命题的个数有〔 〕A.0个B.1个C.2个D.3个6．()()3,0,3,0,6M N PM PN --=，那么动点P 的轨迹是〔 〕 A ．一条射线B ．双曲线右支C ．双曲线D ．双曲线左支7．在正方体1111ABCD A B C D -中，异面直线1A B 与1AD 所成角的大小为〔 〕A ．30︒B ．45︒C ．60︒D ．90︒8. 圆：012222=+--+y x y x 上的点到直线2=-y x 的间隔 最小值是〔 〕 A ． 2 B ．21+ C ．12- D ．221+9．过椭圆22221(0)x y a b a b+=>>的左焦点1F 作x 轴的垂线交椭圆于点P ，2F 为其右焦点，假设1230F F P ∠=，那么椭圆的离心率为〔 〕 A ．22B ．13C ．12D ．3310．不管m 取任何实数，直线()0121:=++--m y x m l 恒过一定点，那么该定点的坐标 是〔 〕A ．()3,2B ．()3,2-C ．()0,2-D ．⎪⎭⎫ ⎝⎛-21,1 11．中国古代数学经典?九章算术?系统地总结了战国、秦、汉时期的数学成就，书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑．如图为一个阳马与一个鳖臑的组合体，PA ⊥平面ABCE ，四边形ABCD 为正方形，2AD =，1ED =，假设鳖臑P ADE -的体积为1，那么阳马P ABCD -的外接球的外表积等于〔 〕A ．17πB ．18πC ．19πD ．20π 12.椭圆C 的焦点为121,0,0F F -()，(1)，过2F 的直线与C 交于,A B 222AF F B =,1AB BF =，那么椭圆C 的方程为〔 〕A ．22143x y +=B ．22541x y +=C ．2212x y +=D ．22132x y +=二、填空题〔一共计20分〕13．求过点〔2，3〕且在x 轴和y 轴截距相等的直线的方程 ． 14. 双曲线224640x y -+=上的一点P 到它的一个焦点的间隔 等于1，那么点P 到另一个焦点的间隔 为_______15. 四棱锥S ABCD -中， 底面ABCD 为平行四边形，E 是SA 上一点，当点E 满足条件：____ ______时，SC 平面EBD .16．给出以下命题，①命题“假设5a b +≠，那么2a ≠或者3b ≠〞为真命题； ②命题“假设1x =，那么20x x -=〞的否命题为真命题； ③假设平面α上不一共线的三个点到平面β间隔 相等，那么αβ；④假设α，β是两个不重合的平面，直线l α⊂，命题:p l β，命题:q αβ，那么p是q 的必要不充分条件；⑤平面α过正方体1111D C B A ABCD -的三个顶点1,,B D A ，且α与底面1111A B C D 的交线为l ，那么l ∥11B D 。
吉林省吉林市第一中学2022-2023学年高二上学期11月考试数学试题(平行班)
吉林省吉林市第一中学2022-2023学年高二上学期11月考试数学试题（平行班）一、单选题1．抛物线28x y =-的准线方程是（ ） A ．132x =B ．=2y -C ．132y =D ．2y =2．下列说法中，错误的是（ ） A ．直线53y x =-在y 轴上的截距为3-B 10y -+=的一个方向向量为()3-C ．过点()3,4且在x ，y 轴上的截距相等的直线方程为70x y +-=D ．()1,3A ，()2,5B ，()2,3C --三点共线3．如图，在四棱锥P ABCD -中，四边形ABCD 是平行四边形，F 是棱PD 的中点，且2BE EC =u u u r u u u r ，则EF =u u u r（ ）A ．1126AP AB AD --u u u r u u u r u u u r B ．1126AP AB AD -++u u ur u u u r u u u rC ．1126AP AB AD -+u u u r u u u r u u u r D ．1126AP AB AD -+-u u ur u u u r u u u r4．已知()1,1,1a =r 为平面α的一个法向量，()1,0,0A 为α内的一点，则点()1,1,2D 到平面α的距离为（ ）AB CD 5．若双曲线22221x y a b-=的焦点()2,0F （ ）A ．3y x =±B ．y =C ．13y x =±D ．y x = 6．已知抛物线2:6C y x =，过点()1,1P 的直线l 与抛物线C 交于,A B 两点.若PA PB =，则直线l 的斜率是（ ） A ．3B ．3-C ．13D ．13-7．已知圆22:(3)(3)4C x y -+-=，一条光线从点()1,3A -处射到直线:0l x y +=上，经直线l 反射后，反射光线与圆C 有公共点，则反射光线斜率的取值范围是（ ） A ．(]3,0,4∞∞⎡⎫-⋃+⎪⎢⎣⎭B ．30,4⎡⎤⎢⎥⎣⎦C ．(]4,0,3⎡⎫-∞+∞⎪⎢⎣⎭UD ．40,3⎡⎤⎢⎥⎣⎦8．在平面直角坐标系xOy 中，点F 是椭圆()2222:10x y C a b a b+=>>的左焦点，A 为椭圆的上顶点，过点A 作垂直于AF 的直线分别与x 轴正半轴和椭圆交于点M ，N ，若3A M M N =u u r u u r ，则椭圆C 的离心率e 的值为（ ）A B C ．12D ．13二、多选题9．已知22:60C x y x +-=，则下述正确的是（ ） A ．圆C 的半径3r =B ．点(在圆C 的内部C ．圆C 与圆222460x y x y +++-= 的公共弦所在直线方程为4230x y +-=D ．圆()22:14C x y '++=与圆C 相交10．已知椭圆22:143x y C +=的左､右焦点分别为12F F 、，P 为椭圆C 上不同于左右顶点的任意一点，则下列说法正确的是（ ）A ．12PF F ∆的周长为8B ．存在点P ，使得1 2.5PF =C ．12PF PF ⋅u u u r u u u u r的取值范围为[)2,3D ．12||||PF PF 的取值范围为(]3,411．2022年4月16日9时56分，神舟十三号返回舱成功着陆，返回舱是宇航员返回地球的座舱，返回舱的轴截面可近似看作是由半圆和半椭圆组成的“曲圆”，如图在平面直角坐标系中半圆的圆心在坐标原点，半圆所在的圆过椭圆的焦点()0,2F ，椭圆的短轴与半圆的直径重合，下半圆与y 轴交于点G ．若过原点O 的直线与上半椭圆交于点A ，与下半圆交于点B ，则（ ）A ．椭圆的长轴长为B ．ABF △面积的最大值是8C ．线段AB 长度的取值范围是4,2⎡+⎣D ．AFG V 的周长为4+12．在平面直角坐标系xOy 中，方程22x y +=对应的曲线为E ，则（ ）A ．曲线E 是封闭图形，其围成的面积小于B ．曲线E 关于原点中心对称C ．曲线E 上的点到直线4x y +=D ．曲线E三、填空题13．已知抛物线C ：()220x py p =>，若C 上一点()0,3M x 到焦点F 的距离为6，则p 的值为.14．.已知(),P m n 是圆22:86230C x y x y +--+= 15．已知抛物线24x y =-，P 为该抛物线上的任意一点，以P 为圆心的圆始终与直线1y =相切，则此圆过定点.16．已知双曲线2213x y -=的左右焦点分别为1F ､2F ，P 为双曲线右支上一点，点Q 的坐标为()2,3-，则1PQ PF +的最小值为.17．已知双曲线22:14x y C m-=与直线2y x =无交点，则m 的取值范围是．18．如图，在四棱锥P ABCD -中，PD ⊥平面ABCD ，底面ABCD 为直角梯形，23PD CD AD AB ====，AB CD ∥，90CDA ∠=︒.点E ，F 分别在棱PD ，PB 上，且3DE DP =u u u r u u u r ，3BF BP =u u u r u u u r，若过点A ，E ，F 的平面与直线PC 交于点G ，且PG PC λ=u u u r u u u r ，则λ=.四、解答题19．在四棱锥P ABCD -中，PA ⊥平面ABCD ，四边形ABCD 是矩形，22AP AB AD == ，E 是线段AP 的中点，F 是线段BC 上一点，且EF 垂直FD ．(1)确定点F 的位置；(2)求二面角C EF D --的余弦值．20．在平面直角坐标系xOy 中，圆C 经过(0,0),(1,1),(4,2)O A B 三点． (1)求圆C 的方程；(2)若经过点39,22⎛⎫⎪⎝⎭的直线l 与圆C 相交于M ，N 两点，且=120?MCN ∠，求直线l 的方程．21．在平面直角坐标系xOy 中，椭圆E ：22221(0)x ya b a b+=>>的左顶点到右焦点的距离是3，离心率为12．(1)求椭圆E 的标准方程；(2)l 经过椭圆E 的右焦点，且与椭圆E 相交于A ，B 两点．已知点()3,0P -，求PA PB ⋅u u u r u u u r的值．22．已知过抛物线22(0)y px p =>的焦点，斜率为()11,A x y 和()()2212,B x y x x <两点，且||9AB =．（1）求该抛物线的方程；（2）O 为坐标原点，C 为抛物线上一点，若OC OA OB λ=+u u u r u u u r u u u r，求λ的值．23．在平面直角坐标系xOy 中，已知双曲线()2222:10,0x y C a b a b -=>>的右焦点为()3,0，且经过点().(1)求双曲线C 的标准方程；(2)已知A ，B 是双曲线C 上关于原点对称的两点，垂直于AB 的直线l 与双曲线C 相切于点P ，当点P 位于第一象限，且PAB V 被x 轴分割为面积比为3:2的两部分时，求直线AB 的方程.。
吉林省2024-2025学年高二上学期第一次月考数学试卷含答案
2024—2025学年上学期高二年级数学学科阶段验收考试试卷（答案在最后）考试时间：90分钟满分：120分命题人：一、单项选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的．1.若随机试验的样本空间为{}Ω0,1,2=，则下列说法不正确的是（）A.事件{}1,2P =是随机事件B.事件{}0,1,2Q =是必然事件C.事件{}1,2M =--是不可能事件D.事件{}1,0-是随机事件【答案】D 【解析】【分析】根据随机事件，必然事件，不可能事件的概念判断即可.【详解】随机试验的样本空间为{}Ω0,1,2=，则事件{}1,2P =是随机事件，故A 正确；事件{}0,1,2Q =是必然事件，故B 正确；事件{}1,2M =--是不可能事件，故C 正确；事件{}1,0-是不可能事件，故D 错误.故选：D2.已知点()1,0A ，(1,B -，则直线AB 的倾斜角为（）A.5π6B.2π3C.π3 D.π6【答案】B 【解析】【分析】由两点坐标求出斜率，由倾斜角与斜率的关系即可求【详解】0tan 11AB k α-===--，()0,πα∈，故直线AB 的倾斜角2π3α=.故选：B3.投壶是从先秦延续至清末的汉民族传统礼仪和宴饮游戏，在春秋战国时期较为盛行.如图为一幅唐朝的投壶图，甲、乙、丙是唐朝的三位投壶游戏参与者，假设甲、乙、丙每次投壶时，投中的概率均为0.6且投壶结果互不影响.若甲、乙、丙各投壶1次，则这3人中至少有2人投中的概率为（）A.0.648B.0.432C.0.36D.0.312【答案】A 【解析】【分析】由独立事件概率乘法公式可得.【详解】记甲、乙、丙投中分别即为事件123,,A A A ，由题知()()()()()()1231230.6,0.4P A P A P A P A P A P A ======，则3人中至少有2人投中的概率为：()()()()123123123123P P A A A P A A A P A A A P A A A =+++320.630.60.40.648=+⨯⨯=.故选：A.4.设,A B 是一个随机试验中的两个事件，且()()()131,,+252P A P B P A B ===，则()P AB =（）A.13B.15C.25D.110【答案】D 【解析】【分析】先利用和事件的概率公式求出()P AB ，然后利用()()()P AB P A P AB =-求解即可.【详解】因为1()2P A =，3()5P B =，所以()251,()2P A P B ==，又()()()()()122512P A B P A P B P AB P AB +=+-=+-=，所以()25P AB =，所以()()()1102512P P P A AB A B ==-=-.故选：D.5.若()2,2,1A ，()0,0,1B ，()2,0,0C ，则点A 到直线BC 的距离为（）A.5B.5C.5D.5【答案】A 【解析】【分析】由题意得()2,2,0BA = ，()2,0,1BC =-，再根据点线距离的向量公式即可求解.【详解】()2,2,0BA = ，()2,0,1BC =- ，则BA 在BC上的投影向量的模为BA BC BC⋅= 则点A 到直线BC5=．故选：A.6.某乒乓球队在长春训练基地进行封闭式集训，甲、乙两位队员进行对抗赛，每局依次轮流．．．．发球，连续赢2个球者获胜，通过分析甲、乙过去对抗赛的数据知，甲发球甲赢的概率为23，乙发球甲赢的概率为14，不同球的结果互不影响，已知某局甲先发球．则该局打4个球甲赢的概率为（）A.13B.16C.112 D.524【答案】C 【解析】【分析】由于连胜两局者赢，则可写出四局的结果，计算即可.【详解】由于连胜两局者赢，甲先发球可分为：该局：第一个球甲赢、第二个球乙赢、第三个球甲赢、第四个球甲赢，则概率为22133231441⨯⨯⨯=；故选：C.7.据史书记载，古代的算筹是由一根根同样长短和粗细的小棍制成，如图所示，据《孙子算经》记载，算筹记数法则是：凡算之法，先识其位，一纵十横，百立千僵，千十相望，万百相当．即在算筹计数法中，表示多位数时，个位用纵式，十位用横式，百位用纵式，千位用横式，以此类推．例如⊥‖表示62，＝T 表示26，现有6根算筹，据此表示方式任意表示两位数（算筹不剩余且个位不为0），则这个两位数不小于50的概率为（）A.13B.12C.23D.35【答案】B 【解析】【分析】根据6根算筹，分为五类情况：51,42,33,24,15+++++，逐一分类求解满足要求的两位数，即可求解概率.【详解】根据题意可知：一共6根算筹，十位和个位上可用的算筹可以分为51,42,33,24,15+++++一共五类情况；第一类：51+，即十位用5根算筹，个位用1根算筹，那十位可能是5或者9，个位为1，则两位数为51或者91；第二类：42+，即十位用4根算筹，个位用2根算筹，那十位可能是4或者8，个位可能为2或者6，故两位数可能42，46，82，86；第三类：33+，即十位用3根算筹，个位用3根算筹，那么十位可能是3或者7，个位可能为3或者7，故两位数可能是33，37，73，77；第四类：24+，即十位用2根算筹，个位用4根算筹，那么十位为2或6，个位可能为4或者8，则该两位数为24或者28或者64或者68，第五类：15+，即十位用1根算筹，个位用5根算筹，那十位是1，个位为5或者9，则两位数为15或者19；综上可知：用6根算筹组成的满足题意的所有的两位数有：15，19，24，28，33，37，42，46，51，64，68，73，77，82，86，91共计16个，则不小于50的有：51，64，68，73，77，82，86，91共计8个，故概率为81=162，故选：B.8.正三棱柱111ABC A B C -中，12,3,AB AA O ==为BC 的中点，M 为棱11B C 上的动点，N 为棱AM上的动点，且MN MOMO MA=，则线段MN 长度的取值范围为（）A.4⎡⎫⎢⎣⎭B.,27⎢⎣⎦C.34747⎢⎣⎦D.【答案】B 【解析】【分析】根据正三棱柱建立空间直角坐标系，设动点坐标，结合线线关系求线段MN 的表达式，利用函数求最值即可.【详解】因为正三棱柱11ABC A B C -中,O 为BC 的中点，取11B C 中点Q ，连接OQ ，如图，以O 为原点，,,OC OA OQ 为,,x y z轴建立空间直角坐标系，则()()((110,0,0,,1,0,,1,0,O A B C -，因为M 是棱11B C上一动点，设(M a ，且[1,1]a ∈-，所以(()0OM OA a ⋅=⋅=，则OA OM ⊥，因为ON AM ⊥，且MN MOMO MA=所以在直角三角形OMA 中可得：~OMN AMO 即222MO MN MA===，于是令tt =∈，2233tt t t-==-，t ∈，又符合函数3=-y t t 为增增符合，所以在t ∈上为增函数，所以当t =min 32t t ⎛⎫-== ⎪⎝⎭，即线段MN 长度的最小值为62，当t =时，max 37t t ⎛⎫-== ⎪⎝⎭，即线段MN长度的最大值为7，故选：B.【点睛】关键点睛：1.找到~OMN AMO ，再利用函数单调性求出最值.2.建系，设出动点(M a ，利用空间向量法求出ON AM ⊥，再结合线线关系求线段MN 的表达式，利用函数求最值即可.二、多项选择题：本大题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9.下列命题中正确的是（）A.若表示两个空间向量的有向线段的终点不同，则这两个向量可能相等；B.在所有棱长都相等的直平行六面体1111ABCD A B C D -中，BD ⊥平面11ACC A ；C.对于空间三个非零向量,,a b c，一定有()()a b c a b c ⋅⋅=⋅⋅r r r r r r 成立；D.在棱长为2的正方体1111ABCD A B C D -中，点,M N 分别是棱11A D ，AB 的中点，则异面直线MD 与NC 所成角的余弦值为25．【答案】ABD 【解析】【分析】由相等向量的概念即可判断选项A ，利用线面垂直的判定定理证明即可判断选项B ，由数量积的性质即可判断选项C ，建立空间直角坐标系利用向量的坐标即可计算异面直线MD 与NC 所成角的余弦值判断选项D.【详解】若表示两个空间向量的有向线段的终点不同，而当两向量方向和长度相等时，这两个向量相等；故A 正确；在所有棱长都相等的直平行六面体1111ABCD A B C D -中，即直棱柱1111ABCD A B C D -中底面为菱形，因为BD AC ⊥，1AA ⊥平面ABCD ，BD ⊂平面ABCD ，所以1AA BD ⊥，又1AA AC A = ，所以BD ⊥平面11ACC A ；故B 正确；对于空间三个非零向量,,a b c ，有()a b c c λ⋅⋅= ，()a b c a μ⋅⋅=，所以不一定有()()a b c a b c ⋅⋅=⋅⋅成立，故C错误；建立如图所示的空间直角坐标系，则()0,0,0D ，()1,0,2M ，()2,1,0N ，()0,2,0C ，所以()1,0,2DM = ，()2,1,0NC =-，所以2cos ,5DM NC ==-，所以异面直线MD 与NC 所成角的余弦值为25，故D 正确.故选：ABD.10.连续抛掷一枚质地均匀的骰子两次，用数字x 表示第一次抛掷骰子的点数，数字y 表示第二次抛掷骰子的点数，用(),x y 表示一次试验的结果．记事件A =“7x y +=”，事件B =“3x ≤”，事件C =“()21N xy k k *=-∈”，则（）A.()14P C =B.A 与B 相互独立C.A 与C 为对立事件D.B 与C 相互独立【答案】AB 【解析】【分析】用列举法列出所有可能结果，再结合互斥事件、对立事件、相互独立事件及古典概型的概率公式计算可得．【详解】依题意依次抛掷两枚质地均匀的骰子，基本事件总数为6636⨯=个；其中事件A =“7x y +=”包含的样本点有：()1,6，()2,5，()3,4，()4,3，()5,2，()6,1共6个；事件C =“()*21Nxy k k =-∈”，包含的样本点有：()1,1，()3,3，()5,5，()1,3，()1,5，()3,1，()3,5，()5,1，()5,3共9个，事件B =“3x ≤”，包含的样本点有：()1,1，()1,2，()1,3，()1,4，()1,5，()1,6，()2,1，()2,2，()2,3，()2,4，()2,5，()2,6，()3,1，()3,2，()3,3，()3,4，()3,5，()3,6共18个，对于A ，()91364P C ==，故A 正确；对于B ，事件AB 包含的样本点有()1,6，()2,5，()3,4共3个，所以()()()6118131,,3663623612P A P B P AB ======，所以()()()P A P B P AB =，所以A 与B 相互独立，故B 正确；对于C ，A C U 包含的样本点个数满足691536+=<，所以A 与C 不为对立事件，故C 错误；对于D ，事件BC 包含的样本点有：()1,1，()1,3，()1,5，()3,1，()3,3，()3,5，共6个，而()14P C =，()12P B =，()61366P BC ==，从而()()()1816P P P BC B C ≠==，所以B 与C 不相互独立，故D 错误.故选：AB.11.在棱长为1的正方体1111ABCD A B C D -中，P 为棱1BB 上一点，且12B P PB =，Q 为正方形11BB C C 内一动点（含边界），则下列说法中正确的是（）A.若1D Q ∥平面1A PD ，则动点Q 的轨迹是一条长为3的线段B.存在点Q ，使得1D Q ⊥平面1A PD C.三棱锥1Q A PD -的最大体积为518D.若12D Q =，且1D Q 与平面1A PD 所成的角为θ，则sin θ【答案】ACD 【解析】【分析】在111,BC CC 取点,E F ，使得1112,2C E B E C F CF ==，证得平面//DEF 平面1A PD ，进而得到1//D Q 平面1A PD ，可判定A 正确；以1D 为原点，建立空间直角坐标系，求得平面1A PD 的一个法向量(3,2,3)m =-，根据1D Q m λ= ，得出矛盾，可判定B 不正确；利用向量的数量积的运算及三角形的面积公式，求得16A PD S =,在求得点Q 到平面1A PD的最大距离max d =，结合体积公式，可判定C 正确；根据题意，求得点点Q 的轨迹，结合线面角的公式，求得11(,1,)22Q 时，取得最大值，进而可判定D 正确.【详解】对于A 中，如图所示，分别在111,BC CC 取点,E F ，使得1112,2C E B E C F CF ==，可得1//EF B C ，因为11//A D B C ，所以1//EF A D ，因为1A D ⊂平面1A PD ，EF ⊄平面1A PD ，所以//EF 平面1A PD ，又由11//D F A P ，且1A P ⊂平面1A PD ，1D F ⊄平面1A PD ，所以1//D F 平面1A PD ，又因为1EF D F F ⋂=，且1,EF D F ⊂平面DEF ，所以平面//DEF 平面1A PD ，且平面DEF ⋂平面11BCC B EF =，若1//D Q 平面1A PD ，则动点Q 的轨迹为线段EF ，且223EF =，所以A 正确；对于B 中，以1D 为原点，以11111,,D A D C D D 所在的直线分别为,,x y z 轴，建立空间直角坐标系，如图所示，可得12(1,0,0),(0,0,1),(1,1,)3A D P ，则112(1,0,1),(0,1,)3A D A P =-= ，设(,1,)(01,01)Q x z x z ≤≤≤≤，可得1(,1,)D Q x z =，设(,,)m a b c = 是平面1A PD 的一个法向量，则110203m A D a c m A P b c ⎧⋅=-+=⎪⎨⋅=+=⎪⎩，取3c =，可得3,2z b ==-，所以(3,2,3)m =-，若1D Q ⊥平面1A PD ，则1//D Q m，所以存在R λ∈，使得1D Q m λ= ，则3[0,1]2x z ==-∉，所以不存在点Q ，使得1D Q ⊥平面1A PD ，所以B 错误；对于C 中，由112(1,0,1),(0,1,3A D A P =-=，可得1111132,33A D A P A D A P ==⋅=，则11cos ,A D A P =11sin ,A D A P = ，所以111111sin 2236A PD S A D A P DA P =⋅∠=⨯ ,要使得三棱锥1Q A PD -的体积最大，只需点Q 到平面1A PD 的距离最大，由1(1,1,)AQ x z =- ，可得点Q 到平面1A PD的距离1)5A Q m d x z m ⋅==+-，因为01,01x z ≤≤≤≤，所以当0x z +=时，即点Q 与点1C重合时，可得max d =，所以三棱锥1Q A PD -的最大体积为111533618A PD S =⋅=，所以C 正确；对于D 中，在正方体中，可得11D C ⊥平面11BCC B ，且1C Q ⊂平面11BCC B ，所以111D C C Q ⊥，则12C Q ==，所以点Q 的轨迹是以1C为圆心，以2为半径的圆弧，其圆心角为π2，则1(,0,)C Q x z =，所以12C Q == ，即2212x z +=，又由1(,1,)D Q x z =，设1D Q 与平面1A PD 所成的角θ，所以111sin cos ,m D Q m D Q m D Qθ⋅===，因为2212x z +=，可得222()2()x z x z +≤+，当且仅当x z =时，等号成立，所以1x z +≤，即12x z ==时，1D Q 与平面1A PD 所成的角最大值，sin θ=D 正确.故选：ACD.【点睛】方法点睛：求解立体几何中的动态问题与存在性问题的策略：1、解答方法：一般时根据线面平行，线面垂直的判定定理和性质定理，结合圆或圆锥曲线的定义推断出动点的轨迹，有时也可以利用空间向量的坐标运算求出动点的轨迹方程；2、对于线面位置关系的存在性问题，首先假设存在，然后再该假设条件下，利用线面位置关系的相关定理、性质进行推理论证，寻找假设满足的条件，若满足则肯定假设，若得出矛盾的结论，则否定假设；3、对于探索性问题用向量法比较容易入手，一般先假设存在，设出空间点的坐标，转化为代数方程是否有解的问题，若由解且满足题意则存在，若有解但不满足题意或无解则不存在，同时，用已知向量来表示未知向量，一定要结合图形，以图形为指导思想是解答此类问题的关键.三、填空题：本大题共3小题，每小题5分，第14题第一个空2分，第二个空3分，共15分．12.已知()3,2,1a =- ，()2,1,2b =r，当()()2ka b a b +⊥- 时，实数k 的值为____________．【答案】6【解析】【分析】由题意依次算得22,,a b a b ⋅ 的值，然后根据()()2ka b a b +⊥-列方程即可求解.【详解】因为()3,2,1a =-，()2,1,2b = ，所以()2294114,4149,3221126a ba b =++==++=⋅=⋅+⋅+-⋅=，因为()()2ka b a b +⊥-，所以()()()()22221214186122120ka b a b ka b k a b k k k +⋅-=-+-⋅=-+-=-=，解得6k =.故答案为：6.13.柜子里有3双不同的鞋子，分别用121212,,,,,a a b b c c 表示6只鞋，从中有放回地．．．．取出2只，记事件M =“取出的鞋是一只左脚一只右脚的，但不是一双鞋”，则事件M 的概率是____________．【答案】13【解析】【分析】列举法写出试验的样本空间，根据古典概型的概率公式直接可得解.【详解】设111,,a b c 表示三只左鞋，222,,a b c 表示三只右鞋，则从中有放回取出2只的所有可能为：()()()()()()111211121112,,,,,,,,,,,a a a a a b a b a c a c ()()()()()()212221222122,,,,,,,,,,,a a a a a b a b a c a c ()()()()()()111211121112,,,,,,,,,,,b a b a b b b b b c b c ()()()()()()212221222122,,,,,,,,,,,b a b a b b b b b c b c ()()()()()()111211121112,,,,,,,,,,,c a c a c b c b c c c c ()()()()()()212221222122,,,,,,,,,,,c a c a c b c b c c c c ，共计36种，其中满足取出的鞋一只左脚一只右脚，但不是一双鞋的有12种，()121363P M ∴==.故答案为：13.14.已知正四面体ABCD 的棱切球1T （正四面体的中心与球心重合，六条棱与球面相切）的半径为1，则该正四面体的内切球2T 的半径为______；若动点,M N 分别在1T 与2T 的球面上运动，且满足MN x AB y AC z AD =++，则2x y z ++的最大值为______．【答案】①.3②.26+【解析】【分析】第一空：将正四面体ABCD 放入正方体中，由等体积法可知，只需求出正四面体的表面积以及体积即可列式求解该正四面体的内切球2T 的半径；第二空：由不等式可知，()maxmin222MN x y z AT MN x y z x y z AT AT AT++++≤++==≤，只需求出max MN 、minAT 即可.【详解】第一空：连接,AD EF ，设交点为M ，则M 是AD 中点，如图所示，将正四面体ABCD 放入正方体中，由对称性可知正方体中心就是正四面体ABCD 的中心，设正方体棱长为2a ，则棱切球球心到正四面体ABCD 的六条棱的距离都等于a ，设正四面体ABCD 的棱切球1T 的半径为1r ，所以11r a ==，正方体棱长为2，AD =，而正四面体ABCD 的体积为1182224222323A BCD V -⎛⎫=⨯⨯-⨯⨯⨯⨯⨯=⎪⎝⎭，正四面体ABCD的表面积为(21422A BCD S -=⨯⨯⨯=设该正四面体的内切球2T 的半径为r，则由等体积法可知，1833⨯=，解得33r =；第二空：取任意一点T ，使得()22x y z AT MN xAB y AC z AD xAO y AC z AD ++==++=++，所以点T 在面OCD 内（其中O 是AB 中点），所以()13213x y z AT MN r r ++=≤+=+，而点A 到平面OCD 的距离为d AO ==所以()1232226x y z AT x y z x y z AT+++++≤++=≤+，等号成立当且仅当2x y z ++是正数且,T O重合且13MN =+ ，综上所述，2x y z ++的最大值为26+.故答案为：33，2626+.【点睛】关键点点睛：第二空的关键是得出()maxmin222MN x y z AT MN x y z x y z AT AT AT++++≤++==≤，由此即可顺利得解.四、解答题：本大题共4小题，共47分．解答应写出文字说明，证明过程或演算步骤．15.如图，在三棱柱111ABC A B C -中，,M N 分别是111,A B B C 上的点，且1112,2A M MB B N NC ==．设1,,AB a AC b AA c ===．（1）试用,,a b c 表示向量MN；（2）若11190,60,1BAC BAA CAA AB AC AA ∠=∠=∠====，求异面直线MN 与AC 的夹角的余弦值．【答案】（1）122333a b c-++（2）11【解析】【分析】（1）由空间向量的基本定理求解即可；（2）先用基向量,,a b c 表示AC 与MN ，然后求解MN 与AC 以及数量积MN AC ⋅，然后计算夹角的余弦值即可.【小问1详解】由图可得：()()1111111112123333MN MB BB B N A B AA B C AB AA AA AC AB=++=++=-++- 1122122333333AB AC AA a b c =-++=-++.【小问2详解】由（1）可知122333MN a b c =-++ ，因为11190,60,1BAC BAA CAA AB AC AA ∠=∠=∠====，所以0a b ⋅=，12a c ⋅= ，12b c ⋅= ，2222212214444814424110333999999999999MN a b c a b c a b a c b c ⎛⎫=-++=++-⋅-⋅+⋅=++--+= ⎪⎝⎭ ，所以113MN = ，AC b = ，1AC =，212212221·133333333MN AC a b c b a b b c b ⎛⎫⋅=-++=-⋅++⋅=+= ⎪⎝⎭所以cos ,11MN AC MN AC MN AC⋅==，所以异面直线MN 与AC的夹角的余弦值为11.16.如图，在正四棱柱1111ABCD A B C D -中，122AA AB ==，,E F 分别为1BB ，1CC的中点．（1）证明：1A F ∥平面CDE ；（2）求三棱锥1A CDE -的体积；（3）求直线1A E 与平面CDE 所成的角．【答案】（1）证明过程见解析（2）16（3）π6【解析】【分析】（1）借助正四棱柱的性质可建立空间直角坐标系，求出空间向量1A F与平面CDE 的法向量后，借助空间向量计算即可得；（2）求出空间向量1A E与平面CDE 的法向量后，借助空间向量夹角公式计算即可得直线1A E 与平面CDE 所成的角的正弦值，进一步求得三棱锥的高以及底面积即可得解.（3）由（2）可知直线1A E 与平面CDE 所成的角的正弦值，从而即可得解.【小问1详解】在正四棱柱1111ABCD A B C D -中，AB ，AD ，1AA 两两垂直，且122AA AB ==，以A 为坐标原点，AB ，AD ，1AA 所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系，则()1,1,0C ，()0,1,0D ，()10,0,2A.因为E ，F 分别为11,BB CC 的中点，所以()1,0,1E ，()1,1,1F ，则()1,0,0CD =- ，()0,1,1CE =- ，()11,1,1A F =-，设平面CDE 的法向量为(),,m x y z = ，则00CD m CE m ⎧⋅=⎪⎨⋅=⎪⎩，即00x y z -=⎧⎨-+=⎩，令1y =，则有0x =，1z =，即()0,1,1m =，因为()11011110A F m ⋅=⨯+⨯+-⨯= ，所以1A F m ⊥ ，又1⊄A F 平面CDE ，所以1//A F 平面CDE ；【小问2详解】由（1）可知，()11,0,1A E =-，1111cos ,2A E m A E m A E m⋅==-，所以1A E 与平面CDE 所成角的正弦值为12.注意到1A E =所以点1A 到平面CDE122=，而()1,0,0CD =- ，()0,1,1CE =-，从而0CD CE =⋅，1,CD CE == 所以CD CE ⊥，三角形CDE的面积为1122⨯=，所以三棱锥1A CDE -的体积为113226⨯⨯=；【小问3详解】由（2）可知，1A E 与平面CDE 所成角的正弦值为12，所以直线1A E 与平面CDE 所成的角为π6.17.2023年10月31日，东北师大附中以“邂逅数学之美，闪耀科技之光”为主题的第17届科技节在自由、青华两校区开幕.在科技节中数学教研室组织开展了“送书券”活动．该活动由三个游戏组成，每个游戏各玩一次且结果互不影响．连胜两个游戏可以获得一张书券，连胜三个游戏可以获得两张书券．游戏规则如下表：游戏一游戏二游戏三箱子中球的颜色和数量大小质地完全相同的红球4个，白球2个（红球编号为“1，2，3，4”，白球编号为“5，6”）取球规则取出一个球有放回地依次取出两个球不放回地依次取出两个球获胜规则取到白球获胜取到两个红球获胜编号之和不超过m 获胜（1）分别求出游戏一，游戏二的获胜概率；（2）甲同学先玩了游戏一，当m 为何值时，接下来先玩游戏三比先玩游戏二获得书券的概率更大．【答案】（1）13，49（2）m 可能取值为7,8,9,10,11【解析】【分析】（1）利用列举法，结合古典概型的概率公式即可得解；（2）利用互斥事件与独立事件的概率公式求得先玩游戏二与先玩游戏三获得书券的概率，从而得到游戏三获胜的概率，由此得解.【小问1详解】设事件A 表示“游戏一获胜”，B 表示“游戏二获胜”，C 表示“游戏三获胜”，游戏一中取出一个球的样本空间为{}1Ω1,2,3,4,5,6=，则()1Ω6n =，()2n A =，()2163P A ∴==，所以游戏一获胜的概率为13．游戏二中有放回地依次取出两个球的样本空间(){}21Ω,,Ωx y x y =∈，则()2Ω36n =，而(){}{},,1,2,3,4B x y x y =∈，所以()16n B =，()164369P B ∴==，所以游戏二获胜的概率为49．【小问2详解】设M 表示“先玩游戏二，获得书券”，N 表示“先玩游戏三，获得书券”，则M ABC ABC ABC =⋃⋃，且ABC ，ABC ，ABC 互斥，,,A B C 相互独立，()()()()()P M P ABC ABC ABC P ABC P ABC P ABC ∴=⋃⋃=++()()()()()()()()()11P A P B P C P A P B P C P A P B P C ⎡⎤⎡⎤=-+-+⎣⎦⎣⎦()()()1424141393939P C P C P C ⎡⎤=⨯-+⨯+⨯⎣⎦()482727P C =+，则N AC B ACB ACB =⋃⋃，且,AC B ACB ACB 互斥，,,A B C 相互独立，()P N =()()()()P ACB ACB ACB P ACB P ACB P ACB ⋃⋃=++()()()()()()()()()11P A P C P B P A P C P B P A P C P B ⎡⎤⎡⎤=-+-+⎣⎦⎣⎦()()()152414393939P C P C P C =⨯⨯+⨯⨯+⨯⨯()1727P C =，若要接下来先玩游戏三比先玩游戏二获得书券的概率更大，则()()P N P M >，即()()1748272727P C P C >+，解得()49P C >，设游戏三中两次取球的编号和为X ，则()26113C 15P X ===，()26114C 15P X ===，()26225C 15P X ===，()26226C 15P X ===，()26337C 15P X ===，()26228C 15P X ===，()26229C 15P X ===，()261110C 15P X ===，()261111C 15P X ===，所以当3m =时，()()143159P C P X ===<，不合题意；当4m =时，()()()2434159P C P X P X ==+==<，不合题意；当5m =时，()()()()44345159P C P X P X P X ==+=+==<，不合题意；当6m =时，()()()()()643456159P C P X P X P X P X ==+=+=+==<，不合题意；当7m =时，()()()()()()9434567159P C P X P X P X P X P X ==+=+=+=+==>，符合题意；所以当7m ≥时，都有()49P C >，所以符合题意的m 的取值有7,8,9,10,11.18.球面三角学是研究球面三角形的边、角关系的一门学科．如图，球O 的半径为R ，A 、B 、C 为球面上的三点，设a O 表示以O 为圆心，且过B 、C 的圆，劣弧BC 的长度记为a ，同理，圆b O ，c O 的劣弧AC 、AB 的长度分别记为b ，c ，曲面ABC （阴影部分）叫做球面三角形．如果二面角,,C OA B A OB C B OC A ------的大小分别为,,αβγ，那么球面三角形的面积为()2++πABC S R αβγ=- 球面．（1）若平面OAB 、平面OAC 、平面OBC 两两垂直，求球面三角形ABC 的面积；（2）若平面三角形ABC 为直角三角形，AC BC ⊥，设1AOC θ∠=，2BOC θ∠=，3AOB θ∠=．①求证：123cos cos cos 1θθθ+-=；②延长AO 与球O 交于点D ，若直线DA ，DC 与平面ABC 所成的角分别为ππ,43，,(0,1]BE BD λλ=∈，S 为AC 的中点，T 为BC 的中点．设平面OBC 与平面EST 的夹角为θ，求cos θ的最大值及此时平面AEC 截球O 的面积．【答案】（1）2π2R （2）①证明见解析；②cos 5θ=，253π78R 【解析】【分析】（1）根据题意结合相应公式分析求解即可；（2）①根据题意结合余弦定理分析证明；②建系，利用空间向量求线面夹角，利用基本不等式分析可知点E ，再利用空间向量求球心O 到平面AEC 距离，结合球的性质分析求解.【小问1详解】若平面,,OAB OAC OBC 两两垂直，有π2αβγ===，所以球面三角形ABC 面积为()22ππ2ABC S R R αβγ=++-= 球面.【小问2详解】①证明：由余弦定理有：2222122222222232cos 2cos 2cos AC R R R BC R R R AB R R R θθθ⎧=+-⎪=+-⎨⎪=+-⎩，且222AC BC AB +=，消掉2R ，可得123cos cos cos 1θθθ+-=；②由AD 是球的直径，则,AB BD AC CD ⊥⊥，且AC BC ⊥，CD BC C ⋂=，,CD BC ⊂平面BCD ，所以AC ⊥平面BCD ，且BD ⊂平面BCD ，则AC BD ⊥，且AB AC A ⋂=，,AB AC ⊂平面ABC ，可得BD ⊥平面ABC ，由直线DA ，DC 与平面ABC 所成的角分别为ππ,43，所以ππ,43DAB DCB ∠=∠=，不妨先令R =，则2AD AB BD BC AC =====，由AC BC ⊥，AC BD ⊥，BC BD ⊥，以C 为坐标原点，以CB ，CA 所在直线为x ，y 轴，过点C 作BD 的平行线为z 轴，建立如图空间直角坐标系，设(,BE t t =∈，则())()0,2,0,,0,0,0,A B C D ，可得()20,1,0,,0,02S T ⎛⎫ ⎪ ⎪⎝⎭，)26,,1,22E t O ⎛⎫ ⎪ ⎪⎝⎭，则),22CB CO ⎛⎫== ⎪ ⎪⎝⎭，,1,0,22ST TE t ⎛⎫⎛⎫=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭设平面OBC 法向量()111,,m x y z =，则11110022m CB m CO x y z ⎧⋅==⎪⎨⋅=++=⎪⎩，取12z =-，则110y x ==，可得()2m =- ，设平面EST 法向量()222,,n x y z =，则222202202n ST x y n TE x tz ⎧⋅=-=⎪⎪⎨⎪⋅=+=⎪⎩，取2x =，则22,1y t z ==-，可得),,1n t =- ，因为cos cos ,m n m n m n θ⋅======，令(]1,1,13m m=+∈，则()2218mt t-==，可得()2221888293129621218m mt m mm mm+===≤=+-+--+-+，当且仅当3,m t==取等．则cosθ5=，此时点E，可得CE=，()0,2,0CA=，设平面AEC中的法向量(),,k x yz=，则20k CE zk CA y⎧⋅==⎪⎨⎪⋅==⎩，取1x=，则0,y z==-，可得(1,0,k=-，可得球心O到平面AEC距离为AO kdk⋅==设平面AEC截球O圆半径为r，则2225326r R d=-=，所以截面圆面积为225353πππ2678r R==.【点睛】方法点睛：1.利用空间向量求线面角的思路:直线与平面所成的角θ主要通过直线的方向向量与平面的法向量的夹角ϕ求得，即sin cosθϕ=.2.利用空间向量求点到平面距离的方法:设A为平面α内的一点，B为平面α外的一点，n为平面α的法向量，则B到平面α的距离AB ndn⋅=.。
吉林省长白山一高中2021-2022学年高二上学期第二次月考数学理试卷 Word版含答案
高二上学期其次次月考数学（理科）试题一、选择题：本大题共10个小题，每小题5分，共50分。
在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知函数2()43,f x x x =-+集合{(,)()()0}M x y f x f y =+≤，集合{(,)()()0}N x y f x f y =-≥,则若在集合M 所表示的区域内撒100颗黄豆，落在集合M N ⋂所表示的区域的黄豆约有多少（ ） A.12 B.25 C. 50 D. 752.某校现有高一同学210人，高二同学270人，高三同学300人，用分层抽样的方法从这三个班级的同学中随机抽取n 名同学进行问卷调查，假如已知从高一同学中抽取的人数为7，那么从高三同学中抽取的人数应为（ ）A. 10 B . 9C.8D.73. 在区间[-1，1]上随机取一个数x ，2cosxπ的值介于0到21之间的概率为 A.31 B. π2C. 21D. 324.六件不同的奖品送给5个人, 每人至少一件,不同的分法种数是 ( )A.45C B. 65 C .1556.AA D. 5526A C5.如图是将二进制数11111（2）化为十进制数的一个程序框图，推断框内应填入的条件是（ ）A ．i ≤5B ．i ≤4C ．i ＞5D ．i ＞46.为调查甲乙两个网络节目的受欢迎程度，随机选取了8天，统计上午8:00-10:00的点击量。
茎叶图如图，设甲、乙的中位数分别为12,x x ，方差分别为12,D D ,则（ ）A.1212,x x D D <<B.1212,x x D D >>C.1212,x x D D <>D.1212,x x D D ><7.学校小卖部为了争辩气温对饮料销售的影响，经过统计，得到一个卖出饮料数与当天气温的对比表：摄氏温度 －1 3 8 12 17 饮料瓶数3405272122依据上表可得回归方程y bx a =+中的b 为6，据此猜测气温为30℃时销售饮料瓶数为（ ）A. 141B. 191C. 211D. 2418.高二班级进行一次演讲赛共有10位同学参赛，其中一班有3位，二班有2位，其它班有5位，若接受抽签的方式确定他们的演讲挨次，则一班有3位同学恰好被排在一起（指演讲序号相连），而二班的2位同学没有被排在一起的概率为：（ ） A.110 B.120 C.140 D.1120 9. 已知1010221010)1()1()1()3(x a x a x a a x +++++++=+ ，则a 9= （ ）A. 20B. 21C.31D. 3210. 用辗转相除法求459和357的最大公约数，需要做除法的次数是（ ） A.1 B.2 C.3 D.4第Ⅱ卷（100分）二．填空题：本大题共5小题，每小题5分，共25分。
吉林省长白山一高2022学年高二数学全册综合测试2 新人教A版必修2
必修2全册综合测试2时间120分钟，满分150分。
一、选择题本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的1．已知空间两点2a20m3in流完．关于油槽剩余量Qm3和流出时间tmin之间的关系可表示为9．如图为四棱锥和它的三视图，反映物体的长和高的是A．俯视图B．主视图C．左视图D．都可以10．点5a12a27cm6cm1C1C2a0.4m3in，故油槽剩余油量Q和流出时间tmin之间的关系式为Q＝20－，故选B9[答案] B[解析]由实物图可以知道正面看到的边是长，所以可以反映长的图是主视图和俯视图，能反映高的是主视图和左视图，故选B10[答案] C[解析]∵点5a12a5a12a25a144a12a[解析]如图所示，正三棱锥．16[答案]M∈FH[解析]连结B1D1、FH∵N、H分别为BC、CD的中点，∴NH∥BD，又∵F为C1D1的中点，∴FH∥DD1，FH∩NH＝H，FH⊂面FHN，NH⊂面FHN，∴面FHN∥面B1BDD1，∴当M∈FH时，MN∥面B1BDD117[解析]当的斜率不存在时，方程为＝5，与圆C相切，∴的斜率必存在，设为，则的方程－＋5－5＝0如图所示，|OH|是圆心到直线的距离，|OA|是圆的半径，|AH|是弦长|AB|的一半，在Rt△AHO中，|OA|＝5|AH|＝错误!|AB|＝错误!×4错误!＝2错误!∴|OH|＝错误!＝错误!，∴错误!＝错误!，解得＝错误!或＝2故直线的方程为－2＋5＝0或2－－5＝018[解析]解法一：过点a，b，则满足6a＋b－23＝0①又由题设知圆心M在直线2：5－3＝0上，则5a－3b＝0②联立式①②，解得a＝3，b＝5，即圆心M3,5，因此半径r＝|故AMNE是平行四边形，∴MN∥AE∵AE⊂平面N⊄平面N∥平面N又CD∥AB，∴MN⊥CD3∵N⊥N⊥CD，∴MN⊥平面1M＝错误!，∴MN∥AC ∴BD⊥MN∵DD1⊥平面ABCD，MN⊂面ABCD，∴DD1⊥MN∴MN⊥平面BDD1∵无论N⊥BP2存在点P，且P为DD1的中点，使得平面APC1⊥平面ACC1∵BD⊥AC，BD⊥CC1，∴BD⊥平面ACC1取BD1的中点E，连结PE，则PE∥BD∴PE⊥面ACC1又∵PE⊂面APC1，∴面APC1⊥面ACC1。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
吉林省延边市长白山第一高级中学2021-2022高二数学上学期学科竞
赛试题
时间：120分钟 分值：150分 一、选择题（每题5分，共60分）
1．命题:(1,),23x
p x ∀∈+∞> ，则p ⌝ 是（ ）
A.(1,),2
3x
x ∀∈+∞ B.(,1],2
3x
x ∀∈-∞ C.0
0(1,),2
3x x ∃∈+∞
D.0
0(,1],2
3x x ∃∈-∞
2．已知23:,522:≥=+q p ,则下列判断中，错误的是 （ ）
A ．p 或q 为真，非q 为假
B ． p 或q 为真，非p 为真
C ．p 且q 为假，非p 为假
D ． p 且q 为假，p 或q 为真 3．“x y =”是“||||x y =”的（ ）条件 A ．充要 B ．充分不必要
C ．必要不充分
D ．既不充分也不必要
4. 过椭圆2
2
41x y +=的一个焦点1F 的直线与椭圆交于,A B 两点，则A 与B 和椭圆的另一个焦点2F 构成的2ABF ∆的周长为（ ）
A. 2
B. 4
C. 8
D. 5．已知m ，n 为两条不同的直线，α，β为两个不同的平面，对于下列四个命题： ①m α⊂，n ⊂α，m β，n βα
β⇒ ②n m ∥，n m αα⊂⇒
③α
β，m α⊂，n m n β⊂⇒ ④m α∥，n m
n α⊂⇒
其中，真命题的个数有（ ）
A.0个
B.1个
C.2个
D.3个
6．已知()()3,0,3,0,6M N PM PN --=，则动点P 的轨迹是（ ） A ．一条射线
B ．双曲线右支
C ．双曲线
D ．双曲线左支
7．在正方体1111ABCD A B C D -中，异面直线1A B 与1AD 所成角的大小为（ ）
A ．30︒
B ．45︒
C ．60︒
D ．90︒
8. 圆：01222
2
=+--+y x y x 上的点到直线2=-y x 的距离最小值是（ ） A ． 2 B ．21+ C ．12- D ．221+
9．过椭圆22
221(0)x y a b a b
+=>>的左焦点1F 作x 轴的垂线交椭圆于点P ，2F 为其右焦点，
若1230F F P ∠=，则椭圆的离心率为（ ） A ．
2
2
B ．13
C ．12
D ．
3
3
10．不论m 取任何实数，直线()0121:=++--m y x m l 恒过一定点，则该定点的坐标 是（ ）
A ．()3,2
B ．()3,2-
C ．()0,2-
D ．⎪⎭
⎫ ⎝⎛-
21,1 11．中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就，书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑．如图为一个阳马与一个鳖臑的组合体，已知PA ⊥平面ABCE ，四边形ABCD 为正方形，2AD =，1ED =，若鳖臑P ADE -的体积为1，则阳马P ABCD -的外接球的
表面积等于（ ）
A ．17π
B ．18π
C ．19π
D ．20π
12.已知椭圆C 的焦点为121,0,0F F -()，(1)，过2F 的直线与C 交于,A B 两点.若
222AF F B =,1AB BF =，则椭圆C 的方程为（ ）
A ．22143x y +=
B ．2254
1x y +=
C ．2
212x y +=
D ．22132
x y +=
二、填空题（共计20分）
13．求过点（2，3）且在x 轴和y 轴截距相等的直线的方程 ． 14. 双曲线2
2
4640x y -+=上的一点P 到它的一个焦点的距离等于1，那么点P 到另一个焦点的距离为_______
15. 四棱锥S ABCD -中， 底面ABCD 为平行四边形，E 是SA 上一点，当点E 满足条件：____ ______时，SC 平面EBD .
16．给出以下命题，
①命题“若5a b +≠，则2a ≠或3b ≠”为真命题； ②命题“若1x =，则20x x -=”的否命题为真命题； ③若平面α上不共线的三个点到平面β距离相等，则αβ；
④若α，β是两个不重合的平面，直线l α⊂，命题:p l β，命题:q α
β，则p 是q 的
必要不充分条件；
⑤平面α过正方体1111D C B A ABCD -的三个顶点1,,B D A ，且α与底面1111A B C D 的交线为
l ，
则l ∥11B D 。
其中，真命题的序号是 三、解答题（共70分）
17．（共10分）求下列双曲线的实轴和虚轴长、离心率、焦点坐标、顶点坐标渐进线方程。
（1）2
2
416x y -= （2）2
2
981y x -=
18．（共12分）已知
1:123
x p --≤，()22:2100q x x m m -+-≤>，若p ⌝是q ⌝的充分
而不必要条件，求实数m 的取值范围．
19．（共12分）如图，在正方体1111ABCD A B C D -中，,,,E F G H 分别是1111,,C ,BC CC D A A 的中点。
求证：
（1）求证：EG ∥平面11BB D D ；
（2）求异面直线BF 与1HB 所成角的余弦值。
20. （共12分）已知双曲线C 和椭圆22
141
x y +=有公共的焦点，且离心率为3。
（1）求双曲线C 的方程。
（2）经过点()2,1M 作直线l 交双曲线C 于A ， B 两点，且M 为AB 的中点，求直线l 的方程。
21．（共12分）如图， ABCD 是正方形，O 是正方形的中心， PO ⊥底面ABCD ，E 是PC 的中点。
2,2PO AB ==
求证：
（1）PA ∥平面BDE ； （2）平面PAC ⊥平面BDE ； （3）求二面角E BD A --的大小。
22. （共12分） 已知在平面直角坐标系xOy 中，动点P 与两定点
(2,0),(2,0)A B -连线的斜率之积为1
2-
，记点P 的轨迹为曲线C 。
（1）求曲线C 的方程；
（2）若过点(1,0)-的直线l 与曲线C 交于,M N 两点，曲线C 上是否存在点E 使得四边形
OMEN 为平行四边形？若存在，求直线l 的方程，若不存在，说明理由。
高二数学答案
1.C
2.C
3.B
4.B
5.A
6.A
7.C
8.C
9.D 10.B 11.A 12.D 13.
3
50
2
y x x y =+-=或 14. 17 15.E 为中点 16.①④⑤ 17.
3
(1)831
2
x
±±±实轴长，虚轴长4，离心率，焦点坐标（2，0），
顶点坐标（4，0），渐近线方程y=
22
(2)8623
3x
±±±实轴长1，虚轴长6，离心率，焦点坐标（0，），
顶点坐标（0，9），渐近线方程y=
18．3m ≤
19.（1）取BD 的中点O ，连接EO 、D 1O ，则OE ∥1D C ，OE ＝
112
D C ．又D 1G ∥DC ，D 1G ＝1
2DC ，
∴OE ∥D 1G ，OE ＝D 1G ，∴四边形OEGD 1是平行四边形，∴GE ∥D 1O ．又D 1O ⊂平面BB 1D 1D ，∴EG ∥平面BB 1D 1D ． （2）
20.(1)
2
2
1
2
y x -= (2)47y x =-
21.(1),(2)证明略（3）34
π
22. 解：（1）设P （x ,y ）,有PA k ·PB k =-12得2y x +·2y
x -=-12得2242
x y +
=1（x ≠±2）∴C 的方程为22
42
x y +
=1（x ≠±2） （2）假设存在符合条件的点E （00x y ，）由题意知直线l 的斜率不为零设直线l 的方程为
x =my 2M 坐标为（11x y ，）、点N 坐标为（22x y ，）由22
1
24
x my x y =-⎧⎨+=⎩得：（2m +2）
2y -2my -3=0,△>0∴1y +2222
m y m =
+则121(x x m y +=+2
)2y -=-24
2m +由四边形OMEN 为平行四边形，得OE OM ON =+∴E （-224222m
m m -++，）
点E 坐标代入C 方程得：4220m m +==0，解得20m =∴此时直线l 的方程为1x =-，但
2x ≠±，所以不存在.。