第三章-控制系统的李雅普诺夫稳定性分析
合集下载
Lyapunov稳定性理论李雅普诺夫
渐近稳定
A的所有特征值：
需 lim eAt 0. t
e1t
te1t e1t
1 t e2 1t 2 te1t
0 0
0
0
e1t
0 0
e2t 0
e3t
结论3：
不稳定
A有一个特征值：
或
的特征值有重根
e1t
te1t e1t
1 t 2e1t 2 te1t
0 0
0
0
e1t
0 0
e2t 0
稳定性： 控制系统本身处于平衡状态。受到扰动，产生偏差，
在扰动消失后，由偏差状态逐渐恢复到原来平衡状态的性能。
偏差逐渐变大，不能恢复到原来的平衡状态，则不稳定。 稳定性是动态系统的一个重要性能，保证系统的稳定性 通常是控制器设计的最基本要求。
1
经典控制理论对稳定性分析的局限性
（1）局限于描述线性定常系统
任给一个球域 ，若存在一个球域 ，使得从 出发的 轨迹不离开 ，则称系统的平衡状态是李雅普诺夫意义下稳定 的。
初始状态有界，随时间 推移，状态向量距平衡 点的距离可以维持在一 个确定的数值内，而到 达不了平衡状态。
任给一个球域 ，若存在一个球域 ，使得从 出发的 轨迹不离开 ，则称系统的平衡状态是李雅普诺夫意义下稳定 的。
若
与初始时刻
t
无关，则
0
称系统的平衡状态 是一致
稳定的。
时变系统 与 t0有关
定常系统
与
t
无关
0
李雅普诺夫意义下稳定
考虑系统（4.1），如果对任意的实数 ，都存在另一实
数 ，使当初始状态位于以平衡状态 为球心， 为半径的
闭球域
内，即
A的所有特征值：
需 lim eAt 0. t
e1t
te1t e1t
1 t e2 1t 2 te1t
0 0
0
0
e1t
0 0
e2t 0
e3t
结论3：
不稳定
A有一个特征值：
或
的特征值有重根
e1t
te1t e1t
1 t 2e1t 2 te1t
0 0
0
0
e1t
0 0
e2t 0
稳定性： 控制系统本身处于平衡状态。受到扰动，产生偏差，
在扰动消失后，由偏差状态逐渐恢复到原来平衡状态的性能。
偏差逐渐变大，不能恢复到原来的平衡状态，则不稳定。 稳定性是动态系统的一个重要性能，保证系统的稳定性 通常是控制器设计的最基本要求。
1
经典控制理论对稳定性分析的局限性
（1）局限于描述线性定常系统
任给一个球域 ，若存在一个球域 ，使得从 出发的 轨迹不离开 ，则称系统的平衡状态是李雅普诺夫意义下稳定 的。
初始状态有界，随时间 推移，状态向量距平衡 点的距离可以维持在一 个确定的数值内，而到 达不了平衡状态。
任给一个球域 ，若存在一个球域 ，使得从 出发的 轨迹不离开 ，则称系统的平衡状态是李雅普诺夫意义下稳定 的。
若
与初始时刻
t
无关，则
0
称系统的平衡状态 是一致
稳定的。
时变系统 与 t0有关
定常系统
与
t
无关
0
李雅普诺夫意义下稳定
考虑系统（4.1），如果对任意的实数 ，都存在另一实
数 ，使当初始状态位于以平衡状态 为球心， 为半径的
闭球域
内，即
稳态李雅普诺夫稳定性分析在不确定系统控制中的应用研究
稳态李雅普诺夫稳定性分析在不确定系统控制中的应用研究随着科学技术的快速发展，现代化复杂系统的建模和控制问题变得越来越重要。
不确定性常常是复杂系统中的一个普遍特征，包括参数变化、外部干扰等，而这些因素往往会影响到系统稳定性和性能。
因此，寻找有效的控制方法来保证系统稳定性和性能成为了复杂系统研究中的一个热点问题。
本文将探讨稳态李雅普诺夫稳定性分析在不确定系统控制中的应用研究。
一、稳态李雅普诺夫稳定性分析的基本理论稳态李雅普诺夫稳定性分析是现代系统控制理论中的一个重要分支。
其核心思想是通过研究系统状态变量的稳态变化规律，来判断系统的稳定性特征。
该方法的基本理论可以总结如下：1.1 稳态李雅普诺夫函数稳态李雅普诺夫（LS）函数是指在一定条件下，系统状态变量通过某种方式组合而成的函数。
它可以用来刻画系统在达到稳态时的状态变化规律。
具体而言，稳态LS函数的定义如下：$$V(x)=\int_0^{\infty} \sum_{i=1}^n \frac{\partial V}{\partial x_i}f_i(x,t)p(t)dt$$其中，$x=\left[x_1,x_2,\cdots,x_n\right]^{\mathrm{T}}$是系统状态变量，$f_i(x,t)$是系统状态变量的方程，$p(t)$是某个概率密度函数，$\frac{\partialV}{\partial x_i}$是某个函数。
在该式中，$V(x)$越小，表示稳态时系统的稳定性越强。
1.2 稳态李雅普诺夫函数的性质稳态LS函数具有许多重要的性质，其中最基本的包括：1）非负性：$V(x)\geq0$，且$V(x)=0$当且仅当$x=0$；2）单调性：如果$f_i(x,t)\geq0$，则对于$x_1\neq x_2$，有$V(x_1)-V(x_2)>0$或$V(x_1)=V(x_2)$；3）对称性：如果对于任意的$x$和$y$有$f_i(x,t)=f_i(y,t)$，则$V(x)=V(y)$；4）上界性：如果存在$yu>0$，使得$f_i(x,t)\leq f_i(y,t)$，则有$V(x)\leq V(y)$。
《自动控制原理》第三章 3-4 稳定性分析
a1 a0 0 0 n 0 0 0 0 0 a3 a2 a1 a0 0 0 0 0 0 a5 a4 a3 a2 a1 a0 0 0 0 0 0 0 0 0 0 an an 1 an 2 0 0 0 0 0 0 0 0 an
第三章 线性系统的时域分析法
赫尔维茨稳定判据: 线性系统稳定的充要条件: i 0, i 1,2, n
能源与动力学院
第三章 线性系统的时域分析法
15
3. 劳思-赫尔维茨稳定判据…
例3 2 s 4 s 3 3s 2 5s 10 0
1 5 4 0 1 0 2
系统不稳定
0 5 3
0 0 0 10
能源与动力学院
第三章 线性系统的时域分析法
11
1. 稳定性的基本概念
稳定性：扰动作用 偏离平衡状态 产生初始偏差 扰动消失 恢复到原平衡状态
例1. 单摆 例2. 曲面坡
大范围稳定 小范围稳定
稳定平衡点 不稳定平衡点
能源与动力学院
第三章 线性系统的时域分析法
12
2. 线性系统稳定的充要条件
第三章 线性系统的时域分析法
3
重点回顾
R(s) E(s)
1
n s(s 2n )
2
C(s)
Td s
n s(s 2n )
2
R(s)
E (s )
C(s)
Kt s
能源与动力学院
第三章 线性系统的时域分析法
4
重点回顾
主导极点: 如果在所有的闭环极点中，距虚轴 最近的极点周围没有闭环零点，而其他闭 环极点又远离虚轴，那么距虚轴最近的极 点在系统响应过程中起主导作用，这样的 闭环极点称为主导极点 非主导极点：除主导极点外的其他闭环极点
第三章 线性系统的时域分析法
赫尔维茨稳定判据: 线性系统稳定的充要条件: i 0, i 1,2, n
能源与动力学院
第三章 线性系统的时域分析法
15
3. 劳思-赫尔维茨稳定判据…
例3 2 s 4 s 3 3s 2 5s 10 0
1 5 4 0 1 0 2
系统不稳定
0 5 3
0 0 0 10
能源与动力学院
第三章 线性系统的时域分析法
11
1. 稳定性的基本概念
稳定性：扰动作用 偏离平衡状态 产生初始偏差 扰动消失 恢复到原平衡状态
例1. 单摆 例2. 曲面坡
大范围稳定 小范围稳定
稳定平衡点 不稳定平衡点
能源与动力学院
第三章 线性系统的时域分析法
12
2. 线性系统稳定的充要条件
第三章 线性系统的时域分析法
3
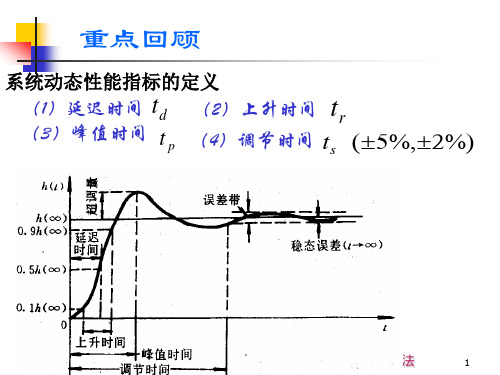
重点回顾
R(s) E(s)
1
n s(s 2n )
2
C(s)
Td s
n s(s 2n )
2
R(s)
E (s )
C(s)
Kt s
能源与动力学院
第三章 线性系统的时域分析法
4
重点回顾
主导极点: 如果在所有的闭环极点中，距虚轴 最近的极点周围没有闭环零点，而其他闭 环极点又远离虚轴，那么距虚轴最近的极 点在系统响应过程中起主导作用，这样的 闭环极点称为主导极点 非主导极点：除主导极点外的其他闭环极点
李雅普诺夫稳定性的定义
定义 (李雅普诺夫渐近稳定性) 若状
x2
态方程
x’=f(x,t)
所描述的系统在初始时刻t0的平衡态xe 是李雅普诺夫意义下稳定的,且系统 状态最终趋近于系统的平衡态xe,即
Limt x(t)=xe
x(0)
x1
则称平衡态xe是李雅普诺夫意义下渐近稳定的。
➢ 若(,t0)与初始时刻t0无关,则称平衡态xe是李雅普诺夫意 义下一致渐近稳定的。
❖ 它是一种具有普遍性的稳定性理论, 不仅适用于线性 定常系统,而且也适用于非线性系统、时变系统、分 布参数系统。
❖ 本节先讨论李雅普诺夫稳定性理论的基础--李雅普 诺夫稳定性定义。
平衡态
❖ 设我们所研究的系统的状态方程为 x’=f(x,t)
其中x为n维状态变量; f(x,t)为n维的关于状态变量向量x和时间t的非线性向量函数。 对该非线性系统,其平衡态的定义如下。
值得指出的是，由于非线性系统的李雅普诺夫稳定性具有局 部性特点,因此在讨论稳定性时,通常还要确定平衡态的稳定邻 域(区域)。
李雅普诺夫稳定性定义
基于上述数学定义和符号,我们有如下 李雅普诺夫意义下稳定性的定义。
x2
x(0) x(0)
x1
定义 (李雅普诺夫稳定性) 若状态方程
x2
x’=f(x,t) 所描述的系统,
➢ 对于任意的>0和任意初始时刻t0,
x(0) x(0)
x1
➢ 都对应存在一个实数(,t0)>0,
➢ 使得对于任意位于平衡态xe的球域 S(xe,)的初始状态x0,
➢ 当从此初始状态x0出发的状态方程的解x都位于球域 S(xe,)内,
则称系统的平衡态xe是李雅普诺夫意义下稳定,
✓ 即逻辑关系式
李雅普洛夫稳定性分析
或任意正实数 0 ，都可以找到另一个正实数 ( , t0 ) 或球
域 S( ) ，当初始状态 x0 满足 x0 xe ( , t0 ) 时，对由此出发
的X的运动轨迹有
lim
t
x
xe
，
则称平衡状态
xe 在李雅普诺
夫意义下是稳定的。
如果 与初始时刻 t0 无关，则称平衡状态是一致稳定的。
2 ）对于给定系统，如果存在李氏函数，它不是唯一的。用 第二法判稳时，找到一个李氏函数就可以。
3 ）李氏函数最简单形式是二次型 V ( x) xT Px ，P是正定实对 称方阵。
4.2 标量函数V(x)的符号性质 标量函数V(x)：
1）正定性：当且仅当x=0时，才有 V (x) 0 ；对任意 非零X，恒有 V (x) 0，则 V ( x) 为正定。
2、内部稳定性：指系统在零输入条件下通过其内部状态变 化所定义的内部稳定性。状态稳定。
外部稳定性只适用于线性系统，内部稳定性不但适用于 线性系统，而且也适用于非线性系统。对于同一个线性系统， 只有在满足一定的条件下两种定义才具有等价性。
不管哪一种稳定性，稳定性是系统本身的一种特性，只 和系统本身的结构和参数有关，与输入－输出无关。
2）平衡状态——状态空间中满足 X&e f ( X e ,t) 0 属性的一 个状态。
3）受扰运动——自治系统因初始扰动X0引起的一类状态运动。 用X0u(t)表示。其呈现为状态空间中从X0出发的一条轨线。
2 李亚普洛夫稳定性定义
2.1 系统的平衡状态 2.2 状态向量范数 2.3 李雅普诺夫意义下稳定性定义（4种）
对非线性系统 X f (X ,t)
当f (X,t)为与X 同维的矢量函数，且对X 具有连续偏导数，则可将
李雅普诺夫关于稳定性的定义
✓
线性定常系统的有界输入有
界输出(BIBO)稳定性
未研究系统的内部状态变化的稳定性，也不能推广 到时变
系统和非线性系统等复杂系统。
➢ 再则，对于非线性系统或时变系统，虽然通过一些 系统转化方法，上述稳定判据尚能在某些特定系统和范 围内应用，但是难以适用于一般系统。
现代控制系统的结构比较复杂，大都存在非线性或时变因 素，即使是系统结构本身，往往也需要根据性能指标的要 求而加以改变，才能适应新的情况，保证系统的正常或最 佳运行状态。
Lyapunov的博士论文被译成法文并于1907年发表，1949年 普林斯顿大学出版社重印了法文版。1992年在Lyapunov的 博士论文发表100周年之际，International Journal of Control （国际控制杂志）以专辑形式发表了Lyapunov论文的英译 版，以纪念他在控制理论领域所作的卓越贡献。
➢ 该方法不仅可用于线性系 统而且可用于非线性时变 系统的分析与设计，已成 为当今控制理论课程的主 要内容之一。
➢ 百余年来Lyapunov理论 得到极大发展, 在数学、 力学、自动控制、机械工 程等领域得到广泛应用。
A.M. Lyapunov是一位天才的数学家。曾从师于大数学家 P.L. Chebyshev（切比雪夫），和A.A. Markov（马尔可夫 ）是同校同学（李比马低两级），并同他们始终保持着良好 的关系。他们共同在概率论方面做出了杰出的贡献。在概率 论中可以看到关于矩的马尔可夫不等式、切比雪夫不等式和 李亚普诺夫不等式等。Lyapunov还在相当一般的条件下证 明了中心极限定理。
✓
经典控制理论讨论的有界输入
有界输出（BIBO）稳定即为外部稳定性 。
Outer stability
5.1_李雅普诺夫稳定性的定义
✓ 本节讨论的李雅普诺夫稳定性即为内部稳定性
概述(5/6)
早在1892年, 俄国学者李雅普诺夫（Aleksandr Mikhailovich Lyapunov , 1857 – 1918) 发表题为“运动稳定性一般问题” 的著名文献, 建立了关于运动稳定性的一般理论
➢ 百余年来, 李雅普诺夫理论 得到极大发展, 在数学、力 学、控制理论、机械工程等 领域得到广泛应用
描述的系统在初始时刻t0, ➢ 对于某个给定的实数>0和任意一个 实数>0,
x1
x(0)
➢ 总存在一个位于平衡态xe的邻域S(xe,)的初始状态x(0), ➢ 使得从x(0)出发的状态方程的解x(t)将脱离球域S(xe,), 则称系统的平衡态xe是李雅普诺夫意义下不稳定的.
Ch.5 李雅普诺夫稳定性 分析
目录
概述 5.1 李雅普诺夫稳定性的定义 5.2 李雅普诺夫稳定性的基本定理 5.3 线性定常系统的李雅普诺夫稳定性分析
目录(1/1)
概述(1/6)
概述
一个自动控制系统要能正常工作,必须首先是一个稳定的系统 一个稳定的系统
➢ 当系统受到外界干扰后, 它的平衡被破坏, 但在外扰去掉 以后, 它仍有能力自动地在平衡态附近继续工作
平衡态
平衡态
平衡态
平衡态(3/4)
例5-1 对于非线性系统
xx12
x1 x1
x2
x23
其平衡态为下列代数方程组
x1x1
0 x2
x23
0
的解, 即下述状态空间中的三个状态为其孤立平衡态
xe,1
0 0
xe,2
0 1
xe,3
0 1
李雅普诺夫稳定性研究系统在 其平衡态附近(邻域)的运动变 化问题
概述(5/6)
早在1892年, 俄国学者李雅普诺夫（Aleksandr Mikhailovich Lyapunov , 1857 – 1918) 发表题为“运动稳定性一般问题” 的著名文献, 建立了关于运动稳定性的一般理论
➢ 百余年来, 李雅普诺夫理论 得到极大发展, 在数学、力 学、控制理论、机械工程等 领域得到广泛应用
描述的系统在初始时刻t0, ➢ 对于某个给定的实数>0和任意一个 实数>0,
x1
x(0)
➢ 总存在一个位于平衡态xe的邻域S(xe,)的初始状态x(0), ➢ 使得从x(0)出发的状态方程的解x(t)将脱离球域S(xe,), 则称系统的平衡态xe是李雅普诺夫意义下不稳定的.
Ch.5 李雅普诺夫稳定性 分析
目录
概述 5.1 李雅普诺夫稳定性的定义 5.2 李雅普诺夫稳定性的基本定理 5.3 线性定常系统的李雅普诺夫稳定性分析
目录(1/1)
概述(1/6)
概述
一个自动控制系统要能正常工作,必须首先是一个稳定的系统 一个稳定的系统
➢ 当系统受到外界干扰后, 它的平衡被破坏, 但在外扰去掉 以后, 它仍有能力自动地在平衡态附近继续工作
平衡态
平衡态
平衡态
平衡态(3/4)
例5-1 对于非线性系统
xx12
x1 x1
x2
x23
其平衡态为下列代数方程组
x1x1
0 x2
x23
0
的解, 即下述状态空间中的三个状态为其孤立平衡态
xe,1
0 0
xe,2
0 1
xe,3
0 1
李雅普诺夫稳定性研究系统在 其平衡态附近(邻域)的运动变 化问题
李雅普诺夫稳定性理论
定义三 对所有的状态(状态空间的所有点)，如 果由这些状态出发的轨迹都具有渐近稳定性，则 称平衡状态xe为大范围渐近稳定。
定义四 :如果从球域 S( )出发的轨迹，无论球
域选得多么小，只要其中有一条轨迹脱离球域， 则称平衡状态xe为不稳定。
❖线性系统：如果它是渐近稳定的，必是有大 范围渐近稳定性(线性系统稳定性与初始条件的 大小无关)。
❖非线性系统：稳定性与初始条件大小密切 相关,系统渐近稳定不一定是大范围渐近稳定。
三. 李雅普诺夫第一法（间接法）
利用状态方程解的特性来判断系统稳定性。
1. 线性定常系统稳定性的特征值判据：
xAx x(0)x0 t 0
李氏稳定的充要条件：
Re(i ) 0 i1,2,n
即系统矩阵A的全部特征值位于复平面左半部。
2) 选取不当，会导V致( x , t ) 不定的结果。
2) 这仅仅是充分条件。
3)
例4：试判断下列线性系统平衡状态的稳定性。
x 1 x 2 x 2 x 1 x 2
解: x 1x 2 0 x1x2 0 即 xe 0
.
设 V(x)x12x2 2 则 V(x) 2x22
.
可见V
( x )与 x1 .
结论：
1) 若 Re(i) 0 i1,2,,n ，则非线
性系统在 x e 处是渐近稳定的，与 g ( x)
2) 无关。
2) 若 Re(i) 0 Re(j ) 0 ij1,,n
3) 则不稳定。
3) 若 Re(i ) 0，稳定性与 g (x)有关，
4)
g(x)50) 则是李雅普诺夫意义下的稳定性。
4.4 线性系统的李雅普诺夫稳定性分析
1．线性定常系统的李雅普诺夫稳定性分析
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1.3 米哈伊洛夫定理 特征矢量幅角变化与稳定性关系 一阶系统 特征方程：D(s) = s + p ＝ 0 D(s)可视为复平面上的向量。
在频域：D(jω) = p + jω 当ω变化时， D(jω)的端点沿虚轴滑动，其相角相 应发生变化。
若特征根为负实 根，系统稳定
D( j )
若特征根为正实 根，系统不稳定
第三章 控制系统的稳定性分析
研究的目的和意义:稳定性是自动控制系统 正常工作的必要条件，是一个重要特征。 要求：在受到外界扰动后，虽然其原平衡 状态被打破，但在扰动消失后，仍然能恢 复到原来的平衡状态，或者趋于另一平衡 状态继续工作。 稳定性：描述初始条件下系统状态方程解 的收敛性，而与输入作用无关。
3
1、经典控制论中的系统稳定性分析方法 2、李雅普诺夫意义下的稳定性
3、判别系统稳定性的李雅普诺夫方法
4、线性系统的李雅普诺夫稳定性分析方法 5、非线性系统的李雅普诺夫稳定性分析方法 6、系统参数最优的李雅普诺夫稳定性分析方法
4
1.经典控制论中的系统稳定性分析
1.1 稳定性的基本概念
1.2 代数判据 1.3 根轨迹法稳定性判据 1.4 Nyquist稳定性判据 1.5 稳定性裕量
D( j )
2
0
2
0 2
2
D(s) a0 s n a1s n1 a2 s n2 ... an1s an D( j) a0 ( j p1)( j p2 )( j pn ) D( j) D( j) D( j) a0 | j p1 | | j p2 | | j pn |
D(s) a 0s 3 a1s 2 .a 2s a 3 0
n
0 0 0 0 an
a0>0时
1 a 1 0
2
a1 a0
a1
a3 a2
a3 a2 a1
a 1a 2 a 0 a 3 0
0 0 a 22 0 a3
3 a 0 0
a0>0时, a1>0, a2>0, a3>0(全部系数数同号) a1a2> a0 a3
特殊情况：第一列出现0。 解决方法：用任意小正数 代之。
• 特殊情况2：某一行元素均为0
D(s) s5 s 4 5s3 5s 2 6s 6 0
各项系数均为正数
s5 s
4
特殊情况：某一行元素均为0
6 6 0
1 1 04 5/ 2 2/5 6
5 5 0 10 6
s3 s2 s1 s0
(a)大范围稳定
否则系统就是小范围稳定的。
(b)小范围稳定
注意：对于线性系统，小范围稳定大范围稳定。
(a)不稳定
临界稳定：若系统在扰动消失后，输出与原始的 平衡状态间存在恒定的偏差或输出维持等幅振荡， 则系统处于临界稳定状态。
注意：经典控制论中，临界稳定也视为不稳定。 原因：(1)分析时依赖的模型通常是简化或线性化； (2)实际系统参数的时变特性； (3)系统必须具备一定的稳定裕量。
D( j )
2
2
二阶系统
特征方程：D(s) = s2 +2ξωns+ ωn2 ＝(s+p1)(s+p2)= 0
实根情形(ξ≥ 1) 当ω由0变化到∞时：
D( j )
2
2
D( j )
2
2
0
共轭虚根情形(0<ξ<1)
设根位于左半s平面
当ω由0变化到∞时， jω+p1的相角变化范围： -φ0 ~ π/2
一阶系统
二阶系统
a1>0(全部系数数同号)
a1>0, a2>0(全部系数数同号) a1>0, a2>0, a3>0(全部系数数同号) a1a2> a0 a3 a1>0, a2>0, a3>0 , a4>0(全部系数数同号)
三阶系统
四阶系统 a a a a a 2 a 2 a 1 2 3 0 3 1 4
ห้องสมุดไป่ตู้
1.1 稳定性的基本概念 稳定性的定义 稳定的充要条件
稳定的必要条件
稳 定 的 摆
不 稳 定 的 摆
稳定性的定义 控制系统在外部扰动作用下偏离其原来的平衡状 态，当扰动作用消失后，系统仍能自动恢复到原 来的初始平衡状态。 注意：以上定义只适 用于线形定常系统。 稳定
不稳定 外加扰动
大范围稳定: 不论扰动引起的初始偏差有多大，当扰动取 消后，系统都能够恢复到原有的平衡状态。
1 2 3
a1 a0 n 0 0 a3 a2 a1 0 a5 a4 a3 0 a n 1 a n 2
n
0 0 0 0 an
一阶系统
D(s) a 0 s a 1 0
1 a1 0 a0>0时 a0>0时, a1>0(全部系数数同号)
k r
nm
a0 ( s pi )[ s ( j j j )][s ( j j j )]
i 1 j 1
理想脉冲函数作用下 R(s)=1。 对于稳定系统,t ∞时,输出量 c(t)=0。 注意：稳定性是控制系统自身的固有特性，取决 于系统本身的结构和参数，与输入无关。
| b1 | c1 | d1
sn s s n 2 s s n 4 s2 s1 s0
n 3 n 1
a0 a1 b1 c1 d1 e1 f1 g1
a2 a3 b2 c2 d2 e2
a4 a5 b3 c3 d3
a0 a1 a1 a1 b1 b1 b1 c1 c1
i 1 j 1 K k
j
P3
P2
P1
S平面
O
P5
Pn
P4
注意：稳定性与零点无关
0<TK<1/4:两个不同 的负实根
TK=1/4:一个负实根， 一个零根
结果：系统稳定
TK>1/4:一对共轭复 根，具有负实部
1.2 代数判据 劳思(routh)判据 赫尔维茨(Hurwitz)判据
解决方法：全0行的上一行 元素构成辅助方程，求导 后方程系数构成一个辅助 系数。 例如： 求导得:
s 4 5s 2 6 0
4s 3 10s1 0
s1, 2 j 2 s 3, 4 j 3
s 5 1
劳斯阵列出现全零行:系统在s平面有对称分布的根 大小相等符号相反的实根
无需求解特征根，直接通过特征方程的系数判别 系统的稳定性。
1.2 代数判据 稳定的必要条件
D(s) a0 s a1s
n
n1
... an1s an
当 a0 0 时，各项系数大于0 且不等于0
劳思阵列
D(s) a 0s a1s
n
n 1
... a n1s a n 0
劳思(routh)判据的特殊情况 • 特殊情况1：第一列出现0
• 特殊情况2：某一行元素均为0
• 特殊情况1：第一列出现0
D(s) s 4 s 3 3s 2 3s 2 0
各项系数均为正数
s4 s3 s2 s1 s0 1 1 0( ) 2 3 2 3 3 2 0 2 0
0 0 a 43 0 0 a4
a a a a a2 a2a 1 2 3 0 3 1 4
a0>0时, a1>0, a2>0, a3>0 , a4>0 (全部系数数同号)
D(s) a 0s n a1s n1 ... a n 1s a n 0
归纳：a0>0时
2
不同特性的控制系统的稳定性分析方法 系统 数学描述方法 稳定性分析方法
单输入单输出线性 传递函数或频率特 定常系统 性（经典） 多变量系统，时变 状态空间（现代） 系统、非线性系统
劳思判据、奈奎斯 特判据、根轨迹判 据等 李雅普诺夫稳定性 理论
其中，李雅普诺夫提出的稳定性定理采用了状态向量来描述， 适用于单变量，线性，非线性，定常，时变，多变量等系统。 应用：自适应，最优控制，非线性控制等
a2 a3
| b2 | c1
|
a0 a1 a1
a4 a5 a5 b3
|
a3 | b2 b2 c2
a1 b1 b1 | b1 c1
|
| d2
b3 c3 c1
|
性质：第一列符号改变次数== 系统特征方程含有 正实部根的个数。
特征方程：
劳斯阵列：
劳思(routh)判据 “第一列中各数” 如果符号相同 系统具有正实部特征根的个数等于 零系统稳定； 如果符号不同 符号改变的次数等于系统具有的正 实部特征根的个数系统不稳定。 控制系统稳定的充分必要条件： 劳思阵列第一列元素不改变符号。 注：通常a0 > 0，因此，劳斯稳定判据可以简述为 劳斯阵列表中第一列的各数均大于零。
四阶系统
D(s) a 0s 4 a1s 3 .a 2s 2 a 3s a 4 0
a0>0时
1 2 3
a1 a0 n 0 0 a3 a2 a1 0 a5 a4 a3 0 a n 1 a n 2
1 a 1 0
变化量：π/2+ φ0
jω+p2的相角变化范围： φ0 ~ π/2 变化量：π/2- φ0