流体绕过颗粒及颗粒床层的流动
第四章12颗粒与流体间的相对流动

本章难点
➢ 非球形颗粒的表示方法; ➢ 干扰沉降速度的计算; ➢ 可压缩滤饼比阻随压强的变化; ➢ 洗涤速率与过滤速率的关系。
第一节 流体绕过颗粒及颗粒床层的流动
1.1 颗粒及颗粒床层的特性 ➢ 单颗粒的特性参数 ➢ 颗粒群(混合颗粒)的特性参数 ➢ 颗粒床层的特性 1.2 流体与颗粒间的相对运动 ➢ 流体绕过颗粒的流动 ➢ 流体通过颗粒床层的流动
于空隙率ε。
(4)床层通道特性 ➢ 固体颗粒堆积所形成的孔道的形状是不规则的、细
小曲折的。
➢ 许多研究者将孔道视作流道,并将其简化成长度为 Le的一组平行细管,并规定:(1)细管的内表面积 等于床层颗粒的全部表面;(2)细管的全部流动等 于颗粒床层的空隙容积。则这些虚拟细管的当量直 径de为:
de
➢ 固体颗粒沉降时,起重要作用的特征数仍是雷诺数。
➢ 静止或流速很慢的流体中,固体颗粒在重力(或离 心力)作用下作沉降运动。此时颗粒的受到以下三 方面的作用力:
(1) 场力F
➢ 重力场
Fg = mg
➢ 离心力场 Fc = mrω2
式中:r——颗粒作圆周运动的旋转半径;
ω——颗粒的旋转角速度;
m——颗粒的质量,对球形颗粒m=πdp3ρp /6。
(2)颗粒群的平均特性参数
➢ 颗粒群的平均粒径有不同的表示法,常用等比表面
积当量直径来表示颗粒的平均直径,则混合颗粒的
平均比表面积αm为:
am
xiai
6 xi d pi
由此可得颗粒群的比表面积平均当量直径 dm为:
1
d m
xi d pi
ai——第i层筛网上颗粒的比表面积, m2/m3 ;
(Re p )
➢ 修正雷诺数的定义为:
化工原理第四章流体通过颗粒层的流动

4.4 过滤原理及设备 4.4.1 过滤原理
过滤将固—液两相的悬浮液分离 成滤饼和滤液。 两种过滤方法 滤饼过滤(表面过滤) 颗粒截留在过虑介质表面。适用于较高浓度的悬浮液 架桥现象——对表面过滤,真正起过滤作用的是滤饼本身,
过滤介质仅给架桥现象提供条件 深层过滤 颗粒靠静电力、表面力吸附于过滤。 介质内部。 适用于低浓度、细颗粒的分离
(2)q与τ的关系;
(3)K与τ的关系;
由 q K c, K
2(q qe ) q c 得K 2c2 2qec
(4)ΔP 与τ的关系。 K
必须注意:使用恒速速率 方程时,应使K与τ严格 对应。
q
τ
τ
ΔP
qe≠0
τ
qe=0,s=0 τ
ΔP
qe=0
τ
qe≠0,s≠0 30 τ
恒压过滤方程 P c,
C.床层特性的影响 (1)空隙率ε: 空隙率ε对压降ΔP 的影响非常大,反映在 ε的可变性大,可靠性差; ε较小的误差,将引起压降明显的误差 (2)比表面积α ΔP ∝α2,对同形状颗粒,dp↓, α越大↑,hf(ΔP )↑。 例:其他条件不变空隙率ε由0.5降为0.4,单位床层压降 增加2.8倍。
4
则
4 u
Re' a(1 ) 4
u
a1
当Re’<2时,λ=k’/Re’,
k’=5.0
代入得: P k / a2 1 2 u
L
3
上式称为康采尼方程(注意适用条件:层流);
欧根在更宽的Re’范围内,得出: ' 4.17 0.29
代入基本式:
Re'
P
L
4.17
a2
1
流体通过颗粒层的流动

反应器 催化剂颗粒层等概念
以上化工操作中均为流体通过颗粒层的流动,与流体
在管道中的流动相比较:阻力增大,速度分布均一,
流动特点:层流,绕流(因速度慢也称爬流)。
爬流:爬流速度很小,流动很 缓慢,颗粒迎流面与背流面的 流线对称。
颗粒层中流体流动特点:
(1)床截面的流体速度分布均匀,床层两端产生很大压降△P 原因:大量颗粒随机堆积,颗粒对流体的流动造成很大 的阻力
真正的过滤介质:架桥作用 。
滤浆
滤饼 过滤介质
滤液
滤饼过滤
(2)深层过滤——本质不同于表面过滤,是依靠吸附作用。
深层过滤 深层过滤主要用于含固量很少的悬浮液 化工生产广泛使用的是滤饼过滤。
3、过滤介质 织物介质: 滤布滤网(截留颗粒dp:5~6μm) 多孔性固体介质:素瓷、多孔塑料(dp: 1~3μm) 堆积介质: 固体颗粒如砂、木炭、非编织纤维如玻璃纤维 ——用于含固量少的悬浮液
2、颗粒床层的数学模型
ΔP
hf
Le de
u12 2
;Le
L,Le L
常数
ΔP 1
L
u
de、u1
流体在固定床内流动的简化模型
Le Δ P 1
Δ P Le u12 de 2
表观流速(空床流速)u与实际流速 u1 的关系 :
uA
u1 A1
u
u1
A1 A
u1
化简得到单位床层高度压降: Δ P ( 1 )a u2
影 响
2 、空隙率随装填情况而变,
L
同种物料同样方式装填,空隙率未必能重复
第四节 过滤原理及设备
一、过滤 固液分离的常用方法是通过过滤获得清净的液体或
作为产品的固体颗粒 1、过滤原理 利用重力或人为造成的压差使悬浮液通过某种多孔性 过滤介质分离悬浮液。 2、两种过滤方式 (1)滤饼过滤——依靠通道尺度小于颗粒直径,滤饼是
860-食品科学基础考试大纲

海南大学硕士研究生入学考试《860-食品科学基础》考试大纲一、考试性质海南大学硕士研究生入学考试初试科目。
二、考试要求考生应全面系统的理解和掌握食品化学与食品工程原理的基本理论,以及各种食品化学理论在食品科学研究中的应用。
并能够应用相关基础理论和基本知识分析和解决食品工程的实际问题。
三、考试方式与分值闭卷、笔试。
满分 150 分。
四、考试内容第一篇食品化学考试大纲绪论1. 食品化学的概念和研究内容。
2. 食品化学的研究方法。
3. 食品化学在食品工业中的作用。
第一章水分1. 食品中的水存在状态及水分含量、水的结构及物理特性。
水和冰的分子结构及对理化性质的影响。
2. 水分活度意义和计算;等温吸湿线的概念及意义;水分活度与食品的稳定性之间的关系。
3.食品的冻结过程,速冻、缓冻和温度波动对食品的影响。
第二章碳水化合物1. 单糖的结构和性质,掌握美拉德褐变反应及影响因素。
单糖的焦糖化反应,与酸或碱的反应,氧化还原反应。
2. 食品中低聚糖的结构和化学性质;多糖的结构与性质;淀粉的结构与性质,淀粉的糊化、老化及改性;果胶的结构及凝胶的形成。
第三章脂质1. 脂肪的结构和组成;脂肪酸和脂肪的命名;天然油脂中脂肪酸的分布;油脂的物理性质;油脂的结晶特性、熔融特性、液晶态及乳化。
2. 掌握脂肪氧化的化学反应机理、影响因素及控制方法,油脂氧化产物的成因。
油脂在高温下的化学变化以及对油脂质量的影响;油脂加工的化学原理与方法。
3. 油脂评价的基本原理和方法。
第四章氨基酸、肽和蛋白质1. 氨基酸、必需氨基酸和常见活性肽的结构、理化性质和功能性质。
2. 蛋白质变性的机理及其影响因素;蛋白质功能性质产生的机理、影响因素和评价方法。
3. 蛋白质在食品贮藏和加工中发生的物理、化学和营养变化以及在食品加工与储藏中如何利用或防止这些变化。
第五章维生素和矿物质1. 脂溶性维生素和水溶性维生素的化学结构特点、性质和来源。
2. 维生素在食品贮存和加工中所发生的物理化学变化,及对食品品质的影响。
流体通过颗粒层的流动(4)全解

过滤介质 滤液
织物介质,如棉、麻、丝、毛、合 成纤维、金属丝等编织 成的滤布; 多孔性固体介质,如素瓷板或管、 烧结金属等。
2018/10/12
滤饼过滤
23
4.4.1过滤操作的分类
(1)饼层过滤(滤饼过滤) 定义:过滤过程中在过滤介质表面形成固体颗粒的滤饼层.
滤浆 滤饼 过滤介质
滤液
滤饼过滤
2018/10/12 24
(2) 床层的各向同性
工业上的小颗粒床层通常是乱堆的,若颗粒是非球 形,各颗粒的定向应是随机的,这样的床层就可视 为各向同性的。 各向同性床层横截面上可供流体通过的实际面积 (或自由截面)与床层截面之比在数值上等于 ,这 是其的重要特点之一。
(3) 床层的比表面
aB=颗粒表面积/床层体积 = S总/ V床 = S总/ V颗×( V颗/ V床) =a(1-)
p ' 1 a K u 3 L 得过滤速率:
2 2
dq p 1 u ' 2 2 d L K 1 a
3
(2) 滤饼的阻力
对于不可压缩滤饼,ε=const,a=const,反映颗粒 物性,因物料而异。 2 2 a 令 ' 1
l u hf d 2
2
范宁方式能否用于计算流体通过固定颗粒床层的 压降呢? (1)流体通过固定颗粒床层压降直接计算时存 在的困难 当流体通过固定颗粒床层时,由于颗粒层内的颗 粒大小不均匀,形状不规则,所形成的通道是弯 弯曲曲的、变截面的、纵横交错的网状结构。 弯曲、变截面的网状结构成为了颗粒层内流体通 道的特点,也成为了压降(流动阻力)直接计算 的困难。因为用范宁公式计算时,无法确定通过 颗粒层的流体通道的边界尺寸。
第4章 颗粒与流体之间的相对流动(10)

第4章 颗粒与流体之间的相对流动1 流体绕过颗粒及颗粒床层的流动 1.1 颗粒床层的特性 1.1.1 单个颗粒的特性球形颗粒是最简单的一种颗粒,它的各有关特性均可用单一参数—直径d 全面表示。
体积 63dVπ=;表面积 2d S π=;比表面积 dVS a 6==(单位体积固体颗粒所具有的表面积称为颗粒的比表面积) 对非球形颗粒,以当量直径d e 来表征其与球形颗粒在某些特性方面的等效。
(1)体积等效直径d ev 使当量球形颗粒的体积等于真实颗粒的体积V P 。
63evP d V π=或36πPev V d =(2)表面积等效直径d es 使当量球形颗粒的表面积等于真实颗粒的表面积S P 。
2es P d S π= 或 πPesS d=(3)比表面积等效直径d ea 使当量球形颗粒的比表面积等于真实颗粒的比表面积a 。
eaPP d VS a 6==或 PP eaS V d 6=球形度φS :体积相同时球形颗粒的表面积与实际颗粒的表面积之比。
相同V PS S S )(=φ0≤φs ≤1。
1.1.2 颗粒群的特性由大量单个颗粒组成的集合—颗粒群。
(1) 粒度分布不同粒径范围内所含粒子的个数或质量称为粒度分布。
一般用粒度表征颗粒的大小,球形颗粒的粒度就是其直径。
颗粒粒度的测量方法有筛分法、显微镜法、沉降法等。
筛分法通常采用一套标准筛进行测量。
常用的泰勒标准筛以筛号(目数)表示筛孔的大小。
目数:每英寸长度上的孔数。
(2)颗粒群的平均直径pm d :以比表面积相等为原则的球形颗粒群的平均直径pm d :∑=PiiPm dx d 1式中:x i —第i 筛号上的筛余量质量分数; 21Pipi Pid d d +=-。
1.1.3 床层特性(1) 床层的空隙率ε:床层中空隙的体积与床层总体积之比。
ε=床层空隙体积/床层总体积=(床层体积-颗粒所占体积)/床层总体积 (2)床层的各向同性各向同性的一个重要特点:床层横截面上可供流体通过的空隙面积(即自由截面)与床层截面之比在数值上等于空隙率ε。
化工原理上册 第3章 流体相对颗粒(床层)的流动及机械分离
τm
AP
(a)
(b)
(c)
图3-5 物体的不同形状和位向对曳力的影响 (a)-平板平行于流向;(b)-平板垂直于流向;(c)-流线型物体
水平方向,颗粒所受曳力:
颗粒微元: dFD p cosdA w sindA
总曳力:FD p cosdA w sindA
A
A
Pcosa dA PdA
τwdA
aB
A VB
V
A a(1 ) (1 )
aB a
3.3 流体和颗粒的相对运动
流体和颗粒相对运动的情况:
① 颗粒静止,流体绕过颗粒流动; ② 流体静止,颗粒流动; ③ 颗粒和流体都运动,维持一定相对速度。
3.3.1 流体绕过颗粒的流动
(1) 曳力 阻力:颗粒对流体的作用力 曳力:流体对颗粒的作用力
② 非球形颗粒的曳力系数 计算方法: ◇ 近似用球形颗粒公式,ds→da 或 dv ◇ 实测ξ-Rep 关系(书P168 图3.3.2)
3.3.2 颗粒在流体中的流动
(1) 颗粒在力场中的受力分析
Fb
① 质量力 Fe mae Vs sae
②
浮力
Fb
m
s
ae
Vs ae
③
曳力
FD
AP
1 2
u 2
1
)3
( 6dV2 / a )1/3 ( 6dV2 )1/3
a
因此, dV
6
a
2)等比表面积当量直径 da 指:与非球形颗粒比表面积相等的球形颗粒的直径
a
as
d
2 s
6
d
3 s
6/ ds
da
因此,da 6 / a
第4章流体通过颗粒层的流动
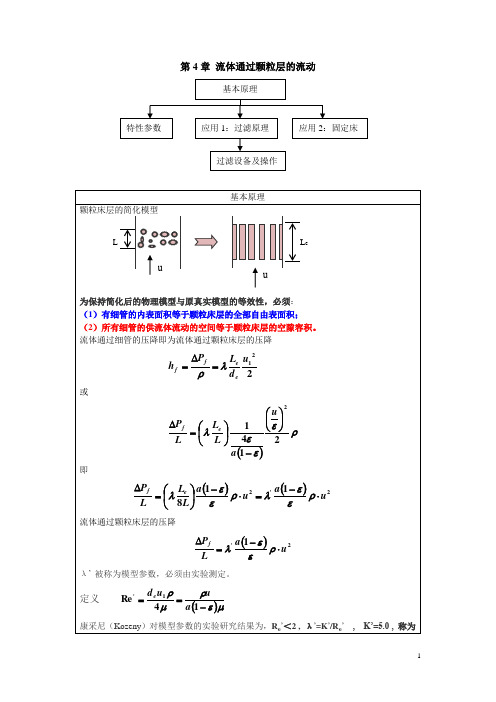
康采尼(Kozeny)对模型参数的实验研究结果为,Re’<2 ,λ’=K’/Re’, K’=5.0 ,称为Kozeny常数。
将模型参数的表达式代入到床层压降的表达式中
欧根(Ergun)在较宽的 范围内, ,获得了关系式
代入到床层压降的表达式中
特性参数
1、颗粒的比表面积
2、颗粒床层的空隙率
3、颗粒床层的比表面积 ,
第4章流体通过颗粒层的流动
基本原理
颗粒床层的简化模型
为保持简化后的物理模型与原真实模型的等效性,必须:
(1)有细管的内表面积等于颗粒床层的全部自由表面积;
(1)
(2)所有细管的供流体流动的空间等于颗粒床层的空隙容积。
流体通过细管的压降即为流体通过颗粒床层的压降
或
即
流体通过颗粒床层的压降
λ’被称为模型参数,必须由实验测定。
单位过滤面积上的滤液体积量
滤饼厚度 、悬浮液中颗粒体积分率 、滤饼空隙率 与单位过滤面积上的滤液体积量 的关系式为
单位过滤面积上过滤速率的表达式则为
定义: , 称为滤饼的比阻。则过滤速率表达式为
或者
考虑过滤介质的阻力后,过滤速率为
令
则
或
定义过滤常数:
自开始即进行恒压过滤,则K为常数,并且 时, ,过滤时间 与累计滤液体积量 (单位面积上累计滤液体积量 )的关系
或
过滤设备及操作
1、板框式压滤机
在保持洗涤水粘度与滤液粘度相同,洗涤操作时的压差与过滤操作时的压差相同时,总面积上的洗涤速率与过滤终了时过滤的速率之间的关系
横穿流洗法, ;置换洗法,
洗涤时间 与过滤时间 的关系
一个生产周期的时间 ,
最佳时间分配:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一节流体绕过颗粒及颗粒床层的流动1.1颗粒、颗粒群及颗粒床层的特性一、单个颗粒的性质形状规则(球形)的颗粒:大小:用颗粒的某一个或某几个特征尺寸表示,如球形颗粒的大小用直径d p表示。
比表面积:单位体积颗粒所具有的表面积,其单位为m2/m3,对球形颗粒为:形状不规则(非球形)的颗粒:(1)颗粒的形状系数:表示颗粒的形状,最常用的形状系数是球形度Φs,它的定义式为:相同体积的不同形状颗粒中,球形颗粒的表面积最小,所以对非球形颗粒而言,总有Φs<1。
当然,对于球形颗粒,Φ=1。
(2) 颗粒的当量直径:a.等体积当量直径d evb.等比表面积当量直径d ea对于非球形颗粒,若体积当量直径为d e:二、颗粒群的特性粒度分布(Particle size distributions)粒度分布测定方法(筛分分析):常用筛分法,再求其相应的平均特性参数。
---泰勒(Tyler)标准筛(表3-1)颗粒粒度(Particle size)对于工业上常见的中等大小的混合颗粒,一般采用一套标准筛进行测量,这种方法称为筛分。
用表格表示:筛孔尺寸——颗粒质量;用图表示:颗粒尺寸——质量分率分布函数:质量分数w i(<d pi)与d pi频率函数:质量分数w i(d pi)与颗粒群的平均特性参数:颗粒群的平均粒径有不同的表示法,常用等比表面积当量直径来表示颗粒的平均直径,则混合颗粒的平均比表面积αm为:由此可得颗粒群的比表面积平均当量直径d m为:三、颗粒床层的特性(1)床层的空隙率:单位体积颗粒床层中空隙的体积(ε),即:ε是颗粒床层的一个重要特性,它反映了床层中颗粒堆集的紧密程度,其大小与颗粒的形状、粒度分布、装填方法、床层直径、所处的位置等有关。
一般颗粒床层的空隙率为0.47~0.7。
(2)床层的比表面积单位体积床层中颗粒的表面积称为床层的比表面积。
(忽略颗粒间的接触面积)影响αb的主要因素:颗粒尺寸。
一般颗粒尺寸越小,αb越大。
(3) 床层的自由截面积与空隙率床层中某一床层截面上空隙所占的截面积(4) 床层的各向同性对于乱堆的颗粒床层,颗粒的定位是随机的,所以堆成的床层可认为各向同性,即从各个方位看,颗粒的堆积都是相同的。
各向同性床层的一个重要特点:床层截面积上可供流体通过的自由截面(空隙截面)与床层截面之比在数值上等于空隙率ε。
壁面处例外——“壁效应”(4)床层通道特性固体颗粒堆积形成的孔道的形状是不规则的、细小曲折的。
许多研究者将孔道视作流道,并将其简化成长度为L e的一组平行细管,并规定:(1)细管的内表面积等于床层颗粒的全部表面;(2)细管的全部流动等于颗粒床层的空隙容积。
则这些虚拟细管的当量直径d e为:影响床层通道特性的因素:与床层颗粒的特性有关。
颗粒的粒度:粒度愈小则所形成的通道数目愈多,通道截面积也愈小;粒度分布的均匀性和颗粒表面状况:粒度分布愈不均匀和表面愈粗糙的颗粒所形成的通道就愈不规则,计算流体流动时应折算成当量直径(也称为水力直径)。
1.2流体与颗粒间的相对运动一、流体绕过颗粒的流动(一)、流体绕颗粒的流动状态(1) 理想流体绕流(2) 实际流体绕流(二)、流体绕颗粒流动时的作用力(1)曳力如图为流体流过固体时,固体表面的受力情况。
经分析,得固体表面上所受的总曳力。
一般,总曳力由形体曳力和表面曳力两部分组成。
工程上大都将形体曳力和表面曳力合在一起,即研究总曳力,并用下式表示:(2) 曳力系数流体沿一定方位绕过形状一定的颗粒时,影响曳力的因素可表示为:其中L为颗粒的特征尺寸,对于光滑球体,L 即为颗粒的直径ds。
应用因次分析可以得出关系式:修正雷诺数的定义为:注意:此式中d p为颗粒直径(对非球形颗粒而言,则取等体积球形颗粒的当量直径),μ、ρ为流体的物性。
ξ-Re p间的关系,经实验测定如图4-6所示.图中球形颗粒(φS=1)的曲线,在不同雷诺数范围内可用公式表示如下:(1) 滞流区(Re p <1):(2) 过渡区(1< Re p <500):(3) 湍流区(500< Re p <2×105):ξ=0.44(4) 边界层内为湍流区(Re p> 2×105):ξ=0.1二、流体通过颗粒床层的流动食品工业中,最常见的流体通过颗粒床层的流动操作有:(1)固定化酶反应:流体(如淀粉溶液等)通过固定床反应器进行,此时组成固定床的颗粒表面载有酶制剂;(2)过滤:悬浮液(如果汁、蔬菜汁及葡萄糖和味精生产中的含晶液体等)的过滤,此时可将由悬浮液中所含的固体颗粒形成的滤饼看作固定床,滤液通过颗粒之间的空隙流动。
1 .流体通过颗粒床层的流动状态流体通过固体颗粒床层时,流动情况复杂,流速分布不均匀(与空管流动比)。
流体在床层内的流动不流畅,产生的旋涡数目要比在直径与床层相等的空管中流动时多很多。
流体在固定床内的流动状态由层流转为湍流是一个逐渐过渡的过程,没有明显的分界线,固定床内常常会呈现某一部分流体的流动可能处于层流状态,但另一部分区域则已处于湍流状态。
2. 流体通过颗粒床层的压降流体通过颗粒床层孔道时,形成阻力的曳力是由两方面引起的:(1)粘滞力(Viscous drag force)(2)惯性曳力(Inertia drag force)总阻力为两者之总和:规定(1) 圆筒形床层的直径为颗粒直径的10-20倍以上,在这个条件下壁效应可以忽略。
(2) 固体颗粒在床层中的堆积是均匀的,因而床层的空隙率也是均匀的。
(3) 固体颗粒是致密的,流体通过颗粒与颗粒及颗粒与器壁的孔道流动,不包括流体通过颗粒本身的毛细管孔隙的扩散运动。
则由床层通道特性可知,流体通过具有复杂几何边界的床层压降等同于流体通过一组当量直径为d e,长度为L e的均匀圆管(即毛细管)的压降。
故有若u为流体的空管流速,通过床层孔道的实际流速u e为:u e=u/ε康采尼方程:仅适用于低雷诺数[(Re)e<2欧根方程:(P97)[应用于较宽的(Re)e范围]欧根方程的误差约为±25%,适用于各种流动条件下的阻力计算,但不适用于细长物体及环状填料。
康采尼或欧根公式可知,床层压降受以下因素的影响:操作变量u、流体物性μ和ρ以及床层特性ε和α,其中受ε的影响最大。
因此,设计计算时空隙率ε的选取应相当慎重。
第二节颗粒在流体中的流动1.固体颗粒沉降过程的作用力固体颗粒沉降时,起重要作用的特征数仍是雷诺数。
静止或流速很慢的流体中,固体颗粒在重力(或离心力)作用下作沉降运动。
此时颗粒的受到以下三方面的作用力:(1) 场力F重力场F g = mg离心力场F c = mrω2式中:r——颗粒作圆周运动的旋转半径;ω——颗粒的旋转角速度;m——颗粒的质量,对球形颗粒m=πd p3ρp /6。
(2) 浮力F b设流体的密度为ρ,则有重力场F b=gmρ/ρp 离心力场F b= rω2mρ/ρp(3) 曳力F D固体颗粒在流体中相对运动时所产生的阻力。
式中:A---颗粒在垂直于其运动方向的平面上的投影面积,m2ξ---阻力系数,无因次;u---颗粒相对于流体的降落速度;2固体颗粒的沉降形态两种沉降形态:滞流和湍流。
✓圆球颗粒直径不大并以极慢的速度沉降时,流体成为一层一层地绕过物体,为滞流沉降。
✓当固体的沉降速度较大时,圆球颗粒背部出现尾迹,产生边界层分离,在球体后面和周围形成大量漩涡,为湍流沉降。
衡量固体颗粒沉降的流动形态的依据也是雷诺数。
u t:颗粒沉降速度用雷诺数判别沉降的流动形态时,对于球形颗粒的沉降,❑当Re t <1时,属于滞流;❑当Re t>500时,为明显而稳定的湍流;❑当1< Re t <500时,为过渡形态3固体颗粒的沉降速度(一) 颗粒的自由沉降速度根据牛顿第二定律,颗粒的重力沉降运动基本方程式应为:上式表明:颗粒的沉降过程分为两个阶段:加速阶段;匀速阶段。
沉降速度(terminal velocity):也称为终端速度,匀速阶段颗粒相对于流体的运动速度。
当du/d =0时,令u= u t,则可得沉降速度计算式对球形颗粒,加速度为零时,应用该式时应具备两个条件:①容器的尺寸要远远大于颗粒的尺寸,因器壁会对颗粒的沉降有阻滞作用;②颗粒不可过分细微,因细微颗粒易发生布朗运动。
由于该式的推导限于自由沉降(Free settling),即,任一颗粒的沉降不受流体中其他颗粒干扰。
沉降速度的求法:求沉降速度通常采用试差法。
①假设流体流动类型;②计算沉降速度;③计算Re,验证与假设是否相符;④如果不相符,则转①。
如果相符,OK !(1)、滞流区(斯托克斯定律区,Re t<1)ξ=24/Re t u t=d p2(ρp-ρ)g/18μ(2)、过渡区(艾伦区,1<Re t<500)ξ=18.5/(Re t0.6)(3)、湍流区(牛顿定律区,500<Ret<2×105)ξ=0.442.摩擦数群法两式相乘,消去u t,即因为一一对应,对于非球形颗粒ψ一定,亦一一对应,所以必亦一一对应。
在坐标上标绘出曲线,由计算值找到曲线上对应的点位置。
再由Re t值,求得,避免了试差。
若已知u t,求颗粒直径d p,也可用类似方法。
在曲线中查得Re t,再根据u t计算d p,即(二)影响沉降速度的因素(以层流区为例)1) 颗粒直径d p:应用:啤酒生产,采用絮状酵母,d p↑→u t↑↑,使啤酒易于分离和澄清。
均质乳化,d p↓→u t↓↓,使饮料不易分层。
加絮凝剂,如水中加明矾。
2) 连续相的粘度μ:应用:加酶:清饮料中添加果胶酶,使μ↓→u t↑,易于分离。
增稠:浓饮料中添加增稠剂,使μ↑→u t↓,不易分层。
加热:3) 两相密度差(ρp-ρ):在实际沉降中:4)颗粒形状非球形颗粒的形状可用球形度φs来描述。
不同球形度下阻力系数与Re的关系见课本图示,Re中的d p用当量直径d e代替。
注意:球形度φs越小,阻力系数ξ越大,但在层流区不明显。
u t非球<u t球。
对于细微颗粒(d<0.5μm),应考虑分子热运动的影响,不能用沉降公式计算u t;沉降公式可用于沉降和上浮等情况。
5) 壁效应(wall effect):当颗粒在靠近器壁的位置沉降时,由于器壁的影响,其沉降速度较自由沉降速度小,这种影响称为壁效应。
6)干扰沉降(hindered settling):当非均相物系中的颗粒较多,颗粒之间相互距离较近时,颗粒沉降会受到其它颗粒的影响,这种沉降称为干扰沉降。
干扰沉降速度比自由沉降的小。
用下述安特里斯公式对沉降速度作修正,可得到实际沉降速度:(7) 液滴或气泡沉降当分散相也是流体时,其粒子可不再视为刚体。
