数学六年级(上)第一单元圆的认识知识点
北师大版六年数学上册《第一单元圆的认识(一)》课堂笔记

北师大版六年级数学上册《第一单元圆的认识(一)》课堂笔记一、圆的定义及特征1. 圆的定义:在同一平面内,到定点的距离等于定长的点的集合。
2. 圆的特征:(1)圆心:圆的中心点,用字母O表示。
(2)半径:连接圆心到圆上任意一点的线段,用字母r表示。
(3)直径:通过圆心并且两端都在圆上的线段,用字母d表示。
(4)圆的半径和直径的关系:在同一个圆内,所有的半径都相等,所有的直径都相等。
直径的长度是半径的2倍,半径的长度是直径的一半。
即:d=2r,r=d/2。
二、圆的性质1. 圆心确定圆的位置,半径确定圆的大小。
2. 在同一个圆内,有无数条半径,有无数条直径。
3. 圆是轴对称图形,有无数条对称轴。
4. 圆周率:圆的周长总是直径的3倍多一些,这个比值是一个固定的数,用字母π表示。
π是一个无限不循环小数,在计算时,通常取3.14。
三、圆的周长和面积1. 圆的周长:围成圆的曲线的长度,用字母C表示。
计算公式:C=2πr。
2. 圆的面积:圆内部的所有点组成的区域的大小,用字母S表示。
计算公式:S=πr²。
四、欣赏与设计1. 利用圆可以设计许多美丽的图案。
2. 圆在实际生活中的应用:例如,钟表的指针、车轮的轮廓等。
五、课堂练习1. 判断题:(1)圆的半径和直径都是直线。
(×)(2)所有的半径都相等,所有的直径都相等。
(×)(3)圆的周长和直径的比值是一个固定的数,叫做圆周率。
(√)2. 选择题:(1)下列图形中,是三棱锥的是:(B)A. 正方体B. 三棱锥C. 圆柱D. 球(2)如图是由5个完全相同是正方体组成的立体图形,它的主视图是:(A)(3)钟表上,8点30分时,时针与分针的夹角是:(C)A. 90°B. 85°C. 75°D. 60°(4)用一副三角板的内角(其中一个三角板的内角是45°,45°,90°,?另一个是30°,60°,90°) 能够画出大于0°且小于180°的不同度数的角共有:(B)A. 8种B. 9种C. 10种D. 11种(5)两条直线相交,只有1个交点,三条直线相交,最多有3个交点,四条直线相交,最多有6个交点,10条直线相交,最多有:(A)A. 45个交点B. 42个交点C. 40个交点D. 36个交点六、总结本节课我们学习了圆的定义、性质、周长和面积的计算方法,以及圆在实际生活中的应用。
人教版六年级上数学《圆的认识》课堂笔记

《圆的认识》课堂笔记以下是整理的关于人教版六年级数学《圆的认识》的课堂笔记,供您参考:一、圆的认识1.圆的概念:圆是由曲线围成的封闭图形,它可以看作是所有到定点(圆心)的距离等于定长(半径)的点的集合。
2.圆心:圆的中心点叫做圆心,用字母“O”表示。
3.半径:连接圆心和圆上任意一点的线段叫做半径,用字母“r”表示。
4.直径:通过圆心且两个端点都在圆上的线段叫做直径,用字母“d”表示。
5.半径与直径的关系:在同一个圆中,直径是半径的2倍,即d=2r。
6.圆的大小比较:两个圆的大小可以通过它们的半径或直径来比较。
两个圆的半径相等时,它们的直径也相等;直径相等时,它们的半径也相等。
7.圆的对称性:圆是一个轴对称图形,它有无数条对称轴,这些对称轴都是经过圆心的直线。
二、圆的周长1.周长的概念:圆的周长是围成圆的曲线的长度,用字母“C”表示。
2.周长公式:圆的周长等于2π乘以半径,即C=2πr。
其中π是一个特殊的数,约等于3.14159。
3.周长的推导公式:根据周长公式和圆的直径与半径的关系,可以推导出周长公式C=πd或C=2πr。
4.周长的应用:通过周长公式可以计算圆的周长,进而求出圆的面积等。
三、圆的面积1.面积的概念:圆的面积是圆所占平面的大小,用字母“S”表示。
2.面积公式:圆的面积等于π乘以半径的平方,即S=πr²。
3.面积的推导公式:根据面积公式和圆的半径与直径的关系,可以推导出面积公式S=π(d/2)²或S=π(r²)。
4.面积的应用:通过面积公式可以计算圆的面积,进而求出圆的周长等。
四、圆的应用1.在生活中,圆的应用非常广泛,如车轮、方向盘、轴承等都是圆形结构;2.在艺术领域,圆也被广泛使用,如穹顶、花窗等都是以圆为基本形状进行设计的;3.在科学研究中,圆也扮演着重要的角色,如天文、物理等领域的研究中经常涉及到圆的形状和性质。
小学六年级上册1单元数学知识点(圆的认识)

小学六年级上册1单元数学知识点(圆的认识)1、圆所占平面的大小叫圆的面积。
把圆等分的份数越多,拼成的图形就越接近平行四边形或长方形。
拼成的平行四边形的底相当于圆周长的一半,高相当于圆的半径;长方形的长相当于圆周长的一半,宽相当于圆的半径。
2、如果用S表示圆的面积, r表示圆的半径,那么圆的面积公式:S圆=pi;r2。
3、半圆的周长不是圆的周长的一半,而是圆的周长的一半再加上一条直径长,即pi;r+2r;pi;r 半圆的面积是圆的面积的一半,即。
24、当长方形、正方形、圆的周长相等时,圆的面积最大,长方形的面积最小。
当长方形、正方形、圆的面积相等时,长方形的周长最大,圆的周长最小。
5、一个圆的半径扩大(缩小)几倍,直径就扩大(缩小)几倍,周长也扩大(缩小)几倍,面积就扩大(缩小)几的平方倍,但圆周率永远不变。
26、一个环形,外圆的半径是R,内圆的半径是r,它的面积是S=pi;中R=r+环的宽度。
环形的周长=外圆周长+内圆周长。
7、几个公式: R2-pi;r2或 S=pi;(R2- r2)。
其C圆=pi;d =2pi;d = 2r pi;S圆=pi;r 2Cdr = r = 2pi; 28、永远记住要带单位,周长是(cm),面积是平方(cm),体积是立方(cm)。
9、常用的3.14的倍数:3.14times;2=6.28 3.14times;3=9.423.14times;4=12.56 3.14times;5=15.7 3.14times;6=18.843.14times;7=21.98 3.14times;8=25.123.14times;9=28.26 3.14times;12=37.683.14times;14=43.963.14times;16=50.24 3.14times;18=56.523.14times;24=75.36 3.14times;25=78.53.14times;36=113.04 3.14times;49=153.863.14times;64=200.96 3.14times;81=254.34希望为大家提供的小学六年级上册1单元数学知识点,能够对大家有用,更多相关内容,请及时关注我们!。
小学数学六年级上册《圆的认识》课件

球体的表面积公式 为:$4pi r^{2}$, 其中$r$为球的半径 。
圆是平面图形,而 球是立体图形。
球体的表面积和体 积计算公式与圆有 关。
球体的体积公式为 :$frac{4}{3}pi r^{3}$,其中$r$为 球的半径。
圆与椭圆的关系
椭圆可以看作是一个长轴和短轴 不同的圆弯曲后形成的平面图形
当圆的直径等于方的对角线长 时,圆的周长等于方的周长, 即2 × π × r = d,其中d是方 的对角线长。
04
圆的实际应用
圆在日常生活中的应用
03
交通工具
餐具
建筑
汽车、火车和飞机等交通工具的轮子都是 圆形的,因为圆可以保证轮子在转动时平 稳,减少摩擦和磨损。
碗和盘子等餐具通常设计成圆形,因为圆 可以容纳更多的食物,并且方便手持和清 洗。
圆形窗户、门和屋顶等建筑元素可以增加 建筑的通风和采光,同时使建筑看起来更 加美观。
圆在科学实验中的应用
01
天文学
天文学家使用圆来描述星球和 星系的运动轨迹,例如地球绕 太阳的公转轨迹就是一个大圆
。
02
物理学
物理学家使用圆来描述物体的 运动状态,例如速度和加速度
等物理量。
03
化学
化学家使用圆来描述化学反应 的平衡状态,例如酸碱中和反 应的平衡常数就是一个圆的方
径。
02
这个公式是通过将圆分割成 无数个小的等长弧线,然后 求和这些弧线的长度来得到
的。
03
圆的周长反映了圆的“长度 ”,是描述圆周长大小的数
学量。
圆和方之间的关系
圆和方之间存在密切的关系, 主要体现在圆的面积和周长与 方的面积和周长的关系上。
当圆的半径等于方的一边长时 ,圆的面积等于方的面积,即 π × r^2 = a^2,其中a是方的 一边长。
数学六年级上册圆的认识

通过圆心且两端都在圆上的线段叫做直径。直径是圆内最长的线段。在同一个圆里,有无数条直径,且所有的直径都相等。直径一般用字母d表示。直径的长度是半径的2倍。
对称性
圆是轴对称图形,有无数条对称轴。
周长(C)
围成圆的曲线的长度叫做圆的周长。圆的周长总是直径的三倍多一些。圆周率π是圆的周长与直径的比值,用字母π表示,π≈3.14。周长公式:C=πd 或 C=2πr。
数学六年级上册圆的认识
类别
内容
定义
在一个平面内,一动点以一定点为中心,以一定长度为距离运动一周所形成的封闭曲线叫做圆。或:在同一个平面内,到定点的距离等于定长的点的集合叫做圆。
圆心(O)
圆中心的点叫做圆心。圆心确定圆的位置。圆心一般用字母O表示。
半径(r)
连接圆心到圆上任意一点的线段叫做半径。半径确定圆的大小。在同一个圆里,有无数条半径,且所有的半径都相等。半径一般用字母r表示。
面积(S)
圆的面积公式为S=πr²。已知圆的直径求面积,则S=π(d÷2)²。已知圆的周长求面积,则S=π(C÷π÷2)²。
其他重要概念
1. 等圆:半径相等的圆叫做等圆,等圆通过平移可以完全重合。2. 同心圆:圆心重合、半径不等的两个圆叫做同心圆。3. 半圆:圆的一半,半圆的弧长等于圆周长的一半,半圆面积等于整圆面积的一半。
六年级数学上册圆的认识知识点总结
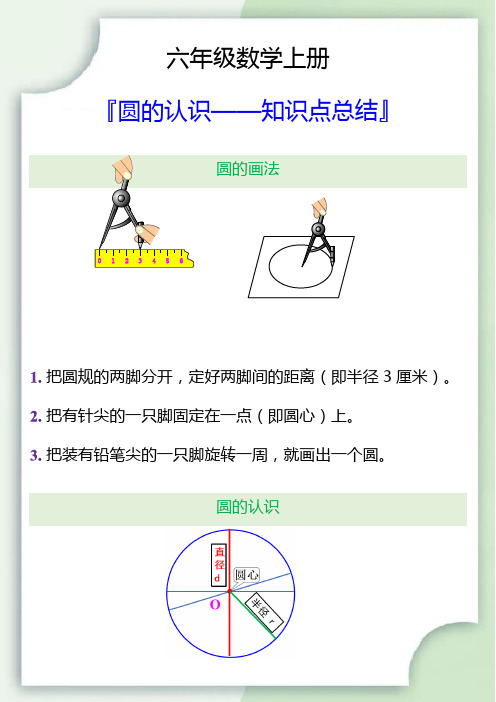
六年级数学上册
『圆的认识——知识点总结』
圆的画法
0123456
把圆规的两脚分开,定好两脚间的距离(即半径3厘米)。
把有针尖的一只脚固定在一点(即圆心)上。
把装有铅笔尖的一只脚旋转一周,就画出一个圆。
圆的认识
圆中心的这一点叫做圆心。
连接圆心和圆上任意一点的线段叫做半径。
通过圆心并且两端都在圆上的线段叫做直径。
在同一个圆里,有(无数)条半径,它们的长度都(相等)。
在同一个圆里,直径是半径的2倍,半径是直径的一半。
六年级数学上册
『圆的认识——知识点总结』
圆的基本概念
1.通过(圆心),并且两端都在(圆上)的线段叫做直径。
从(圆心)到(圆上)上任意一点的线段叫做半径。
同一圆内,直径等于半径的(2倍),半径等于直径的(一半)。
2.圆周率表示圆的(周长)和(直径)的倍数关系,它用字母(π)表示,保留两位小数取近似值约是(
3.14)。
圆周长等
于(直径)乘以(3.14)。
3.用圆规画一个半径是20毫米的圆,圆规两脚之间的距离应取(2)厘米,如果要画直径是20厘米的圆,圆规两脚之间的距离要取(10)厘米。
4.在同一个圆内,有无数条(半径),所有半径长度都(相等)有(无数条)条直径,所有直径的长度都(相等)。
5.(圆心)确定圆的位置,(半径)确定圆的大小。
圆的周长
1.圆一周的长度就是圆的周长。
2.经我国数学家祖冲之的发现,任意一个圆的周长与它的直径的比值是一个定值,称为圆周率π(约等于
3.14)。
3.圆的周长C=πd=2πr。
六年级数学上圆的知识点讲解和练习题

一、圆的认识1、 日常生活中的圆2、 画图、感知圆的基本特征(1) 实物画图(2) 系绳画图3、 对比,感知圆的特征:我们以前学过的长方形、正方形、平行四边形、梯形、三角形等,都是曲线段围成的平面图形,而圆是由曲线围成的一种平面图形。
【归纳】:圆是由一条曲线围成的封闭图形二、圆的各部分名称1、 圆心:用圆规画出圆以后,针尖固定的一点就是圆心,通常用字母O 表示,圆心决定圆的位置2、 半径:连接圆心到圆上任意一点的线段叫做半径。
一般用字母r 表示。
把圆规两脚分开,两脚之间的距离就是圆的半径。
3、 直径:通过圆心并且两端都在圆上的线段叫做直径。
一般用字母d 表示。
直径是一个圆内最长的线段三、圆的主要特征1、 在同圆或等圆内,有无数条半径,有无数条直径。
所有的半径都相等,所有的直径都相等。
2、 在同圆或等圆内,直径的长度是半径的2倍,半径的长度是直径的1/2。
用字母表示为:用字母表示为: d =2r r =12d 用文字表示为:直径=半径×2 半径=直径÷23、 如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形。
圆是轴对称图形且有无数条对称轴一、 圆的周长的认识1、 围成圆的曲线的长叫做圆的周长2、 周长与圆的直径有关,圆的直径越长,圆的周长就越大二、 圆周率的意义及圆的周长公式1、 圆周率实验:在圆形纸片上做个记号,与直尺0刻度对齐,在直尺上滚动一周,求出圆的周长。
发现一般规律,就是圆周长与它直径的比值是一个固定数(π)。
3、 圆周率:任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率。
用字母π(pai) 表示。
4、 一个圆的周长总是它直径的3倍多一些,这个比值是一个固定的数。
圆周率π是一个无限不循环小数。
在计算时,一般取π ≈ 。
5、 在判断时,圆周长与它直径的比值是π倍,而不是倍。
世界上第一个把圆周率算出来的人是我国的数学家祖冲之。
六年级上册 圆知识点

六年级上册圆知识点圆,作为几何图形中的一种特殊形式,具有许多独特的属性和特点。
在六年级上册学习中,我们将深入探究圆的知识点,包括圆的定义、圆心、半径、直径以及圆的周长和面积的计算方法等内容。
一、圆的定义圆是指平面上到一个固定点的距离恒定的点的轨迹,该固定点称为圆心,距圆心相等的任意两个点构成的线段称为直径,直径的一半称为半径。
圆的形状特点是闭合的曲线,其上的任意两点与圆心的距离是相等的。
二、圆心、半径和直径圆心是圆的中心点,通常用字母O表示。
半径是从圆心到圆上任意一点的距离,用字母r表示。
直径是穿过圆心的线段,它的两个端点都在圆上,直径的长度等于两倍的半径。
三、圆的周长圆的周长是指圆的边界长度,也被称为圆周长或圆的周长。
我们可以用公式C=2πr来计算圆的周长,其中C表示圆的周长,r表示半径,π是一个恒定的数值,约等于3.14。
四、圆的面积圆的面积是指圆所覆盖的平面的大小,通常用字母A表示。
我们可以用公式A=πr²来计算圆的面积,其中A表示圆的面积,r表示半径,π是一个恒定的数值,约等于3.14。
五、圆的性质1. 圆与直线的关系:圆和直线最多只有两个交点。
2. 圆的切线:从圆外一点引一条与圆相切的线,该线与圆的切点处与切线垂直。
3. 圆的弦:连接圆上的两点得到的线段称为弦,弦的中点与圆心相连,得到的线段称为弦的中线。
4. 弧和弧长:圆上的两点确定的弧,是两点间的圆弧,弧所对应的圆心角称为弧的度数。
弧长是沿着圆的边界所测量的长度。
六、应用圆的知识点在日常生活中有广泛的应用。
例如,在建筑和工程领域中,我们需要绘制和计算圆形的形状和尺寸。
而在数学领域中,圆的知识点也是学习其他几何图形的基础,如圆锥、圆柱、圆环等。
总结:通过六年级上册的学习,我们了解了圆的定义、圆心、半径、直径以及圆的周长和面积的计算方法。
圆是一种特殊的几何形状,有着许多独特的性质和特点。
圆的知识点不仅在数学中有广泛的应用,而且在生活中也能发现圆的身影。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
◆圆的组成1圆心:圆的中心叫圆心,用字母O表示,圆心决定圆的位置2半径:连接圆心和圆上任意一点的线段叫半径,用字母r表示,半径决定圆的大小3直径:通过圆心,两端都在圆上的线段叫直径,用字母d表示,直径是圆内最长的线段。
◆在同一个圆里,可以画无数条半径,无数条直径。
同一个圆中的半径相等,直径也相等,且直径是半径的2倍,半径是直径的1/2。
◆在正方形内画最大的圆,该圆的直径等于正方形边长,在长方形内画最大的圆,该圆的直径等于长方形的宽。
◆半径相等的两个圆叫等圆,等圆周长相等,面积也相等。
圆心重合,半径不等的两个圆叫做同心圆。
◆圆是轴对称图形,每一条直径所在的直线都是圆的对称轴,圆有无数条对称轴。
半圆也是轴对称图形,但半圆只有一条对称轴,垂直于底边的半径所在的直线就是半圆的对称轴。
◆用圆规画圆时,尖的一头是圆心,两脚打开的距离是圆的半径。
◆圆周率:正方形的周长总是边长的4倍,同样圆的周长除以直径的商也是一个固定的常数,这个常数叫圆周率,用字母π表示,也可以说圆的周长是直径的π倍。
圆周率是一个无限不循化小数,计算时通常取3.14◆圆的周长:围成圆的曲线的长度叫做圆的周长,用字母C表示圆的周长总是直径的π倍所以:周长= 直径×3.14 = 2×半径×3.14 计算公式是:C=d×π= 2×π×r◆半圆的周长 = 圆的周长÷2+直径计算公式是:C半圆 = π×r+r◆圆的面积:圆所占平面的大小或圆形物体表面的大小就是圆的面积。
用字母S表示。
把圆切分成若干等分,再拼凑起来就类似于一个平行四边形。
这个平行四边形底刚好是周长的一半,高等于半径。
所以:圆的面积=周长÷2×半径=3.14×半径×半径计算公式:S=C÷2×r=π×r×r◆周长与面积是不同的单位,所以不能比较。
但知道周长可以计算圆的面积,面积= 周长÷2×半径,S=C÷2×r◆应用题要根据实际情况判断题目要求计算周长还是面积◆车轮前进的问题:因为圆上任意一点到圆心的距离都相同,即同一个圆所有的半径都相等,所以用圆来作轮子才能保证车子平稳,轮子在转动时,转动一圈前进的距离就是这个圆的周长。
如果1秒钟轮子转动5圈,则1秒钟车子前进的距离=周长×5◆大小齿轮的问题:如果大齿轮的半径是小齿轮半径的2倍,那么大齿轮周长就是小齿轮周长的2倍。
所以大齿轮转动一圈可以带动小齿轮转动2圈。
◆绕绳法求周长、面积的问题:用绳子绕圆一圈,绳子的长度就是圆的周长,知道周长先求半径,再求面积◆运动跑道的问题:运动圆在跑道上跑步,经过半圆形弯道时,由于跑道的半径不同所以半圆的周长不同。
最外面的半圆周长最大,为保证公平,起跑线不在同一直线上,两条起跑线相差的距离= 圆周长的差。
◆环形面积与周长的计算问题:两个半径不相等的同心圆,它们之间的部分,叫环形。
半径大的圆叫外圆,外圆半径用R表示,半径小的圆叫内圆,内圆半径用r表示。
环形面积=大圆面积-小圆面积=π×R×R-π×r×r. 计算公式 S环形=π×(R×R-r×r)◆阴影部分面积的计算:1看清楚阴影部分是由两个什么图形组合而成的,分别计算两个图形的面积然后相加,2看清楚阴影部分是由哪两个图形重叠剩下的,分别计算两个图形的面积然后相减。
◆半径直径周长面积的关系:◆半径增加到2倍,直径也增加到2倍,周长也增加到2倍,面积增加到2×2=4倍◆应用题要根据实际情况判断题目要求计算周长还是面积◆车轮前进的问题:因为圆上任意一点到圆心的距离都相同,即同一个圆所有的半径都相等,所以用圆来作轮子才能保证车子平稳,轮子在转动时,转动一圈前进的距离就是这个圆的周长。
如果1秒钟轮子转动5圈,则1秒钟车子前进的距离=周长×5◆大小齿轮的问题:如果大齿轮的半径是小齿轮半径的2倍,那么大齿轮周长就是小齿轮周长的2倍。
所以大齿轮转动一圈可以带动小齿轮转动2圈。
◆绕绳法求周长、面积的问题:用绳子绕圆一圈,绳子的长度就是圆的周长,知道周长先求半径,再求面积◆运动跑道的问题:运动圆在跑道上跑步,经过半圆形弯道时,由于跑道的半径不同所以半圆的周长不同。
最外面的半圆周长最大,为保证公平,起跑线不在同一直线上,两条起跑线相差的距离= 圆周长的差。
◆环形面积与周长的计算问题:两个半径不相等的同心圆,它们之间的部分,叫环形。
半径大的圆叫外圆,外圆半径用R表示,半径小的圆叫内圆,内圆半径用r表示。
环形面积=大圆面积-小圆面积=π×R×R-π×r×r. 计算公式 S环形=π×(R×R-r×r)◆阴影部分面积的计算:1看清楚阴影部分是由两个什么图形组合而成的,分别计算两个图形的面积然后相加,2看清楚阴影部分是由哪两个图形重叠剩下的,分别计算两个图形的面积然后相减。
◆圆的组成1圆心:圆的中心叫圆心,用字母O表示,圆心决定圆的位置2半径:连接圆心和圆上任意一点的线段叫半径,用字母r表示,半径决定圆的大小3直径:通过圆心,两端都在圆上的线段叫直径,用字母d表示,直径是圆内最长的线段。
◆在同一个圆里,可以画无数条半径,无数条直径。
同一个圆中的半径相等,直径也相等,且直径是半径的2倍,半径是直径的1/2。
◆在正方形内画最大的圆,该圆的直径等于正方形边长,在长方形内画最大的圆,该圆的直径等于长方形的宽。
◆半径相等的两个圆叫等圆,等圆周长相等,面积也相等。
圆心重合,半径不等的两个圆叫做同心圆。
◆圆是轴对称图形,每一条直径所在的直线都是圆的对称轴,圆有无数条对称轴。
半圆也是轴对称图形,但半圆只有一条对称轴,垂直于底边的半径所在的直线就是半圆的对称轴。
◆用圆规画圆时,尖的一头是圆心,两脚打开的距离是圆的半径。
◆圆周率:正方形的周长总是边长的4倍,同样圆的周长除以直径的商也是一个固定的常数,这个常数叫圆周率,用字母π表示,也可以说圆的周长是直径的π倍。
圆周率是一个无限不循化小数,计算时通常取3.14◆圆的周长:围成圆的曲线的长度叫做圆的周长,用字母C表示圆的周长总是直径的π倍所以:周长= 直径×3.14 = 2×半径×3.14 计算公式是:C=d×π= 2×π×r◆半圆的周长 = 圆的周长÷2+直径计算公式是:C半圆 = π×r+r◆圆的面积:圆所占平面的大小或圆形物体表面的大小就是圆的面积。
用字母S表示。
把圆切分成若干等分,再拼凑起来就类似于一个平行四边形。
这个平行四边形底刚好是周长的一半,高等于半径。
所以:圆的面积=周长÷2×半径=3.14×半径×半径计算公式:S=C÷2×r=π×r×r◆周长与面积是不同的单位,所以不能比较。
但知道周长可以计算圆的面积,方法是用周长÷2×半径,S=C÷2×r圆的认识单元知识整理1. 圆的认识(1)直径是圆中所有线段中最长的一条。
(2)半径和直径的关系:同一个圆里,直径是半径的两倍,半径是直径的一半。
(3)在同一个圆里,有无数条半径,所有半径的长度都相等。
(4)在同一个圆里,有无数条直径,所有直径的长度都相等。
(5)画圆时,圆规针尖固定的一点是圆心,圆规两脚之间距离是半径。
圆心确定圆的位置,半径确定圆的大小。
(6)圆是轴对称图形,有无数条对称轴,对称轴就是直径所在的直线。
(7)正方形里最大的圆:圆心是对角线交点,半径是正方形边长的一半。
(8)长方形里最大的圆:圆心是对角线交点,半径是长方形宽的一半。
2. 圆的周长(1)圆周率:任何一个圆的周长除以它直径的商都是一个固定的数,我们把它叫做圆周率,用字母π表示。
π是一个无限不循环小数,π≈3.14。
(2)圆的周长=圆周率×直径=圆周率×半径×2(C=πd或C=2πr)(3)半圆的周长=圆周长的一半+直径( C半圆= πd÷2+d,C半圆= πr+2r(4)常用数据(略,自己背诵)(5)同一个圆里,圆的周长是直径的π倍,圆的周长是半径的2π倍。
3. 圆的面积(1)圆面积公式的推导过程把圆分成若干等份,剪开后,拼成了一个近似的长方形。
长方形的面积与圆的面积相等;长方形的长相当于圆周长的一半,宽相当于圆的半径。
因为:长方形面积=长×宽,所以:圆面积=πr×r=πr2。
即:S=πr2。
要求圆的面积只要知道圆的半径或者知道圆的半径的平方。
4. 半圆的面积是圆面积的一半。
S半圆=πr2÷2 (求半圆面积一定要除以2)C=πr+2r=5.14r=2.57d容易与半圆周长相混淆的是圆周长的一半, d÷2或者直接用 r5. 大小两个圆比较,半径的倍数=直径的倍数=周长的倍数,面积的倍数=半径的倍数26. 周长相等的平面图形中,圆的面积最大;面积相等的平面图形中,圆周长最短。
7、方套圆 S圆占S正的78.5%(200:157)或S圆:S正=3.14:4圆套方 S正占S圆的157:100或S正:S圆=2:3.148. 圆的半径增加a,周长增加的2πa=6.28a;圆的直径增加a,周长增加πa=3.14a。
