螺旋桨势流理论计算方法的比较
螺旋桨基础理论分解
作用在桨叶上的力及力矩
三、螺旋桨的作用力 由上面的分析可知,在给定螺旋桨的进速VA和转速n时. 如能求得诱导速度ua及ut,则可根据机翼理论求出任意半 径处叶元体上的作用力,进而求出整个螺旋桨的作用力。 取半径r处dr 段的叶元体进行讨论,其速度多角形如图3 一10 所示。当水流以合速度VR、攻角α K流向此叶元体时 ,便产生了升力dL和阻力dD。将升力dL分解为沿螺旋桨轴 向的分力dLa和旋转方向的分力dLt,阻力dD 相应地分解 为dDa和dDt 。因此该叶元体所产生的推力dT及遭受的旋 转阻力dF是:
对于有限翼展机翼,由于机翼上下表面的压差作用, 下表面高压区的流体会绕过翼梢流向上表面的低压区.翼 梢的横向绕流与来流的共同作用,使机翼后缘形成旋涡层 。这些旋涡称为自由涡。它们在后方不远处卷成两股大旋 涡而随流速V 延伸至无限远处,如图3 一8 所示。
2-7
作用在桨叶上的力及力矩
由于自由涡的存在,在空间产生一个诱导速度场。在机翼 后缘处,诱导速度垂直于运动方向,故也称下洗速度。由 于产生下洗速度,使机翼周围的流动图形有所改变,相当 于无限远处来流速度V 发生偏转,真正的攻角发生变化, 如图3 一9 所示。由于机翼处下洗速度un/2 ,使得原来 流速V 改变为VR,真正的攻角由α ’k改变为α k, α ’k为 三元的名义弦线攻角,α k 称为有效几何攻角。 △α =α ’k-α k称为下洗角, 一般约为2º ~3º,因此可近 似地2认- 8为
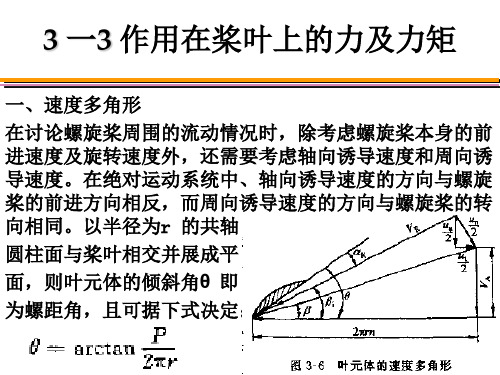
3 一3 作用在桨叶上的力及力矩
一、速度多角形 在讨论螺旋桨周围的流动情况时,除考虑螺旋桨本身的前 进速度及旋转速度外,还需要考虑轴向诱导速度和周向诱 导速度。在绝对运动系统中、轴向诱导速度的方向与螺旋 桨的前进方向相反,而周向诱导速度的方向与螺旋桨的转 向相同。以半径为r 的共轴 圆柱面与桨叶相交并展成平 面,则叶元体的倾斜角θ 即 为螺距角,且可据下式决定:
螺旋桨推力计算模型根据船舶原理知通过资料

螺旋桨推力计算模型根据船舶原理知通过资料螺旋桨是船舶的主要推进器件,它的淌水特性对船舶的推力性能具有重要影响。
螺旋桨推力计算模型可以根据船舶原理和相关资料提供有效的推力计算方法。
本文将从螺旋桨的基本原理、淌水特性以及推力计算模型等方面进行详细介绍。
一、螺旋桨的基本原理螺旋桨是船舶的主要推进器件,它由一系列螺旋线形成。
当螺旋桨旋转时,水流会被螺旋桨叶片推动并产生一定的反作用力,从而推进船舶前进。
螺旋桨的推力主要来自两个方面:剪切推力和反作用推力。
剪切推力是由于螺旋桨叶片在水中剪切水流所产生的,它与螺旋桨叶片弯曲及鼓波等因素有关;反作用推力是由于螺旋桨旋转所产生的反作用力,它与螺旋桨推进转速、直径和旋转方向等因素有关。
二、螺旋桨的淌水特性1.淌水流场螺旋桨在淌水过程中,会形成一定的淌水流场。
这个流场受到螺旋桨叶片形状、转速和船舶运动速度等因素的影响,它对螺旋桨推力的大小和方向有重要影响。
2.淌水损失由于螺旋桨叶片与水之间存在一定的摩擦和阻力,螺旋桨在淌水过程中会产生一定的淌水损失。
淌水损失会降低螺旋桨的效率,因此需要通过推力计算模型来准确估计淌水损失。
3.淌水性能参数为了描述螺旋桨的推力性能,可以引入一些淌水性能参数,如推力系数、功率系数和效率等。
这些参数可以通过实验和理论模型来确定,从而有效评估螺旋桨的推力性能。
三、螺旋桨推力计算模型为了准确计算螺旋桨的推力,研究者们提出了不同的推力计算模型。
这些模型主要基于流体动力学原理和大量实验资料,可以较为准确地估计螺旋桨的淌水特性和推力性能。
推力计算模型可以通过以下几个步骤进行:1.确定船舶参数首先,需要确定船舶的一些参数,如船舶的船体形状、质量、速度和运动状态等。
这些参数将用于计算螺旋桨的推力。
2.建立淌水流场模型根据螺旋桨叶片形状和转速等参数,可以建立螺旋桨的淌水流场模型。
这个模型可以通过数值计算方法或实验测试来确定。
3.计算推力系数和淌水损失根据淌水流场模型,可以计算螺旋桨的推力系数和淌水损失。
螺旋桨轴承力计算方法的对比分析

p r o p e l l e r s [ J ] . C h i n e s e J o u r n a l o f S h i p R e s e a r c h , 2 0 1 5 , 1 0 ( 1 ) : 8 3 - 8 7 .
螺旋桨 轴承 力计算方法 的对 比分析
朱鹏 , 毕毅 , 叶金 铭
中 图分 类 号 : U 6 6 4 . 3 3 文献标志码 : A D OI : 1 0 . 3 9 6 9 / j . i s s n . 1 6 7 3 — 3 1 8 5 . 2 0 1 5 . O 1 . 0 1 2
Co mp a r i s o n An a l y s i s o f Thr e e Ki nd s o f Co mp u t a t i o n a l M e t h o d s f o r t he Be a r i n g Fo r c e o f Pr o p e l l e r s
pl a c e a t t h e e n d o f a s t a n d a r d mo l d o f SUBOFF. Wi t h t h e h e l p o f CFD, q u a s i s t e a d y e mp i r i c a l f o r mu l a,a n d t he l i f t i n g l i n e t h e o r y me t h o d,t h e be a r i n g f o r c e c a n b e p r e di c t e d . Ba s e d o n t h e c a l c u l a t i o n r e s u l t s ,t h i s pa - p e r a n a l y z e s t h e e f f e c t s o f t h e b l a d e n umb e r o f p r o p e l l e r o n t h e b e a r i n g f o r c e a s we l l a s t h e r e l a t i v e s t r e n g t h o f t h e f o r c e i n v a r i o us d i r e c t i o ns . F i n a l l y , t h e a d v a n t a g e s o f a l l t h r e e k i n d s o f me t h o d s a r e s u m ma r i z e d, a n d i t i s o b s e r v e d t h a t t h e l i f t i n g l i n e t h e o r y me t h o d a n d t h e CFD a r e mo r e s u i t a b l e t h a n q u a s i s t e a d y me t h o d f o r e n g i n e e r i n g a p p l i c a t i o n s,e s p e c i a l l y or f t h e h i g hl y s k e we d b l a d e .M e a n wh i l e,t h e l i ti f n g l i n e t h e o y r
螺旋桨水动力学性能分析与优化设计

螺旋桨水动力学性能分析与优化设计螺旋桨是水上船只中最重要的推进装置,其性能直接关系到船舶的推进效率和航行速度。
螺旋桨水动力学性能分析与优化设计是船舶研究领域中的重要分支,对于减少能源消耗、提高运输效率、降低污染排放具有重要作用。
一、螺旋桨水动力学性能分析的基础理论1.1 计算流体力学计算流体力学(CFD)是一种通过数字计算方法来解决流体力学问题的数学模型。
在螺旋桨被设计和研究时,CFD成为了一种重要的工具。
其模型基于Navier-Stokes方程和欧拉方程,模拟了流场和流动的变化,从而分析了流体运动的影响和经济性能的评估。
1.2 螺旋桨理论螺旋桨的理论基础是流体力学中的速度势流和双曲型等势流。
速度势流指的是在流体中的一个点上速度向量可以分解为势函数的梯度,而双曲型等势流涉及到一个坐标系中,速度的散度和旋度是相等的。
1.3 失速失速指的是在较小的流速下,螺旋桨进入了抵抗气蚀和附面效应的状态。
能够有效地分析并求出失速将对设计螺旋桨的截面和轴设置具有重要意义。
二、螺旋桨水动力学性能分析的关键参数2.1 推力和速度推力和速度是螺旋桨水动力学性能分析中的两个关键参数。
推力是螺旋桨提供给船体的推进力,影响到船舶的加速度和航行速度。
速度可以用来计算泥和水的扰动实体质量。
2.2 轮廓设计螺旋桨轮廓设计对其性能影响非常大,包括叶片的数量、截面形状和翼型等。
良好的轮廓设计能够提高螺旋桨的效率,减小水动力噪音,提高抵抗力和附面效应。
2.3 旋转速度旋转速度是螺旋桨的打动驱动力,影响了传动效率和螺旋桨效率。
高速旋转通常会导致较大的失速和流量噪音,而低速旋转也可能会导致螺旋桨产生过多垂直力。
2.4 推力系数推力系数是推力与密度、直径、旋转速度和旋转等效面积的关系。
推力系数是成尺寸和旋转速度的一种无因次数,用于描述螺旋桨的推进效率。
三、螺旋桨水动力学性能优化的方法3.1 优化设计算法优化设计算法是一种通过数学模型和计算机程序来找到最优解的方法。
螺旋桨基础理论.

理想螺旋桨理论(尾流旋 转的影响)
根据动能定理可知,质量为d ,的流体在旋转运动时动能 的改变应等于旋转力dF 。在单位时间内所作的功,即
式中:ut1为桨盘处的周向诱导速度。 将式(3 一14 )代入上式中,并经简化后可得
上式表明,螺旋桨盘面处的周向诱导速度等于盘面后任一 截面处(包括远后方)的周向诱导速度的一半。
(3 一9 )代人式(3 一7 )可得效率的表达式为:
由式(3 一9 )及式(3 一10 )可见,若己知推进器的 载荷系数σ T,便可以确定诱导速度ua(或ua1)及效率 η A.图3 一2 表示与载荷系数σ T之间的关系曲线。σ T愈 小则效率愈高.
理想推进器理论
在推力Ti和速度VA一定的条件下,要取得小的载荷系数必 须增大盘面积 A0 ,对螺旋桨来说需增大直径 D ,从而 提高效率。这一结论具有重要的现实意义。
理想推进器理论
为VA+ua1,而压力降为p1,当水流经过盘面时,压力突 增为p '1(这一压力突变是由于推进器的作用而产生), 而水流速度仍保持连续变化。水流离开盘面以后,速度将 继续增大而压力下降。到推进器的远后方(CC1剖面)处 ,速度将达到最大值VA+ua.而压力回复至p0,图3 一1 ( b )和3 一1 ( c )分别表示流管中水流速度和压力的 分布情况。流管内水流轴向速度的增加使流管截面形成收 缩,而流管内外的压力差由其边界面的曲度来支持。由于 假定推进器在无限深广的流体中运动,故流管以外两端无 限远处的压力和水流速度可视为不变。
理想推进器理论
根据动量定理,作用在流体上的力等于单位时间内流体动 量的增量。而流体的反作用力即为推力,故推进器所产生 的推力
以上各式中,ρ 为流体的密度。 为了寻求盘面处速度增量ua1与无限远后方速度增量ua的 关系,在推进器盘面前和盘面后分别应用伯努利方程.在 盘面远前方和紧靠盘面处有下列关系式:
船舶螺旋桨的设计与计算过程.解析

某沿海单桨散货船螺旋桨设计计算说明书刘磊磊20081013202011年7月某沿海单桨散货船螺旋桨设计计算说明书1.已知船体的主要参数船长 L = 118.00 米 型宽 B = 9.70 米 设计吃水 T = 7.20 米 排水量 △ = 5558.2 吨 方型系数 C B = 0.658 桨轴中心距基线高度 Zp = 3.00 米由模型试验提供的船体有效马力曲线数据如下:航速V (kn ) 13 14 15 16 有效马力PE (hp ) 2160 2420 3005 40452.主机参数型号 6ESDZ58/100 柴油机 额定功率 Ps = 5400 hp 额定转速 N = 165 rpm 转向 右旋 传递效率 ηs=0.983.相关推进因子伴流分数 w = 0.279 推力减额分数 t = 0.223 相对旋转效率 ηR = 1.0船身效率 0777.111=--=wtH η4.可以达到最大航速的计算采用MAU 四叶桨图谱进行计算。
取功率储备10%,轴系效率ηs = 0.98 螺旋桨敞水收到马力: P D = 4762.8 hp根据MAU4-40、MAU4-55、MAU4-70的Bp --δ图谱列表计算:项 目 单位 数 值 假定航速V kn 1314 1516V A =(1-w)V kn 9.373 10.09410.81511.536Bp=NP D 0.5/V A 2.569.013042 69.01304 69.0130422569.01304225Bp268.96548323.7116 384.6505072451.9996707MAU 4-40δ75.6 72.10878 64.87977369 60.744 P/D 0.64 0.667321 0.685420561 0.720498 ηO 0.5583333 0.582781 0.6057068060.62606P TE =P D ·ηH ·ηOhp 2863.9907 2989.395 3106.994626 3211.4377 MAU 4-55δ74.629121 68.63576 63.56589147 59.341025 P/D 0.6860064 0.713099 0.740958466 0.7702236 ηO 0.5414217 0.567138 0.590941438 0.6111996 P TE =P D ·ηH ·ηOhp 2777.2419 2909.156 3031.255144 3135.1705 MAU 4-70δ73.772563 67.77185 63.0305555658.68503P/D 0.69254 0.723162 0.754280639 0.7861101 ηO 0.5210725 0.54571 0.565792779 0.5828644 P TE =P D ·ηH ·ηOhp2672.86012799.2382902.2542 2989.8239据上表的计算结果可绘制PT E 、δ、P/D 及ηO 对V 的曲线,如下图所示。
螺旋桨片条理论简介

螺旋桨片条理论简介螺旋桨片条理论(Standard Strip Analysis)又称为涡流理论是在儒可夫斯基螺旋桨涡流理论基础上,将普朗特(Prandtl)有限翼展理论应用于螺旋桨涡流模型中提出的螺旋桨特性计算理论。
根据有限翼展理论,一个产生升力的有限翼展机翼,当前方来流绕过机翼时将改变方向,引起气流下洗(Airflow downwash),下洗角取决于机翼升力大小、机翼截面尾迹沿(Trailing Edge)的切线方向和机翼展长。
在无限翼展情况下,机翼扰流无下洗角,机翼扰流仅取决于叶型剖面形状。
下洗角的产生会使螺旋桨叶素相对气流攻角减小,在后面的螺旋桨特性计算中此下洗角称为干涉角。
叶素分析法就是在某半径处剖开螺旋桨桨叶,取出径向一段微元段,利用翼型升阻特性数据对此微元(即叶素)进行受力分析。
由于在航空涡桨发动机控制系统仿真实验过程中,需要建立实时计算的航空螺旋桨模型,一般使用的计算流体力学CFD方法是无法完成计算的,但是又无法避免螺旋桨建模,所以就会使用螺旋桨片条理论进行实时模型的建立,简化螺旋桨模型计算过程,提高实时仿真效率,并通过实验数据进行仿真验证。
片条叶素的示意图如右图所示。
图中叶素段被单独示出,c标示叶素厚度,b标示叶素弦长,叶素的本质是一段机翼翼型。
叶素具有翼型的升力系数、阻力系数,通过对翼型的升力和阻力的计算,可以得到叶素的整体受力,最后积分整个螺旋桨的受力情况。
[编辑本段]详细内容螺旋桨片条理论的关键是将螺旋桨叶片半径剖开(即所谓叶素,构成叶片的片段形状要素)后对叶片的气动特性进行分析,得到截面的力学量变化,如右图所示。
图中β角就是气流下洗干涉角度,图中标示的螺旋桨运行状态时最常用的螺旋桨前进状态,其他的螺旋桨共作状态有:静拉力状态,零拉力状态,制动状态,自转状态,风车状态,全部的工作状态一共六种。
图中V0 ——螺旋桨来流空速α——叶片实际攻角β——叶片的下洗角(Airflow downwash)dLp ——叶片叶素的升力(通过升力系数得到)dDp ——叶片叶素的阻力(通过阻力系数得到)dFp ——叶素的扭矩方向力分量dT' ——叶素的前进推力方向力分量dRp ——叶素受力的合力φ——干涉角β和空气角度φ0角度和φ0——actg(V0/2nπr)2nπr——螺旋桨转速旋转分量v ——干涉角度的气流速度和向量va ——干涉角度的气流速度轴向分量vt ——干涉角度的气流速度周向分量θ——螺旋桨桨叶角度螺旋桨片条理论计算的最关键步骤是计算干涉角度β,计算的根本是求解一个非线性方程f(β)=0,由于百度百科无法提供公式编辑,所以请参阅《空气螺旋桨理论及其应用》(刘沛清编著,北航社)[编辑本段]理论发展螺旋桨理论经历了如下的发展历程:来源于《空气螺旋桨理论及其应用》1- 基于力学原得出的螺旋桨起动理论(19世纪及以前)仅仅实现了功率和拉力与螺旋桨在气流中所起速度建立的联系,而不能把桨叶尺寸和几何关系与其在空气中所激起的速度联系起来,所以这些理论没有设计上的意义。
不同湍流模型在螺旋桨水动力性能计算中的应用与比较_黄胜

第30卷第5期 哈 尔 滨 工 程 大 学 学 报 V o l .30№.52009年5月 J o u r n a l o f H a r b i n E n g i n e e r i n g U n i v e r s i t y M a y 2009d o i :10.3969/j .i s s n .1006-7043.2009.05.002不同湍流模型在螺旋桨水动力性能计算中的应用与比较黄 胜,王 超,王诗洋(哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001)摘 要:为了研究不同湍流模型在螺旋桨水动力性能预报中的适用性,运用计算流体力学软件对粘性流场中螺旋桨的敞水性能进行了计算研究.分别采用标准模型k -ε、R N G k -ε模型和雷诺应力方程模型(R S M )模拟了敞水螺旋桨在不同进速系数下的推力系数、转矩系数等.由3种湍流模型的预报结果与试验值的对比得出:标准模型对螺旋桨水动力性能的数值预报存在明显的缺陷;R N G k -ε模型相对于标准k -ε模型有所改进,但这种改进仍然没有抛弃基于涡粘性假设的基础,对预报精度的改进是有限的;而R S M 模型完全抛弃了涡粘性假设,完全求解雷诺应力的微分输运方程,并且考虑了壁面对雷诺应力分布的影响,因此具有较其他2种模型更强的模拟能力.关键词:螺旋桨;水动力性能;湍流模型;粘性流场中图分类号:U 661.31 文献标识码:A 文章编号:1006-7043(2009)05-0481-05A p p l i c a t i o na n dc o m p a r i s o no f d i f f e r e n t t u r b u l e n c e m o d e l s i n t h ec o m p u t a t i o no f a p r o p e l l e r 's h yd r o d y n a m i c pe rf o r m a n c eH U A N GS h e n g ,W A N GC h a o ,W A N GS h i -y a n g(C o l l e g e o f S h i p b u i l d i n g E n g i n e e r i n g ,H a r b i nE n g i n e e r i n gU n i v e r s i t y ,H a r b i n 150001,C h i n a )A b s t r a c t :I n o r d e r t o e v a l u a t e t h e a p p l i c a b i l i t y o f t u r b u l e n t m o d e l s w h e n p r e d i c t i n g t h e h y d r o d y n a m i c p e r f o r m a n c e o f p r o p e l l e r s ,c o m p u t a t i o n a l f l u i d d y n a m i c s (C F D )s o f t w a r e w a s u s e d t o c a l c u l a t e t h e h y d r o d y n a m i c p e r f o r m a n c e o f a p r o p e l l e r i n t h e v i s c o u s f l o wr e g i o n .T h e s t a n d a r d m o d e l ,t h e R N Gm o d e l a n d t h e R e y n o l d s s t r e s s m o d e l (R S M )w e r e u s e d r e s p e c t i v e l y t o s i m u l a t e t h r u s t a n d t o r q u e c o e f f i c i e n t s a t d i f f e r e n t a d v a n c e c o e f f i c i e n t s .C o m p a r i s o n s b e -t w e e nt h e c o m p u t e d r e s u l t s a n d e x p e r i m e n t a l d a t a s h o wt h a t t h e s t a n d a r d m o d e l h a s o b v i o u s l i m i t a t i o n w h e n p r e d i c -t i n g t h e h y d r o d y n a m i c p e r f o r m a n c e o f a p r o p e l l e r ;t h e R N Gm o d e l b r i n g s l i m i t e d i m p r o v e m e n t s i n p r e c i s i o n o f p r e -d i c t i o n r e l a t i v e t o t h e s t a n d a r d m o d e l .H o w e v e r ,R S M f u l l y a b a n d o n s t h e e d d yv i s c o s i t y h y p o t h e s i s t o s o l v e t h e R e y n o l d s s t r e s s 's d i f f e r e n t i a l t r a n s p o r t e q u a t i o n s a n d c o n s i d e r s t h e w a l l 's i n f l u e n c e o n t h e d i s t r i b u t i o no f R e y n o l d s s t r e s s ,s o i t s i m u l a t e s b e t t e r t h a n t h e o t h e r t w o m o d e l s .K e y w o r d s :p r o p e l l e r ;h y d r o d y n a m i c p e r f o r m a n c e ;t u r b u l e n t m o d e l ;v i s c o u s f l o w 收稿日期:2008-04-05.基金项目:国家自然科学基金资助项目(10702016).作者简介:黄 胜(1945-),男,教授,博士生导师;王 超(1982-),男,博士研究生,E -m a i l :z h i t a o 0213@s i -n a .c o m . 对船舶螺旋桨水动力理论研究,目前已经形成了升力线理论、升力面理论和面元法3种经典的理论方法,为螺旋桨水动力性能的研究构建了坚实的理论基础.但三者均为基于流体无粘性假设的势流理论方法.随着计算机技术的推广普及和计算方法的新发展,计算流体力学(C F D )技术取得了蓬勃的发展,通过对通用R A N S 方程的数值求解来获得粘性流场全场信息已经成为可能,这为螺旋桨水动力性能的研究提供了新的途径.文中运用C F D 软件对粘性流场中敞水螺旋桨的水动力性能进行计算研究,其中湍流模型分别采用标准k -ε模型、R N Gk -ε模型和雷诺应力方程模型(R S M ),对某一标准螺旋桨的水动力性能进行了预报,并将计算结果与试验测量值作了比较.由分析结果得出3种模型中以R S M 模型的预报结果最为合理,但同实验值仍有一定的差别,分析认为同湍流模型本身的原因外,与边界条件的设置、旋转模型的选取以及网格划分的质量等均有一定的关系.1 控制方程假定流体是不可压的,则流场的连续方程和动量方程分别为[1]u ix i=0,(1)ρ (u i u j ) x j =- P x j +ρg i +ρ x j [μ( u i x j + u j x i)-u ′i u ′j].(2)式中:u i 、u j为速度分量时均值(i ,j =1,2,3),P 为压力时均值,ρ为流体密度,μ为流体粘性系数,g i 为重力加速度分量,-ρu ′i u ′j为雷诺应力项.方程中的雷诺应力项属于新的未知量,因此,要使方程封闭,必须对该应力项作某种假设,即建立应力的表达式(或引进新的湍流模型方程),通过表达式或湍流模型,把应力项中的脉动值与时均值联系起来.2 湍流模型的选取目前湍流的内在机理还没有真正被人们所了解,迄今尚未认定一种解决湍流问题的最佳方法[2-6],而且目前关于螺旋桨粘性绕流场数值计算方面的可供参考文献较少,文中选取理论上发展较为完善的二方程湍流模型以及R S M 湍流模型来封闭R A N S 方程.2.1 标准k -ε模型标准模型是个半经验公式,主要是基于湍流动能和扩散率.k 方程是个精确方程,ε方程是个由经验公式导出的方程.k-ε模型假定流场完全是湍流,分子之间的粘性可以忽略,因而标准k -ε模型只对完全是湍流的流场有效.湍动能k 方程为ρd k d t = x i μ+μt σkk x i +G k +G b -ρε-Y M .(3)湍动能耗散率ε方程为ρd εd t = x i μ+μt σk+ ε x i +C 1εεk (G k +C 3εG b )-C 2ερε2k.(4)式中:G k 表示由于平均速度梯度引起的湍动能产生;G b 是用于浮力影响引起的湍动能产生;Y M 可压速湍流脉动膨胀对总的耗散率的影响;湍流粘性系数μt =ρC μk2ε;作为默认值常数,C 1ε=1.44、C 2ε=1.92、C μ=0.09;湍动能k 与耗散率ε的湍流普朗特数分别为σk =1.0、σε=1.3.可以通过调节“粘性模型”面板来调节这些常数值.2.2 R N Gk -ε模型Y a k h o t 和O r s z a g [1]把重整化群(R N G )方法引入到湍流研究中建立了一个新的湍流模型,其方程如下:ρk t +x j(ρU j k )=-23ρk u k x k + x j (μe f f σk kx j )+G k -ρε,(5) ρε t + x j(ρU j ε)=-[(23C ε1-C ε3+23C μC η·k u k ε x k )ρε u k x k + x j (μe f f σε εx j )]+ρεk [(C ε1-C η)G k -C ε2ρε].(6)式中:C ε1=1.42,C ε2=1.68,C ε3=[-1+2C ε1-3m 1(n-1)+(-1)δ6C μC ηη]/3,C η=η(1-η/η0)1+βη3,η=S k /ε,S =2S i j S i j ,η0=4.28,β=0.015,C μ=0.085.2.3 雷诺应力方程模型基本的雷诺应力模型(R S M )即线性的R S M 模型,压力应变项的模拟采用线性代数式,耗散项用标量耗散率.R S M 湍流模型方程如下: t (ρu i u j )+ x k (ρU k u i u j )=D i j +P i j +Υi j -εi j .(7)其中,D i j 、P i j 、Υi j 、εi j分别为扩散项、产生项、压力应变项和耗散项,分别表示如下:D i j = x k (μt σk u ′i u ′j x k),P i j =-(u ′i u ′k ) U j x k +u ′j u ′k( U ix k),Υi j =-C 1εαi j +C 2ε(αi k αk j -13αk l αk l δi j )+C 3k S i j +C 4k (αi k S j k +αj k S i k -23αk l αk l δi j )+C 5(αi k W j k +αj k W i k ).压力应变项包括了雷诺应力的各向异性张量的二次方项:C 1=3.4+1.8P k k /ε,C 2=4.2,C 3=45-1.3Υ1/2α,C 4=1.35,C 5=0.4,αi j =u ′i u ′j 2k -13δij ,Υα=αi j αi j,S i j =12( U j x i + U i x j ),W i j =12( U i x j - U j x j).模型中压力应变项的系数依赖于雷诺应力的变化和湍能的产生,而雷诺应力的变化和湍能产生又与壁面作用密切相关,因此R S M 模型体现了壁面效应对雷诺应力分布的影响.耗散过程主要发生在小尺度涡区.较长时间以·482·哈 尔 滨 工 程 大 学 学 报 第30卷来一直认为在高雷诺数下,小尺度涡团结构趋于各向同性,因而可以忽略各向异性的耗散,即认为湍流的切应力耗散趋于零,而粘性作用只引起湍流正应力即湍能的耗散.这样耗散张量ε就可以化为标量形式,即εi j =23ρεδi j.(8)目前最为广泛采用的ε模型为ρε t + x k (ρU k ε)= x k (μt σε εx k)-C ε1k ερu ′i u ′j U i x j-C ε2ρε2k .(9)式中,右端分别为扩散项、产生项、耗散项.系数为:C ε1=1.44,C ε2=1.92,C ε3=-1,C ε=1.33.与双方程k -ε模型比较,雷诺应力方程湍能的模拟不需要任何输运方程求解,而是通过雷诺应力得到:k=1/2·u ′i u ′j.3 计算模型的建立3.1 几何模型与计算域的创建作为对比计算所选用的模型是D T M BP 4119螺旋桨,其尺寸如表1所示,数据取自文献[7].表1 D T M BP 4119螺旋桨的几何参数T a b l e 1 D i me n s i o n s o f D T MBP 4119p r o p e l l e r几何参数D T M BP 4119直径/m0.305叶数3螺距比(0.7R )1.084毂径比0.2纵倾角/(°)0侧斜角/(°)0叶剖面N A C A 66m o d 文中采用F O R T R A N 语言编制程序,计算出螺旋桨表面的型值点,将原始的型值点数据转换为特定的格式数据,然后输入到与F l u e n t 软件配套的前处理器G a m b i t 软件,进行实体几何建模.在建模过程中使用的是直角坐标系O-X Y Z ,X 轴方向代表来流方向,它沿着螺旋桨的旋转轴指向下游,Y 轴与螺旋桨的某一桨叶的叶面参考线一致,Z 轴服从右手定则.文中研究的是在粘性流场中螺旋桨的水动力性能,因此需要把模型置于流场域中.计算域的内边界取在桨毂和叶片表面上,其中桨毂被简化为中间为圆柱面,两端为椭球面;外边界面即外流计算的无穷远边界,取在直径约为螺旋桨直径5倍的圆柱体表面上.为了计算的需要,又把整个流域分成2个小域,这样便于在划分网格时进行局部加密,提高计算结果的准确度.图1给出了螺旋桨计算流域的三维视图.3.2 网格的划分网格划分是C F D 模拟过程中较为耗时的环节,也是直接影响模拟精度和效率的关键因素之一.高质量的网格是实现数值模拟成功的首要条件.过疏或过密的网格都会极大影响计算结果.过疏的网格往往会得到不精确甚至完全错误的结果;过密的网格会使计算量增大,使计算难以收敛.文中在划分网格时使用了局部加密的方法,对于桨叶与桨毂连接处以及叶梢部分等)进行加密,以便捕捉到重要的流场信息;而对于出口段f l u i d 2的网格,将其密度适当降低,便于控制总网格数.这样,在网格模型总节点数一定的情况下可以提高计算精度,还可以避免流场变化平缓区域的计算资源浪费.螺旋桨桨叶表面网格划分如图2所示.图1 螺旋桨及整个流域三维图F i g .1 T h e t h r e e d i m e n s i o nc h a r t o f p r o p e l l e r a n d f u l l f l o wf i e ld图2 螺旋桨桨叶与桨毂网格划分F i g .2 G r i d d i v i s i o no f b l a d e a n dh u b3.3 边界条件的设置在螺旋桨的敞水计算中,整个计算区域均相对某个参考坐标系作旋转运动,而螺旋桨周围不存在与其相互干扰的物体,因此可选用F l u e n t 软件提供的运动参考坐标系模型(即M R F 模型).在进口边界处设置为速度进口条件,出口边界定义为压力出口,圆柱体侧面设为壁面,f l u i d 1和f l u i d 2的交界面设为i n t e r i o r 面.壁面设为无滑移固壁条件,在近壁区采用标准壁面函数并考虑壁面粗糙度的影响[3].计算域内的流体则按M R F 模型设置为绕轴以角速度n 旋转.·483·第5期 黄 胜,等:不同湍流模型在螺旋桨水动力性能计算中的应用与比较4 螺旋桨敞水性能计算结果与分析4.1 敞水性能曲线计算结果及与试验的对比进速系数J 分别取为0.5、0.7、0.833、0.9、1.1,螺旋桨转速为一定值,n=600r /m i n ,进速系数的变化通过改变来流流速大小来实现.通过F L U E N T 模拟计算,从计算结果中提取出不同进速系数J 情况下的螺旋桨推力与转矩,进而求出桨的推力系数K T 、转矩系数K Q 以及敞水效率η.表2列出了在不同进速系数时的螺旋桨推力与扭矩.把通过公式转换求得的特性曲线结果与试验值[7]一起绘制成图,见图3、图4以及图5.表2 计算结果T a b l e 2 T h er e s u l t s o f c a l c u l a t i o nJT标准k -εR N Gk -ε雷诺应力方程模型Q 标准k -εR N G k -ε雷诺应力方程模型0.5218.36256.70254.3912.083813.188713.08040.7171.04191.17184.8659.7222910.07449.85770.8113.99130.88129.377.219957.55587.48810.9100.58105.04107.8826.575416.31006.44541.115.6523.9728.592.572752.70822.7623 在图3、4中可以看出:采用标准k -ε湍流模型所计算的推力系数K T 与转矩系数K Q 较试验值均偏小,平均偏差分别为15.93%与5%;而采用R N G k -ε模型和R S M 湍流模型的计算的K T 与K Q 较试验值有所偏大,但与试验值比较接近,最大偏差不超过5%.在图5中可以看到:采用标准k -ε湍流模型所计算的敞水效率η与试验值偏差较大,最大偏差可达到43.5%,而采用R N G k -ε模型和R S M 湍流模型的敞水效率η在进速系数为0.5~0.83与试验值吻合得较好,最大偏差不过4.7%,超过0.833之后偏差也越来越大.图3 推力系数曲线F i g .3 T h e c u r v e s o f p r o p e l l e r 's t h r u s t c o e f f i c i e n t总的来说,在考察的进速系数范围内(0.5~1.1),采用R N G k -ε模型和R S M 湍流模型所计算的结果与试验结果比较接近,推力系数K T 、转矩系数K Q的计算结果与试验结果基本上一致,只是在斜率上稍有偏差;而敞水效率η在0.5≤J ≤0.833的情况下两者基本重合,J 超过0.833后差距逐渐变大.图4 扭矩系数曲线F i g .4 T h e c u r v e s o f p r o p e l l e r 's t o r q u ec o e f f i c i e n t图5 敞水效率曲线F i g .5 T h ec u r v e s o f p r o p e l l e r 's o p e nw a t e r e f f i c i e n c y图6 敞水性能曲线F i g .6 T h e c u r v e s o f p r o p e l l e r 's o p e n w a t e r p e r f o r m a n c e4.2 R S M 湍流模型的再次验证由上述对p 4119的计算结果可以看出,R S M 湍流模型可以较好地模拟螺旋桨的敞水性能.为了更好地验证上文论点,又对另一类型螺旋桨的敞水性能进行了计算.螺旋桨的参数为:B 4-70桨,纵倾角为15°,P /D =1.0,D =4.26m ,n=240r /m i n .图6中给出了B 4-70桨的敞水性能曲线,其中实线表示计算值,虚线为实验值.从图6中可以看·484·哈 尔 滨 工 程 大 学 学 报 第30卷出:数值计算结果与实验值[8]8非常接近,偏差最大处是进速系数为1.0处的敞水效率值,但相对误差没有超过4%.因而,可以再次验证R S M湍流模型比较适合于螺旋桨的敞水性能的模拟计算.4.3 误差分析对于整个计算过程来说,影响计算结果的因素较多,比如:模型建立的好坏、网格质量、湍流模型的不同、湍流流动的近壁处理方法的不同、边界条件选取以及各种参数的设置等等.下面分析主要的几个因素:1)湍流模型的不同.虽然标准k-ε湍流模型应用多、计算量合适、有较多数据积累和相当精度,但对于流向有曲率变化问题以及有较强压力梯度的有旋问题等复杂流动模拟效果欠缺.R N Gk-ε湍流模型对方程进行了改善,同时考虑了湍流漩涡,可以较好地模拟射流撞击、二次流与有旋流等中等复杂流动,但它受到涡旋粘性各向同性假设限制.而只有R S M湍流模型考虑的物理机理更仔细,包含了湍流各向异性影响,可以更加准确地模拟有旋流问题[1].2)网格质量的问题.有限体积法求解R A N S方程所得的流场变量值,其实是离散在计算域内各节点上的速度、压力、湍流度等近似于理想解的流场信息,所以要想求得较为准确的数值解,就需要在计算域中划分出能正确反映螺旋桨边界形状且具有一定分辨率的计算网格.高质量的网格是实现数值模拟成功的首要条件,过疏或过密的网格都会极大影响计算结果.过疏的网格往往会得到不精确甚至完全错误的结果;过密的网格会使计算量增大,使计算难以收敛.3)近壁处理方法的选取.壁面是涡量和湍流的主要来源,因而,近壁的处理明显影响数值模拟的结果.近壁区域一般分为3层:粘性底层、完全湍流区和混合区.近壁处理的方法分为壁面函数法(标准壁面函数和非平衡壁面函数)与双层区模型法.在模拟计算过程中,壁面函数法不求解层流底层和混合区,而是采用半经验公式来求解层流底层与完全湍流之间的区域,从而精度将有所降低,但计算量大为减小;双层区模型法不依赖壁面法则,可以求解整个区域,但要求模型的网格非常密,这将大大增加计算量.由于受到计算机处理能力的限制,文中只采用了标准壁面函数法来处理近壁区域,这难免对计算结果造成一定的影响.5 结论通过3种湍流模型的计算结果与实验数据的比较可以看出:1)标准k-ε模型对螺旋桨水动力性能的数值预报存在明显的缺陷,表明该模型不太适合于模拟计算螺旋桨的旋流流动;2)R N G k-ε模型相对于标准k-ε模型有所改进,但这种改进仍然没有抛弃基于涡粘性假设的基础,因此其对预报精度的改进是有限的;3)雷诺应力方程模型完全抛弃了涡粘性假设,完全求解雷诺应力的微分输运方程,并且考虑了壁面对雷诺应力分布的影响,因此具有较其它两种模型更强的模拟能力;4)影响数值计算结果的因素很多,包括:湍流模型的不同、网格质量的好坏、近壁区域的处理方式以及边界条件的选取等.5)该文初步探讨了几种湍流模型在螺旋桨水动力性能预报中的应用,分析了各自在模拟计算中优缺点.为今后计算相关问题时,对于选取何种湍流模型起到一定的指导作用.参考文献:[1]王福军.计算流体动力学分析———C F D软件原理与应用[M].北京:清华大学出版社,2004:113-142.[2]龚 吕,姚 征,吴 曼.船舶反弯扭螺旋桨水力特性的数值模拟与分析[J].上海理工大学学报,2007,29(1):65-69.G O N GLǜ,Y A O Z h e n g,WU M a n.N u m e r i c a l a n a l y s i sf o rh y d r a u l i cc h a r a c t e r i s t i c so fm a r i n ep r o p e l l e ru n d e rr e v e r s e b e n t a n dt w i s t[J].J.U n i v e r s i t y o f S h a n g h a i f o r S c i e n c ea n dT e c h n o l o g y,2007,29(1):65-69.[3]H U A N GS h e n g,Z H U X i a n g y u a n g,G U O C h u n y u.C F Ds i m u l a t i o n o fp r o p e l l e r a n d r u d d e r p e r f o r m a n c e w h e n u s i n ga d d i t i o n a l t h r u s t f i n s[J].J o u r n a l o f M a r i n e S c i e n c ea n d A p p l i c a t i o n,2007,6(4):27-31.[4]王 超,黄 胜,解学参.基于C F D方法的螺旋桨水动力性能预报[J].海军工程大学学报,2008,20(4): 107-112.WA N GC h a o,H U A N GS h e n g,X I EX u e s h e n.P r e d i c t i o n o f t h e h y d r o d y n a m i c p e r f o r m a n c e o f p r o p e l l e r b yC F D[J].J o u r n a lo fN a v a l U n i v e r s i t y o fE n g i n e e r i n g,2008,20(4):107-112.[5]刘志华,熊 鹰.基于多块混合网格的R A N S方法预报螺旋桨敞水性能的研究[J].水动力学研究与进展(A 辑),2007,22(4):450-456.L I U Z h i h u a,X I O N G Y i n g.S t u d yo nt h ep r e d i c t i o no f p r o p e l l e ro p e n-w a t e rp e r f o r m a n c e u s i n gR A N S f o r m u l aa n d m u l t i-b l oc k h y b r id me s h e s[J].J o u r n a l o fh y d r o d y n a m i c s(S e r.A),2007,22(4):450-456.[6]冯学梅,陈凤明.使用F L U E N T软件的螺旋桨敞水性能计算和考察[J].船舶,2006,(1):14-19.F E NG X u e m e i,CH E N G F e n g m i n g.C a l c u l a t i o n o fp r o p e l l e r o p e n w a t e r p e r f o r m a n c e b y C F D s o f t w a r eF L U E N T[J].S h i pa n db o a t,2006,(1):14-19.[7]苏玉民,黄 胜.船舶螺旋桨理论[M].哈尔滨:哈尔滨工程大学出版社,2003:162-163.[8]盛振邦,刘应中.船舶原理[M].上海:上海交通大学出版社,2004:118-123.[责任编辑:郑可为]·485·第5期 黄 胜,等:不同湍流模型在螺旋桨水动力性能计算中的应用与比较。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
螺旋桨势流理论计算方法的比较一、螺旋桨的升力线理论最早的螺旋桨升力线理论是Lerbs 在1952年提出的,虽然它有无法考虑侧斜和纵倾的局限,但作为这样一个具有经典性的理论,我们从中可以了解很多螺旋桨理论中的基本而重要的特性。
反之,对于可以考虑任意形状的升力线理论(如侧斜、纵倾等),一旦学习了升力线理论后,必然非常容易理解。
1、螺旋桨升力线模型把螺旋桨桨叶看作有限翼展的机翼,并以一根径向的升力线(即一条附着涡线)来代替螺旋桨桨叶,升力线的环量随半径方向是变化的,故自升力线上每一点有自由涡线下泄。
在叶梢处,因叶面和叶背压力趋于相等,故不存在升力(亦即环量为零)。
至于叶根部分,因与桨毂连在一起,处理上比较复杂。
有人认为:桨毂虽能阻挡同一叶片压力面和吸力面之间的压力中和,但由于根部处叶与叶之间很靠近,一叶之压力面将与相邻叶片之吸力面发生压力的中和,因此该处的环量也为零;但也有人认为在根部环量并不一定为零,因而在处理上有些不同。
由于螺旋桨运转时一边前进,一边旋转,故在升力线处下泄的自由涡线呈螺旋线状,无数螺旋线状自由涡线组成螺旋面涡片。
每个叶片后面有一个螺旋状涡片,Z 个叶子就有Z 个螺旋涡片。
又因为螺旋桨叶片是对称的,故螺旋桨后面的螺旋涡片也是对称的。
事实上,螺旋桨后面的自由涡片是不稳定的,在离螺旋桨稍远处即卷成二个漩涡带,一个在叶梢附近,一个在叶根附近,分别称为梢涡和根涡,各叶的根涡汇集成一个总的轴向漩涡带,而梢涡则成螺旋状涡管,梢涡数目与叶数相同。
在理论研究时,为方便起见,假定螺旋桨涡片并不卷起,一直延伸到无穷远。
2、桨叶上的力和转矩以升力线涡线系代替螺旋桨,认为此涡系所诱导的速度场与螺旋桨运动所诱导的速度场相同,如果能够计算出自由涡系在桨叶上(即升力线上)的诱导速度,那么,考虑了此诱导速度之后,可将桨叶上每一个叶元体当作二因次机翼来处理,应用茹可夫斯基升力公式可以求出作用在桨叶上的力和力矩。
设螺旋桨的进速为A V ,角速度为ω,如在半径r 处截取dr 微段,则此dr 微段的轴向速度为A V ,周向速度为r ω,相对于静水的合速度为0V =0V 与周向速度的夹角β称为进角,可由下式表示:tan A V r βω=。
设所有自由涡片对升力线处的诱导速度为a u ,t u ,r u 。
由于径向诱导速度r u 与附着涡环量()r Γ方向相同,不产生升力,所以对水动力学的计算不起作用。
轴向诱导速度a u 的方向与螺旋桨前进方向相反,使桨叶与附近水流的轴向相对速度增加。
周向诱导速度t u 的方向与螺旋桨旋转方向相同,使桨叶与附近水流的相对周向速度减小。
因此,考虑自由涡系的诱导速度以后,水流与螺旋桨叶元体的相对速度为R V 。
R V 与周向速度的夹角i β称为水动力螺距角,可由下式表示:tan A a i tV u r u βω+=-。
若忽略离心力的影响,则作用在dr 微段上的升力可表达为:其方向与R V 垂直。
在实际流体中,除了升力外尚有翼型阻力(包括摩擦阻力和漩涡阻力),以dD 表示,方向与R V 相同。
以ε表示翼型的阻升比,即dD dL ε=或dD dL ε=⋅。
将dL 和dD 的合力在轴向投影,则得到叶元体所产生的推力dT 为: 将dL 和dD 的合力在周向投影,则得到叶元体所产生的旋转阻力dF 为:因而,dF 所形成的转矩dQ 为:因cos R i t V r u βω=-,sin R i A a V V u β=+故作用在dr 微段上的推力和转矩为:将dT 和dQ 沿半径r 积分,即得一个叶片的推力和转矩,乘以叶数Z 即得整个螺旋桨发出的推力T 和吸收的转矩Q ,即:其中h r 为桨毂半径。
3、环量分布上述公式中环量分布()r Γ和自由涡系在升力线处的诱导速度之间有一定的关系,可以通过Biot-Savart 定理或速度势理论建立这种关系。
所以,问题就归结为求解环量分布。
而环量分布可按二因次机翼模型求解。
二因次机翼的环量分布可表示为:其中()y Γ为y 处的环量分布,()a y 为y 处机翼对于来流速度的攻角,0()a y 为y 处机翼剖面的零升力角,()b y 为y 处机翼剖面的弦长,V 为来流速度的大小,114w w wl d dy y y dy πΓ⋅-⎰表示由自由涡系在升力线处引起的诱导速度。
4、螺旋桨升力面理论修正根据升力线理论设计出来的螺旋桨在实际使用中一般都达不到预期的推力,究其原因,在于升力线理论中未能考虑环量的面分布和桨叶厚度的影响,因此没有满足桨叶表面的边界条件。
为了克服这一缺点,在20世纪50年代曾采用比较粗糙的近似方法对剖面的拱度或攻角进行适当的修正,这种修正称为升力面修正。
升力面修正通常包括下列两项:由环量的面分布引起的修正,称为宽度修正;由厚度影响引起的修正称为厚度修正。
二、螺旋桨的升力面理论螺旋桨的升力面理论最早可以追溯到1955年Ginzel 发表的宽叶螺旋桨理论。
至今无论是升力面模型的建模,以及数学处理和数值计算方法上均有很大发展。
螺旋桨升力面理论有涡分布法,偶极子分布法和加速度势法等。
经过多年的应用实践,现在普遍采用的是涡分布法。
虽然面元法的发展比升力面方法在理论上更为完善,尤其是压力分布的预报计算显著优于后者,但就螺旋桨合力的计算而言,两者基本具有同样的计算精度,因此升力面理论方法目前仍是螺旋桨理论设计所采用的主要工具。
随着计算机速度和内存的不断提高和扩大,涡格法(V ortex Lattice Method ,即VLM )得到越来越广泛的应用。
至今,各学者所发表的各种涡升力面理论的论文,就原理而言都是一致的,而主要差别仅在于涡模型包括尾涡处理和数值方法两方面。
本小节就升力面涡格法求解水动力学性能的一般步骤对涡格法进行简要的介绍。
1、涡格法模型及控制方程首先确定坐标系,给出螺旋桨桨叶形状(包括拱弧面及厚度分布等)的数学表达式。
坐标系一般选择固定于螺旋桨的柱面坐标系,坐标点用(,,)x r θ来表示,ox 轴沿桨轴方向指向螺旋桨的下游,θ为螺旋桨周向,r 为径向。
桨叶对流体的作用由涡和源汇的联合分布模拟。
为了便于计算,在桨叶拱弧面上分布离散的线涡、线源,以涡模拟升力,而源汇代表桨叶厚度的影响。
在桨叶区分布马蹄涡及源汇,并设置控制点。
拱弧面上自桨毂到叶梢分成m 等分,自导边到随边分成n 等分。
在每个涡格中将马蹄涡的展向涡段布置在每格的1/4弦向格长位置处,而控制点置于3/4弦向格长及1/2展向格长位置,Weissinger 证明了这样做已隐含着库塔条件的满足。
对于马蹄涡的弦向涡线则沿涡格线分成直线涡段,亦即说整个弦向涡的几何形状用折线代替。
尾流区的涡系模型较为复杂。
在决定自由涡系的诱导速度时,首先必须知道自由涡线的形状,而自由涡线的形状又依赖于诱导速度的大小,即诱导速度和自由涡线形状是相互依赖的,所以不得不作些近似假定。
在实际处理中,一般将螺旋桨分为三种类型:轻载螺旋桨,中载螺旋桨和重载螺旋桨。
为了考虑螺旋浆尾流收缩等非线性影响,将螺旋浆尾流分成两个区域,分别称为过渡区和远尾流区。
在过渡尾流区内,可以模拟尾涡片的变形现象,如尾涡的收缩、尾涡螺旋线的螺距角的变化等等。
在远尾流区,可以对尾涡作进一步的简化,如假定尾涡为螺旋梢涡和直线毂涡。
为求解布置于涡格上的马蹄涡涡强分布,须在控制点满足物面边界条件,并对所有的控制点方程联立求解。
即:其中IJ v Γ和QIJ v 分别表示所有的马蹄涡和源汇对第(,)I J 个涡格控制点的诱导速度的叠加,IJ n 表示第(,)I J 个涡格控制点的法向矢量,0v 表示流场的入流速度。
IJ v Γ的表达式可以写为如下的离散格式:其中,si j u ,1,,()n c c i l i l l j uu +=-∑,1,,w w i j i j u u +-分别表示单位涡强的第(,)i j 个马蹄涡的展向涡段、弦向涡段以及尾涡段对第(,)I J 个涡格控制点的诱导速度,可根据Biot-Savart 定理求得,而,i j Γ表示第(,)i j 个马蹄涡的涡强,为待求的未知量。
Biot-Savart 定理的表达式为: 其中p 为场点,q 为长为L 的涡段上任一点,q Γ为q 点处的涡强。
Q IJ v 与布置在桨叶上的所有源汇有关,而源汇分布则可通过螺旋桨的几何形状确定。
由源汇引起的诱导速度的表达式为:其中p 为场点,q 为长为L 的源汇段上任一点,q Q 为q 点处的源强。
2、速度及压力分布在求得所有的马蹄涡涡强以及源汇强度分布后,即可求得由涡和源汇所引起的诱导速度,再加上来流速度,可得到整个流场内的速度分布。
为求解螺旋桨的水动力学性能,仅需求得桨叶表面的速度分布即可。
为方便计算,可将求解速度控制点取在马蹄涡展向涡段的中点处。
根据Biot-Savart 定理可求得所有涡段(除自身涡段)对控制点的诱导速度,而自身涡段则会引起桨叶上下表面的切向速度跳跃,即:ijij c γΓ=∆,2ijt ij u t γ±±=其中ij Γ包含由第(,)i j 个涡格内设置的马蹄涡离散所得到的展向涡段和弦向涡段(不包括尾涡),c ∆表示涡段所在涡格的宽度(垂直于涡段方向),ij t 垂直于直线涡段且与叶面相切。
除本身以外的源汇在控制点上产生的诱导速度可以很方便的求出,而自身源汇则会引起桨叶上下表面的法向速度跳跃,其速度跳跃值为:ijij Q q c =∆,2ij n ij q u n ±±=其中ij Q 为第(,)i j 个涡格内的源汇强度,c ∆表示源段所在涡格的宽度,ij n 为第(,)i j 个涡格内速度控制点的法线方向。
最终得到桨叶拱弧面(包括上下表面)的速度分布为:其中0V 表示来流速度,u V 表示所有涡及源汇所引起的诱导速度(包括自身奇点引起的拱弧面上下表面的速度跳跃)。
在求得速度分布后,利用伯努利方程即可求得压力分布:3、推力及扭矩推力为所有叶元体所受茹可夫斯基力和拉格雷力的合力在轴向投影的叠加,旋转阻力为茹可夫斯基力和拉格雷力的合力在周向的投影,扭矩为所有叶元体所受旋转阻力与各自半径的乘积叠加后得到。
为了减小由于薄翼假定及理想流体假定所带来的误差,还须考虑导边吸力影响及粘性力修正。
螺旋桨上受力是通过作用在每个线涡和线源单元的受力来进行的,所用到的是每个展向、弦向元素中点的平均速度,并不包括本身奇点引起的诱导速度。
库塔-茹可夫斯基力的表达式为:其中Kij F ∆为第(,)i j 个涡格上所受到的库塔-茹可夫斯基力,ij l ∆和ij Γ包含由第(,)i j 个涡格内设置的马蹄涡离散所得到的展向涡段和弦向涡段(不包括尾涡、叶梢分离涡和导边分离涡,因为它们的作用力已不在桨叶上),ij V 为所求涡段中点的当地速度(不包括本身涡段引起的诱导速度)。
