三角函数图像与应用
三角函数的几何表示

在微积分中,三角函数用于解决与极坐标相关的 问题。
线性代数
在矩阵运算中,三角函数用于计算特征值和特征 向量。
三角函数在金融领域的应用
复利计算
01
在金融领域,复利计算涉及到指数函数和三角函数的结合使用。
期权定价
02
在期权定价模型中,三角函数用于计算期权的价值。
风险管理
03
在风险管理领域,三角函数用于计算风险值(VaR)和压力测试。
三角恒等式是三角函数之间的基本关系式,如sin^2 x + cos^2 x = 1、sin(x+y) 和cos(x+y)分别等于sin x cos y + cos x sin y等。
三角恒等式是三角函数运算的基础,对于简化复杂的三角函数表达式、证明性质 以及解决实际问题非常有用。
THANKS FOR WATCHING
简谐运动
物体在平衡点附近的往复 运动可以用三角函数来描 述。
工程中的三角函数应用
结构设计
在工程中,三角函数常用 于结构设计,如梁的弯曲、 拱桥的设计等。
信号处理
在通信和信号处理中,三 角函数用于频谱分析和滤 波器设计。
测量
在测量领域,三角函数用 于角度和距离的测量。
数学中的三角函数应用
解析几何
在解析几何中,三角函数用于解决与角度和长度 相关的问题。
正割函数的图像
正割函数图像是正弦函数的倒数,其周期为$pi$弧度。
在直角坐标系中,正割函数图像呈现为一个双曲线,随着角度的增加,函数值逐渐减小并趋 近于0。
正割函数图像关于原点对称。
余割函数的图像
余割函数图像是余弦函数的倒数,其周期同样为$pi$ 弧度。
常见三角函数图像及其性质
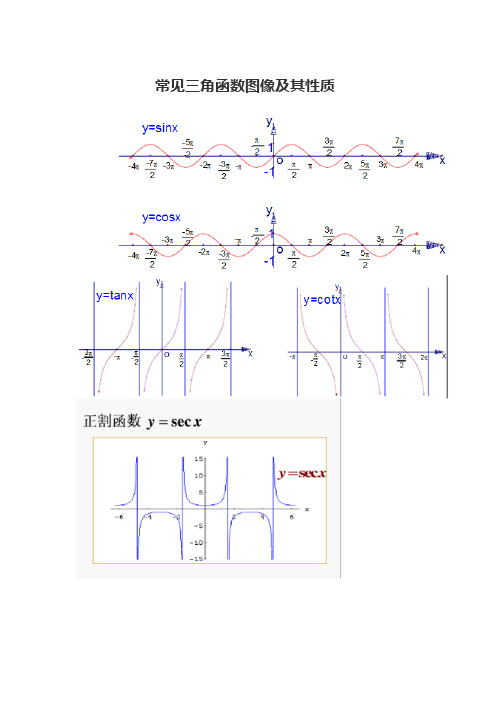
常见三角函数图像及其性质三角函数介绍正弦函数主词条:正弦函数格式:sin(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角对边长度比斜边长度的比值求出,函数值为上述比的比值,也是csc(θ)的倒数函数图像:波形曲线值域:[]1,1-余弦函数主词条:余弦函数格式:cos(θ)作用:在直角三角形中,将大小为(单位为弧度)的角邻边长度比斜边长度的比值求出,函数值为上述比的比值,也是sec(θ)的倒数函数图像:波形曲线值域:[]1,1-正切函数主词条:正切函数格式:tan(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角对边长度比邻边长度的比值求出,函数值为上述比的比值,也是cot(θ)的倒数。
函数图像:上图平面直角坐标系反映值域:()∞-∞,+余切函数主词条:余切函数格式:cot(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角邻边长度比对边长度的比值求出,函数值为上述比的比值,也是tan(θ)的倒数值域:()∞-∞,+正割函数主词条:正割函数格式:sec(θ)作用:在直角三角形中,将斜边长度比大小为θ(单位为弧度)的角邻边长度的比值求出,函数值为上述比的比值,也是cos(θ)的倒数函数图像:上图平面直角坐标系反映值域:(][)∞-1-,1∞,+余割函数主词条:余割函数格式:csc(θ)作用:在直角三角形中,将斜边长度比大小为θ(单位为弧度)的角对边长度的比值求出,函数值为上述比的比值,也是sin(θ)的倒数值域:(][)∞-1-∞,+,1。
三角函数的图象与性质 (共44张PPT)

(
)
3 3 A.-2,2 3 3 3 3 C. - , 2 2
解析: 当 故
π π 1 π π 5π x∈0,2 时, 2x- ∈- 6, 6 , sin2x-6 ∈-2,1, 6
上是减函数 - π , 0 C.在[0,π]上是增函数,在
)
π π π π D.在2,π和-π,-2上是增函数,在-2,2 上是减函数
3.(2015· 皖南八校模拟)函数 f(x)=cos 2x+2sin x 的最大值与最小值 的和是 A.-2 3 C.- 2
4.求函数 y=cos x+sin
2
π x|x|≤4 的最大值与最小值.
π 2 2 解:令 t=sin x,∵|x|≤ ,∴t∈- , . 4 2 2
∴y=-t
2
1 2 5 +t+1=-t-2 + , 4
1- 2 1 5 2 ∴当 t= 时,ymax= ,当 t=- 时,ymin= . 2 4 2 2 ∴函数 y=cos x+sin
sin 2x>0, 解析:由 2 9-x ≥0,
π kπ<x<kπ+ ,k∈Z, 2 得 -3≤x≤3.
π π ∴-3≤x<- 或 0<x< . 2 2 ∴函数 y=lg(sin 2x)+ 9-x
2
π π 的定义域为-3,2 ∪0,2 .
2
π 1- 5 x通法]
1.三角函数定义域的求法 求三角函数定义域实际上是构造简单的三角不等式(组),常借 助三角函数线或三角函数图象来求解.
2.三角函数值域的不同求法 (1)利用 sin x 和 cos x 的值域直接求;
三角函数的图像变换

cosθ = 邻边/斜边,在单位圆中表示为x坐标。
正切函数(tangent)
三角函数的周期性
tanθ = 对边/邻边,表示为正弦与余弦之比。
正弦、余弦函数周期为2π,正切函数周期为 π。
三角函数在各象限表现
第一象限
所有三角函数值均为正。
第三象限
正弦、余弦函数值为负,正切函数值为正。
第二象限
正弦函数值为正,余弦、正切函数值为负。
伸缩变换对正弦函数影响
横向伸缩
改变正弦函数图像的周期长度。缩小周期使得函数图像更加紧密,扩大周期则 使得函数图像更加稀疏。
纵向伸缩
改变正弦函数图像的振幅大小。增大振幅使得函数图像波动范围更大,减小振 幅则使得函数图像波动范围更小。
周期性与相位调整方法
周期性调整
通过改变正弦函数的周期来调整图像的疏密程度。可以通过调整函数中的系数来 实现周期的变化。
相位调整
通过改变正弦函数的相位来调整图像出现的位置。可以通过在函数中添加常数项 来实现相位的调整。同时,利用三角函数的和差化积公式,也可以实现相位的调 整。
03 余弦函数图像变换分析
余弦函数基本图像特征
波形图像
余弦函数图像呈现周期性波动,具有典型的波形 特征。
振幅和周期
余弦函数的振幅和周期是确定其图像形状和尺寸 的关键参数。
拓展:其他类型周期函数图像变换
锯齿波和方波
除了正弦波和余弦波外,还有其 他类型的周期函数如锯齿波和方 波等,它们的图像变换同样具有 实际应用价值。
周期函数的合成与分解
通过三角函数的线性组合可以合 成其他类型的周期函数;反之, 其他类型的周期函数也可以通过 傅里叶级数展开成三角函数的线 性组合。
三角函数认识ppt课件

辅助角公式
总结词
用于将三角函数式化为单一三角函数的形式。
详细描述
辅助角公式是三角函数中常用的化简工具,它可以将复杂的三角函数式化为单一三角函数的形式,便于计算和理 解。具体公式如下:sin(x+y)=sinxcosy+cosxsiny,cos(x+y)=cosxcosy-sinxsiny, tan(x+y)=(tanx+tany)/(1-tanxtany)。
三角函数认识ppt课件
目录
• 三角函数的定义 • 三角函数的图像与性质 • 三角函数的应用 • 三角函数的变换公式 • 三角函数的特殊值
01
三角函数的定义
角度与弧度的关系
角度制
以度(°)为单位,规定一周为 360度,每度分为60分,每分为 60秒。
弧度制
以弧度(rad)为单位,规定圆的 周长为2π弧度。角度与弧度的转 换公式为:1° = π/180 rad。
三角函数的基本恒等式
正弦、余弦、正切之间的基本恒等式。
利用这些恒等式,可以方便地进行三角函数的转换和化简,对于解决三角函数问 题非常有用。
THANK YOU
积的和差公式
总结词
用于计算两个角的三角函数值的乘积之和或之差。
详细描述
积的和差公式也是三角函数中常用的公式之一,它可以计算两个角的三角函数值 的乘积之和或之差。具体公式如下:sin(x-y)=sinxcosy-cosxsiny,cos(xy)=cosxcosy+sinxsiny,tan(x-y)=(tanx-tany)/(1+tanxtany)。
详细描述
和差角公式是三角函数中非常重要的公式之一,它可以将两个角的三角函数值 相加或相减,得到新的三角函数值。具体公式如下: sin(x+y)=sinxcosy+cosxsiny,cos(x+y)=cosxcosy-sinxsiny, tan(x+y)=(tanx+tany)/(1-tanxtany)。
高考数学《图像变换在三角函数中的应用》基础知识与典型例题分析

高考数学《图像变换在三角函数中的应用》基础知识与典型例题分析在高考中涉及到的三角函数图像变换主要指的是形如()sin y A x ωϕ=+的函数,通过横纵坐标的平移与放缩,得到另一个三角函数解析式的过程。
要求学生熟练掌握函数图像变换,尤其是多次变换时,图像变化与解析式变化之间的对应联系。
一、基础知识:(一)图像变换规律:设函数为()y f x =(所涉及参数均为正数) 1、函数图像的平移变换:(1)()f x a +:()f x 的图像向左平移a 个单位 (2)()f x a −:()f x 的图像向右平移a 个单位 (3)()f x b +:()f x 的图像向上平移b 个单位 (4)()f x b −:()f x 的图像向下平移b 个单位 2、函数图像的放缩变换:(1)()f kx :()f x 的图像横坐标变为原来的1k(图像表现为横向的伸缩) (2)()kf x :()f x 的图像纵坐标变为原来的k 倍(图像表现为纵向的伸缩) 3、函数图象的翻折变换: (1)()fx :()f x 在x 轴正半轴的图像不变,负半轴的图像替换为与正半轴图像关于y 轴对称的图像(2)()f x :()f x 在x 轴上方的图像不变,x 轴下方的部分沿x 轴向上翻折即可(与原x 轴下方图像关于x 轴对称)(二)图像变换中要注意的几点:1、如何判定是纵坐标变换还是横坐标变换?在寻找到联系后可根据函数的形式了解变换所需要的步骤,其规律如下: ① 若变换发生在“括号”内部,则属于横坐标的变换 ② 若变换发生在“括号”外部,则属于纵坐标的变换例如:()31y f x =+:可判断出属于横坐标的变换:有放缩与平移两个步骤()2y f x =−+:可判断出横纵坐标均需变换,其中横坐标的为对称变换,纵坐标的为平移变换2、解析式变化与图像变换之间存在怎样的对应?由前面总结的规律不难发现: (1)加“常数”⇔ 平移变换(2)添“系数”⇔放缩变换 (3)加“绝对值”⇔翻折变换3、多个步骤的顺序问题:在判断了需要几步变换以及属于横坐标还是纵坐标的变换后,在安排顺序时注意以下原则:① 横坐标的变换与纵坐标的变换互不影响,无先后要求 ② 横坐标的多次变换中,每次变换只有x 发生相应变化 例如:()()21y f x y f x =→=+可有两种方案方案一:先平移(向左平移1个单位),此时()()1f x f x →+。
4.4三角函数的图像性质及应用
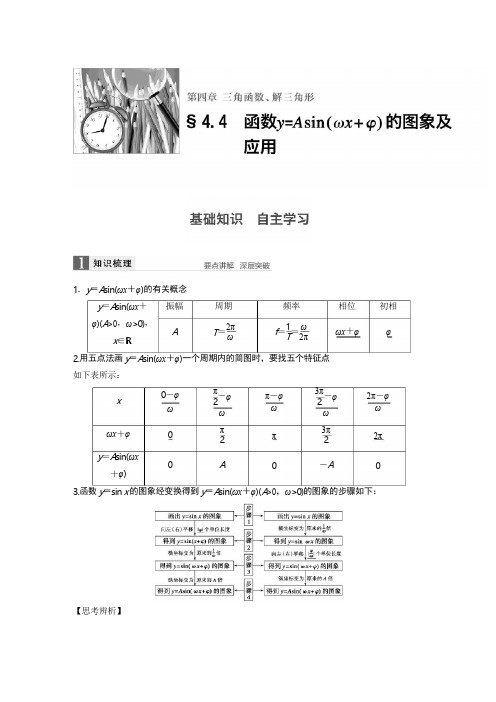
-φ-φ1.y=A sin(ωx+φ)的有关概念y=A sin(ωx+φ)(A>0,ω>0),x∈R振幅A周期2πT=ω频率1ωf=T=2π相位ωx+φ初相φ2.用五点法画y=A sin(ωx+φ)一个周期内的简图时,要找五个特征点如下表所示:x0-φωπ2ωπ-φω3π2ω2π-φωωx+φy=A sin(ωx+φ)π2Aπ3π2-A2π0 3.函数y=sin x的图象经变换得到y=A sin(ωx+φ)(A>0,ω>0)的图象的步骤如下:【思考辨析】(2)y =sin ⎝x -4⎭的图象是由 y =sin ⎝x +4⎭的图象向右平移个单位得到的.(√ )1.y =2sin ⎝2x -4⎭的振幅、频率和初相分别为2.已知函数 f (x )=sin ⎝2x +6⎭.若 y =f (x -φ) (0<φ< )是偶函数,则 φ=解析 因为 y =f (x -φ)=sin ⎣2(x -φ)+6⎦=sin ⎝2x -2φ+6⎭是偶函数,所以-2φ+ = +k π, k ∈Z ,得 φ=- - ,k ∈Z .又 0<φ< ,所以 φ= .3.(2015· 湖南改编)将函数 f (x )=sin 2x 的图象向右平移 φ⎝0<φ<2⎭个单位后得到函数 g (x )的]判断下面结论是否正确(请在括号中打“√”或“×”)(1) 利用图象变换作图时“先平移,后伸缩”与“先伸缩,后平移”中平移的长度一致.( × )⎛ π⎫ ⎛ π⎫ π 2(3)由图象求解析式时,振幅 A 的大小是由一个周期内的图象中的最高点的值与最低点的值确定的.( √ )(4)函数 f (x )=A sin(ωx +φ)的图象的两个相邻对称轴间的距离为一个周期.( × )(5)函数 y =A cos(ωx +φ)的最小正周期为 T ,那么函数图象的两个相邻对称中心之间的距离为T2.( √ )⎛ π⎫1 π答案 2,π,-4.⎛ π⎫ π 2.答案π3⎡ π⎤ ⎛ π⎫ π π 6 2π k π π π6 2 2 3⎛ π⎫π图象,若对满足|f (x 1)-g (x 2)|=2 的 x 1,x 2,有|x 1-x 2|min =3,则 φ=.答案π6解析 因为 g (x )=sin [2 x -φ =sin(2x -2φ),所以|f (x 1)-g (x 2)|=|sin 2x 1-sin(2x 2-2φ)|=2.因为-1≤sin 2x 1≤1,-1≤sin(2x 2-2φ)≤1,所以 sin 2x 1 和 sin(2x 2-2φ)的值中,一个为 1,另一个为-1,不妨取 sin 2x 1=1,sin(2x 2-2φ)π π=-1,则 2x 1=2k 1π+2,k 1∈Z,2x 2-2φ=2k 2π-2,k 2∈Z,2x 1-2x 2+2φ=2(k 1-k 2)π+π,(k 1⎪⎪因为0<φ<,所以0<-φ<,则φ=.答案y=10sin⎝8x+4⎭+20,x∈[6,14]所以A=×(30-10)=10,b=×(30+10)=20,所以ω=.又×10+φ=2π,4所以y=10sin⎝8x+4⎭+20,x∈[6,14].5.(2014·安徽)若将函数f(x)=sin(2x+)的图象向右平移φ个单位,所得图象关于y轴对称,答案3π-k2)∈Z,π得|x1-x2|=⎪(k1-k2)π+2-φ⎪.πππ222ππ故当k1-k2=0时,|x1-x2|min=2-φ=3,π64.(教材改编)如图,某地一天从6~14时的温度变化曲线近似满足函数y=A sin(ωx+φ)+b,则这段曲线的函数解析式为.⎛π3π⎫解析从图中可以看出,从6~14时的是函数y=A sin(ωx+φ)+b的半个周期,121212π又2×ω=14-6,π8π83π解得φ=,⎛π3π⎫π4则φ的最小正值是.8解析∵函数f(x)=sin(2x+)的图象向右平移φ个单位得到g(x)=sin[2(x-φ)+]=sin(2x+又∵g(x)是偶函数,∴-2φ=kπ+(k∈Z).∴φ=--(k∈Z).当k=-1时,φ取得最小正值.例1已知函数y=2sin⎝2x+3⎭.(3)说明y=2sin⎝2x+3⎭的图象可由y=sin x的图象经过怎样的变换而得到.解(1)y=2sin⎝2x+3⎭的振幅A=2,周期T==π,初相φ=.(2)令X=2x+,则y=2sin⎝2x+3⎭=2sin X.6y=2sin⎝2x+3⎭πππ444-2φ),ππ42kππ283π8题型一函数y=A sin(ωx+φ)的图象及变换⎛π⎫(1)求它的振幅、周期、初相;(2)用“五点法”作出它在一个周期内的图象;⎛π⎫⎛π⎫2ππ23π⎛π⎫3列表如下:xXy=sinX⎛π⎫π-π12π212π3π7π123π2-1-25π62π描点画出图象,如图所示:(3)方法一 把 y =sin x 的图象上所有的点向左平移 个单位长度,得到 y =sin ⎝x +3⎭的图象; 再把 y = sin ⎝x +3⎭ 的图象上所有点的横坐标缩短到原来的sin ⎝2x +3⎭的图象;最后把 y =sin ⎝2x +3⎭上所有点的纵坐标伸长到原来的 2 倍(横坐标不变 ),即可得到 y =2sin ⎝2x +3⎭的图象.方法二 将 y =sin x 的图象上所有点的横坐标缩短为原来的 倍(纵坐标不变),得到 y =sin 2x再将 y =sin 2x 的图象向左平移 个单位长度,得到 y =sin ⎣2⎝x +6⎭⎦=sin ⎝2x +3⎭的图象;再将 y =sin ⎝2x +3⎭的图象上所有点的纵坐标伸长为原来的 2 倍(横坐标不变),即得到 y =2sin ⎝2x +3⎭的图象.设 z =ωx +φ,由 z 取 0, ,π, π,2π 来求出相应的 x ,通过列表,计算得出五点坐标,描(1)把函数 y =sin(x + )图象上各点的横坐标缩短到原来的 (纵坐标不变),再将图象向右平移 个单位长度,那么所得图象的一条对称轴方程为(填正确的序号).①x =- ;②x =- ;③x = ;④x = .(2)设函数 f (x )=cos ωx ( ω>0),将 y =f (x )的图象向右平移 个单位长度后,所得的图象与原图π ⎛ π⎫ 3⎛ π⎫ 1 2倍 ( 纵坐标不变 ) ,得到 y =⎛ π⎫⎛ π⎫⎛ π⎫12的图象;π ⎡ ⎛ π⎫⎤ ⎛ π⎫ 6⎛ π⎫⎛ π⎫思维升华 (1)五点法作简图:用“五点法”作 y =A sin(ωx +φ)的简图,主要是通过变量代换,π 3 2 2点后得出图象.(2)图象变换:由函数 y =sin x 的图象通过变换得到 y =A sin(ωx +φ)的图象,有两种主要途径:“先平移后伸缩”与“先伸缩后平移”.π 162π3π π π π2 4 8 4π3象重合,则 ω 的最小值等于.答案 (1)① (2)6解析(1)将y=sin(x+)图象上各点的横坐标缩短到原来的(纵坐标不变),得到函数y=sin(2x+);再将图象向右平移个单位长度,得到函数y=sin[2(x-)+]=sin(2x-),故x 2(2)由题意可知,nT=(n∈N*),例2(1)已知函数y=A sin(ωx+φ)(A>0,ω>0,|φ|<)的图象上一个最高点的坐标为(2,2),答案(1)y=2sin⎝8x+4⎭(2)f(x)=2sin(2x+)⎫解析(1)由题意得A=2,=6-2,所以T=16,ω==.又sin⎝8×2+φ⎭=1,所以+φ=+2kπ(k∈Z).又因为|φ|<,所以φ=.41234π162πππππ63362π=-是其图象的一条对称轴方程.π32ππ∴n·ω=3(n∈N*),∴ω=6n(n∈N*),∴当n=1时,ω取得最小值6.题型二由图象确定y=Asin(ωx+φ)的解析式π2由这个最高点到其右侧相邻最低点间的图象与x轴交于点(6,0),则此函数的解析式为.(2)函数f(x)=A sin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数f(x)的解析式为.⎛ππ⎫π3T2ππ⎛ππ4T84πππ224(2)由题图可知A=2,T7πππ=-=,所以T=π,故ω=2,因此f(x)=2sin(2x+φ),又⎝12π,- 2⎭为最小值点, ∴2× π+φ=2k π+ ,k ∈Z ,∴φ=2k π+ ,k ∈Z ,∴φ= .故 f (x )= 2sin(2x + ).则 A = ,b = .(2)求 ω,确定函数的最小正周期 T ,则可得 ω= . “最大值点”(即图象的“峰点”)时 ωx +φ= ;“最小值点”(即图象的“谷点”)时 ωx +φ= .函数 f (x )=2sin(ωx +φ)⎝ω>0,-2<φ<2⎭的部分图象如图所示,则 φ=3解析 ∵ = π- π,⎛ 7 ⎫7 3π12 2π3又|φ|<π,π3π3思维升华 确定 y =A sin(ωx +φ)+b (A >0,ω>0)的步骤和方法:(1)求 A ,b ,确定函数的最大值 M 和最小值 m ,M -m M +m2 22πT(3)求 φ,常用的方法有:①代入法:把图象上的一个已知点代入(此时 A ,ω,b 已知)或代入图象与直线 y =b 的交点求 解(此时要注意交点在上升区间上还是在下降区间上).②特殊点法:确定 φ 值时,往往以寻找“最值点”为突破口.具体如下:π23π 2π答案 -T 1152 12 12∴T =π.2π又 T = ω (ω>0),2π∴ ω =π,⎛ ππ⎫.由五点作图法可知当x=π时,2即2×π+φ=,∴φ=-.y).若初始位置为P0⎝2,⎭,当秒针从P(注:此时t=0)正常开始走时,那么点P的纵坐答案y=sin⎝-30t+6⎭位是.又函数周期是60(秒)且秒针按顺时针旋转,即T=⎪ω⎪=60,所以|ω|=π⎪2π⎪ππ63030所以y=sin⎝-30t+6⎭.例4已知关于x的方程2sin2x-3sin2x+m-1=0在⎝2,π⎭上有两个不同的实数根,则m ∴ω=2.512πωx+φ=,5π122π3题型三三角函数图象性质的应用命题点1三角函数模型的应用例3如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置P(x,⎛31⎫2标y与时间t的函数关系式为.⎛ππ⎫解析设点P的纵坐标y与时间t的函数关系式为y=sin(ωt+φ).由题意可得,函数的初相,即ω=-,⎛ππ⎫命题点2方程根(函数零点问题)⎛π⎫的取值范围是.答案(-2,-1)解析方程2sin2x-3sin2x+m-1=0可转化为m=1-2sin2x+3sin2x=cos2x+3sin2x=2sin⎝2x+6⎭,x∈⎝2,π⎭.设2x+=t,则t∈⎝6π,6π⎭,6=sin t,t∈⎝6π,6π⎭,有两个不同的实数根.∴y=和y=sin t,t∈⎝6π,6π⎭的图象有两个不同交点,如图:2由图象观察知,的范围为(-1,-),解析由例4知,的范围是⎣-1,2⎭,∴-2≤m<1,图象的两相邻对称轴间的距离为.(1)求f⎝8⎭的值;(2)求函数y=f(x)+f⎝x+4⎭的最大值及对应的x的值.=2⎣2=2sin⎝ωx+φ-6⎭.⎛π⎫⎛π⎫π⎛713⎫∴题目条件可转化为m⎛713⎫2m⎛713⎫m122故m的取值范围是(-2,-1).引申探究例4中,“有两个不同的实数根”改成“有实根”,则m的取值范围是.答案[-2,1)m⎡1⎫2∴m的取值范围是[-2,1).命题点3图象性质综合应用例5已知函数f(x)=3sin(ωx+φ)-cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且函数y=f(x)π2⎛π⎫⎛π⎫解(1)f(x)=3sin(ωx+φ)-cos(ωx+φ)⎡31⎤sin(ωx+φ)-2cos(ωx+φ)⎦⎛π⎫因为f(x)是偶函数,则 φ- = +k π(k ∈Z ),所以 φ= +k π(k ∈Z ),又因为 0<φ<π,所以 φ= ,ωx +=2cos ωx .所以 f (x )=2sin 2⎭⎝因此 f =2cos = 2.⎝8⎭x +(2)y =2cos 2x +2cos 2⎣ ⎝ 4⎭⎦2x +=2cos 2x +2cos 2⎭⎝-2x =2 2sin ⎝4 ⎭2x -=-2 2sin4⎭⎝令 2x - =2k π- (k ∈Z ),y 有最大值 2 2,所以当 x =k π- (k ∈Z )时,y 有最大值 2 2.设函数 f (x )=3sin(ωx +φ)(ω>0,- <φ< )的图象关于直线 x = 对称,它的周期①f (x )的图象过点(0, );π π6 22π32π3⎛ π⎫ 2π π由题意得 ω =2· 2,所以 ω=2.故 f (x )=2cos 2x .⎛π⎫ π4⎡ ⎛ π⎫⎤⎛ π⎫=2cos 2x -2sin 2x⎛π ⎫⎛ π⎫ π π4 2π8思维升华 (1)三角函数模型的应用体现在两方面:一是已知函数模型求解数学问题;二是把实际问题抽象转化成数学问题,建立数学模型再利用三角函数的有关知识解决问题.(2)方程 根的个数可转化为两个函数图象的交点个数.(3)研究 y =A sin(ωx +φ)的性质时可将 ωx +φ 视 为一个整体,利用换元法和数形结合思想进行解题.π π 2π2 2 3是 π,则下列说法正确的是.(填序号)32②f (x )在[ , ]上是减函数;③f (x )的一个对称中心是( ,0);∴f (x )=3sin(2x +φ),f ( )=3sin( +φ),则 sin( +φ)=1 或-1.又 φ∈(- , ), +φ∈( , π),∴ +φ= ⇒φ= ,∴f (x )=3sin(2x + ).①:令 x =0⇒f (x )= ,正确.②:令 2k π+ <2x + <2k π+ ,k ∈Z⇒k π+ <x <k π+ ,k ∈Z .令 k =0⇒ <x < ,即 f (x )在( , )上单调递减,而在( , )上单调递增,错误.③:令 x = ⇒f (x )=3sin π=0,正确.④:应平移 个单位长度,错误.典例 (14 分)已知函数 f (x )=2 3sin( + )·cos( + )-sin(x +π).π 2π12 35π12④将 f (x )的图象向右平移|φ|个单位长度得到函数 y =3sin ωx 的图象.答案 ①③2π解析 ∵周期为 π,∴ ω =π⇒ω=2,2π 4π3 34π3π π 4π 5π 112 23 6 64π 3π π3 2 6π 632π π 3π2 6 2π 2π6 3π 2π63π 2π π π6 3 12 65π12π124.三角函数图象与性质的综合问题x π x π2 4 2 4(1)求 f (x )的最小正周期;(2)若将f(x)的图象向右平移个单位长度,得到函数g(x)的图象,求函数g(x)在区间[0,π]上(2)将f(x)解析式中的x换成x-,得g(x),然后利用整体思想求最值.解(1)f(x)=23sin(+)·cos(+)-sin(x+π)=3cos x+sin x[4分]=2sin(x+),[6分]于是T==2π.[7分](2)由已知得g(x)=f(x-)=2sin(x+),[9分]∵x∈[0,π],∴x+∈[,],∴sin(x+)∈[-,1],[12分]∴g(x)=2sin(x+)∈[-1,2].[13分]a sinα+b cosα=a2+b2sin(α+φ)(其中tanφ=),或a sinα+b cosα=a2+b2cos(α-φ)(其中tanφ=),在历年高考中使用频率是相当高的,几乎年年使用到、考查到,应特别加以关注.(sin x·aπ6的最大值和最小值.思维点拨(1)先将f(x)化成y=A sin(ωx+φ)的形式再求周期;π6规范解答xπxπ2424π32π1ππ66ππ7π666π162π6故函数g(x)在区间[0,π]上的最大值为2,最小值为-1.[14分]解决三角函数图象与性质的综合问题的一般步骤:第一步:(化简)将f(x)化为a sin x+b cos x的形式;第二步:(用辅助角公式)构造f(x)=a2+b2·b+cos x·);a2+b2a2+b2第三步:(求性质)利用f(x)=a2+b2sin(x+φ)研究三角函数的性质;第四步:(反思)反思回顾,查看关键点、易错点和答题规范.温馨提醒(1)在第(1)问的解法中,使用辅助角公式baab(2)求g(x)的最值一定要重视定义域,可以结合三角函数图象进行求解.±1.函数y=cos⎝2x-3⎭的部分图象可能是⎫[方法与技巧]1.五点法作图及图象变换问题(1)五点法作简图要取好五个关键点,注意曲线凸凹方向;(2)图象变换时的伸缩、平移总是针对自变量x而言,而不是看角ωx+φ的变化.2.由图象确定函数解析式由图象确定y=A sin(ωx+φ)时,φ的确定是关键,尽量选择图象的最值点代入;若选零点代入,应根据图象升降找“五点法”作图中第一个零点.3.对称问题函数y=A sin(ωx+φ)的图象与x轴的每一个交点均为其对称中心,经过该图象上坐标为(x,A)的点与x轴垂直的每一条直线均为其图象的对称轴,这样的最近两点间横坐标的差的绝对值是半个周期(或两个相邻对称中心的距离).[失误与防范]1.由函数y=sin x的图象经过变换得到y=A sin(ωx+φ)的图象,如先伸缩,再平移时,要把x前面的系数提取出来.2.复合形式的三角函数的单调区间的求法.函数y=A sin(ωx+φ)(A>0,ω>0)的单调区间的确定,基本思想是把ωx+φ看做一个整体.若ω<0,要先根据诱导公式进行转化.3.函数y=A sin(ωx+φ)在x∈[m,n]上的最值可先求t=ωx+φ的范围,再结合图象得出y =A sin t的值域.A组专项基础训练(时间:40分钟)⎛π.2x -,∴当2x - =0,解析∵y =cos 3⎭⎝即 x = 时,函数取得最大值 1,结合图象看,可使函数在 x = 时取得最大值的只有④. 解析 取 K ,L 中点 N ,则 MN = ,因此 A = .由 T =2 得 ω=π.∵函数为偶函数,0<φ<π,∴φ= ,∴f (x )= cos πx ,3.已知函数 f (x )=2sin(ωx +φ)(ω>0,且|φ|< )的部分图象如图所示,则函数 解析 由函数的图象可得 T = π- π,又图象过点( π,2),∴2sin(2× π+φ)=2, ∴φ=- +2k π,k ∈Z ,∵|φ|< ,△KLM 为等腰直角三角形,∠KML =90°,KL =1,则 f ( )的值为.答案3 ∴f ( )= cos = .答案 [k π- ,k π+ ],k ∈Z答案 ④⎛ π⎫ π 3π π6 62.设偶函数 f (x )=A sin(ωx +φ)(A >0,ω>0,0<φ<π)的部分图象如图所示,1641212π 2121 1 π 3 62 6 4π2f (x )的单调递增区间是.π 5π12 121 2 54 3 12∴T =π,则 ω=2.5 512 12π3π2∴取 k =0,则 φ=- ,即得 f (x )=2sin(2x - ),∴f (x )的单调增区间为 2k π- ≤2x - ≤2k π+ ,k ∈Z ,即单调递增区间为[k π- ,k π+ ],k ∈Z .4.已知曲线 f (x )=sin ωx + 3cos ωx (ω>0)相邻的两条对称轴之间的距离为 ,且曲线关于点 (x 0,0)中心对称,若 x 0∈⎣0,2⎦,则 x 0==2⎝ sin ωx + =2sin ⎝ωx +3⎭.∵曲线 f (x )=2sin ⎝ωx+3⎭相邻的两条对称轴之间的距离为 ,∴f (x )=2sin ⎝2x +3⎭. 又 x 0∈⎣0,2⎦,∴x 0= . 5.函数 f (x )=sin(2x +φ)⎝|φ|<2⎭的图象向左平移 个单位后所得函数图象的解析式是奇函数,则函数 f (x )在⎣0,2⎦上的最小值为 答案 - 3解析 由函数 f (x )的图象向左平移 个单位得 g (x )=sin ⎝2x +φ+3⎭的图象,π π3 3π π π2 3 2π 5π12 12π2⎡ π⎤.答案π3解析 f (x )=sin ωx + 3cos ωx⎛1 2 3 ⎫ 2 cosωx ⎭⎛ π⎫⎛ π⎫ π 22π∴最小正周期 T =π= ω ,∴ω=2,⎛ π⎫∵曲线关于点(x 0,0)中心对称;π∴2x 0+3=k π(k ∈Z ),k π π∴x 0= 2 -6(k ∈Z ),⎡ π⎤ π 3⎛ π⎫ π 6⎡ π⎤.2π ⎛ π⎫ 6因为是奇函数,所以 φ+ =k π,k ∈Z ,又因为|φ|< ,所以 φ=- ,2x -.所以 f (x )=sin 3⎭⎝0,,所以 2x - ∈ - ,,又 x ∈⎣ 2⎦ ⎣ 33 ⎦ ∴ω= =100π.∴I =10sin(100πt +φ).,10 ,∵图象过点⎝300⎭∴sin( +φ)=1, +φ=2k π+ ,k ∈Z ,∴φ=2k π+ ,k ∈Z ,又∵0<φ< ,∴φ= .100πt +,∴I =10sin6⎭⎝所以当 x =0 时,f (x )取得最小值为- 3.ω>0,0<φ< ) 的图象如右图所示,则当 t =秒时,电流强度是解析由图象知 A =10, = - = , ∴10sin(100π× +φ)=10,当 t = 秒时,I =-5 安.7.若函数 f (x )=sin(ωx +φ) (ω>0 且|φ|< )在区间⎣6, 3 ⎦上是单调递减函数,且函数从 1 减小2到-1,则 f ⎝4⎭= .答案3π3π π2 3⎛ π⎫⎡ π⎤ π ⎡ π 2π⎤ 326. 电流强度 I ( 安 ) 随时间 t ( 秒 ) 变化的函数I = A sin(ωt + φ)(A >0 ,π 12 100安.答案 -5T4 1 12 300 300 1002πT⎛ 1 ⎫ 1300π π π3 3 2π6π π2 6⎛ π⎫1100π ⎡π 2π⎤⎛π⎫2解析由题意可得,函数的周期为2×⎝3-6⎭=π,⎛⎫∴f(x)=sin⎝2x+6⎭,∴f⎝4⎭=sin⎝2+6⎭=cos=.8.已知函数f(x)=A sin(ωx+φ)(A>0,ω>0,|φ|<)在一个周期内的图象如图所示.若方程可得φ=答案或π解析由图象可知y=m和y=f(x)图象的两个交点关于直线x=或x=π对称,9.(2015·天津)已知函数f(x)=sin2x-sin2⎝x-6⎭,x∈R.(2)求f(x)在区间⎣-3,4⎦上的最大值和最小值.1-cos⎝2x-3⎭解(1)由已知,有f(x)=-⎛sin2x-所以f(x)的最小正周期T==π.⎛2ππ⎫2π即ω=π,∴ω=2,∴f(x)=sin(2x+φ).πππ由sin⎝2×6+φ⎭=1,|φ|<26,⎛π⎫⎛π⎫⎛ππ⎫π362π2f(x)=m在区间[0,π]上有两个不同的实数x1,x2,则x1+x2的值为.π433π263π4∴x1+x2=3或3π.⎛π⎫(1)求f(x)的最小正周期;⎡ππ⎤⎛π⎫1-cos2x221⎛13=2⎝2cos2x+2⎫1sin2x⎭-2cos2x=311π⎫44cos2x=2sin⎝2x-6⎭.2π2⎡ππ⎤⎡ππ⎤⎛π⎫1 (2)因为f(x)在区间⎣-3,-6⎦上是减函数,在区间⎣-6,4⎦上是增函数,且f⎝-3⎭=-4,4 所以 f (x )在区间⎣-3,4⎦上的最大值为 最小值为- .10.设函数 f (x )= 3- 3sin 2ωx -sin ωx cos ωx (ω>0),且 y =f (x )图象的一个对称中心到最近 的对称轴的距离为 .(2)求 f (x )在区间⎣π, 2 ⎦上的最大值和最小值.解 (1)f (x )= 3- 3sin 2ωx -sin ωx cos ωx= - 3× - sin 2ωx = 3 cos 2ωx - sin 2ωx=-sin ⎝2ωx -3⎭.依题意知 =4× ,ω>0,所以 ω=1.(2)由(1)知 f (x )=-sin ⎝2x -3⎭.当 π≤x ≤ 时, ≤2x - ≤ .⎛2 故 f (x )在区间⎣π, 2 ⎦上的最大值和最小值分别为 ,-1.11.已知函数 f (x )=A sin(ωx +φ) (A >0,|φ|< ,ω>0)的图象的一部分如图所⎛ π⎫1⎛π⎫3f ⎝-6⎭=-2,f ⎝4⎭=,⎡ π π⎤34 ,1 22π 4(1)求 ω 的值; ⎡ 3π⎤231-cos 2ωx 1 2 2 2 12 2⎛π⎫2π π 2ω 4⎛ π⎫3π 5π π 8π 2 3 3 3 所以- 3 π⎫2 ≤sin ⎝2x -3⎭≤1.所以-1≤f (x )≤ 3.⎡ 3π⎤3 2B 组 专项能力提升(时间:20 分钟)π 2示,则该函数的解析式为 .答案 f (x )=2sin ⎝2x +6⎭∴1=2sin(ω·0+φ),即 sin φ= .∵|φ|< ,∴φ= .又∵ π 是函数的一个零点,且是图象递增穿过 x 轴形成的零点,∴ ω+ =2π,∴ω=2. ∴f (x )=2sin ⎝2x +6⎭. 的交点中,若相邻交点距离的最小值为 ,则 f (x )的最小正周期为.解析 f (x )= 3sin ωx +cos ωx =2sin(ωx + )(ω>0).由 2sin(ωx + )=1 得 sin(ωx + )= ,∴ωx + =2k π+ 或 ωx + =2k π+ π(k ∈Z ).故 f (x )的最小正周期 T = =π.13.已知函数 f (x )=cos ⎝3x +3⎭,其中 x ∈⎣6,m ⎦,若 f (x )的值域是⎣-1,- 答案 ⎣ 9 ,18⎦⎛ π⎫解析 观察图象可知:A =2 且点(0,1)在图象上,1 π π2 2 611 11π π12 12 6⎛ π⎫12.(2014· 天津改编)已知函数 f (x )= 3sin ωx +cos ωx (ω>0),x ∈R .在曲线 y =f (x )与直线 y =1π3答案 ππ6π π 16 6 2π π π 56 6 6 6π π π 5令 k =0,得 ωx 1+6=6,ωx 2+6=6π,2π∴x 1=0,x 2=3ω.π 2π π由|x 1-x 2|=3,得3ω=3,∴ω=2.2π2值范围是.⎡2π 5π⎤解析 画出函数的图象.⎛ π⎫ ⎡π ⎤ ⎡ 3⎤ 2 ⎦ ,则 m 的取由 x ∈⎣6,m ⎦,可知 ≤3x + ≤3m + ,且 f ⎝ 9 ⎭=cos π=-1,=- 要使 f (x )的值域是⎣-1,-2 ⎦ 所以 π≤3m + ≤ π,则 ≤m ≤ ,即 m ∈⎣ 9 ,18⎦.14.已知 f (x )=sin ⎝ωx +3⎭ (ω>0),f ⎝6⎭=f ⎝3⎭,且 f (x )在区间⎝6,3⎭上有最小值,无最大值, 答案 146 3 π解析 依题意,x = = 时,y 有最小值,∴sin ⎝4ω+3⎭=-1,∴ ω+ =2k π+ (k ∈Z ),∴ω=8k + (k ∈Z ),∵f (x )在区间⎝6,3⎭上有最小值,无最大值, 15.已知函数 f (x )= 3sin ωx cos ωx +cos 2ωx - (ω>0),其最小正周期为 . (2)将函数 f (x )的图象向右平移 个单位长度,再将图象上各点的横坐标伸长到原来的 2 倍(纵坐标不变),得到函数 y =g (x )的图象,若关于 x 的方程 g (x )+k =0 在区间[0, ]上有且只有一解 (1)f (x )= 3sin ωx cos ωx +cos 2ωx -⎡π ⎤ 5π π π 6 3 3⎛π⎫ 5π 3 因为 f ⎝6⎭=cos 6 2⎛2π⎫,⎡ 3⎤ ,π 7 2π 5π3 6 9 18⎡2π 5π⎤⎛ π⎫ ⎛π⎫ ⎛π⎫ ⎛π π⎫则 ω=.3π π + 2 4⎛π π⎫π π 3π4 3 2143⎛π π⎫π π π 14 ∴3-4<ω,即 ω<12,令 k =0,得 ω= 3 .1 π2 2(1)求 f (x )的表达式;π8π2个实数解,求实数 k 的取值范围.12=sin2ωx+-=sin(2ωx+),所以ω=2,所以f(x)=sin(4x+).(2)将f(x)的图象向右平移个单位长度后,得到y=sin(4x-)的图象;再将所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到y=sin(2x-)的图象,所以g(x)=sin(2x-),因为0≤x≤,所以-≤2x-≤,cos2ωx+11所以g(x)∈[-3又g(x)+k=0在区间[0,]上有且只有一个实数解,即函数y=g(x)与y=-k在区间[0,]上≤-k<或-k=1,解得-3<k≤或k=-1,,]∪{-1}.3π2226π2πππ由题意知f(x)的最小正周期T=2,T=2ω=ω=2,π6ππ83ππ33πππ2π23332,1].ππ22有且只有一个交点,由正弦函数的图象可知-32233 22所以实数k的取值范围是(-33 22。
三角函数的图像及其变换

振幅变换
振幅变换
通过将三角函数中的系数乘以一 个常数,可以改变函数图像的形 状和大小。例如,将正弦函数 y=sin(x)变为y=2sin(x),图像的 高度变为原来的两倍。
总结词
振幅变换可以改变函数图像的大 小和形状,但不影响位置。
详细描述
振幅变换通常通过乘以一个常数来实 现。例如,对于正弦函数y=sin(x),乘 以2得到y=2sin(x),图像的高度变为 原来的两倍。同样地,对于余弦函数 y=cos(x),乘以2得到y=2cos(x),图 像的高度也变为原来的两倍。
与复数的联系
三角函数与复数之间有着密切的联系。例如,复数的三角形式就是由三角函数来表示的,这使得复数 的一些性质和运算可以通过三角函数来理解和实现。
此外,在复分析中,三角函数也起着重要的作用,如在求解某些复数域上的微分方程时,经常需要用 到三角函数。
谢谢
THANKS
应用
正切函数在解决实际问题和数学 问题中也有应用,例如在几何学 和三角学中的角度和长度计算。
02 三角函数的图像
CHAPTER
正弦函数的图像
01
正弦函数图像是周期函数,其基本周期为$2pi$,在$[0, 2pi]$ 区间内呈现波形。
02
正弦函数图像在$x$轴上的交点是$(frac{pi}{2} + kpi, 0)$,其
周期变换
总结词
详细描述
通过改变三角函数的周期,可以改变
函数图像的形状和位置。例如,将正 弦函数和余弦函数的周期从2π变为4π, 图像将变为原来的两倍长,但形状和
周期变换可以改变函数图像的长度, 但不影响形状和位置。
位置保持不变。
周期变换通常通过乘以一个常数来实现。例 如,将函数y=sin(x)变为y=sin(2x),周期 从2π变为π,图像长度减半。同样地,对于 余弦函数,将y=cos(x)变为y=cos(2x),周 期从2π变为π,图像长度也减半。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图像的应用
(08’四川,15)已知函数 f ( x) sin(w x ) (w 0) 在
61
(0,
4
3
)
单调递增,在 ( 4
3
,
2
)
单调递减,
则w__2___.
wx
6
6
2
x
0
4
3
f (x)
例2.函数 y Asin(w x )(w 0, )的部分图 像如图所示,则函数表达式为y____4_2s_i_n_(8__x___4_).
2
(
3 2
,
0)
( , 1)
(2 ,1)
2 x
例1:用“五点法”作y sin(2x ) , x [ , ] 的简
图.
2x
3
3
22
2
32
0
2
4
3
x
5
2 12 6 12 3 2
y sin(2x ) 3 1 0
3
2
y
1 03
2
2
5
12
1
6 o 1 12
32
D.
x
1. 函数 y sin(w x )(w 0,| | ) 的图像如 图所示,则函数的解析式是_y__s_2i_n_(2_x___3_)__.
y
1
7
12
o
x
12
1
(09’海南,16)已知函数 f ( x) 2sin(w x ) 的图像
如图所示,则 f (7 ) __0___ .
12
y
2
7
12
o
4
2
5 x
4
精品文档 欢迎下载
读书破万卷,下笔如有神--杜甫
4
令k=1,则
2
4
2 3
12 12
f (0) Acos( )
2 A
42
f ( ) Acos( 3 ) 2 A
2
24
2
f ( ) 2
23
(09’辽宁,8)已知函数 f (x) Acos(w x ) 的图像如图
所示,f ( ) 2 , 则 f(0)等于(
23
C
)
A. 2
中分别选定了一个适当的区间,各自作出三
个函数 y sin 2x, y sin( x ), y sin( x )
6
3
的图像如下。结果发现其中有一位同学作出
的图像有错误,那么有错误的图像是( )
y sin 2x
A.
x
y sin( x )
6
B.
x
y sin( x )
3
C√. x
向_左_平移__2__个单位长度而得到.
五点作图法
1. y sin x (0 x 2 )的简图
y
( ,1)
最高点
1-
2
o (0, 0)
( , 0)
(2 , 0)
与x轴 的交点
2 x
-
1 -
(
3 2
,
1)
最低点
2. y cos x (0 x 2 )的简图
y
1 -(0,1)
o
1 -
( ,0)
B. 1
2 C.
1 D.
3
2
3
2
y
o
12
2
3
32
7 11
x
12
12
(06’福建9)已知函数 f ( x) 2sinw x(w 0)
在区间[ , ]上的最小值是-2,则ω的最小
34
值等于( B)
(A)2 (B) 3
3y
2
2
2w
o
(C)2 (D)3
3
3 2w
2w
x
即w 3
2
2
(2010’江西)如图,四位同学在同一个坐标系
y
4
2 o
6
x
4
变式训练:(09’辽宁,8)已知函数 f ( x) Acos(w x )
的图像如图所示,f ( ) 2 , 则 f(0)等于(
23
C
)
A. 2
B. 1
C. 2
D. 1
分析:
3
2
y
3
2
T 2
3
w 3
(11 , 0)是第二个关键点
12
o
2
x 7 11
11 2k , k Z
正弦余弦函数的图像及其应用
知识结构
正弦线
作精确的图像
平移
正弦函数的图像
余弦函数的图像
作简图
“五点法”作图
利用正弦线作出正弦函数的图像
6
4
y-
1
2
o-
-1
正弦曲线
2
4
6
x
利用变换法作余弦函数的图像
y-
ห้องสมุดไป่ตู้
余弦曲线
-
-
1
-
6
4
2
o
-1
2
4
6
y cos x sin( x )
2
y=cosx的图像可通过把y=sinx的图像
