第五节 理论板数的求法
第五节理论板数的求法

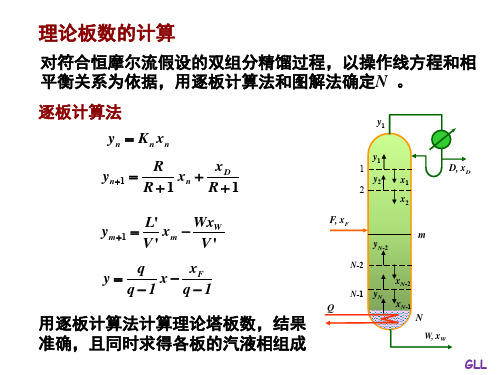
第五节理论板数的求法所谓求理论塔板数,就是利用前面讨论的平衡关系,和操作关系,计算达到指定分离要求所须的汽化-冷凝次数。
(1)逐板计算法每利用一次平衡关系和一次操作关系,即为一块理论板。
提馏段也是一样。
(2)图解法通常采用直角梯级图解法,其实质仍然是以平衡关系与操作关系为依据,将两者绘在图上,便可图解得出达到指定分离任务所须的理论塔板数及加料板位置。
图解步骤如下:①作平衡线与对角线②作精馏段操作线,即连的直线。
③作进料线,过④作提馏段操作线,即连所得直线即是。
⑤从点开始,在平衡线与操作线之间作直角梯级,直到超过点。
有多少直角梯级,就有多少块理论板数。
跨越点的阶梯为加料板。
如图所示,共有5.2块理论板,第三块板为加料板。
图解法示意图a. 回流比与吉利兰图b. 回流比的影响因素(1)回流比对理论板数的影响。
如图。
回流比对的影响,操作线靠近平衡线,反之,,操作线远离平衡线,即正比于(2)回流比对设备费与操作费的影响,塔直径,冷凝器,蒸馏釜设备费,塔高下降,设备费,冷却水量,加热蒸汽量,操作费须选一个合适回流比,使总费用最省。
如图所示。
费用示意图1线为“设备费~R”的关系式2线为“操作费~R”的关系式3线为“总费用~R”的关系式。
c. 全回流与最小回流比全回流——当时,则,此时称为全回流。
这时精馏段与提馏段操作线方程均与对角线重合,此时理论板数最少。
最小回流比——当减小时,,当减至两操作线交点逼近平衡线时,此时,此时R称为最小回流比。
最小回流比推导图解之得,………………与是平衡线与进料线之交点。
最小回流比是指对于一定分离要求的最小回流比,分离要求变动了(例如变了),对应的亦要改变。
d. 吉利兰图法求理论板数吉利兰图是一种经验关联图,它总结了八种不同的物系,个组分,操作压力由真空个大气压,进料由过冷液体过热蒸汽。
它如何归纳得到,本章并不关心,重点是如何应用它?下面是吉利兰图法应用举例。
【例】某二元理想混合液其平均相对挥发度为。
理论板层数的计算

1、图解法
2021/10/24
2、解析法求理论板层数
1)理论板数的解析表达式
当吸收涉及的浓度区间内平衡关系为直线Y * mX b 时
在 I ~ II 层板间任一截面到塔顶范围内作组分A的衡算
VYII LX 0 LX1 VYI
YII
L V
(
X
1
X 0 ) YI
若相平衡关系可采用 Y * mX b 表示
2021/10/24
XI
YI
m
b
,
X
0
Y0* b m
YII
L V
(YI
Y0* m
)
YI
L A mV YII A(YI Y0*) YI
YII ( A 1)YI AY0*
2021/10/24
在 II ~ III 板间任一截面到塔顶范围内作组分A的衡算
VYIII LX 0 LX II VYI
A
N 1
A
1
1
(YI
Y0*)
Y2 Y0* YN1 Y0*
A 1 AN1 1
YI Y0* YN1 Y0*
1
A A N 1
1
1
1
YN 1 YI AN 1 A YN 1 Y0* AN 1 1
2021/10/24
——克列姆塞尔方程
YN1 Y1,YI Y2 Y0* mX2 b Y2*
Y1 Y2 Y1 Y2*
ANT 1 A ANT 1 1
相对吸收率 溶质的吸收率与理论最大吸收率的比值
Y1 Y2
Y1 Y2*
分析相对吸收率与吸收率的区别与联系
2021/10/24
ANT 1 A ANT 1 1
图解法求理论板数(图文运用)

一、图解法求理论板数图解法计算精馏塔的理论板数和逐板计算法一样,也是利用汽液平衡关系和操作关系,只是把气液平衡关系和操作线方程式描绘在y x -相图上,使繁琐数学运算简化为图解过程。
两者并无本质区别,只是形式不同而己。
(1)精馏段操作线的作法 由精馏段操作线方程式可知精馏段操作线为直线,只要在x y -图上找到该线上的两点,就可标绘出来。
若略去精馏段操作线方程中变量的下标, 11+++=R x x R R y D 上式中截距为1+R x D ,在图7-12中以c 点表示。
当D x x =时,代入上式得D x y =,即在对角线上以a 点表示。
a 点代表了全凝器的状态。
联ac 即为精馏段操作线。
(2)提馏段操作线的作法 由q 线ef ,即可求得它和精馏段操作线的交点,而q 线是两操作线交点的轨迹,故这一交点必然也是两操作线的交点d,联接bd 即得提馏段操作线。
(3)图解法求理论板数的步骤①在直角坐标纸上绘出待分离的双组分混合物在操作压强下的y x -平衡曲线,并作出对角线。
如图7-14所示。
②依照前面介绍的方法作精馏段的操作线ac ,q 线ef ,提馏段操作线bd 。
③从a 点开始,在精馏段操作线与平衡线之间作水平线及垂直线构成直角梯级,当梯级跨过d 点时,则改在提馏段与平衡线之间作直角梯级,直至梯级的水平线达到或跨过b 点为止。
④梯级数目减一即为所需理论板数。
每一个直角梯级代表一块理论板,这结合逐板计算法分析不难理解。
其中过d 点的梯级为加料板,最后一级为再沸器。
因再沸器相当于一块理论板,故所需理论板数应减一。
在图7-14中梯级总数为7。
第四层跨过d 点,即第4层为加料板,精馏段共3层,在提馏段中,除去再沸器相当的一块理论板,则提馏段的理论板数为4-1=3。
该分离过程共需6块理论板(不包括再沸器)。
图解法较为简单,且直观形象,有利于对问题的了解和分析,目前在双组分连续精馏计算中仍广为采用。
但对于相对挥发度较小而所需理论塔板数较多的物系,结果准确性较差。
理论板数

简捷算法
简捷算法
吉利兰(Gilliland)关联图 前面讲到回流比的两个极限:Rmin与全回流,与此对应,回流比为Rmin时所需的理论板数为无穷多,全回 流时所需的理论板数Nmin为最少,实际回流比R在Rmin与无穷大之间.理论板数N在Nmin与无穷多之间。 根据对物系的分离要求,用前述方法很容易计算出Rmin和Nmin,困难在于如何按照选定的回流比R,求算所 需的理论塔板数N。通过对R,N,Rmin和Nmin之间关系的广泛研究,得出表示上述4个参数的相互关联图(图 3.33),此图称为吉利兰图。图中N与Nmin为不包括再沸器的理论板数。 应用吉利兰图可以简便地计算出精馏所需的理论板数,这种方法称为简捷法。它的另一个优点是也可以用于 多组分精馏的计算。这种方法的误差较大,一般只能对所需理论板数作大致的估计,因为简便,所以在初步设计 或进行粗略估算时常常使用。 简捷法求理论塔板数的步骤 1.根据物系性质及分离要求,求出Rmin,选择合适的R。 2.求出全回流下所需理论板数Nmin。对于接近理想体系的混合物,可以应用芬斯克方程计算。 3.
计算理论塔板数的方法有逐板计算法、图解法和芬斯克公式一吉利兰图的方法有时又称(简捷算法),这几 种方法目前都得到普遍的应用。
计算方法
逐板计算法
图解法
逐板计算法
逐板计算法的依据是气液平衡关系式和操作线方程。该方法是从塔顶或者塔底开始,交替利用平衡关系式和 操作线方程。逐级推算气液相的组成来确定理论塔板数。
理论板数
化工术语
01 介绍
03 简捷算法
目录
理论板数的计算
Rmin 1 x D (1 x D ) 1 0.98 2.5( 1 0.98 ) 1.237 1 xF 1 x F 2.5 1 0 . 501 1 0 . 501
R-Rmin 4 1.237 0.553 R1 41
对第二层理论板: y2 K 2 x2
1 2 F, xF
y1 L, xD y1 y2 x1 x2
全凝器
D, xD
R x 第二与第三层之间的气液相 y3 x2 D R1 R1 浓度满足操作关系:
……直至xn≤xq,换操作线方程
yN-2
N-2
m
平衡 作线 平衡 作现 x D y1 相 x1 操 y2 相 x2 操 y2 xn
双组分溶液 略去下标A、B N min
x D 1 xW lg 1 x x D W lg
芬斯克方程
理论板数的简捷算法 在精馏塔设计中,利用 Rmin 和Nmin 估算所需的理论塔板数。 吉利兰 (Gilliland) 关联图 用8个物系,由逐板计算 结果绘制。 精馏条件: 组分数目=2~11
yA xA y x B n1 B n
xA xA yA 离开第 1 块板的汽液平衡为: y 1 x x B 1 B 1 B D yA yA y 1 y B 1 B 2 yA xA 1 2 y x B 1 B 2 yA yA y 1 2 y B B 1 3
yN-2
N-2
蒸馏第5节-计算

M F 0.4504 78 (1 0.4504) 92 85.69kg / kmol
8570 F 100.0kmol/ h 85.69
2013-7-14 12
F D W
FxF Dx D Wxw
100.0 D W
100.0 0.4504 D 0.9787 W 0.0212
2013-7-14 17
3)q值与提馏段操作线方程
L L q F
L L qF
提馏段操作线方程为:
L qF W ym1 xm xw L qF W L qF W
2013-7-14
18
4)q线方程 由精馏段和提馏段操作线方程,可得到两操作线交点的坐 标;再由物料之间的关系,可以得到坐标x,y值之间的关系 ,即两操作线交点的轨迹方程:
(3)汽液混合物进料(c)
q 1 q 0 ~1
LF q F
2013-7-14
16
(4)对于饱和蒸汽进料 (d)
L L
V V F
q 0
(5)过热蒸汽进料 (e)
q
c pV (tF td ) r
q0
对于饱和液体、汽液混合物及饱和蒸汽三种进料而言,q 值就等于进料中的液相分率。
D 44.3kmol / h
(2)上升蒸汽量及回流量
W 55.7kmol / h
精馏段:L RD 3 44.8 134.5kmol/ h
V L D 134.5 44.83 179.3kmol/ h
2013-7-14 24
(3)提馏段操作线方程 饱和蒸汽进料时
,塔底产品中含甲苯不低于98.2%,每小时处理的原料量为 8570kg。操作回流比为3,试计算: (1)塔顶及塔底的产品量; (2)精馏段上升蒸汽量及回流液量;
1章蒸馏4第五节两组分连续精馏的计算(简捷法)+其他精馏

会形成另外一条温度分 布曲线。 布曲线。 受外界影响温度变化 最大的板——灵敏板。 灵敏板。 最大的板 灵敏板 t t
例:
1. 某精馏塔在操作时,加料热状态由原来的饱和液体 进料改为冷液进料,且保持F, xf,回流比R 和提馏段 上升蒸汽量V'不变,则此时D ,xD ,W 。 (增加,不变,减少,无法确定) 2. 某精馏塔在操作时,加料热状态由原来的饱和液 体进料改为冷液进料,且保持F, xf,V,D不变,则此 时xD ,xw ,R ,L/V 。 (增加,不变, 减少)
xn1 xn EML = (1-51a) xn1 x *n
实验时, 通常在R 下测取单板效率。 实验时 通常在 ∞下测取单板效率。
3、点效率 EO 、
中 国 矿 业 大 学 化 工 学 院 化 工 系
指塔板上各点的局部效率。以气相推动力为例: 指塔板上各点的局部效率。以气相推动力为例:
Байду номын сангаас
y yn+1 EOV = * yo yn+1
1. 全塔效率 E (总板效率 总板效率) 总板效率 是塔内各单板效率的平均值: 是塔内各单板效率的平均值:
中 国 矿 业 大 学 化 工 学 院 化 工 系
xD, , D
E= (NT / NP)×100% × 实际板数: 实际板数: NP= NT / E 目前公认的较为符合实际的是美国 化工学会的预测板效率的A Ch. 化工学会的预测板效率的 A.I.Ch.E 法和奥康奈尔法 法和奥康奈尔法。 奥康奈尔
Y = 0.545827 0.591422X + 0.002743/ X (1-50)
N Nmin = N +2
上式适用于 0.01<X<0.9
化工原理下1.4 理论板计算(逐板、图解

W xW
➢直线:过点(xW,xW)、截 踞WxW/(L’-W )
xW
a
d
b
xD
R 1
c
xW L W
xW g
xD
精馏塔的操作线
8
二、梯级图解法
提馏段操作线的截距数值很小,因此提馏段操作 线不易准确作出,且这种作图法不能直接反映进料 热状况的影响。
9
q 线方程
精馏段操作线方程 V y = Lx + D xD
xD yq
yq xq
一、全回流和最小回流比
非正常平衡曲线最小回流比的求法
27
2)解析法 对于相对挥发度为常数的情况
Rm
xD yq
yq xq
yp
q q 1
xp
1 q 1
xF
yq
xq 1 ( 1)xq
Rm
1 [ xD
1 xq
(1 xD )]
yB
xB
(
x x
A B
)
D
(
yA yB
)1
1(
xA xB
)1
1(
yA yB
)2
1
2(
xA xB
)2
1 1
2( 2
yyBA3)(3xx
A B
)3
1 1
2 3( 2 3L
yA yB L
)4
W
(
xA xB
)W
(
yA yB
)n1
y q x xF q1 q1
q 线的意义 精馏段操作线与提馏段
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五节 理论板数的求法
所谓求理论塔板数,就是利用前面讨论的平衡关系,()n n x f y =和操作关系,
()()m n n x f y x f y ''='=+或1计算达到指定分离要求所须的汽化-冷凝次数。
(1)逐板计算法
每利用一次平衡关系和一次操作关系,即为一块理论板。
提馏段也是一样。
(2)图解法
通常采用直角梯级图解法,其实质仍然是以平衡关系与操作关系为依据,将两者绘在y x -图上,便可图解得出达到指定分离任务所须的理论塔板数及加料板位置。
图解步骤如下: ①作平衡线与对角线
②作精馏段操作线111++
+=+R x x R R y D n n ,即连()D D D x x A R x C ,1,0与⎪⎭⎫ ⎝⎛+的直线。
③作进料线11---=q x x q q
y F
,过()d AC q q x x e F F 于的直线交点,作斜率为1,- ④作提馏段操作线W L Wx x W L L y W m m -'--''
=
+1,即连()d x x B W W 与,所得直线即是。
⑤从A 点开始,在平衡线与操作线之间作直角梯级,直到超过B 点。
有多少直角梯级,就有多少块理论板数。
跨越d 点的阶梯为加料板。
如图所示,共有5.2块理论板,第三块板为加料板。
图解法示意图
a. 回流比与吉利兰图
b. 回流比的影响因素
(1)回流比R 对理论板数T N 的影响。
如图。
回流比对T N 的影响
↑
+↓1R x R D ,,操作线靠近平衡线,↑T N 反之,
↓
+↑1R x R D ,,操作线远离平衡线,↓T N 即 T N 正比于R 1
(2)回流比对设备费与操作费的影响 ()D R D L V 1+=+=
↑↑V R ,,塔直径↑,冷凝器↑,蒸馏釜↑ 设备费↑
↓↑T N R ,,塔高下降,设备费↓
↑↑V R ,,冷却水量↑,加热蒸汽量↑, 操作费↑
须选一个合适回流比R ,使总费用最省。
如图所示。
费用示意图
1线为“设备费~R”的关系式 2线为“操作费~R”的关系式 3线为“总费用~R”的关系式。
c. 全回流与最小回流比)(min R
全回流——当0→D 时,则∞→R ,此时称为全回流。
这时精馏段与提馏段操作线方程均与对角线)(x y =重合,此时理论板数最少)(m N 。
最小回流比——当R 减小时,↓+)1(R R ,当R 减至两操作线交点逼近平衡线时,此
时∞→T N ,此时R称为最小回流比min R 。
最小回流比推导图
min
11R R h d ah
R R 即为时,如图所示,当=+
q D q
D x x y x h d ah R R --=
=+∴1min min 1
()()q D q D q D y x y x R R x x -+-=-min min ()q D q D q D y x y x x x R -=+--min
解之得,
q q q
D x y y x R --=
min ………………)(X
q x 与q y 是平衡线与进料线之交点。
最小回流比是指对于一定分离要求的最小回流比,
分离要求变动了(例如D x 变了),对应的min R 亦要改变。
d. 吉利兰图法求理论板数
吉利兰图是一种经验关联图,它总结了八种不同的物系,112→个组分,操作压力由真空40→个大气压,进料由过冷液体→过热蒸汽。
它如何归纳得到,本章并不关心,重点是如何应用它?下面是吉利兰图法应用举例。
【例】某二元理想混合液其平均相对挥发度为3.1=α。
若进料组成5.0=F x ,要求馏出液组成为9.0=D x ,釜液组成1.0=W x ,泡点进料,回流比R 取为0.8。
试求所需理论板数。
解:(1)求全回流时的理论板数m N ,
m N 用芬斯克公式求得的全回流时的理论板数
()()1log 11log -⎥⎦⎤⎢⎣⎡--=αW W D D m x x x x N 75.1513
.1log 9.01.01.09.0log =-⎥⎦⎤
⎢⎣⎡=
(不包括再沸器)
(2)求最小回流比m R ,
()565
.05.03.015.03.111=⨯+⨯=-+=q q q x x y αα
154
.55.0565.0565
.09.0=--=
--=
q q q
D m x y y x R 316
.018154.581=+-=+-∴R R R m 由吉利兰图查得32
.02=+-N N N m
,如图所示。
解得 24=N
吉利兰图
式中,N ——所要求的理论板数, R , min R ——分别为回流比与最小回流比
e. 芬斯克公式推导
全回流时,最少理论板数的计算式。
如图所示。
芬斯克公式推导图
对于二元理想溶液,则有
A B
B A B B A A x x
p p x p x p ⋅==
α 而
B A B A B A x x P p P p y y ⋅==α
对于第一块理论板
1111B A B A x x
y y ⋅=α
对于第二块理论板22
2
2B A B A x x
y y ⋅=α 而全回流时,1212B B A A x y x y ==,
22
222221111B A B A B A B A B A x x x x y y x x y y ⋅=⎪⎪⎭
⎫ ⎝⎛⋅⋅=⋅=⋅=∴
ααααα
同理,对于第一块板的1A y 与第三块板的1A x
33333222211B A B A B A B A x x y y x x
y y ⋅=⋅=⋅=ααα
继续下去,对于第一块板的1A y 与第N 块板的AN x
AN BN B A N BN AN N B A x x y y x x y y ⋅=⇒⋅=1111αα
⎥
⎦⎤
⎢⎣⎡⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝
⎛=⋅∴AN BN B A x x y y N 11ln ln α
全回流时,D
B D A x y x y -==1,11
W
BN W AN x x x x -==1,
α
ln 11ln ⎥⎦
⎤⎢⎣⎡⎪⎪⎭⎫
⎝⎛-⎪⎪⎭⎫ ⎝⎛-=
∴W W
D D x x x x N (包括再沸器的最小理论板数)
α为塔顶与塔底的α的几何平均值W D ααα⋅= 若只计算精馏段的理论板数,则将上式中的W x 改为F x
α
ln 11ln ⎥⎦
⎤⎢⎣
⎡⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=F
F D D x
x x x N 精。
